正弦量的有效值
- 格式：ppt
- 大小：82.00 KB
- 文档页数：1
下载文档原格式
合集下载
正弦量的三要素和有效值
１．振幅值 正弦量的最大值称为振幅值，用大写字母表示，
如Im 、Um。
首页
2．角频率、周期、频率 正弦量在单位时间内所经历的电角度，称为角频率，用ω 表示，单位是弧度/秒，即
t
正弦量完成一次周期变化所需要的时间，称为周期，用T 表示，单位是秒。
正弦量在1秒钟内完成周期性变化的次数，称为频率，用 f 表示，单位是赫兹。
选零点为计时起点，则初相ψ =0，如图3-7所示是不同初相时
几种正弦电流的解析式和波形图。
首页
i
Im
i Im sint
0
t
a)
i i Im sin(t π 6)
i
i Im sin(t π 2)
0
t
b)
i i Im sin(t π 6)
0
t
0
t
π/6
π/6
首页
例3-3 两个同频率正弦电流的波形如图3-6所示，试写出 它们的解析式，并计算二者之间的相位差。
解 解析式
i/A 10 i1
i1
10 s in(314t
π )A 4
8
i2
i2
8 s in(314t Nhomakorabeaπ )A 4
0
4
4
0.02s
相位差
ωt/rad
i1
i2
π 4
(
c)
d)
图3-3 初相不同的几种正弦电流的波形图 a)初相为0; b)初相为π/2; c)初相为π/6; d)初相为-π/6
首页
注意：正弦量的初相、相位以及解析式都与参考方向有 关。改变参考方向，就是将正弦量的初相加上或减去π。
如Im 、Um。
首页
2．角频率、周期、频率 正弦量在单位时间内所经历的电角度，称为角频率，用ω 表示，单位是弧度/秒，即
t
正弦量完成一次周期变化所需要的时间，称为周期，用T 表示，单位是秒。
正弦量在1秒钟内完成周期性变化的次数，称为频率，用 f 表示，单位是赫兹。
选零点为计时起点，则初相ψ =0，如图3-7所示是不同初相时
几种正弦电流的解析式和波形图。
首页
i
Im
i Im sint
0
t
a)
i i Im sin(t π 6)
i
i Im sin(t π 2)
0
t
b)
i i Im sin(t π 6)
0
t
0
t
π/6
π/6
首页
例3-3 两个同频率正弦电流的波形如图3-6所示，试写出 它们的解析式，并计算二者之间的相位差。
解 解析式
i/A 10 i1
i1
10 s in(314t
π )A 4
8
i2
i2
8 s in(314t Nhomakorabeaπ )A 4
0
4
4
0.02s
相位差
ωt/rad
i1
i2
π 4
(
c)
d)
图3-3 初相不同的几种正弦电流的波形图 a)初相为0; b)初相为π/2; c)初相为π/6; d)初相为-π/6
首页
注意：正弦量的初相、相位以及解析式都与参考方向有 关。改变参考方向，就是将正弦量的初相加上或减去π。
正弦量的瞬时值、幅值和有效值(精)
电路基础
正弦量的瞬时值、幅值和有效值
3.2 正弦量的三要素
u U m sin(t u ) i I m sin(t i )
其中u、i分别为电压和电流的瞬时值; Um、Im分别为 电压和电流的幅值（或最大值）; ω为角频率; φu, φi分别
为电压和电流的初相角, 如图所示。
注意： 交流电压、电流表测量数据为有效值 交流设备名牌标注的电压、电流均为有效值
u ~
i
R
+ U _
I
R
பைடு நூலகம்
通入正弦交流电，T时 间内，电流热效应：
T
通入直流电，T时间内， 电流热效应：
Q = I2 RT
Q
2 i Rdt 0
则有： 同理：
I
Im 2
U U m 2
E
Em 2
1.瞬时值、最大值、有效值
i I m sin t
母u, i, e 表示 。 母带下标m表示, 如：Im, 有效值。以大写字母I、U、
瞬时值 : 描述正弦量在任一瞬间的值 ，以小写字 最大值 ：瞬时值中的最大数值，也称幅值 ,以大写字 Um, Em. 有效值 : 与交流热效应相等的直流定义为交流电的 E表示 。
正弦量的瞬时值、幅值和有效值
3.2 正弦量的三要素
u U m sin(t u ) i I m sin(t i )
其中u、i分别为电压和电流的瞬时值; Um、Im分别为 电压和电流的幅值（或最大值）; ω为角频率; φu, φi分别
为电压和电流的初相角, 如图所示。
注意： 交流电压、电流表测量数据为有效值 交流设备名牌标注的电压、电流均为有效值
u ~
i
R
+ U _
I
R
பைடு நூலகம்
通入正弦交流电，T时 间内，电流热效应：
T
通入直流电，T时间内， 电流热效应：
Q = I2 RT
Q
2 i Rdt 0
则有： 同理：
I
Im 2
U U m 2
E
Em 2
1.瞬时值、最大值、有效值
i I m sin t
母u, i, e 表示 。 母带下标m表示, 如：Im, 有效值。以大写字母I、U、
瞬时值 : 描述正弦量在任一瞬间的值 ，以小写字 最大值 ：瞬时值中的最大数值，也称幅值 ,以大写字 Um, Em. 有效值 : 与交流热效应相等的直流定义为交流电的 E表示 。
《电工基础》练习及答案(7初识正弦交流电)
《电工技术基础与技能》复习题 7．初识正弦交流电 一、选择题：1．人们常说的交流电压220V 是指交流电压的（ ）A ．最大值B ．有效值C ．瞬时值D ．平均值 2．关于交流电的有效值，下列说法正确的是（ ） A ．最大值是有效值的3倍B ．有效值是最大值的2倍C ．最大值为311V 的正弦交流电，就其热效应而言，相当于一个220V 的直流电D ．最大值为311V 的正弦交流电，可以用220V 的直流电代替3．一个电容器的耐压为250V ，把它接入正弦交流电中使用，加在它两端的交流电压的有效值可以是（ ）。
A ．150VB ．180VC ．220VD ．都可以 4．已知V t u )6314sin(2100π-=，则它的角频率、有效值、初相分别是（ ）A ．62100/314π-、V 、s rad B ．6100/100ππ-、V 、s radC ．610050π-、V 、Hz D ．6100/314π、V 、s rad5．某正弦交流电的初相角20πϕ-=，在t =0时，其瞬时值将（ ）A ．大于零B ．小于零C ．等于零D ．不能确定 6．A t i ωsin 51=与A t i )30sin(52︒-=ω的相位差是（ ） A ．30° B ．－30° C ．0° D ．无法确定 7．两个同频率正弦交流电21、i i 的有效值各为40A 和30A ，当21、i i 的有效值为50V时，1i 与2i 的相位差是（ ）A ．0°B ．180°C ．45°D ．90° 8．某交流电压V t u )4100sin(100ππ+=，当s t 1.0=时的值是（ ）A ．V 7.70-B ．V 7.70C ．V 100D ．V 100-9．某正弦交流电压的有效值为380V ，频率为50Hz ，在t =0时的值为380V ，则该正弦电压的表达式为（ ）A ．V t u )90314sin(380︒+=B ．V t u 314sin 380=C ．V t u )45314sin(2380︒+=D ．V t u )45314sin(2380︒-= 10．如右图所示的矢量图中，交流电压1u 与2u 的相位关系是（ ）A ．1u 比2u 超前75°B ．1u 比2u 滞后75°C ．1u 比2u 超前30°D ．无法确定11．一个电热器接在10V 的直流电源上，产生一定的热功率。
正弦量的三要素
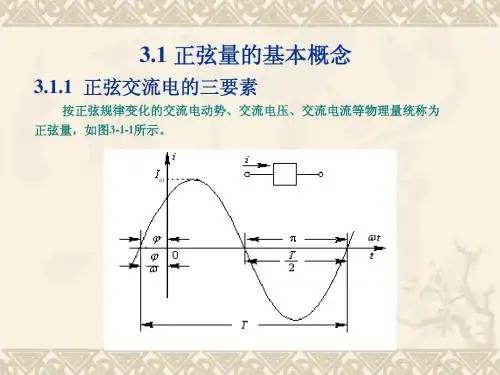
4.1正弦交流电的基本概念正弦量：按正弦规律变化的物理量的统称。
正弦电流、正弦电压、正弦电动势：随时间按正弦规律变化的电流、电压、电动势。
正弦交流电路：电路中所有电压、电流、电动势都是正弦量的电路。
在一定的参考方向下，正弦电流可表示为sin()m i i I t ω=+ψ正弦电流的波形图正弦量的主要特征：大小、变化的快慢及变化的进程一、周期、频率与角频率周期：正弦量完成一个循环的变化所需要的时间。
用T 表示，单位为秒（s ）。
频率：正弦量在单位时间内变化所完成的循环数。
用f 表示，单位为赫兹（Hz ）。
角频率：正弦量在单位时间内变化的角度，即每秒变化的弧度数。
用ω表示，单位为弧度/秒（rad/s ）。
三者之间的关系：周期、频率和角频率都是表示正弦量变化快慢的量，周期愈大，正弦量变化愈慢；角频率愈大，频率愈高，正弦量变化愈快。
【例3－1】 已知电流，试求该电流的周期T 和频率。
1f T=22f Tπωπ==解：100100 5022110.0250Z Zrad sf H H T s s f ωπωπππ=======二、瞬时值、幅值与有效值瞬时值：随时间变化的电压或电流在某一时刻的数值。
幅值：正弦量在变化过程中出现的最大瞬时值，又称最大值。
大写字母加下标m 来表示，如Im 、Um 、Em 。
有效值：如果一个周期性电流i 通过某一电阻R ，在一个周期内产生的热量与另一个直流电流I 通过电阻R 在相等的时间内产生的热量相等，则将此直流电流的数值I 称为该周期性电流的有效值。
大写字母表示，如I 、U 、E 。
由此可得到周期电流的有效值设i = Imsin(ωt +ψi )时mI ===周期量的有效值等于它的瞬时值的平方在一个周期内的平均值的平方根，因此有效值又称均方根值。
mI == 220I RTTi Rdt =⎰I =U m==E m ==【例3－2】 已知电压u = 311sin(100πt +6π) V ，试求电压的有效值U 及t=0.01s 时电压的瞬时值。
电压有效值和峰值的关系
电压有效值和峰值的关系
一、峰峰值是指一个周期内信号最高值和最低值之间差的值，就是最大和最小之间的范围。
它描述了信号值的变化范围的大小。
有效值(Effective value)在相同的电阻上分别通以直流电流和交流电流，经过一个交流周期的时间，如果它们在电阻上所消耗的电能相等的话，则把该直流电流（电压）的大小作为交流电流（电压）的有效值，正弦电流（电压）的有效值等于其最大值（峰值）的1/√2，约0.707倍。
峰值Vp（Peak）。
峰值是指一个周期内信号最高值或最低值到平均值之间差的值。
一般来说，峰值对上下对称的信号才有定义。
可以看到，峰值等于峰峰值的一半。
二、有效值在相同的电阻上分别通过直流电流和交流电流，经过一个交流周期的时间，如果它们在电阻上所消耗的电能相等的话，则把该直流电流(电压)的大小作为交流电流(电压)的有效值，正弦电流(电压)的有效值等于其最大值(幅值)的1/√2，约0.707倍。
在正弦交流电流电中根据热等效原理，定义电流和电压的有效值为其瞬时值在一个周期内的方均根值。
(1)有效值也称为方均根值。
(2)正弦量的有效值等于其最大值被2的平方根去除。
(3)非正弦量的有效值，等于它的直流分量、基波和各高次谐波有效值平方和的平方根值(还有一种定义方式，将直流分量、基波定义分别为零次谐波和一次谐波。
在这个前提下，非正弦量的有效值就等于它的各次谐波有效值平方和的平方根值)。
正弦量的三要素
设一交变电流i通过电阻R,在一个周期内该电阻消耗的 电能是:
W~ = ∫ i Rdt = R∫ i dt
2 2 0 0
T
T
i
R
如果有一个直流电流I通过同一电阻R,在同一时间T内 所消耗的电能为：
W = I RT
2
I
R
在一个周期时间内,W～=W—, 于是
R∫ i dt = I RT
2 2 0
T
1 T 2 I= ∫0 i dt T
最大值（幅值） 最大值（幅值）:在一个周期里 最大的瞬时值叫最大值, 最大的瞬时值叫最大值,它是交 流电的振幅,通常用大写字母并 流电的振幅, 加注下标m表示。 加注下标m表示。如Im、Um及Em。 可见， 可见，最大值实际上就是最大的 瞬时值，也是与时间有关的量。 瞬时值，也是与时间有关的量。
Im
ω
= 2πf
Um
ψu
e = Em sin( ωt +ψe )V
Em
ψe
相位差：两个同频率的正弦交流电在相位上的差值 定义位相位差,用φ表示。
ui = (ωt +ψu ) (ωt +ψi ) =ψu ψi
同频率的两个正弦交流电的相位差等于它们的 初相之差。 i, u i, u
ψi ψu
0
t
ψu 0
Im i t4 t
t3 0 t1 t2
.
每秒时间内重复变化的周期数称 T 为频率,用字母 表示,它的单位是赫 为频率 用字母 f 表示 它的单位是赫 简称赫,周期和频率互为倒数 兹(Hz),简称赫 周期和频率互为倒数 简称赫 周期和频率互为倒数, 1 2π 即有 f = ωT = 2π ω = = 2πf T T 的交流电(称为工频交流电),其角 例如频率 f =50Hz的交流电 称为工频交流电 其角 的交流电 称为工频交流电 频率和周期分别为： 频率和周期分别为 ω=2π f=314 rad/s T=0.02s
正弦量的基本概念
Q I 2 RT Q i 2 R dt
0 T
I RT i R dt
2 2 0
T
1 I T 1 U T
T
0
i dt u dt
2
2
T
0
正弦量的有效值
1 I T
T
0
I sin tdt
2 m 2
2 Im T
T
0
1 cos 2t dt 2
2 Im (T 0) 2T
6
3
(1)t=100ms时，
π π u ab (t ) 300 sin(2000 πt )mV , iab (t ) 5 sin(2000 πt )mV 6 3
π π u ab (0.1) 300 sin(2000 π 0.1 ) 300 sin 150 mV 6 6 π π iab (0.1) 5 sin(2000 π 0.1 ) 5 sin 4.33m 3 3
u/V 250 200 u2 u1
0 3
6
2
t
i 例 3-1 图3-1-4给出正弦电压u ab 和正弦电流ab 的 波形。(1)写出u ab 和i ab 的解析式并求出它们在 i t=100ms时的值。(2)写出 ba 的解析式并求出 t=100ms时的值。
由波形可知电压和电流的最大值分别为300mV和 5mA，频率都为1kHz，角频率为2000πrad/s，初 π π 相分别为 和 ，它们的解析式分别为
π 2π iba (t ) iab 5 sin(2000 πt π) 5 sin(2000 πt )mA 3 3
当t＝100ms时
正弦电路的电压电流及相量表示
解：电压u（t）与电流i1（t）的相位差为
=（-180o）-（- 45o ）= -135o＜0
所以u（t）滞后i1（t）135o 。
电压u（t）与电流i2（t）的相位差为
= -180o - 60o = -240o 由于规定||≤π，所以u（t）与i2（t）的相位 差应为 = -240o+360o = 120o＞0，因此u（t）超前 i2（t）120o 。
四、正弦量的有效值 有效值的提出： 正弦量的有效值是根据它的热效应确定的。以正 弦电压u（t）为例，它加在电阻R两端，如果在一个 周期T内产生的热量与一个直流电压U加在同一电阻上 产生的热量相同，则定义该直流电压值为正弦电压 u （t）的有效值。用大写字母“U”表示。 有效值的定义式：
1 U T
本讲作业
1、复习本讲内容；
2、预习下一讲内容——正弦电路的相量分析法； 3、书面作业：习题8-1，8-2，8-4，8-5。
8.2 正弦量的相量表示
一、相量表示法的提出 前面学过的解析式（三角函数表示法）和正弦量 的波形图（正弦曲线表示法）都不便于分析计算正弦 电路。为了解决这个问题，引入了正弦量的第三种表 示方法——相量表示法。 二、相量表示法采用的形式 相量表示法，实际上采用的是复数表示形式。
三、相量表示方法 模等于正弦量的有效值（或振幅），幅角等于 正弦量的初相的复数，称为该正弦量的相量。相量 用该正弦量的符号上加一圆点“ · ”来表示，说明它 是时间的函数，以便与一般复数相区别。 振幅相量 相量的模为正弦量的振幅，称振幅相量，以 I m 、 Um 等表示。其振幅相量表达式为
将u3（t）的解析式整理如下： u3（t）= 5cos（100πt + 60o） = 5sin（100πt + 60o + 90o） = 5sin（100πt + 150o ）V 所以得到
正弦量的瞬时值、幅值和有效值(精)
i Im sin t
瞬时值 : 描述正弦量在任一瞬间的值 ，以小写字
母u, i, e 表示 。
最大值 ：瞬时值中的最大数值，也称幅值 ,以大写字 母带下标m表示, 如：Im, Um, Em.
有效值 : 与交流热效应相等的直流定义为交流电的 E表示 。
注意：
有效值。以大写字母I、U、
电路基础
正弦量的瞬时值、幅值和有效值
3.2 正弦量的三要素
u Um sin(t u ) i Im sin(t i )
其中u、i分别为电压和电流的瞬时值; Um、Im分别为 电压和电流的幅值（或最大值）; ω为角频率; φu, φi分别 为电有效值
交流电压、电流表测量数据为有效值 交流设备名牌标注的电压、电流均为有效值
~u i R
+
U IR _
通入正弦交流电，T时
间内，电流热效应：
T
Q i2Rdt
0
则有：
I Im 2
同理：
U
Um 2
通入直流电，T时间内， 电流热效应：
Q = I2 RT
E Em 2
知识回顾 Knowledge Review
瞬时值 : 描述正弦量在任一瞬间的值 ，以小写字
母u, i, e 表示 。
最大值 ：瞬时值中的最大数值，也称幅值 ,以大写字 母带下标m表示, 如：Im, Um, Em.
有效值 : 与交流热效应相等的直流定义为交流电的 E表示 。
注意：
有效值。以大写字母I、U、
电路基础
正弦量的瞬时值、幅值和有效值
3.2 正弦量的三要素
u Um sin(t u ) i Im sin(t i )
其中u、i分别为电压和电流的瞬时值; Um、Im分别为 电压和电流的幅值（或最大值）; ω为角频率; φu, φi分别 为电有效值
交流电压、电流表测量数据为有效值 交流设备名牌标注的电压、电流均为有效值
~u i R
+
U IR _
通入正弦交流电，T时
间内，电流热效应：
T
Q i2Rdt
0
则有：
I Im 2
同理：
U
Um 2
通入直流电，T时间内， 电流热效应：
Q = I2 RT
E Em 2
知识回顾 Knowledge Review
教案：正弦交流电的三要素
教案纸
电压与电流的相位差为：2
)6
(3
πππϕϕϕ=--=-=i u
相位差的存在，表示两个正弦量的变化进程不同。
两个正弦量，根据相位差的不同，可以有以下几种不同的变化进程:
（1）当ϕ= 0，即ϕu = ϕi 时，两个正弦量的变化进程相
同，称为电压u 与电流i 同相；
（2）当ϕ> 0，即
ϕ
u
>
ϕ
i
时，电压u 比电流i 先到达零值
或正的最大值，称电压u 比电流i 在相位上超前ϕ角。
反过来也可以称电流i 比电压u 滞后ϕ角，
（3）当ϕ=2
π
时，两正弦量的变化进程相差90°称它们为正交，
（4）当ϕ=π时，两正弦量的变化进程刚好相反，称它们为反相，
【例题】 已知两正弦电动势分别是:
e 1=100V t )60100sin(2︒+π，e 2V t )30100sin(265︒-=π。
求：（1）各电动势的最大值和有效值；
（2）频率、周期、相位、初相位、相位差； 解：（1）最大值 V Em 21001= V Em 2652= 有效值 V E 1002
21001==
V E 652
2652==
（2）频率
Hz
f
f 50210022
1
===
=
π
π
πω 周期 s f T T 02.050
1
121==== 相位
)60100(1︒+=t πα )30100(2
︒-=t πα
初相位︒=601
ϕ ︒-=302
ϕ
相位差︒=︒--︒=-=
90)30(602
1
ϕ
ϕϕ。