当前位置：文档之家 › 中职拓展模块三角公式及应用测试题(2020年整理).pptx

中职拓展模块三角公式及应用测试题(2020年整理).pptx

  • 格式：pptx
  • 大小：34.16 KB
  • 文档页数：2

下载文档原格式

  / 2

合集下载

中职数学-三角函数复习课件

中职数学-三角函数复习课件

sin2α=2sinαcosα.
cos2α=cos²α-sin²α=2cos²α-1=1-2sin²α
知识点10:正弦定理(掌握)
知识点11:余弦定理(掌握)
a²= b²+c²-2bccosA
b²= a²+c²-2accosB
c²= a²+b²-2abcosC
知识点12:正弦函数的变换规律(掌握)
上下拉伸（压缩）A倍
上下平衡
a个单位
() = ( + ) +
改变函数周期
=
2

改变相位(左右平移)

例：已知函数 = 3 sin 2 − 4 + 1,求函数的最大值，最小
值，周期，及取得最大值、最小值时x的取值
解: ∵ −1 ≤ ≤ 1

∴ −1 ≤ sin(2 − ) ≤ 1
【2022广东】函数f(x)=4sin(6x+5π/6)的最小正周期为（ ）
A.π/6 B. π/3
C. π/2
D. 5π/6
【2022广东】已知角的顶点与原点重合，始边与轴非负半轴重
合，角的终边经过点(1，2)，求2的值是（ ）
A.-3/5
B. -4/5
C. 3/5
D. 4/5
【2022广东】若 = 2，则
余弦函数 =
定义域:R; 奇函数(原点对称)
定义域:R;
值域:[-1,1]
值域:[-1,1]
图像:
图像:
周期: = 2
周期: = 2


单调增区间:[− 2 + 2, 2 + 2]( ∈ )

单调减区间:[ 2 + 2,

职高三角函数解三角形练习题

职高三角函数解三角形练习题

职高三角函数解三角形练习题三角函数（Trigonometric functions）是数学中一个重要的概念，常被用于解决与三角形相关的问题。

在职业高中的数学学习中，解三角形练习题是一项重要的训练内容。

本文将通过几个实例来演示如何运用三角函数来解答这些练习题。

一、已知两边长度求角度假设有一个三角形 ABC，已知边 AC 的长度为 10cm，边 BC 的长度为 12cm，请问∠ABC 的度数是多少？解答：首先，我们可以使用余弦定理来求得∠ABC 的度数。

余弦定理表示：c^2 = a^2 + b^2 - 2ab*cosC其中，a 和 b 是两个已知边的长度，c 是这两边所夹角的对边的长度，C 是所求的角度。

将已知数据代入公式：12^2 = 10^2 + 12^2 - 2*10*12*cosC化简得：144 = 244 - 240*cosC继续化简：cosC = (244 - 144) / (2*10*12)cosC = 100 / 240cosC = 5/12使用反余弦函数（arccos）可以求得角度 C 的弧度，即：C = arccos(5/12)最后，将弧度转化为度数，可得：C ≈ 69.3°所以，∠ABC 的度数约为 69.3°。

二、已知一个角度求边长假设有一个三角形 PQR，其中∠P = 30°，边 PQ 的长度为 5cm，请问边 PR 的长度是多少？解答：在这个问题中，我们可以运用正弦定理来求边 PR 的长度。

正弦定理表示：a/sinA = b/sinB = c/sinC其中，a、b、c 分别表示三角形中对应的边的长度，A、B、C 分别表示对应的角度。

将已知数据代入公式：5/sin30° = PR/sin(180°-30°-30°)化简得：5/sin30° = PR/sin120°sin30° = PR/(√3/2)通过计算，可得：PR ≈ (5 * √3) / 2所以，边 PR 的长度约为 4.33cm。

高中数学课件《三角公式》中职总复习

高中数学课件《三角公式》中职总复习

（1）sin αcos α；
（2）s2insinα－α－2ccoossαα.
【解析】（1）解法一：由已知可得方程组
得sin α=3cos α，cos2α=110. 故sin αcos α=3cos αcos α=3cos2α=130.
典例解析
解法二：sin αcos α=ssinin2αα+ccoossα2α=tatna2nαα+1=323+1=130. 解法三：因为tan α=3，所以sin α=3cos α. 所以sin αcos α=ssinin2αα+ccoossα2α=9co3s2cαo+s2cαos2α=9+31=130. （2）因为tan α=csoins αα=3，所以sin α=3cos α. 所以2sisninαα－－2ccooss αα=36ccoossαα－－2ccoossαα=5.
又因为α∈(π2,π)，所以cos α=- 23.
典例解析
【例2】已知α∈(π2,π)，sinα2+cosα2= 26.
（2）因为-
π 2
<α-β<
π 2
，cos(α-β)=
1−sin2(α−β)= 45,
所以cos β=cos［α-(α-β)］=cos αcos(α-β)+sin αsin(α-β)
典例解析
【例2】已知α∈(π2,π)，sinα2+cosα2= 26.
（1）求cos α的值；
（2）若sin(α-β)=-35，β∈(π2,π)，求cos β的值.
【解析】（1）因为（sinα2+cos
α 2
）2=1+2sin
α 2
cos
α 2

高教版中职数学(拓展模块)1.3《正弦定理与余弦定理》ppt课件1

高教版中职数学(拓展模块)1.3《正弦定理与余弦定理》ppt课件1

整 体 建
余弦定理： a2 b2 c2 2bc cos A；
构
b2 a2 c2 2ac cos B；
c2 a2 b2 2ab cosC．
自 我 反 思
学习方法
目 标 检 测
学习行为
学习效果
自
在△ABC中，a=20，b=29，c=21，求角B．
我
反
思
B 90.
A

b sin
B

c sin C
．
动 脑
当三角形为钝角三角形时，不妨设角A为钝角，如图所示，以A为原
点，以射线AB的方向为x轴正方向，建立直角坐标系，则BC BA AC，
思 两边取与单位向量j的数量积，得 j BC j （BA+BC）=j BA j BC．
考
由于< j，BC 90 B，j BA，< j，AC A 90，
目 标 检 测
继
读书部分：阅读教材相关章节
续
探
书面作业：教材习题1.3（必做）
索
活
学习与训练1.3（选做）
动
实践调查：编写一道有关余弦定
探
究
理或正弦定理的习题
识
对角，利用正弦定
解 sin B bsin A 15 2 sin 45 1．理求另一边的对角
典
a
30
2 时，要讨论这个角
型 例
由 b a ，知B A，故 30 B 180，的 发所取 生以值 错B 范误45.围或，B 避13免5．
题
运
1．已知ABC 中，A 45，B 30，b= 3 ，求C和a.
探

中职拓展模块三角公式及应用测试题

中职拓展模块三角公式及应用测试题

中职拓展模块三角公式及应用测试题姓名_______得分______一、选择题：（本大题共10小题，每小题4分，共40分）1、sin （－6π19）的值是（ ） A ． 21 B ．－21 C ．23 D ．－232、cos118cos58sin118sin58+=o o o o （ ）A ．-BC ．12-D ．123、已知=-=-ααααcos sin ,45cos sin 则（ ） A ．47B ．169-C ．329-D ．329 4、将函数x y 4sin =的图象向左平移12π个单位，得到)4sin(ϕ+=x y 的图象，则ϕ等于（ ）A ．12π-B ．3π-C ．3πD ．12π 5、οοοο50tan 70tan 350tan 70tan -+的值等于( ) A ．3 B ．33C ．33- D ．3- 6、函数)4sin(π+=x y 的单调递增区间是（ ） A 、],2[ππ B 、]4,0[π C 、 ]0,[π- ]2,4[ππ 7、sin170sin160cos10sin 70-=o o o o （ ）A ．12-B ．12C ．2-D ．28、2(sin cos )1y x x =--是 （ ）A ．最小正周期为2π的偶函数B ．最小正周期为2π的奇函数C ．最小正周期为π的偶函数D ．最小正周期为π的奇函数9、函数x x x f cos sin )(-=的最大值为 （ ）A ．1B ． 2C ．3D ．210、若角α的终边经过点(12)P -，，则tan 2α的值为（ ）．A ．1B ．4/3C ． 3/4D ．2二、填空题（每小题4分，共20分）11、已知()cos cos 2,f x x x x R =-∈的最大值是 12、等于则)2cos(),,0(,31cos θππθθ+∈=_________ 13、若α是第三象限角，则)πcos()πsin(21αα---=_________ 14、函数()3sin 25f x x π⎛⎫=- ⎪⎝⎭的最大值为 ；最小值为15、函数),2,0)(sin(R x x A y ∈π<ϕ>ωϕ+ω=的部分图象如上图所示，则函数表达式为__________________三、解答题（共40分）15、（10分）已知,1)cos(,31sin -=+=βαα求sin(2)αβ+的值 16 4cos ,sin 526ππααπα⎛⎫=-<<- ⎪⎝⎭已知,且求的值。

人教版中职数学(拓展模块)1.4《三角公式的应用

人教版中职数学(拓展模块)1.4《三角公式的应用
两角和差与倍角公式
昌硕高级中学 吴忠
引例:
(1) cos 400 cos 200 sin 400 cos 700
1
2
(2) sin100 cos350 cos100 cos550
2
2
(3) sin150 3 cos150 2
(4)ABC中, tan A 1 , tan B 2.则C 450
(2)已知向量 a (cosx,sin x),b (cosx,cosx),c (1,0).
（I）若 x ,求向量a, c 的夹角；
6
（II）当 x [ , 9 ] 时，求函数 f (x) 2a b 1 的最大值
28
问题5:
求y sin2 x sin x cos x的值域.


π 4

2
问题4:
(1)已知向量 a (2cosx,cos2x),b (sinx,1) ，（ 0 ），令 f (x) a b ，
且 f (x) 的周期为 ．
(1) 求 f( )的值；(2)写出 f(x)在[ , ] 上的单调递增区间．
4
22
已知: 0 ,sin cos 1 ,
5
你能想出几种方法求tan的值
❶生难字。
华歆．(xīn)
辄．(zhé)
Байду номын сангаас
携．(xié)
拯．(zhěng) 尊君在不．(fǒu)
❷重点词语理解。
①与友期．行(约定)
②太丘舍去．(离开)
③时．年七岁(当时)
④尊．君．在不(古代尊称对方的父亲)
变式1: 在(1)中,若0 x ,求此函数值域.

中职数学基础模块上第五章三角函数检测题(2020年整理).pptx

中职数学基础模块上第五章三角函数检测题(2020年整理).pptx

6、把 7500 换算为弧度=
。
7、比较大小： sin 3500 cos1600
0
8、若 sin cos 3 ，则 sin cos
。
5
9、化简： 1cos2 （ 是第三象限角）=
。
10、函数 y tan x 是
函数（奇偶性）
二、选择题（每题 10 分，共 50 分）
11、若 sin 0 ，且 tan 0 ，则 是（ ）
14、函数 y 3 sin x 的最大值是（
）
2
A、 3 B、 1 C、 5 D、 7
2
2
2
2
15、若 ( , )，则 sin ,cos, tan 的大小顺序是（ ）
42
A、 sin cos tan
B、 sin cos tan
C、 cos tan sin
D、 tan sin cos
三、解答题（每题 10 分，共 50 分）
17、计算： sin 4200 cos3900 tan 4050
18、已知tan 3 ，求 3sin cos 的值
sin 2cos
19、用“五点法”作出函数 y 4sin x ， x[0,2 ] 的简图。
20、求出函数 y 3cos x 2 的最大值和最小值。
中职数学基础模块上第五章三角函数检测题
班级
姓名
一、填空题（每空 10 分，共 100 分）
1、 7500 是第
象限的角
2、 9000 化为角度制是
rad.
3、 11 化为角度制是
6
度。
3r
4、在半径为r 的圆中，弧长为
的圆弧所对的圆心角等于 4
弧度。
5、角 终边上一点的坐标是（3，4),则sin 。

三角函数公式及其应用拓展模块复习课件

三角函数公式及其应用拓展模块复习课件
练习：计算
1.cos750 _______,tan150 ______ tan 750 ________ 2.cos700 cos100 sin 700 sin100 ____________ 3.sin700 cos100 cos700 sin100 ____________
4. 3 tan150 ___________ 1 3 tan150
变形：a 2R sin A, b 2R n B, c 2R sin C
a : b : c sin A : sin B : sin C A B a b sin A sin B
余弦定理：
a 2 b 2 c 2 2bc cos A b2 a 2 c 2 2ac cosB c 2 a 2 b2 2ab cosC
5
（1）.sin2 2sincos，sin 2sin cos
22
（2）已知cos 1 ,求sin 2 和cos2 的值
2
2
2
（3）已知函数y sinx cosx 的周期为2，求的值.
6 6
二倍角公式
（2）.cos2 cos2 sin 2
（cos sin )cos sin
1.x _________,则x ________ y ______,第一个点为________ 2.x _________,则x ________ y ______,第二个点为________ 3.x _________,则x ________ y ______,第三个点为________ 4.x _________,则x ________ y ______,第四个点为________ 5.x _________,则x ________ y ______,第五个点为________

中职数学 拓展模块 第1章 三角公式及应用

中职数学 拓展模块 第1章 三角公式及应用
－sinβ)，因此向量OB=(cos α,sin α)，向量OC =(cos β,－sin β), 且 OB =1, OC =1，于是
OB· OC = OB · OC ·cos(α+β)=cos(α+β)，
1.1 和角公式
学习提示
设向量 a =(x1,y2), b =(x2,y2)，且< a , b >=θ，则 a · b =| a |·| b |·cos θ，又 由于 a · b =x1x2+y1y2，则| a |·| b |·cos θ=x1x2+y1y2.
1.1 和角公式
例14 不用计算器,求下列各式的值： （1） sin15°cos15°； （2）2sin222.5°－1.
解 （1）sin15°cos15°= 1/2 ×(2sin15°cos15°) = 1/2 sin(2×15°)= 1/2 sin30°= 1/4 .
（2）2sin222.5°－1=－(1－2sin222.5°) =－cos(2×22.5°)=－cos45°=－ 2 .
1.2 正弦型函数
1.2.1 正弦型函数的概念和性质
我们已经学习了正弦函数y=sin x和余弦函数y=cos x.在物 理学和电学中，我们经常会遇到形如y=Asin(ωx+φ)(A>0,ω>0) 的函数，这类函数称为 正弦型函数 .它与正弦函数y=sin x有着 密切的关系.
我们先来讨论正弦型函数的周期. y=Asin(ωx+φ)(A>0,ω>0)中，令
.
1 tan15
2.已知tan α= 1/2 ,tan（α-β）=- 2 /5 ，求tan（2α-β）
的值.
3.已知：tan α、tan β分别是关于x的二次方程x2-5x+6=0的

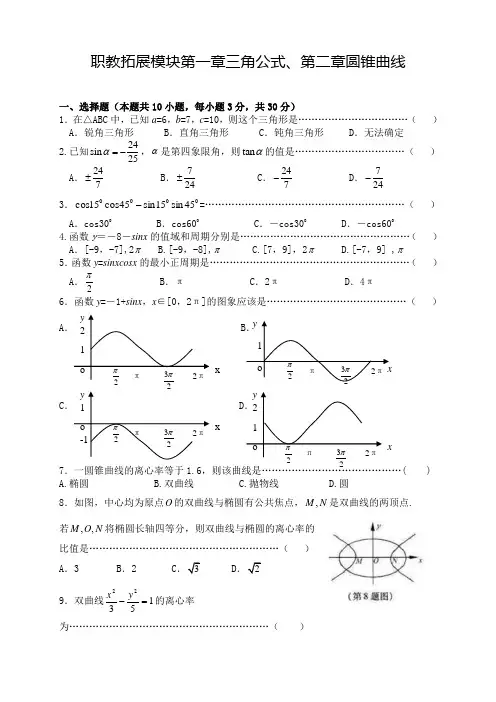
职教拓展模块第一章三角公式、第二章圆锥曲线

职教拓展模块第一章三角公式、第二章圆锥曲线

职教拓展模块第一章三角公式、第二章圆锥曲线一、选择题（本题共10小题，每小题3分，共30分）1．在△ABC 中，已知a =6，b =7，c =10，则这个三角形是……………………………（ ）A ．锐角三角形B ．直角三角形C ．钝角三角形D ．无法确定2.已知24sin 25α=-，α是第四象限角，则tan α的值是……………………………（ ） A ．247± B ．724± C ．247- D ．724- 3．000045sin 15sin 45cos 15cos -=……………………………………………………（ ）A ．cos300B ．cos600C ．－cos300D ．－cos6004.函数y ＝－8－sinx 的值域和周期分别是……………………………………………（ ）A ．[-9，-7],2π B.[-9，-8],π C.[7，9]，2π D.[-7，9] ,π5．函数y =sinxcosx 的最小正周期是……………………………………………………（ ）A ．2π B ．π C ．2π D ．4π 6．函数y =－1+sinx ，x ∈[0，2π]的图象应该是……………………………………（ ） A ． B ．C ． D． 7．一圆锥曲线的离心率等于1.6，则该曲线是……………………………………( ) A.椭圆 B.双曲线 C.抛物线 D.圆 8．如图，中心均为原点O 的双曲线与椭圆有公共焦点，,M N 是双曲线的两顶点. 若,,M O N 将椭圆长轴四等分，则双曲线与椭圆的离心率的比值是…………………………………………………（ ）A ．3B ．2C ．3D ．29．双曲线15322=-y x 的离心率为……………………………………………………（ ）o 2π 2π23π2ππ 2π 1 2 x y o 2π 2π23π2ππ 2π 1 x y o 2π 2π23π2ππ 2π 1 -1 x y o 2π 2π23π2ππ 2π 1 2 x yA.210B.322C.36 D.362 10.已知一直线经过椭圆11422=+y x 的右焦点F 2交椭圆于A 、B 两点，则△ABF 1的周长为…………………………………………………………………………………………（ ）A.4B.6C.8D.10二、填空题：(每小题3分，共18分）11．已知α为第一象限的角，sin α＝35，则tan α＝ . 12．函数y =x x sin cos 3-的最大值为 ，周期为 ． 13.oo15tan 115tan 1-+的值等于 ． 14.椭圆1162522=+y x 上的一点到一个焦点的距离是7，则到另一个焦点的距离是 .15．双曲线16422=-y x 的渐近线方程为 ．16．抛物线24y x =的焦点坐标是 ．三、解答题：(共6题，共52分）17．（本题满分12分）计算：（1）若1sin cos 3αα=，求①2(sin cos )αα-；②2(sin cos )αα+.（2）已知3tan =α，求4sin cos 2sin 3cos αααα-+的值.18.（本题满分8分）在△ABC 中，已知a =4cm ，b =34cm ，A=30 o ，解三角形.19.（本题满分8分）已知椭圆的长轴是短轴长的3倍，并过点（0，-3），求该椭圆的标准方程.20.（本题满分8分）已知双曲线的焦点坐标是（-6，0），（6，0），且经过点A （-5，2），求该双曲线的标准方程、实轴长、虚轴长和渐近线方程.21．（本题满分8分）求以双曲线191622=-y x 的焦点为顶点，顶点为焦点的椭圆方程.22.（本题满分8分）若抛物线px y 22=的焦点与椭圆192522=+y x 的右焦点重合，求抛物线的方程.。

三角公式及应用中职

三角公式及应用中职

三角公式及应用中职三角公式及应用一、三角公式1、余弦定理：在△ABC中，若a、b、c分别表示三边的长度，则有：a²=b²+c²-2bc·cosA。

2、正弦定理：在△ABC中, a/sin(A)=b/sin(B)=c/sin(C)。

3、正切定理：在△ABC中，a·cotA=b·cotB=c·cotC。

4、勾股定理：在直角三角形中，斜边的平方等于两直角边的平方之和，即：c²=a²+b²。

二、三角函数1、余弦函数：它是由复变函数和三角函数组合而成，用cosθ表示，记为cosx或y=cosx（x为弧度）。

2、正弦函数：它是三角函数之一，用sinθ表示，记为sinx或y=sinx（x为弧度）。

3、正切函数：它是由复变函数和三角函数组合而成，用tanθ表示，记为tanx或y=tanx（x为弧度）。

4、反余弦函数：它是一种特殊的反函数，用arccos x表示，记为y=arccos x（x为弧度）。

5、反正弦函数：它是一种特殊的反函数，用arcsin x表示，记为y=arcsin x（x为弧度）。

6、反正切函数：它是一种特殊的反函数，用arctan x表示，记为y=arctan x（x为弧度）。

三、三角公式的应用1、物理：可用来求出反射角、折射角、夹角等相关角度，并设计各类专用仪器；2、几何：我们可以用三角公式推导一些三角形的各种属性；3、天文：可以用来确定地球与太阳之间的日周期，以及其他天体的运行；4、测绘：可以用来解决道路、河流的测量和绘制；5、工程：可以应用来解决建筑计算和设计中遇到的各种三角形问题。

职高数学基础模块上册第五章《三角函数》(2020年整理).pptx

职高数学基础模块上册第五章《三角函数》(2020年整理).pptx

C、 k 360 0 180 0 (k Z ) D、 k 180 0 (k Z )
23、若 A 为△ABC 的一个内角，则下列三角函数中，只能取正值的是（ ） A、sinA B、cosA C、tanA D、cotA
24、若角 的终边经过点 p(0, m)(m 0), 则下列各式中无意义的是（ ）
3
,sin(- )= .
3
18.cos =
4
, cos(- )= .
4
19.-120 是第 象限的角，210 是第 象限的角。
20．若 是第三象限的角，则 sin 0 ,cos 0,tan 0（用“<”或“>”符号
填空）
21. 若 cos <0,则 为第 或第 象限的角。
班级学号姓名
22．若 tan >0，则 为第 或第 象限的角。 23. 若 sin >0 且 tan >0，则 为第 象限的角。 24. 正弦函数 Y=sinX 在区间（0， ）上为单调 函数。
值域
8. 若 是第四象限角， cos 3 ，则 Sin =
5
9.已知：tan =1 且 ∈（0, ），则 =
2
，tan =
。
10.已知 Cos = 1 则 Cos( )=
3
.Cos(- )=
11.若点 p(3,5) 是角 终边上一点，则 sin ，Cos =
12.y=Sinx 且 x∈[0,2 ]则当 x= 13.y=Sinx 且 x∈[0,2 ]则当 x=
Sin >0 且 Cos >0 则 为（ ）的角
A． 第一象限 B.第二象限 C.第三象限 D.第四象限
3．tan >0 则 为（ ）的角

(2020年整理)中职拓展模块三角公式及应用测试题(1).doc

(2020年整理)中职拓展模块三角公式及应用测试题(1).doc

合职校XXXX 春高16级数学第一学月测试题（A 、B 卷总150分记分）班级_______姓名_______得分______ （A 卷）（共100分）一、选择题：（本大题共10小题，每小题4分，共40分）1、sin （－6π19）的值是（ ） A ． 21 B ．－21 C ．23 D ．－232、cos118cos58sin118sin58+=o o o o （ ）A ．BC ．12-D ．12 3、已知=-=-ααααcos sin ,45cos sin 则（ ）A ．47B ．169-C ．329-D ．329 4、将函数x y 4sin =的图象向左平移12π个单位，得到)4sin(ϕ+=x y 的图象，则ϕ等于（ ）A ．12π-B ．3π-C ．3πD ．12π 5、οοοο50tan 70tan 150tan 70tan -+ 的值等于( )A ．3B ．33C ．33-D ．3- 6、函数)4sin(π+=x y 的单调递增区间是（ ）A 、],2[ππB 、]4,4[ππ-C 、 ]0,[π-D 、]2,4[ππ 7、sin170sin160cos10sin 70-=o o o o （ ）A ．12-B ．12C ．2-D ．28、2(sin cos )1y x x =--是 （ ）A ．最小正周期为2π的偶函数B ．最小正周期为2π的奇函数C ．最小正周期为π的偶函数D ．最小正周期为π的奇函数9、函数x x x f cos sin )(-=的最大值为 （ ）A ．1B ． 2C ．3D ．210、若角α的终边经过点(12)P -，，则tan 2α的值为（ ）． A ．1 B ．4/3 C ． 3/4 D ．2二、填空题（每小题4分，共20分）11、已知()cos cos 2,f x x x x R =-∈的最大值是12、等于则)2cos(),,0(,31cos θππθθ+∈=_________ 13、若α是第三象限角，则)πcos()πsin(21αα---=_________ 14、函数()3sin 25f x x π⎛⎫=- ⎪⎝⎭的最大值为 ；最小值为15、函数),2,0)(sin(R x x A y ∈π<ϕ>ωϕ+ω=的部分图象如图所示，则函数表达式为__________________三、解答题（共40分）15、（10分）已知,1)cos(,31sin -=+=βαα求sin(2)αβ+的值16 4cos ,sin 526ππααπα⎛⎫=-<<- ⎪⎝⎭已知,且求的值。

人教版中职数学(拓展模块)1.4《三角公式的应用》ppt课件1

人教版中职数学(拓展模块)1.4《三角公式的应用》ppt课件1

2019/10/17
教学资料精选
11
谢谢欣赏！
2019/10/17
教学资料精选
12
实地听完整堂课。
•
3、课前预习
•
课前预习新课内容，找出不理解的地方标记下来。预习后尝试做课后练习题，不要怕出错，因为老师还没有讲，出错也是正常的。
•
关键是，出错了你就知道上课时应该重点听哪里，注意力自然就能集中了。
•
4、即便上课时不理解也不要放弃
•
有些同学觉得老师讲的听不懂，就干脆不再听讲，按照自己的方法去学习。其实这样做真的很傻，因为不听讲就非常容易和同学们的学习进度脱节，这就会直接导致考试时成绩下降。原因是，老师讲的内容不一定都在教材中体现，有相当一部分重点内容
4
5
4
问:做完这两题后对你有什么启发?
学会分析已知条件中的角和要求角之间的关系(拆角拼角).如:
,2 ( ) ( ),( x) ( x) , 2 等
4
42Βιβλιοθήκη 2问题3:(1) tan150 tan 300 tan150 tan 300
是老师在上课时补充讲解的，如果不听讲很可能就会错过这些重点。
•
所以，上课的时间一定要专注于课堂，决不能打开别的习题集去学习，这样才是高效率的学习，才是提高成绩最快的方法。因此，困难也要先听课，那对你将来的自学一定会很有帮助，哪怕你只是记住了一些经常出现的术语，上课的内容好像马上就忘光
了，但等到你日后自己学习的时候，也能让你回想起很多内容。
变式1: 在(1)中,若0 x ,求此函数值域.

变式2
:
求y

s in 2

中职数学三角函数 (1)ppt课件

中职数学三角函数 (1)ppt课件

cos
2
学习 提示
利 用 基 本 关 系 式 sin 2 cos2 1 求三角函数的值时，需要进行开平方运
算，所以必须要明确角 所在的象限.
返回
完整版课件
15
此课件下载可自行编辑修改，供参考！ 感谢您的支持，我们努力做得更好！
r r r r x x
由于点 P，P 在同一象限内，
所以它们的坐标符号相同，因此得
y P
r P' y
r' y'
O x' x x
xx， yy， yy． r r r r x x
完整版课件
8
所以当角 不变时，不论点 P 在角
的终边上的位置如何，这三个比值都是定值，
只依赖于 的大小，与点 P 在 角 终
完整版课件
12
1.2.3 界线角的三角函数值
三角函数 0
sin 0
π π 3π 2π
2
2
1 0 -1
0
cos 1
0 -1 0
1
tan 0 不存在 0 不存在 0
完整版课件
13
三角
三
三角
角
1.3
三角
同角三角函数的关系
同角三角函数的基本关系
sin2 cos2 1,
tan sin , π kπ (k Z ).
式 比，即
l r
(rad) .
这里，角 的正负由其终边的旋转方向决定.
一般地，正角的弧度数是一个正数，负角的弧度数是一
个负数，零角的弧度数是 0.
完整版课件
4
π=180°
换算公式
1 π (rad) 0.017 45(rad), 180
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2
D． 9 32
3、在 ABC 中，若 A 120 ， AB 5 ， BC 7 ，则 ABC 的面积为（ ）
A．7.5
B．8
C．8.5 D．9
4、将函数 y sin 4x 的图象向左平移 个单位，得到 y sin( 4x ) 的图象，
12
则 等于（ ）
A．
12
B．
3
C．
3
D．
12
5、 tan 70 tan 50 3 tan 70 tan 50 的值等于( )
A． 3
B． 3 3
C． 3 3
6、函数 y sin( x ) 的单调递增区间是（ ）
4
A、[ , ]
2
B、[0, ]
4
C、 [,0]
7、 sin170 sin160 cos10 sin 70 （ ）
A． 1 2
3 13、若 α 是第三象限角，则 1 2 sin(π ) cos(π ) = 14、函数 y Asin( x )( 0, , x R) 的部分图象如上图所示，则函数表
2
达式为
三、解答题（共 40 分）
15、（10 分）已知sin 1 , cos( ) 1, 求 sin(2 ) 的值
中职拓展模块三角公式及应用测试题
姓名
得分
一、选择题：（本大题共 10 小题，每小题 4 分，共 40 分）
1、sin（－ 19π ）的值是（ ）
6
A． 1 2
B．－ 1 2
C． 3 2
D．－ 3 2
2、已知sin cos 5 ,则sin cos （ ）
4
A． 7 4
B． 9 16
C． 9 32
3
1
16、（10 分）若 sin( ) 3 ，求 sin2θ的值。
2
5
18、（12 分）已知函数 f (x) 2cos x(sin x cos x) 1，xR ． （Ⅰ）求函数 f (x) 的最小正周期； （Ⅱ）求函数 f (x) 的最小值和最大值
17、（12 分）已知三角形 ABC 中， A 450 , B 300 , c 10, 求 b 的值。
A．1 B． 2 C． 3 D．2
10、若角 的终边经过点 P(1，2) ，则 tan 2 的值为（ ）．
A．1 B．4/3 C． 3/4 D．2 二、填空题（每小题 4 分，共 16 分）
11、已知 f (x) cos x cos 2x, x R 的最大值是
12、 cos 1 , (0, ),则cos( 2)等于
B． 1 2
C． 3 2
8、 y (sin x cos x)2 1是 （ ）
D． 3[ , ]42Fra bibliotekD． 32
A．最小正周期为2π 的偶函数 B．最小正周期为2π 的奇函数
C．最小正周期为π 的偶函数
D．最小正周期为π 的奇函数
9 、 函 数 f (x) sin x cos x 的 最 大 值 为 （ ）