版第5章定积分及其利用单元自测题答案

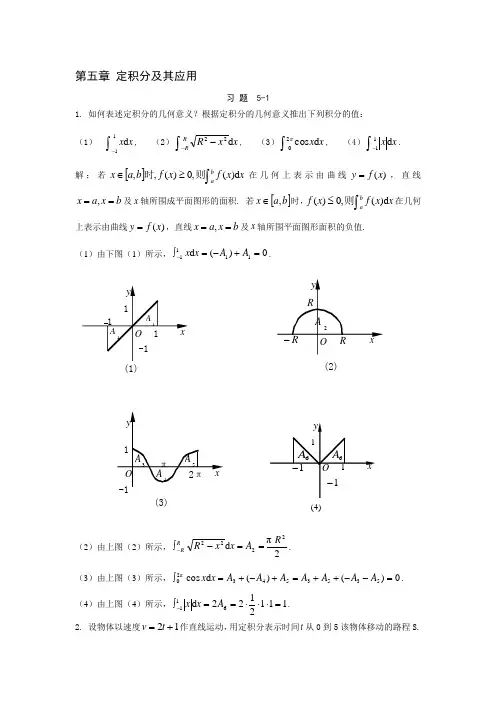
第五章 定积分及其应用习 题 5-11. 如何表述定积分的几何意义？根据定积分的几何意义推出下列积分的值： （1）⎰-x x d 11, （2）⎰--x x R R R d 22, （3）⎰x x d cos 02π, （4）⎰-x x d 11.解：若[]⎰≥∈x x f x f b a x ab d )(,0)(,,则时在几何上表示由曲线)(x f y =，直线b x a x ==,及x 轴所围成平面图形的面积. 若[]b a x ,∈时，⎰≤x x f x f ab d )(,0)(则在几何上表示由曲线)(x f y =，直线b x a x ==,及x 轴所围平面图形面积的负值. （1）由下图（1）所示，0)(d 1111=+-=⎰-A A x x .（2）由上图（2）所示，2πd 2222R A x x R R R==-⎰-.（3）由上图（3）所示，0)()(d cos 5353543π20=--++=+-+=⎰A A AA A A A x x . （4）由上图（4）所示，1112122d 611=⋅⋅⋅==⎰-A x x . 2. 设物体以速度12+=t v 作直线运动，用定积分表示时间t 从0到5该物体移动的路程S.( 2 )( 1 )( 3 )(4)解：=s ⎰+t t d )12(053. 用定积分的定义计算定积分⎰bax c d ,其中c 为一定常数.解：任取分点b x x x x a n =<<<<= 210,把],[b a 分成n 个小区间],[1i i x x -)2,1(n i =，小区间长度记为x ∆i =i x -1-i x )2,1(n i =,在每个小区间[]i i x x ,1-上任取一点i ξ作乘积i i x f ∆⋅)(ξ的和式：∑∑==--=-⋅=∆⋅n i ni i iiia b c x xc x f 111)()()(ξ,记}{max 1i n i x ∆=≤≤λ, 则)()(lim )(lim d 0a b c a b c x f x c ni i i b a-=-=∆⋅=∑⎰=→→λλξ.4. 利用定积分定义计算120d x x ⎰.解：上在]1,0[)(2x x f =连续函数，故可积，因此为方便计算，我们可以对[]0,1 n 等分，分点i i n i nix ξ;1,,2,1,-==取相应小区间的右端点，故 ∑∑∑===∆=∆=∆ni i i ni i i ni i i x x x x f 12121)(ξξ=∑∑===ni ni in n n i 1232111)(=311(1)(21)6n n n n ⋅++ =)12)(11(61nn ++ 当时0→λ（即时∞→n ），由定积分的定义得： 120d x x ⎰=31．5. 利用定积分的估值公式，估计定积分⎰-+-1134)524(x x x d 的值.解：先求524)(34+-=x x x f 在[]1,1-上的最值，由0616)(23=-='x x x f , 得0=x 或83=x . 比较 35093(1)11,(0)5,(),(1)781024f f f f -====的大小，知min max 5093,111024f f ==，由定积分的估值公式，得[])1(1d )524()]1(1[max 1134min --⋅≤+-≤--⋅⎰-f x x x f ,即14315093(425)d 22512x x x -≤-+≤⎰. 6. 利用定积分的性质说明⎰1d xe x与⎰1d 2x e x ，哪个积分值较大？解：在[]0,1区间内：22xx x x e e ≥⇒≥ 由性质定理知道：⎰1d xe x≥⎰1d 2x e x7. 证明：⎰---<<2121212d 22x e ex 。

第五章 定积分及其应用【内容提要1．定积分的概念和性质（1）定积分的定义设 )(x f 是定义在 [,]a b 上的函数，在区间 [,]a b 内任意插入 1n - 个 分点0121,n n a x x x x x b -=<<<<<=将其分成 n 个小区间。

记1(1,2,,)i i i x x x i n -∆=-=，max{}i x λ=∆，在每个小区间上任取一点 1[,]i i i x x ξ-∈，下列和式的极限01lim()niii f x λξ→=∆∑存在，且与小区间的划分及 iξ 的选取无关，则称函数)(x f 在 [,]a b 上可积，并称该极限值为 )(x f 在 [,]a b 上的定积分 ，记作() d baf x x ⎰，即01() d l i m() d nbiiai f x x f x x λξ→==∆∑⎰，其中 )(x f 称为被积函数，() d f x x称为被积表达式，x 称为积分变量，a 称为积分下限，b 称为积分上限，[,]a b 称为积分区间。

（2）定积分的性质1）常数因子可以提到积分号外()d ()d bbaakf x x k f x x =⎰⎰ （k 为常数）。

2）函数代数和的积分等于它们积分的代数和。

[()()]d ()d ()d b bbaa a f x g x x f x x g x x ±=±⎰⎰⎰3）对任意单个实数 ,,,a b c 恒有()d ()d ()d bcb aacf x x f x x f x x =+⎰⎰⎰。

4）若在区间 [,]a b 上，被积函数 ()f x K ≡，那么()d d d ()bb baaaf x x K x K x K b a ===-⎰⎰⎰特别地，当 1K = 时，()d d bbaaf x x K x b a ==-⎰⎰5）如果在区间 [,]a b 上， ()()f x g x ≤，则()d ()d bbaaf x xg x x ≤⎰⎰ (a b <)。

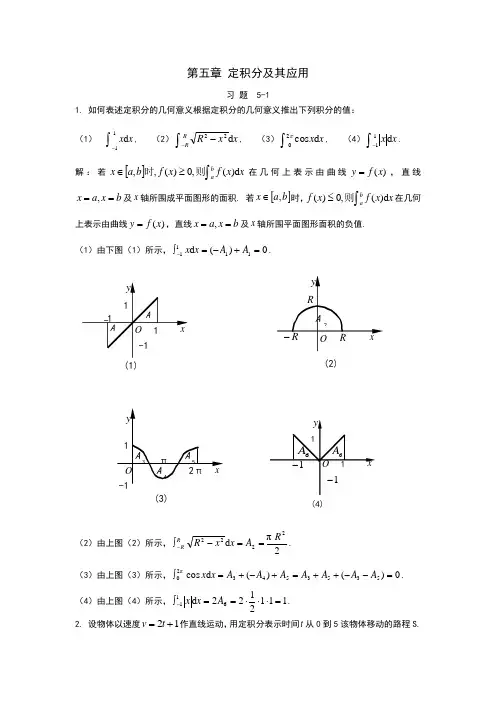
第五章 定积分及其应用习 题 5-11. 如何表述定积分的几何意义根据定积分的几何意义推出下列积分的值： （1）⎰-x x d 11, （2）⎰--x x R R R d 22, （3）⎰x x d cos 02π, （4）⎰-x x d 11.解：若[]⎰≥∈x x f x f b a x ab d )(,0)(,,则时在几何上表示由曲线)(x f y =，直线b x a x ==,及x 轴所围成平面图形的面积. 若[]b a x ,∈时，⎰≤x x f x f ab d )(,0)(则在几何上表示由曲线)(x f y =，直线b x a x ==,及x 轴所围平面图形面积的负值. （1）由下图（1）所示，0)(d 1111=+-=⎰-A A x x .（2）由上图（2）所示，2πd 2222R A x x R R R==-⎰-.（3）由上图（3）所示，0)()(d cos 5353543π20=--++=+-+=⎰AA A A A A A x x .（4）由上图（4）所示，1112122d 611=⋅⋅⋅==⎰-A x x .2. 设物体以速度12+=t v 作直线运动，用定积分表示时间t 从0到5该物体移动的路程S.( 2 )( 1 )( 3 )(4)解：=s ⎰+t t d )12(053. 用定积分的定义计算定积分⎰bax c d ,其中c 为一定常数.解：任取分点b x x x x a n =<<<<= 210,把],[b a 分成n 个小区间],[1i i x x -)2,1(n i =，小区间长度记为x ∆i =i x -1-i x )2,1(n i =,在每个小区间[]i i x x ,1-上任取一点i ξ作乘积i i x f ∆⋅)(ξ的和式：∑∑==--=-⋅=∆⋅n i ni i iiia b c x xc x f 111)()()(ξ,记}{max 1i n i x ∆=≤≤λ, 则)()(lim )(lim d 0a b c a b c x f x c ni i i b a-=-=∆⋅=∑⎰=→→λλξ.4. 利用定积分定义计算120d x x ⎰.解：上在]1,0[)(2x x f =连续函数，故可积，因此为方便计算，我们可以对[]0,1 n 等分，分点i i n i nix ξ;1,,2,1,-==取相应小区间的右端点，故∑∑∑===∆=∆=∆n i i i n i i i ni i i x x x x f 12121)(ξξ=∑∑===ni ni in n n i 1232111)(=311(1)(21)6n n n n ⋅++ =)12)(11(61nn ++ 当时0→λ（即时∞→n ），由定积分的定义得： 120d x x ⎰=31．5. 利用定积分的估值公式，估计定积分⎰-+-1134)524(x x x d 的值.解：先求524)(34+-=x x x f 在[]1,1-上的最值，由0616)(23=-='x x x f , 得0=x 或83=x . 比较 35093(1)11,(0)5,(),(1)781024f f f f -====的大小，知min max 5093,111024f f ==，由定积分的估值公式，得[])1(1d )524()]1(1[max 1134min --⋅≤+-≤--⋅⎰-f x x x f ,即14315093(425)d 22512x x x -≤-+≤⎰. 6. 利用定积分的性质说明⎰1d xe x与⎰1d 2x e x ，哪个积分值较大解：在[]0,1区间内：22xx x x e e ≥⇒≥ 由性质定理知道：⎰10 d x e x≥⎰10 d 2x e x7. 证明：⎰---<<2121212d 22x e ex 。

第五章 定积分及其应用主要内容内容提要：一、定积分的定义 二、定积分的简单性质⎰⎰⎰±=±bab ab adx x g dx x f dx x g x f )()()]()([⎰⎰=bab a dx x f k dx x kf )()(0)(=⎰a a dx x f⎰⎰-=ba ab dx x f dx x f )()(⎰⎰⎰+=bcc ab adx x f dx x f dx x f )()()(当)(x f 是奇函数时，0)(=⎰-a a dx x f ；当)(x f 是偶函数时，⎰⎰=-aa adx x f dx x f 0)(2)(．三、微积分基本公式C x F dx x f +=⎰)()( ⇒)()()()(a F b F x F dx x f ba b a-==⎰．四、定积分的计算：方法与不定积分相同． 1．换元积分法（1）定积分的凑微分法⎰⎰='bab ax d x f dx x x f )())(()())((ϕϕϕϕ⎰=)()()()(b a du u f x u ϕϕϕ)()()(b a u F ϕϕ=（2）定积分的第二类换元法 令)(a ϕα=，)(b ϕβ=，则⎰⎰'=b adt t t f t x dx x f )())(()()(ϕϕϕβα2．分部积分法⎰⎰='bab ax dv x u dx x v x u )()()()(⎰-=b aba x du x v x v x u )()()]()([⎰'-=b aba dx x u x v x v x u )()()]()([五、积分上限函数的导数：（1）)()(x f dt t f xa ='⎪⎭⎫ ⎝⎛⎰ （2）)())(()()(x u x u f dt t f dx d x u a '=⎰（3）)('))(()('))(()()()(x x f x x f dt t f dx d x x ϕϕψψψϕ-=⎰六、反常积分 1、⎩⎨⎧≤>⎰∞+1,1,1p p x dx p 发散收敛； 2、⎩⎨⎧≥<-⎰1p ,1p ,)a x (dxba p 发散收敛 七、定积分的应用（微元法） 1．平面图形的面积．2．体积：只要求旋转体的体积． 3．弧长第五章 定积分及其应用单元自测题一、填空题： 1．=⎰-xdx x sin 4ππ0 。

《高等数学》单元自测题答案 第五章 定积分及其应用一、填空题： 1、0； 2、≤； 3、65； 4、)sin(362x x ； 5、2+e ． 二、选择题：1、D ； 2 、C ； 3、B ； 4、C ； 5、D 。

三、计算题：1、解 令t x sin 2=，则tdt dx cos 2=，且 当0=x 时，0=t ；当2=x 时，2π=t 。

所以，⎰⎰⋅-=-20232023cos 2sin 44sin 84πtdt t t dx x x⎰⎰⋅-=⋅⋅=2022203cos cos )1(cos 32cos 2cos 2sin 8ππttd t tdt t t1564)cos 31cos 51(322035=-=πt t 。

2、解⎰⎰⎰⎰+=+=+---20322322223cos 20cos )cos (πππππππxdx xdx xdx dx x x34)sin 31(sin 2sin )sin 1(2203202=-=-=⎰ππt x x d x 。

3、解⎰⎰⎰--=-⋅=210221021021112arcsin )arcsin (arcsin dx xx x xd x x xdx π123121221121)1(211221022122-+=-⋅+=--+=⎰πππxx x d 。

4、解31)11lim (31)131(31314=--=⋅-=+∞→+∞∞+⎰xx x dx x 。

5、解 2)arcsin(ln )(ln 1ln )(ln 111212π==-=-⎰⎰ee e x x x d x x dx 。

四、应用题：1、已知函数)(x f 在 12=x 的某邻域内可导，且0)(lim 12=→x f x ，1004)(lim 12='→x f x ，求3121212)12(])([limx dtdu u tf x tx -⎰⎰→。

解 []2121231212123121212)12(3)(lim )12(])([lim )12(])([lim x du u xf x dt du u tf x dt du u tf x x xt x xt x --='-'⎥⎦⎤⎢⎣⎡=-⎰⎰⎰⎰⎰→→→ [])12(6)]([)(lim )12(3)(lim 121221212x x f x du u f x du u f x x x x x --+='--'⎥⎦⎤⎢⎣⎡=⎰⎰→→ 20086)()(2lim 6)]()([)(lim 1212='+=-'+--=→→x f x x f x f x x f x f x x 。

第5章 定积分及其应用§5.1 定积分的概念习 题 5－11.填空题：（1）函数()f x 在区间[,]a b 上的定积分是积分和的极限，即()baf x dx ⎰＝（ ）.（2）定积分的值只与（ ）及（ ）有关，而与（ ）的记法无关. （3）区间[,]a b 的长度的定积分的表示是（ ）. （4）被积函数()f x 在区间[,]a b 上连续是定积分()baf x dx ⎰存在的（ ）.（5）定积分的几何意义（ ）. 2.利用定积分的定义计算下列积分： （1）2baxdx ⎰； （2）1x e dx ⎰.3.利用定积分的定义计算由抛物线21y x =+，直线x a =、x b =（b a >）及x 轴所围成的图形的面积.4.利用定积分的几何意义，证明下列等式： （1）1310x -=⎰； （2）sin 0xdx ππ-=⎰；（3）4π=⎰； （4）11arctan 0xdx -=⎰；（5）11124x dx xdx -=⎰⎰ ； （6）2202cos 2cos xdx xdx πππ-=⎰⎰.5.利用定积分的几何意义求a⎰(0)b >的值.6. 将下列极限表示成定积分： （1）()201lim3nii i i x λξξ→=-∆∑，λ是[]7,5-上的分割；（2）01limni i x λ→=，λ是[]0,1上的分割.7.将下列和式的极限表示成定积分：（1）111lim 12n n n n n →∞⎛⎫+++ ⎪+++⎝⎭； （2）112lim p p p p n n n +→∞+++（0p >）；（3）)221limn n n →∞+； （4）n .8.有一河，宽为200米，从一岸到正对岸每隔20米测量一次水深，测得数据如下（图5-1-8）.试用梯形公式求此河横截面积的近似值.图5-1-8§5.2 定积分的性质习 题 5－21. 证明定积分的性质： （1）()()bb aakf x dx k f x dx =⎰⎰ （k 为常数）； （2）1b baadx dx b a ⋅==-⎰⎰. 2. 估计下列积分值：（1）421(2)x dx +⎰； （2）3244(1sin )x dx ππ+⎰； （3）arctan x xdx ；（4）21x edx ⎰； （5）2211x dx x +⎰； （6）20sin x dx x π⎰. 3. 设()f x 及()g x 在[],a b 上连续，证明： (1) 若在[],a b 上，()0f x ≥，且()0baf x dx =⎰，则在[],a b 上，()0f x ≡；（2）若在[],a b 上，()0f x ≥，且()f x 不恒等于零，则()0baf x dx >⎰；（3）若在[],a b 上，()()f x g x ≤，且()()bbaaf x dxg x dx =⎰⎰，则在[],a b 上，()()f x g x ≡．4. 根据定积分性质及第3题的结论，比较下列每组积分的大小：（1）320sin xdx π⎰，220sin xdx π⎰； （2）221x dx ⎰，231x dx ⎰；（3）21ln xdx ⎰，221(ln )x dx ⎰； （4）10x e dx ⎰，21x e dx ⎰；（5）1xe dx ⎰，()101x dx +⎰； （6）20xdx π⎰，20sin xdx π⎰；（7）20sin xdx π⎰，02sin xdx π-⎰； （8）2cos xdx π-⎰，20cos xdx π⎰；（9）10xdx ⎰，()01ln 1x dx +⎰ （10）()01ln 1x dx +⎰，011xdx x+⎰；. 5. 利用积分中值定理求下列极限： （1）sin limn pnn x dx x+→∞⎰； （2）120lim 1nn x dx x →∞+⎰； （3）10lim 1n xx n x e dx e →∞+⎰.6. 设()f x 在[],a b 上连续，()0baf x dx =⎰．证明：()f x 在[],a b 上在[],a b 内至少存在一个零点．7. 设()f x 在[]0,1上连续，在()0,1内可导，且1233()(0)f x dx f =⎰．证明：在()0,1内至少存在一点ξ，使得()0f ξ'=．8. 设()f x 在[],a b 上连续，在(),a b 内可导，且存在(),c a b ∈，使得()()()caf x dx f b c a =-⎰．证明：在(),a b 内至少存在一点ξ，使得()0f ξ'=．§5.3 微积分基本公式习 题 5-31. 设0()cos xx t tdt ϕ=⎰，求(0)ϕ'，4πϕ⎛⎫' ⎪⎝⎭. 2．求下列函数的一阶导数： （1）0()sin xtx e dt ϕ=⎰； （2）223()t xx e dt ϕ-=⎰；（3）2()x x ϕ=⎰； （4）2x y =；（5）32x xy =⎰； （6）()cos 2sin ()cos xxx t dt ϕπ=⎰；（7）22x txy t e dt -=⎰； （8）2()xe xy f t dt =⎰．3. 求下列函数的二阶导数：（1）()330sin xy t x tdt =-⎰； （2）258sin ()xy t f x dt dy t ⎛⎫= ⎪⎝⎭⎰⎰．4. 利用洛必达法则，求下列极限：（1）20cos limxx t dt x→⎰； （2）201lim arctan xx tdt x+→⎰；（3）202limsin 2x t x x e dt x x→-⎰； （4）()2202002sin limln 1x x xt dtt t dt→⎡⎤+⎣⎦⎰⎰；（5）121ln 1lim (1)xx tdtt x →-⎰＋； （6）232lim(sin )x x x t dtt t t dt→-⎰⎰；（7）22201lim ()x t x x t t edt x -→+∞+⎰； （8）()222020lim xt xx t e dt te dt→⎰⎰．5. 设函数()y y x =由方程00cos 0y xte dt tdt +=⎰⎰所确定，求dydx． 6. 设函数()y y x =由方程20cos y x x y tdt -+=⎰所确定，求dy dx．7. 设0sin t x udu =⎰，0cos t y udu =⎰，求dydx.8．设20()(1)xt f x t t e dt -=-⎰，问x 为何值时，()f x 有极值？9. 求函数0()(4)xF x t t dt =-⎰在[1,5]-上的最大值与最小值.10. 计算下列各定积分： （1）24211()x dx x+⎰； （2）()13213x x dx --⎰； （3）332(21)x dx --⎰； （4）1(21)xe dx +⎰； （5）12111dx x -+⎰； （6）240tan xdx π⎰；（7）10⎰； （8）21201x dx x +⎰； （9）20cos 2x dx π⎛⎫ ⎪⎝⎭⎰； （10）41dx ⎰； （11）420213311x x dx x -+++⎰； （12）211e dx x ---+⎰； （13）20sin x dx π⎰； （14）设21,01()1,10x x f x x x ⎧+ ≤≤=⎨+ -≤<⎩，求11()f x dx -⎰． 11. 设()f x 连续，若()f x 满足1()()x f xt dt f x xe =+⎰，求()f x ．12. 设13201()()1f x x f x dx x =++⎰，求()f x 与10()f x dx ⎰． 13. 设0ln(1)()(0)xt f x dt x t+=>⎰，求1()f x f x ⎛⎫+ ⎪⎝⎭． 14. 设1sin ,0()20,0x x f x x x ππ⎧ ≤≤⎪=⎨⎪ <>⎩或，求0()()x x f t dt ϕ=⎰在(,)-∞+∞内的表达式．§5.4 定积分的换元积分法与分部积分法习 题 5－41. 用换元积分法求下列定积分： （1）122(115)dxx --+⎰； （2）101xx e dx e +⎰； （3）220sin cos x xdx π⎰； （4）022122dx x x -⎰＋＋； （5）1⎰； （6）2120t te dx -⎰； （7）1221xe dx x ⎰； （8）35201x dx x +⎰； （9）2502353x x dx x +-+⎰；(10)6e e⎰； （11）21e ⎰； (12)320sin cos d πθθθ⎰；(13)1(14)；(15)ax ⎰；(16)3⎰(17)⎰；（18）0；(19) 0⎰； (20)； (21)3122(1)xdx -+⎰；(22)1；(23)41⎰；(24)1⎰－；(25)⎰； (26)2⎰； (27)-⎰； (28)()223min 2,x dx -⎰（29）2sin sin cos xdx x xπ+⎰；（30）0π⎰. 2. 用分部积分法求下列定积分： （1）ln 2x xe dx ⎰； （2）1ln e x xdx ⎰；（3）41⎰； （4）1arctan x xdx ⎰； （5）220sin x xdx π⎰； （6）324sin xdx xππ⎰； （7）220cos x xdx π⎰； （8）1530ln x xdx ⎰ ；（9）230x e dx ；(10)22(1)x - ； (11)220cos x e xdx π⎰； (12)1sin(ln )ex dx ⎰ ；(13)22ln (1)e exdx x -⎰； (14)12(1)ln (1)e x x dx -++⎰；(15)221log x xdx ⎰；(16)20sin x x dx π⎰； (17)1ln eex dx ⎰ ； (18)()242sec 1tan x xdx x π+⎰；(19)161⎰； (20)122(1)m xdx -⎰(m 为自然数).3. 利用积分区间的对称性以及函数的奇偶性，计算下列定积分：（1）22sin cos 2x xdx ππ-⎰；（2）22ππ-⎰；（3）6sin x xdx ππ-⎰；（4）1⎰； （5）x dx ； （6）221cos xdx x ππ-+⎰；（7）522cos xdx ππ-⎰； （8）325425sin 21x xdx x x -+⎰＋； （9）)sin x x dx ππ-⎰＋.（10）244cos 1x xdx e ππ--+⎰.4.已知()f x 是连续函数，证明 （1）1()()[()]baf x dx b a f a b a x dx =-+-⎰⎰；（2）200()[()(2)]aaf x dx f x f a x dx =+-⎰⎰；（3）()2321()2aa x f x dx xf x dx =⎰⎰（0a >）．5. 设()f x 是连续函数，证明 (1) 当()f x 是偶函数时，则0()()xx f t dt ϕ=⎰为奇函数；（2）当()f x 是奇函数时，则0()()xx f t dt ϕ=⎰为偶函数．6. 证明：220()2()aaax dx x dx ϕϕ-=⎰⎰，其中()x ϕ为连续函数.7. 证明：110(1)(1)m n n m x x dx x x dx ϕϕ-=-⎰⎰.8. 证明：20sin 2sin nn xdx xdx ππ=⎰⎰.9. 证明：112211111xx dx dx x x =++⎰⎰（0x >）. 10. 设31sin ()x t f x dt t =⎰，求120()x f x dx ⎰.若1sin ()n x t f x dt t=⎰，求110()n x f x dx -⎰.11. 若()f x ''在[0,]π连续，(0)2f =，()1f π=，证明：[()()]sin 3f x f x xdx π''+=⎰.12. 当0x >时，()f x 可导，且满足方程11()1()xf x f t dt x=+⎰， 求()f x .§5.5 广义积分习 题 5－51 计算下列瑕积分.(1)41dx x +∞⎰； (2)0e +∞⎰； （3）2122dx x x +∞-∞++⎰； （4）211(1)dx x x +∞+⎰； (5)1+∞⎰； (6) 0sin px e xdx ω+∞-⎰(0,0p ω>>)；(7)21arctan xdx x+∞⎰；(8) 1⎰(9)1e⎰（10）10⎰；（11）21⎰；（12）()22011dx x -⎰.2. 求当k 为何值时，瑕积分()21ln kdx x x +∞⎰收敛？当k 为何值时，该瑕积分发散？又当k 为何值时，该瑕积分取得最小值？3. 计算瑕积分0n x n I x e dx +∞-=⎰（n 为自然数）.4. 求c 为何值时，使2lim xc tx x c te dt x c -∞→+∞+⎛⎫= ⎪-⎝⎭⎰. 5.求2+∞⎰.6. 计算下列式子：（1）(7)2(4)(3)ΓΓΓ； （2）3(3)()29()2ΓΓΓ； （3）40x x e dx +∞-⎰； （4）2220x x e dx +∞-⎰. 7. 用Γ函数表示下列积分，并指出积分的收敛范围.（1）nxe dx +∞-⎰（0n >）； （2）101ln pdx x ⎛⎫⎪⎝⎭⎰； （3）22x dx +∞--∞⎰；(4)mn x x edx +∞-⎰； (5)10⎰； (6)311dx x +∞+⎰. §5.6 定积分的几何应用习题5-6１. 求由下列各组曲线所围成平面图形的面积：（１）1xy =，y x =，2x =; （2）x y e =，xy e -=，1x =; （3）2y x =，2x y +=; （4）3y x =，1y =，2y =，0x =;（5）0y =，1y =，ln y x =，0x =; (6)22x y =，228x y +=;(7) ln y x =,y 轴,ln y a =,ln y b =( 0b a >>)；(8) 23y x =+，2y x =. 2. 直线x k =平分由2y x =，0y =，1x =所围之面积，求k 之值． 3. 求抛物线243y x x =-+-及在点(0,3)-和(3,0)处切线所围成图形的面积. 4. 求抛物线22y px =及其在点,2p p ⎛⎫⎪⎝⎭处的法线所围成的图形的面积. 5. 求曲线33cos ,sin x a t y a t ==，).0(>a 所围成图形的面积. 6. 求曲线2cos r a θ=).0(>a 所围成图形的面积.7. 求曲线2(2cos r a θ=＋）).0(>a 所围成图形的面积. 8. 求对数螺线r ae θ=（0a >，πθπ-≤≤）及射线θπ=所围成图形的面积.9. 计算阿基米德螺线r a θ= (0a >)上相应于θ从0到2π的一段弧与极轴所围成的图形(如图5-6-22)的面积.图5-6-22 图5-6-2310.求由下列各曲线所围成图形的公共部分的面积. (1) 3cos r θ=及1cos r θ=+；(2) r θ=及2cos 2r θ=.11. 圆1r =被心形线1cos r θ=+分割成两部分，求这两部分的面积. 12.设sin y x =，02x π≤≤.问：为t 何值，图5-6-23中阴影部分的面积1s 与2s 之和最小？最大？13.求由下列已知曲线围成的平面图形绕指定的轴旋转而成的旋转体的体积.（1）2xy a =，0y =，x a =，2x a =（0a >），绕x 轴. （2）22(2)1x y +-=，绕x 轴.（3）ln y x =，0y =，x e =，绕x 轴和y 轴. （4）224x y +=，24(1)x y =--，0y >，绕x 轴. （5）5xy =，6x y +=，绕x 轴.（6）cos y x =，0x =，x π=，x 轴，绕y 轴.14. 求摆线(sin )(1cos )x a t t y a t =-⎧⎨=-⎩（02t π≤≤，0a >）的一拱与0y =所围成的图形绕直线2y a =旋转而成的旋转体的体积.15. 由心形线4(1cos )ρθ=+和直线0θ=及2πθ=所围成图形绕极轴旋转而成的旋转体的体积.16. 一个棱锥体的底面是长为2a 的正方形，高为h ，求此棱锥体的体积 (如图5-6-24).图5-6-24 图5-6-2517.设直线y ax b =+(0a >，0b >)与直线0x =，1x =及0y =所围成的梯形面积等于A ，试求a 、b ，使这个梯形绕x 轴旋转所得旋转体的体积最小.18.在由椭圆域2214y x +≤绕y 轴旋转而成的椭球体上，以y 轴为中心轴打一个圆孔，使剩下的部分的体积恰好等于椭球体体积的一半，求圆孔的直径.19.设有一锥体，其高为h ，上、下底都为椭圆，椭圆的轴长分别为2a 、2b 与2A 、2B ，求这锥体的体积.20.作半径为r 的球的外切正圆锥，问此圆锥的高h 为何值时，其体积V 最小？求出此最小值(如图5-6-25).21.把星形线232323x y a +=所围成的图形绕x 轴旋转(图5-6-26)，计算所得旋转体的体积.图5-6-26 图5-6-27 22.用积分的方法证明图5-6-27所示球缺的体积为2()3H V H R π=-. 23.求圆盘222x y a +≤绕x b =-(0b a >>)旋转而成的旋转体的体积.24.证明：由平面图形x a =，x b =，0a b ≤<，0()y f x ≤≤绕y 轴旋转而成的旋转体的体积为2()baV xf x dx π=⎰.25.利用24题的结论，计算sin y x =(0x π≤≤)和x 轴所围成的图形绕y 轴旋转所成的旋转体的体积.习题5－71. 已知边际成本'2()25309C q q q =+-，固定成本为55，试求总成本()C q ，平均成本与变动成本.2. 已知边际收入为'()30.2R q q =-，q 为销售量，求总收入函数()R q ，并确定最高 收入的大小.3. 某产品生产q 个单位是总收入R 的变化率为'()200100qR q =-，求： （1）生产50个单位时的总收入；（2）在生产100个单位的基础上，再生产100个单位时总收入的增量.4. 已知某商品每周生产q 个单位时，总成本变化率为'()0.412C q q =-（元/单位），固 定成本500，求总成本()C q . 如果这种商品的销售单价是20元，求总利润()L q ，并问每周生产多少单位时才能获得最大利润？图5-7-56. 设某城市人口总数为F ，已知F 关于时间t （年）的变化率为dF dt =，假设在计算的初始时间(0)t =，城市人口数为100（万），试求t 年中该城市人口总数.7. 若边际消费倾向在收入为Y 时为1232Y -，且当收入为零时总消费支出070c =.（1）求消费函数()c Y ；（2）求收入由100增加到196时消费支出的增加数.8. 设储蓄边际倾向（即储蓄额S 的变化率）是收入y 的函数 '()0.3S y =， 求收入从100元增加到900元时储蓄的增加额.9. 如果需求曲线为2()500.025D q q =-，并已知需求量为20个单位，试求消费者剩余CS .10. 假设某国某年洛伦兹曲线近似地由3y x =（01x ≤≤）表示，试求该国的基尼系数.11. 某投资项目的成本为100万元，在10年中每年可收益25万元，投资率为5%，试 求这10年中该项投资的纯收入的贴现值.12. 一位居民准备购买一栋别墅，现价为300万元，如果以分期付款的方式，要求每年 付款21万元，且20年付清，而银行贷款的年利率为4%，按连续复利计息，请你帮这位购5. 某新产品的销售率由下式给出()10090x f x e -=-，式中x 是产品上市的天数，前四天的销售总数是曲线()y f x =与x 轴在之间的面积（如图5-7-5），求前四天总的销售量.房者作一决定：是采用一次付款合算还是分期付款合算？总习题五1．求下列极限：(1) limnn k →∞=. (2) 21lim inni n i nen ne→∞=+∑；（3）11lim n n i n →∞= （4）112lim p p p p n n n +→∞+++（0p >）； （5）lim n →∞2．利用积分中值定理求下列极限： （1）sin lim0n pnn xdx x +→∞=⎰； （2）222lim n x n n x dx e+→∞⎰．3．求下列极限：（1）101lim (1sin 2)xtx t dt x →+⎰； （2）lim ()x a x a x f t dt x a →-⎰（其中()f x 连续）；（3）()2arctan lim xx t dt→＋ (4) ()2210limxt t x e dt→+∞⎰．4．（已知[]02()1()1xf t dt f x -=-⎰，求(0)f '．5． 已知()2021,0()0,x t e dtx f x x x ⎧-⎪≠=⎨⎪=0⎩⎰，求(0)f '． 6．设()f t 在0t ≤≤+∞上连续，若220()(1)x f t dt x x =+⎰，求(2)f ．7． 求函数0()(3)xF x t t dt =-⎰在[1,5]-上的最大值与最小值．8. 证明：111ln(1)11ln 23n n n+=++++<+． 9. 设()f x 、()g x 在区间[,]a b 上均连续，证明：（1）()222()()()()bbbaaaf xg x dxf x dxg x dx ≤⋅⎰⎰⎰（柯西－施瓦茨不等式）；（2）[]()()()111222222()()()()bbba aaf xg x dxf x dxg x dx +≤+⎰⎰⎰（闵可夫斯基不等式）.10. 设函数()f x 在区间[,]a b 上连续，且()0f x >，证明：11ln ()ln ()b b a a f x dx f x dx b a b a ⎡⎤≥⎢⎥--⎣⎦⎰⎰. 11. 设()f x 在[0,]a （0a >）上有连续导数，且(0)0f =，证明：2()2aMa f x dx ≤⎰，其中0max ()x aM f x ≤≤'=.12. 设()f x 在[0,1]上连续且单调减少，试证：对任何(0,1)a ∈，有1()()af x dx a f x dx ≥⎰⎰.13. 设()x ϕ在[,]a b 上连续，()()()xaf x x b t dt ϕ=-⎰，证明：必存在(,)a b ξ∈，使得()f ξ'=0.14.设()f x 在区间[,]a b 上连续，()g x 在区间[,]a b 上连续且不变号.证明至少存在一点[,]a b ξ∈，使下式成立()()()()bbaaf xg x dx f g x dx ξ=⎰⎰（积分第一中值定理）.15. 计算下列定积分：（1）3(1sin )x dx π-⎰； （2）e ；（3）⎰； （4）0ax ⎰ (0a >)；（5）20sin 1cos x xdx xπ++⎰； （6）40ln(1tan )x dx π+⎰；（7）a⎰(0a >)； （8）；（9）121(21)x x dx -++⎰； （10）sin )x x dx ππ-⎰（11）42213||||1x x dx x -⎛⎫-+ ⎪+⎝⎭⎰； （12）设2,01()2,12x x f x x x ⎧ ≤≤=⎨-<<⎩，求20()f x dx ⎰.16.利用函数的奇偶性计算定积分121(x dx -+⎰. 17. 利用函数的周期性计算定积分2(sin 2)(tan 1)a ax x dx π++⎰.18. 设函数()f x 在(,)-∞+∞内连续，并满足条件()sin xu f x u e du x -=⎰，求()f x .19. 计算下列各题： （1）设(5)2f =，5()3f x dx =⎰，求5()xf x dx '⎰．（2）已知2()tan f x x =，求40()()f x f x dx π'''⎰.20. 证明()[()()]aaaf x dx f x f x dx -=+-⎰⎰，并求下列定积分：（1）441sin dx x ππ-+⎰； （2）244sin 1x x dx e ππ--+⎰； （3）244cos 1nxx dx e ππ--+⎰（n 为正整数）. 21. 设()f x 在区间[,]a b 上连续，且()f x 关于2a bx +=对称的点处取相同的值.证明： 2()2()a b baaf x dx f x dx +=⎰⎰.22. 证明：112211111xx dt dt t t =++⎰⎰（0x >）. 23. 判断下列瑕积分的敛散性：(1)1+∞⎰；(2)2+∞⎰；(3)2cos ln xdx x+∞⎰；(4) 0+∞⎰；(5)3(1)(2)dxx x x +∞--⎰；(6)1+∞⎰；(7)120ln 1xdx x -⎰； (8)1ln 11eex dx x --⎰.24. 已知sin 2x dx x π+∞=⎰，求220sin x dx x+∞⎰. 25. 求介于直线0x =，2x π=之间由曲线sin y x =和cos y x =所围成的平面图形的面积.26. 求椭圆22113x y +=和22113x y +=的公共部分的面积. 27. 求曲线x y e =及该曲线的过原点的切线和x 轴的负半轴所围成的平面图形的面积. 28. 设曲线21:1L y x =-(01)x ≤≤、及x 轴和y 轴所围成的区域被曲线21:L y ax =分为面积相等两部分，其中a 是大于零的常数，试确定a 的值.29. 求由柱体222x y a +≤与222x z a +≤(0a >)的公共部分所围成图形的体积.30.将曲线r =绕x 轴旋转而成的旋转体的体积. 31. 将抛物线2y x ax =-在横坐标0与c （0c a >>）之间的弧段绕x 轴旋转，问c 为 何值时，所得旋转体体积V 等于弦OP （P 为抛物线与x c =的交点）绕x 轴旋转所得锥体体积.32. 设抛物线2y ax bx c =++通过点(0,0)，且当[0,1]x ∈时，0y ≥.试确定a b c 、、 的值，使得该抛物线与直线1x =，0y =所围成图形的面积为13，且使该图形绕x 轴旋转而成的旋转体的体积最小.33.一位居民准备购买一栋别墅价值为300万元，若首付为50万元，以后分期付款，每年付款数目相同，10年付清，而银行贷款的年利率为6%，按连续复利计息，每年应付款多少？（0.60.5448e-≈）34. 某公司投资2000万建成一条生产线，投产后，在t 时刻的追加成本和追加收益分别为23()52g t t =+ （百万/年）23()17t t ϕ=- （百万/年）试确定该生产线在何时停产可获得最大利润？最大利润是多少？.35.生产某种产品的固定成本为50万元，边际成本与边际收益分别为216100=-+（万元/单位产品）MC Q Q=-（万元/单位产品）MR Q894试确定工厂应将产量定为多少个单位时，才能获得最大利润？并求最大利润.。

(A层次）1. 4.7. 兀f 。

2 s in x cos3 xdx ; r xdx -1✓5-4x ，e 2dx f 1 x ✓l +I n x ;10. f 一冗九x 4s in 汕； 冗13. f f-�dx; 4 Sill X 冗16. f 。

2产co sx dx ;冗第五章定积分2. f 。

a x 2✓a 2—x 2dx; 5.「I✓x dx +l ；8. f -o 2 x 2 + d 2xx + 2 ; 冗11. f� 冗4c os 4xdx ;14. 17. 2f14 Jn X｀dx ;f 。

兀(xsinx)2dx ;冗19. f� ✓cosx-cos 3 xdx;20. f 。

4 smx dx · 1 + S lll . X ， 22. 4If 0 2 xln l +x dx ; l -x25. f +00dx0 (1 + x 2 XI + xa \ (B层次）23. f +oo l +x 2 dx · -oo 1 +X 4' 心(a�o )。

3. 6.9. 厂dx1 X 飞l +x2 r dx｀3 斤言-1;f。

冗✓1+ c os2xdx;3· 212 fs x sm xdx · ·-5 x 4 + 2x 2 + 1' 15. f 。

1 xa rct gxdx ; 18. {es in(lnx 雇21. 24. f 。

冗xs mx dx .1 +C OS 2X 冗f 。

2 ln sin x dx ;d y 1. 求由f 。

:e r dt+f x costd t=O所确定的隐函数对x 的导数odx 2. 当x 为何值时，函数I(x)= f x t e -t 2dt有极值？。

3.d厂cos矿t。

dx si n x(}Ix+l, x�14. 设八x )�{归，X > 1'求l。

勹(x )dx 。

2f x(a rc tg t) 2d t5. lirn 。

第五章 定积分的应用典型习题解答与提示习 题 5-21．（1）)10S x dx =⎰； （2）()10xS e e dx =-⎰； （3）()12332S x x dx -=--⎰；（4）(0]aS dx =⎰； （5）()544sin cos S x x dx ππ=-⎰。

2．（1）3ln 22-； （2）12e e+-； （3）()121413S x dx -=-=⎰； （4）2424182y S y dy -⎛⎫=+-= ⎪⎝⎭⎰。

3．()0332234sin cos 8S a td a t a ππ==⎰。

4．（1）()22214cos 42S d ππθθπ-==⎰； （2）()223013sin 324S a d a ππθθ=⨯=⎰；（3）()2121521cos 2424S d πππθθπ⎡⎤=++=-⎢⎥⎣⎦⎰，252244S πππ⎛⎫=--=- ⎪⎝⎭。

5．（1）32,85x y V V ππ==； （2）()11102484xdx x dx πππ--=⎰⎰；（3）22sin 2xdx πππ=⎰； （4）()()2222301cos [sin ]5a t d a t t a πππ--=⎰。

6．（1）()()33222[11]3aS b a ==+-+⎰； （2）(0ln 1S ==+⎰。

习 题 5-31．()0.060.0018J W kxdx ==⎰。

2．()2R hRkmM mMhW dx k x R R h +==+⎰。

3．()()5209.81512250J W x dx =⨯-=⎰。

4．()()215109.81557697.5J 15x W x dx π⎛⎫=-= ⎪⎝⎭⎰。

5．()()39.82[32]205.8N F x dx =⨯+-=⎰。

6．取圆心为原点，x 轴正向向下，()39.82176.4N F =⨯=⎰。

习 题 5-41．（1）总收益函数为()20200200100200QQQ Q R Q MRdQ dQ Q ⎛⎫==-=-⎪⎝⎭⎰⎰， 故50Q =个单位时，总收益()25050200509987.5200R R ==⨯-=； （2）200220010010020019850200Q R MRdQ Q ⎛⎫==-= ⎪⎝⎭⎰V 。

定积分及其应用题一 题面：求由曲线2(2)y x =+与x 轴，直线4y x =-所围成的平面图形的面积． 答案：323．变式训练一题面：函数f (x )＝⎩⎪⎨⎪⎧x ＋2(－2≤x <0)，2cos x ⎝ ⎛⎭⎪⎫0≤x ≤π2的图象与x 轴所围成的封闭图形的面积为( )A.52 B ．2 C ．3D ．4答案：D. 详解：画出分段函数的图象，如图所示，则该图象与x 轴所围成的封闭图形的面积为12×2×2＋∫π202cos x d x ＝2＋2sin x |π20＝4.变式训练二 题面：由直线y ＝2x 及曲线y ＝3－x 2围成的封闭图形的面积为( ) A ．2 3 B ．9－2 3 C.353D.323答案： 详解：注意到直线y ＝2x 与曲线y ＝3－x 2的交点A ，B 的坐标分别是(－3，－6)，(1,2)，因此结合图形可知，由直线y ＝2x 与曲线y ＝3－x 2围成的封闭图形的面积为⎠⎛－31(3－x 2－2x )d x ＝⎝ ⎛⎭⎪⎫3x －13x 3－x 2⎪⎪⎪1－3＝3×1－13×13－12－⎣⎢⎡3×－3－13×－33]－－32＝323，选D.题二 题面：如图所示，在边长为1的正方形OABC 中任取一点P ，则点P 恰好取自阴影部分的概率为( )．A ．14B ．15C ．16D ．17变式训练一题面：函数f (x )＝sin(ωx ＋φ)的导函数y ＝f ′(x )的部分图象如图所示，其中，P 为图象与y 轴的交点，A ，C 为图象与x 轴的两个交点，B 为图象的最低点．若在曲线段ABC 与x 轴所围成的区域内随机取一点，则该点在△ABC 内的概率为________． 答案：π4.详解：设A (x 0,0)，则ωx 0＋φ＝π2，∴x 0＝π2ω－φω. 又y ＝ωcos(ωx ＋φ)的周期为2πω， ∴|AC |＝πω，C ⎝ ⎛⎭⎪⎫π2ω－φω＋πω，0.依题意曲线段ABC 与x 轴围成的面积为 S ＝－∫π2ω－φω＋πωπ2ω－φωωcos(ωx ＋φ)d x ＝2. ∵|AC |＝πω，|y B |＝ω，∴S △ABC ＝π2. ∴满足条件的概率为π4.变式训练二 题面：（2012•福建）如图所示，在边长为1的正方形OABC 中任取一点P ，则点P 恰好取自阴影部分的概率为（ ）A ．B ．C ．D ．答案：C. 详解：根据题意，正方形OABC 的面积为1×1=1， 而阴影部分由函数y=x 与y=围成，其面积为∫01（﹣x ）dx=（﹣）|01=，则正方形OABC 中任取一点P ，点P 取自阴影部分的概率为=； 故选C ．金题精讲 题一 题面：（识图求积分，二星）已知二次函数y ＝f (x )的图象如图所示，则它与x 轴所围图形的面积为( )．A ．2π5B ．43C ．32D ．π2答案：变式训练一题面：如图求由两条曲线y ＝－x 2，y ＝－14x 2及直线y ＝－1所围成的图形的面积．答案：43. 详解：由⎩⎪⎨⎪⎧y ＝－x 2，y ＝－1，得交点A (－1，－1)，B (1，－1)．由⎩⎨⎧y ＝－14x2，y ＝－1，得交点C (－2，－1)，D (2，－1)．∴所求面积S ＝2⎣⎢⎡⎦⎥⎤∫10⎝ ⎛⎭⎪⎫－14x 2＋x 2d x ＋⎠⎛12⎝ ⎛⎭⎪⎫－14x 2＋1d x ＝43.变式训练二 题面：例1求在[0,2]π上，由x 轴及正弦曲线sin y x =围成的图形的面积. 答案：4. 详解：作出sin y x =在[0,2]π上的图象如右 sin y x =与x 轴交于0、π、2π，所 求积2200sin |sin |(cos )|(cos )|4s xdx xdx x x ππππππ=+=---=⎰⎰题二 题面：（作图求积分，四星）求曲线36y x x =-与曲线2y x =所围成的图形的面积． 交点的横坐标分别为2,0,3-，12112S =．变式训练一题面：求曲线2y x =，y x =及2y x =所围成的平面图形的面积. 答案：76. 详解：作出2y x =，y x =及2y x =的图如右 解方程组22y x y x=⎧⎨=⎩ 得24x y =⎧⎨=⎩0x y =⎧⎨=⎩ 解方程组2y x y x =⎧⎨=⎩得11x y =⎧⎨=⎩ 00x y =⎧⎨=⎩∴所求面积12201(2)(2)s x x dx x x dx =-+-⎰⎰ 12201(2)xdx x x dx =+-⎰⎰212320111|()|23x x x =+- 76=答：此平面图形的面积为76变式训练二 题面：求由抛物线28(0)y x y =>与直线6x y +=及0y =所围成图形的面积. 答案：403. 详解：作出28(0)y x y =>及6x y +=的图形如右：解方程组2860y x x y ⎧=⎨+-=⎩得24x y =⎧⎨=⎩解方程组600x y y +-=⎧⎨=⎩ 得60x y =⎧⎨=⎩∴所求图形的面积62(6)s x dx =+-⎰⎰32262022140|(6)|323x x x +-= 题三x题面： （1）由曲线y x =，直线2y x =-及y 轴所围成的图形的面积为_______．（2）由曲线2y x =与直线2y x =-所围成的封闭图形的面积为_______． 答案：（1）163；（2）92．变式训练一题面： 设f （x ）=，函数图象与x 轴围成封闭区域的面积为（ ）A ．B ．C ．D ．答案：C.详解：根据题意作出函数的图象：根据定积分，得所围成的封闭区域的面积S=故选C变式训练二 题面：已知函数的图象与x 轴所围成图形的面积为（ ）A．1/2 B．1C．2D．3/2答案：D.详解：由题意图象与x轴所围成图形的面积为102(1)cosx dx xdxπ--++⎰⎰21021()|sin|2x x xπ-=-++112=+32=.故选D．题四题面：（导数与积分结合，二星）设函数()mf x x ax=+的导函数为()21f x x'=+，则21()f x dx-⎰的值等于______．答案：56．变式训练一题面：设函数f(x)＝x m＋ax的导函数f′(x)＝2x＋1，则⎠⎛12f(－x)d x的值等于()A.56B.12C.23D.16答案：A. 详解：由于f (x )＝x m ＋ax 的导函数f ′(x )＝2x ＋1，所以f (x )＝x 2＋x ，于是∫21f (－x )d x＝∫21(x 2－x )d x ＝⎝ ⎛⎭⎪⎫13x 3－12x 2⎪⎪⎪21＝56.变式训练二 题面：设函数f (x )＝x m ＋ax 的导函数f ′(x )＝2x ＋1，则⎠⎛12f (－x )d x 的值等于( )A.56B.12C.23D.16答案：A. 详解：由于f (x )＝x m ＋ax 的导函数为f ′(x )＝2x ＋1，所以f (x )＝x 2＋x ，于是⎠⎛12f (－x )d x ＝⎠⎛12 (x 2－x )d x ＝⎪⎪⎪⎝ ⎛⎭⎪⎫13x 3－12x 221＝56.题五 题面：（化简后求积分，四星）（1）求21sin 2xdx π-20sin cos x x dxπ=-⎰原式4204(cos sin )(sin cos )x x dx x x dx πππ=-+-⎰⎰22 2.=（2）440(sin cos )22x xdx π+⎰变式训练一题面：与定积分∫3π01－cos x d x 相等的是( ) A.2∫3π0sin x 2d x B.2∫3π0⎪⎪⎪⎪⎪⎪sin x 2d x C.⎪⎪⎪⎪⎪⎪2∫3π0sin x 2d x D ．以上结论都不对答案：B. 详解：∵1－cos x ＝2sin 2x2，∴∫3π01－cos x d x ＝∫3π02 ⎪⎪⎪⎪⎪⎪sin x 2d x ＝2∫3π0⎪⎪⎪⎪⎪⎪sin x 2d x .变式训练二题面：40cos xdx π=⎰________.答案：22.详解：因为40cos xdx π=⎰sin x ⎪⎪⎪⎪π40＝sin π4＝22，所以∫π40cos x d x ＝22. 题六 题面：（定积分的运用，三星）函数f (x )＝sin(ωx ＋φ)的导函数y ＝f ′(x )的部分图象如图所示，其中，P 为图象与y 轴的交点，A ，C 为图象与x 轴的两个交点，B 为图象的最低点．(1)若φ＝π6，点P 的坐标为⎝⎛⎭⎫0，332，则ω＝________；(2)若在曲线段ABC 与x 轴所围成的区域内随机取一点，则该点在△ABC 内的概率为________．[解析] (1)函数f (x )＝sin(ωx ＋φ)求导得，f ′(x )＝ωcos(ωx ＋φ)，把φ＝π6和点⎝⎛⎭⎫0，332代入得ωcos ⎝⎛⎭⎫0＋π6＝332解得ω＝3．(2)取特殊情况，在(1)的条件下，导函数f ′(x )＝3cos ⎝⎛⎭⎫3x ＋π6，求得A ⎝⎛⎭⎫π9，0， B ⎝⎛⎭⎫5π18，－3，C ⎝⎛⎭⎫4π9，0，故△ABC 的面积为S △ABC ＝12×3π9×3＝π2，曲线段与x 轴所围成的区域的面积S ＝－⎪⎪⎪f (x ) 4π9π9＝－sin ⎝⎛⎭⎫4π3＋π6＋sin ⎝⎛⎭⎫3π9＋π6＝2，所以该点在△ABC 内的概率为P ＝S △ABC S ＝π4. 同类题一题面：设y ＝f (x )是二次函数，方程f (x )＝0有两个相等的实根，且f ′(x )＝2x －2.(1)求y ＝f (x )的表达式；(2)求y ＝f (x )的图象与两坐标轴所围成图形的面积．答案：(1) f (x )＝x 2－2x ＋1.(2) 13.详解：(1)设f (x )＝ax 2＋bx ＋c (a ≠0)，则f ′(x )＝2ax ＋b .又f ′(x )＝2x －2，所以a ＝1，b ＝－2，即f (x )＝x 2－2x ＋c .又方程f (x )＝0有两个相等实根，所以Δ＝4－4c ＝0，即c ＝1.故f (x )＝x 2－2x ＋1.(2)依题意，所求面积为S ＝⎠⎛01(x 2－2x ＋1)d x ＝(13x 3－x 2＋x )|10＝13.同类题二题面：设y =f （x ）是二次函数,方程f （x ）=0有两个相等的实根，且f ′（x ）=2x +2.（1）求y =f （x ）的表达式；（2）求y =f （x ）的图象与两坐标轴所围成图形的面积.（2）若直线x =－t （0＜t ＜1＝把y =f （x ）的图象与两坐标轴所围成图形的面积二等分，求t 的值.答案：（1）f （x ）=x 2+2x +1.（2）13. （3）t =1－321. 详解： （1）设f （x ）=ax 2+bx +c ，则f ′（x ）=2ax +b ，又已知f ′（x ）=2x +2∴a =1，b =2.∴f （x ）=x 2+2x +c又方程f （x ）=0有两个相等实根，∴判别式Δ=4－4c =0，即c =1.故f （x ）=x 2+2x +1.（2）依题意，有所求面积=31|)31()12(0123201=++=++--⎰x x x dx x x . （3）依题意，有x x x x x x t t d )12(d )12(2021++=++⎰⎰---， ∴023123|)31(|)31(t t x x x x x x ---++=++，－31t 3+t 2－t +31=31t 3－t 2+t ，2t 3－6t 2+6t －1=0，∴2（t －1）3=－1，于是t =1－321.思维拓展题一题面：（几何法求积分，四星）（1）计算0⎰，121sin x xdx -⎰；（2）求椭圆22221x y a b +=的面积．0044b S a ==⎰⎰，转化为圆的面积．同类题一题面：求定积分11dx -⎰的值. 答案：2π． 详解：11dx -⎰表示圆x 2＋y 2＝1在第一、二象限的上半圆的面积． 因为2S π=半圆，又在x 轴上方．所以11dx -⎰＝2π．同类题二题面：20)ax dx -⎰的值是（ ） A. 143π- B. 143π+ C. 123π- D. 12π- 答案：A.详解：积分所表示的几何意义是以（1，0）为圆心，1为半径第一象限内圆弧与抛物线y=x 2在第一象限的部分坐标轴围成的面积，故只需求出圆的面积乘以四分之一与抛物线在第一象限的部分与x 轴和直线x=1围成的图形的面积之差．即20)ax dx-⎰ 1231001|443x dx x ππ=-=-⎰ 143π=-.故答案选A。

定积分自测题A 答案与提示一、选择题 1. 答案：A 2. 答案：C提示：4422(1sin )6cos 6x dx x ππππππ---=+=⎰.3. 答案：C提示：232()23x x F x e x e x '=⋅-⋅. 4. 答案：A提示：令u =则11()2f dx f u udu =⎰⎰.5. 答案：B提示：()f x '是偶函数，sin ()f x '是偶函数，(sin )f t 是奇函数，0(sin )xf t dt ⎰是奇函数. sin ()t f t +是奇函数，0[sin ()]xt f t dt +⎰是偶函数.sin ()t f t dt ⋅是偶函数，sin ()xt f t dt ⋅⎰是奇函数.6. 答案：B提示：1100ln(1)1dx x x =--=+∞-⎰. 7. 答案：D提示：111121111(1)()()()()0aa a a a a a af t dt f t d t f u du t t t t ++-+=++==⎰⎰⎰.8. 答案：A提示：2021101()3x f x dx e dx xdx e --=+=-⎰⎰⎰.二、填空题1．答案：12π提示：令sin ,[,]22x t t ππ=∈-，则12222211cos 2cos 22t tdt dt πππππ---+===⎰⎰⎰.2. 答案：1π提示：21arctan 1A dx A x A x π+∞+∞-∞-∞===+⎰. 3. 答案：1x -提示：对等式1()2()f x x f t dt =+⎰积分，得111()2()f x dx xdx f t dt =+⎰⎰⎰，则11()2f t dt =-⎰.即得()1f x x =-.4.112π-提示：622006111sin sin sin 122212xdx x dx x dx πππππ⎛⎫⎛⎫-=-+-=- ⎪ ⎪⎝⎭⎝⎭⎰⎰⎰.5. 答案：2a提示：02()()lim lim22xx x f at dtf ax ax x →→==⎰. 6. 答案：4提示：1211(2)()(2)(2)(2)4(2)n xf x dx xf x dx t f t d t tf t dt ''''===⎰⎰⎰⎰.7.答案：623x x x e --提示：32623x t x x de dt e x e dx---=⋅-.8. 答案：12e e+-提示：1110001()2x x x x e e dx e e e e ---=+=+-⎰.三、计算题166200011.sin sin(cos sin)212xdx x t t tdt t t tππ==-+=-⎰解：22lnln222.2(arctan)arctan122udx du u u c cuπ=-+=++∴==-⎰⎰解：32121210013.(1)1()()(1)x t t tf x e dx t x f t e dt e e dt te dt e e e+-=-=+=+-⎰⎰⎰⎰解：221111ln(1)1ln(1)1114.ln(1)ln2(1)11(1)22x xdx x d dxx x x x+∞+∞+∞+∞++=-+=-+=+++++⎰⎰⎰解：11110005.arctan ln(1x==-=⎰解：22110001max min6.()2(1)00,1,1(0)0(1)(1)(1)()()(1)0xt t tf x x x e x x x ff f t e dt e f f t e dt t ef e f-+∞+∞-----'=-===-===-=-=+∞=-∞=-====⎰⎰解：令得又因此7.解：10≤≤x时⎰=x dt t fxF)()(=⎰-x t dtexe--=110≤≤x时⎰=x dt t fxF)()(=⎰-10dte t⎰+x tdt1212--=ex所以⎩⎨⎧≤≤-≤≤-=--2111)(12xexxexFx四、证明题1．证明：由积分中值定理有11()()(1)axf x dx a fξξ=⎰设()()F x xf x=，则()()()()()(1)(1)F x xf x F x f x xf x F f''==+=，又()(1)(2)axf x dx af=⎰而11112()(1)()(1)a f af F Fξξξ∴==由（），（）得即所以由罗尔定理存在1,(1)(0,1)()0.F ξξξ'∈⊂=使得2. 证明：2221()1(1)()()(()1)0,()12()0()()f x F x f x f x f x f x f x f x +'=+=-≥+≥>()211(2)()0()()0()()ab bbaaF x F a dt dt F b f t dt f t f t '∴≥==-<=>⎰⎰⎰()0[,]F x a b ∴=在内至少有一个根，()20,()[,]F x F x a b '≥>因所以在上是单调增函数，()[,]F x a b 故在内只有一根。

129第五章 定积分及其应用§5.1 学习的要求1. 理解定积分的概念及几何意义，了解可积的条件．2. 掌握定积分的基本性质．3. 理解变上限积分是变上限的函数，掌握对变上限积分求导数的方法．4. 熟练掌握牛顿—莱布尼茨公式．5. 掌握定积分的换元积分法和分部积分法6. 理解无穷区间的广义积分，掌握其计算方法．7. 熟练掌握定积分求平面图形面积和掌握平面图形绕坐标轴旋转所成的旋转体体积 8. 会用定积分求变力直线做功和不均匀细棒的质量．§5.2内容提要一、 定积分的概念 （一）定积分的概念定义 设函数)(x f y =在区间],[b a 上有定义，用任一组分点： 01....a x x =<<,i n x x b <<<=把区间],[b a 分成n 个小区间),...3,2,1](,[1n i x x i i =-在每个小区],[1i i x x -上任意取一点i ξi i i x x ≤≤-ξ1() 用函数值)(i f ξ与该区间的长度1--=∆i i i x x x 相乘,作和式i ni i x f ∑=∆1)(ξ 如果不论对区间],[b a 采取何种分法及i ξ如何选取,当 {}0(max (1)i x x x i n ∆→∆=∆≤≤)时，和式的极限存在，则称函数)(x f 在],[b a 上可积,此极限称为函数在区间],[b a 上的定积分(简称积分).记为dx x f ba)(⎰，即1()()limnbiiai x f x dx f x ξ=∆→=∆∑⎰，其中变量x 称为积分变量,)(x f 称为被积函数,dx x f )(称为被积表达式b a ,分别称为积分下限和积分上限, ],[b a 称为积分区间.⎰badx x f )( 是 一个常量(b a ,为常数)，其值只与被积函数和积分上下限有关,与积分变量用什么字母无关.(二).几何意义 1. 若)(x f ≥0,定积分⎰ba dx x f )(表示曲线)(x f y =,直线x =a 和x =b 以及x 轴所围成的曲边梯形的面积. 2. 若)(x f ≤0,定积分⎰badx x f )(表示相应曲边梯形面积的负值.(三) 定积分存在定理定理 如果函数)(x f 在区间],[b a 上连续,则)(x f 在],[b a 上的定积分必定存在. 二 、定积分的性质130 性质1 若],,[b a x ∈恒有)(x f =1，则有⎰⎰-==⋅bab aa b dx dx 1．性质2 ⎰ba dx x f )(=-⎰abdx x f )(．性质3 ⎰=badx x kf )(⎰badx x f k )( （k 是常数）性质4⎰⎰⎰±=±b ab abadx x f dx x f dx x f x f )()()]()([2121推论1 112[()()]()()()bb bbn n aaaaf x f x dx f x dx f x dx f x dx ±±=±±±⎰⎰⎰⎰性质5 ],[b a c ∈∀,则⎰badx x f )(=⎰c adx x f )(+⎰bcdx x f )(推论2 c b a ,,为任意的常数⎰badx x f )(=⎰c adx x f )(+⎰bcdx x f )(.性质6(积分中值定理) 若函数)(x f 在],[b a 上连续,则至少存在一点ξ()b a ,(∈ξ),使⎰badx x f )(=))((a b f -ξ三 、牛顿—莱布尼茨公式 (一) 积分上限函数1. 定义 设)(x f 在],[b a 上连续,],,[b a x ∈则)(t f 在],[x a 上可积 , 即⎰xadt t f )(存在,因此⎰xadt t f )(是上限x 的函数,记为()x φ=⎰xadt t f )(，称)(x φ为积分上限函数(或变上限积分) ．2.积分上限函数的导数设)(x f 在],[b a 上连续, )(x φ在],[b a 上可导,则⎰∈==xa b a x x f dt t f dxd x ].,[),()()('φ )(x φ就是)(x f 在],[b a 上的一个原函数．(二)牛顿—莱布尼茨公式定理 如果函数()F x 是连续函数)(x f 在区间],[b a 上的任一原函数, 则)()()(a F b F dx x f ba-=⎰,这个公式称为牛顿—莱布尼茨公式,也称为微积分学基本定理. 公式表明:一个连续函数在区间],[b a 上的定积分等于它的任一原函数在区间],[b a 上的增量.四. 定积分的换元法和分部积分法 (一) 定积分的换元法设函数)(x f 在区间],[b a 上连续,令)(t x φ=,如果 (1) )(t φ在[βα,]上连续,当],[βα∈t 时, )(t φ的值不超出],[b a ,且有连续导函数)('t φ；(2) b a ==)(,)(βφαφ， 则⎰badx x f )(=⎰βαφφdx t t f )('))((．用)(t x φ=进行变换时,积分限也要随之换成新变量t 的积分限,不必像不定积分那样将变量还原.131(二)定积分的分部积分法设函数),(x u )(x v 在],[b a 上具有连续的一阶导数 ),('),('x v x u 则''bb aaba uv dx u vdx uv =-⎰⎰；或bbaaba udv vdu uv =-⎰⎰ ．(三)偶，奇函数在对称区间],[a a -上的积分(1)当)(x f 是],[a a -上连续的偶函数时，⎰⎰-=aaadx x f dx x f 0)(2)(；(2)当)(x f 是],[a a -上连续的奇函数时，⎰-=aadx x f 0)(．五．广义积分(反常积分)(一) 无穷区间上的积分(无穷积分)定义 设)(x f 在区间[,)a +∞上连续,取b a >,若极限lim ()bab f x dx →∞⎰,则称此极限值为 )(x f 在),[+∞a 上的广义积分,记作 ⎰+∞adx x f )(=lim ()bab f x dx →∞⎰；(1)类似地,可以定义如下反常积分⎰∞-bdx x f )(=lim()baa f x dx →-∞⎰； (2)⎰-∞∞-dx x f )(=⎰∞-cdx x f )(+⎰+∞cdx x f )(lim()caa f x dx →-∞=⎰+lim()bcb f x dx →+∞⎰， (3)其中c 为任何实数；当(1)(2)(3)式右端极限存在时,反常积分收敛,否则是发散的. (二) 无界函数的积分定义 设)(x f 在],(b a 上连续,且lim ()x af x +→=∞，取0>ε若极限0lim ()ba f x dxεε+→⎰存在,则称此极限为无界函数)(x f 在],[b a 上的广义积分,记作⎰badx x f )(=0lim ()ba f x dx εε++→⎰．类似地,可定义在x b =附近无界函数()f x 的反常积分⎰b adx x f )(=0lim ()b af x dx εε-→⎰，以及在(a ,b )内一点x c =附近无界函数()f x 的反常积分⎰badx x f )(=⎰c adx x f )(+⎰bcdx x f )(=0lim ()c af x dx εε-→⎰+0lim ()bc f x dx εε++→⎰．六 定积分的应用(二) 定积分的元素法.(1) 任取],[b a 上的代表性的小区间[,]x x dx + ,作出欲求量Q 在此小区间上增量Q ∆的近似值即微元： dx x f dQ )(= .(2)求积分，Q =⎰badx x f )(.注:关键是找出微元,例如求面积要找出“面积微元”,求体积要找出“体积微元”等. (三)定积分的几何应用1)平面图形的面积(1)直角坐标系下的面积公式①由曲线(),()(()())y f x y g x f x g x ==≥与)(,b a b x a x <==所围成的图形面积132 S=⎰-badx x g x f )]()([；②由曲线 (),()(()())x y x y y y φϕφϕ==≥与)(,d c d y c y <==所围成的图形面积[()()]dcs y y dy φϕ=-⎰.(2)极坐标系下的面积,求立体的体积由曲线],,[),(βαθθ∈=r r 与两条射线βθαθ==, 所围成的曲边扇形的面积 21()2s r d βαθθ=⎰. 2)已知平行截面的面积,求立体的体积设某立体由一曲面和垂直于x 轴的两个平面 b x a x ==,围成，用垂直于x 轴的平面去截这个立体，若截面面积()A x (b x a ≤≤)是已知的连续函数,则该立体体积()baV A x dx =⎰．3)旋转体的体积①连续曲线))((b x a x f y ≤≤=与b x a x =-,及x 轴所围成的图形绕x 轴旋转一周所得的旋转体体积⎰=bax dx x f V )(2π②连续曲线))((d y c y x ≤≤=φ与d y c y ==,及y 轴所围成的图形绕y 轴旋转一周所得的旋转体体积⎰=dcy dy y V )(2φπ．（三）定积分在物理上的应用 1.变力沿直线作功变力)(x f 作用于物体,使物体由点a x =移动到b x =,)(x f 在],[b a 上连续,由微元法，任取],[b a 上的小区间[,],x x dx +其上的变力)(x f 近似看着常数,得功元素dx x f dw )(=，以a 到b 求定积分,得所求的功 w =⎰badx x f )(．2.非均匀直线细棒的质量.直线细棒的线密度为∈=x x ),(ρρ],[b a ,在],[b a 上由微元法,任取],[b a 上的小区间[,],x x dx +其上的密度近似看着常数,得质量元素 dx x dm )(ρ=，从a 到b 求定积分,得到所求的直线细棒的质量m =⎰badx x )(ρ．3. 非均匀细棒的转动惯量细棒AB 的方程为,b kx y +=密度∈=x x ),(ρρ],[b a ,任取],[b a 上的小区间],[dx x x +,视该小区间上密度与],[dx x x +对应的细棒段CD 到转轴x 轴的距离y 为常数,得转动惯量微元dx x b kx k dx x k ydI x )()(1)(12222ρρ++=+=转动惯量为 ⎰++=bax dx x b kx k I )()(122ρ§5.3基本例题及分析133例1.比较下列积分的大小关系.(1)⎰21sin dx x x 与⎰212)sin (dx x x ； (2)⎰⎰++1010)1ln(1dx x dx xx 与． 分析 在积分上下限都相同的情况下，积分大小由被积函数的大小决定． 比较两个函数的大小可以根据函数本身的图形关系、利用单调函数的定义等方法来判断.解 (1)当0x >时sin x x <，当1<x <2时,有1sin >x x ，即有 ,sin )sin (2xx x x > 则⎰⎰<21212)sin (sin dx x x dx x x . (2) 令0)0(),1ln(1)(=+-+=F x x xx F ，,)1(11)1(1)('22x xx x x F +-=+-+= 当0x >时,0)('<x F 时,()F x 单调下降,0)0()(,0=<>F x F x ，即)1l n (1x xx+<+， 则⎰⎰+<+1010)1ln(11dx x dx x ．例2.估计积分1214xe ⎰的值.解 当]21,41[∈x 时, x y =单增, x y arcsin=单增, u e y =是单增,所以x xe x f y arcsin )(==在]21,41[也是单增的,因此)21()()41(f x f f <<,由641111(),()4422f e f e ππ==，得 6411()42e f x e ππ<<，同时积分得42141681)(161ππe dx x f e <<⎰. 例3.设)(x f 在a x =处连续,求极限ax dt t f xaax -⎰→)(lim．分析 x a →时，分子趋向()aaf t dt ⎰（=0），所以是型极限，一般对变上限积分很常用“(())()xaf t dt f x '=⎰”这种运算方式，所以很自然想到用洛必达法则求解.解 这是型未定式，用洛必达法则求解. 原式=)(1)(lim)'())((lim'a af x xf a x dt t tf ax xa ax ==-→→⎰.134 例 4. 设)(x f 在 ],[b a 上连续,且)(x f >0,证明：方程⎰⎰=+xaxbdt t f dt t f 0)(1)( 在区间),(b a 内恰有一个根.分析 证明根的存在可以考虑零点定理：连续函数的端点函数值符号相反则函数至少有一个零点（即函数值为0的点），如果函数是单调函数，则只能有一次穿过x 轴.本例中出现变上限积分，一般要用到它的导数，注意变上限积分函数的自变量由变上限确定.证 设 )(x F =⎰⎰+xaxbdt t f dt t f )(1)(,由于)(x f 连续, )(x f >0,则)(1x f 连续,所以)(x F 在],[b a 上也连续.又因为11()0,()()0()()ab b b a a F a dt dt F b f t dt f t f t ==-<=>⎰⎰⎰，由零点定理可知, )(x F =0在),(b a 内至少有一个根.又.0)(1)()('>+=x f x f x F 则)(x F 在],[b a 上单增，()0F x =在 ],[b a 上最多有一个根,由上述证明可知：)(x F 在),(b a 内恰好有一个根.例5. 计算下列积分 (1)⎰94sin dx xx ； (2)⎰2052sin cos πxdx x ；(3)⎰-adx x a x222(a >0)； (4) ⎰---1221x x dx ；(5)⎰-+1)1ln(e dx x ； (6)⎰-+223)cos (sin ππdx x x .分析 （1）题出现了复合函数和其中间变量的导数，比较明显是用凑微分法；另外也项，可以尝试第二换元法.（2）题先用倍角公式化简后明显是用凑微分法的情形.（32xdx -的组成，所以用第二换元法的三角代换法．（4）题同（3）题，另外注意到和(arcsin )x '=.（5）题是幂函数乘对数函数的积分，显然用分部积分．（6）题的上下限是对称区间，根据奇偶函数在对称区间的积分来做.解:(1)法一:,21x d dx x=⎰⎰-=-==949494)3cos 2(cos 2cos 2sin 2sin xx d x dx xx .法二:(用第二换元法). 令,2,,2tdt dx t x x t === 当x =4时, t =2;当x =9时t =3,则93332422sin 22sin 2cos 2(cos 2cos3)t tdt tdt tt ===-=-⎰⎰⎰.(2)原式=2⎰⎰=-=-=2020276672cos 72cos cos 2sin cos πππx x xd xdx x .135(3)令tdt a dx t t a x cos ),20(,sin =≤≤=π,当x =0时, t =0;当x =a 时, t =2π,则22422220(sin )(cos )(cos )sin cos axa t a t a t dt at tdt ππ==⎰⎰⎰4422201cos 4sin 2442a a t tdt dt ππ-==⎰⎰4420sin 4()8416a t a t ππ=-=.(4)法一:用第二换元积分法,令sec ,sec tan x t dx t tdt ==，当2-=x 时,π32=t ;当1-=x 时, t =π,则⎰⎰⎰---=-=-=-12323223)1()tan (sec tan sec 1πππππdt dt t t t t x x dx . 法二:运用恒等变形和凑微分法. 当[2,1],x ∈--x =-1()x'==,令1u x =，则1121/----=⎰⎰11/2arcsin ()263u πππ--==---=-. (5)1111ln(1)ln(1)(1)[(1)ln(1)](1)ln(1)e e e e x dx x d x x x x d x ----+=++=++-++⎰⎰⎰11001(1)11e e e x dx e x x --=-+=-=+⎰ . (6)积分区间关于点对称, x 3sin 是奇函数,x 3cos 是偶函数.原式=/2/232/2/2sin cos 02cos 2xdx xdx xdx πππππ--+=+=⎰⎰⎰.例6.求证(sin )(sin )2xf x dx f x dx πππ=⎰⎰．分析 等式两边被积函数均含有)(sin x f ,注意到sin()sin t t π-=，如果t x -=π，其上下限互换了，并注意到定积分与积分变量用什么符号无关.证 令t x -=π，,dt dx -=,当0=x 时, t =π;当x =π时, t =0.00(sin )()(sin())()()(sin )xf x dx t f t dt t f t dt ππππππ=---=--⎰⎰⎰=()(sin )(sin )(sin )t f t dt f t dt tf t dt πππππ-=-⎰⎰⎰,而定积分与积分变量无关,得⎰⎰=ππ00)(sin )(sin dx x xf dt t tf ，整理得⎰⎰=πππ)(sin 2)(sin dx x f dx x xf .例7.计算⎰∞-0sin xdx e x ．136 分析 被积函数的指数函数乘正弦函数，两次同型的分部积分就可以解出原函数．本题是广义积分，其实就是先求定积分，然后取上限或下限的极限.解:由不定积分⎰⎰---+-=xdxe x e xdx e x x x cos sin sin =dx x e x e x e xx x )sin (cos sin -+-----⎰，则⎰++-=--c x x e dx ex x)cos (sin 21sin ,⎰⎰∞-∞→-=00sin lim sin b xb x xdx e xdx e . 则 0lim[(/2)(sin cos )]x bb e x x -→∞-+=2/1)2/12cos sin (lim =++-∞→b b eb b 则⎰∞-0sin xdx e x 收敛,其值为1/2.例8.求曲线24x y -=与直线x =4, x 轴, y 轴在区间[0,4]上围成图形的面积S . 解S =42424222330224(4)(4)(4(34)16x dx x dx x dx x x x x -=-+-=-+-=⎰⎰⎰.例9.求由曲线θ2cos 22=r 所围成图形在r =1内的面积.分析 本题没有明确指出极坐标下θ的变化范围，那么肯定要根据已知条件找出来，注意2r >0. 题意是求两个图形围成的图形面积，而r =1是一个半径为1的圆，它和曲线一定要相交，所以首先要求出交点，从而确定积分的限.解 由 θ2cos 22=r 0≥ ,则 cos20θ≥,2,2244ππππθθ-≤≤-≤≤.令 {22cos21r r θ==，得6πθ±= ,交点(1,6π±).由于对称性,先计算第一象限内的部分.当6/0πθ<<时, r =1 ,阴影部分面积⎰⎰===660211212121πππθθd d r A ；当46πθπ<<时,,2cos 22θ=r 阴影部分的面积为2442661112cos 2(1222A r d d ππππθθθ===⎰⎰323)(421-+=+=πA A A .例10.求由曲线22x y -=与直线0),0(=≥=x x x y . 围成的平面图形绕x 轴旋转而成的旋转体体积.分析 两曲线围成图形的旋转体体积可以看成大的旋转体去掉小的旋转体，曲线绕x 轴旋转，任意点x 处的截面半径是()r y f x ==,旋转体体积微元是22()y dx f x dx ππ=.解 解方程组{22y xy x ==-且x 0≥,得x =1.则所求旋转体的体积为111222240(2)(45)x V x dx x dx x x dx πππ=--=-+⎰⎰⎰137=π513058(4)23515x x x π-+=例11.自地面垂直向上发射火箭,火箭质量为m , 试计算将火箭发射到距离地面高度为h 处所做的功.解:设地球质量M ,半径为R ,坐标原点在地心,地球对于r 点处火箭的引力大小为2rMmGf = (r 是地心到火箭的距离) ． 火箭从r 处到dr r +处. 引力近似看成不变,为2)(rMmG r f =, 则功元素为dr r f dW )(=，2111()()()R R R R RRRRhhhhMm W dW f r dr Gdr GMm GMm r rR R h++++====-=-+⎰⎰⎰．§5.4 教材习题选解习题 5-11、判断题（1）定积分⎰ba x f )(由被积函数)(x f 与积分区间],[b a 确定． （√）（2）定积分⎰b a dx x f )(是x 的函数． （×） （3）若⎰=b adx x f 0)(，则0)(=x f ． （×）（4）定积分⎰badx x f )(在几何上表示相应曲边梯形面积的代数和． （√）2、选择题（根据右图（见教材P122图）写出答案）： （1）⎰=bdx x f 0)(（B ）；（A ）21A A +； （B ）21A A -； （C ）12A A +； （D ）231A A A -+． （2）⎰=dcC dx x f )()(；（A ）32A A +； （B ）32A A -； （C ）23A A -； （D ）213A A A -+． （3）⎰=d dx x f 0)(（C ）．（A ）321A A A ++；（B ）321A A A -+；（C ）321A A A +-；（D ）213A A A +-．习题 5-21、判断题 （1）⎰⎰=2112)()(dx x f dx x f ；（×）138 （2）当c x f =)(时，⎰⎰+=11)()(a adx x f dx x f ；（√）（3）⎰⎰=babadx x f k dx x kf )()(只对非零常数k 成立；（×）（4）⎰⎰⎰±=±bababadx x f k dx x f k dx x f k x f k )()()]()([22112211；（√）(5)⎰⎰⎰--+=ππππππ2339929sin sin sin xdx xdx xdx ． (√)2、已知⎰=10341dx x ，⎰=10231dx x ，⎰=1021xdx ，⎰=201cos πxdx ，⎰=201sin πxdx ，求定积分：（1）130(421)x x dx ++⎰；（2）120(2)x dx +⎰；（3）11(3)3x dx +⎰； （4）130(1)x dx +⎰； （5）220sin 2x dx π⎰； （6）20(sin cos )a x b x dx π+⎰．解 （1）⎰⎰⎰⎰=+⨯+⨯=++=++101010103331212414124)124(dx xdx dx x dx x x ；（2）⎰⎰⎰⎰⎰=+⨯+=++=++=+1010*******2231642143144)44()2(dx xdx dx x dx x x dx x ； （3）⎰⎰⎰=+=⨯+⨯=+=+101010611629131213313)313(dx xdx dx x ；（4）⎰⎰⎰⎰⎰⎰+++=+++=+10101010123231333)133()1(dx xdx dx x dx x dx x x x dx x419121331341=+⨯+⨯+=； （5）2222200001cos 11111sin cos (2)22222224x x dx dx dx xdx ππππππ-==-=⨯-=-⎰⎰⎰⎰； （6）⎰⎰⎰+=⨯+⨯=+=+2020211cos sin )cos sin (πππb a b a xdx b xdx a dx x b x a ．3、设)(x f 和)(x g 在],[b a 上连续，且)()(0x g x f ≤≤试用定积分的几何意义说明⎰⎰≤babadx x g dx x f )()(．解 令)()()(x f x g x h -=，则在],[b a 上，≥)(x h 0，()0b ah x dx ∴≥⎰，即⎰⎰⎰≥-=-b a b a badx x f dx x g dx x f x g 0)()())()((，()()bbaaf x dxg x dx ≤⎰⎰．4、用第3题的结论比较定积分的大小： （1）⎰21xdx 与⎰212dx x ；（2）⎰43ln xdx 与⎰432)(ln dx x ；（3）⎰20πxdx 与⎰20sin πxdx ；（4）⎰10sin xdx 与⎰12sin xdx ．139解（1） 在[1，2]上，x x >2，⎰⎰<∴21212dx x xdx ．(2) 在[3，4]上，ln 1x >，知2ln (ln )x x <∴⎰43ln xdx <⎰432)(ln dx x ．(3) 在]20[π，上，x x x f sin )(-=，'()1cos 0f x x =-≥，即()f x 在]2,0[π是增函数，显然在]20[π，上，当0=x 时，)(x f 取到最小值0，即在]20[π，上0sin )(≥-=x x x f ，有sin x x ≤，则220sin xdx xdx ππ>⎰⎰．（4） 在[0，1]上，0sin 1x <<，2sin sin x x >⎰⎰>∴1012sin sin xdx xdx ．习题 5-31、判断题 （1）当⎰=Φxadt t f x )()(时，)()('x f x =Φ；（√）（2）对任意函数)(x f 有⎰-=baa Fb F dx x f )()()(；（×）（3）⎰=--122)11(πdx x；（×）（4）0sin 20=⎰kxdx π． （√）2、计算定积分（2）)0()13(211>+-⎰+a dx x x x a ；（3）⎰+2142)1(dx xx ；（4）4dx +⎰； (5)⎰+33121x dx ； (6)⎰--212121xdx ； (7)⎰>+a a x a dx 3022)0(； (8)⎰-4221x dx； (9)⎰-1024xdx ； (10)⎰-+++11241133dx x x x ； （11）⎰23sin πxdx ； （12）dx x |sin |20⎰π；（13）⎩⎨⎧>-≤=1,121,)(2x x x x x f ，求⎰20)(dx x f ； （14）⎰+π0)cos 3sin 2(dx x x ； （15）⎰402tan πxdx ；（16）⎰++212123dx xx x ； （17）⎰+π02)2cos (dx xe x ．140 解（2）1211(3)a x x dx x +-+⎰1123|)|ln 2(++-=a x x x0211)1ln(2)1()1(23-+-+++-+=a a a)1ln(22523++++=a a a a ．(3) ⎰+2142)1(dx x x 8212463)3131(3183138)3131(2133==--⨯-=-=-x x ．(4) ⎰⎰+=+=+94942232194)2132()()1(x x dx x x dx x x)1621832()81212732(⨯+⨯-⨯+⨯= 6145621110)8316()28118(=+=+-⨯=．(5) ⎰+33121xdx663arctan 331πππ=-==x ．(6)⎰--212121x dx 3)6(6arcsin 2121πππ=--==-x． (7)220dx a x +aa a xaa 3031arctan130ππ=-⋅==． (8)⎰-4221x dx 5ln 213ln 31ln 2153ln 21|11|ln 2142-=-=+-=x x ． (9) ⎰-1024xdx60arcsin 21arcsin 2arcsin 10π=-==x ． (10) ⎰-+++11241133dx x x x ⎰-++++-+=112222143)1(3)1(3dx x x x x x ⎰⎰⎰--+++++=1111222141)1(23x dx x x d dx 1111211113arctan 4)1ln(233----++-=x x x x 2604[()]2444πππ=-++--=-．(11)⎰23sin πxdx⎰=---=-=-=2020203232)10()10(31cos cos 31)(cos )1(cos πππx x x d x ．141(12)dx x |sin |20⎰π⎰⎰+-=-=ππππππ0202cos cos sin sin xx xdx xdx4)11()11(=+++=．(13) ⎰⎰⎰=-+=-+=-+=21212121032312)02(31)(3)12()(x x x dx x dx x dx x f ．(14)⎰+π)cos 3sin 2(dx x x ⎰⎰+-=+=ππππ0sin 3cos 2cos 3sin 2x x xdx xdx4)00(3)11(2=-++=(15)⎰402tan πxdx ⎰-=-=-=4040241)(tan )1(sec οππx x dx x ．(16)⎰++212123dx xxx 42121)2t t t dt =++)13253(2)222322453(2)3253(22135++-+⋅+⋅=++=t t t1568215142-=． (17) ⎰+π02)2cos (dx x e x ⎰⎰++=ππ002cos 1dx x dx e x 12)00(21)02()1(sin 2121000-+=-+-+-=++=πππππππe e x x e x．3、设k 为正整数，证明：（1）sin 0kxdx ππ-=⎰；（2）⎰-=ππ0cos kxdx ．证明 ：（1）⎰⎰---=---=-==ππππππππ0))cos((cos 1cos 1)(sin 1sin k k k kx k kx kxd k kxdx ； （2）⎰⎰---=--===ππππππππ0))sin((sin 1sin 1)(cos 1cos k k k kx k kx kxd k kxdx ．4、设某公司拟在市场推出一种新产品，据市场预测，产品最终可占有全国市场的4%，即每年可销售480万元，产品刚上市时大家陌生，故开始时达不到预测数，若收益函数变化率])1(11[480)('3+-=t t R （万元/年），问第二年的收益为多少？第三年呢？ 解 第二年的收益为：⎰⎰+-=21213])1(11[480)('dt t dt t R32446]4121191212[480])1(121[480212=⋅--⋅+=+⋅+=t t （万）， 第三年的收益为：142 ⎰⎰+-=32323])1(11[480)('dt t dt t R 31468]91212161213[480])1(121[480212=⋅--⋅+=+⋅+=t t （万）．习题 5-41、判断题：（1）定积分换元时要交换上、下限；（×）（2）⎰-=++2232110)2)(cos 1(ππdx x x x ；（√） （3）222sin 4cos x u udu π=⎰⎰；（√） （4）dx xdx x e e +-=+⎰⎰--11)1ln(11；（×） （5）⎰-=--124)1(πdx x ． （√）2、计算定积分（1）⎰+2024t dt； （2）⎰+10431dx x x ； （3）dt t t ⎰-211； （4）31e ⎰； （5）21211cos dt t tππ⎰； （6）⎰203cos sin πxdx x ； （7）⎰+ωπϕω02)(sin dt t ； （8）⎰-222cos cos ππxdx x ； （9）222)1(x xdx+⎰； （10）⎰-121dx x ； （11）⎰>-2022)0(a a xa dx．解(1)⎰+224t dt ⎰⎰===40402821sec 4)tan 2(tan 2πππdu u u d u t ． (2) ⎰+10431dx x x ⎰=+=++=1014442ln 41)1ln(411)1(41x x x d ． (3) dt tt ⎰-21121122220011(1)2111u u u d u du t u u u =+-+==+++⎰⎰ 22arctan 22)111(21010102π-=-=+-=⎰u u du u ．(4)31e⎰222221122221111111()2222t t t t t t d e t e dt dt tx etet e-----=⋅=====⋅⎰⎰⎰．143(5)22111cos dt t t ππ⎰2121111cos ()sin sin sin 12d t t t ππππππ=-=-=-=-⎰． (6)⎰203cos sin πxdx x ⎰=-===2204341)01(41sin 41)(sin sin ππxx xd ． (7)20sin ()tdt πωωϕ+⎰1cos 2()2tdt πωωϕ-+=⎰11cos 2()(2())24t t d t ππωωωϕωϕω=-++⎰ 011sin 2()[sin(22)sin 2]24242t πωπππωϕπϕϕωωωωω=-+=-+-=． (8) ⎰-222cos cos ππxdx x 222222sin 213sin 61)cos 3(cos 21ππππππ---+=+=⎰x x dx x x 32)11(21)11(61=++--=． (9) 2220)1(x xdx +⎰222201(1)(1)2x d x -=++⎰52)151(211121202=--=+-=x ． (10) ⎰-1021dx x ⎰⎰⎰+===202022022cos 1cos )(sin cos sin πππdu u udu u ud u x 42sin 414)2(2cos 4121202020πππππ=+=+=⎰u u ud u ． 969323 (11)20a ⎰⎰⎰===60606cos )sin (sin πππdu u a u a d ua x ． 3、计算定积分： （1）10xxe dx -⎰； （2）0sin t tdt π⎰； （3）120arcsin xdx ⎰；（4）1arctan x xdx ⎰； (5)⎰202cos πxdx e x ； (6)⎰π2sin xdx x ．解(1) 11111102()1xx xx xxe dx xdx e xee dx e ee ------=-=-+=--=-⎰⎰⎰；(2)00sin (cos )cos cos sin t tdt td t t ttdt tπππππππ=-=-+=+=⎰⎰⎰．(3)111122220001arcsin arcsin (arcsin )26xdx x xxd x π=-=⋅-⎰⎰⎰112222011(1)(1)1122122122x d x πππ-=++-=+⋅+-⎰．144 (4) 211112220000111arctan arctan (arctan )22821x dx x xdx x x x d x x π=-=-+⎰⎰⎰ 112001111(1)[arctan )]8218242dx x x x πππ=--=--=-+⎰． (5)⎰22cos πxdx e x ⎰⎰-==202022022)(sin sin )(sin πππx x x e xd x e x d e⎰⎰⎰-+=+=-=202020220222)(cos 2cos 2)(cos 2sin 2πππππππx xxxe xd x e e x d e e xdx e e22024cos x e e xdx ππ=--⎰，⎰-=∴202)2(51cos πx x e xdx e ． (6)⎰π2sin xdx x ⎰⎰+-=-=πππ22cos 2cos )(cos xdx x x x x d x222202(sin )2sin 2sin 2cos 4xd x x xxdx xππππππππ=+=+-=+=-⎰⎰．4、求定积分（1）⎰--+12511x dx ；（2）⎰-10221dt t t ；（3）⎰414ln dx xx ；（4）11ln e x dx x +⎰；（5）⎰-ππxdx x 34sin ；（6）⎰-+11231)1cos (dx x x ．解(1) ⎰--+12511x dx 6ln 51)1ln 6(ln 51|511|ln 51511)511(511212=-=+=++=----⎰x x x d ．(2) ⎰-1221dt t t ⎰⎰⋅=⋅=202022)cos (sin )(sin cos sin sin ππdu u u u ud u u t 222220000111cos 411sin 2cos 444288u udu du u udu ππππ-===-⎰⎰⎰201sin 4163216u πππ=-=． (3) ⎰414ln dx xx 2222221111ln 1()ln ln 4t d t tdt t t t dt t t ==-⎰⎰ 12ln 22ln 221-=-=t ．(4) 11ln ex dx x +⎰2211113(1ln )(1ln )(1ln )[(11)1]222e e x d x x =++=+=+-=⎰．145(5) ⎰-ππxdx x 34sin 0=（奇函数）．(6)⎰-+11231)1cos (dx x x ⎰⎰⎰--=+=+=11111231220)cos (dx dx dx x x （奇函数）． 5、证明在区间],[a a -上，若)(x f 为偶函数，则⎰⎰-=aaadx x f dx x f 0)(2)(．证明00()()()aa a af x dx f x dx f x dx --=+⎰⎰⎰，对0()()af x d x -⎰，令x u =-，有00()()()()()()()()()()aaaaaf x d x f u d u f u d u f u d u f u d u -=--=-=-=⎰⎰⎰⎰⎰，又因为积分与变量形式无关，知()()()()aaf u d u f x d x =⎰⎰，从而⎰⎰-=aaadx x f dx x f 0)(2)(．6、设k 为自然数，试证： （1）2cos kxdx πππ-=⎰；（2）2sin kxdx πππ-=⎰．证明 （1）⎰⎰⎰----+=+=ππππππππkxdx x dx kx kxdx 2cos 212122cos 1cos 2111cos 2(2)sin 2(00)444kxd kx kxk kkππππππππ--=+=+=+-=⎰． （2）21cos 211sin cos 2222kx kxdx dx xkxdx ππππππππ-----==-⎰⎰⎰ ⎰--=--=-=-=ππππππππ)00(412sin 41)2(2cos 41k kx k kx kxd k ．7、证明：⎰⎰>+=+11122)0(11x x x x dx x dx ． 证明 1211111112212211()1111111x t x x x x x d dx t t dt dt x t t t t==-=-+=+++⎰⎰⎰⎰ 11221111x xdt dx t x ==++⎰⎰．（积分与变量形式无关，只与积分上下限和函数有关）习题 5-51、某河床的横断面如下图所示（图形见教材P134），为了计算最大排洪量，需要计算它的横断面的面积，试根据图示的测量数据（单位：m ）用梯形法计算其横断面面积．解26.67277279.529.55.225.21.121.10(4)(36+++++++++++≈⎰dx x f146 )22.222.21.421.46.6++++++)2.21.46.6779.55.21.1(4+++++++= 6.145=（2m ）． 2、用矩形法，梯形法与抛物线法近似计算定积分⎰21xdx ，以求2ln 的近似值（取10=n ，被积函数值取四位小数）．解 取10=n ，分点为：10=x ，1.11=x ，2.12=x ，…，9.19=x ，210=x 且101=∆x矩形法：用外接矩形21(1 3.4595+2.7282)0.7187710x ≈+=⎰，或者用内接矩形211(0.5 3.4595+2.7282)0.6687710dx x ≈+=⎰梯形法：2111( 1.5000 3.4595+2.7282)0.6938102dx x ≈⨯+=⎰，抛物线法：211(1.50002 2.72824 3.4595)0.69316*5dx x ≈+⨯+⨯=⎰．习题 5-61、计算反常积分 （1）41x dx ⎰∞+；（2）dx e ax-+∞⎰0（0a >）；（3）⎰∞+a dx x x ln （0a >）；（4）⎰∞+∞-++222x x dx ； （5）⎰-121x xdx ；（6）⎰-e x x dx 12)(ln 1；（7）xdx e xsin 0-+∞⎰；（8）⎰242cos ππx dx ． 解(1)41x dx ⎰∞+31)1lim (3131331341=--=-==--+∞→∞+--∞+⎰b x dx x b ．147(2) dx eax-+∞⎰ae e a e aax d e a ab b axax 1)lim (11)(1000=--=-=--=-+∞→∞+--∞+⎰．(3) ⎰∞+adx x x ln +∞=-===+∞→∞+∞+⎰)ln ln lim (21ln 21)(ln ln 222a b x x xd b aa （发散）．(4) ⎰∞+∞-++222x x dx∞+∞-∞+∞-+=+++=⎰)1arctan(1)1()1(2x x x dlim arctan(1)lim arctan(1)a b a b →+∞→-∞=+-+πππ=--=)2(2．(5)⎰-121x xdx101)1(1lim 211)1(21201022=-+---=---=+→⎰εεxx d ． (6)⎰-ex x dx 12)(ln1101(ln )lim arcsin(ln )122ee x x εεππ+→-===-=⎰．(7)xdx e xsin 0-+∞⎰(cos )cos cos ()xxx e d x e xxd e +∞+∞+∞---=-=-+⎰⎰00lim cos cos 0(sin )a x a e a e e d x +∞--→+∞=-+-⎰01sin sin xx e xxde +∞+∞--=-+⎰xdx e e b e x bb sin 0sin sin lim 10-∞+-+∞→⎰-+-=xdx e x sin 10-+∞⎰-=，21sin 0=∴-∞+⎰xdx e x ． (8) ⎰242cos ππx dx 2242004sec lim tan lim tan()12xdx x πππεπεεπε++-→→===--=+∞⎰（发散）． 2、求分开数值为1C 的两个相反电荷所需要的能量，假定正负电荷开始相距1m ，将一个电荷移动至另一个电荷的无穷远处．解 设两个相反电荷的横坐标分别为0，1，则将2C 移至无穷远处所需能量为2221111()(lim ()1)a C k dx kC kC kC x xa+∞+∞→+∞=-=-+=⎰．习题 5-71、判断题（1）微元dx x f dA )(=是所求量A 在任意微小区间].[dx x x +上部分量A ∆的近似值；（√）148 （2）由曲线2x y =与3x y =围成图形面积为⎰-=13)(dx x x A ； （×）（3）由曲线3x y =与x y =在[0，1]上围成图形绕y 轴旋转所得旋转体体积⎰-=126)(dy y y V ππ； （√）（4）)(x f y =在任意微小区间],[dx x x +上的弧微分为21y ds '+=． （×） 2、将阴影部分的面表用定积分表示出来（图形见教材P144）： 解 （4）令223x x =+，有(1)(3)0x x +-=，∴两曲线交点横坐标为1-=a ，3=b ，∴ ⎰--+=312)32(dx x x A ．4、求由曲线围成图形的面积（1）xy 1=与直线x y =及2=x ；（2）x e y =，xe y -=与直线1=x ； （3）x y ln =，2ln =y ，7ln =y ，0=x ；（4）22,4y x x y =+=；（5）2x y =与直线x y =及x y 2=．解(1) ⎰-=---=-=-=212122ln 23)021(2ln 2|)|ln 2()1(x x dx x x A ．(2) 21)11(1)()(11-+=+-+=+=-=⎰--e e e e e e dx e e A xxxx(3) 由ln y x =，有yx e =，则⎰=-===7ln 2ln 7ln 2ln 527yy edy e A ．(4) 由242y y =-有2280y y +-=，即(2)(4)0y y -+=， 解得两曲线交点纵坐标为4-=a ，2=b ，从而2232244(4)(4)18226y y y A y dx y --=--=--=⎰．(5) 显然2x y =与x y =交点横坐标为0，1，2x y =与x y 2=交点横坐标为0，2，⎰⎰⎰⎰-+=-+-=1021102122)2()2()2(dx x x xdx dx x x dx x x A67)311()384(21)3(2213212=---+=-+=x x x ．5、求由曲线围成图形的面积： （1）θρcos 2=，0=θ，6πθ=；（2）)cos 1(2θρ+=a ，0=θ，πθ2=．解(1) 266001(2cos )(1cos 2)2A d d ππθθθθ==+⎰⎰66011sin 2262264ππππθθ=+=+⋅=+．149(2) θθθθθππd a d a A )cos cos 21(2)]cos 1(2[212202220++=+=⎰⎰ 2203cos 22(2cos )22a d πθθθ=++⎰ππθθθπ222026)003(2)42sin sin 223(2a a a =++=++=．6、求曲线围成图形绕指定轴旋转所得旋转体的体积：（1）042=+-y x ，0=x 及0=y ，绕x 轴；（2）42-=x y ，0=y 绕x 轴；（3）12222=+by a x ，绕x 轴；（4）x y =2，y x =2，绕y 轴；（5）x y sin =，x y cos =及x 轴上的线段]2,0[π绕x 轴旋转．解(1) 因为 dx x dV 2)42(+=π，所以3222222(24)4(44)4(24)3x V x dx x x dx x x πππ---=+=++=++⎰⎰8324(88)33ππ=--+-=．(2) 因为 dx x dV 22)4(-=π，所以dx x x V )168(2422+-=⎰-π2235)16385(-+-=x x x ππ15512=．(3) 因为 2222(1)x dV y dx b dx aππ==-，所以a aa a x a xb dx a x b V ---=-=⎰)31()1(322222ππ234ab π=．(4) 因为 dy y y dy y dy y dV )()()(4222-=-=πππ，所以2514013()()02510y y V y y dy πππ=-=-=⎰．(5) 因为 xdx dV 2sin π=，]4,0[π∈x ，xdx dV 2cos π=，]2,4[ππ∈x ，224204sin cos V xdx xdx πππππ=+⎰⎰4(1cos 2)2x dx ππ=-⎰)2(4)2cos 1(224-=++⎰πππππdx x ．7、有一铸铁件，它是由三条线：抛物线2110y x =，11012+=x y 与直线10=y 围成的图形，绕y 轴旋转而成的旋转体，算出它的重量（长度单位是厘米(cm)，铁的比重是7.8g/cm 3）．。