钢结构第4章(带答案)
- 格式:doc
- 大小:31.00 KB
- 文档页数:1

P1084.1解: 示意图要画焊缝承受的剪力V=F=270kN ;弯矩M=Fe=270⨯300=81kN.mI x =[0.8⨯(38-2⨯0.8)3]/12+[(15-2)⨯1⨯19.52]⨯2=13102cm 4=腹板A e =0.8⨯(38-2⨯0.8)=29.12 cm 2截面最大正应力σmax =M/W= 81⨯106⨯200/13102⨯104=123.65 N/mm 2≤f t w =185N/mm 2剪力全部由腹板承担τ=V/A w =270⨯103/2912≤=92.72 N/mm 2 =f v w =125N/mm 2腹板边缘处”1”的应力σ1=(M/W)(190/200)=123.65(190/200)=210.19=117.47腹板边缘处的折算应力应满足1.1w zs t f σ=≤=2≤1.1f t w =203.5N/mm 2焊缝连接部位满足要求4.2解:(1) 角钢与节点板的连接焊缝“A ”承受轴力N=420kN连接为不等边角钢长肢相连 题意是两侧焊肢背分配的力N 1=0.65 ⨯420=273 kN肢背分配的力N 2=0.35 ⨯420=147 kNh fmin =1.5(t max )1/2=1.5(10)1/2=4.74mmh fmax =1.2(t min )=1.2(6)=7.2mm取h f =6mm肢背需要的焊缝长度l w1=273⨯103/(2⨯0.7⨯6⨯160)+2⨯6=203.12+12=215.13mm肢尖需要的焊缝长度l w2=147⨯103/(2⨯0.7⨯6⨯160)+2⨯6=109.38+12=121.38mm端部绕角焊2h f 时,应加h f (书中未加)取肢背的焊缝长度l w1=220mm ;肢尖的焊缝长度l w2=125mm 。
l wmax =60h f =360mm ;l wmin =8h f =48mm ;焊缝“A ”满足要求4.3解:节点板与端板间的连接焊缝“B ”承受拉力N 对焊缝“B ”有偏心,焊缝“B ”承受拉力N=(1.5/1.8) ⨯420=350kN ;剪力V=(1/1.8) ⨯420=233.33 kN ;弯矩M=350⨯50=17.5 kN.mh fmin =1.5(t max )1/2=1.5(20)1/2=6.71mmh fmax =1.2(t min )=1.2(10)=12mm焊缝“B ”h f =7mm焊缝“B ”A 点的力最大焊缝“B ”承受的剪应力τ=233.33⨯103/(2⨯0.7⨯7⨯386)=61.68 N/mm 2焊缝“B ”承受的最大正应力σ=N/Ae+M/W=350⨯103/(2⨯0.7⨯7⨯386)+17.5⨯106⨯200/(2⨯0.7⨯7⨯3863/12)=92.52+71.91 =164.43 N/mm 2验算焊缝“B ”的强度=148.19 N/mm 2<f f w 焊缝“B ”满足要求。

第四章4. 1有哪些因素影响轴心受压杆件的稳定系数? 答:①残余应力对稳定系数的影响;②构件的除弯曲对轴心受压构件稳定性的影响; ③构件初偏心对轴心轴心受压构件稳定性的影响; ④杆端约束对轴心受压构件稳定性的影响;4.3影响梁整体稳定性的因素有哪些?提高梁稳定性的措施有哪些? 答:主要影响因素:①梁的侧向抗弯刚度y EI 、抗扭刚度t GI 和抗翘曲刚度w EI 愈大,梁越稳定; ②梁的跨度l 愈小,梁的整体稳定越好;③对工字形截面,当荷载作用在上翼缘是易失稳,作用在下翼缘是不易失稳; ④梁支撑对位移约束程度越大,越不易失稳; 采取措施:①增大梁的侧向抗弯刚度,抗扭刚度和抗翘曲刚度; ②增加梁的侧向支撑点,以减小跨度;③放宽梁的受压上翼缘,或者使上翼缘与其他构件相互连接。
4.6简述压弯构件中等效弯矩系数mx β的意义。
答:在平面内稳定的计算中,等效弯矩系数mx β可以把各种荷载作用的弯矩分布形式转换为均匀守弯来看待。
4.10验算图示焊接工字形截面轴心受压构件的稳定性。
钢材为Q235钢,翼缘为火焰切割边,沿两个主轴平面的支撑条件及截面尺寸如图所示。
已知构件承受的轴心压力为N =1500kN 。
解:由支承条件可知0x 12m l =,0y 4m l =23364x 1150012850025012225012476.610mm 12122I +⎛⎫=⨯⨯+⨯⨯+⨯⨯⨯=⨯ ⎪⎝⎭3364y 5001821225031.310mm 1212I =⨯+⨯⨯⨯=⨯2225012500810000mm A =⨯⨯+⨯=x 21.8cm i ===,y 5.6cm i ===0x x x 12005521.8l i λ===,0y y y 40071.45.6l i λ===,翼缘为火焰切割边的焊接工字钢对两个主轴均为b 类截面,故按y λ查表得=0.747ϕ整体稳定验算:3150010200.8MPa 215MPa 0.74710000N f A ϕ⨯==<=⨯,稳定性满足要求。
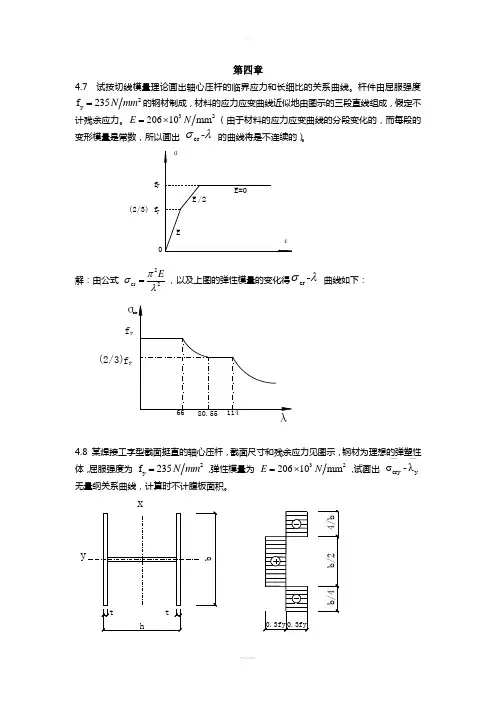
第四章4.7 试按切线模量理论画出轴心压杆的临界应力和长细比的关系曲线。
杆件由屈服强度2y f 235N mm =的钢材制成,材料的应力应变曲线近似地由图示的三段直线组成,假定不计残余应力。
320610mm E N =⨯2(由于材料的应力应变曲线的分段变化的,而每段的变形模量是常数,所以画出 cr -σλ 的曲线将是不连续的)。
解:由公式 2cr 2Eπσλ=,以及上图的弹性模量的变化得cr -σλ 曲线如下:4.8 某焊接工字型截面挺直的轴心压杆,截面尺寸和残余应力见图示,钢材为理想的弹塑性体,屈服强度为 2y f 235N mm =,弹性模量为 320610mm E N =⨯2,试画出 cry y σ-λ——无量纲关系曲线,计算时不计腹板面积。
f yyf (2/3)f y(2/3)f yx解:当 cr 0.30.7y y y f f f σ≤-=, 构件在弹性状态屈曲;当 cr 0.30.7y y y f f f σ>-=时,构件在弹塑性状态屈曲。
因此,屈曲时的截面应力分布如图全截面对y 轴的惯性矩 3212y I tb =,弹性区面积的惯性矩 ()3212ey I t kb =()322232232212212ey cryy y y yI t kb E E E k I tb πππσλλλ=⨯=⨯= 截面的平均应力 2220.50.6(10.3)2y ycr y btf kbt kf k f btσ-⨯⨯==-二者合并得cry y σ-λ——的关系式cry cry342cry σ(0.0273)σ3σ10y λ+-+-= 画图如下4.10 验算图示焊接工字型截面轴心受压构件的稳定性。
钢材为Q235钢,翼缘为火焰切割边,沿两个主轴平面的支撑条件及截面尺寸如图所示。
已知构件承受的轴心压力为0.6f yfyλσ0.20.40.60.81.0cryN=1500KN 。
解:已知 N=1500KN ,由支撑体系知对截面强轴弯曲的计算长度 ox =1200cm l ,对弱轴的计算长度 oy =400cm l 。
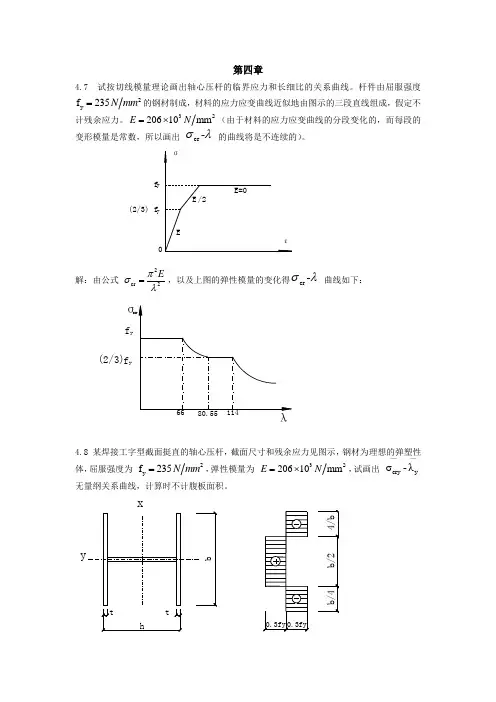
第四章4.7 试按切线模量理论画出轴心压杆的临界应力和长细比的关系曲线。
杆件由屈服强度2y f 235N mm =的钢材制成,材料的应力应变曲线近似地由图示的三段直线组成,假定不计残余应力。
320610mm E N =⨯2(由于材料的应力应变曲线的分段变化的,而每段的变形模量是常数,所以画出 cr -σλ 的曲线将是不连续的)。
解:由公式 2cr 2Eπσλ=,以及上图的弹性模量的变化得cr -σλ 曲线如下:4.8 某焊接工字型截面挺直的轴心压杆,截面尺寸和残余应力见图示,钢材为理想的弹塑性体,屈服强度为 2y f 235N mm =,弹性模量为 320610mm E N =⨯2,试画出 cryy σ-λ——无量纲关系曲线,计算时不计腹板面积。
f yyf (2/3)f y(2/3)f yx解:当 cr 0.30.7y y y f f f σ≤-=, 构件在弹性状态屈曲;当 cr 0.30.7y y y f f f σ>-=时,构件在弹塑性状态屈曲。
因此,屈曲时的截面应力分布如图全截面对y 轴的惯性矩 3212y I tb =,弹性区面积的惯性矩 ()3212ey I t kb =()322232232212212ey cryy y y yI t kb E E E k I tb πππσλλλ=⨯=⨯= 截面的平均应力 2220.50.6(10.3)2y ycr y btf kbt kf k f btσ-⨯⨯==-二者合并得cry y σ-λ——的关系式cry cry342cry σ(0.0273)σ3σ10y λ+-+-= 画图如下4.10 验算图示焊接工字型截面轴心受压构件的稳定性。
钢材为Q235钢,翼缘为火焰切割边,沿两个主轴平面的支撑条件及截面尺寸如图所示。
已知构件承受的轴心压力为N=1500KN 。
0.6f yfyλσ0.20.40.60.81.0cry解:已知 N=1500KN ,由支撑体系知对截面强轴弯曲的计算长度 ox =1200cm l ,对弱轴的计算长度 oy =400cm l 。


第4章 习题一、单选题1、发生弯扭屈曲的理想轴心受压构件截面形式为( )A.双轴对称工字形截面B.单角钢截面C.H 型钢截面D.箱形截面2、梁整体失稳的方式为( )A.弯曲失稳B.剪切失稳C.扭转失稳D.弯扭失稳4、图示压弯构件弯矩作用平面外稳定计算公式f W M A N x b x tx y ≤ϕβ+ϕ中,tx β的取值是( A ) 所考虑构件段无横向荷载作用时,|M ||M |,M /M 35.065.01212tx <+=β所考虑构件段无端弯矩但有横向荷载作用时0.1tx =β悬臂构件0.1tx =βD.EX tx N /N 2.01-=β5、对格构式轴压杆绕虚轴的整体稳定计算时,用换算长细比λox 代替λ,这是考虑() A.格构柱剪切变形的影响 B.格构柱弯曲变形的影响C.缀材剪切变形的影响D.缀材弯曲变形的影响6、实腹式偏心压杆在弯矩作用平面外的失稳是( )A.弯扭屈曲B.弯曲屈曲C.扭转屈曲D.局部屈曲7、梁受压翼缘的自由外伸宽度b1/t ≤y f 23515是为了保证翼缘板的( )A.抗剪强度B.抗弯强度C.整体稳定D.局部稳定8、轴心受压杆设计公式A Nϕ≤f 中的ϕ为( )A.y k f σB.R k γσC.f kσ D.p k f σ9、通常轴心受压缀条式格构柱的横缀条不受力,但一般仍设置。
其理由是( )A.起构造作用B.可以加强柱的整体抗弯刚度C.对单肢稳定起作用D.以上三种原因都有10、实腹式偏心压杆弯矩作用平面外的整体稳定计算公式f W M A N x 1b x tx y ≤ϕβη+ϕ中,W1x 应取( )A.弯矩作用平面内最小受压纤维的毛截面模量B.弯矩作用平面外最小受压纤维的毛截面模量C.弯矩作用平面内最大受压纤维的毛截面模量D.弯矩作用平面外最大受压纤维的毛截面模量11、当仅讨论截面形式对轴心受压杆的失稳影响时,一般来说,图示的四种截面中最易发生扭转失稳的截面为( B )12、如图所示焊接组合工字形轴心压杆,一般情况下(当板件不是很薄时)杆件的整体失稳形式是( )A.绕y 轴的弯扭失稳B.绕y 轴的弯曲失稳C.绕x 轴的弯曲失稳D.绕z 轴的扭转失稳13、某竖直向下均布荷载作用下的两端简支工字形钢梁,关于荷载作用位置对其整体稳定性的影响,叙述正确的是( )A.当均布荷载作用于上翼缘位置时稳定承载力较高B.当均布荷载作用于中和轴位置时稳定承载力较高C.当均布荷载作用于下翼缘位置时稳定承载力较高D.荷载作用位置与稳定承载力无关14、偏心受压构件稳定计算公式中的等效弯矩系数βmx 与下列哪项有关?( )A.端弯矩和横向荷载B.端弯矩和轴向荷载C.长细比和横向荷载D.长细比和轴向荷载15、单轴对称的轴心受压构件,当绕对称轴失稳时,其整体失稳形式通常是()A.弯曲失稳 B.扭转失稳C.弯扭失稳 D.塑性失稳16、某双轴对称截面的压弯构件承受如图所示不同工况的弯矩作用,图中所示的弯矩大小均相等,仅考虑弯矩作用平面内稳定性时,其轴向受压承载力最大的情况为()A.(a) B.(b)C.(c)D.(d)17、简支梁符合下列哪种条件时,可不必验算梁的整体稳定性?()A.有钢筋混凝土板密铺在梁的受压翼缘上,并与其牢固连接,能阻止受压翼缘的侧向位移时B.有钢筋混凝土板密铺在梁的受拉翼缘上,并与其牢固连接,能阻止受拉翼缘的侧向位移时C.除了梁端设置侧向支承点外,且在跨中有一个侧向支承点时D.除了梁端设置侧向支承点外,且在跨间有两个以上侧向支承点时18、关于残余应力对轴心受压构件承载力的影响,下列说法正确的是()A.残余应力对轴压构件的强度承载力无影响,但会降低其稳定承载力B.残余应力对轴压构件的稳定承载力无影响,但会降低其强度承载力C.残余应力对轴压构件的强度和稳定承载力均无影响D.残余应力会降低轴压构件的强度和稳定承载力19、某工字形截面钢梁在某固定集中荷载作用下局部压应力很大,无法满足局压验算要求时,可采用的最经济、有效的措施是()A.增加梁腹板厚度B.增加梁翼缘板厚度C.增设纵向加劲肋D.增设支承加劲肋20、对于单轴对称压弯构件,当弯矩作用在对称轴平面内,且使较大翼缘受压时,应补充验算fNNWMANExxxxmx≤'--)/25.11(22γβ,原因是()A.防止受压塑性区的开展而导致构件平面内失稳B.防止受拉塑性区的开展而导致构件平面内失稳C.防止受压塑性区的开展而导致构件平面外失稳D.防止受拉塑性区的开展而导致构件平面外失稳21、双肢格构式轴心受压柱,虚轴为x-x轴,实轴为y-y轴,确定两单肢间距离时应根据()A.强度条件B.=xλyλC.=x λoy λD.=ox λy λ22、梁采用Q235钢,梁受压翼缘的自由外伸宽度与其厚度之比即b1/t ≤13,是为了保证翼缘板的( )A.整体稳定B.局部稳定C.抗弯强度D.抗剪强度23、工字型截面组合梁,计算所得06.1b =ϕ,表明( )A.梁的刚度能满足要求 B .应用b ϕ'代替b ϕ验算梁的整体稳定C.梁的整体稳定能满足要求 D .梁不会发生强度破坏24、下图所示简支梁,除截面和荷载作用位置不同外,其它条件均相同,则以哪种情况的整体稳定性最好?( D )25、如图所示实腹式柱头,设置加劲肋的目的是( )A.提高柱腹板局部稳定B.提高柱的刚度C.传递梁的支座反力D.提高柱的承载力二、填空题1、工字形截面梁按弹性设计时,应使翼缘的宽厚比b1/t1≤ 15 。

4.1 验算由2∟63×5组成的水平放置的轴心拉杆的强度和长细比。
轴心拉力的设计值为270kN ,只承受静力作用,计算长度为3m 。
杆端有一排直径为20mm 的孔眼,用于螺栓承压型连接。
钢材为Q235钢。
如截面尺寸不够,应改用什麽角钢?计算时忽略连接偏心和杆件自重的影响。
解:拉杆2L63×5,查附表7.4单角钢毛面积为:6.14 cm 2故:22n cm 28.10228.1210205214.62A =-=⨯⨯⨯-⨯=-钢材Q235,2215mmN f =强度验算:22232156.2621028.1010270mm N f mm N A N n =>=⨯⨯==σ该拉杆强度不满足。
试改用2∟70×6单角钢毛面积为:8.16 cm 2故:221392240163262021016.82mm A n =-=⨯⨯-⨯⨯=强度验算:223215194139210270mm N f mm N A N n =<=⨯==σ强度满足要求。
静力作用只需验算竖向平面内的长细比,按一般建筑结构系杆考虑,容许长细比为400 (或按其他构件300、350); 由附表7.4cm i x 15.2=长细比验算:[]4005.13915.2300=<===λλx o i l长细比满足要求。
点评:1、实际设计应多方案,在满足要求的方案中选重量最轻的。
如果选用的规格是所有角钢规格中最轻的就是最优设计。
OK4.3 验算图示高强螺栓摩擦型连接的钢板净截面强度。
螺栓直径20mm ,孔径22mm ,钢材为Q235-A.F ,承受轴心拉力N=600kN (设计值)。
解:钢板厚度14mm ,拼接板厚度2×10mmQ235—A.F 查表得2mm N 215f =钢板最外列螺栓处:()224369243360142234080804014mm A n =-=⨯⨯-+++⨯=()n n 5.01N N 1-='==600(1-0.5×3/9)=500kN验算净截面强度:2232153.205243610500mm N f mm N A N n =<=⨯='=σ钢板净截面强度满足要求。
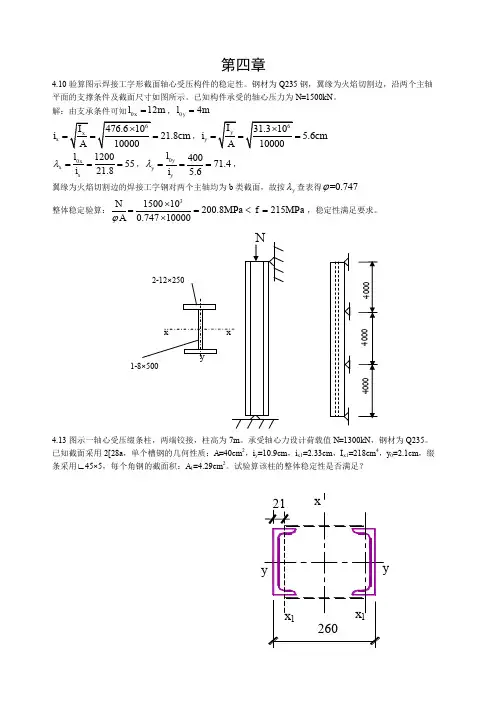
第四章4.10验算图示焊接工字形截面轴心受压构件的稳定性。
钢材为Q235钢,翼缘为火焰切割边,沿两个主轴平面的支撑条件及截面尺寸如图所示。
已知构件承受的轴心压力为N=1500kN。
解:由支承条件可知0x 12ml=,0y 4ml=x21.8cmi===,y5.6cmi===0xxx12005521.8liλ===,0yyy40071.45.6liλ===,翼缘为火焰切割边的焊接工字钢对两个主轴均为b类截面,故按yλ查表得=0.747ϕ整体稳定验算:3150010200.8MPa215MPa0.74710000NfAϕ⨯==<=⨯,稳定性满足要求。
4.13图示一轴心受压缀条柱,两端铰接,柱高为7m。
承受轴心力设计荷载值N=1300kN,钢材为Q235。
已知截面采用2[28a,单个槽钢的几何性质:A=40cm2,i y=10.9cm,i x1=2.33cm,I x1=218cm4,y0=2.1cm,缀条采用∟45×5,每个角钢的截面积:A1=4.29cm2。
试验算该柱的整体稳定性是否满足?解:柱为两端铰接,因此柱绕x 、y 轴的计算长度为:0x 0y 7m l l == 格构柱截面对两轴均为b 类截面,按长细比较大者验算整体稳定既可。
由0x 65.1λ=,b 类截面,查附表得0.779ϕ=,整体稳定验算:32130010208.6MPa 215MPa 0.77924010N f A ϕ⨯==<=⨯⨯⨯ 所以该轴心受压的格构柱整体稳定性满足要求。
4.15某压弯格构式缀条柱如图所示,两端铰接,柱高为8m 。
承受压力设计荷载值N =600kN ,弯矩100kN m M =⋅,缀条采用∟45×5,倾角为45°,钢材为Q235,试验算该柱的整体稳定性是否满足? 已知:I22a A=42cm 2,I x =3400cm 4,I y1=225cm 4; [22a A=31.8cm 2,I x =2394cm 4,I y2=158cm 4; ∟45×5 A 1=4.29cm 2。

第四章 格构式轴心受压构件一.填空和选择题1.格构式轴心受压构件的等稳定性的条件 y ox λλ= 。
2.对于缀板式格构柱,单肢不失稳的条件是 max 15.0λλ< ,且不大于40 。
3.缀条式格构柱的缀条设计时按 轴心受压 构件计算。
4.对于缀条式格构柱,单肢不失稳的条件是 max 17.0λλ< 。
5.格构式轴压构件绕虚轴的稳定计算采用了大于x λ的换算长细比ox λ是考虑(D )。
A 格构构件的整体稳定承载力高于同截面的实腹构件B 考虑强度降低的影响C 考虑单肢失稳对构件承载力的影响D 考虑剪切变形的影响6.为保证格构式构件单肢的稳定承载力,应(B )。
A 控制肢间距B 控制截面换算长细比C 控制单肢长细比D 控制构件计算长度7.格构式轴压柱等稳定的条件是(D )A .实轴计算长度等于虚轴计算长度B .实轴计算长度等于虚轴计算长度的2倍C .实轴长细比等于虚轴长细比D .实轴长细比等于虚轴换算长细比8.格构式柱中缀材的主要作用是(B )A 、保证单肢的稳定B 、承担杆件虚轴弯曲时产生的剪力C 、连接肢件D 、保证构件虚轴方向的稳定9.格构柱设置横隔的目的是( A )A 保证柱截面几何形状不变B 提高柱抗扭刚度C 传递必要的剪力D 上述三种都是10.由二槽钢组成的格构式轴压缀条柱,为提高虚轴方向的稳定承载力应(D )A .加大槽钢强度B .加大槽钢间距C .减小缀条截面积D .增大缀条与分肢的夹角二.简答题:1现行钢结构设计规范关于轴心压杆整体稳定设计如何考虑这些因素的影响?原因是什么?残余应力,初偏心,初弯曲,使得构件的整体稳定承载力下降。
2.格构式轴压柱应满足哪些要求,才能保证单肢不先于整体失稳?柱对实轴的长细比y λ和对虚轴的换算长细比ox λ均不得超过容许长细比[λ]:缀条柱的分肢长细比1λ<0.7m ax λ缀板柱的分肢长细比1λ<0.5m ax λ且不应大于403.格构柱绕虚轴的稳定设计为什么要采用换算长细比?格构式轴压柱绕虚轴失稳时,剪力主要由缀材分担,柱的剪切变形较大,剪力造成的附加绕曲影响不能忽视,故对虚轴失稳计算采用换算长细比。

钢结构第二版课后习题答案【篇一:钢结构基础(第二版)课后习题第四章答案】q235钢,翼缘为火焰切割边,沿两个主轴平面的支撑条件及截面尺寸如图所示。
已知构件承受的轴心压力为n=1500kn。
l?4m解:由支承条件可知l0x?12m,0y11?500?12?64ix??8?5003??250?123?2?250?12476.6?10 mm12122?? 50031iy??8?2??12?2503?31.3?106mm412122a?2?250?12?500?8?10000mmix??21.8cmiy5.6cm,l0y400l0x120071.4?x?55?y?i5.6ix21.8y,,2翼缘为火焰切割边的焊接工字钢对两个主轴均为b类截面,故按y查表得?=0.747n1500?103200.8mpa?f?215mpa整体稳定验算:?a0.747?10000,稳定性满足要求。
4.13图示一轴心受压缀条柱,两端铰接,柱高为7m。
承受轴心力设计荷载值n=1300kn,钢材为q235。
已知截面采用2[28a,单个槽钢的几何性质:a=40cm2,iy=10.9cm,ix1=2.33cm,解:柱为两端铰接,因此柱绕x、y轴的计算长度为:l0x?l0y?7m22b26??ix?2?ix1?a??y02?218?40??2.19940.8cm422l0y700l0x70064.263.1ix???11.1cmyxiy10.9ix11.10x格构柱截面对两轴均为b类截面,按长细比较大者验算整体稳定既可。
由?0x?65.1,b类截面,查附表得??0.779,65.1n1300?103208.6mpa?f?215mpa2整体稳定验算:?a0.779?2?40?10 所以该轴心受压的格构柱整体稳定性满足要求。
4.17焊接简支工字形梁如图所示,跨度为12m,跨中6m处梁上翼缘有简支侧向支撑,材料为q345钢。
集中荷载设计值为p=330kn,间接动力荷载,验算该梁的整体稳定是否满足要求。
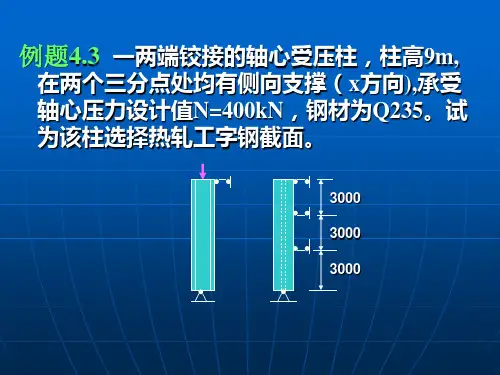
第四章4.7 试按切线模量理论画出轴心压杆的临界应力和长细比的关系曲线。
杆件由屈服强度2y f 235N mm =的钢材制成,材料的应力应变曲线近似地由图示的三段直线组成,假定不计残余应力。
320610mm E N =⨯2(由于材料的应力应变曲线的分段变化的,而每段的变形模量是常数,所以画出 cr -σλ 的曲线将是不连续的)。
解:由公式 2cr 2Eπσλ=,以及上图的弹性模量的变化得cr -σλ 曲线如下:4.8 某焊接工字型截面挺直的轴心压杆,截面尺寸和残余应力见图示,钢材为理想的弹塑性体,屈服强度为 2y f 235N mm =,弹性模量为 320610mm E N =⨯2,试画出 cryy σ-λ——无量纲关系曲线,计算时不计腹板面积。
f yyf (2/3)f y(2/3)f yx解:当 cr 0.30.7y y y f f f σ≤-=, 构件在弹性状态屈曲;当 cr 0.30.7y y y f f f σ>-=时,构件在弹塑性状态屈曲。
因此,屈曲时的截面应力分布如图全截面对y 轴的惯性矩 3212y I tb =,弹性区面积的惯性矩 ()3212ey I t kb =()322232232212212ey cryy y y yI t kb E E E k I tb πππσλλλ=⨯=⨯= 截面的平均应力 2220.50.6(10.3)2y ycr y btf kbt kf k f btσ-⨯⨯==-二者合并得cry y σ-λ——的关系式cry cry342cry σ(0.0273)σ3σ10y λ+-+-= 画图如下4.10 验算图示焊接工字型截面轴心受压构件的稳定性。
钢材为Q235钢,翼缘为火焰切割边,沿两个主轴平面的支撑条件及截面尺寸如图所示。
已知构件承受的轴心压力为N=1500KN 。
0.6f yfyλσ0.20.40.60.81.0cry解:已知 N=1500KN ,由支撑体系知对截面强轴弯曲的计算长度 ox =1200cm l ,对弱轴的计算长度 oy =400cm l 。
钢结构试题第4章习题第4章习题⼀、单选题1、发⽣弯扭屈曲的理想轴⼼受压构件截⾯形式为()A.双轴对称⼯字形截⾯B.单⾓钢截⾯C.H 型钢截⾯D.箱形截⾯2、梁整体失稳的⽅式为()A.弯曲失稳B.剪切失稳C.扭转失稳D.弯扭失稳4、图⽰压弯构件弯矩作⽤平⾯外稳定计算公式fW MA N x b x tx y ≤?β+?中,tx β的取值是( A)所考虑构件段⽆横向荷载作⽤时,|M ||M |,M /M 35.065.01212tx <+=β所考虑构件段⽆端弯矩但有横向荷载作⽤时0.1tx =β悬臂构件0.1tx =βD.EX tx N /N 2.01-=β5、对格构式轴压杆绕虚轴的整体稳定计算时,⽤换算长细⽐λox 代替λ,这是考虑( ) A.格构柱剪切变形的影响 B.格构柱弯曲变形的影响C.缀材剪切变形的影响D.缀材弯曲变形的影响6、实腹式偏⼼压杆在弯矩作⽤平⾯外的失稳是( )A.弯扭屈曲B.弯曲屈曲C.扭转屈曲D.局部屈曲7、梁受压翼缘的⾃由外伸宽度b1/t ≤y f 23515是为了保证翼缘板的( )A.抗剪强度B.抗弯强度C.整体稳定D.局部稳定8、轴⼼受压杆设计公式A N≤f 中的?为( )A.y kf σ B.R k γσ C.f kσ D.p k f σ9、通常轴⼼受压缀条式格构柱的横缀条不受⼒,但⼀般仍设置。
其理由是()A.起构造作⽤B.可以加强柱的整体抗弯刚度C.对单肢稳定起作⽤D.以上三种原因都有10、实腹式偏⼼压杆弯矩作⽤平⾯外的整体稳定计算公式f W M A N x 1b x tx y ≤?βη+?中,W1x 应取( )A.弯矩作⽤平⾯内最⼩受压纤维的⽑截⾯模量B.弯矩作⽤平⾯外最⼩受压纤维的⽑截⾯模量C.弯矩作⽤平⾯内最⼤受压纤维的⽑截⾯模量D.弯矩作⽤平⾯外最⼤受压纤维的⽑截⾯模量11、当仅讨论截⾯形式对轴⼼受压杆的失稳影响时,⼀般来说,图⽰的四种截⾯中最易发⽣扭转失稳的截⾯为( B )12、如图所⽰焊接组合⼯字形轴⼼压杆,⼀般情况下(当板件不是很薄时)杆件的整体失稳形式是( )A.绕y 轴的弯扭失稳B.绕y 轴的弯曲失稳C.绕x 轴的弯曲失稳D.绕z 轴的扭转失稳13、某竖直向下均布荷载作⽤下的两端简⽀⼯字形钢梁,关于荷载作⽤位置对其整体稳定性的影响,叙述正确的是( )A.当均布荷载作⽤于上翼缘位置时稳定承载⼒较⾼B.当均布荷载作⽤于中和轴位置时稳定承载⼒较⾼C.当均布荷载作⽤于下翼缘位置时稳定承载⼒较⾼D.荷载作⽤位置与稳定承载⼒⽆关14、偏⼼受压构件稳定计算公式中的等效弯矩系数βmx 与下列哪项有关?( )A.端弯矩和横向荷载B.端弯矩和轴向荷载C.长细⽐和横向荷载D.长细⽐和轴向荷载15、单轴对称的轴⼼受压构件,当绕对称轴失稳时,其整体失稳形式通常是()A.弯曲失稳 B.扭转失稳C.弯扭失稳 D.塑性失稳16、某双轴对称截⾯的压弯构件承受如图所⽰不同⼯况的弯矩作⽤,图中所⽰的弯矩⼤⼩均相等,仅考虑弯矩作⽤平⾯内稳定性时,其轴向受压承载⼒最⼤的情况为()A.(a) B.(b)C.(c)D.(d)17、简⽀梁符合下列哪种条件时,可不必验算梁的整体稳定性?()A.有钢筋混凝⼟板密铺在梁的受压翼缘上,并与其牢固连接,能阻⽌受压翼缘的侧向位移时B.有钢筋混凝⼟板密铺在梁的受拉翼缘上,并与其牢固连接,能阻⽌受拉翼缘的侧向位移时C.除了梁端设置侧向⽀承点外,且在跨中有⼀个侧向⽀承点时D.除了梁端设置侧向⽀承点外,且在跨间有两个以上侧向⽀承点时18、关于残余应⼒对轴⼼受压构件承载⼒的影响,下列说法正确的是()A.残余应⼒对轴压构件的强度承载⼒⽆影响,但会降低其稳定承载⼒B.残余应⼒对轴压构件的稳定承载⼒⽆影响,但会降低其强度承载⼒C.残余应⼒对轴压构件的强度和稳定承载⼒均⽆影响D.残余应⼒会降低轴压构件的强度和稳定承载⼒19、某⼯字形截⾯钢梁在某固定集中荷载作⽤下局部压应⼒很⼤,⽆法满⾜局压验算要求时,可采⽤的最经济、有效的措施是()A.增加梁腹板厚度B.增加梁翼缘板厚度C.增设纵向加劲肋D.增设⽀承加劲肋20、对于单轴对称压弯构件,当弯矩作⽤在对称轴平⾯内,且使较⼤翼缘受压时,应补充验算fNNWMANExxxxmx≤'--)/25.11(22γβ,原因是()A.防⽌受压塑性区的开展⽽导致构件平⾯内失稳B.防⽌受拉塑性区的开展⽽导致构件平⾯内失稳C.防⽌受压塑性区的开展⽽导致构件平⾯外失稳D.防⽌受拉塑性区的开展⽽导致构件平⾯外失稳21、双肢格构式轴⼼受压柱,虚轴为x-x轴,实轴为y-y轴,确定两单肢间距离时应根据()A.强度条件B.=xλyλC.=x λoy λD.=ox λy λ22、梁采⽤Q235钢,梁受压翼缘的⾃由外伸宽度与其厚度之⽐即b1/t ≤13,是为了保证翼缘板的()A.整体稳定B.局部稳定C.抗弯强度D.抗剪强度23、⼯字型截⾯组合梁,计算所得06.1b =?,表明( )A.梁的刚度能满⾜要求 B .应⽤b ?'代替b ?验算梁的整体稳定C.梁的整体稳定能满⾜要求 D .梁不会发⽣强度破坏24、下图所⽰简⽀梁,除截⾯和荷载作⽤位置不同外,其它条件均相同,则以哪种情况的整体稳定性最好?( D )25、如图所⽰实腹式柱头,设置加劲肋的⽬的是( )A.提⾼柱腹板局部稳定B.提⾼柱的刚度C.传递梁的⽀座反⼒D.提⾼柱的承载⼒⼆、填空题1、⼯字形截⾯梁按弹性设计时,应使翼缘的宽厚⽐b1/t1≤ 15 。
钢结构第4章作业参考答案4.1 验算由2L63×5组成的水平放置的轴心拉杆的强度和长细比。
轴心拉力的设计值为270KN ,只承受静力作用,计算长度为3m 。
杆端有一排直径为20mm 的孔眼(图4.37),钢材为Q235钢。
如截面尺寸不够,应改用什么角钢?注:计算时忽略连接偏心和杆件自重的影响。
解:查表2228.12,215cm A mm N f == 有孔洞,∴危险截面是孔洞所在的正截面 22102852021028.12mm A n =⨯⨯-⨯=∴此截面能承受的最大轴力为:KN N KN f A N n 27002.2212151028][=<=⨯=⋅= ∴不满足要求改用Q235,2L63×6,查得A=14.58cm 2,cm i cm i y x 98.2,93.1==22125852021058.14mm A n =⨯⨯-⨯=∴2232156.214125810270mm N f mm N A N f n =<=⨯==∴实实际应力长细比: 350][4.15593.1300=<===λλx x i l 350][7.10098.2300=<===λλy y i l满足要求。
4.2 一块━400×20的钢板用两块拼接板━400×12进行拼接。
螺栓孔径为22mm ,排列如图4.38所示。
钢板轴心受拉,N=1350KN (设计值)。
钢材为Q235钢,解答下列问题:(1)钢板1-1截面的强度够否?(2)是否还需要验算2-2截面的强度?假定N 力在13个螺栓中平均分配,2-2截面应如何验算?(3)拼接板的强度够否?解:查表得t=20钢板220205mm N f =,t=12钢板220215mm N f = (1)在1-1截面,20厚钢板266802022320400mm A n =⨯⨯-⨯=220232051.2026680101350mm N f mm N A N n =<=⨯=∴12厚拼接板2801612)223400(2mm A n =⨯⨯-⨯=212232154.1688016101350mm N f mm N A N n =<=⨯=∴所以,1-1截面强度满足设计要求。
第4章 受弯构件正截面承载力 2.已知梁的截面尺寸为b×h=200mm×500mm ,混凝土强度等级为C25,22/9.11,/27.1mm N f mm N f c t ==,截面弯矩设计值M=125KN.m 。
环境类别为一类。
求:(1)当采用钢筋HRB335级2/300mm N f y =时,受拉钢筋截面面积;(2)当采用钢筋HRB400级2/360mm N f y =时,受拉钢筋截面面积.解:(1)由公式得26204652009.110.110125⨯⨯⨯⨯==bh f Mc s αα=0.243 283.00.243211211=⨯--=--=s αξ858.0)243.0211(5.0)2-1(15.0s =⨯-+⨯=⨯+⨯=αγs2601044465858.030010125/mm h f M A s y s =⨯⨯⨯==γ选用钢筋421017,18mm A s =Φ2m i n 200500200%2.01044mm bh A s =⨯⨯=>=ρ (2)2870360/1044300mm A s =⨯=。
3.已知梁的截面尺寸为b×h=250mm×450mm;受拉钢筋为4根直径为16mm 的HRB335钢筋,即Ⅱ级钢筋,2/300mm N f y =,A s =804mm 2;混凝土强度等级为C40,22/1.19,/71.1mm N f mm N f c t ==;承受的弯矩M=89KN.m 。
环境类别为一类。
验算此梁截面是否安全。
解:f c =19.1N/mm 2,f t =1.7 N/mm 2,f y =300 N/mm 2 则,满足适用条件。
55.0121.01.190.13000077.01=<=⨯⨯==b cyf f ξαρξ()(),安全。
m KN M m KN bh f M c u .89.49.93121.05.01121.04152501.190.15.012201=>=⨯-⨯⨯⨯⨯⨯=-=ξξα5.已知梁截面尺寸为200mm×400mm ,混凝土等级C30,2/3.14mm N f c =,钢筋采用HRB335,2/300mm N f y =,环境类别为二类,受拉钢筋为3φ25的钢筋,A s =1473mm 2,受压钢筋为2φ6的钢筋,A ’s = 402mm 2;承受的弯矩设计值M=90 KN.m 。
第4章 轴心受力构件
1 轴心受压构件整体失稳的形式有弯曲失稳、扭转失稳、弯扭失稳。
2 在计算构件的局部稳定时,工字形截面的轴压构件腹板可以看成四边受弹性嵌固的矩形板,其翼缘板的外伸部分可以看成是三边简支一边自由的矩形板。
3 柱脚中靴梁的主要作用是增加底板的刚度降低底板的弯矩。
4 实腹式工字形截面轴心受压柱翼缘的宽厚比限值,是根据翼缘板的临界应力等于柱的整体临界应力导出的。
5 轴心受压构件腹板的宽厚比的限制值,是根据腹板的临界应力等于柱的整体临界应力的条件推导出的。
6 当临界应力cr σ小于比例极限时,轴心受压杆属于弹性屈曲问题。
7 因为残余应力减小了构件的刚度 ,从而降低了轴心受压构件的整体稳定承载力。
8 格构式轴心压杆中,绕虚轴的整体稳定应考虑剪切的影响,以ox λ代替x λ进行计算。
9 当工字形截面轴心受压柱的腹板高厚比y w f t h 235)5.025(0λ+>时,可能使腹板失稳。
10 在缀板式格构柱中,缀板的线刚度不能小于单肢线刚度的6倍。
11 焊接工字形截面轴心受压柱腹板局部稳定的限值y w f t h 235)5.025(0λ+≤。
某柱=x λ57,=y λ62,应把62代人上式计算。
12 双肢缀条格构式压杆绕虚轴的换算长细比12
27A A x ox +=λλ,其中1A 代
表2个缀条的面积和·。