习题2与答案

习题二⒉１描述以下四个概念的区别：头指针变量，头指针，头结点，首结点（第一个结点）。

解：头指针变量和头指针是指向链表中第一个结点（头结点或首结点）的指针；在首结点之前附设一个结点称为头结点；首结点是指链表中存储线性表中第一个数据元素的结点。

若单链表中附设头结点，则不管线性表是否为空，头指针均不为空，否则表示空表的链表的头指针为空。

2.2简述线性表的两种存储结构有哪些主要优缺点及各自使用的场合。

解：顺序存储是按索引直接存储数据元素，方便灵活，效率高，但插入、删除操作将引起元素移动，降低了效率；而链式存储的元素存储采用动态分配，利用率高，但须增设表示结点之间有序关系的指针域，存取数据元素不如顺序存储方便，但结点的插入和删除十分简单。

顺序存储适用于线性表中元素数量基本稳定，且很少进行插入和删除，但要求以最快的速度存取线性表中的元素的情况；而链式存储适用于频繁进行元素动态插入或删除操作的场合。

2.3 在头结点为h的单链表中，把值为b的结点s插入到值为a的结点之前，若不存在a，就把结点s插入到表尾。

Void insert(Lnode *h,int a,int b){Lnode *p,*q,*s;s=(Lnode*)malloc(sizeof(Lnode));s->data=b;p=h->next;while(p->data!=a&&p->next!=NULL){q=p;p=p->next;}if (p->data==a){q->next=s;s->next=p;}else{p->next=s;s->next=NULL;}}2.4 设计一个算法将一个带头结点的单链表A分解成两个带头结点的单链表A和B，使A中含有原链表中序号为奇数的元素，而B中含有原链表中序号为偶数的元素，并且保持元素原有的相对顺序。

Lnode *cf(Lnode *ha){Lnode *p,*q,*s,*hb;int t;p=ha->next;q=ha;t=0;hb=(Lnode*)malloc(sizeof(Lnode));s=hb;while(p->next!=NULL){if (t==0){q=p;p=p->next;t=1;}else{q->next=p->next;p->next=s->next; s->next=p; s=p;p=p->next; t=0;}}s->next=NULL;return (hb);}2.5设线性表中的数据元素是按值非递减有序排列的，试以不同的存储结构，编写一算法，将x插入到线性表的适当位置上，以保持线性表的有序性。

第二章习题一、选择题2.非线性度是表示定度曲线（ ）的程度。

A.接近真值B.偏离其拟合直线C.正反行程的不重合3.测试装置的频响函数H （j ω）是装置动态特性在（ ）中的描述。

A ．幅值域 B.时域 C.频率域 D.复数域5.下列微分方程中（ ）是线性系统的数学模型。

A.225d y dy dx t y x dt dt dt ++=+ B. 22d y dx y dt dt+= C.22105d y dy y x dt dt -=+ 6.线性系统的叠加原理表明（ ）。

A.加于线性系统的各个输入量所产生的响应过程互不影响B.系统的输出响应频率等于输入激励的频率C.一定倍数的原信号作用于系统所产生的响应，等于原信号的响应乘以该倍数7.测试装置能检测输入信号的最小变化能力，称为（ ）。

A.精度B.灵敏度C.精密度D.分辨率8.一般来说，测试系统的灵敏度越高，其测量范围（ ）。

A.越宽B. 越窄C.不变10.线性装置的灵敏度是（ ）。

A.随机变量B.常数C.时间的线性函数12.输出信号与输入信号的相位差随频率变化的关系就是系统的（ ）。

A.幅频特性B.相频特性C.传递函数D.频率响应函数13.时间常数为τ的一阶装置，输入频率为 1ωτ=的正弦信号，则其输出与输入间的相位差是（ ）。

A.-45° B-90° C-180°14.测试装置的脉冲响应函数与它的频率响应函数间的关系是（ ）。

A.卷积B.傅氏变换对C.拉氏变换对D.微分16.对某二阶系统输入周期信号 000()sin()x t A t ωϕ=+，则其输出信号将保持（）。

A.幅值不变，频率、相位改变B.相位不变，幅值、频率改变C.频率不变，幅值、相位可能改变18.二阶系统的阻尼率ξ越大，则其对阶越输入的时的响应曲线超调量（）。

A.越大B.越小C.不存在D.无关19.二阶装置引入合适阻尼的目的是（）。

A.是系统不发生共振B.使得读数稳定C.获得较好的幅频、相频特性20.不失真测试条件中，要求幅频特性为（），而相频特性为（）。

1、将全部成本分为固定成本、变动成本和混合成本所采用的分类依据是A.成本核算目标B.成本的可辨认性C.成本的性态D.成本的经济用途正确答案：C2、管理会计中对成本相关性的正确解释是A.与决策方案有关的成本特性B.与归集对象有关的成本特性C.与资产价值有关的成本特性D.与控制标准有关的成本特性正确答案：A3、下列项目中，只能在发生当期予以补偿、不可能递延到下期的成本是A.间接成本B.产品成本C.直接成本D.期间成本正确答案：D4、下列成本估计方法中，可以用于研究各种成本性态的方法是A.历史成本分析法B.契约检查法C.工业工程法D.账户分析法5、单位固定成本在相关范围内的变动规律为A.随业务量的增加而增加B.随业务量的减少而减少C.随业务量的增加而减少D.不随业务量的变动而变动正确答案：C6、在各类固定成本中，能够在不改变企业生产经营能力的前提下降低其总额的是A.单位固定成本B.约束性固定成本C.半固定成本D.酌量性固定成本正确答案：D7、在管理会计中，单耗相对稳定的外购零部件成本应当归属于A.约束性固定成本B.酌量性固定成本C.技术性变动成本D.酌量性变动成本正确答案：D8、为排除业务量因素的影响，在管理会计中反映变动成本水平的指标一般是A.单位变动成本B.变动成本率C.变动成本的总额与单位额D.变动成本总额9、在应用高低点法进行成本性态分析时，选择高点坐标的依据是A.最高的业务量B.最高的业务量或最高成本C.最高的成本D.最高的业务量和最高的成本正确答案：A10、在应用历史资料分析法进行成本性态分析时，必须首先确定a,然后才能计算出b 的方法是A.回归直线法B.直接分析法C.高低点法D.散布图法正确答案：D11、混合成本可以用直线方程y=a+bx模拟，其中bx表示A.固定成本B.变动成本总额C.单位变动成本D.单位固定成本正确答案：B12、已知某项成本的习性模型为：y=1000+2x，当业务量x由1000单位上升为2000单位时，该项成本的增加量为A.2000B.5000C.1000D.3000正确答案：A13、在前后期产量和成本水平均不变的条件下，若本期完全成本法计算下的利润小于变动成本法计算下的利润，则意味着A.本期生产量等于本期销售量B.本期生产量大于本期销售量C.期末存货量大于期初存货量D.期末存货量小于期初存货量正确答案：D14、在其他条件相同的情况下，变动成本法计算下的单位产品成本比完全成本法计算下的单位产品成本A.无法确定B.相同C.大D.小正确答案：D15、在变动成本法下，其利润表所提供的中间指标是A.期间成本B.营业毛利C.营业利润D.贡献毛益正确答案：D16、如果某期按变动成本法计算的营业利润为5 000元，该期产量为2000件，销售量为1 000件，期初存货为零，固定性制造费用总额为2 000元，则按完全成本法计算的营业利润为A.6 000元B.1 000元C.5 000元D.0正确答案：A17、若某企业连续三年按变动成本法计算的营业利润分别为10 000元、12 000元和11 000元，则下列表述中正确的是A.第二年的产量比第三年多B.第一年的产量比第二年少C.第三年的销量最小D.第二年的销量最大正确答案：D18、下列各项中，不属于变动成本法与完全成本法本质区别的是A.应用的前提条件不同B.销货成本水平不同C.计算出的营业利润不同D.损益确定程序不同正确答案：C19、当产品的销售价格、成本水平均不变时，按变动成本法计算的营业利润与当期实现的销售量之间的关系是A.正比例关系B.同方向变动关系C.反比例关系D.反方向变动关系正确答案：B20、已知2015年某企业按变动成本法计算的营业利润为13 500元，假定2016年销量与2015年相同，产品单价及成本水平都不变，但产量有所提高，则该年按变动成本法计算的营业利润A.必然大于13 500元B.可能等于13 500元C.必然小于13 500元D.必然等于13 500元正确答案：D二、多选题1、下列项目中，属于固定成本的有A.按产量法计提的折旧费B.企业管理人员工资C.定期支付的广告费D.按直线法计提的折旧费正确答案：B、C、D2、下列属于约束性固定成本的有A.财产保险B.固定资产折旧C.职工培训费D.科研开发费正确答案：A、B3、由于相关范围的存在，导致固定成本和变动成本的性态均具有以下特点，即A.可转化性B.相对性C.暂时性D.正比例变动性正确答案：A、B、C4、在应用一元直线回归法进行成本形态分析时，相关系数r应满足的条件有A.r等于0B.r等于+ 1C.r为任意值D.r趋近于+ 1正确答案：B、D5、下列项目中，与可能导致完全成本法和变动成本法确定的分期损益出现差异完全无关的因素有A.直接材料B.管理费用C.财务费用D.固定性制造费用正确答案：A、B、C6、下列各项中，属于完全成本法缺点的内容有A.不利于管理者理解信息B.可能导致盲目生产C.可能歪曲各部门降低成本的业绩D.无法揭示利润与销售量之间的依存关系正确答案：A、B、C、D7、变动成本法所提供的信息对强化企业管理有相当大的积极作用，比如可以A.加强成本管理B.调动企业增产的积极性C.简化成本计算D.促进以销定产正确答案：A、C、D8、在应用变动成本法的多种设想中，属于"结合制"的内容有A.单独核算变动性制造费用B.日常核算以变动成本法为基础C.单独核算固定性制造费用D.期末编制完全成本法的会计报表正确答案：A、B、C、D9、下列各项中，属于变动成本法优点的有A.便于分清部门的责任，实施成本控制B.有利于长期决策C.简化产品成本计算D.易于为管理部门所理解和掌握正确答案：A、C、D10、下列说法正确的有A.完全成本发下，全部成本都计入产品成本B.完全成本发下，各会计期发生的全部生产成本要在完工产品和在产品之间分配C.变动成本法下，利润=销售收入—销售成本—固定制造费用—销售和管理费用D.变动成本法提供的资料不能充分满足决策的需要正确答案：B、C、D。

1、中国的法定货币是（）A.港币B.欧元C.人民币D.美元正确答案：C2、在中国境内，可以自由流通的货币是（）A.人民币B.日元C.美元D.欧元正确答案：A3、秦国统一六国后，发行的统一使用法定货币是（）A.圆形方孔的秦半两钱B.布币C.圆形圆孔钱D.刀币正确答案：A4、人民币的单位为（）A.港元B.美元C.日元D.元5、边远地区和交通不便地区的开户单位的库存现金限额，可以多于5天，但不得超过（）天的日常零星开支。

A.5B.30C.15D.20正确答案：C解析：边远地区和交通不便地区的开户单位的库存现金限额，可以多于5天，但不得超过15天的日常零星开支。

二、多选题1、人民币，是指中国人民银行依法发行的货币，包括（）A.外币B.美元C.纸币D.硬币正确答案：C、D2、禁止下列损害人民币的行为（）A.制作、仿制、买卖人民币图样；B.未经中国人民银行批准，在宣传品、出版物或者其他商品上使用人民币图样；C.中国人银行规定的其他损害人民币的行为。

D.故意毁损人民币；正确答案：A、B、C、D3、下列说法正确的有（）A.禁止走私、运输、持有、使用伪造、变造的人民币B.美元在中国境内可以自由流通和兑换C.禁止伪造、变造人民币D.禁止出售、购买伪造、变造的人民币正确答案：A、C、D解析： B、中国境内不允许外币流通，只允许人民币流通。

4、人民币有下列情形之一（）的，不得流通：A.仿冒的人民币B.停止流通的人民币C.不能兑换的残缺的人民币D.不能兑换的污损的人民币；正确答案：A、B、C、D5、下列说法正确的有（）A.人民币发行基金是中国人民银行人民币发行库保存的已经进入流通的人民币B.人民币辅币单位为角、分C.人民币依其面额支付D.人民币由中国人民银行指定的专门企业印制正确答案：B、C、D解析：人民币发行基金是中国人民银行人民币发行库保存的未进入流通的人民币三、判断题1、我国有权发行货币的机构是中国银行。

（×）解析：我国有权发行货币的机构是中国人民银行。

第一章国际贸易理论的微观基础习题（一）选择题1.微观经济学研究的是单个社会的资源配置问题，而国际贸易理论研究的是（）A 一国的资源配置问题B两国范围内的资源配置问题C地区范围内的资源配置问题D世界范围内的资源配置问题2. 一个人在作出选择时，（）A如果边际收益非常大，他或她就不用考虑机会成本B进行最小机会成本的选择C比较该选择活动的边际成本和边际收益D只有当总利益非常大时，他或她才会选择使用其稀缺的资源3.机会成本（）A由自己支付，而与他人无关B对劳务而言是零，因为劳务不会持续太久；对物品而言是正的，因为物品具有长久性C是为了进行某一选择而放弃的评价最高的选择D是为了进行某一选择放弃的所有选择4.如果两个人在商品的生产中具有不同的机会成本，那么他们能够从专业化与交换中（）A都受损B一人受益，一人受损C既不受益，也不受损D都能够受益5. 沿着外凸的生产可能性边界线向下移动时，随着一种物品产量的增加，生产该物品的机会成本将（）A保持不变B增加C减少D无法确定6 .一个国家（），能够在其生产可能性边界线之外的点上进行消费。

A没有任何时候B在充分就业的情况下C同其他国家进行贸易时D所有生产要素全部投入生产的时候7.供给曲线除了表示不同的价格水平所提供的商品数量外，还可以被认为是（）A愿意并有能力支付的曲线B边际收益曲线C供给的最高价格曲线D供给的最低价格曲线8. 在封闭条件下，一国生产技术的改进降低了棉花的生产成本，那么棉花的价格（），棉花的生产数量（）A上升；增加B上升；减少C下降；增加D下降；减少9 .对于两国贸易模型来说，国际均衡价格一定处于两国贸易前的（）A最低相对价格水平之下B最高相对价格水平之上C相对价格水平之间D根据具体情况而定10 .经济学家作出这样的假设：作为一种目标，消费者总是在追求（）A其效用最大化B其收入的最大化C其边际效用的最大化D以上选项均不对（二）简答题1如何理解狭义和广义的国际贸易，国际贸易理论的主要研究对象是什么？2既然国际贸易理论与微观经济学的基本原理存在着一致性，为什么还要区分国际贸易与国内贸易，将国际贸易作为一个独立的问题来研究呢？3用相对价格概念解释经济行为主体是如何摆脱“货币幻觉”的影响的。

当时，F 故X 的分布函数(X)=P (XWx) =10,X < 022—,0<x<I 35 34 - A —,1 < x < 2 35x>2习题3•设在15只同类型零件中有2只为次品，在英中取3次，毎次任取1只，作不放回抽样. 以X 表示取出的次品个数，求： (1) (2) (3) X 的分布律： X 的分布函数并作图; P{X<lhP{I<X <-),P)I<%<-),P{l<x<2}・ 2 2 2 【解】 x=at2・CP(X=O) = »±・C ；5 35 心)半』C ； 35C" 1P(X=2) =卑=丄・C ：5 35故X 的分布律为(2)当 xvO 时，F (X)=P (X<x) =0当OWxvl 时, 当lWxv2时,22 F (X)=P(XWx) =P(X=O)= —3534F (X)=P (XWx) =P(X=O)+P{X=1)= —1 I 22P (X<l) = F(i) = —,2 2 353 3 34 34P (KX <-) = F(-)-F(l) = --- — = 02 2 35 353 3 12P (1<X <-) = P(X = 1) + P(1<X<-)亠2 2 3534 1 P(1<X<2)=F(2)-F(1)-P(X =2) = 1-衣-务=0.4•射手向目标独立地进行了 3次射击，每次击中率为，求3次射击中击中目标的次数的分布 律及分布函数，并求3次射击中至少击中2次的概率. 【解】设X 表示击中目标的次数•则X<K 1. 2, 3.p(x = 0) = (0.2)3 =0・008 p(x =1) = C ；O.8(O.2)2 = 0.096 P(X = 2) = C^(0.8)'0.2 = 0.384 p(x= 3) = (0.8)3 =0.512故X 的分布律为 XP分布函数0, 0.00&F(X ) = W ・104.0.48&P(X > 2) = P(X = 2) + P(X = 3) = 0.8965. （1）设随机变量X 的分布律为P(X=.}=Z.k\尖中后0, r 2,…，人>0为常数，试确定常数G （2）设随机变虽X 的分布律为 p{X=k ）=a/N, k=l. 2,…，N,x<0 0<%<1 1<%<2 2<x<3x>3试确世常数G【解】（1）由分布律的性质知1=》P(X =k) = u》——=ad D k!{2)由分布律的性质知N N\ = ^P{X=k}=^- = aA-l £-1 N即 a =6.甲、乙两人投篮，投中的概率分别为“今^$投3次，求:(1)两人投中次数柑等的概率；(2)甲比乙投中次数多的概率•【解】分别令X、y表示甲、乙投中次数，则XF (3,) y~b(3.(1)p(x = r)= p(x=o,y=o)+p(x=ty = i)+p(x = 2,r=2)+p(X=3.y=3)=(0・4)'(0・3)' + C"0.6(0.4)-C"0.7(03)- +C；(O・6)2O・4C；(O・7)2O・3 + (O・6)3(O・7)3=0.32076⑵ p(x>y)= p(x = i,r=o)+p(x = 2,y=o)+p(x=3,r = o)+p(x = 2,y=i)+p(x=3,y = i)+p(x=xr = 2)=C；O・6(O・4)2(O・3)3 +C；(O・6)2O・4(O・3)3 +(O・6)3(O・3)3 +C；(O・6)2O・4C；O・7(O・3)2 +(O・6)3C；O・7(O・3)2 + (O・6)3C；(O・7)2O・37•设某机场每天有200架飞机在此降落，任一飞机在某一时刻降落的概率设为，且设齐飞机降落是相互独立的.试问该机场需配备多少条跑道，才能保证某一时刻飞机需立即降落而没有空闲跑逍的概率小于(每条跑道只能允许一架飞机降落)【解】设X为某一时刻需立即降落的飞机数，则X~b(200八设机场需配备W条跑逍，则有P(X > TV) <0,01200为 C 爲(0.02)气0.98严"vO.Olt-N'+i利用泊松近似A = np = 200 X 0.02 = 4. » 宀4*P(X>N)= Z ——<0.01 jt-A+i k!査表得WM9.故机场至少应配备9条跑道.8.已知在五重伯努利试脸中成功的次数X 满足P{X=1}=P{X=2},求概率P{X=4}. 【解】设在每次试验中成功的概率为P,则P(X=4) = Ct(-/- = —. '3 3 2439.设事件A 在每一次试验中发生的概率为，当人发生不少于3次时，指示灯发出信号, (1) (2) 【解】 所以进行了 5次独立试验，试求指示灯发出信号的概率：进行了 7次独立试验，试求指示灯发出信号的概率. (1)设X 表示5次独立试验中A 发生的次数，则X~6(5,) 5P(X >3) = XC ；(O ・3)Z(O ・7)I =0.16308(2)令y 表示7次独立试验中人发生的次数，则Y-b (7r)P{Y > 3) = 2^C ；(03/ (0・7)F = 0.35293X-310•某公安局在长度为f 的时间间隔内收到的紧急呼救的次数X 服从参数为(坨)t 的泊松分布，而与时间间隔起点无关(时间以小时计).<1)求某一天中午12时至下午3时没收到呼救的概率； (2)求某一天中午12时至下午5时至少收到1次呼救的概率..3【解】(1) P(X=0) = e"^5(2) P(X >1) = 1-P(X =0) = l-e"^11•设 P{X=k}=C*/(l-p)--\ 后012P{y=m}=CS"(l - 〃)m=0,1,23/4分别为随机变Sx, y 的概率分布，如果已知P{xMi}=#,试求p{Y^i},54【解】因为P(X>l) = j,故P(X<1) = £.P(X<1) = P(X=O) = (1 — “)2(1-卩)冷,P （r> I ） = l-P （r = 0） = 1-（1-/?/= — «.0.802478112•某教科书岀版了 2000册，因装订等原因造成错误的概率为，试求在这2000册书中恰有 5册错误的概率.【解】令X 为2000册书中错误的册数，则XF （2000,・利用泊松近似计算，A = np = 2000 X 0.001 =2p(x= 5” ^^ = 0.00185!3 I13•进行某种试验，成功的概率为一,失败的概率为丄•以X 表示试验首次成功所需试验的次4 4数，试写出X 的分布律，并计算X 取偶数的概率.【解】X =12…人…P(X = 2) + P(X=4)+…+ P(X=2幻 + … =1.2+(1/2+...+(丄严4 4 4 4 4 43 4 1 =—• =— 4-（$5414. 有2500名同一年龄和同社会阶层的人参加了保险公司的人寿保险.在一年中每个人死亡 的概率为，毎个参加保险的人在1月1日须交12元保险费，而在死亡时家属可从保险 公司领取2000元赔偿金•求： （1） 保险公司亏本的概率；（2） 保险公司获利分别不少于10000元、20000元的概率. 【解】以“年”为单位来考虑.（1）在1月1日，保险公司总收入为2500X12=30000元. 设1年中死亡人数为X,则X~b （25g,则所求概率为故得从而P(2000X >30000) = P(X>15) = \-P(X < 14)由于I)很大，p很小• A=np=5.故用泊松近似，有M e时P(X > 15)^1-工^^总0・000069*•<)k!(2) P(保险公司获利不少于10000)=P(3OOOO-2OOOX > 10000) = P(X < 10)即保险公司获利不少于10000元的概率在98%以上P (保险公司获利不少于 20000) = P(30000-2000X > 20000) = P(X <5)5 ■呻迄一“.6窗即保险公司获利不少于20000元的概率约为62%15.已知随机变量X的密度函数为/(x)=^e ni, 8*+8. 求：(1〉人值：(2) P{O<X<1}; (3)F(x)・【解】(1)由/(x)d.r = 1得=J = 2J0 Ae"*d.v = 2A/?(0 < X < 1)=丄[「dx =丄(1 一 e")2" 2当 x<0 时，F(x) = J — e*dv = — e"2 2当心0时，F(x) = J ■^e~'^Av = J ¥&+[£「血十产F(x) =17•在区间[0, o]上任意投掷一个质点，以X表示这质点的坐标，设这质点落在[0, g] 中任意小区间内的概率与这小区间长度成正比例，试求X的分布函数.【解】由题意知X-U[0.o],密度函数为八1 2P(X>3) = J^-dv = -故所求概率为厂C 净出；(討=等19•设顾客在某银行的窗口等待服务的时间X(以分钟计)服从指数分布£(-).某顾客在窗口等待服务，若超过10分钟他就离开•他一个月要到银行5次，以y 表示一个月内他未等 到服务而离开窗口的次数，试写出Y 的分布律，并求P{g?l}・ 【解】依题意知X~E(-) •即英密度函数为^5-e 蔦 X > 0 0,x<0该顾客未等到服务而离开的概率为1 2P(X>10) = p-e"'dLv = e-'y~b(5・r),即其分布律为f(x) = 一，0<x<« a0, 其他故当xvO 时F (X)=0当 0 WxWo 时 F(x)=『f(t}dt = J ； yaM =J^idZ = - 当 x>a 时，F (X)=1 即分布函数0,x<0F(x)=Q<x<a x>a18•设随机变量X 在［2, 值大于3的概率. 【解】XP ⑵5),即5］上服从均匀分布•现对X 进行三次独立观测，求至少有两次的观测2<%<5/W = b'0, 其他P （y = £） = C （mi-r ）Lk =0,12345P （r> I ） = l-P （y = 0） = l-（l-e--/=0.516720.某人乘汽车去火车站乘火车，有两条路可走.第一条路程较短但交通拥挤，所需时间X 服 从W （40, 102）；第二条路程较长，但阻塞少，所需时间X 服从W （50, 4?）. （1） 若动身时离火车开车只有1小时，问应走哪条路能乘上火车的把握大些 （2） 又若离火车开车时间只有45分钟，问应走哪条路赶上火车把握大些 【解】（1）若走第一条路，X-N （40. 102）,则若泄:第二条路，X-N （50, 42）,则p(X<60) = Px-40 60-40----- < ------- 10 10= 0(2) = 0.97727P(X<60) = P(X-5Q 60-50、---------- <I 4= 0(2.5) = 0.9938 卄故走第二条路乘上火车的把握大些. （2） 若 X"/（40, 102〉，贝I]P{X < 45) = pf X二° <45 j = 0(0.5) = 0.6915若 X~N (50, 42〉，则p(X <45) = P(X-5Q 45-501---------- <I 4= 0(-1.25)= 1-0(1.25) = 0.1056故走第一条路乘上火车的把握大些.21•设 X~N (3, 22),CD 求 P{2<X<5}» P{ 4<X<10}> P{|X| >2}, P{X>3}; (2)确总 c 使 P{X>c}=P{X^c}.【解】（1）P （2<X<5） = P=0(1) — 0 —一 =0 ⑴-1 + 0 -I 2丿 (2 = 0.8413-1 + 0.6915 = 0.5328 12P(-4<X <10) = P(-4-3X-3 10-3、 -------- < ----------- < -----------I 2 22 J2 12丿=0.9996P(l Xl>2) = P(X>2) + P(X <-2)P(X>3) = P(^^^>—) = 1-0(0) = 0.52 2⑵C=322•由某机器生产的螺栓长度（cm ） X-N C ）,规定长度在±内为合格品,求一螺栓为不合格品 的概率•=1-0(2) + 0(-2) = 2[1- 0(2)] =0.045623•—工厂生产的电子管寿命X （小时）服从正态分布N （160, 02）,若要求P{120VXW200} 允许。

《微机原理》习题2 （P40）参考答案2.1为什么说计算机只能“识别”二进制数，并且计算机内部数的存储及运算也都采用二进制？解：因为二进制是计算机刚出现时就奠定的计算机内的进位记数制，之所以选用它来表示计算机内的信息，是因为两个状态的物理器件容易制造和实现，将这两个状态抽象为数字就可用0、1来表示；此外，采用二进制的运算规则较为简单，容易实现。

2.2在进位记数制中，“基数”和“位权（或权）”的含义是什么？一个以b为基数的任意进制数N，它按位权展开式求值的一般通式是如何描述的？解：在进位记数制中，常常要用“基数”（或称底数）来区别不同的数制，而进位制的基数就是该进位制所用的字符或数码的个数。

在一个进位记数制中，每一位都有特定的权，称为位权或简称权。

每个位权由基数的 n次幂来确定。

数N的按位权展开式的一般通式为：N=±（ki×b i）式中，ki为第i位的数码；b为基数；b i为第位的位权；n为整数的总位数；m 为小数的总位数。

2.3将下列十进制数分别转化为二进制数。

（1）147 （2）4095 （3）0.625 (4) 0.15625解：(1) 147 D=10010011 B(2) 4095 D=111111111111 B(3) 0.625 D=0.101 B(4) 0.15625 D=0.00101 B2.4将下列二进制数分别转换为BCD码。

（1）1011 (2) 0.01 (3) 10101.101 (4) 11011.001解：(1) 1011 B=1×23+0×22+1×21+ 1×20=11 D=(0001 0001)BCD(2) 0.01 B=1×2-2=0.25 D=(0.0010 0101)BCD(3) 10101.101 B =1×24+1×22+1×20+1×2-1+1×2-3 =21.625 D=(0010 0001.0110 0010 0101)BCD(4) 11011.001B=1×24+1×23+1×21+1×20+1×2-3=27.125D=(0010 0111.0001 0010 0101)BCD2.5将下列二进制数分别转换为八进制数和十六进制数。

一、单选题1、人刚刚能够感受到某个刺激变化所需的最小量被称为（）。

A.绝对阈限B.差别阈限C.感受性D.感觉对比正确答案：B2、在香水柜台工作的售货员，工作一段时间后觉得自己鼻子“失灵”了，这种现象是（）。

A.感觉对比B.感觉钝化C.感觉变化D.感觉适应正确答案：D3、（）是将外界物理能量转化为人类大脑可以识别的神经编码的过程。

A.感觉B.知觉C.情绪D.思维正确答案：A4、在知觉的过程中，（）凸显在前方，具有边缘和轮廓。

A.背景B.图像C.图形正确答案：C5、感觉信息已变化，但知觉依然会对信息重组，发现事物不变的本质，这表现了知觉的（）。

A.选择性B.模糊性C.恒常性D.理解性正确答案：C6、“一目十行”指的是注意力的（）。

A.稳定性B.广度C.强度D.持久性正确答案：B7、用来研究注意力偏向和轨迹的常用仪器是（）。

A.fMRIB.ERPC.EEGD.眼动仪正确答案：D8、眼动仪实验最后的产物是（）。

A.透视图B.剖面图C.热点图正确答案：C9、“有限理性”思想的提出者是（）。

A.赫伯特·西蒙B.丹尼尔·卡尼曼C.特沃斯基D.理查德·塞勒正确答案：A10、同一个问题用不同语言产生“损失”或者“获益”的表达，依然会使人产生对风险的不同态度。

这种现象被称为（）。

A.风险厌恶B.框架效应C.成本沉没D.禀赋效应正确答案：B二、多选题1、让夜晚作业的工人晚上沐浴在（）色的灯光下，白天带上（）色眼镜，有助于他们调节生物钟。

A.红色B.蓝绿色C.琥珀色D.白色正确答案：B、C2、“前景理论”的提出者是（）。

A.赫伯特·西蒙B.丹尼尔·卡尼曼C.特沃斯基D.理查德·塞勒正确答案：B、C三、判断题1、声强超过听觉的上感觉阈限（120分贝），带来的是痛觉。

（√）2、错觉和幻觉一样都是知觉的扭曲，是知觉的特殊形式。

（×）3、研究者发现，人们有追求社会公平的偏好，甚至以损失个人利益为代价。

习 题 二2-1 何为等效变换？两电路等效需要满足什么条件？答：用一个较为简单的电路替代原电路，从而使分析的问题得以简化，这就是电路的等效变换。

两电路等效需要满足的条件是：电路对外的伏安特性不变。

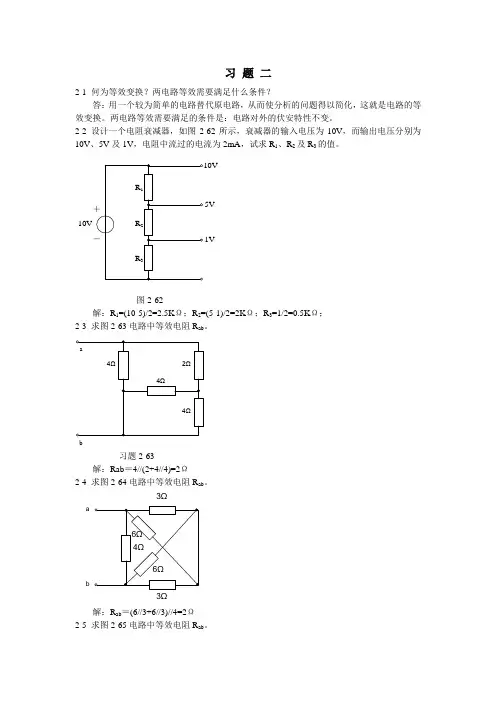
2-2 设计一个电阻衰减器，如图2-62所示，衰减器的输入电压为10V ，而输出电压分别为10V 、5V 及1V ，电阻中流过的电流为2mA ，试求R 1、R 2及R 3的值。

10V5V1V图2-62解：R 1=(10-5)/2=2.5K Ω；R 2=(5-1)/2=2K Ω；R 3=1/2=0.5K Ω； 2-3 求图2-63电路中等效电阻Rab 。

b习题2-63解：Rab ＝4//(2+4//4)=2Ω2-4 求图2-64电路中等效电阻R ab 。

3Ω3Ωba解：R ab ＝(6//3+6//3)//4=2Ω 2-5 求图2-65电路中等效电阻R ab 。

ba图2-65解：R ab ＝3//3//3=1Ω2-6 求图2-66电路中①S 打开；②S 闭合时等效电阻R ab 。

36Ω24ΩbaS图2-66解：S 打开：R ab ＝0.5*（36+24）＝30Ω S 闭合：R ab ＝36/2+24/2＝30Ω2-7 图2-67中，试求：①R=0时的电流I ；②I=0时的电阻R ；③R ＝∞时的电流I 。

3Ω4Ω图2-67解：① I 总=6/((3*6)/(3+6))=3A ，∴I ＝（6/（3+6））* I 总＝2A; ② 3/6=4/R ，∴R=8Ω③ I 总=6/(4+3*6/(3+6))=1A ，I=－(3/(3+6))* I 总=－1/3A 2-8 电路如图2-68所示，已知30Ω电阻中电流为0.2A ，试求此电路的总电压U 和总电流I 。

60Ω图2-68解：I=(0.2+30*0.2/60)+ (0.2+30*0.2/60)*(10+60*30/(60+30))/15=0.9AU=0.9*10+(0.2+30*0.2/60)*(10+60*30/(60+30))=18V2-9 将图2-69所示电路中星形与三角形网络进行等效变换。