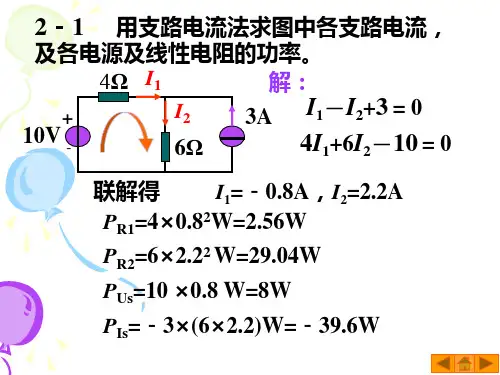
习题第二章答案

习题集第二章参考答案一、单项选择题1、 D2、 D3、 B4、 D5、 C6、 B7、 A 8、 B9、 C10、 B11、 C12、 B13、 D14、 C15、 D16、 A17、 B18、 A19、 B20、 D21、 C22、 D23、 B24、 D25、 D26、 B27、 C28、 B29、 A30、 B31、 A32、 B33、 A34、 C二、填空题1 进程2 就绪执行阻塞3 等待的事件发生的4 进程控制块5 进程控制块（或PCB）6 99 1 1007 就绪8 静止阻塞9 阻塞就绪10 共享存储器，管道通信，消息传递11 信号量12 [1-n，1]13 进程控制块（PCB）14 同步互斥信号量15 wait(mutex)signal(mutex)16 顺序性，封闭性，可再现性17 并发18 临界区19 wait, signal20 1，(1-n）或-(n-1)21 722 wait signal23 阻塞就绪三、判断题×√1×2√3×4×5×6×7√8×9×10√11√12×13√四、简答题1、解释进程的顺序性和并发性。

答：进程的顺序性是指进程在顺序的处理器上的执行是严格按序的，只有在前一个操作结束后才能开始后继操作。

进程并发性是指一组进程可以轮流占用处理器，一个进程的工作没有全部完成之前，另一个进程就可开始工作。

把这样的一组进程看做是同时执行的，把可同时执行的进程称为并发进程。

所以，进程的顺序性是对每个进程而言的，进程的并发性是对一组具有顺序性的进程而言的。

一组进程并发执行时各进程轮流占用处理器交替执行，占用处理器的进程按各自确定的顺序依次执行指令。

2、简述进程与程序的区别和联系。

答：区别：（1）进程能真实地描述并发，而程序不能。

（2）动态性是进程的基本特征，进程实体具有创建、执行和撤销的生命周期，而程序只是一组有序指令的集合，存放在某种介质上，是静态的。

第二章习题答案第二章作业1. 已知煤的空气干燥基成分：Cad=60.5% ，Had=4.2%，Sad=0.8%，Aad=25.5%，Mad=2.1%和风干水分=3.5%，试计算上述各种成分的收到基含量。

（Car=58.38%，Har=4.05%，Sar=0.77%，Aar=24.61%，Mar=5.53%) f100 Mar100 3.5 3.5 2.1 5.53% 解：Mar M Mad*****f arK 100 Mar100 5.53 0.965 100 Mad100 2.1Car KCad 0.965 60.5 58.38%Har KHad 0.965 4.2 4.05%Sar KSad 0.965 0.8 0.77%Aar KAad 0.965 25.5 24.61%2, 已知煤的空气干燥基成分：Cad=68.6%，Had=3.66%，Sad=4.84%，Oad=3.22%，Nad=0.83%，Aad=17.35%，Mad=1.5%，Vad=8.75%，空气干燥基发热量Qnet,ad=*****kJ/kg和收到基水分Mar=2.67%，煤的焦渣特性为3类，求煤的收到基其他成分,干燥无灰基挥发物及收到基低位发热量，并用门捷列夫经验公式进行校核。

（Car=67.79%，Har=3.62%，Sar=4.78%，Oar=3.18%，Nar=0.82%，Aar=17.14%，Vdaf=10.78%，Qnet，ar=*****kJ/kg;按门捷列夫经验公式Qnet,ar=*****kJ/kg) 解：从空气干燥基转换为收到基的换算系数K 100 Mar100 2.67 0.9881 100 Mad100 1.5Car KCad 0.9881 68.6 67.79%Har KHad 0.9881 3.66 3.62%Sar KSad 0.9881 4.84 4.78%Oar KOad 0.9881 3.22 3.18%Nar KNad 0.9881 0.83 0.82%Aar KAad 0.9881 17.35 17.14%从空气干燥基转换为干燥无灰基的换算系数*****K 1.2323 100 Mad Aad100 1.5 17.35Vdaf KVad 1.2323 8.75 10.78%Qnet,ar (Qnet,ad 25Mad) 100 Mar100 2.67 25Mar (***** 25 1.5) 25 2.67 *****kJ/kg 100 Mad100 1.5门捷列夫公式Qnet,ar 339Car 1030Har 109(Oar Sar) 25Mar 339 67.79 10303.62 109 (3.184.78) 25 2.67 *****.06kJ/kg4，某工厂贮存有收到基水分Mar1=11.34%及收到基低位发热量Qnet,ar1=20XX年7kJ/kg的煤100t，由于存放时间较长，收到基水分减少到Mar2=7.18%，问这100t煤的质量变为多少？煤的收到基低位发热量将变为多大？*****. 4% x 00.718解：设减少的水分为x（t），，所以x=4.48t，100 x100t煤变为100-4.48=95.52t，由收到基转为干燥基：*****Qnet,d1 (Qnet,ar1 25Mar1) (20XX年7 25 11.34) *****kJ/kg 100 Mar1100 11.34由干燥基转为收到基：100 Mar2100 7.18Qnet,ar2 Qnet,d1 25Mar2 ***** 25 7.18 *****kJ/kg *****7，一台4t/h的链条炉，运行中用奥氏烟气分析仪测得炉膛出口处RO2=13.8%，O2=5.9%，CO=0；省煤器出口处RO2=10.0%，O2=9.8%，CO=0。

第二章参考答案1.原子间的结合键共有几种？各自特点如何？2.为什么可将金属单质的结构问题归结为等径圆球的密堆积问题?答:金属晶体中金属原子之间形成的金属键即无饱和性又无方向性, 其离域电子为所有原子共有,自由流动,因此整个金属单质可看成是同种元素金属正离子周期性排列而成,这些正离子的最外层电子结构都是全充满或半充满状态,电子分布基本上是球形对称,由于同种元素的原子半径都相等,因此可看成是等径圆球。

又因金属键无饱和性和方向性, 为使体系能量最低，金属原子在组成晶体时总是趋向形成密堆积结构,其特点是堆积密度大,配位数高,因此金属单质的结构问题归结为等径圆球的密堆积问题.3.计算体心立方结构和六方密堆结构的堆积系数。

(1) 体心立方 a ：晶格单位长度 R ：原子半径a 34R = 34R a =，n=2, ∴68.0)3/4()3/4(2)3/4(23333===R R a R bccππζ (2)六方密堆 n=64. 试确定简单立方、体心立方和面心立方结构中原子半径和点阵参数之间的关系。

解：简单立方、体心立方和面心立方结构均属立方晶系，点阵参数或晶格参数关系为90,=====γβαc b a ，因此只求出a 值即可。

对于（1）fcc(面心立方)有a R 24=, 24R a =， 90,=====γβαc b a(2) bcc 体心立方有：a 34R = 34R a =； 90,=====γβαc b a(3) 简单立方有：R a 2=， 90,=====γβαc b a74.0)3(3812)3/4(6)2321(6)3/4(633hcp =⋅=⋅R R R R a a c R ππξ＝R a a c 238==5. 金属铷为A2型结构，Rb 的原子半径为0.2468 nm ，密度为1.53g·cm-3，试求：晶格参数a 和Rb 的相对原子质量。

解：AabcN nM=ρ 其中, ρ为密度, c b a 、、为晶格常数, 晶胞体积abc V =，N A 为阿伏加德罗常数6.022×1023 mol -1，M 为原子量或分子量，n 为晶胞中分子个数，对于金属则上述公式中的M 为金属原子的原子量，n 为晶胞中原子的个数。

第二章 孔、轴极限与配合思考题与习题答案2-1题解：（1）由题已知m m 039.0ES += m m 002.0+=es 0mm EI = m m 002.0-=ei 又由D D ES up -= d d up -=esD D EI low -= d d low -=eim m 50d D ==∴50.039mm D ES D up =+= mm 002.50d es d up =+= 50m m D EI D low =+= mm 977.49d ei d low =+= 由极限偏差作公差图，如图：（2）()[]mm 062.0mm 023.0039.0ei -ES d D X low up m ax +=--+==-= ()mm 002.0mm 002.00es -ES d D Y up low m ax -=-==-= ∴该配合为过渡配合2-2题已知：公称尺寸150Φmm ，090.0X m ax +=mm ，018.0X m in +=mm 求： 此配合解： ①没有特殊要求，取基孔制②根据公式s h m in m ax f T T X -X T +==得072.0018.0090.0T T s h =-=+mm查表2-1可知，公称尺寸为150Φ时，0.040IT7=,025.0IT6=mm 高精度等级时，孔应比轴低一级。

所以取孔为IT7，轴为IT6， 由于是基孔制，则0EI =,根据EI -ES T h =， 则0.04000.040EI T ES h +=+=+=mm ③确定轴的基本偏差因为es -EI X m in =，所以初步得到轴的基本偏差018.0X es m in -=-=mm 查表2-3可知，当公称尺寸为150Φmm 时，轴的基本偏差为g 时，014.0es -=，与初步得到轴的基本偏差较为接近。

根据ei es T s -=，可得 s T es ei -==-0.014-0.025=0.039所以，孔轴的配合为()()014.0039.0040.006g H7150--+Φ2-3题已知：公称尺寸25Φmm ，086.0X m ax +=mm ，023.0X m in +=mm 求： 孔、轴公差等级及基孔制和基轴制时的配合。

电工学第二章习题一、填空题1． 两个均为40F μ的电容串联后总电容为 80 F μ，它们并联后的总电容为 20F μ。

2. 表征正弦交流电振荡幅度的量是它的 最大值 ；表征正弦交流电随时间变化快慢程度的量是 角频率ω ；表征正弦交流电起始位置时的量称为它的 初相 。

三者称为正弦量的 三要素 。

3. 电阻元件上任一瞬间的电压电流关系可表示为 u = iR ；电感元件上任一瞬间的电压电流关系可以表示为dtdiLu =L ；电容元件上任一瞬间的电压电流关系可以表示为dtduCi =C 。

由上述三个关系式可得， 电阻 元件为即时元件； 电感 和 电容 元件为动态元件。

4. 在RLC 串联电路中，已知电流为5A ，电阻为30Ω，感抗为40Ω，容抗为80Ω，那么电路的阻抗为 50Ω ，该电路为 容 性电路。

电路中吸收的有功功率为 750W ，吸收的无功功率又为 1000var 。

二、选择题1. 某正弦电压有效值为380V ，频率为50Hz ，计时始数值等于380V ，其瞬时值表达式为（ B ）A 、t u 314sin 380=V ；B 、)45314sin(537︒+=t u V ；C 、)90314sin(380︒+=t u V 。

2. 一个电热器，接在10V 的直流电源上，产生的功率为P 。

把它改接在正弦交流电源上，使其产生的功率为P/2，则正弦交流电源电压的最大值为（D ） A 、； B 、5V ； C 、14V ； D 、10V 。

3. 提高供电电路的功率因数，下列说法正确的是（ D ）A 、减少了用电设备中无用的无功功率；B 、减少了用电设备的有功功率，提高了电源设备的容量；C 、可以节省电能；D 、可提高电源设备的利用率并减小输电线路中的功率损耗。

4. 已知)90314sin(101︒+=t i A ，︒+=30628sin(102t i ）A ，则（ C ）A 、i1超前i260°；B 、i1滞后i260°；C 、相位差无法判断。

第二章习题答案2.1.1 质点的运动学方程为j t i t r j i t r ˆ)14(ˆ)32()2(ˆ5ˆ)23()1(-+-=++=求质点的轨迹并用图表示解：（1）⎭⎬⎫=+=523y t x 平行于x 轴的直线：y=5(2)⎭⎬⎫-=-=1432t y t x 消去t 的轨迹方程：0534=-+y x2.1.2 质点的运动学方程为kj e i e r t t ˆ2ˆˆ22++=-。

(1)求质点的轨迹。

（2）求自t = -1 至t = 1质点的位移解：（1）由运动方程得质点轨迹的参数方程为 )3()2()1(222⎪⎩⎪⎨⎧===-z ey e x tt （1）x （2）消去t ，得轨迹方程 ⎩⎨⎧==21z xy（2）自t = -1 至t = 1质点的位移：je e i e e r r r k j e i e r k j e i e r t t ˆ)(ˆ)(ˆ2ˆˆˆ2ˆˆ,1,1222211221221-------+-=-=∆++=++==-= 2.1.3 质点的运动学方程为j t i t r ˆ)32(ˆ42++=。

（1）求质点的轨迹；（2）求自t=0至t=1质点的位移解：由质点的运动方程⎩⎨⎧+==)2(32)1(42t y t x （1） 质点的轨迹：消去t 得：2)3(-=y x（2） 位移：ji r r r j i r j r t t ˆ2ˆ4ˆ5ˆ4ˆ3101221+=-=∆+====2.2.1 雷达站于某瞬时测得飞机位置为R 1=4100m ，θ1=33.70，0.75s 后测得R 2=4240m ，θ2=29.30，R 1,R 2均在铅直平面内，求飞机瞬时速度的近似值和飞行方向（α角）。

解：取雷达站位置为原点，飞机在两个时刻的位置矢量分别为r 1和r 2，则| r 1|=R 1, | r 2|=R 2，如图所示由余弦定理，在0.75s 时间间隔内飞机的位移的大小为mR R R R r r r r r 4.349)3.297.33cos(42404100242404100)cos(2)cos(200222121222121212221≈-⨯⨯-+=--+=--+=∆θθθθ飞机的瞬时速度的大小：==∆∆≈smt r v 75.04.349465.8m/s飞机的瞬时速度方向：由正弦定理)3.297.33sin(4.349sin 4240)sin(sin 00212-=⇒-∆=γθθγr r100001207.341806.11193.0arcsin 18090,93.04.4sin 4.3494240sin ≈--=∴≈-=∴>∴>≈=γθαγγγr r另解：利用矢量在直角坐标系中的正交分解. 选平面直角坐标系,取雷达站的位置为坐标原点,x 轴沿水平方向,y 轴铅直向上,则在两个时刻飞机的位置矢量分别可表示为ji j i jR i R r ji j i jR i R r ˆ98.2074ˆ57.3697ˆ3.29sin 4240ˆ3.29cos 4240ˆsin ˆcos ˆ86.2274ˆ01.3411ˆ7.33sin 4100ˆ7.33cos 4100ˆsin ˆcos 00222220011111+=⨯+⨯=+=+=⨯+⨯=+=θθθθ 飞机飞行0.75s 后的位移矢量为j i r r r ˆ88.199ˆ56.28612-=-=∆飞机瞬时速度的大小的近似值:s m t rv /8.46575.038.34975.088.19956.28622=≅+=∆∆≈飞机瞬时速度的方向与x 轴的夹角:09.3482.038.34956.286ˆcos =∴==∆⋅∆=ααr i r2.2.2 一圆柱体沿抛物线轨道运动.抛物线的轨道方程为y=x 2/200(长度:mm).第一次观测到圆柱体在x=249mm 处,经过时间2ms 后圆柱体移到x=234mm 处.求圆柱体瞬时速度的近似解：第一次观测时，x=249mm, y=x 2/200=(249)2/200≈310mm ，j i r ˆ310ˆ2491+=2ms 后，x=234mm, y=x 2/200=(234)2/200≈273.78mm ，j i r ˆ78.273ˆ2342+=圆柱体的位移：mm r j i r r r 2.3922.3615ˆ22.36ˆ152212≈+=∆--=-=∆∴ms mm msmm t r v /6.1922.39==∆∆≈速度与x 轴的夹角：5.112383.02.3915ˆcos -≈∴-≈-=∆⋅∆=ααr i r2.2.3 一人在北京音乐厅内听音乐，离演奏着17m 。

第二章2-1 试证明图P2-1中周期性信号可以展开为 （图略）04(1)()cos(21)21nn s t n t n ππ∞=-=++∑ 证明：因为()()s t s t -=所以000022()cos cos cos 2k k k k k k kt kt s t c c c kt T πππ∞∞∞======∑∑∑101()00s t dt c -=⇒=⎰ 1111221111224()cos ()cos cos sin 2k k c s t k tdt k tdt k tdt k πππππ----==-++=⎰⎰⎰⎰ 0,24(1)21(21)n k n k n n π=⎧⎪=⎨-=+⎪+⎩所以 04(1)()cos(21)21nn s t n t n ππ∞=-=++∑2-2设一个信号()s t 可以表示成()2c o s (2)s t t t πθ=+-∞<<∞试问它是功率信号还是能量信号，并求出其功率谱密度或能量谱密度。

解：功率信号。

222()cos(2)sin (1)sin (1)[]2(1)(1)j ft j j s f t e dt f f e e f f τπττθθπθτπτπτπτπτ---=+-+=+-+⎰ 21()lim P f s τττ→∞= 2222222222sin (1)sin (1)sin (1)sin (1)lim 2cos 24(1)(1)(1)(1)f f f f f f f f ττπτπτπτπτθπτπτπτ→∞-+-+=++-+-+ 由公式22sin lim ()t xt x tx δπ→∞= 和 sin lim ()t xt x x δπ→∞= 有()[(1)][(1)]441[(1)(1)]4P f f f f f ππδπδπδδ=-++=++- 或者001()[()()]4P f f f f f δδ=-++2-3 设有一信号如下：2exp()0()00t t x t t -≥⎧=⎨<⎩ 试问它是功率信号还是能量信号，并求出其功率谱密度或能量谱密度。

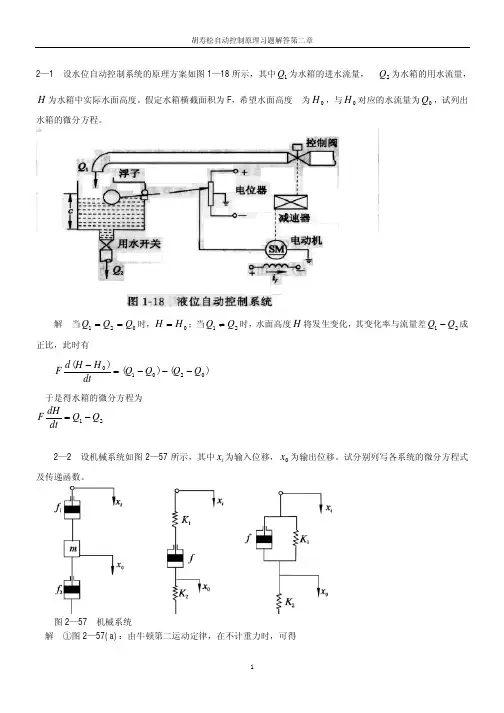
集成电路版图设计习题答案第2章 集成电路制造工艺【习题答案】1．硅片制备主要包括（直拉法）、（磁控直拉法）和（悬浮区熔法）等三种方法。

2．简述外延工艺的用途。

答：外延工艺的应用很多。

外延硅片可以用来制作双极型晶体管，衬底为重掺杂的硅单晶（n +），在衬底上外延十几个微米的低掺杂的外延层（n ），双极型晶体管（NPN ）制作在外延层上，其中b 为基极，e 为发射极，c 为集电极。

在外延硅片上制作双极型晶体管具有高的集电结电压，低的集电极串联电阻，性能优良。

使用外延硅片可以解决增大功率和提高频率对集电区电阻要求上的矛盾。

图 外延硅片上的双极型晶体管集成电路制造中，各元件之间必须进行电学隔离。

利用外延技术的PN 结隔离是早期双极型集成电路常采用的电隔离方法。

利用外延硅片制备CMOS 集成电路芯片可以避免闩锁效应，避免硅表面氧化物的淀积，而且硅片表面更光滑，损伤小，芯片成品率高。

外延工艺已经成为超大规模CMOS 集成电路中的标准工艺。

3．简述二氧化硅薄膜在集成电路中的用途。

答：二氧化硅是集成电路工艺中使用最多的介质薄膜，其在集成电路中的应用也非常广泛。

二氧化硅薄膜的作用包括：器件的组成部分、离子注入掩蔽膜、金属互连层之间的绝缘介质、隔离工艺中的绝缘介质、钝化保护膜。

4．为什么氧化工艺通常采用干氧、湿氧相结合的方式？答：干氧氧化就是将干燥纯净的氧气直接通入到高温反应炉内，氧气与硅表面的原子反应生成二氧化硅。

其特点：二氧化硅结构致密、均匀性和重复性好、针孔密度小、掩蔽能力强、与光刻胶粘附良好不易脱胶；生长速率慢、易龟裂不宜生长厚的二氧化硅。

湿氧氧化就是使氧气先通过加热的高纯去离子水（95℃），氧气中携带一定量的水汽，使氧化气氛既含有氧，又含有水汽。

因此湿氧氧化兼有干氧氧化和en +SiO 2n -Si 外延层 n +Si 衬底水汽氧化的作用，氧化速率和二氧化硅质量介于二者之间。

实际热氧化工艺通常采用干、湿氧交替的方式进行。

第二章 流体输送机械1．用离心油泵将甲地油罐的油品送到乙地油罐。

管路情况如本题附图所示。

启动泵之前A 、C 两压力表的读数相等。

启动离心泵并将出口阀调至某开度时，输油量为39 m 3/h ，此时泵的压头为38 m 。

已知输油管内径为100 mm ，摩擦系数为0.02；油品密度为810 kg/m 3。

试求（1）管路特性方程；（2）输油管线的总长度（包括所有局部阻力当量长度）。

解：（1）管路特性方程甲、乙两地油罐液面分别取作1-1’与2-2’截面，以水平管轴线为基准面，在两截面之间列柏努利方程，得到2e e H K Bq =+由于启动离心泵之前p A =p C ,于是g p Z K ρ∆+∆==0则 2e e H Bq = 又 e 38H H ==m])39/(38[2=B h 2/m 5=2.5×10–2 h 2/m 5则 22e e 2.510H q -=⨯（q e 的单位为m 3/h ）（2）输油管线总长度2e 2l l u H d gλ+= 39π0.0136004u ⎡⎤⎛⎫⎛⎫=⨯ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦m/s=1.38 m/s于是 e 22229.810.1380.02 1.38gdH l l u λ⨯⨯⨯+==⨯m=1960 m 2．用离心泵（转速为2900 r/min ）进行性能参数测定实验。

在某流量下泵入口真空表和出口压力表的读数分别为60 kPa 和220 kPa ，两测压口之间垂直距离为0.5 m ，泵的轴功率为6.7 kW 。

泵吸入管和排出管内径均为80 mm ，吸入管中流动阻力可表达为2f,0113.0h u -=∑（u 1为吸入管内水的流速，m/s ）。

离心泵的安装高度为2.5 m ，实验是在20 ℃，98.1 kPa习题1 附图的条件下进行。

试计算泵的流量、压头和效率。

解：（1）泵的流量由水池液面和泵入口真空表所在截面之间列柏努利方程式（池中水面为基准面），得到∑-+++=10,211120f h u p gZ ρ将有关数据代入上式并整理，得48.3581.95.2100010605.3321=⨯-⨯=u184.31=u m/s则 2π(0.08 3.1843600)4q =⨯⨯⨯m 3/h=57.61 m 3/h(2) 泵的扬程29.04m m 5.081.9100010)22060(3021=⎥⎦⎤⎢⎣⎡+⨯⨯+=++=h H H H(3) 泵的效率s 29.0457.6110009.81100%100036001000 6.7Hq g P ρη⨯⨯⨯==⨯⨯⨯=68%在指定转速下，泵的性能参数为：q =57.61 m 3/h H =29.04 m P =6.7 kW η=68% 3．对于习题2的实验装置，若分别改变如下参数，试求新操作条件下泵的流量、压头和轴功率（假如泵的效率保持不变）。

第二章课后习题自动化朱秀红1.AT89系列的单片机的内部数据存储器可以分为哪几个不同的区域？各有什么特点？CPU是如何对不同空间进行寻址的？单片机的片内数据存储器地址范围是00H-FFH，有256B。

对于51系列高128B 被特殊功能寄存器占用。

对于52系列，高128B与特殊功能寄存器地址重叠，相同的地址，物理上是分开独立的。

存储器划分和特点：（1）低128B RAM区（00H--7FH）1）工作寄存器组区(00H--1FH)：最低的32个单元是4个通用工作寄存器组，每个寄存器组包括8个寄存器，编号为R0--R7，PSW中的RS0和RS1用来确定当前使用哪一个寄存器组。

某一个时刻只能使用其中一个寄存器组，系统复位后指向工作寄存器组02）位寻址区（20H--2FH):位地址的表示形式：一种采用位地址的表示形式；一种采用字节地址（20H--2FH）.位数的表示形式特点：该区域每个单元可以作为一般用户RAM区RAM单元整体使用;该区域的每一位可以作为单独的可寻址位单独使用3）用户RAM区（30H--7FH）:可供用户作为数据存储区，这区域的操作指令丰富，数据处理灵活方便，是非常宝贵的资源。

但是，如果堆栈指针初始化时设置在这个区域，要留出足够的字节单元作为堆栈区，以防止在数据存储时，破坏堆栈的内容。

寻址方式：低128B（00H--7FH）可通过直接和间接寻址方式访问高128B（80H--FFH）直接寻址方式访问特殊功能寄存器（SFR）；间接寻址访问高128B RAM（2）高128B的特殊功能寄存器（SRF）区1）在该区域中除了SFR之外剩余的空闲单元用户不得使用2）必须使用直接寻址的方式对SFR进行访问，可使用寄存器名称3）具有位地址和位名称的SFR才可以位寻址SFR“字节地址.位”直接使用位地址表示；使用位名称表示；使用SFR“字节地址.位”形式表示；使用SFR“名称.位”表示2.PSW包含哪些程序状态信息？这些状态信息的作用是什么？PSW是一个8位的寄存器，包含各种程序状态信息，相当于一个标志寄存器，以供程序查询和判别CY AC F0 RS1 RS0 0V --- PCY(PSW.7):进位标志，在执行某些算术和逻辑指令时可以被硬件和软件置位和清零，CY在布尔处理机中被认为是位累加器AC(PSW.6):辅助进位标志，当进行加法或减法操作时而产生低4位向高4位数进位或借位时，AC将被硬件置位，否则被清零F0(PSW.5):用户标志位。

第二章 词法分析2.1 完成下列选择‎题： (1) 词法分析器的‎输出结果是 。

a. 单词的种别编‎码 b. 单词在符号表‎中的位置 c. 单词的种别编‎码和自身值 d. 单词自身值 (2) 正规式M1和‎M 2等价是指‎ 。

a. M1和M2的‎状态数相等b. M1和M2的‎有向边条数相‎等c. M1和M2所‎识别的语言集‎相等d. M1和M2状‎态数和有向边‎条数相等 (3) DFA M(见图2-1)接受的字集为‎ 。

a. 以0开头的二‎进制数组成的‎集合b. 以0结尾的二‎进制数组成的‎集合c. 含奇数个0的‎二进制数组成‎的集合d. 含偶数个0的‎二进制数组成‎的集合 【解答】(1) c (2) c (3) d图2-1 习题2.1的DFA M2.2 什么是扫描器‎？扫描器的功能‎是什么？ 【解答】 扫描器就是词‎法分析器，它接受输入的‎源程序，对源程序进行‎词法分析并识‎别出一个个单‎词符号，其输出结果是‎单词符号，供语法分析器‎使用。

通常是把词法‎分析器作为一‎个子程序，每当词法分析‎器需要一个单‎词符号时就调‎用这个子程序‎。

每次调用时，词法分析器就‎从输入串中识‎别出一个单词‎符号交给语法‎分析器。

2.3 设M=({x,y}, {a,b}, f, x, {y})为一非确定的‎有限自动机，其中f 定义如‎下： f(x,a)={x,y} f{x,b}={y} f(y,a)=Φ f{y,b}={x,y} 试构造相应的‎确定有限自动‎机M ′。

【解答】 对照自动机的‎定义M=(S,Σ,f,So,Z)，由f 的定义可‎知f(x,a)、f(y ,b)均为多值函数‎，因此M 是一非‎确定有限自动‎机。

先画出NFA ‎ M 相应的状态‎图，如图2-2所示。

图2-2 习题2.3的NFA M用子集法构造‎状态转换矩阵‎，如表表2-1 状态转换矩阵‎1b将转换矩阵中‎的所有子集重‎新命名，形成表2-2所示的状态‎转换矩阵，即得到 M ′=({0,1,2},{a,b},f,0,{1,2})，其状态转换图‎如图2-3所示。

第2章 习题2-1 a) 试证明均匀形核时，形成临界晶粒的△G K 与其临界晶核体积V K 之间的关系式为2K K V V G G ∆=-∆； b) 当非均匀形核形成球冠形晶核时，其△G K 与V K 之间的关系如何？a) 证明 因为临界晶核半径 2K Vr G σ=-∆ 临界晶核形成功 32163()K V G G πσ∆=∆ 故临界晶核的体积 3423K K K Vr G V G π∆==∆ 所以 2K K V V G G ∆=-∆ b) 当非均匀形核形成球冠形晶核时，SL 2K Vr G σ=-∆非 临界晶核形成功 3324(23cos cos )3()K SL V G G πσθθ∆=-+∆非故临界晶核的体积 331(23cos cos )3K K V r πθθ=-+非（） 3333SL 3281(23cos cos )(23cos cos )33()SL K V V V V V G G G G σπσπθθθθ∆=--+∆=-+∆∆() 所以 2K K V V G G ∆=-∆非 2-2 如果临界晶核是边长为a 的正方体，试求出其△G K 与a 的关系。

为什么形成立方体晶核的△G K 比球形晶核要大？解：形核时的吉布斯自由能变化为326V V G V G A a G a σσ∆=∆+=∆+ 令()0d G da∆= 得临界晶核边长4K V a G σ=-∆ 临界形核功3333222244649632()6()()()()K tK V K V V V V V V G V G A G G G G G G σσσσσσσ∆=∆+=-∆+-=-+=∆∆∆∆∆ 2K Vr G σ=-∆，球形核胚的临界形核功 332242216()4()33()K bV V V V G G G G G σσπσππσ∆=-∆+=∆∆∆ 将两式相比较3232163()13262()K K b V t V G G G G πσπσ∆∆==≈∆∆ 可见形成球形晶核得临界形核功仅为形成立方形晶核的1/2。