高二数学抛物线公式总结
- 格式:doc
- 大小:27.50 KB
- 文档页数:4







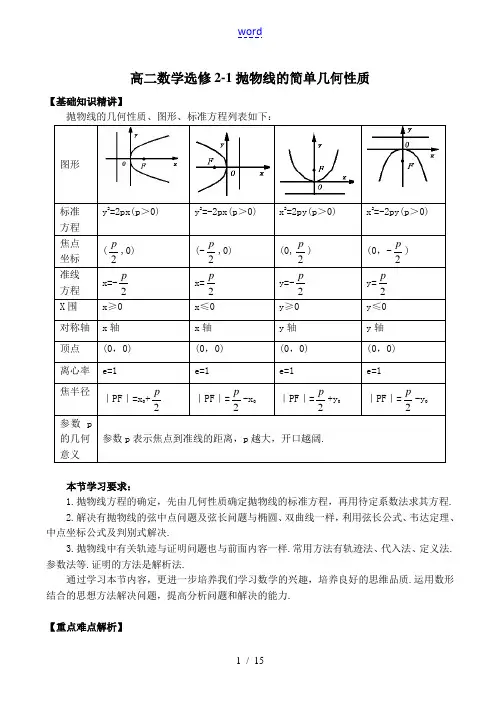
高二数学选修2-1抛物线的简单几何性质【基础知识精讲】抛物线的几何性质、图形、标准方程列表如下: 图形标准 方程 y 2=2px(p >0)y 2=-2px(p >0)x 2=2py(p >0)x 2=-2py(p >0)焦点 坐标 (2p,0) (-2p,0) (0,2p ) (0,-2p ) 准线 方程 x=-2px=2p y=-2py=2p X 围x ≥0x ≤0 y ≥0 y ≤0 对称轴 x 轴 x 轴 y 轴 y 轴 顶点(0,0)(0,0) (0,0) (0,0) 离心率 e=1 e=1e=1e=1焦半径 |PF |=x 0+2p |PF |=2p -x 0 |PF |=2p +y 0 |PF |=2p -y 0 参数p 的几何 意义参数p 表示焦点到准线的距离,p 越大,开口越阔.本节学习要求:1.抛物线方程的确定,先由几何性质确定抛物线的标准方程,再用待定系数法求其方程.2.解决有抛物线的弦中点问题及弦长问题与椭圆、双曲线一样,利用弦长公式、韦达定理、中点坐标公式及判别式解决.3.抛物线中有关轨迹与证明问题也与前面内容一样.常用方法有轨迹法、代入法、定义法.参数法等.证明的方法是解析法.通过学习本节内容,更进一步培养我们学习数学的兴趣,培养良好的思维品质.运用数形结合的思想方法解决问题,提高分析问题和解决的能力.【重点难点解析】1.抛物线的几何性质和椭圆、双曲线比较起来,差别较大,它的离心率等于1;它只有一个焦点、一个顶点、一条对称轴、一条准线;它没有中心.通常称抛物线为无心圆锥曲线,而称椭圆和双曲线为有心圆锥曲线.应熟练掌握抛物线的四种标准方程.本节重点是抛物线的简单几何性质,难点是几何性质的灵活应用.例1 已知抛物线顶点在原点,对称轴为x 轴,抛物线上的点(x 0,-8)到焦点的距离等于17,求抛物线方程.分析 设方程为y 2=2px(p >0)或y 2=-2px(p >0)则 x 0+2p =17或2p-x 0=17 即 x 0=17-2p 或x 0=2p-17将(17-2p ,-8)代入y 2=2px解得 p=2或p=32 将(2p -17,-8)代入y 2=-2px 解得 p=2或p=32∴所求抛物线方程为y 2=±4x 或y 2=±64x.例2 求抛物线y 2=4x 中斜率为2的平行弦中点的轨迹方程.分析 本例可设平行弦的纵截距为参数、运用判别式及韦达定理、中点坐标公式来求,也可设点参数运用点差法求解.设AB 是抛物线中斜率为2的平行弦中任一条弦,A(x 1,y 1),B(x 2,y 2)AB 中点M(x,y)由⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=--=+=+==2224421212121222121x x y y yy y x x x x y xy 得:y=1 代入y 2=4x 得x=41 ∴轨迹方程为y=1(x >41)例3 设点A 和B 为抛物线y 2=4px(p >0)上原点以外的两个动点.已知OA ⊥OB ,OM ⊥AB 于M ,求点M 的轨迹方程,并说明表示什么曲线.分析 设A(4pt 21,4pt 1),B(4pt 22,4pt 2),OA 、OB 的斜率分别为k OA 、k OB 则 k OA =11t ,k OB =21t由OA ⊥OB ,得 k OA ·k OB =211t t =-1⇒t 1t 2=-1① ∵点A 在AB 上,得直线AB 的方程为 y-4pt 1=211t t + (x-4pt 21)② 由OM ⊥AB ,得直线OM 方程为 y=-(t 1+t 2)x ③设点M(x,y),则x,y 满足②③两式 将②化为:y(t 1+t 2)=x+4pt 1t 2=x-4p ④ 由③×④得:x 2+y 2-4px=0 ∵A 、B 是原点以外的两点 ∴x ≠0∴点M 的轨迹是以(2p,0)为圆心,以2p 为半径的圆(去掉原点).【难题巧解点拨】例1 已知抛物线y 2=2px 上两点A 、B ,BC ⊥x 轴交抛物线于C ,AC 交x 轴于E ,BA 延长交x 轴于D ,求证:O 为DE 中点.分析 只需证出D 、E 两点的横坐标互为相反数即可,设A(2pt 21,2pt 1),B(2pt 22,2pt 2)则 C(2pt 22,-2pt 2) AC :y-2pt 1=211t t -(x-2pt 21) 令y=0,得x D =2pt 1t 2 BA :y-2pt 1=211t t + (x-2pt 21) 令y=0,得x E =-2pt 1t 2 ∴x D +x E =0即O 为DE 中点.例2 设抛物线过定点A(0,2)且以x 轴为准线. (Ⅰ)试求抛物线顶点M 的轨迹C 的方程;(Ⅱ)如果点P(a,1)不在线段y=1(-2≤x ≤2)上,那么当a 取何值时,过P 点存在一对互相垂直的直线同时与曲线C 各有两个交点?分析 (Ⅰ)设抛物线顶点M(x,y),y >0,则其焦点为F(x,2y). 据抛物线定义有22)22(-+y x =2即 42x +(y-1)2=1(y ≠0)∴抛物线顶点M 的轨迹C 的方程是42x +(y-1)2=1(y ≠0) (Ⅱ)过P 点的直线可设为l :y-1=k(x-a).由已知P(a,1)不在曲线C 上,则⎩⎨⎧=-++-=4)1(41)(22y x a x k y 消去y ,得x 2+4k 2(x-a)2=4 即(1+4k 2)x 2-8k 2ax+4(k 2a 2-1)=0 ∴△=16[k 2(4-a 2)+1]过点P 存在一对互相垂直的直线同时与曲线C 各有两个不同的交点的充要条件是关于斜率k 的不等式组⎪⎩⎪⎨⎧>+->+-01)4(101)4(2222a ka k 有解 ∵点P 不在直线y=1(-2≤x ≤2)上,∴|a |>2,4-a 2<0.∴上不等式组可化为⎪⎩⎪⎨⎧->-<4,412222a k a k∴a 2-4<412-a 解a 2<5又|a |>2,∴2<|a |<5 即a ∈(-5,-2)∪(2,5)【命题趋势分析】本节与椭圆、双曲线的相同内容相似,都是高考的重要内容.圆锥曲线的基础知识;直线与圆锥曲线的位置关系、弦长、中点弦及弦的中点的轨迹问题;圆锥曲线中的有关最值问题等等.本章内容为高考压轴题的高频题.【典型热点考题】例1 抛物线y=x 2的弦AB 保持与圆x 2+y 2=1相切移动,求过A 、B 的抛物线的切线交点的轨迹方程.分析一 如图,设抛物线弦AB 与圆x 2+y 2=1相切于P(x 0,y 0),则过P 点的圆的切线方程为x 0x+y 0y=1.由⎩⎨⎧==+2001xy y y x x 得y 0x 2+x 0x-1=0设A 的坐标为(x 1,x 21),B(x 2,x 22),由韦达定理,得 x 1+x 2=-00y x ,x 1·x 2=-01y又过A 、B 两点的抛物线的切线方程分别为 y+x 12=2x 1x,y+x 22=2x 2x , 则两切线交点Q(x,y)是方程组⎪⎩⎪⎨⎧=+=+xx x y x x x y 22212122②①①-②得x 21-x 22=2(x 1-x 2)x. ∴ 2x=x 1+x 2=-y x ③①×x 2-②×x 1得(x 2-x 1)y+x 1x 2(x 1-x 2)=0 ∴y=x 1x 2=-1y ④ 由③、④得x 0=y x 2,y 0=-y1∵P(x 0,y 0)在圆x 2+y 2=1上, ∴(y x 2)2+(-y1)2=1 即 y 2-4x 2=1,这是双曲线.由条件知,所求轨迹是焦点在y 轴上,a=1、b=21的双曲线的下支的一部分. 分析二设抛物线的弦AB 与圆切于点P(x 0,y 0),则过P 点的圆的切线AB 的方程为 x 0x+y 0y=1①设过A 、B 两点的抛物线切线交点为Q(α,β)则AB 为抛物线的切点弦,其方程为 y+β=2αx ② 由①、②表示同一直线,于是有α20x =10-y =β1 ∴x 0=βα2 y 0=-β1 ∵P(x 0,y 0)在圆x 2+y 2=1上,∴(βα2)2+(-β1)2=1, 即β2-4α2=1,故 y 2-4x 2=1(x ∈R,y <0)例2 某蔬菜基地种植西红柿,由历年市场行情得知,从2月1日起的300天内,西红柿市场售价与上市时间的关系用如图甲所示的一条折线表示;西红柿的种植成本与上市时间的关系用如图乙所示的抛物线段表示.(1)写出如图甲所示市场售价与时间的函数关系式P =f(t);写出如图乙所示种植成本与时间的函数关系式Q =g(t).(2)认定市场售价减去种植成本为纯收益,问何时上市的西红柿纯收益最大? (注:市场售价和种植成本的单位:元/102kg ,时间单位:天)解:(1)f(t)=⎩⎨⎧≤<-≤≤-.300200,3002,2000,300t t t tg(t)=2001 (t-150)2+100,0≤t ≤300. (2)设t 时刻的纯收益为h(t),则由题意得h(t)=f(t)-g(t),即h(t)=⎪⎪⎩⎪⎪⎨⎧≤<-+-≤≤++-.300200,21025272001,2000,2175********t t t t t t当0≤t ≤200时,配方整理得 h(t)=-2001(t-50)2+100, 所以,当t =50时,h(t)取得区间[0,200]上的最大值100; 当200<t ≤300时,配方整理得 h(t)=-2001(t-350)2+100 所以,当t =300时,h(t)取得区间(200,300]上的最大值87.5.综上,由100>87.5可知,h(t)在区间[0,300]上可以取得最大值100,此时t =50,即从2月1日开始的第50天时,上市的西红柿纯收益最大.【同步达纲练习】A 级一、选择题1.若A 是定直线l 外的一定点,则过A 且与l 相切圆的圆心轨迹是( ) A.圆 B.椭圆 C.双曲线一支 D.抛物线2.抛物线y 2=10x 的焦点到准线的距离是( ) B.5D.103.已知原点为顶点,x 轴为对称轴的抛物线的焦点在直线2x-4y+11=0上,则此抛物线的方程是( )A.y 2=11xB.y 2=-11xC.y 2=22xD.y 2=-22x4.过抛物线y 2=2px(p >0)的焦点且垂直于x 轴的弦AB ,O 为抛物线顶点,则∠AOB( ) A.小于90°B.等于90° C.大于90°D.不能确定5.以抛物线y 2=2px(p >0)的焦半径|PF |为直径的圆与y 轴位置关系为( ) A.相交B.相离C.相切D.不确定 二、填空题6.圆心在抛物线y 2=2x 上,且与x 轴和该抛物线的准线都相切的圆的方程是.7.若以曲线252x +162y =1的中心为顶点,左准线为准线的抛物线与已知曲线右准线交于A 、B 两点,则|AB |=.8.若顶点在原点,焦点在x 轴上的抛物线截直线y=2x+1所得的弦长为15,则此抛物线的方程是.三、解答题9.抛物线x 2=4y 的焦点为F ,过点(0,-1)作直线l 交抛物线A 、B 两点,再以AF 、BF 为邻边作平行四边形FABR ,试求动点R 的轨迹方程.10.是否存在正方形ABCD ,它的对角线AC 在直线x+y-2=0上,顶点B 、D 在抛物线y 2=4x 上?若存在,试求出正方形的边长;若不存在,试说明理由.AA 级一、选择题1.经过抛物线y 2=2px(p >0)的所有焦点弦中,弦长的最小值为( ) A.p B.2pC.4pD.不确定2.直线y=kx-2交抛物线y 2=8x 于A 、B 两点,若AB 的中点横坐标为2,则|AB |为( ) A.15B.415C.215D.423.曲线2x 2-5xy+2y 2=1( ) A.关于x 轴对称B.关于y 轴对称C.关于原点对称,但不关于y=x 对称D.关于直线y=x 对称也关于直线y=-x 对称4.若抛物线y 2=2px(p >0)的弦PQ 的中点为(x 0,y 0)(y ≠0),则弦PQ 的斜率为( ) A.-0x p B.0y p C.px -D.-px 0 5.已知抛物线y 2=2px(p >0)的焦点弦AB 的两端点坐标分别为A(x 1,y 1),B(x 2,y 2),则2121x x y y 的值一定等于( )A.4B.-4C.p 2D.-p 2二、填空题6.抛物线y 2=4x 的弦AB 垂直于x 轴,若AB 的长为43,则焦点到AB 的距离为.7.以椭圆52x +y 2=1的右焦点F 为焦点,以原点为顶点作抛物线,抛物线与椭圆的一个公共点是A ,则|AF |=.8.若△OAB 为正三角形,O 为坐标原点,A 、B 两点在抛物线y 2=2px 上,则△OAB 的周长为. 三、解答题9.抛物线y=-22x 与过点M(0,-1)的直线l 相交于A 、B 两点,O 为坐标原点,若直线OA和OB 斜率之和为1,求直线l 的方程.10.已知半圆的直径为2r ,AB 为直径,半圆外的直线l 与BA 的延长线垂直,垂足为T ,且|TA |=2a(2a <2r),半圆上有M 、N 两点,它们与直线l 的距离|MP |、|NQ |满足条件|MP |=|AM |,|NQ |=|AN |,求证:|AM |+|AN |=|AB |.【素质优化训练】 一、选择题1.过点A(0,1)且与抛物线y 2=4x 有唯一公共点的直线的条数为( ) A.1 B.2 C.3 D.42.设抛物线y=ax 2(a >0)与直线y=kx+b 相交于两点,它们的横坐标为x 1,x 2,而x 3是直线与x 轴交点的横坐标,那么x 1、x 2、x 3的关系是( )A.x 3=x 1+x 2B.x 3=11x +21x C.x 1x 2=x 2x 3+x 3x 1D.x 1x 3=x 2x 3+x 1x 2 3.当0<k <31时,关于x 的方程x 2=kx 的实根的个数是( ) A.0个 B.1个 C.2个 D.3个4.已知点A(1,2),过点(5,-2)的直线与抛物线y 2=4x 交于另外两点B 、C ,则△ABC 是( ) A.锐角三角形 B.钝角三角形 C.直角三角形 D.不确定5.将直线x-2y+b=0左移1个单位,再下移2个单位后,它与抛物线y 2=4x 仅有一个公共点,则实数b 的值等于( )A.-1B.1C.7D.9 二、填空题6.抛物线y 2=-8x 被点P(-1,1)所平分的弦所在直线方程为.7.已知抛物线y 2=2x 的弦过定点(-2,0),则弦AB 中点的轨迹方程是. 8.已知过抛物线y 2=2px 的焦点F 的弦AB 被F 分成长度为m 、n 的两部分,则m 1+n1=. 三、解答题9.已知圆C 过定点A(0,p)(p >0),圆心C 在抛物线x 2=2py 上运动,若MN 为圆C 在x 轴上截得的弦,设|AM |=m,|AN |=n ,∠MAN=θ.(1)当点C 运动时,|MN |是否变化?写出并证明你的结论?(2)求m n +nm的最大值,并求取得最大值时θ的值和此时圆C 的方程.10.已知抛物线y 2=4ax(0<a <1)的焦点为F ,以A(a+4,0)为圆心,|AF |为半径在x 轴上方作半圆交抛物线于不同的两点M 和N ,设P 为线段MN 的中点,(Ⅰ)求|MF |+|NF |的值;(Ⅱ)是否存在这样的a 值,使|MF |、|PF |、|NF |成等差数列?如存在,求出a 的值,若不存在,说明理由.【生活实际运用】1.已知点P(x 0,y 0)在抛物线含焦点的区域内,求证以点P 为中点的抛物线y 2=2px(p >0)的中点弦方程为yy 0-p(x+x 0)=y 20-2px 0注:运用求中点弦的方法不难求出结论,这一结论和过抛物线y 2=2px 上点的切线方程有什么联系?若P(x 0,y 0)为非对称中心,将抛物线y 2=2px 换成椭圆22a x +22b y =1或双曲线22a x -22by =1,它们的中点弦存在的话,中点弦方程又将如何?证明你的结论.中点弦方程在高考中多以选择题、填空题的形式出现.2.公园要建造一个圆形的喷水池,在水池中央垂直于水面安装一个柱子OA ,O 恰在圆形水面中心,OA=1.25米.安置在柱子顶端A 处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路经落下,且在过OA 的任一平面上抛物线路径如图所示,为使水流形状较为漂亮,设计成水流在到OA 距离1米处达到距水面最大高度2.25米.如果不计其它因素,那么水池的半径至少要多少米,才能使喷出的水流不致落到池外?分析 根据图形的对称性,设出并求出一边的抛物线的方程,便可求出水池的半径. 以OA 所在直线为y 轴,过O 点作oy 轴的垂直线ox 轴,建立直角坐标系如图依题意A(0,1.25),设右侧抛物线顶点为则B(1,2.25),抛物线与x 轴正向交点为C ,OC 即圆型水池的半径.设抛物线ABC 的方程为 (x-1)2=-2p(y-2.25) 将A(0,1.25)代入求得p=21 ∴抛物线方程为(x-1)2=-(y-2.25) 令y=0,(x-1)2=1.52,x=2.5(米)即水池的半径至少要2.5米,才能使喷出的水流不致落到池外.【知识验证实验】1.求函数y=136324+--x x x -124+-x x 的最大值.解:将函数变形为y=222)2()3(---x x -222)1(-+x x ,由几何意义知,y 可以看成在抛物线f(x)=x 2上的点P(x,x 2)到两定点A(3,2)和B(0,1)的距离之差,∵|PA |-|PB |≤|AB |,∴当P 、A 、B 三点共线,且P 在B 的左方时取等号,此时P 点为AB 与抛物线的交点,即P 为(6371-,183719-)时,y max =|AB |=10. 2.参与设计小花园的喷水池活动. 要求水流形状美观,水流不落池外.【知识探究学习】1.如图,设F 是抛物线的焦点,M 是抛物线上任意一点,MT 是抛物线在M 的切线,MN 是法线,ME 是平行于抛物线的轴的直线.求证:法线MN 必平分∠FME ,即φ1=φ2.解:取坐标系如图,这时抛物线方程为y 2=2px.(p >0),因为ME 平行x 轴(抛物线的轴),∴φ1=φ2,只要证明φ1=φ3,也就是△FMN 的两边FM 和FN 相等.设点M 的坐标为(x 0,y 0),则法线MN 的方程是y-y 0=-py 0(x-x 0),令y=0,便得到法线与x 轴的交点N 的坐标(x 0+p,0),所以|FN |=|x 0+p-2p |=x 0+2p ,又由抛物线的定义可知,|MF |=x 0+2p,∴|FN |=|FM |,由此得到φ1=φ2=φ3,若M 与顶点O 重合,则法线为x 轴,结论仍然成立.2.课本第124页阅读材料: 圆锥曲线的光学性质及其应用参考答案: 【同步达纲练习】A 级1.D2.B3.D4.C5.C6.(x-21)2+(y ±1)2=17.3100 8.y 2=12x 或y 2=-4x 9.解:设R(x,y),∵F(0,1),∴平行四边形FARB 的中心为C(2x ,21+y ),l :y=kx-1,代入抛物线方程,得x 2-4kx+4=0,设A(x 1,y 1),B(x 2,y 2),则x 1+x 2=4k,x 1x 2=4,且△=16k 2-16>0,即|k|>1 ①,∴y 1+y 2=42221x x +=42)(21221x x x x -+=4k 2-2,∵C为AB 的中点.∴⎪⎪⎩⎪⎪⎨⎧-=+=+=+=1222122222121k y y y k x x x ⇒⎩⎨⎧-==3442k y k x 消去k 得x 2=4(y+3),由①得,|x |>4,故动点R 的轨迹方程为x 2=4(y+3)(|x |>4).10.解:设存在满足题意的正方形.则BD :y=x+b,代入抛物线方程得x 2+(2b-4)x+b 2=0,∴△=(2b-4)2-4b 2=16-16b >0,∴b <1, ①,设B(x 1,y 1),D(x 2,y 2),BD 中点M(x 0,y 0),则x 1+x 2=4-2b,∴x 0=2-b,y 0=x 0+b=2,∵M 在AC 直线上,∴(2-b)+2-2=0,∴b=2与①相矛盾,故不存在满足要求的正方形.AA 级1.B2.C3.D4.B5.B6.27.95-188.123p9.解:设l :y=kx-1,代入y=-22x ,得x 2+2kx-2=0,设A(x 1,y 1),B(x 2,y 2),则x 1+x 2=-2k,x 1x 2=-2,又11x y +22x y =111x kx -+221x kx -=2k-2121x x x x +=2k-22--k =k=1,∴直线l 的方程为y=x-1. 10.证明:由|MP |=|AM |,|NQ |=|AN |知M 、N 在以l 准,A 为焦点的抛物线上,建立直角坐标系,设抛物线方程为y 2=2px ,又|TA |=2a=p,∴抛物线方程为y 2=4ax ,又圆的方程为(x-a-r)2+y 2=r 2,将两方程相减可得:x 2+2(a-r)x+a 2+2ar=0,设M(x 1,y 1),N(x 2,y 2),则x 1+x 2=2r-2a,∴|AM |+|AN |=|PM |+|QN |=x 1+x 2+2a=2r,即|AM |+|AN |=|AB |【素质优化训练】1.C2.C3.D4.C5.C6.4x+y+3=07.y 2=x+2(在已知抛物线内部的部分) 8.2p9.解:(1)设圆心C(x 0,y 0),则x 20=2py 0,圆C 的半径|CA |=2020)(p y x -+,其方程为(x-x 0)2+(y-y 0)2=x 20+(y 0-p)2,令y=0,并将x 20=2py 0,代入,得x 2-2x 0x+x 20-p 2=0,解得x m =x 0-p,x N =x 0+p,∴|MN |=|x N -x M |=2p(定值)(2)∵m=|AM |=220)(p p x +-,n=|AN |=220)(p p x ++,∴m 2+n 2=4p 2+2x 20,m ·n=4044x p +,∴m n +n m =mn n m 22+=40422424x p x p ++=20202)(4y p p y p p ++=220)(2y p y p ++=222021y p py ++≤22,当且仅当y 0=p 时等号成立,x 0=±2p ,此时△M 为等腰直角三角形,且∠M=90°,∴∠MAN=21∠M=45°,故当θ=45°时,圆的方程为(x-2 p)2+(y-p)2=2p 2或(x+2p)2+(y-p)2=2p 210.解:(1)由已知得F(a,0),半圆为[x-(a+4)]2+y 2=16(y ≥0),设M(x 1,y 1),N(x 2,y 2),则|MF |+|NF |=x 1+x 2+2a=2(4-a)+2a=8(2)若|MF |、|PF |、|NF |成等成数列,则有2|PF |=|MF |+|NF |,另一方面,设M 、P 、N 在抛物线的准线上的射影为M ′、P ′、N ′,则在直角梯形M ′MNN ′中,P ′P 是中位线,又有2|P ′P |=|M ′M |+|N ′N |=|MF |+|FN |,因而|PF |=|P ′P |,∴P 点应在抛物线上,但P点是线段MN的中点,即P并不在抛物线上,故不存在使|MF|、|PF|、|NF|成等差数列的a值.。


高二数学《抛物线》知识精讲 人教版一. 本周教学内容: 《抛物线》 教学目标:1. 理解并掌握抛物线的定义及其标准方程。
2. 理解并掌握抛物线的性质,并会画图。
3. 掌握抛物线单元中的相关知识,并会综合应用。
能力训练:1. 掌握抛物线的定义及标准方程、几何性质的综合应用。
2. 会求轨迹方程及抛物线的实际应用问题。
3. 准确把握抛物线标准方程的四种形式,进一步巩固待定系数法。
4. 进一步培养学生数形结合的能力,并能灵活运用常用的一些数学变换方法解决综合性问题。
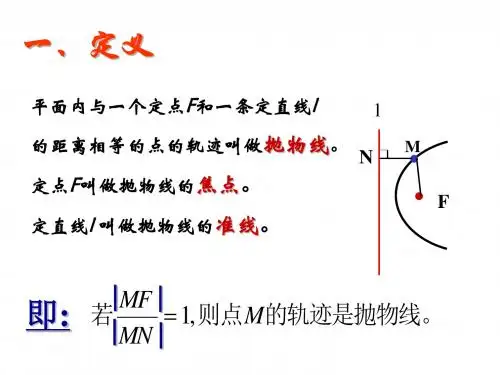
教学过程: 知识提要: 1. 抛物线的定义:平面内与一个定点F 和一条定直线l 的距离相等的点的轨迹叫做抛物线,定点F 叫抛物线的焦点,直线l 叫抛物线的准线。
2. 抛物线的标准方程:(1)顶点在原点,焦点在x 轴正半轴上:y 2=2px ,(p>0)。
(2)顶点在原点,焦点在x 轴负半轴上:y 2=-2px ,(p>0)。
(3)顶点在原点,焦点在y 轴的正半轴上:x 2=2py ,(p>0)。
(4)顶点在原点,焦点在y 轴负半轴上,x 2=-2py ,(p>0)。
3. 抛物线的几何性质:(1)焦点在x 轴正半轴上的抛物线y 2=2px ,(p>0)的几何性质: ①范围:x ≥0,y ∈R 。
②对称性:图形关于x 轴对称。
③顶点:0(0,0)。
④离心率:e=1。
⑤准线:。
x p=-2说明:其实从图形上就可以反映前三条性质,下面列表给出四种形式的性质:图形 =2px(p>0)=2py(p>0)二. 重点、难点:重点:抛物线的定义,标准方程,几何性质的综合运用。
难点:抛物线的几何性质在解题及证题中的运用。
【典型例题分析】 例1. 选择题:1. 抛物线y=ax 2(a ≠0)的焦点坐标是( )A aB aC aD a.().().().()140140014014,,,,--解:把方程化为:≠,与对照。
高二数学抛物线公式总结
同学们进入高二要求背诵的公式也逐渐增多,为此查字典数学网整理了高二数学抛物线公式总结,请参考。
1.抛物线的定义摘
定义:平面内到一定点(F)和一条定直线(l)的距离相等的点的轨迹叫抛物线。
这个定点F叫抛物线的焦点,这条定直线l 叫抛物线的准线。
需强调的是,点F不在直线l上,否则轨迹是过点F且与l 垂直的直线,而不是抛物线。
2.抛物线的方程
对于以上四种方程:应注意掌握它们的规律:曲线的对称轴是哪个轴,方程中的该项即为一次项;一次项前面是正号则曲线的开口方向向x轴或y轴的正方向;一次项前面是负号则曲线的开口方向向x轴或y轴的负方向。
3.抛物线的几何性质
以标准方程y2=2px为例
(1)范围:x
(2)对称轴:对称轴为y=0,由方程和图像均可以看出;
(3)顶点:O(0,0),注:抛物线亦叫无心圆锥曲线(因为无中心);
(4)离心率:e=1,由于e是常数,所以抛物线的形状变化是由方程中的p决定的;
(6)焦半径公式:
抛物线上一点P(x1,y1),F为抛物线的焦点,对于四种抛物线的焦半径公式分别为(p0):
(7)焦点弦长公式:
对于过抛物线焦点的弦长,可以用焦半径公式推导出弦长公式。
设过抛物线y2=2px(pO)的焦点F的弦为AB,A(x1,y1),B(x2,y2),AB的倾斜角为,则有
①|AB|=x1+x2+p
以上两公式只适合过焦点的弦长的求法,对于其它的弦,只能用弦长公式来求。
(8)直线与抛物线的关系:
直线与抛物线方程联立之后得到一元二次方程:
ax2+bx+c=0,当a0时,两者的位置关系的判定和椭圆、双曲线相同,用判别式法即可;但如果a=0,则直线是抛物线的对称轴或是和对称轴平行的直线,此时,直线和抛物线相交,但只有一个公共点。
(9)抛物线y2=2px的切线:
①如果点P(x0,y0)在抛物线上,则y0y=p(x+x0);
(10)参数方程
教师范读的是阅读教学中不可缺少的部分,我常采用范读,让幼儿学习、模仿。
如领读,我读一句,让幼儿读一句,边读边记;第二通读,我大声读,我大声读,幼儿小声读,边
学边仿;第三赏读,我借用录好配朗读磁带,一边放录音,一边幼儿反复倾听,在反复倾听中体验、品味。
理解参数方程的概念,了解某些常用参数方程中参数的几何意义或物理意义,掌握参数方程与普通方程的互化方法.会根据给出的参数,依据条件建立参数方程.
唐宋或更早之前,针对“经学”“律学”“算学”和“书学”各科目,其相应传授者称为“博士”,这与当今“博士”含义已经相去甚远。
而对那些特别讲授“武事”或讲解“经籍”者,又称“讲师”。
“教授”和“助教”均原为学官称谓。
前者始于宋,乃“宗学”“律学”“医学”“武学”等科目的讲授者;而后者则于西晋武帝时代即已设立了,主要协助国子、博士培养生徒。
“助教”在古代不仅要作入流的学问,其教书育人的职责也十分明晰。
唐代国子学、太学等所设之“助教”一席,也是当朝打眼的学官。
至明清两代,只设国子监(国子学)一科的“助教”,其身价不谓显赫,也称得上朝廷要员。
至此,无论是“博士”“讲师”,还是“教授”“助教”,其今日教师应具有的基本概念都具有了。
高二数学抛物线公式总结就分享到这里了,更多高二数学公式请继续关注查字典数学网高中频道!
死记硬背是一种传统的教学方式,在我国有悠久的历史。
但随着素质教育的开展,死记硬背被作为一种僵化的、阻碍学生能力发展的教学方式,渐渐为人们所摒弃;而另一方面,老师们又为提高学生的语文素养煞费苦心。
其实,只要应用得当,“死记
硬背”与提高学生素质并不矛盾。
相反,它恰是提高学生语文水平的重要前提和基础。