6.3温度的变化

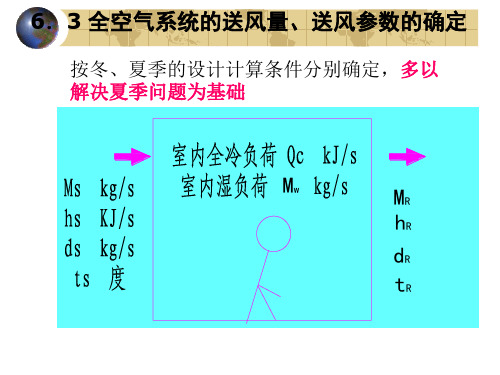
h Rd Rt RM R按冬、夏季的设计计算条件分别确定，多以解决夏季问题为基础M w6.3.1夏季空调送风量的确定（a ）房间通风示意图(b)室内空气状态变化过程RSDh Rh S d S (Kg/s)(Kg/s)(Kg/s)由室内状态R（t R.φR）送风温差Δt s=t R-t S热湿比线ε确定送风状态S送风温差Δt s大小的影响：Δt s大，则送风量小，导致室内气流分布均匀性差、稳定性差。

所以对温湿度控制严格的场合，应减少送风温差Δt s ，加大送风量M s。

舒适性空调，Δt s尽可能加大。

送风口高度≤5m，Δt s应<10℃；>5m，Δt s应<15℃送风温差与换气次数（规范）换气次数n=G/V（次/h）送风温差Δt s ：影响空调精度和人体舒适性换气次数n与气流均匀性有关，与送风温差有类似作用。

送风状态点应在热湿比线上①冬夏季相同（设计、运行便利②冬季送风量减少（节能，满足最小换气的要求，且送风温度尽量控制在45℃以下。

冬季送风量 送风状态。

6.3.3 冬季空调送风状态点和送风量的确定冬季室内空气状态变化过程冬季送风量ε’思考题如何确定送风量和送风状态点？已知某空调房间余热量Q c=3314w，余湿量M w=0.264g/s，室内全年维持空气状态参数为：t R=(22±1)℃，φR=（55±5）%，当地大气压力为101325Pa，要求确定该房间夏季送风状态S与送风量M s。

新风量(仅讨论无工业污染物发生的民用建筑和一般工业建筑)（1）经热湿处理，消耗大量能量。

应尽可能少处理新风的代价（以上海为例）夏季：室内28℃，60%，每处理1kg/h新风，年耗冷量21618KJ制冷系数按2.8计算，年耗电9度冬季：室内20℃，60%每处理1kg/h新风，年耗热量89430KJ/年，电加热24.8度蒸汽加热35KG油2.2Kg（2）为了室内空气品质，应尽可能增加新风量6.4.1最小风量确定的原则最小新风量，应满足①释污染物，保证人员对空气品质的要求；（即：卫生要求）②补充局部排风，保证室内正压的要求。

6.3温度的变化年级：七年级学科：数学执笔：贾峪一中冯雅利课型：新授审核人：市三中赵智强时间：2008年12月18日【学习目标】知识目标：意识到温度变化与时间的关系，了解两个变量之间的对应关系,初步形成函数的思想。

学会根据图像观察反映温度变化的一些特征，学会用语言描述这些特征。

能力目标：学会对实际生活中的例子用两变量之间关系的图像进行描述表达，初步形成函数与图像的对应关系。

主动尝试用图像来反映两变量之间关系，解决自己身边的一个实际问题。

情感目标：学会与他人合作与交流。

体会数学来源于生活，用于生活；体验用所学数学知识来解决实际问题的感受，激发学生学习数学的兴趣。

【学习重点】把实际问题转化为数学图像，再根据图像来研究实际问题。

【学习难点】从图像中获得一些信息与在现实情景下用语言进行描述之间的等价转化；用图像法来反映两变量之间关系，解决自己身边的一个实际问题，根据图像的特点来研究实际问题。

【学习方法】启发-——自主探究相结合【学习过程】一．情境引入师：我们生活在一个变化的世界中，我们常常见到由图像来反映实际生活的例子。

如，在股市里，常常见到大盘、个股的走势图；在医院里，测量器显示人的心率随时间的变化而变化的图像；电视台反馈各栏目的收视率常用图像来表示；人的体温随时间的变化而变化等。

可见在日常生活中，人们经常用图像来表示一些量与量之间的关系。

老师在课前请同学们收集一些用图像来反映两变量之间的关系的实例卡片，下面请同学们展示一下自己的收集情况。

二．自学探究1．学生展示课前制作的卡片。

（卡片内容有气温随时间变化而变化、体温随时间变化而变化等温度变化的图像……）2．从学生收集的一些图像中选几幅反映温度变化的图像展示。

时间/时展示课题：温度的变化。

做一做3．教师引导，观察上述图像，回答下列问题（设计成问题串）：（1）上午9时的温度是多少？12时呢？（2）这一天的最高温度是多少？是在几时达到的？最低温度呢？（3）这一天的温差是多少？从最低温度到最高温度经过了多少时间？（4）在什么时间范围内温度在上升？在什么时间范围内温度在下降？（5）图中的A点表示的是什么？B点呢？学生分四人一小组讨论，相互交流。

06.热对流教学设计含反思6.热对流【主要概念】热总是从高温处传向低温处，热传递的方式有多种，液体和气体主要通过热对流的形式传递热量。

【涉及课标】6.3.3 热可以在物体内和物体间传递，通常热从温度高的物体传向温度低的物体●说出生活中常见的热传递的现象，知道热通常从温度高的物体传向温度低的物体。

●举例说明影响热传递的主要因素，举例它们在日常生活和生产中的应用。

【教材分析】本课着重探究的是液体和气体的热传递方式——对流。

液体或气体中较热部分和较冷部分之间通过循环流动使温度趋于均匀的过程叫对流，即流体(气体或液体）通过自身各部分的宏观流动实现热量传递的过程。

对流产生的原因在于物质的热胀冷缩，流体受热后体积变大，质量不变，密度变小，在浮力作用下向上浮起，温度低的流体密度较大，向下流动。

教学内容包括四个部分：第一部分是复习导入，让学生用上节课热传导的原理来分析热在水中是如何传递的，引发学生思维冲突，聚焦对流现象。

第二部分是探究热在水中是怎样传递的。

把木屑放入水中加热，水升温后观察木屑在水中的运动方式，借助木屑的运动方向推测液体的流动方向，经过分析初步建立热对流的概念。

第三部分是探究热在空气中是怎样传递的，在空气中点燃一支香，用玻璃罩倒扣住，观察香冒出的烟是怎样流动的，进一步完善流体通过热对流传递热量。

第四部分是使学生运用所学的知识解释生活中的热对流现象和拓展活动，制作一个走马灯并尝试解释原理。

【学情分析】学生上一节课完成了热传导内容的学习，明白了热总是从高温处传向低温处，热量在物体内部或两个物体之间会以传导的形式传递。

由上节课的学习经验，学生会觉得液体和气体也会是通过传导的方式传递热量。

这是学习热对流这种热传递方式的一个障碍。

学生在以前学过固体和液体及气体的性质，知道液体和气体能够流动，是液体和气体区别于固体的重要特性，这为学生解释液体和气体在传递热的过程中可能发生流动奠定了基础。

学生在日常生活中可能注意到开锅后热气向上流动、打开冰箱门冷空气会向下流向脚面的现象，但他们往往没有认识到这是一种热传递的方式，而仅仅是热的物体和冷的物体运动了，不知道它们在运动的过程中传递了热量；同时，他们注意到的现象是一个局部，要么是上升、要么是下降，而没有注意到或者说无法观察到高温流体上升会伴随着低温流体下降，低温流体下降会伴随着高温流体上升。

6.3 温度的变化●教学目标（一）教学知识点1.经历从图象中分析变量之间的关系的过程，进一步体会变量之间的关系.2.结合具体情境理解图象上的点所表示的意义.3.能从图象中获取变量之间关系的信息，并能用语言进行描述.（二）能力训练要求1.培养学生从图象中获取信息的广泛性和准确性.2.在具体情境中锻炼学生对变量之间关系的敏感和语言描述的合理.（三）情感与价值观要求从解决大量实际问题和学生感兴趣的问题中提高学生用数学的意识，体验数学所蕴含的数学美.●教学重点1.用图象表示两个变量之间的关系.2.从图象中获取变量之间关系的信息，并能用语言合理地表示，并能结合具体情境理解图象上的点所表示的数学意义.●教学难点根据图象得出事物变化的规律.●教学方法自主探索法本节课的重点是使学生获得对图象反映变量之间关系的体验，学生可借助于以前读统计图的经验发现两个变量的关系，并尽可能多地从图象中获取信息.●教具准备投影片四张第一张：人的体温的变化（记作投影片§6.3 A）第二张：某天温度变化情况（记作投影片§6.3 B）第三张：骆驼体温变化（记作投影片§6.3 C）第四张：某港口0~12时水深情况（记作投影片§6.3 D）●教学过程Ⅰ.创设情景，引入新课［师］我们都知道，人的正常体温是36.5 ℃左右，这是一个很粗略的说法.你知道人的体温是随时间变化的吗？一天之中，在凌晨2时到6时之间，人的体温最低；在下午5时到8时之间，人的体温最高.在正常情况下，人体温度变化的幅度大约是0.6 ℃.如果变化幅度超过1 ℃，特别是在“非典”时期，那就要被“隔离”观察.在了解人体体温随时间变化的情况之前，我们不妨先来看一下一天天气温度变化的情况.（板书§6.3 温度的变化）Ⅱ.讲授新课——由学生根据读统计图的经验来自主探索图象中变量之间的关系1.气温变化的情况出示投影片（§6.3 A）请你根据图象，与同伴讨论某地某天温度变化情况.（1）上午9时的温度是多少？12时呢？（2）这一天的最高温度是多少？是几时到达的？最低温度呢？（3）这一天的温差是多少？从最低温度到最高温度经过了多长时间？（4）在什么时间范围内温度在上升？在什么时间范围内温度在下降？（5）图中的A点表示的是什么？B点呢？（6）你能预测次日凌晨1时的温度吗？说说你的理由.图6－7［师］上述问题反映的是哪两个变量的关系？［生］是时间和温度这两个变量的关系，其中时间是自变量，温度是因变量.［师］根据图6－7，同学们可先自己获取上述六个问题的答，并与同伴交流.［生］（1）上午9时的温度是27 ℃，12时是31 ℃.［师］你是如何从图中读出的？［生］在水平的数轴上找到9，它是表示时间的，过9的一条竖直的线与曲线交于一点，过这一点又有一条水平的线与竖直方向的数轴交于一点，此点表示的正是27 ℃.［师］很好.［生］（2）这一天最高的温度是37 ℃,是在15时达到的.因为最高温度应在曲线的最高点处达到，即C点是最高点，过这个点的水平方向就找到最高温度是37 ℃，竖直方向就找到了达到这温度的时间.同样，最低点D,就表示在3时，这天的气温达到最低温度23 ℃.［生］（3）这天的温差应为最高温度－最低温度=37 ℃－23 ℃=14 ℃.而经过的时间应为3时至15时.（4）温度上升，从图中反映的是曲线上升，观察可得3时到15时温度在上升；温度下降，从图中反映的是曲线下降，观察同样可以得出0时到3时、15时到24时温度在下降.［生］（5）图中A点表示的是21时的温度为31 ℃，B点表示的是0时的温度是26 ℃.（6）次日凌晨的温度应和前一日凌晨的温度相差不多，所以根据今天的凌晨1时的温度便可预测明日凌晨1时的温度约为24 ℃.［师］同学们观察图6－7，可知曲线上的点所表示的意义，谁能用自己的语言描述一下呢？［生］曲线上的点表示的是某一时刻这天的温度.［师］而这样的点我们用一条光滑的曲线按时间顺序把它们连起来，就表示了温度随时间变化而变化的情况，它就是温度与时间关系的图象.因此我们又得到了表示变量之间关系的又一种方法——图象法.用这种方法表示变量之间的关系，有何优点.同学们不妨交流一下.［师生共析］用这种方法表示，很直观，一眼就可看出什么时间，一天温度达到最高；什么时间，一天温度达到最低.同时，还能观察出在什么时段内温度在上升，什么时段温度在下降.直观、形象、生动.2.骆驼的体温［师］骆驼被称为“沙漠之舟”，它的体温随时间变化而发生较大的变化，下面是骆驼的体温随时间变化的图象，我们根据它来分析变量之间的关系.（出示投影片§6.3 B）（图中25时表示次日凌晨1时）图6－8（1）一天中，骆驼体温变化范围是什么？它的体温从最低上升到最高需要多少时间？（2）从16时到24时，骆驼的体温下降了多少？（3）在什么时间范围内骆驼的体温在上升？在什么时间范围内骆驼的体温在下降？（4）你能看出第二天8时骆驼的体温与第一天8时有什么关系吗？其他时刻呢？（5）A点表示的是什么？还有几时的温度与A点所表示的温度相同？（6）你还知道哪些关于骆驼的趣事？与同伴交流.［师］在回答上述六个问题之前，我们先来看一下在这个问题中，哪是自变量，哪是因变量？［生］时间是自变量，骆驼的体温是因变量.［师］联系某天气温变化的图象，我们可以注意在用图象表示变量之间关系时，一般用水平方向上的数轴（即横轴）上的点表示________，用竖直方向的数轴（即纵轴）上的点表示________.［生］用横轴上的点表示自变量，用纵轴上的点表示因变量.［师］下面我就根据图象分析骆驼体温的变化.［生］（1）一天中骆驼体温变化的范围是35 ℃到40 ℃.它的体温从最低上升到最高需要16时－4时.即需要12个小时（或40－28=12时）.（2）16时的温度最高是40 ℃，24时骆驼的体温下降到了37 ℃，共下降了3 ℃.（3）每天4时到16时体温在上升，0时到4时、16时到24时，体温在下降.（4）从图象中可以看出第二天8时的体温与第一天8时的体温是相同的，其他时刻也是如此.也就是说骆驼在每天的体温变化规律是相同的.因为图象从24时开始复制了0时到24时的图象.（5）A点表示的是12时的温度，与A点表示的温度相同的时刻还有20时的温度及次日12时和20时的温度.（6）一提起骆驼，就想到了沙漠.骆驼之所以称为“沙漠之舟”，是由于骆驼耐饥、耐渴、耐劳又耐风沙，这些特殊的能力而使它成为人类的好朋友.［生］骆驼最明显的特征是长有两个驼峰，一次进食后可以维持较长时间，它的脚掌很大，适宜沙漠行走.骆驼在沙漠上行走总是不紧不慢，踏着很稳健的步伐，但从不停留，靠着一种坚强的意志，到达目的地，我们应学习骆驼这种吃苦耐劳，锲而不舍的精神.……［师］同学们讲了很多关于骆驼的趣事，我们也都知道骆驼是人类的好朋友，人类应该和它们友好相处.在我国的珍稀野生动物中，生命力最强的就是在大漠戈壁深处独来独往，靠喝盐水生存的野骆驼.有关骆驼方面的有关资料同学们可到网上查找.我们研究了体温随时间变化的情况，还记得刚上课时，老师提到的，人的体温也是随时间变化的.同学们可打开课本阅读P174的读一读，你会更好地了解人体正常体温的变化情况.阅读后，和同伴交流你从中获取的信息.Ⅲ.随堂练习出示投影片（§6.3 C）1.海水受日月的引力而产生潮汐现象，早晨海水上涨叫做潮，黄昏海水上涨叫做汐，合称潮汐.潮汐与人类的生活有着密切的联系.下面是某港口从0时到12时的水深情况.图6－9（1）大约什么时刻港口的水最深？深度约是多少？（2）大约什么时刻港口的水最浅？深度约是多少？（3）在什么时间范围内，港口水深在增加？（4）在什么时间范围内，港口水深在减少？（5）A，B两点分别表示什么？还有几时水的深度与A点所表示的深度相同？（6）说一说这个港口从0时到12时的水深是怎样变化的.解：（1）在凌晨3时港口水最深，深度约为7.5米；（2）上午9时港口水最低，深度约为2.4米；（3）在凌晨0时到3时，上午9时到12时，港口的水深在增加；（4）凌晨3时到上午9时，港口的水深在减少.（5）A点表示上午6时港口的水深为5米，B点表示中午12时港口的水深为4.3米，0时水的深度与A点所表示的深度相同.（6）（只要描述的是变化过程合理即可）凌晨0时到3时水深在增加；凌晨3时到上午9时水深在降低；上午9时到12时水深又开始增加.2.如图6－10，向高为H的圆柱形空水杯中注水，表示注水量y与水深x的关系的图象是下面的哪一个？图6－10解：根据题意可知，x是自变量，y是因变量，当水深x为0时，注水量y 也为0；同时，y随x的增大而增大，因此，应选A.Ⅳ.课时小结这节课从图象中分析了两个变量之间的关系，结合温度的变化直观而形象地从图象中获得了变量之间的有关信息.用图象来直观地反映变量之间的关系是表格法、关系式法所无法代替的.Ⅴ.课后作业1.课本习题6.3 第1题;2.观察章头图《青春期男女孩身高曲线》并回答相应的问题;3.收集生活中用图象法表示的两个变量之间的关系，并从中获取更多的信息.Ⅵ.活动与探究某气象研究中心观测一场沙尘暴从发生到结束的全过程.开始时风速平均每小时增加2千米，4小时后，沙尘暴开始经过开阔荒漠地，风速变为平均每小时增加4千米，一段时间，风速保持不变.当沙尘暴经过绿色植被区时，其风速每小时平均减少1千米，最终停止.结合风速和时间的图象，回答下列问题:图6－11（1）在纵轴（）内填入相应的数值；（2）沙尘暴从发生到结束，共经过了多少小时？（3）写出当x≥25时，风速y（千米/时）与时间x（小时）之间的关系式.［过程］此题是一个关于环境恶化的一个问题.从题中可以增强同学们的“环保意识”.要回答上述几个问题，首先要读懂题，第二要读懂图.［结果］（1）开始时风速平均每小时增加2千米，由图象可知，0时的速度为0千米/时，4小时后，速度y=2×4=8千米/时，所以在y轴的第一个空应填8.接着4时到10时经过荒漠地，每小时平均增加4千米，所以10时，风速已变为8+4×（10－4）=32（千米/时）.第二空应填32.（2）由图象可知，当风速为32千米/时时，遇到绿色植被区时，其风速每小时平均减少1千米，最后停止，即风速变为0千米/时，需32小时.所以沙尘暴从发生到结束需25+32=57（小时）（3）当x≥25时，y=57－x.●板书设计§6.3 温度的变化一、图象是表示变量之间关系的又一种方法.1.直观、形象.2.通常用水平方向的数轴上的点表示自变量，用竖直方向的数轴上的点表示因变量.二、随堂练习（由学生板演）。

6.3．温度的变化一、学习目标：1、经历从图象中分析变量之间关系的过程，进一步体会变量之间的关系；结合具体情境，理解图象上的点所表示的意义。

2、能利用图象对所研究的对象过去的情况作一个回顾，对未来的情况作一个预测；领悟数形结合思想，培养学生观察能力和联想能力。

二、学习重点:结合具体情境，理解图象上的点所表示的意义。

并能从图象中获取变量间关系的信息，三、学习难点:能从图象中获取变量之间关系的信息，并能用语言进行描述。

四、学习方法:观察法，启发式教学法，分组讨论法 五、学习过程: （一）、新课引入:两变量之间的数量关系，除了可用关系式法和表格法来表示外，是否还有第三种表示方法呢？这就是本课将要解决的新问题。

本课的学习目标是：1.经历从图象中探究变量之间关系的过程，进一步体会变量之间的关系； 2、结合具体情境，能理解图象上的点所表示的意义。

3、能从图象中获取变量之间关系的信息，并对未来的情况作一个预测。

（二）、新课：1、典型例题：某地某天温度变化的情况如下图所示：观察下表回答下列问题： （1）、上午9时的温度是多少？12时呢？（2）、这一天的最高温度是多少?是在几时达到的?最低温度呢?（3）这一天的温差是多少？从最高温度到最低温度经过了多长时间？ （4）、在什么时间范围内温度在上升？在什么时间范围内温度在下降？ 5）、图中的A 点表示的是什么？B 点呢？（6）、你能预测次日凌晨1时的温度吗？说说你的理由。

点拔: 1).前图表示了温度随时间的变化而变化的情况，它是温度与时间之间关系的图象。

2).图象法是我们表示变量之间关系的 又一种方法，它的特点是非常直观。

3).在用图象表示变量之间的关系时，通常用水平方向的数轴（称为横轴）上的点表示自变量，用竖直方向的数轴（称为纵轴）上的点表示因变量。

2、巩固训练：如下图，是骆驼的体温随时间变化而变化的关系图，据图回答下列问题： （1）、一天中，骆驼体温的变化范围是什么？它的体温从最低上升到最高需要多少时间？（2）、从16时到24时，骆驼的体温下降了多少？（3）、在什么时间范围内骆驼的体温在上升？在什么时间范围内骆驼的体温在下降？（4）、你能看出第二天8时骆驼的体温与第一天8时有什么关系吗？其它时刻呢？（5）、A 点表示的是什么？还有几时的温度与A 点所表示的温度相同？点拔：骆驼的体温随时间变化而变化的的关系图，可以预测它第二天某时刻的体温。