江苏省高邮市送桥中学 必修5导学案 1.1正弦定理(2)

第一章 解三角形§1.1 正弦定理和余弦定理1.1.1正弦定理 【学习目标】1. 掌握正弦定理的内容；2. 掌握正弦定理的证明方法；3. 会运用正弦定理解斜三角形的两类基本问题．【学习过程】1、课前准备试验：固定∆ABC 的边CB 及∠B ，使边AC 绕着顶点C 转动．思考：∠C 的大小与它的对边AB 的长度之间有怎样的数量关系？显然，边AB 的长度随着其对角∠C 的大小的增大而 ．能否用一个等式把这种关系精确地表示出来？2、新课导学 ※ 学习探究探究1：在初中，我们已学过如何解直角三角形，下面就首先来探讨直角三角形中，角与边的等式关系. 如图，在Rt ∆ABC 中，设BC =a ，AC =b ，AB =c ，根据锐角三角函数中正弦函数的定义， 有sin a A c =，sin b B c =，又sin 1cC c==， 从而在直角三角形ABC 中，sin sin sin a b cA B C==．探究2：那么对于任意的三角形，以上关系式是否仍然成立？可分为锐角三角形和钝角三角形两种情况：当∆ABC 是锐角三角形时，设边AB 上的高是CD ，根据任意角三角函数的定义，有CD =sin sin a B b A =，则sin sin a bA B=， 同理可得sin sin c bC B=，从而sin sin a bA B =sin c C=．类似可推出，当∆ABC 是钝角三角形时，以上关系式仍然成立．请你试试导.新知：正弦定理在一个三角形中，各边和它所对角的 的比相等，即sin sin a bA B =sin c C=． （1）正弦定理说明同一三角形中，边与其对角的正弦成正比，且比例系数为同一正数，即存在正数k 使sin a k A =， ，sin c k C =；（2）sin sin a b A B =sin c C =等价于 ，sin sin c bC B =，sin a A =sin c C ． （3）正弦定理的基本作用为：①已知三角形的任意两角及其一边可以求其他边，如sin sin b Aa B=；b = ．②已知三角形的任意两边与其中一边的对角可以求其他角的正弦值，如sin sin aA B b=；sin C = ．（4）一般地，已知三角形的某些边和角，求其它的边和角的过程叫作解三角形．【学习评价】1．满足a =4，A=045，B=060的△ABC 的边b 的值为（ ） A 62 B 232+ C 13+ D 132+2．△ABC 中6=a ，36=b ，A=030，则边c = （ ） A 6 B 12 C 6或12 D 363．在△ABC 中，若C B A cos sin 2sin ⋅=，C B A 222sin sin sin +=，则△ABC 的形状是（ ）A ．直角三角形B 。

1.1 正弦定理教学目标：(1)掌握正弦定理及其证明，会初步运用正弦定理解斜三角形，培养数学应用意识；(2)在问题解决中，培养学生的自主学习和自主探索能力；(3)提供适当的问题情境，激发学生的学习热情，培养学生学习数学的兴趣，在合作学习中，学会学习，学会交流，相互评价，提高学生的合作意识与交流能力。

教学重点：正弦定理及其证明过程 教学难点：正弦定理的推导与证明教学过程： 一．问题情境引言：从金字塔的建造到尼罗河两岸的土地丈量，从大禹治水到都江堰的修建，从天文观测到精密仪器的制造，人们都离不开对几何图形的测量，设计和计算。

测量河流两岸码头之间的距离，确定待建隧道的长度，确定卫星的角度与高度等等问题，都可以转化为求三角形的边与角的问题，这就需要我们进一步探索三角形的边角关系。

探索1：在Rt △ABC ，C=900，那么边角之间有哪些关系？sinA=c a ，sinB=c b，sinC=cc =1，……即c=A a sin ，c=B b sin ，c=Ccsin ， ∴A a sin =B b sin =Cc sin 探索2：在任意三角形里, A a sin =B b sin =Ccsin 还成立吗？ （几何画板演示） 二.学生活动 数学实验：分组一：对于锐角三角形验证结论是否成立？c b a DBA C分组二：对于钝角三角形验证结论是否成立？数学猜想：A a sin =B b sin =Ccsin ; 三.建构数学:数学证明: 证法一：证明二：（等积法）在任意斜△ABC 当中S △ABC =A bc B ac C ab sin 21sin 21sin 21== 两边同除以abc 21即得：A a sin =B b sin =Ccsin 正弦定理：在任一个三角形中，各边和它所对角的正弦比相等， 即A a sin =B b sin =Ccsin =2R （R 为△ABC 外接圆半径）a bcOBCADb ac DA BC b ac 过程：sinB=AD c ，sinC=sin （1800-C ）=ADb，得csinB=bsinC ，得b sinB =c sinC 同理可得：a sinA =csinC 所以a sinA =b sinB =c sinC所以a sinA =b sinB =c sinC同理可得：a sinA =csinC得b sinB =csinC 得csinB=bsinC ，sinB=AD c ，sinC=AD b，过程：cba DDBACBC证明三：（外接圆法） 如图所示，∠Ａ＝∠Ｄ ∴R CD DaA a 2sin sin === 同理B b sin =2R ，Ccsin ＝2R 证明四：（向量法）探索3：观察正弦定理的结构，看它有什么特点？你能用语言把它叙述出来吗？定理中的正弦改成余弦，结论还成立吗？正弦定理结构和谐、对称，体现了数学的和谐美与对称美； 若改成余弦，除正三角形外，其余三角形都不成立。

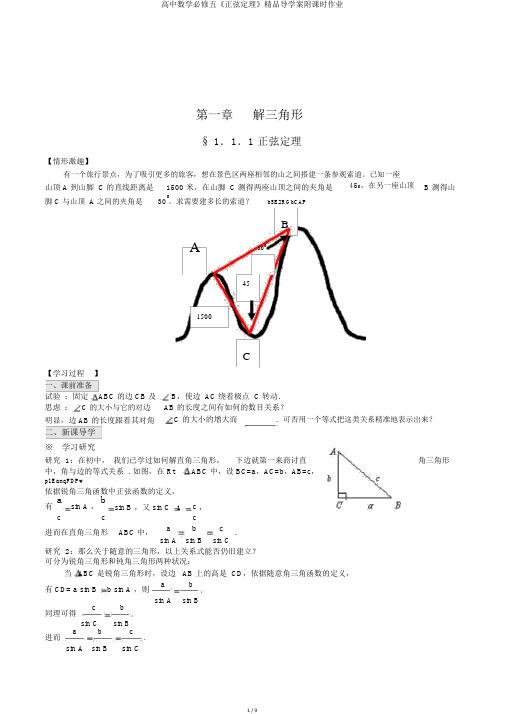
第一章 解三角形§ 1．1．1 正弦定理【情形激趣】有一个旅行景点，为了吸引更多的旅客，想在景色区两座相邻的山之间搭建一条参观索道。

已知一座 山顶 A 到山脚 C 的直线距离是 1500 米，在山脚 C 测得两座山顶之间的夹角是脚 C 与山顶 A 之间的夹角是 30 。

求需要建多长的索道？b5E2RGbCAP450，在另一座山顶B 测得山BA300451500C【学习过程 】 一、课前准备试验 ：固定 ABC 的边 CB 及 思虑 ： C 的大小与它的对边 明显，边 AB 的长度跟着其对角B ，使边 AC 绕着极点 C 转动． AB 的长度之间有如何的数目关系？C 的大小的增大而．可否用一个等式把这类关系精准地表示出来？二、新课导学 ※ 学习研究研究 1：在初中， 我们已学过如何解直角三角形， 下边就第一来商讨直 角三角形中，角与边的等式关系 . 如图，在 Rt ABC 中，设 BC=a ，AC=b ，AB=c ，p1EanqFDPw依据锐角三角函数中正弦函数的定义，有asin A ，bsin B ，又 sin C 1c ， ccc进而在直角三角形 ABC 中，ab c．sin A sin B sin C研究 2：那么关于随意的三角形，以上关系式能否仍旧建立？ 可分为锐角三角形和钝角三角形两种状况：当 ABC 是锐角三角形时，设边 AB 上的高是 CD ，依据随意角三角函数的定义，有 CD= a sin B b sin A ，则 a bsin A ，cb sin B 同理可得，sin C sin B 进而 a b csin A sin B ．sin C近似可推出，当ABC 是钝角三角形时，以上关系式仍旧建立．请你试一试推导.1.表达正弦定理的内容：2.正弦定理的变形①边化角： a = ， b = ， c = ；DXDiTa9E3d②角化边：sin ， sin ， sin C ； RTCrpUDGiT3.正弦定理的推论： a : b : c进而知正弦定理的基本作用为：①②一般地，已知三角形的某些边和角，求其余的边和角的过程叫作_______【沟通释疑】（二）合作商讨种类一已知两角及一边解三角形例 1. 在ABC 中，已知 A 45 ， B 60 ，a42cm，解三角形．变式：在ABC 中，已知 B 45 ， C 60 ， a 12cm，解三角形．规律总结：种类二已知两边及此中一边的对角解三角形例 2. 在ABC中， c6, A 45 , a2,求 b和 B, C ．变式：在ABC中， b3, B 60 , c1, 求a 和A, C ．规律总结：种类三判断三角形的形状例 3在ABC 中，已知a2tan B b 2 tan A ，试判断三角形的形状。

2009年9月1 日执笔人:女兆东盐审核人：祁正权必修5 §1.1正弦定理（1）第1课时一、学习目标1.理解正弦定理的推理过程；2.掌握正弦定理的内容；3.能运用正弦定理解决一些简单的三角形问题。

二、学法指导1.要注意定理的几种证法，自己能够发现通过探索、讨论研究，发现证明方法；2.体会向量是一种处理问题的工具三、课前预习1.在AA3C中，已知a,b分别为ZA,ZB所对的边，则a >b = A____ B o sin A sin B2.正弦定理：在二角形中，即===（）3.一般的，把二角形的二个角A,B,C和它们的对边a, b,c叫做二角形的元素。

已知二角形的几个元素求其他元素的过程叫做一4,正弦定理的证明方法有哪些？四、课堂探究探索1我们前面学习过直角三角形中的边角关系，在RtAABC中，设C =90° ,贝U sinA=. sinB=, sinC=即：探索2对于任意三角形，这个结论还成立吗？探索3这个结论对于任意二角形可以证明是成立的.不妨设C为最大角，若C为真角，我们已经证得结论成立，如何证明。

为锐角、钝角时结论也成立？证法1若C为钥用（图（1））,过点A作ADLB C于4An A nD ,此时有sinB = — , sinC=千，所以/ : Vh r 8 ------------ b_ 尸csinB=bsinC ,即一^ =」一.同理可得（i）csin B sin Ca c。

b c--- = --------- ，所以 ----- = ------ = ------- •sin A sin C sin A sin B sin C若。

为鲤角（图（2））,过点A作AD LBC ,交8C的延长线于此4 n AT）时也有sin8=——，且sinC = sin（180。

—C）=——.同样可得c b= = .综上可知，结论成立.sin A sin B sin C证法2利用三角形的面积转换，先作出三边上的高AD、BE、CF ,则AD = c sin 3 , BE =asinC , CF =bsinA . 所以S MBC = —ab sin C = —ac sin B = —bcsmA ,1n h c 每项同除以一a"c即得：2sin A sin B sin C探索4充分挖掘三角形中的等量关系，可以探索出不同的证明方法.我们知道向量也是解决问题的重要工具，因此能否从向量的角度来证明这个结论呢？在AA3C中，有而=瓦5+京.设C为最大角，过点A作AD1B C于。

第2课时：正弦定理(2)【学习目标】1、会利用正弦定理证明简单三角形问题；2、会利用正弦定理求解简单斜三角形边角问题；3、会利用正弦定理判断三角形解的个数。

【学习重点】正弦定理应用【预习内容】a sin A ＝bsin B＝csin C已知两角一边或已知两边和其中一边的对角求解三角形中其它的量. 【新知学习】1、在Rt△ABC中，斜边c等于Rt△ABC外接圆的直径，故有asin A ＝bsin B＝csin C=2R，这一关系对于任意三角形也能成立吗？【新知深化】1、asin A ＝bsin B＝csin C=2R2、如何利用正弦定理解决两边及邻角问题.评述：(1)要求学生注意考虑问题的全面性.对于角B为钝角的排除也可以结合三角形小角对小边性质而得到.(2)综合上述问题要求学生自我总结正弦定理的适用范围，已知两角一边或两边与其中一边的对角.(3)对于已知两边夹角这一类型，将通过下一节所学习的余弦定理求解.【新知应用】例1、在△ABC中，已知a＝28，b＝20，A＝120°，求sin B和c例2、根据下列条件解三角形：（1）已知60,1b B c ==︒=；（2）已知45,2c A a ==︒=例3. 已知135cos ,53sin ==B A ，求C cos ；【新知回顾】 通过本节学习，我们一起研究了利用正弦定理所能解决的两类有关三角形问题：已知两角一边；已知两边和其中一边的对角.【教学反思】第2课时：正弦定理(2)课后作业1. （1）△ABC 中,2,2,4a b A π===，求B ，c ；（2）△ABC 中，23,6,6a b A π===，求B ，c ；2.根据下列条件解三角形：（1）b ＝13，a ＝26，B ＝30°；（2）014,76,60a b B ===3. 在△ABC 中，已知060,B =且2b =，则此三角形的外接圆半径为 。

4. 在△ABC 中，已知031,60,3a A c ===，解三角形。

江苏省高邮中学高一数学正弦定理学案一07-4-28教学目的：1、掌握正弦定理内容及证明正弦定理的方法，体会转化与联系的数学思想。

2、会运用正弦定理解决两类基本的解三角形问题，明白为什么解的情况不一样。

教学重点：数学思想的理解及利用正弦定理解三角形。

教学难点：正弦定理的证明教学过程：一、问题情境：1.复习：在Rt ΔABC 中，∠C=90 ，试判定A a sin ，B b sin 与Cc sin 之间的大小关系？ 2.猜想：对任意三角形ABC 上述关系是否成立？如何证明：（1） 转化为直角三角形来证明。

（2） ΔABC 的面积公式可以证明吗？（3） 能利用向量的方法来证明？二、讲解新课：1．正弦定理：A a sin = B b sin = Cc sin • 正弦定理适合任意三角形，是勾股定理的推广。

2．利用正弦定理，可解决两类三角形问题：（1）已知两角与一边，求另两边与另一角。

（2）已知两边和其中一边的对角，求其他边角。

• 三角形有三条边和三个角，可看成是六个元素，则最少几个元素可能确定一个三角形。

• 由其中三个元素求另外三个元素的过程叫解斜三角形。

• 类型（2）的解的情况不唯一。

三、知识运用：例1．① 在ΔABC 中 已知23,45,7500===c B A ，求b a C ,,②在ΔA BC 中 ，已知060,67,14===B b a ，解三角形ABC 。

③在ΔABC 中 ，已知045,332,2===B b c ，解三角形ABC 。

•对于②③能否从图形来分析为什么解的个数不一样，分析类型（２）产生多解的原因。

例２．在ΔABC 中 ，已知,45,250==A c 试判断当a 分别取25,3310,5,10时解的个数。

例３．在ΔABC 中 ，已知0150,3,2===C b a ，求ABC S ∆四、课堂练习：１．在ΔABC 中 已知12,120,3000===b B A ，求b a C ,,２．在ΔABC 中 ，已知060,32,2===B b a ，解三角形ABC 。

1.1 正弦定理(1)【学习目标】1、掌握正弦定理推导过程，会利用正弦定理证明简单三角形问题，能利用计算器进行运算；2、通过三角函数、正弦定理、向量数量积等多处知识间联系来体现事物之间的普遍联系与辩证统一.【学习重点】正弦定理证明及应用.【预习内容】引例：在Rt△ABC中，角C为直角，a,b,c分别是角A、B、C的对边，由直角三角形的边角关系可知：sinA= ;sinB= ;sinC=sin900= ;问题1：能否通过表达式变形得出下列关系a sinA＝bsinB＝csinC那么，在任意三角形中，这一关系式是否成立呢?这也是我们这一节课将要研究的问题. 【新知学习】对于asinA＝bsinB＝csinC这一关系的证明，我们一起来看下面的证法.尝试：（1）转化为直角三角形中的边角关系；（2）建立直角坐标系，利用三角函数的定义；（3）通过三角形的外接圆，将任意三角形问题转化为直角三角形问题；（4）利用向量的投影或向量的数量积（产生三角函数）证明1：通过作BC边上的高AD将任意三角形中的边角关系转化为直角三角形中的边角关系，由于垂足D的位置不同，所以要分类讨论。

探究1：不妨设角C为最大角。

若C=900，我们已经证得结论成立。

若C为锐角呢?探究2：若C为钝角呢？证明2：用向量方法证明。

证明的关键是将向量等式转化为数量等式。

在向量的数量积中，由向量的投影可产生三角函数，从而得到相应的边角关系。

正弦定理：asinA＝bsinB＝c sinC【新知应用】例1、在△ABC中，A＝30°，C＝105°，a＝10，求b、c【新知回顾】通过本节学习，我们一起研究了正弦定理的证明方法，同时了解了向量的工具性作用，并且明确了利用正弦定理所能解决的两类有关三角形问题：已知两角一边；已知两边和其中一边的对角.【教学反思】1.1 正弦定理(1)课后作业1.一个三角形的两个内角分别为030和045，如果045角所对的边长为8，则030角所对的边的长是 。