一道尺规作图题的多种作图方法

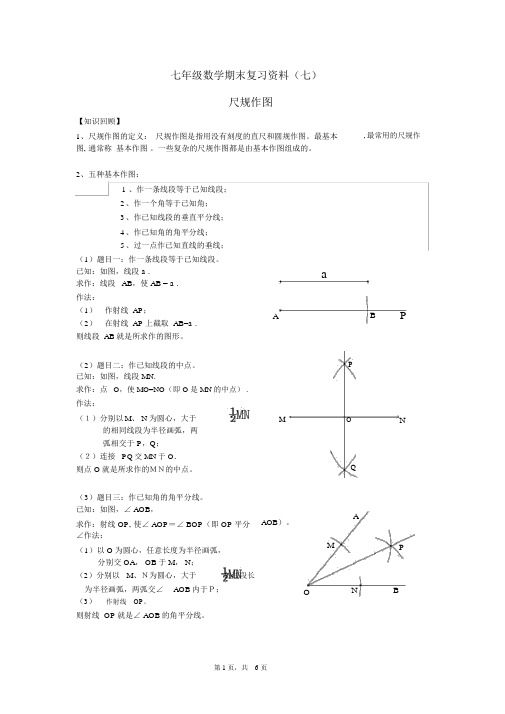
七年级数学期末复习资料（七）尺规作图【知识回顾】1、尺规作图的定义：尺规作图是指用没有刻度的直尺和圆规作图。

最基本图, 通常称基本作图。

一些复杂的尺规作图都是由基本作图组成的。

,最常用的尺规作2、五种基本作图：1 、作一条线段等于已知线段；2、作一个角等于已知角；3、作已知线段的垂直平分线；4、作已知角的角平分线；5、过一点作已知直线的垂线；（1）题目一：作一条线段等于已知线段。

已知：如图，线段 a .求作：线段AB，使 AB = a .作法：（1）作射线 AP；（2）在射线 AP上截取 AB=a .则线段 AB就是所求作的图形。

（2）题目二：作已知线段的中点。

已知：如图，线段 MN.求作：点O，使 MO=NO（即 O是 MN的中点） .作法：（１）分别以M、 N为圆心，大于的相同线段为半径画弧，两弧相交于 P，Q；（２）连接PQ交 MN于 O．则点 O就是所求作的ＭＮ的中点。

（3）题目三：作已知角的角平分线。

已知：如图，∠ AOB，求作：射线 OP, 使∠ AOP＝∠ BOP（即 OP平分∠作法：（1）以 O为圆心，任意长度为半径画弧，分别交 OA， OB于 M， N；（2）分别以M、Ｎ为圆心，大于的线段长为半径画弧，两弧交∠AOB内于Ｐ；（3）作射线OP。

则射线 OP就是∠ AOB的角平分线。

aAMAOB）。

MOB PPO NQAPN B（4）题目四：作一个角等于已知角。

已知：如图，∠ AOB。

求作：∠ A’ O’ B’，使 A’ O’ B’ =∠ AOBBB' N N'N'O MA O'M'A'O'M'A'O'M' A'①②③作法：（1）作射线O’ A’；（2）以 O为圆心，任意长度为半径画弧，交OA于M，交OB于N；（3）以 O’为圆心，以 OM的长为半径画弧，交 O’ A’于 M’；（4）以 M’为圆心，以 MN的长为半径画弧，交前弧于N’；（5）连接 O’ N’并延长到 B’。

尺规作图的方法和步骤
尺规作图的方法和步骤
在几何里把限定用直尺和圆规来画图，称为尺规作图，最基本最常用的尺规作图，称基本作图。

2. 基本作图包括：
①作一角等于已知角；
②平分已知角；
③经过一点作已知直线的垂线；
④作线段的垂直平分线；
⑤若两已知圆相交，可求其交点。

原理都是已经证明的定理，如平分角，利用的就是边边边公理，以定点为圆心化圆交角两点，角平分线的任一点，到两点的距离相等的原理（很容易证明这是个全等三角形）。

作图公法
以下是尺规作图中可用的基本方法，也称为作图公法，任何尺规作图的步骤均可分解为以下五种方法：
通过两个已知点可作一直线。

已知圆心和半径可作一个圆。

若两已知直线相交，可求其交点。

若已知直线和一已知圆相交，可求其交点。

若两已知圆相交，可求其交点。

看完这些正多边形的尺规作图⽅法，你还不认为数学也是⼀种艺术吗？荟思正多边形的尺规作图，虽然是⼀个很纯粹的数学问题，但同时也极具艺术欣赏价值！尺规作图问题是⾮常古⽼的数学问题，早在两千多年前的古希腊时期就开始研究了。

⼈们好奇什么样的图形可以⽤尺规作图的⽅法得到，什么样的图形不可以。

对于可以尺规作图的图形，很好办，想尽办法得到作图⽅法就解决问题了。

对于那些还没想到作图⽅法的图形就⽐较为难，因为不知道是因为不存在这样的作图⽅法，还是因为作法太复杂，所以还没⼈能发现这样的⽅法。

例如三等分⾓问题，就是很长时间⾥都找不到作图⽅法，最终证明是不可能办到的。

再次特别强调⼀下，在尺规作图问题中，直尺是不带刻度的，我们只能⽤它来画直线。

在各种图形中，正多边形是⼤家⽐较感兴趣的⼀类。

由于圆规可以画圆，⽽所有正多边形都可以内接于圆，因此它的所有顶点都在圆周上。

这样看来，正多边形应该很有希望⽤尺规作图。

⽽且，前⼏个正多边形的作图⽅法很快就构造出来了，步骤也不算复杂。

然⽽还是有很多正多边形没有找到尺规作图的⽅法，因此⾃然要问，是否存在不可能尺规作图的正多边形。

相对于同时期的其他⽂明，古希腊数学更富思辨精神。

尽管当时的数学问题都是源于⽣活，但古希腊⼈并不⽴⾜于解决⽣活问题，⽽是考虑⼀般的理想情形。

边数较多的多边形在实际问题中⼏乎不会出现，但他们仍然对这些多边形的尺规作图很感兴趣，并且还执着地规定直尺不能带刻度。

这个问题在经过漫长的两千年后，才最终被天才的⾼斯在24岁时完全解决。

根据⾼斯的结论，⼀个正多边形可以尺规作图，当且仅当边数是费马素数或者两个不同的费马素数的乘积，或者是这些数的2的乘幂倍（即2倍，4倍，8倍，16倍，等等）。

请注意，⾼斯的结论给出的是⼀个充分必要条件。

换句话说，费马素数的数量决定了能尺规作图的奇数边正多边形的个数。

根据⾼斯的结论，边数不超过20的18个正多边形中，可以尺规作图的⼀共有11个，边数分别是3,4,5,6,8,10,12,15,16,17,20。

BPAaO QPNMON MBPA 尺规作图【知识回顾】1、尺规作图的定义：尺规作图是指用没有刻度的直尺和圆规作图。

最基本,最常用的尺规作图,通常称基本作图。

一些复杂的尺规作图都是由基本作图组成的。

2、五种基本作图：1、作一条线段等于已知线段；2、作一个角等于已知角；3、作已知线段的垂直平分线；4、作已知角的角平分线；5、过一点作已知直线的垂线； （1）题目一：作一条线段等于已知线段。

已知：如图，线段a . 求作：线段AB ，使AB = a .作法：（1） 作射线AP ；（2） 在射线AP 上截取AB=a . 则线段AB 就是所求作的图形。

（2）题目二：作已知线段的中点。

已知：如图，线段MN.求作：点O ，使MO=NO （即O 是MN 的中点）. 作法：（１）分别以M 、N 为圆心，大于的相同线段为半径画弧， 两弧相交于P ，Q ； （２）连接PQ 交MN 于O ． 则点O 就是所求作的ＭＮ的中点。

（3）题目三：作已知角的角平分线。

已知：如图，∠AOB ，NMBOA③②①A'A'N'O'B'M'O'A'N'M'M'O'求作：射线OP, 使∠AOP ＝∠BOP （即OP 平分∠AOB ）。

作法：（1）以O 为圆心，任意长度为半径画弧，分别交OA ，OB 于M ，N ；（2）分别以M 、Ｎ为圆心，大于 的线段长 为半径画弧，两弧交∠AOB 内于Ｐ； （3） 作射线OP 。

则射线OP 就是∠AOB 的角平分线。

（4）题目四：作一个角等于已知角。

已知：如图，∠AOB 。

求作：∠A ’O ’B ’，使A ’O ’B ’=∠AOB作法：（1）作射线O ’A ’；（2）以O 为圆心，任意长度为半径画弧，交OA 于M ，交OB 于N ； （3）以O ’为圆心，以OM 的长为半径画弧，交O ’A ’于M ’； （4）以M ’为圆心，以MN 的长为半径画弧，交前弧于N ’； （5）连接O ’N ’并延长到B ’。

尺规作图欧阳光明（2021.03.07）【知识回顾】1、尺规作图的定义：尺规作图是指用没有刻度的直尺和圆规作图。

最基本,最常用的尺规作图,通常称基本作图。

一些复杂的尺规作图都是由基本作图组成的。

2、五种基本作图：1、作一条线段等于已知线段；2、作一个角等于已知角；3、作已知线段的垂直平分线；4、作已知角的角平分线；5、过一点作已知直线的垂线； （1）题目一：作一条线段等于已知线段。

已知：如图，线段a .求作：线段AB ，使AB = a . 作法：（1） 作射线AP ；（2）在射线AP 上截取AB=a .则线段AB 就是所求作的图形。

（2）题目二：作已知线段的垂直平分线。

已知：如图，线段MN.a求作：点O ，使MO=NO （即O 是MN 的中点）. 作法： （１）分别以M 、N 为圆心，大于MN 21的相同线段为半径画弧， 两弧相交于P ，Q ；（２）连接PQ 交MN 于O ．则点PQ 就是所求作的ＭＮ的垂直平分线。

（3）题目三：作已知角的角平分线。

已知：如图，∠AOB ，求作：射线OP, 使∠AOP ＝∠BOP （即OP 平分∠AOB ）。

作法：（1）以O 为圆心，任意长度为半径画弧，分别交OA ，OB 于M ，N ；（2）分别以M 、Ｎ为圆心，大于MN21的线段长为半径画弧，两弧交∠AOB 内于Ｐ；（3）作射线OP 。

则射线OP 就是∠AOB 的角平分线。

（4）题目四：作一个角等于已知角。

已知：如图，∠AOB 。

求作：∠A ’O ’B ’，使A ’O ’B ’=∠AOB 作法：（1）作射线O ’A ’；（2）以O 为圆心，任意长度为半径画弧，交OA 于M ，交OB 于N ；（3）以O ’为圆心，以OM 的长为半径画弧，交O ’A ’于M ’； （4）以M ’为圆心，以MN 的长为半径画弧，交前弧于N ’； （5）连接O ’N ’并延长到B ’。

则∠A ’O ’B ’就是所求作的角。

O尺规作图【知识回顾】1、尺规作图的定义：尺规作图是指用没有刻度的直尺和圆规作图。

最基本,最常用的尺规作图,通常称基本作图。

一些复杂的尺规作图都是由基本作图组成的。

2、五种基本作图：1、作一条线段等于已知线段 ；2、作一个角等于已知角 ；3、作已知线段的垂直平分线 ；4、作已知角的角平分线 ；5、过一点作已知直线的垂线 ；（1）题目一：作一条线段等于已知线段。

已知：如图，线段 a .a求作：线段 AB ，使 AB = a . 作法：（1） 作射线 AP ； （2） 在射线 AP 上截取 AB=a . 则线段 AB 就是所求作的图形。

（2） 题目二：作已知线段的中点。

已知：如图，线段 MN.求作：点 O ，使 MO=NO （即 O 是 MN 的中点）. 作法：（１）分别以 M 、N 为圆心，大于MN的相同线段为半径画弧， 两弧相交于 P ，Q ； （２）连接 PQ 交 MN 于 O ．则点 O 就是所求作的ＭＮ的中点。

（3） 题目三：作已知角的角平分线。

已知：如图，∠AOB，求作：射线 OP, 使∠AOP＝∠BOP（即 OP 平分∠AOB）。

作法：（1） 以 O 为圆心，任意长度为半径画弧，分别交 OA ，OB 于 M ，N ；（2） 分别以 M 、Ｎ为圆心，大于的线段长 为半径画弧，两弧交∠AOB 内于Ｐ； （3） 作射线 OP 。

则射线 OP 就是∠AOB 的角平分线。

（4） 题目四：作一个角等于已知角。

已知：如图，∠AOB。

求作：∠A’O’B’，使 A’O’B’=∠AOB作法：① （1） 作射线 O’A’； ① ①（2） 以 O 为圆心，任意长度为半径画弧，交 OA 于 M ，交 OB 于 N ； （3） 以 O’为圆心，以 OM 的长为半径画弧，交 O’A’于 M ’； （4） 以 M’为圆心，以 MN 的长为半径画弧，交前弧于 N ’； （5） 连接 O’N’并延长到 B ’。

则∠A ’O ’B ’就是所求作的角。

初中数学尺规作图方法大全尺规作图是一种用没有刻度的直尺和圆规作图的方法。

最基本的尺规作图通常称为基本作图，而一些复杂的尺规作图则是由基本作图组成的。

基本作图包括五种：作一条线段等于已知线段、作一个角等于已知角、作已知线段的垂直平分线、作已知角的角平分线、过一点作已知直线的垂线。

第一个问题要求作一条长度等于已知线段a的线段AB。

作法是先作射线AP，然后在射线AP上截取AB=a。

这样就得到了所求的线段AB。

第二个问题要求作已知线段MN的中点O。

作法是以M、N为圆心，大于MN的相同线段为半径画弧，两弧相交于P、Q，然后连接PQ交MN于O。

这样就得到了所求的点O。

第三个问题要求作已知角AOB的角平分线OP。

作法是以O为圆心，任意长度为半径画弧，分别交OA、OB于M、N，然后分别以M、N为圆心，大于AOB的线段长为半径画弧，两弧交AOB内于P，最后作射线OP。

这样就得到了所求的角平分线OP。

第四个问题要求作一个角等于已知角AOB。

作法是先作射线O'A'，然后以O为圆心，任意长度为半径画弧，交OA于M，交OB于N，再以O’为圆心，以OM的长为半径画弧，交O’A’于M’，以M’为圆心，以MN的长为半径画弧，交前弧于N’，最后连接O’N’并延长到B’。

这样就得到了所求的角A’O’B’。

最后一个问题要求经过点P作直线CD，使得CD经过点P且CD⊥AB。

作法是以P为圆心，任意长为半径画弧，交AB于M、N，然后分别以M、N为圆心，大于MN的长为半径画弧，两弧交于点Q，最后过D、Q作直线CD。

这样就得到了所求的直线CD。

题六：已知直线AB及外一点P，求作直线CD，使CD经过点P，且CD⊥AB。

作法：1）以P为圆心，任意长为半径画弧，交AB于M、N；2）分别以M、N为圆心，大于MN长度的一半为半径画弧，两弧交于点Q；3）过P、Q作直线CD。

则直线CD就是所求作的直线。

题目七：已知三边作三角形。

已知：线段a，b，c，求作△ABC，使AB=c，AC=b，BC=a。

初二尺规作图五个方法
尺规作图，是一种利用尺规来绘制图形的一种方法。

它包括五种方法：
一、直线图法：用尺规将两个点之间的直线绘制出来，即可构成图形。

可以用来绘制简单的几何图形，如矩形、梯形、三角形等。

二、折线图法：用尺规将多个点之间的折线绘制出来，即可构成图形。

可以用来绘制复杂的曲线图形，如抛物线、椭圆等。

三、圆弧图法：用尺规将一个圆或一些圆弧绘制出来，即可构成图形。

可以用来绘制圆形的几何图形，如圆、圆环等。

四、线环图法：用尺规将一个线环绘制出来，即可构成图形。

可以用来绘制复杂的几何图形，如圆环、环形等。

五、投影法：用尺规将投影绘制出来，即可构成图形。

可以用来绘制立体图形，如体积图、投影图等。

以上就是尺规作图的五种方法。

尺规作图是一种简单实用的绘图方法，可以用来绘制各种几何图形和立体图形。

它的最大优势在于可以准确控制作图的尺寸和准确性，从而获得精确的图形。

由于尺规作图的优点，在日常工作中，它被广泛应用于设计图纸、绘制图形等方面。

尺规作图的五种方法都是绘图中必不可少的工具，因此，在绘制图形时，应该根据自身的需求充分考虑这五种方法，以求最佳的作图效果。