大学物理实验讲义

大学物理实验讲义实验12用霍尔效应法测量磁场实验名称：用霍尔效应法测量磁场实验目的：1. 学习使用霍尔效应测量磁场；2. 熟悉实验仪器和操作方法。

实验器材：1. 霍尔效应磁场测量仪；2. 电磁铁；3. 直流电源；4. 万用表。

实验原理：霍尔效应是指将电流通过一个导体时，如果该导体处于垂直于磁场方向的磁场中，导体上将会产生一个电压，这个电压称为霍尔电压。

霍尔电压与磁场的强度具有一定的关系，可以通过测量霍尔电压来测量磁场的强度。

根据霍尔效应的原理，可得到以下公式：\[E_H = K \cdot B \cdot I\]其中，E_H为霍尔电压，K为霍尔常数，B为磁场强度，I为通过导体的电流。

实验步骤：1. 连接实验仪器。

将实验仪器的电源接入直流电源，将电磁铁的输入端接入直流电源的正极，将输出端接入实验仪器的霍尔电压测量端。

2. 调节电磁铁的电流。

通过调节直流电源的电流大小，控制电磁铁的磁场强度。

3. 测量霍尔电压。

通过实验仪器的读数，记录下给定电流下的霍尔电压。

4. 重复步骤2和步骤3，分别记录不同电流下的霍尔电压值。

5. 绘制电流与霍尔电压的图线。

6. 根据拟合直线的斜率和霍尔常数的关系，计算磁场强度。

注意事项：1. 实验过程中，要注意安全，避免触电和磁场对身体的影响。

2. 测量时需保持实验环境的恒温和较低的干扰。

3. 操作仪器时要注意仪器的使用说明，避免操作不当导致误差。

4. 测量结果的精度和准确性取决于实验仪器的精度、操作人员的技术水平和实验环境的条件等因素。

实验结果：根据测量所得的电流和霍尔电压数据，绘制出电流与霍尔电压的图线。

利用图线的斜率和霍尔常数的关系，计算出磁场的强度。

电子与场带电粒子在电场和磁场中运动是在近代科学技术应用的许多领域中都经常遇到的一种物理现象。

在下面的实验中，主要研究电子在各种电场和磁场中的运动规律。

在这个实验中，把电子看作是遵从牛顿运动定律的经典粒子。

因为在下面实验中，电子的运动速度总是远小于光速（3.00×108 m/s），所以不必考虑相对论效应，而且由于实验中电子运动的空间范围远比原子的尺度要大，也可不必考虑量子效应。

【实验目的】1.了解示波管的构造和工作原理，研究静电场对电子的加速作用。

2.定量分析电子束在横向匀强电场作用下的偏转情况。

3.定量分析电子束在横向磁场作用下的偏转。

4.定量分析电子束在纵向磁场作用下螺旋运动，测定荷质比。

【实验仪器】DH4521电子束测试仪、电源线、10芯专用电缆、52尼康线。

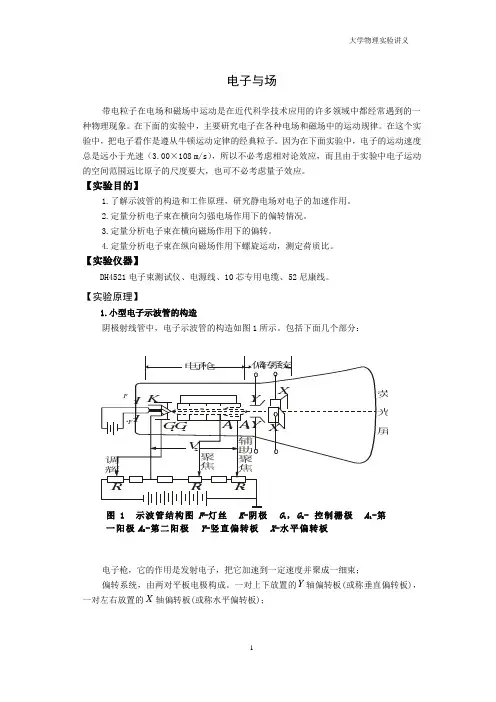
【实验原理】1.小型电子示波管的构造阴极射线管中，电子示波管的构造如图1所示。

包括下面几个部分：图 1 示波管结构图F-灯丝K-阴极G1，G2- 控制栅极A1-第一阳极A2-第二阳极Y-竖直偏转板X-水平偏转板电子枪，它的作用是发射电子，把它加速到一定速度并聚成一细束；偏转系统，由两对平板电极构成。

一对上下放置的Y轴偏转板(或称垂直偏转板)，一对左右放置的X轴偏转板(或称水平偏转板)；荧光屏，用以显示电子束打在示波管端面的位置。

以上这几部分都密封在一只玻璃壳之中。

玻璃壳内抽成高真空，以免电子穿越整个管长时与气体分子发生碰撞，故管内的残余气压不超过610-大气压。

电子枪的内部构造如图2所示。

电子源是阴极，图中用字母K 表示。

它是一只金属圆柱筒，里面装有加热用的灯丝，两者之间用陶瓷套管绝缘。

当灯丝通电时可把阴极加热到很高温度。

在圆柱筒端部涂有钡和锶氧化物，此材料中的电子在加热时较容易逸出表面，并能在阴极周围空间自由运动，这种过程叫热电子发射。

与阴极共轴布置着的还有四个圆筒状电极，电极1G 离阴极最近，称为控制栅，正常工作时加有相对于阴极K 大约-5～-20伏的负电压，它产生的电场是要把阴极发射出来的电子推回到阴极去。

实验09 用牛顿环测曲率半径光的干涉现象证实了光在传播过程中具有波动性;光的干涉现象在工程技术和科学研究方面有着广泛的应用;获得相干光的方法有两种：分波阵面法例如杨氏双缝干涉、菲涅尔双棱镜干涉等和分振幅法例如牛顿环等厚干涉、迈克尔逊干涉仪干涉等;本实验主要研究光的等厚干涉中的两个典型干涉现象,即牛顿环和劈尖干涉,它们都是用分振幅方法产生的干涉,其特点是同一条干涉条纹处两反射面间的厚度相等,故牛顿环和劈尖都属于等厚干涉;在实际工作中,通常利用牛顿环来测量光波波长,检查光学元件表面的光洁度、平整度和加工精度,利用劈尖来测量微小长度、薄膜的厚度和固体的热膨胀系数等;实验目的22λδ+=K K d 8-1式中2λ是因为光线由光疏媒质空气进入光密媒质玻璃在交界面反射时有一位相π的突变而引起的附加光程差半波损失;由图8-1所示的几何关系,有： 因为K d R >>,故可略去2K d 项而得：Rr d KK 22= 8-2根据干涉条件,两束相干光当光程差为波长的整数倍时互相加强,光程差为半波长的奇数倍时互相抵消,因此,第K 级明环和暗环的形成条件是：λδK = 为明环 8-32)12(λδ+=K 为暗环 8-4由公式8-1、8-2、8-3、8-4可求得第K 级明环和暗环的半径为： 明环： 2)12(λR K r K -= ,3,2,1=K 8-5暗环： λKR r K =,2,1,0=K 8-6从公式8-5、8-6可知,在平凸透镜凸面与平面玻璃的接触点即0=K r 处,干涉圆环为暗环,实际观察到的是一个暗圆斑;2. 透镜曲率半径R 的测量方法及系统误差的处理方法如果已知入射光波长λ,则只要设法测得明环或是暗环的半径K r ,就可以由8-5、8-6式求得平凸透镜的曲率半径R 值,反之,当曲率半径R 已知时,则可求得波长λ值;但是,由于玻璃的弹性形变及接触处不干净等原因,使接触处不可能是一个几何点,即中心点的半径不为零,这使得在环心处平凸透镜与平面玻璃之间有一附加厚度其符号可正可负,环心的干涉结果会是一个较大的暗斑,这种情况均导致每环半径K r 发生变化,这时如果仍用8-5、8-6式进行计算,就势必造成较大的系统误差;改用下述方法进行测量,就能消除这个系统误差;假设用暗环进行测量,测出第m 级和n 级的暗环半径m r 和n r ,设这些数据带有上述系统误差,但我们可以认为：r 是测准了的,误差主要是在级数m 和n 上,由于加上了一个附加厚度,使得在理想的点接触时,本该是第x m +环之处,我们现在看到的是第m 环,本该是第x n +环之处,我们现在看到的是第n 环;按8-5、8-6式本该有：上面两式是准确的,把它们平方后相减可得即 λ)(22n m r r R n m --=若用环的直径来表示,则上式可写为λ)(422n m D D R nm --= 8-78-7式只涉及两环级数之差,而不决定于级数本身,从而消除了因级数不准带来的系统误差;另一方面,由8-7式可以发现,只要级数差)(n m -一定,则暗环的直径平方差也是一定值,例如=-=-=-)()()(212222211221210220D D D D D D ,这样,在测量中,可测量多个暗环的m D 和n D 值,然后用逐差法求出多个)(22n m D D -,以平均值)(22n m D D -代进8-7式计算R ,可以进一步减小测量误差,从而有利于进一步提高R 的测量结果的精确度;上面的讨论对于明条纹也有同样的结果; 3. 劈尖干涉玻璃板,包线,这样,二光束相遇时,2δ=nd 要形成暗条纹,则 d =由上式可知,当此时d 总数;在N 不太多的情况下可以直接数出来;但一般情况N 数目很大,故先测出单位长度上的暗条纹数0N ,再测出两玻璃板交接线至待测物间的距离L ,则L N N 0=,于是nL N d 20λ= 8-8 如劈尖间的媒质为空气,则1=n ;仪器介绍JCD 2-A 型读数显微镜 1. 读数显微镜概述读数显微镜即为测量显微镜;显微镜通常起放大物体的作用,而读数显微镜除放大物体外,还能测量物体的大小;读数显微镜的规格型号很多,但基本结构是相同的;本实验使用的是JCD 2-A 型读数显微镜,测量范围为0~50mm,最小分度值为0.01mm 与螺旋测微计相同,可估读到0.001mm;读数显微镜的优点是既有螺旋测微计的测量精度,又不会使被测物体变形、受损,还兼有低倍率显微镜的作用; 2. JCD 2-A 型读数显微镜的外型结构手轮10可使反射镜11的方向适当即目镜视场中背景光亮度适当；显微镜的高度和水平位置均可调节,松开锁紧手轮13和16,显微镜可在竖直方向和水平方向移动；测得数可从标尺18和测微手轮17读得：从标尺上读得的mm位读数加上从测微手轮上读得的数即为最后的测得数,测微手轮的结构与读数方法与螺旋测微计类似,测微手轮每转动一周,显微镜就横移1mm的距离,测微手轮的圆周等分为100小格,因此每一小格表示0.01mm,加上估读的一位,测微手轮可读到0.001mm,因此最后结果可读出五位有效数字;实验内容与要求能通过牛顿环的中心,并依次与各暗环相切;（4）开始测量;由于接近牛顿环中心处的圆环宽度变化很大,不易测准,故可以从10=K 开始测量;又因为暗环较易对准,所以实验时是测量暗环直径D ;选择牛顿环的测量范围为29~10=K 共20个环,为了消除空程差螺距差,注意只能往一个方向进行测量,这时可安排测量顺序如下：转动测微手轮使十字叉丝向左移动到第32环以外,然后倒回到第29环,使十字叉丝与暗环的左侧或右侧相切,对准并读数,记为左29x ,然后缓慢移动十字叉丝至第28环,读出左28x ,逐条依次测量i x ,直至测读出左10x ；继续向原方向转动测微手轮,越过牛顿环的中心区域至第10环,读出右10x ,至第11环,读出右11x ,逐条依次测量i x ,直至测读出右29x ,将全部测量数据填入下面的数据表格中;（5n m 22nm D D -、R σ,并求相对误差r E ;（6）根据实验室给定的牛顿环曲率半径标称值1.855=标R mm,按照0-30式计算百分差r δ; 2. 用劈尖干涉法测量微小物体的厚度（1）将劈尖取代牛顿环放置在读数显微镜的玻璃平台上,在目镜视场中找到干涉条纹,调节调焦手轮,使条纹清晰;移动劈尖,使干涉条纹和叉丝竖线平行;（2）旋转测微手轮,使十字叉丝沿某一方向移动,测出21条干涉暗条纹之间的总长度0L ,在不同位置分别测量4次;（3）计算单位长度的暗条纹数0N 001L n N -=,测4次求平均值0N ; （4）测出由劈尖的顶端开始0=K 至待测物的总长度L ,连续测4次,求平均值L ; （5）按8-8式计算待测物的厚度d ; （6）计算误差;注意事项1. 测量时,只能往一个方向缓慢转动读数显微镜的测微手轮,中途切不可反转,以免带来空程差螺距差;2. 测量中途,如眼睛感到疲劳,可稍作休息再行读数,以保证测量数据的准确性;3. 爱护仪器,各光学镜面不得用手或其它物体触摸;4. 牛顿环装置上的三个压紧螺丝不可拧得太紧,以防压碎镜片;5. 本实验所使用的钠灯光源是冷光源,点亮之后不要轻易关掉它,关掉之后也不能马上再启动,必须先拿开灯罩冷却几分钟后才能再次启动;思考问题课前预习题1. 牛顿环与劈尖干涉有什么相同与不同之处2. 为什么牛顿环的各环宽度不等试解释牛顿环内疏外密的现象;3. 如果本实验观测到的牛顿环中心不是暗斑而是亮斑,试分析其可能性;这种情况对测量R 有没有影响课后思考题4. 牛顿环是非等间隔的干涉环,为什么在实验中仍用逐差法处理数据5. 在牛顿环实验中,假如平玻璃板上有微小的凸起,则凸起处空气薄层的厚度减小,导致等厚干涉条纹发生畸变;试问这时的牛顿环暗环将局部内凹还是局部外凸为什么6. 怎样利用劈尖干涉现象测表面平整度。

大学物理实验讲义（）目录实验1 复摆 (4)预习报告 (8)实验2 弦振动的研究 (9)预习报告 (13)实验3 速度和加速度的测量 (14)预习报告 (21)实验4 动量守恒定律的验证 (22)预习报告 (27)实验5 空气中声速的测量 (28)预习报告...................................................... 错误!未定义书签。

实验6 RLC电路的稳态特性 (24)预习报告...................................................... 错误!未定义书签。

实验报告.. (34)实验7 油滴法测定基元电荷 (46)预习报告 (53)实验8 用双臂电桥测量低值电阻 (54)预习报告...................................................... 错误!未定义书签。

实验9 牛顿环. (60)预习报告 (67)实验10 光电效应及普朗克常数的测定 (68)预习报告 (73)实验11 单缝衍射 (60)预习报告...................................................... 错误!未定义书签。

实验12 多缝的夫琅和费衍射. (79)预习报告...................................................... 错误!未定义书签。

实验报告——速度和加速度的测量 (83)实验报告——牛顿环 (88)实验1 复摆伽利略首先证明了，当空气的摩擦阻力可以忽略不计时，所有自由下落物体都将以同一加速度下落，这就是重力加速度。

重力加速度是一个重要的基本物理常数，测量重力加速度的实验很多，有自由落体测定和气垫导轨等，还有简单方便的单摆和复摆实验。

单摆是根据摆的长度和摆动的周期计算出重力加速度。

复摆是一个任意形状的刚体，受重力作用绕着固定转轴在竖直面内往复摆动，利用复摆的共轭性，通过作图法进行测算得到重力加速度。

大一物理实验讲义知识点实验一：测量物体质量和密度1. 实验目的：通过测量物体质量和尺寸，计算物体的密度。

2. 实验原理：- 质量的测量：使用天平测量物体的质量，保证天平的零位和精确读数。

- 密度的计算：物体的密度可以通过质量与体积之间的关系计算得到，公式为密度=质量/体积。

3. 实验步骤：1) 清洁天平，使其保持干净并调整到零位。

2) 使用天平测量物体的质量，记录下数值。

3) 测量物体的尺寸（如长、宽、高），计算出物体的体积。

4) 根据质量和体积的测量结果，计算物体的密度。

4. 实验注意事项：- 天平要保持干净、水平放置，并调整到零位。

- 测量物体尺寸时，要使用合适的测量工具，并保证测量的准确性。

- 计算密度时，注意单位的转换和小数点的精确性。

实验二：测量光的折射角1. 实验目的：通过测量光的入射角和折射角，验证光的折射定律。

2. 实验原理：- 光的入射角和折射角：当光从一个介质射入另一个介质时，入射角和折射角之间满足折射定律，即入射角的正弦与折射角的正弦之比等于两介质的折射率之比。

- 折射率：介质的折射率定义为光速在真空中的速度与光速在该介质中的速度之比。

3. 实验步骤：1) 准备一个光学平台，并安装一个光源和一个半圆柱形容器。

2) 使用一个测量尺测量半圆柱形容器的半径，并记录下数值。

3) 调整光源和半圆柱形容器的位置，使光线通过容器，并测量入射角和折射角。

4) 根据测量结果，计算光在该介质中的折射率，并与理论值进行比较。

4. 实验注意事项：- 在测量光线入射角和折射角时，要保证准确的读数和测量。

- 使用合适的测量工具，如测量尺和角度测量器。

- 调整光源和容器位置时，要小心操作，避免光线的偏移或干扰。

实验三：测量力的大小和方向1. 实验目的：通过测量物体受力的大小和方向，了解力的性质和作用。

2. 实验原理：- 力的大小：力是物体之间相互作用的结果，可以通过测力计或弹簧秤等工具来测量力的大小。

- 力的方向：力的方向可以通过测量物体所受力的方向来确定，力是矢量量值。

大学物理学实验(讲稿)（力、热、光、电）**: ***授课时间:所在院系: 物理与电子信息学院预备知识：不确定度的概念：不确定度是由于测量误差的存在而造成对被测量值不能确定的程度。

因此，我们应将测量中的不可靠量值叫误差，导致测量结果的不可靠量值叫不确定度。

一、 直接测量量的不确定度计算：A 类不确定度：（随机误差）)1()(2--=∑N N x xu iA （通用式）B 类不确定度：（未定系统误差）3仪∆=B u （p=0.683） （通用式）总不确定度：22B A u u u +=（通用式）仪∆获得的三个途径：（1）由仪器或说明书给出（指以前称为仪器误差）。

（2）由仪器的准确度等级给出：100量程）（等级仪⨯=∆（3）估计连续读数的仪器：分度值仪21=∆；非连续读数的仪器：分度值仪=∆； 数子式仪器：仪∆取末位数字的21±±或。

单次测量的不确定度计算：由于00)(==-A i u x x 故，3仪∆==B u u二、 间接测量量的不确定度计算：设：...),,(z y x f N = 传递公式：...)()()(222222+∂∂+∂∂+∂∂=z y x N u zf u y f u x f u 例如：园柱体的密度公式为h d m v m 24πρ==则222)()2()()(hu d u m u u h d m ++=ρρ ρρρρ⨯=)()(u u （单位）式中：—待测物体的直径。

—d —待测物体的高度。

—h —待测物体的质量。

—m三、 测量结果表示：3)18.091.8()(cm g u ±=±=ρρρ （第一位为1时可多取1位）3)05.080.7()(cm gu ±=±=ρρρ （测量值不足两位补零与不确定度位数对齐）实验一 单摆一、实验目的1、用单摆测定本地的重力加速度；2、掌握用作图法验证理论公式；3、了解测量中主要误差来源及处理方法。

实验1 拉伸法测量杨氏模量杨氏弹性模量(以下简称杨氏模量)是表征固体材料性质的重要的力学参量，它反映材料弹性形变的难易程度，在机械设计及材料性能研究中有着广泛的应用。

其测量方法有静态拉伸法、悬臂梁法、简支梁法、共振法、脉冲波传输法，后两种方法测量精度较高；本实验采用静态拉伸法测量金属丝的杨氏模量，因涉及多个长度量的测量，需要研究不同测量对象如何选择不同的测量仪器。

【实验目的】1. 学习用静态拉伸法测量金属丝的杨氏模量。

2. 掌握钢卷尺、螺旋测微计和读数显微镜的使用。

3. 学习用逐差法和作图法处理数据。

4.掌握不确定度的评定方法。

【仪器用具】杨氏模量测量仪（包括砝码、待测金属丝）、螺旋测微计、钢卷尺、读数显微镜【实验原理】1. 杨氏模量的定义本实验讨论最简单的形变——拉伸形变，即棒状物体(或金属丝)仅受轴向外力作用后的伸长或缩短。

按照胡克定律：在弹性限度内，弹性体的应力S F 与应变LL δ成正比。

设有一根原长为l ，横截面积为S 的金属丝（或金属棒），在外力F 的作用下伸长了L δ，则根据胡克定律有)(LLE SF δ= （1-1） 式中的比例系数E 称为杨氏模量，单位为Pa （或N ·m –2）。

实验证明，杨氏模量E 与外力F 、金属丝的长度L 、横截面积S 的大小无关，它只与制成金属丝的材料有关。

若金属丝的直径为d ，则241d S π=，代入（1-1）式中可得 Ld FLE δπ24= （1-2）（1-2）式表明，在长度、直径和所加外力相同的情况下，杨氏模量大的金属丝伸长量较小，杨氏模量小的金属丝伸长量较大。

因此，杨氏模量反映了材料抵抗外力引起的拉伸（或压缩）形变的能力。

实验中，测量出L d L F δ、、、值就可以计算出金属丝的杨氏模量E 。

2. 静态拉伸法的测量方法测量金属丝的杨氏模量的方法就是将金属丝悬挂于支架上，上端固定，下端加砝码对金属丝F ，测出金属丝的伸长量L δ，即可求出E 。

大学物理实验讲义(太阳能科学与工程系光伏工程教研室2010年3月)目录写在前面 (2)一、物理实验的地位和作用 (2)二、物理实验课的教学目的 (2)三、物理实验课的基本程序 (3)实验一扭摆法测定刚体转动惯量 (5)【实验目的】 (5)【实验原理】 (5)实验二悬丝耦合弯曲共振法测定金属材料杨氏模量 (11)【实验目的】 (11)【实验原理】 (11)实验三电表改装与校准 (19)【实验目的】 (19)【实验原理】 (19)实验四示波器原理及使用 (26)【实验目的】 (26)【实验原理】 (26)实验五霍尔效应实验组合仪的使用 (30)【实验目的】 (30)【实验原理】 (30)实验六迈克尔逊干涉实验仪的使用 (38)【实验目的】 (38)【实验原理】 (38)写在前面一、物理实验的地位和作用科学的理论来源于科学的实验,并受到科学实验的检验,物理学的理论,就是通过观察、实验、抽象、假说等研究方法，并通过实验的检验而建立起来的。

观察和实验是物理学中的重要研究方法。

观察就是对自然界中发生的某种现象，在不改变自然条件的情况下，按照原来的样子加以观察研究。

而实验则是人们按照一定的研究目的，借助按规定的仪器设备，人为地控制或模拟自然现象，使自然现象以比较纯粹或典型的形式表现出来，进而对其进行反复地观察和测试，探索其内部规律的一种方法。

物理学从本质上说是一门实验科学，无论是物理规律的发现，还是物理理论的验证，都有待迂实验。

物理实验不仅在物理学的发展中占有重要的地位，而且在推动其它自然科学、工程技术的发展中也起着重要作用。

特别在不少交叉学科中，物理试验的构思、方法和技术与化学、生物学、天文学等学科的相互结合已取得丰硕的成果。

此外，物理实验还是众多高技术发展的源泉、原子能、半导体、激光、超导和空间技术等最新科技成果，都是与物理实验密切相关的。

二、物理实验课的教学目的根据《高等学校工程专科物理实验课程教学的基本要求》，结合我校的实际，对各专业不同的需要选取一定数量和实用内容的实验项目。

大学物理实验讲义实验12-用霍尔效应法测量磁场实验目的：1.熟悉霍尔效应的基本原理。

2.掌握用霍尔效应法测量磁场的方法。

3.了解LCR电路的基本原理及其在霍尔效应实验中的应用。

实验原理：1.霍尔效应当一个半导体片被放置在一个磁场中时，正常的电流方向将被改变，这是霍尔效应的重要特征。

在一个横向磁场中，电子将受到一个力，使它们沿一个轴移动，这个轴垂直于电流和磁场之间的平面。

由于电荷的分布而产生的电压称为霍尔电压，它与磁感应强度和电流成正比。

2.LCR谐振电路LCR谐振电路是一种电路，可以在给定频率下将电压最小化。

它包括一个电感，一个电容和一个电阻器。

在特定的谐振频率下，当电感和电容的电流达到平衡时，电阻器的电流将为零。

这时电路的表现出来的阻抗是最小的，因此在谐振频率下可以测量出磁场。

实验器材：霍尔效应实验装置、电源、导线、万用表、量角器、磁铁。

实验步骤：1.首先将霍尔效应实验装置放在静磁场中，并用万用表确认磁场的磁感应强度。

2.将红色电缆夹子连接到霍尔片上的直流电极，将黑色夹子连接到其左边的垂直电极，用导线将电缆夹子连接到电源上。

3.用万用表检查电源输出电压的值。

将电源输出电压调整到所需的范围。

4.将量角器放在霍尔片上，测量电流通过载流电极时，霍尔片的垂直电极与磁场之间的夹角。

5.打开电源，调整电流强度至所需范围。

6.将电阻器调至LCR电路上的电阻元件的最佳位置。

7.使用万用表或示波器测量在谐振频率下所具有的最小值。

8.再次使用量角器，测量电流通过霍尔片时，霍尔电压与磁场之间的夹角。

9.用霍尔电压和磁感应强度计算出霍尔常数。

1.通过等式VH = IBZH / e d，我们可以计算出横向电场的霍尔电压，其中IB是电流，ZH是霍尔电阻，e是电子的带电量，d是半导体晶片的厚度。

3.使用等式R = V/IH计算出霍尔电阻。

实验结果分析：通过实验数据处理，我们可以计算出霍尔电阻和霍尔常数，并使用它们来确定磁场的强度。

实验01 塞曼效应实验在物理学的发展过程中，人类为光本性的探讨经过了相当曲折的过程。

1845 年，法拉第发现光的振动面在磁场中发生旋转，揭示了光学现象与磁学现象之间存在联系，启发人类不能孤立地研究光，必须将光学现象和其它物理现象联系起来考虑。

1860 年，麦克斯韦的理论研究指出光的电磁本质，1892 年赫兹的实验证实了光是电磁波。

1896年塞曼（zeeman）在强磁场和精密的光谱仪器，使原子光谱分裂成数条完全偏振的光谱现象，此现象被称为塞曼效应，洛仑兹电子论对其的解释，使洛仑兹的“电子论取得了它最伟大的胜利”（劳厄）。

塞曼效应在对光本性认识中的作用被认为是继X光(1895)之后物理学最重要的发现之一。

1902 年塞曼因这一成就与洛仑兹共获诺贝尔物理奖。

塞曼效应是研究原子结构和能级参数的重要手段，也是激光技术、测量技术中的重要手段。

∆≤0.14cm-1），故采用法布里-玻罗标由于塞曼效应分裂谱线的间距极小（波数间距γ~∆值。

准具来分析谱线的精细结构，并用照相或摄谱装置记录测量塞曼分裂线的波数间距γ~【实验目的】1、观察汞546.1 nm 光谱线的塞曼效应；2、了解用法布里-波罗干涉仪测量波长差值的方法；3、测量汞546.1 nm 塞曼分裂光谱线的波长差，并且测定e /m的值。

【仪器用具】由笔形汞灯、汞灯支架、汞灯电源、可移动永久磁铁、聚光透镜、可切换滤光片盘、偏振片、FP标准具、成像透镜、观测目镜、测微千分表、CCD摄像头等部件组成三、实验原理1896年，塞曼（P. Zeeman）发现把光源放置于足够强的磁场中时，磁场作用于光体，使其光谱发生变化，可把每一条谱线分裂成几条偏振化的谱线，这种现象称为塞曼效应。

塞曼效应实验证实了原子具有磁矩和空间取向量子化，这一现象得到洛仑兹理论的解释。

1902年塞曼因这一发现与洛仑兹共享诺贝尔物理学奖。

1、原子的磁矩原子由原子核和电子组成，电子绕原子核具有轨道运动和自旋运动，相应的轨道角动量、轨道磁矩、自旋角动量及自旋磁矩可表示为：μL = eP L / 2m (1)P L = [ L (L+1)]1/2 h / 2π(2)μS = eP S / m (3)P S = [ S ( S +1)] h / 2π(4)式中L为轨道量子数，S 为自旋量子数，e为电子电荷，m为电子质量，h为普朗克常数。

用稳恒电流场模拟静电场1、知识介绍在科学研究及实际生产中，常常需要确定带电体周围的静电场分布，这些任意形状的带电体在空间的电场分布（即电场强度和电势的分布）比较复杂，一般很难写出它们的数学表达式，理论计算非常困难。

例如在电子管、示波管、电子显微镜以及各种显示器内部电极形状的设计和研究制造中，都需要了解各电极或导体间的电场分布情况，采用数学方法进行计算十分复杂，一般通过实验的手段来确定。

但直接对静电场进行测量也是相当困难，对于静电场，测量仪器只能采用静电式仪表，而实验中一般采用磁电式仪表，有电流才有反应。

静电场中无电流，磁电式仪表不会起作用，且一旦将仪器放入静电场中，探针上会产生感应电荷。

这些电荷所产生的电场将叠加到原来的待测静电场中，即测量仪器的介入会导致原静电场分布发生畸变。

为避免数学方法的复杂性以及直接测量的不现实性，实验中采取模拟法测绘静电场。

模拟法就是采用一个和待测对象有相似的数学形式或物理规律的模型或装置来代替实际的待测对象，且该模型或装置在实验室条件下较容易实现。

相似模型中各个变量和原型中相应变量有相似关系，既包括几何形状相似，也包括质量、时间、力、温度、电流、电场等的相似。

图7-1 垂直风洞模拟空中跳伞图7-2 汽车模拟风洞实验模拟法一般分为物理模拟和数学模拟两大类。

物理模拟具有生动形象的直观性，并可使观察的现象反复出现，尤其是对于那些难以用数学表达式准确描述的对象进行研究时，常常采用物理模拟方法。

数学模拟是指模型和原型遵循相同的数学规律，满足相似的数学方程和边界条件。

本实验模拟构造了一个和原静电场完全一样的稳恒电流场，当用探针去测模拟场时，原场不受干扰，因此可间接地测出模拟场中各点的电势，连接各等电势的点作出等势线。

根据电场线和等势线的垂直关系，描绘出电场线，这样就可以由等势线的间距确定电场线的疏密和指向，即可形象地了解电场情况。

理论和实验都能证明，只要电极的形状和大小，相对位置和边界条件一致，这两个场的分布应该是一样的。

大学物理实验讲义-弦振动与驻波研究弦振动与驻波研究【实验目的】1．观察在弦上形成的驻波；2．确定弦线振动时驻波波长与张力的关系； 3．学习对数作图和最小二乘法进行数据处理。

【实验原理】在一根拉紧的弦线上，其中张力为T ，线密度为μ，则沿弦线传播的横波应满足下述运动方程：2222x yT t y ∂∂=∂∂μ(1)式中x 为波在传播方向（与弦线平行）的位置坐标，y 为振动位移。

将(1)式与典型的波动方程22222x y V t y ∂∂=∂∂相比较，即可得到波的传播速度: μTV =若波源的振动频率为f ，横波波长为λ，由于波速λf V =，故波长与张力及线密度之间的关系为：μλTf1=(2)为了用实验证明公式(2)成立，将该式两边取对数，得：11lg lg lg lg 22T f λμ=-- (3)固定频率f 及线密度μ，而改变张力T ，并测出各相应波长λ，作lg λ-lg T 图，若得一直线，计算其斜率值（如为21），则证明了λ∝21T的关系成立。

弦线上的波长可利用驻波原理测量。

当两个振幅和频率相同的相干波在同一直线上相向传播时，其所叠加而成的波称为驻波，一维驻波是波干涉中的一种特殊情形。

在弦线上出现许多静止点，称为驻波的波节。

相邻两波节间的距离为半个波长。

【实验仪器】1、可调频率数显机械振动源；2、振动簧片；3、弦线（铜丝）；4、可动刀片支架；5、可动刀口支架；6、标尺；7、固定滑轮；8、砝码与砝码盘；9、变压器;10、实验平台；11、实验桌9123456781011图1 实验装置示意图图2 可调频率数显机械振动源面板图 （1、电源开关 2、频率调节 3、复位键 4、幅度调节 5、频率指示）实验装置如图1所示，金属弦线的一端系在能作水平方向振动的可调频率数显机械振动弦线上驻波实验仪电 源ON复位 幅度 调节上海复旦天欣科教仪器有限公司频率调节H Z1 2 3 45FD-SWE-II源的振簧片上，频率变化范围从0-200Hz 连续可调，频率最小变化量为0.01Hz ，弦线一端通过定滑轮⑦悬挂一砝码盘⑧；在振动装置(振动簧片)的附近有可动刀片支架④，在实验装置上还有一个可沿弦线方向左右移动并撑住弦线的可动刀口⑤。

【实验目的】(1)掌握游标卡尺的读数原理和使用方法，学会测量不同物体的长度。

(2)掌握千分尺(螺旋测微器)和物理天平的使用方法。

(3)测量规则固体密度。

(4)用流体静力称衡法测量液体的密度。

(5)学会正确记录和处理实验数据，掌握有效数字记录、运算和不确定度估算。

记下游标卡尺的量程和最小分(刻)度值，卡尺零点校正：松开游标紧固螺钉。

合拢刀口，记下零点偏差值）（初L 用游标卡尺)02.0(mm 铜套的高H 、外径D 、内径d ，各测六次取其平均值，如果存在初读值需校正。

该情况下总的不确定度可取U B =0.02mm ，各直接测量的结果表达式X=X ±U B (X)计算体积V 和估算不确定度体积：V=H )d D (422⋅- 不确定度：22222)]()(4[))( 2())( 2()(H U d D d U d H D U D H V U -++=πππ 测量结果表达为：V=V ±U(V)()()()232122221321223221)()()()()()()(m U m m m U m m m U m m m m -+-+-⋅-=水()[]()()()221312221321m m m m m m m m m m --ρ=∂ρ∂-+-ρ=∂ρ∂水水图1-5中的游标卡尺读数为多少？我们知道当主、附尺的零刻度线重合时，被测物长度为零，由此推断被测物的长度应等于主、附尺零刻度线之间的距离(即图中L)。

故用游标卡尺测取读数时首先应读取游标零刻度线在主尺上所截取的读数值，图中游标零刻度线在主尺上所截取的读数值L 0=15.0mm,但还有从15.0mm 刻度线到游标零刻度线之间的小段距离ΔL 读不出来。

为此，可利用线段相减的原理求ΔL ，第二步从主、附尺上找出主、附尺的重合线，读出附尺的格数m ，由图知m=5格，于是按线段相减原理：图1-7 螺旋测微器mm nmb a m mb ma L 5.01.05)(=⨯==-=-=∆ 最后，得到被测物体的长度即读数值L 为：mm namL L L L 5.155.00.1500=+=+=∆+= (1-4) 我们称(1-4)式为游标卡尺的读数原理，它对角度游标也。

11机本大学物理实验（上）讲义收获在于努力！目录第一章测量误差及数据处理-------------------------------------------------------------------------------------------------- 3§1-1 测量与误差 ------------------------------------------------------------------------------------------------------------------ 31.1.1 测量--------------------------------------------------------------------------------------------------------------------------- 31.1.2 测量结果--------------------------------------------------------------------------------------------------------------------- 31.1.3 测量值——算术平均值 -------------------------------------------------------------------------------------------------- 41.1.4 误差--------------------------------------------------------------------------------------------------------------------------- 51.1.5 误差处理方法 -------------------------------------------------------------------------------------------------------------- 61.1.6 不确定度的简化估算方法 ----------------------------------------------------------------------------------------------- 61.1.6 仪器量程精密度准确度 ----------------------------------------------------------------------------------------------- 9§1-2有效数字及运算规则 ---------------------------------------------------------------------------------------------------- 101.2.1 有效数字的基本概念 ---------------------------------------------------------------------------------------------------- 101.2.2直接测量的读数原则 ----------------------------------------------------------------------------------------------------- 101.2.3 有效数字运算规则 ------------------------------------------------------------------------------------------------------- 111.2.4 测量结果数字取舍规则 ------------------------------------------------------------------------------------------------- 12§1-3实验数据处理基本方法 ------------------------------------------------------------------------------------------------- 121.3.1 列表法----------------------------------------------------------------------------------------------------------------------- 121.3.2 图解法----------------------------------------------------------------------------------------------------------------------- 121.3.3 逐差法----------------------------------------------------------------------------------------------------------------------- 141.3.4 最小二乘法----------------------------------------------------------------------------------------------------------------- 14第二章实验课题---------------------------------------------------------------------------------------------------------------- 15§实验1学习使用万用表------------------------------------------------------------------------------------------------------- 15§实验2学习使用电子示波器------------------------------------------------------------------------------------------------- 23§实验3弦线上驻波实验------------------------------------------------------------------------------------------------------- 31§实验4拉伸法测细丝的杨氏模量 ------------------------------------------------------------------------------------------ 35§实验5用扭摆法测定物体转动惯量---------------------------------------------------------------------------------------- 38§实验6霍尔效应---------------------------------------------------------------------------------------------------------------- 44第一章 测量误差及数据处理本章介绍测量误差估计、实验数据处理和实验结果的表示等初步知识。

大学物理实验讲义(密度测定)密度是物质的一种常用的物理量，是物质质量与体积之比。

在实验中，可以通过测定物质的重量和体积来求出其密度。

本实验利用吊秤法和水位计法分别测定不同物质的密度。

一、吊秤法测定密度实验器材：电子称、吊秤装置、砝码、试样（铁块、铜块、铝块、锌块等）。

实验原理：将试样通过挂钩架悬挂于天平下方，测得其重量；然后将试样完全浸入量满水的容器中，测出水位上升高度，根据密度的定义可以求得物质的密度。

实验步骤：1. 确定天平的零点，将待测试样挂于吊秤上，并测出其质量（m）。

2. 将已盛满水的容器放在桌面上，用木棍调整水平度并记录水位读数（h_1）。

3. 将试样放入容器中，让其完全浸入水中，此时水位上升高度为h_2。

4. 用吊秤将试样取出，记录重量（m_1）。

5. 计算物质密度ρ：ρ = m / (V_s - V_w )其中V_s为试样的体积，V_w为水的体积。

实验注意事项：1. 确保吊秤的准确性，及时校准天平的零点。

2. 确保试样完全浸入水中，避免空气被浸入水中影响实验结果。

3. 确保容器平衡稳定，避免水的波动和震动影响实验结果。

实验器材：水位计、烧杯、试样（木块、塑料块、泥土等）。

1. 用水注满烧杯，记录水面高度为h_1。

2. 将待测试样放置于水中，记录水位的高度为h_2。

1. 测量时注意正确读取水位计的读数，避免读错或者漏读。

本实验通过吊秤法和水位计法分别测定了不同物质的密度，验证了密度的定义。

实验中要注意保证实验器材的精度和稳定性，并严格按照实验步骤操作，避免误差的发生，从而取得高精度的实验结果。