迈克耳孙干涉仪实验报告
- 格式:doc
- 大小:42.00 KB
- 文档页数:3

迈克耳孙干涉仪的调节和使用实验报告大家好,今天我要给大家分享一下我最近做的一次实验——迈克耳孙干涉仪的调节和使用。
这次实验可真是让我大开眼界,原来科学实验可以如此有趣!好了,废话不多说,让我们开始吧!我要给大家介绍一下迈克耳孙干涉仪是什么。
迈克耳孙干涉仪是一种利用光的干涉现象来测量物体长度的仪器。
它的主要原理是:当两束光波相遇时,如果它们的光程差相等,那么它们就会发生相长干涉;如果它们的光程差相差半个波长,那么它们就会发生相消干涉。
通过测量干涉条纹的形态和位置,我们就可以计算出物体的长度。
接下来,我要给大家讲解一下实验的具体步骤。
我们需要准备两台迈克耳孙干涉仪,一台作为基准仪,另一台作为待测仪。
然后,我们需要将待测仪放置在一个已知长度的标准尺上。
这时,我们就可以开始调节基准仪了。
具体方法是:用一个已知长度的标准尺放在待测仪和基准仪之间,然后调整基准仪的高度和角度,使得两台干涉仪的光程差为半个波长。
这样一来,干涉条纹就会出现在标准尺上。
接下来,我们只需要观察干涉条纹的位置和形态,就可以计算出待测仪的长度了。
在实验过程中,我遇到了一些有趣的问题。
比如说,当我第一次调整基准仪的时候,总是调不好。
后来我才发现,原来是我没有注意观察干涉条纹的变化。
原来,只有在干涉条纹稳定后,我们才能准确地测量出待测仪的长度。
这让我深刻地体会到了“熟能生巧”的道理。
我还发现了一个有趣的现象。
那就是,当我把待测仪移动到不同位置时,干涉条纹的位置和形态都会发生变化。
这让我想到了那句老话:“人生就像一场戏,每天都有新花样。
”在这个世界上,没有什么是一成不变的,我们要学会适应变化,才能不断地进步。
总的来说,这次迈克耳孙干涉仪的实验让我收获颇丰。
我不仅学会了如何调节和使用干涉仪,还体会到了科学实验的乐趣。
我相信,只要我们用心去探索,就一定能够揭开自然界的神秘面纱。
我要感谢我的老师和同学们的支持和帮助,是你们让我在这个实验中取得了成功。

迈克耳孙干涉仪实验报告一、实验目的本实验的目的是研究大电流的特性,熟悉并使用米克尔孙干涉仪完成电流度量的实验,并采集测量数据,以证实熟悉的物理原理。
二、实验原理米克尔孙干涉仪是一种用于测量大电流的传感器,它采用了米克尔孙定律理论,简单地讲,当电流通过米克尔孙仪时,电流就会形成米克尔孙磁场,经过一定距离后,这个磁场耦合到被测量的磁棒上,由磁棒变化量来表征电流的大小,从而进行度量。
三、实验仪器和材料1. 测试用米克尔孙棒:由磁棒组成的2类装置,用作测量大电流的特性,其特性由米克尔孙定律决定。
2. 示波器:一种用于研究电流的仪器,可以显示持续变化的电流和电压的变化情况以及一些不可见的参数。
3. 多功能电源:一种可以提供稳定电压和电流的电源,用于测试米克尔孙棒,可以模拟各种实际电路中的调制过程。
四、实验步骤1. 熟悉米克尔孙棒结构,了解它的工作原理和测量原理。
2. 将米克尔孙仪连接多功能电源、示波器和计算机。
3. 根据计划,调整多功能电源,使其依次输出不同电压和电流,对米克尔孙仪进行测试。
4. 测量和记录米克尔孙仪的输出参数,包括电压、电流和振幅等。
5. 根据实验结果,计算最大变化量等参数。
6. 将实验数据进行处理和分析。
五、实验结果1. 实验中,采用多功能电源逐步改变电流和电压,获得了不同参数的测量结果,其结果如下所示:2. 通过实验,得出了米克尔孙仪的变化量与电压的关系:随着电压的增加,变化量呈线性增加趋势,与电压的增加趋势一致。
3. 通过实验处理,得出拟合的变化量的方程为Y=AX+B,其中,A,B分别为 0.3, 0.2.六、总结通过本次实验,我们可以准确地测量出米克尔孙仪的变化量,并用于证明其物理原理,同时也掌握了多功能电源、示波器等仪器的使用方法,受益匪浅。

迈克尔逊干涉仪实验报告英文回答:Michelson Interferometer Experiment Report。
Introduction。
The Michelson interferometer is an optical instrument that uses interference to measure the wavelength of light and the speed of light. It was invented by Albert A. Michelson in 1881. The interferometer consists of a light source, two mirrors, and a beam splitter. The light source is split into two beams by the beam splitter. One beam is reflected by one mirror and the other beam is reflected by the other mirror. The two beams are then recombined by the beam splitter and the interference pattern is observed.Methods。
This experiment determined the speed of light using aMichelson interferometer. The following apparatus was used: 1A Michelson interferometer。
2A helium-neon laser。
3A power supply。
4A photodetector。
5A digital oscilloscope。

迈克尔孙实验报告篇一:迈克尔孙干涉仪实验实验报告实验题目:迈克尔逊干涉仪实验成绩:一、实验目的1、学习迈克尔逊干涉仪的使用;2、测量He-Ne激光器发出光波的波长。
二、实验仪器用具计算机及其仿真软件三、实验原理(一)光的干涉对于薄膜干涉,当光程差满足正式时,将分别出现明暗相间的条纹,即明条纹暗条纹(1)在迈克尔逊干涉仪中M1与M2的像之间可以视为薄膜,由(1)式可知,相邻两条明条纹或暗条纹之间的光程差为,对应薄膜之间的厚度差为e??/2。
因此当视野中移过n条干涉条纹时,则M1移动的距离为h?ne?n?2(2)实验时只需测出当视野中移过n条干涉条纹时,M1移动的距离,即可以利用(2)来测量光波的波长。
四、实验内容一、启动软件:二、仪器调节三、实验内容及步骤测量He-Ne激光器发出的光波波长1、在窗口中右键,选择“测量He-Ne激光波长”;2、在迈克尔孙干涉仪侧面右键,选择“导轨侧面毫米刻度尺读数”、左键单击“刻度盘读数窗口”和“微动手轮”,弹出对应窗口;3、右击微动手轮(左击或右击均可,右击是让干涉条纹从中心冒出,便于观察),选择干涉条纹的一个参考位置,记下三者之和的初始读数为x1?;4、继续右击微动手轮,让干涉条纹从中心冒出,当连续冒出n?100个干涉条纹时,刻度尺三者之和的读数为x2? ;5、M1移动的距离为h?x2?x1? ;6、利用(2)计算He-Ne激光器发出的光波波长??2h? n相对误差为 E?,其中He-Ne激光的波长为6.328?10m。
?7篇二:迈克尔逊干涉仪的使用实验报告学生物理实验报告实验名称迈克尔逊干涉仪的使用学院专业班级报告人学号同组人学号同组人学号同组人学号理论课任课教师实验课指导教师实验日期报告日期实验成绩批改日期篇三:迈克尔孙干涉仪实验报告迈克耳孙干涉仪实验报告实验目的1、了解迈克尔逊干涉仪的结构及工作原理,掌握其调试方法2、学会观察非定域干涉、等倾干涉、等厚干涉及光源的时间相干性,空间相干性等重要问题。

迈克耳孙干涉仪实验报告
实验报告:
迈克耳孙干涉仪实验报告
一、实验目的
本实验旨在探究迈克耳孙干涉仪的工作原理,通过测量光程差的改变对光干涉的现象进行观测,验证光的波动性。
二、实验原理
迈克耳孙干涉仪是一种利用光的干涉现象测量长度、精密测量折射率和表面形貌的仪器。
该仪器由光源、光路、反射镜、分束器等部分组成。
实验中将激光通过分束器分为两路,经过反射后合并。
若光程差为波长λ的整数倍,则两束光相长干涉,能够产生干涉条纹;若光程差为波长λ的奇数倍,则两束光相消干涉,无光强信号输出。
通过调整移动反射镜的距离,可以改变两束光之间的光程差,
从而改变干涉条纹的位置和间距。
三、实验步骤
1.将迈克耳孙干涉仪放在水平台上,调整仪器平衡,保证反射
镜和分束器都放在同一水平线上。
2.利用反射镜将激光分为两路,并调整两路光的光程差至相等。
3.调整反射镜位置,使两路光在同一点空间叠加,观察干涉条
纹的出现。
4.移动反射镜,改变光程差,观察干涉条纹的变化。
5.记录不同光程差下的干涉条纹位置,计算出相应的波长,并
根据波长变化计算出光的折射率。
四、实验结果
在实验中,我们测量了不同光程差下的干涉条纹位置,并计算出了光的波长和折射率。
实验结果表明,光的波动性和干涉现象得到了很好的验证。
五、实验结论
本实验利用迈克耳孙干涉仪探究了光的干涉现象,通过测量干涉条纹位置计算出相应的光程差、波长和折射率等参数,验证了光的波动性和干涉现象。
通过本实验,我们加深了对光学基础理论的理解,对光学实验技能有了更深入的认识。

实验一迈克尔逊干涉仪实验报告_2011.5.17英文回答:Michelson Interferometer Experiment Report_2011.5.17。
Abstract。
The Michelson interferometer is a device that uses interference to measure the wavelength of light. It was invented by Albert A. Michelson in 1881. The interferometer consists of two mirrors that are placed at a distance of about 2 meters apart. A beam of light is split into two beams, and each beam is reflected by one of the mirrors. The two beams are then recombined, and the interference pattern is observed.Materials。
Michelson interferometer。
Light source。
Detector。
Procedure。
1. Set up the Michelson interferometer.2. Align the mirrors so that the beams of light are parallel.3. Adjust the distance between the mirrors so that the interference pattern is visible.4. Measure the distance between the bright fringes.Results。

迈克尔逊干涉仪实验报告数据处理篇一:迈克尔逊干涉仪实验报告迈克尔逊干涉仪的调整与应用1. 原始数据及处理1.1 测量钠光灯波长(?Na?589.3nm)不确定度计算:?A?2.48?x?mm, ?B?0.00004mm?U?d?mm U??U2U?d=4.4nm,Ur????100%=0.74%. ?N?1.2 双线的波长差:??Na?0.59nm 2.思考题及分析:2.1、为什么白光干涉不易观察到?答:两光束能产生干涉现象除满足同频、同向、相位差恒定三个条件外,其光程差还必须小于其相干长度。
而白光的相干长度只有微米量级,所以只能在零光程附近才能观察到白光干涉。
2.2、为什么M1和M2没有严格垂直时,眼睛移动干涉条纹会吞吐?答:因为没有严格垂直时,会形成一个披肩状的光学腔。
各处的光程差不相同,其干涉条纹的级数也会不同。
所以眼睛移动时,干涉条纹会吞吐。
2.3、讨论干涉条纹吐出或吞入时的光程差变化情况。
答:吞入时,光程差变小。
而吐出时,光程差则变大。
2.4、为什么要加补偿板?答:因为分束板的加入,使其中一路光束比另一光束附加了一定的光程。
所以加入与分束板厚度相同的补偿板来补偿这部分光程差。
2.5、如何设计一个实验,利用迈克尔逊干涉仪测玻璃的折射率?答:以白光发生干涉现象时,确定零光程处。
测定在光路中加入玻璃与否,白光产生干涉时M2镜移动的距离。
再根据所加入玻璃的厚度,计算出玻璃的折射率。
2.6、试根据迈克尔逊干涉仪的光路,说明各光学元件的作用,并简要叙述调出等倾干涉、等厚干涉和白光干涉条纹的条件及程序.答:分束板:将光束分为两路光束。
补偿板:补偿因分束板产生的光程差。
粗调螺丝:调节使其与M1镜大致垂直。
细调拉丝:精密调节M2镜的方位,使使其与M1M2镜的方位,镜严格垂直。
鼓轮:调节M2镜的位置,使光学腔的厚度改变。
等倾干涉:光学腔应严格平行。
等厚干涉:此时光学腔为披肩状。
白光干涉:零光程处附近。
2.7、如何利用干涉条纹“吞”、“吐”现象,测定单色光的波长? 答:数一定量的“吞”或“吐”,再根据公式??2?d?N计算。

迈克耳孙干涉仪实验报告迈克耳孙干涉仪实验报告引言:迈克耳孙干涉仪是一种经典的光学实验装置,由德国物理学家阿尔伯特·迈克耳孙于1887年发明。
该实验装置通过利用光的干涉现象,可以精确测量光的波长、光速以及其他光学参数。
本实验报告将详细介绍迈克耳孙干涉仪的原理、实验步骤以及实验结果的分析。
一、实验原理:迈克耳孙干涉仪的原理基于光的干涉现象。
当光线经过一块透明介质表面时,会发生折射和反射。
当入射光线的角度满足一定条件时,反射光线和透射光线会发生干涉现象,产生明暗条纹。
迈克耳孙干涉仪利用这种干涉现象来测量光的波长。
二、实验装置:迈克耳孙干涉仪主要由一个分束器、两个反射镜和一个透明介质构成。
分束器将入射光线分成两束,分别经过两个反射镜反射后再次汇聚,形成干涉条纹。
三、实验步骤:1. 调整仪器:首先,调整迈克耳孙干涉仪的各个部件,确保光线的传输正常。
调整分束器使得光线分成两束,经过反射后再次重合。
调整透明介质的位置,使得干涉条纹清晰可见。
2. 测量干涉条纹:用目镜观察干涉条纹的变化。
通过调整反射镜的位置,可以改变干涉条纹的间距和形状。
记录下不同位置的干涉条纹,并测量它们的间距。
3. 计算波长:根据干涉条纹的间距和实验装置的参数,可以计算出入射光线的波长。
利用迈克耳孙干涉仪的公式,可以得到波长的精确数值。
四、实验结果分析:通过实验,我们得到了一系列干涉条纹的数据。
根据这些数据,我们可以计算出入射光线的波长。
在实验中,我们还可以改变透明介质的折射率,观察干涉条纹的变化。
通过对实验结果的分析,我们可以得到一些有趣的结论。
在实验中,我们发现干涉条纹的间距与入射光线的波长成正比。
这符合光的波动性质,也验证了迈克耳孙干涉仪的原理。
通过计算,我们得到了入射光线的波长为X纳米。
这个结果与已知的光的波长相符合,验证了实验的准确性。
此外,我们还发现透明介质的折射率对干涉条纹的形状有一定影响。
当折射率增大时,干涉条纹的间距会变大,条纹也会更加清晰。

实验预习与原始数据记录一、原理简述1.迈克耳孙干涉仪的结构和原理:A和B为材料、厚度完全相同的平行板,A的一面镀上半反射膜,M1、M2为平面反射镜,M2是固定的,M1和精密丝杆相连,使其可前后移动,最小读数为10−4mm,可估计到10−5mm,M1和M2后各有几个小螺丝可调节其方位。
2.透明薄片折射率(或厚度)的测量:(1). 白光干涉条纹干涉条纹的明暗决定于光程差与波长的关系,用白光光源,只有在d=0的附近才能在M1、M2′交线处看到干涉条纹,这时对各种光的波长来说,其光程差均为λ/2(反射时附加λ/2),故产生直线黑褐色纹,即所谓的中央条纹,两旁有对称分布的彩色条纹。
(2)固体透明薄片折射率或厚度的测定当视场中出现中央条纹之后,在M1与A之间放入折射率为n、厚度为l的透明物体,则此时程差要比原来增大∆L=2l(n−1),因而中央条纹移出视场范围,如果将M1向A前移d,使d=∆L/2,则中央条纹会重新出现,测出d及l,可由下式d=l(n−l)求出折射率n。
二、预习中的问题列举自误差的主要来源是什么?三、原始数据记录表1中心每“生成”或“吞进”30个干涉条纹M1镜的位置表2条纹从不可见到次不可见时M1的位置读数将中央黑褐纹移到中间,M1的位置(mm)=30.89650放置玻璃薄片,再将中央黑褐纹移动至中心,M1的位置(mm)=30.89100移除玻璃薄片,找到d=0的位置,观察到中央是直线黑褐纹两边对称分布彩色花纹的直线干涉条纹,M1的位置(mm)=30.89600放置水晶薄片,再将中央黑褐纹移动至中心,M1的位置(mm)=30.89065表3 中心每“生成”或“吞进”30个干涉条纹时M1镜的位置实验名称:迈克尔逊干涉仪实验日期 2023.11.12 教师签字同组者审阅日期一、实验目的1.了解迈克尔逊干涉仪的构造原理并掌握其调节方法2.通过实验观察等倾干涉、等厚干涉、自然光干涉和非定域干涉条纹3.了解光源的时间相干性问题二、实验仪器与实验方法实验仪器:HeNe激光器,Na光源,白光源,小孔光阑,短焦透镜(扩束镜),迈克耳孙干涉仪实验内容:1. 观察非定域干涉条纹2.测量He-Ne激光的波长3.测钠黄光波长及钠黄光双线的波长差,观察条纹的可见度的变化;4.测量钠黄光的相干长度,观察氦氖激光的相干情况;5.调节观察白光干涉条纹,测定透明薄片的折射率.三、测量内容及数据处理1.用逐差法处理数据,根据相应公式计算钠光的波长λ(nm)=589.26λ=∆D1+∆D2+∆D3390×12=0.02650+0.02650+0.02655345×1000000≈589.26(nm)2.用逐差法处理数据,根据相应公式计算钠光双线的波长差d(nm)=0.60d=λ2∆D1+∆D22=589.2620.57918+0.581852×11000000≈0.60(nm)3.两种薄片的折射率:玻璃:N=30.89650−30.891000.01+1=1.55水晶:N=30.89100−30.890650.01+1=1.544.用逐差法处理数据,根据相应公式计算He-Ne激光的波长λ(nm)=632.89λ=∆D1+∆D2+∆D3390×12=0.02848+0.02850+0.02846345×1000000≈632.89(nm)四、小结(结论、误差分析及建议等)结论:钠光的波长λ=589.26nm钠光双线的波长差d=0.60nm玻璃的折射率为1.55水晶的折射率为1.54He-Ne激光的波长λ=632.89nm误差分析:1.d0、d30对应的圆心处干涉圆环不会完全一致而产生误差;2.读数误差。

迈克尔逊干涉仪实验报告一、实验目的1、了解迈克尔逊干涉仪的结构和工作原理。
2、掌握迈克尔逊干涉仪的调节方法。
3、观察等倾干涉、等厚干涉条纹,并测量激光的波长。
二、实验原理迈克尔逊干涉仪是一种利用分振幅法产生双光束干涉的精密光学仪器。
其原理基于光的干涉现象。
从光源 S 发出的一束光,经分光板 G1 分成两束光,反射光 1 射向平面镜 M1,透射光 2 射向平面镜 M2。
M1 和 M2 反射回来的光在分光板 G1 的半透膜处相遇,发生干涉。
若 M1 和 M2 严格垂直,则形成等倾干涉条纹。
此时,干涉条纹是一组同心圆环,圆心处条纹级次最高。
干涉条纹的光程差为:$\Delta = 2d\cos\theta$其中,d 为 M1 和 M2 之间的距离,θ 为入射光与 M1 法线的夹角。
当 M1 和 M2 有一定夹角时,形成等厚干涉条纹。
此时,干涉条纹是平行于 M1 和 M2 交线的直条纹。
通过测量干涉条纹的变化,可以计算出光的波长。
三、实验仪器迈克尔逊干涉仪、HeNe 激光器、扩束镜、毛玻璃屏等。
四、实验步骤1、仪器调节调节迈克尔逊干涉仪的底座水平。
点亮 HeNe 激光器,使激光束大致垂直于干涉仪的入射窗口。
放置扩束镜和毛玻璃屏,在屏上观察激光光斑,调节 M1 和 M2 背后的螺丝,使光斑重合。
观察干涉条纹,若没有出现条纹,微调 M1 或 M2 的位置,直到出现清晰的干涉条纹。
2、测量激光波长转动微调鼓轮,使条纹中心“冒出”或“缩进”,记录条纹变化的条数N 和对应的微调鼓轮的读数变化Δd。
重复测量多次,计算平均值,根据公式$\lambda =\frac{2\Delta d}{N}$计算激光的波长。
3、观察等倾干涉和等厚干涉条纹缓慢调节 M1 的位置,观察等倾干涉条纹的变化。
调节 M1 和 M2 之间的夹角,观察等厚干涉条纹。
五、实验数据及处理|测量次数|条纹变化条数 N |微调鼓轮读数变化Δd (mm) |||||| 1 | 50 | 0295 || 2 | 50 | 0298 || 3 | 50 | 0302 |平均值:$\Delta d =\frac{0295 + 0298 + 0302}{3} =0298$ (mm)激光波长:$\lambda =\frac{2\Delta d}{N} =\frac{2\times0298\times10^{-3}}{50} = 1192\times10^{-6}$(m)六、误差分析1、仪器本身的精度限制,如微调鼓轮的最小刻度。
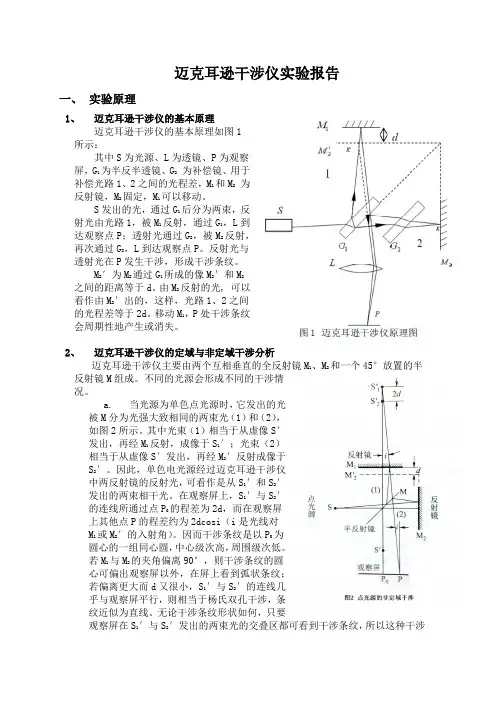
迈克耳逊干涉仪实验报告一、 实验原理1、迈克耳逊干涉仪的基本原理迈克耳逊干涉仪的基本原理如图1所示:其中S 为光源、L 为透镜、P 为观察屏,G 1为半反半透镜、G 2 为补偿镜、用于补偿光路1、2之间的光程差,M 1和M 2 为反射镜,M 2固定,M 1可以移动。
S 发出的光,通过G 1后分为两束,反射光由光路1,被M 1反射,通过G 1,L 到达观察点P ;透射光通过G 2,被M 2反射,再次通过G 2,L 到达观察点P 。
反射光与透射光在P 发生干涉,形成干涉条纹。
M 2′为M 2通过G 1所成的像M 2′和M 2之间的距离等于d 。
由M 2反射的光, 可以看作由M 2′出的,这样,光路1、2之间的光程差等于2d 。
移动M 1,P 处干涉条纹会周期性地产生或消失。
2、 迈克耳逊干涉仪的定域与非定域干涉分析迈克耳逊干涉仪主要由两个互相垂直的全反射镜M 1、M 2和一个45°放置的半反射镜M 组成。
不同的光源会形成不同的干涉情况。
a. 当光源为单色点光源时,它发出的光被M 分为光强大致相同的两束光(1)和(2),如图2所示。
其中光束(1)相当于从虚像S ′发出,再经M 1反射,成像于S 1′;光束(2)相当于从虚像S ′发出,再经M 2′反射成像于S 2′。
因此,单色电光源经过迈克耳逊干涉仪中两反射镜的反射光,可看作是从S 1′和S 2′发出的两束相干光。
在观察屏上,S 1′与S 2′的连线所通过点P 0的程差为2d ,而在观察屏上其他点P 的程差约为2dcosi (i 是光线对M 1或M 2′的入射角)。
因而干涉条纹是以P 0为圆心的一组同心圆,中心级次高,周围级次低。
若M 1与M 2的夹角偏离90°,则干涉条纹的圆心可偏出观察屏以外,在屏上看到弧状条纹;若偏离更大而d 又很小,S 1′与S 2′的连线几乎与观察屏平行,则相当于杨氏双孔干涉,条纹近似为直线。
无论干涉条纹形状如何,只要观察屏在S 1′与S 2′发出的两束光的交叠区都可看到干涉条纹,所以这种干涉称为“非定域干涉”。
迈克尔孙干涉仪实验报告迈克尔孙干涉仪实验报告引言:光学是一门研究光的传播和性质的学科,而干涉是光学中的重要现象之一。
迈克尔孙干涉仪是一种经典的干涉仪器,它能够用来观察光的干涉现象,并通过干涉条纹的变化来分析光的性质。
本实验旨在通过迈克尔孙干涉仪的搭建和实验操作,探究干涉现象的基本原理,并对光的干涉现象进行观察和分析。
一、实验器材和原理1. 实验器材:迈克尔孙干涉仪、激光器、半反射镜、平板玻璃、光屏、光源、调节器等。
2. 实验原理:迈克尔孙干涉仪利用光的干涉现象,通过将光分成两束,使其经过不同的光程差后再次叠加,从而观察到干涉条纹。
其中,光程差是指光线在两个路径上行进的距离差。
二、实验步骤1. 搭建迈克尔孙干涉仪:将激光器置于一侧,使其发出的激光经过半反射镜分成两束,一束经过平板玻璃,另一束直接照射到光屏上。
通过调节器调整光程差,使两束光线再次叠加于光屏上。
2. 观察干涉条纹:调整迈克尔孙干涉仪,使两束光线的光程差逐渐增加或减小,观察光屏上的干涉条纹的变化。
可以通过调整平板玻璃的位置或倾斜角度来改变光程差。
3. 分析干涉条纹:根据观察到的干涉条纹,可以得出干涉现象的一些特点。
例如,干涉条纹的间距与光的波长有关,间距越小代表光的波长越短;干涉条纹的形状也可以反映出光的相位差等信息。
三、实验结果和讨论在实验中,我们观察到了明暗相间的干涉条纹,这些条纹呈现出一定的规律性。
通过调整光程差,我们发现干涉条纹的间距随着光程差的变化而变化,这与光的波长有关。
当光程差为波长的整数倍时,干涉条纹明亮;当光程差为波长的半整数倍时,干涉条纹暗淡。
此外,我们还观察到干涉条纹的形状会随着光程差的改变而变化。
当光程差为零时,干涉条纹呈现出等距离的直线状;当光程差逐渐增大时,干涉条纹会呈现出弯曲的形状。
这些现象可以通过迈克尔孙干涉仪的原理进行解释。
实验中还可以通过调整平板玻璃的位置或倾斜角度来改变光程差,从而观察到不同的干涉条纹。
迈克耳孙干涉仪实验报告一、实验目的1.了解迈克耳孙干涉仪的原理和结构。
2.观察和研究平行光束通过迈克耳孙干涉仪时的干涉现象。
3.通过实验结果验证光的干涉理论。
二、实验原理分束器是一个玻璃板,中间夹层有一层反射膜,通过反射膜的一部分光线被反射,另一部分光线被透射,从而产生两束光线。
合束器是两个平行的玻璃板,其中间夹层同样有一层反射膜,使两束光线再次重合。
当两束光线重合后,它们会产生干涉现象。
干涉是由于两束光线相遇的位置和相位差引起的。
当两束光线的相位差相等时,会形成明纹,相位差差π时,会形成暗纹。
三、实验步骤1.将迈克耳孙干涉仪摆放好,确保设备稳定。
2.打开光源,调节光源的亮度,使光线足够明亮。
3.调节分束器上的反射镜,使两束光线分离。
4.调节合束器上的反射镜,使两束光线再次重合。
5.观察和记录干涉图样。
6.调节光源的亮度,观察干涉图样的变化。
7.调节分束器和合束器上的反射镜,改变光线的路径,观察干涉图样的变化。
四、实验结果与分析在实验过程中,观察到了干涉图样。
当两束光线重合时,形成了一系列明纹和暗纹。
明纹是由光的叠加增强形成的,暗纹是由光的叠加抵消形成的。
通过调节光源的亮度,可以观察到明纹和暗纹的变化。
光源越亮,明纹越亮,暗纹越暗;光源越弱,明纹越暗,暗纹越亮。
通过调节分束器和合束器上的反射镜,可以改变光线的路径,观察到干涉图样的变化。
当两束光线重合的位置发生变化时,干涉图样也会发生相应变化。
这表明干涉图样的形成与光线的路径密切相关。
五、实验总结通过这次实验,我们对迈克耳孙干涉仪的原理和结构有了深入了解。
我们观察到了明纹和暗纹的形成,并通过调节光源亮度和光线的路径,观察到了干涉图样的变化。
在实验过程中,我们还发现,光的干涉现象是光的波动性质的体现。
干涉图样的形成与光的相位差有关,相位差相等时形成明纹,相位差差π时形成暗纹。
这次实验让我们更加深入地理解了光的干涉现象,也提高了我们的实验技能。
同时,实验过程中也发现了一些问题,如实验条件的稳定性,需要进一步完善实验装置,以获得更准确的实验结果。
迈克尔逊干涉仪实验报告
实验目的:
本实验旨在通过迈克尔逊干涉仪观察干涉现象,探究光的干涉原理,并验证干涉现象对光波相位的影响。
实验仪器与原理:
本实验使用迈克尔逊干涉仪,该仪器由半透镜、半反射镜、全反射镜等部件组成。
当光波经过半透镜后,一部分光被反射,一部分光穿过。
被反射的光和穿过的光在半反射镜和全反射镜处相遇,形成干涉现象。
实验步骤与结果:
1. 调整迈克尔逊干涉仪,使光路达到稳定状态。
2. 观察干涉条纹,并记录不同位置的条纹亮度和位置。
3. 通过调整半透镜和半反射镜的位置,观察干涉条纹的变化。
4. 测量干涉条纹的间距和角度,计算光波的波长和相位差。
实验结论:
通过实验观察和数据分析,我们验证了干涉现象对光波相位的影响。
同时,根据实验结果计算出了光波的波长和相位差,验证了干涉原理的基本公式。
实验总结:
本次实验通过迈克尔逊干涉仪观察了光的干涉现象,加深了对光波干涉原理的理解。
同时,实验过程中也发现了一些操作技巧和注意事项,为今后的实验提供了经验和启示。
自查情况:
本次实验报告经过反复检查和修改,确保了内容的准确性和完整性。
同时,实验数据和结论也经过多次确认,保证了实验结果的可靠性。
【实验报告】迈克耳孙干涉仪
迈克耳孙干涉仪是一种非常重要的实验仪器,在光学实验中得到了广泛应用。
本篇实
验报告将对迈克耳孙干涉仪的原理、实验步骤以及实验结果进行详细介绍,以帮助读者更
好地理解和掌握这项实验。
一、实验原理
迈克耳孙干涉仪主要由激光器、分束器、反射镜、半反射镜、透镜以及像面等基本组
成部分组成。
当激光束被分束器分成两束光后,其中一束光经过反射镜反射回来,并与另
一束来自半反射镜的光在像面上发生干涉。
如果两束光程的差为光的波长的一半,那么它
们将在相遇时形成相消干涉,否则将形成相位差相加的相位干涉。
二、实验步骤
1. 打开激光器,将激光束照射到分束器上,使其被分成两束光。
2. 将其中一束光经过反射镜反射回来,与另一束来自半反射镜的光在像面上发生干涉。
3. 通过移动反射镜或调整半反射镜的位置,使两束光程差为光的波长的一半。
4. 观察像面上的干涉条纹,记录相关数据。
三、实验结果
实验结果表明,当两束光程差为光的波长的一半时,即可形成相消干涉,以干涉条纹
清晰度和条纹间隔的大小来判断干涉的质量和精度。
我们可以通过调整分束器与反射镜之
间的距离和半反射镜的反射率等参数,进一步优化干涉质量和精度。
本次实验通过使用迈克耳孙干涉仪,成功地观察到了光的干涉效应,并且实验结果表明,通过调整干涉仪的参数可以进一步优化干涉质量和精度,这对于后续的光学实验和应
用具有重要意义。
因此,在进行光学实验时,迈克耳孙干涉仪是一个非常重要的实验仪器,需要认真掌握和使用。
迈克尔逊干涉仪(实验报告)一、实验目的1、掌握迈克尔逊干涉仪的调节方法并观察各种干涉图样。
2、区别等倾干涉、等厚干涉和非定域干涉,测定He-Ne 激光波长二、实验仪器迈克尔逊干涉仪、He-Ne 激光器及光源、小孔光阑、扩束镜(短焦距会聚镜)、毛玻璃屏等。
(图一)(图二)三、实验原理①用He-Ne 激光器做光源,使激光通过扩束镜会聚后发散,此时就得到了一个相关性很好的点光源,射到分光板P1和P2上后就将光分成了两束分别射到M1 和M2 上,反射后通过P1 、P2 就可以得到两束相关光,此时就会产生干涉条纹。
②产生干涉条纹的条件,如图 2 所示, B 、 C 是两个相干点光源,则到A 点的光程差δ=AB-AC=BCcosi , 若在A 点出产生了亮条纹,则δ =2dcosi=k λ (k 为亮条纹的级数) ,因为i 和k 均为不可测的量,所以取其差值,即λ =2 Δ d/ Δ k。
四、实验步骤1、打开激光电源,先不要放扩束镜,让激光照到分光镜P1 上,并调节激光的反射光照射到激光筒上。
2、调节M2 的位置使屏上两排光中最亮的两个光点重回,并调至其闪烁。
3、将扩束镜放于激光前,调节扩束镜的高度和偏角,使光能照在P1分光镜上,看显示屏上有没有产生同心圆的干涉条纹图案。
没有的话重复2 、3 步骤,直到产生同心圆的干涉条纹图案。
4、微调M2是干涉图案处于显示屏的中间。
5、转动微量读数鼓轮,使M1 移动,可以看到中心条纹冒出或缩进,若看不到此现象,先转动可度轮,再转动微量读数鼓轮。
记下当前位置的读数d0 ,转动微量读数鼓轮,看到中心条纹冒出或缩进30 次则记一次数据,共记录10 次数据即d0、d1 (9)6、关闭激光电源,整理仪器,处理数据。
五、实验数据处理数据记录:数据处理:Δd0=d5-d0=0.05202mm Δd1=d6-d1=0.05225mmΔd2=d7-d2=0.04077mm Δd3=d8-d3=0.04077mmΔd4=d9-d4=0.05071mmΔd(平均)=(Δd0+Δd1+Δd2+Δd3+Δd4)/5 =0.047304mmA类不确定度σ=5.99355*10-6mΔk=150所以λ(平均)=2Δd(平均)/Δk =630.72 nmB类不确定度:UΔB=0.5*10-7 m总不确定度:UΔd =6.01437*10-6 mUλ =2UΔd/Δk =80.1916 nm所以λ=λ(平均)+Uλ=630.72 + 80.1916 nmEλ=(632.8-630.72)/632.8 *100% =0.329%遇到失意伤心事,多想有一个懂你的人来指点迷津,因他懂你,会以我心,换你心,站在你的位置上思虑,为你排优解难。
迈克尔逊干涉仪实验报告
实验目的:
本实验旨在通过使用迈克尔逊干涉仪,观察和分析光的干涉现象,以及验证干涉仪的工作原理。
实验仪器和材料:
1. 迈克尔逊干涉仪。
2. 激光光源。
3. 互动式干涉仪软件。
4. 平面镜。
5. 半反射镜。
6. 透镜。
7. 旋转平台。
8. 光电探测器。
9. 调节螺钉。
实验步骤:
1. 将激光光源接入迈克尔逊干涉仪的光路中,使光线通过半反
射镜分成两束光线。
2. 通过调节平面镜和半反射镜的位置,使得两束光线分别经过
不同的光程后再次汇聚在光电探测器上。
3. 使用互动式干涉仪软件记录并分析干涉条纹的变化。
4. 通过旋转平台,改变其中一束光线的光程差,观察干涉条纹
的变化。
实验结果:
通过实验观察和数据记录,我们成功观察到了明显的干涉条纹,
并且发现随着光程差的改变,干涉条纹的间距也相应发生了变化。
通过软件分析,我们得到了干涉条纹的间距与光程差的关系曲线。
实验分析:
根据实验结果,我们验证了迈克尔逊干涉仪的工作原理,即光程差的改变会导致干涉条纹的变化。
同时,我们也通过实验观察到了光的干涉现象,加深了对光学干涉的理解。
实验结论:
本次实验通过使用迈克尔逊干涉仪,成功观察和分析了光的干涉现象,并验证了干涉仪的工作原理。
实验结果符合预期,达到了预期的实验目的。
同时,通过本次实验,我们对光学干涉有了更深入的认识。