【优秀毕设】工程力学《剪力图与弯矩图》
- 格式:doc
- 大小:347.00 KB
- 文档页数:16



轴,。
以表(a)(c)(1)(2) (3)≤ (4) 以剪力图是平行于轴的直线。
段的剪力为正,故剪力图在轴上方;段剪力为负,故剪力图在轴之下,如图8-12(b )所示。
由式(2)与式(4)可知,弯矩都是的一次方程,所以弯矩图是两段斜直线。
根据式(2)、(4)确定三点,, ,由这三点分别作出段与段的弯矩图,如图8-12(c )。
例8-4 简支梁受集度为的均布载荷作用,如图8-13(a )所示,作此梁的剪力图和弯矩图。
图8-13解 (1)求支反力 由载荷与支反力的对称性可知两个支反力相.即(2)列出剪力方程和弯矩方程 以梁左端为坐标原点,选取坐标系如图所示。
距原点为的任意横截面上的剪力和弯矩分别为x C l x AC x BC x x 0=x 0)(=x M a x =l Fabx M =)(l x =0)(=x M AC BC AB q A x解 (1)求支反力 由静力平衡方程,得(2)列剪力方程和弯矩方程 由于集中力作用在处,全梁内力不能用一个方程来表示,故以为界,分两段列出内力方程段0<≤ (1)0≤< (2)段 ≤< (3)≤≤(4) (3) 画剪力图和弯矩图 由式(1)、(3)画出剪力图,见图8-14(b );由式(2)(4)画出弯矩图,见图8-14(c )。
二、弯矩、剪力与分布载荷集度之间的微分关系在例8-4中,若将的表达式对取导数,就得到剪力。
若再将的∑=0)(x M A ∑=0)(x M B m C C AC l mF x F A Q ==)(x a xl m x F x M A ==)(x a BC l mF x F A Q ==)(a x l mx l mm x F x M A -=-=)(a x l )(x M x )(x F Q )(x F Q表达式对取导数,则得到载荷集度。
这里所得到的结果,并不是偶然的。
实际上,在载荷集度、剪力和弯矩之间存在着普遍的微分关系。
现从一般情况出发加以论证。






基础篇之六第6章 剪力图与弯矩图杆件承受垂直于其轴线的外力或位于其轴线所在平面内的力偶作用时,其轴线将弯曲成曲线,这种受力与变形形式称为弯曲(bemding )。
主要承受弯曲的杆件称为梁(beam )。
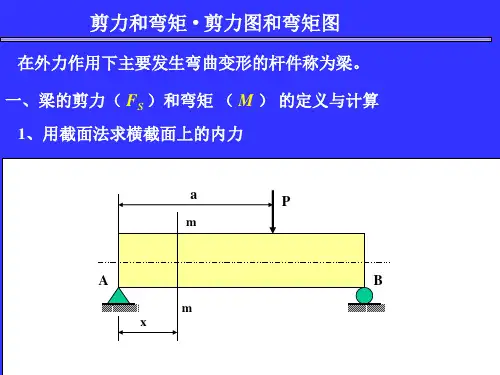
在外力作用下,梁的横截面上将产生剪力和弯矩两种内力分量。
在很多情形下,剪力和弯矩沿梁长度方向的分布不是均匀的。
对梁进行强度计算,需要知道哪些横截面可能最先发生失效,这些横截面称为危险面。
弯矩和剪力最大的横截面就是首先需要考虑的危险面。
研究梁的变形和刚度虽然没有危险面的问题,但是也必须知道弯矩沿梁长度方向是怎样变化的。
本章首先介绍怎样力系简化的方法确定梁横截面上的剪力和弯矩,以此为基础建立剪力方程和弯矩方程;然后导出然后讨论载荷、剪力、弯矩之间的微分关系;在上述两方面的基础上,介绍绘制剪力图与弯矩图的方法与过程。
此外,本章还将计算刚架内力图的绘制方法。
6-1 承弯构件的力学模型与工程中的承弯构件材料力学中将主要承受弯曲的杆件简化为梁,可以说梁就是承受弯曲的杆件的力学模型。
有些结构或者结构的局部,形式上不属于杆件,但是,进行总体结构设计时,有时也需要将其视为梁。
从这个意义上讲,梁又是一个广义的概念——泛指主要承受弯曲的构件、部件以及结构整体等等。
根据梁的支承形式和支承位置不同,梁可以分为:悬臂梁(图6-1a )、简支梁(图6-1b )、外伸梁(图6-1c 、d )。
悬臂梁的一端固定、另一端自由(没有支承或约束)。
简支梁的一端为固定铰支座、另(b) 简支梁AB固定铰支座辊轴支座AB固定铰支座辊轴支座外伸端外伸端AB固定铰支座辊轴支座外伸端(a) 悬臂梁(c) 一端外伸梁(d) 两端外伸梁图8-1 梁的力学模型一端为辊轴支座。
外伸梁有一个固定铰支座和一个辊轴支座,这两个支座中有一个不在梁的端点、或者两个都不在梁的端点,分别称为一端外伸梁和两端外伸梁。
工程结构的设计中,可以看作梁的对象很多。
图6-2中所示之直升机旋翼的桨叶,桨叶可以看成一端固定、另一端自由的悬臂梁,在重力和空气动力作用下桨叶将发生弯曲变形。

梁的剪力和弯矩 剪力图和弯矩图1、 剪力和弯矩剪力:沿截面切线方向的内力F S 称为剪力,剪力符号规定为:截面上的剪力如果有使考虑的脱离体有顺时针转动的趋势则为正,反之为负(图9-2)。
弯矩:作用面垂直于横截面的内力偶矩M 称为弯矩,弯矩符号规定为截面上的弯矩如果使考虑的脱离体向下凸(或者说使梁下边受拉,上边受压)为正,反之为负(图9-3)。
2、 列方程作梁的剪力图和弯矩图。
剪力方程和弯矩方程可以表示剪力和弯矩随横截面位置变化的规律。
)(S S x F F =和 )(x M M = (9-1)剪力图和弯矩图是将剪力和弯矩随横截面位置变化情况用图形表示出来。
在载荷无突变的一段杆的各截面上内力按相同的规律变化,各段的分界点为各段梁的控制截面,必须分段列出梁的剪力方程和弯矩方程。
列方程作梁的剪力图和弯矩图的步骤为:(1)、求支座反力; (2)、确定坐标原点,分段列剪力方程和弯矩方程; (3)、计算控制点处的剪力值和弯矩值,标注在图上; (4)、根据各段的剪力方程和弯矩方程作剪力图和弯矩图,并说明剪力和弯矩的最大值。
3、利用弯矩、剪力、荷载集度之间的关系作梁的剪力图和弯矩图。
弯矩、剪力、荷载集度之间的微分关系为)(d )(d S x q x x F =, )(d )(d S x F x x M =,)(d )(d 22x q x x M = (9−2) 剪力图和弯矩图的规律为表9−1梁上的外力情况 剪力图上的特征弯矩图上的特征弯矩极值所在截面的可能位置水平线段直线段FF FF(a)(b)图9−2MMMM(a)(b)图9−3无外力段 ()()0d d S ==x q xx F ()()常数d d S ==x F xx M q (x )=常数向下的均布荷载 向下方倾斜的直线段()()0d d S <=x q xx F 下凸的二次抛物线()()0d d 22<=x q xx M 在F S =0的截面上q (x )=常数向上的均布荷载 向上方倾斜的直线段()()0d d S >=x q xx F 上凸的二次抛物线()()0d d 22>=x q x x M 在F S =0的截面上F 作用处发生突变,突变值等于FF 作用处发生转折在左右剪力具有不同正负号的截面上集中力偶在M e 作用处无变化M e 作用处发生突变,突变值等于M e在紧靠集中力偶作用处的某一侧截面上利用弯矩、剪力、荷载集度之间的关系作梁的剪力图和弯矩图的步骤为: (1)、求支座反力; (2)、计算控制点处的剪力值和弯矩值,标注在图上; (3)、根据弯矩、剪力、荷载集度之间的关系作剪力图和弯矩图,并标出剪力和弯矩的最大值。