实验四 控制系统的根轨迹分析

时间。这些性能指标和闭环极点的关系如下：
% e 1 2 100% ectg 100%
ts
3
n
3
(为极点实部 )
n
j 1 2n
%和 的关系如下图 %
80
60
若闭环极点落在下图中红线包围
的区域中，有：
% ectg 和ts
3
40
20
0 30 60 90
上述结论也可应用于具有主导极点的高阶系统中。如下例：
是稳定的（为什么？）；
kg 64 kg 14
当 kg 195和14 kg 64 时， 系统是不稳定的。
kg 14 kg 64
kg 195
左图是用Matlab工具绘
制的。
条件稳定系统：参数在一定的范围内取值才能使系统稳定，这 样的系统叫做条件稳定系统。
下面的系统就是条件稳定系统的例子：
A B
这是一个三阶系统，从根轨迹上看出，随着kg 的增加， 主导极点越显著。所以可以用二阶系统的性能指标近似计
算。 下面计算超调量和阻尼角的关系。由于：
% ectg1 100%, 当 % 18%时解得： 60
在根轨迹图上画两条与实轴夹角为 60的直线，与根轨 迹交与A、B两点。 则A、B两点就是闭环共轭主导极点， 这时系统的超调量为18%。通过求A、B两点的坐标，可以 确定这时的根轨迹增益kg ，进而求得开环放大系数k。
[例4-12]单位反馈系统的开环传递函数为：Gk
(s)
s(s
kg 4)( s
6)
若要求闭环单位阶跃响应的最大超调量 % 18% ，试确定 开环放大系数。
[解]：首先画出根 轨迹如右。由图 可以看出：根轨 迹与虚轴的交点 为+j5,-j5，这时的 临界增益 kgp 240 当 kg 240 时， 闭环系统不稳定。

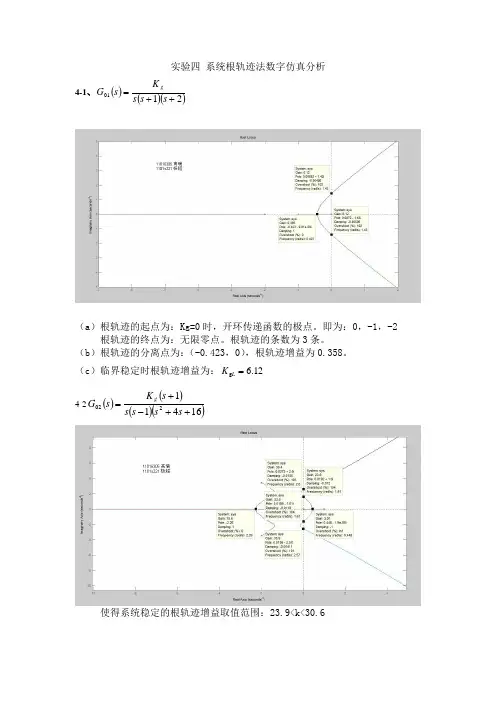
实验四 系统根轨迹法数字仿真分析4-1、()()()2101++=s s s K s G g（a ）根轨迹的起点为：Kg=0时，开环传递函数的极点。

即为：0，-1，-2根轨迹的终点为：无限零点。

根轨迹的条数为3条。

（b ）根轨迹的分离点为：（-0.423，0），根轨迹增益为0.358。

（c ）临界稳定时根轨迹增益为：12.6g =L K4-2()()()()16411202++-+=s s s s s K s G g使得系统稳定的根轨迹增益取值范围：23.9<k<30.64-3 ()()()2303++=s s s K s G g（a ）确定系统具有最大超调量M Pmax 时的根轨迹增益。

系统具有最大超调量M Pmax 时为1.17，根轨迹增益为2.0101.2g =K 17.1max p =，M（b ）确定系统阶跃响应无超调量时的根轨迹增益取值范围。

系统阶跃响应无超调量时的根轨迹增益取值范围为：6.93<k<7.46和0.536<k<0.5822、完成上述各题要求，分析闭环极点在s 平面上的位置与系统动态性能的关系。

答：闭环极点在s 平面上的位置与系统动态性能的关系有：如果闭环系统有两个负实极点，那么单位阶跃响应是指数型的。

如果两个实极点相距较远，则暂态过程主要决定于离虚轴近的极点。

如果闭环极点为一对复极点，单位阶跃响应是衰减振荡型的，它由两个特征参数决定，即阻尼比和自然振荡角频率。

如果θ不变，则随着ωn 的增加，极点将沿矢量方向延伸ξωn 是表征系统指数衰减的系数，它决定系统的调节时间。

如果闭环系统除一对复极点外还有一个零点，则将增大超调量。

如果大于5倍左右，则可以不计零点的影响。

闭环系统中一对相距很近的实极点和零点称为偶子，偶子对系统暂态响应很小，可以忽略不计。

控制系统的根轨迹分析（Matlab）一、实验目的1. 通过实验，进一步理解根轨迹的基本概念以及根轨迹与系统性能之间的关系；2. 学会用Matlab软件绘制系统的根轨迹，并能够根据轨迹线分析系统的性能。

二、实验数据和曲线1.模型一:（1）传递函数（ 2 s^2 + 5 s + 1）*kG（s）= -----------------------s^3 + 6 s^2 + 3 s + 4（2）源代码1：m = [2 5 1];n = [1 6 3 4];g = tf(m,n);rlocus(g);>> m = [2 5 1];n = [1 6 3 4];g = tf(m,n);rlocfind(g);Select a point in the graphics window selected_point =-0.5379 + 0.6615i（3）根轨迹图示因为根均分布在S的左半平面，所以系统稳定。

（4）源代码2：m = [2 5 1];n = [1 6 3 4];g = tf(m,n);rlocus(g);k = 10;g1 = k * g;g2 = feedback(g1,1);step(g2);（5）阶跃响应曲线2.模型二(1)传递函数:KG（s）= ------------------------- s^4 + 5 s^3 + 8 s^2 + 6 s（2）源代码：m = [1];n = [1 5 8 6 0];g = tf(m,n);rlocus(g);m = [1];n = [1 5 8 6 0];g = tf(m,n);rlocfind(g);Select a point in the graphics window selected_point =0.0782 + 1.0683i（3）根轨迹图示系统稳定临界情况在，根轨迹上实部为零时取得。

（4）源代码2：m = [1];n = [1 5 8 6 0];g = tf(m,n);rlocus(g);k = 8;g1 = k*g;g2 = feedback(g1,1);step(g2);（5）阶跃响应曲线三、实验结论通过本次试验，让我第一次接触到了matlab这个软件，了结了它的一些基本用法，和操作步骤。

实验四 控制系统的根轨迹分析一. 实验目的:1. 学习利用MATLAB 语言绘制控制系统根轨迹的方法。

2. 学习利用根轨迹分析系统的稳定性及动态特性。

二. 实验内容:1. 应用MATLAB 语句画出控制系统的根轨迹。

2. 求出系统稳定时，增益K 的范围。

3. 实验前利用图解法画出系统的根轨迹，算出系统稳定的增益范围，与实测值相比较。

4. 应用SIMULINK 仿真工具，建立闭环系统的实验方块图进行仿真。

观察不同增益下系统的阶跃响应，观察闭环极点全部为实数时响应曲线的形状；有共轭复数时响应曲线的形状。

（实验方法参考实验二）5. 分析系统开环零点和极点对系统稳定性的影响。

三. 实验原理:根轨迹分析法是由系统的开环传递函数的零极点分布情况画出系统闭环根轨迹，从而确定增益K 的稳定范围等参数。

假定某闭环系统的开环传递函数为)164)(1()1()()(2++-+=s s s s s K s H s G 利用MATLAB 的下列语句即可画出该系统的根轨迹。

b=[1 1]； ％确定开环传递函数的分子系数向量a1=[l 0]； ％确定开环传递函数的分母第一项的系数a2=[l -1]； ％确定开环传递函数的分母第二项的系数a3=[l 4 16]； ％确定开环传递函数的分母第三项的系数a=conv(al ，a2)； ％开环传递函数分母第一项和第二项乘积的系数 a=conv(a ，a3)； ％分母第一项、第二项和第三项乘积的系数 rlocus(b,a) ％绘制根轨迹，如图（4-l ）所示。

p=1.5i ； ％ p 为离根轨迹较近的虚轴上的一个点。

[k ，poles]=rlocfind(b ，a ，p) ％求出根轨迹上离p 点很近的一个根及所对应的增益K 和其它三个根。

K=22.5031， poles= -1.5229+2.7454i -1.5229-2.7454i0.0229+1.5108i 0.0229-1.5108i再令p=1.5108i ，可得到下面结果:k=22.6464， poles=-1.5189+2.7382i -1.5189-2.7382i0.0189+1.5197i 0.0189-1.5197i再以此根的虚部为新的根，重复上述步骤，几步后可得到下面的结果： k=23.316， poles=-1.5000+2.7040i -1.5000-2.7040i0.0000+1.5616i 0.0000-1.5616i这就是根轨迹由右半平面穿过虚轴时的增益及四个根。

绘制根轨迹如图4-13所示。
第4章 控制系统的根轨迹分析
图4-13 例4-5系统的根轨迹
第4章 控制系统的根轨迹分析
图中根轨迹与虚轴的交点可从系统临界稳定的条件
得到τ=1。τ=1时系统的特征方程为
得与虚轴交点的坐标为jω=±j。从根轨迹得到系统稳定时τ
的取值范围为0<τ<1。
第4章 控制系统的根轨迹分析
θj(j=1,2,3,4)。选取实轴上一点s0,若s0为根轨迹上的点,必满足
相角条件,有
第4章 控制系统的根轨迹分析
图4-5 实轴上根轨迹相角示意
第4章 控制系统的根轨迹分析
下面分别分析开环零、极点对相角条件的影响,进而分
析对实轴上根轨迹的影响。
(1)共轭复数极点p4和p5到点s0的向量的相角和为
φ4+φ5=2π,共轭复数零点到s0点的向量的相角和也为2π。
(2)实轴上,s0点左侧的开环极点p3和开环零点z2到点s0所
构成的向量的夹角φ3和θ2均为零度。
(3)实轴上,s0点右侧的开环极点p1、p2和开环零点z1到点
s0 所构成的向量的夹角φ1、φ2和θ1均为π。
第4章 控制系统的根轨迹分析
第4章 控制系统的根轨迹分析
若系统稳定,由劳斯表的第一列系数,有以下不等式成立:
得0<K* <78.47。
由此可知,当 Kc* =78.47时,系统临界稳定,此时根轨迹穿
过虚轴。K* =78.4ω 值由以下辅助方程确定:
将 K* =78.47代入辅助方程,得
解得s=±j2.16。
第4章 控制系统的根轨迹分析
对于例4-1,其在实轴上的根轨迹一条始于开环极点,止于
开环零点(根轨迹位于-2到-5之间),另两条始于开环极点,止于

j1
s0
j1
jk
s sk
j1
jk
单位阶跃响应为
n
y(t) A0 Akeskt k 1
m
m
Ks zi Kzi
A0
i1 n
s sj
i1 n
GB(0)
sj
j1
s0
j1
m
m
K s zi
Ak
i1 n
s sj
1 s
K sk zi
i1 n
sk sk sj
jk
1
s2
100 8s 100
4 3
os1
1.5
1.7
可求得 0.4, ，n 10
s3
所以 % e 1 2 100% 25%，ts (s3.)5 n 3.5 4 0.9
j
0
利用根轨迹分析控制系统的性能
例11 分析K的变化对系统稳定性的影响
K (s 3) G(s)H (s) s(s 5)(s 6)(s2 2s 2)
增加开环极点的影响 增加极点对根轨迹形状的影响
增加开环零点的影响 增加零点对根轨迹形状的影响
例9 已知某系统闭环传递函数
GB (s) 0.67s 1
1 0.01s2
0.08s 1
试计算在单位阶跃输入时的系统输出超调量 % 和调节时间t。s
解：该闭环系统有三个极点，s1 1.5, s2,3 零4 、j9.2极点 分布如右图。
系统稳定的K的范围为: 0<K<35
例12 分析K的变化对系统的影响。设负反馈系统的开环传递函数为
K s z G(s)H(s) ss p
z p
求系统闭环根轨迹，并分析 p 2, 时z系 统4 的动态性能。

控制系统根轨迹分析控制系统的根轨迹分析是一种常用的工程方法，用于分析系统的稳定性和性能。

在控制系统设计中，了解根轨迹的特性对于确保系统的稳定性和满足性能要求至关重要。

本文将介绍根轨迹分析的基本原理，以及如何应用根轨迹分析来评估和改进控制系统。

1. 根轨迹分析的基本原理根轨迹分析是利用系统的传递函数来描述系统在复平面上的特征。

系统的传递函数可以通过拉普拉斯变换和频域分析获得。

根轨迹是描述系统传递函数极点随控制参数变化所形成的轨迹，它反映了系统的稳定性和性能。

2. 根轨迹的特性根轨迹具有以下几个重要特性：- 根轨迹始于系统的零点，终止于系统的极点。

- 根轨迹通过传递函数的极点数目与零点数目的差值确定的角度。

当角度为奇数时，根轨迹会靠近负实轴；当角度为偶数时，根轨迹会靠近负无穷大。

- 根轨迹与实轴之间的交点表示系统的振荡频率。

3. 根轨迹分析的步骤下面是进行根轨迹分析的基本步骤：1) 将系统的传递函数表示为标准型。

2) 根据系统传递函数的分母和分子系数，确定系统的极点和零点。

3) 绘制根轨迹图，根据极点和零点的位置画出根轨迹的轨迹。

4) 分析根轨迹图，判断系统的稳定性和性能。

4. 根轨迹分析的应用根轨迹分析在控制系统设计中有广泛的应用，主要包括以下几个方面：- 稳定性分析：通过观察根轨迹图，可以判断系统是否稳定。

如果根轨迹位于左半平面，即实部小于零，则系统是稳定的；否则，系统不稳定。

- 性能评估：根轨迹的形状和位置可以提供有关系统响应速度、振荡频率和阻尼比等性能指标的信息。

例如，当根轨迹与虚轴相交时，系统存在振荡。

- 控制器设计：通过根轨迹分析，可以确定合适的控制器增益，以实现所需的系统性能要求。

- 稳定裕度分析：通过改变根轨迹的形状和位置，可以评估系统对参数扰动的敏感性，并提供稳定性裕度的指导。

根轨迹分析作为控制系统设计和分析的重要工具，为工程师提供了直观、可视化的方式来理解和改进系统的性能。

通过合理运用根轨迹分析，可以帮助我们设计出更稳定、高性能的控制系统。

实验四 线性系统的根轨迹一、实验目的1. 熟悉MATLAB 用于控制系统中的一些基本编程语句和格式。

2. 利用MATLAB 语句绘制系统的根轨迹。

3. 掌握用根轨迹分析系统性能的图解方法。

4. 掌握系统参数变化对特征根位置的影响。

基础知识及MATLAB 函数根轨迹是指系统的某一参数从零变到无穷大时，特征方程的根在s 平面上的变化轨迹。

这个参数一般选为开环系统的增益K 。

课本中介绍的手工绘制根轨迹的方法，只能绘制根轨迹草图。

而用MATLAB 可以方便地绘制精确的根轨迹图，并可观测参数变化对特征根位置的影响。

假设系统的对象模型可以表示为nn n n m m m m a s b s a s b s b s b s b K s KG s G ++++++++==--+-11111210)()(ΛΛ 系统的闭环特征方程可以写成： 0)(10=+s KG对每一个K 的取值，我们可以得到一组系统的闭环极点。

如果我们改变K 的数值，则可以得到一系列这样的极点集合。

若将这些K 的取值下得出的极点位置按照各个分支连接起来，则可以得到一些描述系统闭环位置的曲线，这些曲线又称为系统的根轨迹。

1）绘制系统的根轨迹rlocus （）MATLAB 中绘制根轨迹的函数调用格式为：rlocus(num,den) 开环增益k 的范围自动设定。

rlocus(num,den,k) 开环增益k 的范围人工设定。

rlocus(p,z) 依据开环零极点绘制根轨迹。

r=rlocus(num,den) 不作图，返回闭环根矩阵。

[r,k]=rlocus(num,den) 不作图，返回闭环根矩阵r 和对应的开环增益向量k 。

其中，num,den 分别为系统开环传递函数的分子、分母多项式系数，按s 的降幂排列。

K 为根轨迹增益，可设定增益范围。

例3-1：已知系统的开环传递函数924)1()(23++++=*ssssKsG，绘制系统的根轨迹的MATLAB的调用语句如下：num=[1 1]; %定义分子多项式den=[1 4 2 9]; %定义分母多项式rlocus (num,den)%绘制系统的根轨迹grid%画网格标度线xlabel(‘Real Axis’),ylabel(‘Imaginary Axis’) %给坐标轴加上说明title(‘Root Locus’) %给图形加上标题名则该系统的根轨迹如图3-1所示：若上例要绘制K在（1，10）的根轨迹图，则此时的MATLAB的调用格式如下，对应的根轨迹如图3-2所示。

控制系统的根轨迹1．实验目的：1) 掌握MA TLAB 软件绘制根轨迹的方法。

2) 分析参数变化对根轨迹的影响。

3) 利用根轨迹法对控制系统性能进行分析。

2．实验仪器：1) 计算机一台； 2) MA TLAB 软件。

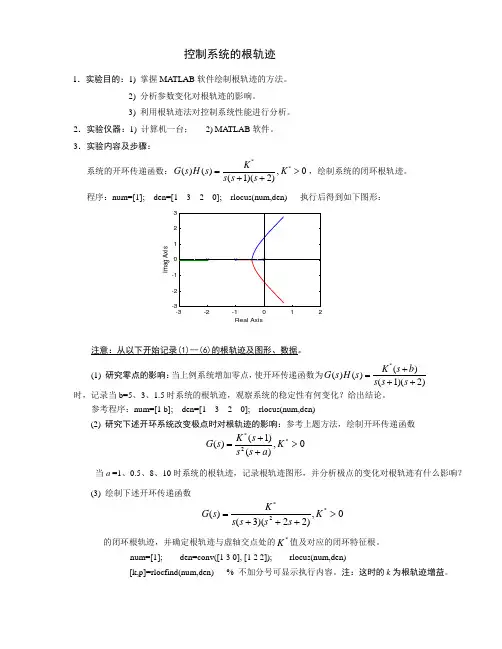
3．实验内容及步骤： 系统的开环传递函数：**()(),0(1)(2)K G s H s K s s s =>++，绘制系统的闭环根轨迹。

程序：注意：从以下开始记录(1)--(6)的根轨迹及图形、数据。

(1) 研究零点的影响：当上例系统增加零点，使开环传递函数为*()()()(1)(2)K s b G s H s s s s +=++时，记录当b=5、3、1.5时系统的根轨迹，观察系统的稳定性有何变化？给出结论。

参考程序：num=[1 b]; den=[1 3 2 0]; rlocus(num,den)(2) 研究下述开环系统改变极点时对根轨迹的影响：参考上题方法，绘制开环传递函数0,)()1()(*2*>++=K a s s s K s G 当a =1、0.5、8、10时系统的根轨迹，记录根轨迹图形，并分析极点的变化对根轨迹有什么影响？(3) 绘制下述开环传递函数0,)22)(3()(*2*>+++=K s s s s K s G的闭环根轨迹，并确定根轨迹与虚轴交点处的*K 值及对应的闭环特征根。

num=[1]; den=conv([1 3 0], [1 2 2]); rlocus(num,den)[k,p]=rlocfind(num,den) % 不加分号可显示执行内容。

注：这时的k 为根轨迹增益。

gtext(‘k=8.2665’) % 单引号内填自己读出的数据也可以采用鼠标直接点击获得。

执行时先画出了根轨迹，并提示用户在图形窗口中选择根轨迹上的一点，以计算出增益K*及 相应的极点。

这时将十字光标放在根轨迹与虚轴的交点处，可得交点处信息：k = 8.2665 p =------------------------- （需要记录该值）再求该系统的K*=5时的阶跃响应和脉冲响应：0,)22)(3()(*2*>+++=K s s s s K s G 输入如下语句：K=5; s1=tf([5], conv([1 3 0],[1 2 2])); sys=feedback(s1,1); %1为负反馈 step(sys); impulse(sys); % 这两个语句分别输入（逐一输入）可以求出5*=K 时的单位阶跃响应、冲激响应，记录两个曲线。

一、实验目的1. 熟悉控制系统根轨迹的基本概念和绘制方法。

2. 掌握利用MATLAB软件绘制和分析控制系统根轨迹的方法。

3. 通过根轨迹分析，了解系统参数变化对系统性能的影响。

4. 培养实验操作能力和数据处理能力。

二、实验原理根轨迹是指当系统的某一参数（如开环增益K）从0变化到无穷大时，闭环系统的特征根在s平面上的变化轨迹。

通过分析根轨迹，可以了解系统在参数变化时的稳定性、瞬态响应和稳态误差等性能。

三、实验设备1. 计算机2. MATLAB软件3. 控制系统实验箱四、实验内容1. 绘制控制系统根轨迹（1）首先，根据实验要求，搭建控制系统的数学模型。

（2）利用MATLAB中的rlocus函数绘制系统的根轨迹。

（3）观察根轨迹的变化规律，分析系统在不同参数下的稳定性。

2. 分析系统性能（1）根据根轨迹，确定系统的稳定裕度，包括增益裕度和相位裕度。

（2）分析系统在不同参数下的瞬态响应，如上升时间、调整时间、超调量等。

（3）分析系统在不同参数下的稳态误差，如稳态误差和稳态误差系数。

3. 改变系统参数，观察根轨迹变化（1）改变系统的参数，如增益、时间常数等。

（2）重新绘制根轨迹，观察根轨迹的变化规律。

（3）分析系统参数变化对系统性能的影响。

五、实验结果与分析1. 绘制控制系统根轨迹（1）根据实验要求，搭建控制系统的数学模型，得到开环传递函数。

（2）利用MATLAB中的rlocus函数绘制系统的根轨迹。

（3）观察根轨迹的变化规律，分析系统在不同参数下的稳定性。

2. 分析系统性能（1）根据根轨迹，确定系统的稳定裕度，包括增益裕度和相位裕度。

（2）分析系统在不同参数下的瞬态响应，如上升时间、调整时间、超调量等。

（3）分析系统在不同参数下的稳态误差，如稳态误差和稳态误差系数。

3. 改变系统参数，观察根轨迹变化（1）改变系统的参数，如增益、时间常数等。

（2）重新绘制根轨迹，观察根轨迹的变化规律。

（3）分析系统参数变化对系统性能的影响。

本科实验报告课程名称：自动控制原理实验名称：实验四控制系统的根轨迹和频域特性分析实验四 控制系统的根轨迹和频域特性分析一、实验目的1．学会利用MATLAB 绘制系统的根轨迹，并对系统进行分析； 2．学会利用MATLAB 对系统进行频域特性分析。

二、实验设备安装Windows 系统和MATLAB 软件的计算机一台。

三、实验内容1．基于MATLAB 的控制系统根轨迹分析 1）利用MATLAB 绘制系统的根轨迹利用rlocus( )函数可绘制出当根轨迹增益k 由0至+∝变化时，闭环系统的特征根在s 平面变化的轨迹，该函数的调用格式为[r,k]=rlocus(num,den) 或 [r,k]=rlocus(num,den,k)其中，返回值r 为系统的闭环极点，k 为相应的增益。

rlocus( )函数既适用于连续系统，也适用于离散系统。

rlocus(num,den)绘制系统根轨迹时，增益k 是自动选取的，rlocus(num,den, k)可利用指定的增益k 来绘制系统的根轨迹。

在不带输出变量引用函数时，rolcus( )可在当前图形窗口中绘制出系统的根轨迹图。

当带有输出变量引用函数时，可得到根轨迹的位置列向量r 及相应的增益k 列向量，再利用plot(r,‘x’)可绘制出根轨迹。

2）利用MATLAB 获得系统的根轨迹增益 在系统分析中，常常希望确定根轨迹上某一点处的增益值k ，这时可利用MATLAB 中的rlocfind( )函数，在使用此函数前要首先得到系统的根轨迹，然后再执行如下命令[k,poles]=rlocfind(num,den) 或 [k,poles]=rlocfind(num,den,p)其中，num 和den 分别为系统开环传递函数的分子和分母多项式的系数按降幂排列构成的系数向量；poles 为所求系统的闭环极点；k 为相应的根轨迹增益；p 为系统给定的闭环极点。

例3-1 已知某反馈系统的开环传递函数为)2)(1()()(++=s s s ks H s G试绘制该系统根轨迹，并利用根轨迹分析系统稳定的k 值范围。

根轨迹的特点和规律
根轨迹具有以下特点和规律： • 根轨迹是一条连续的曲线，代表了特征方程根的轨迹 • 根轨迹始终位于系统开环增益与相位的交点上 • 根轨迹趋近于无限远点的方向，表示系统的稳定性 • 根轨迹与该点的对称位置具有相同的特性
利用根轨迹评价系统性能
根轨迹可以评估系统的稳定性和动态响应性能，通过观察根轨迹的形状和位置，可以得出以下结论：
根轨迹的概念
根轨迹是反映闭环控制系统特征方程根随参数变化而变化的图形。通过观察 根轨迹可以分析系统的稳定性、动态响应和频率响应特性。
如何绘制根轨迹
绘制根轨迹的步骤如下： 1. 得到系统的特征方程 2. 使用根轨迹的绘制规则和技巧，画出根轨迹的大致形状 3. 通过调整系统参数，绘制出完整的根轨迹图形
自动控制原理 4.4 利用根 轨迹分析系统性能
自动控制系统的性能对于系统的稳定性和响应速度至关重要。本章将介绍根 轨迹方法，用于绘制系统的根轨迹图，并利用根轨迹图评估系统的稳定性和 动态响应性能。
系统性能的定义
系统性能是指系统对于输入信号的响应质量和稳定性。主要包括以下几个方 面：时间响应特性、频率响应特性、稳定性和误差特性。
结论和要点
1 根轨迹是分析系统
性能的重要工具
根轨迹反映了系统的稳 定性和动态响应性能。
2 根轨迹的绘制方法
可以通过特征方程和绘 制规则来绘制根轨迹。
3 根轨迹的应用
根轨迹分析在实际控制 系统中具源自广泛的应用。稳定性如果根轨迹位于左半平面，则系统是稳定的。
动态响应
根轨迹的形状和位置可以反映系统的响应速 度和超调量。
频率响应
根轨迹的形状和位置可以反映系统的频率响 应特性。
稳定裕度
根轨迹与虚轴的交点距离表示系统的稳定裕 度。

控制系统根轨迹分析简介控制系统根轨迹分析是一种经典的控制系统稳定性分析方法。

通过分析系统的特征根轨迹，可以评估系统的稳定性、阻尼比、过渡时间等性能指标，从而设计合适的控制器来实现系统的稳定和性能要求。

根轨迹的定义控制系统的根轨迹是由系统的特征根在复平面上随参数变化所形成的轨迹。

特征根是系统传递函数的零点，它们决定了系统的动态特性。

根轨迹对应于特征根的运动轨迹，可以直观地反映系统的稳定性和相应的频率响应。

根轨迹的绘制方法步骤一：计算系统的传递函数首先，需要获得系统的传递函数。

传递函数通常是通过将系统的微分方程进行拉氏变换得到的。

传递函数是 Laplace 域中的函数，它描述了输入和输出之间的关系。

步骤二：确定系统的开环极点和零点根轨迹是由系统的特征根构成的，而特征根由系统的开环极点和零点决定。

开环极点指的是系统传递函数的分母多项式的根，而开环零点指的是系统传递函数的分子多项式的根。

通过确定系统的极点和零点，可以得到系统的特征根。

步骤三：绘制根轨迹根轨迹的绘制可以通过手工计算或数值模拟方法实现。

手工计算方法需要根据系统的传递函数进行复杂的计算，而数值模拟方法可以借助计算机软件进行自动计算和绘制。

绘制根轨迹时，需要遵循以下基本规则： - 根轨迹始于系统的零点。

如果系统有多个零点，那么根轨迹将从每个零点开始。

- 根轨迹与实轴交点的个数等于零点的个数减去极点的个数，这一性质被称为根轨迹的零点和极点计数法则。

- 根轨迹在系统的极点位置是不连续的，并且与极点的关联程度取决于极点的幅度和阶数。

根轨迹的稳定性分析通过观察根轨迹图形，可以评估控制系统的稳定性。

根轨迹的稳定性分析方法主要有以下几种：1. 判据法判据法是判断根轨迹稳定性的基本方法之一。

根轨迹的稳定性与根轨迹图形与实轴的关系有关。

如果根轨迹图形位于实轴的左侧，则系统是稳定的；如果根轨迹图形经过实轴，则系统是不稳定的。

2. Astrom法Astrom法是一种根据根轨迹图形的形态特征进行稳定性判断的方法。

3、根轨迹分析 例一、 （参数根轨迹） 设系统结构如图所示：
试绘制速度反馈系数������������ （由 0→∞）变动时闭环系统的根轨迹，并计算其零极点。 解： （1） 、由该系统图可知系统的开环传递函数为 G(s) H(s)
5(Ta s 1) ，其闭环特性方程 s(5s 1)
为：
D(s) 5s2 s 5Ta s 5 5s2 s 5 5Ta s 0
（2） 、则构造新的单位负反馈系统如图所示，使之具有相同闭环特征方程。
（3） 、在 MATLAB 中建立 M 文件，程序如下： num=[5 0];den=[5 1 5]; sys=tf(num,den); [p,z]=pzmap(sys) rlocus(sys) 运行结果如下：
p = -0.1000 + 0.9950i -0.1000 - 0.9950i
系统根轨迹的影响，并绘制k=1是它们的单位阶跃响应。 解：在MATLAB中建立M文件，程序如下： num=1;den=poly([0 -3]); subplot(2,2,1),rlocus(num,den); num1=[1,1];den1=den; subplot(2,2,2),rlocus(num1,den1); num2=[1,5];den2=den; subplot(2,2,3),rlocus(num2,den2); num3=num2;den3=conv(den2,[1 8]); subplot(2,2,4),rlocus(num3,den3),figure(2); [num,den]=cloop(num,den); [num1,den1]=cloop(num1,den1); [num2,den2]=cloop(num2,den2); [num3,den3]=cloop(num3,den3); t=0:0.1:25; step(num,den,t);hold on step(num1,den1,t);

控制系统的根轨迹分析引言控制系统是现代工程领域中应用广泛的一个重要概念，它用于调节和控制系统的输出，以使其达到预期的目标。

在控制系统设计中，根轨迹分析是一种重要的工具，用于评估系统的稳定性和性能。

本文将介绍控制系统的根轨迹分析方法，包括其基本原理、应用范围以及如何使用根轨迹分析改进控制系统的性能。

根轨迹分析原理根轨迹分析是一种基于系统传递函数的频域分析方法，它用于研究系统在不同参数情况下的稳定性和性能。

根轨迹是系统传递函数极点随参数变化而形成的轨迹图，通过观察根轨迹可以得到系统的稳定性、阻尼比、过渡过程和稳态误差等性能指标。

根轨迹分析基于以下原理： - 控制系统的稳定性取决于系统传递函数极点的位置，当极点全在左半平面时，系统是稳定的。

- 控制系统的阻尼比可以通过观察根轨迹的形状来判断，当根轨迹越接近实轴，阻尼比越小，系统的过渡过程越激烈。

- 控制系统的稳态误差可以通过观察根轨迹的最后一段来判断，当根轨迹趋于无穷远时，稳态误差为零。

根轨迹分析步骤根轨迹分析一般需要经历以下几个步骤： 1. 给定系统的传递函数，通常是一个比例控制器和一个被控对象的组合。

2. 将传递函数的分子和分母分别表示为多项式的形式。

3. 根据系统传递函数的阶数，求解其特征方程的根。

这些根即为根轨迹的起始点。

4. 在复平面上绘制出根轨迹的起始点以及随参数变化而形成的轨迹。

5. 根据根轨迹的形状和位置，判断系统的稳定性、阻尼比和稳态误差等性能指标。

根轨迹分析的应用根轨迹分析在控制系统设计中有广泛的应用，主要有以下几个方面： 1. 系统稳定性评估：通过观察根轨迹的位置，可以判断系统是否稳定。

如果根轨迹全在左半平面，则系统是稳定的。

2. 控制器设计：根轨迹分析可以帮助工程师选择合适的控制器参数，以实现系统的稳定性和性能要求。

3. 系统性能优化：通过分析根轨迹的形状，可以判断系统的过渡过程、阻尼比和稳态误差等性能指标，从而优化系统的性能。

实验四基于MATLAB的根轨迹绘制与性能分析一、实验目的1.了解根轨迹的概念和作用；2.学习使用MATLAB绘制根轨迹；3.通过根轨迹进行系统性能分析。

二、实验原理1.根轨迹的概念根轨迹是指随着系统参数变化，系统极点随参数变化所经过的连续点的轨迹。

根轨迹可以用来表示系统的动态性能，并可以用来分析系统的稳定性、抗干扰能力以及动态响应等。

2.根轨迹的绘制方法根轨迹的绘制方法主要有以下几步：(1)确定系统传递函数的开环极点和零点；(2)根据系统传递函数的特征方程确定根轨迹起始点和抵达无穷远点的分支数量；(3)确定分支的方向；(4)计算根轨迹抵达无穷远点的角度；(5)计算根轨迹与实轴的交点。

三、实验步骤1.准备工作(1)安装MATLAB软件，并确保已安装了Control System Toolbox；(2)准备所需绘制根轨迹的系统传递函数。

2.绘制根轨迹(1)在MATLAB命令窗口中输入以下命令，定义系统传递函数：G = tf([1],[1 2 3]);(2)输入以下命令，绘制系统的根轨迹：rlocus(G);3.性能分析(1)根据根轨迹的形状，可以判断系统的稳定性。

如果根轨迹与实轴相交的次数为奇数，则系统是不稳定的。

(2)根据根轨迹的形状以及相交点的位置，可以判断系统的过渡过程的振荡性和阻尼性。

(3)根据根轨迹抵达无穷远点时的角度，可以判断系统的相对稳定性。

角度接近0或180度时，系统相对稳定。

(4)根据根轨迹抵达实轴的位置，可以判断系统的动态性能。

抵达实轴的位置越远离原点，系统的动态响应越快。

四、实验结果分析通过上述步骤，我们可以得到系统的根轨迹图，并根据根轨迹图进行性能分析。

根据根轨迹的形状、交点位置、角度以及抵达实轴的位置，我们可以判断系统的稳定性、过渡过程的振荡性和阻尼性、相对稳定性以及动态响应速度。

根轨迹分析可以帮助我们设计和优化系统的控制器，从而改善系统的性能。

五、实验总结本实验通过MATLAB绘制根轨迹，并利用根轨迹进行系统性能分析。

控制系统的根轨迹分析摘要:在控制系统的数学模型建立以后，就要进行系统性能的分析了。

通过这一环节，获得原有的系统的各方面性能定性活定量的描述。

我的报告是根轨迹分析方法。

根轨迹是指，当开环系统某一参数（一般为系统的开环系统增益K),从零变到无穷大时，四循环系统特征方程的根在s平面上的轨迹。

因此,从根轨迹，可分析系统的稳定性、稳态性能、动态性能。

在MATLAB中，绘制根轨迹的有关函数有rlocus、r l o c f i n d、pzmap 等。

通过对根轨迹分析法的学习和运用，并根据实例，介绍根轨迹分析法的原理。

运用MATLAB软件绘制根轨迹。

理解并且根轨迹与系统性能之间的关系。

关键词：根轨迹函数、零极点图、稳定性分析、MATLAB绘图、分析仿真The control system of root locus analysisMaShuaiAbstract：After the establishment of mathematical model in control system,analysisof system performance. Through this link, all aspects of the original system performance quantitative live qualitative description. My report isrootlocusmethod.Rootlocusrefers to, when the open loop system a parameter (usually for the system of open loopgainK), from zero to infinity, the fourcirculationsystemrootofcharacteristicequationinthesplane trajectory. From the root locus, therefore,toanalyzethestabilityofsystem,thesteady-state performance and dynamic performance. In MATLAB, the drawing of root locusrlocus, rlocfind and pzmap relating to functions. Through the root locus methodoflearningand using,andaccordingtotheexample,thispaperintroducestheprincipleofrootlocusmethod.U sing theMATLABsoftwareplottherootlocus.Understandandrootlocusandtherelationship between the performance of the system.Key words:Root locus function、zero pole figure、stability analysis and MATLAB graphics、analysis、simulation一 根轨迹法的基本知识：)()(1)()()()(s H s G s G s R s C s +==Φ 特征方程为：0)()(1=+s H s G ；0)()(1=+s den s num k图1-1 单位反馈系统流程图二 根轨迹的零、极点图： )()()()()(11m n p s z s k s H s G n i imj j ≥--=∏∏== （3-16）在绘制根轨迹前，首先将系统的开环传递函数表示成上式的零、极点形式，且在s 平面上，用“o ”表示开环零点的位置；用“×”表示开环极点的位置。