高中数学知识点最全的思维导图
- 格式:doc
- 大小:1.94 MB
- 文档页数:9
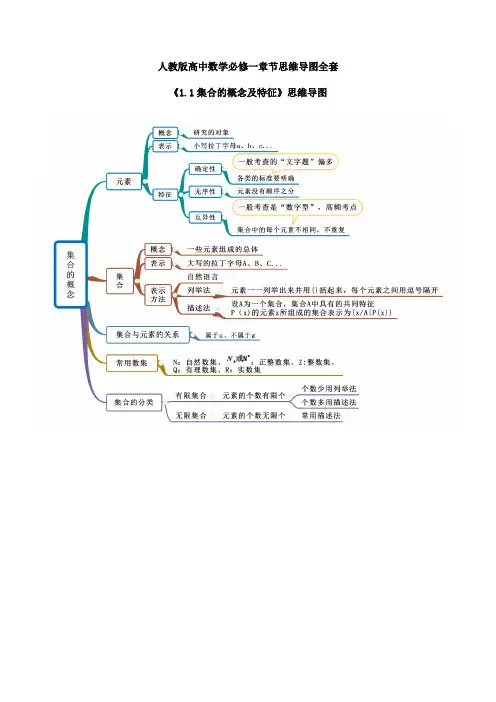
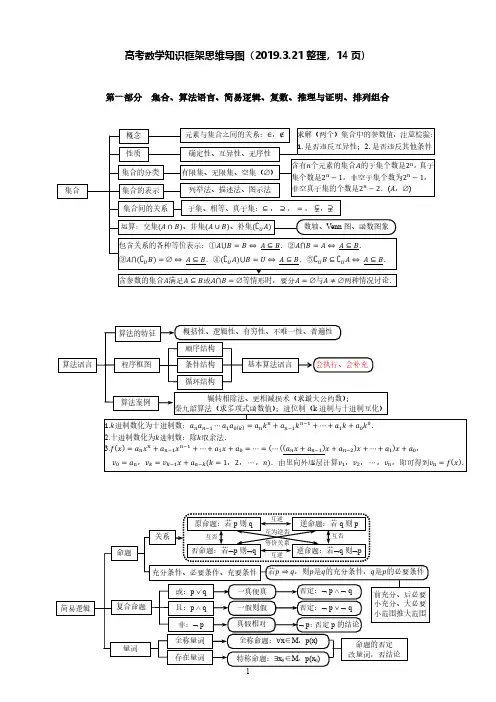

高中函数知识点总结思维导图1. 函数及其性质1.1 函数的定义函数是一种特殊的关系,它将一个集合的元素对应到另一个集合的元素。
函数可以用数学符号或图形表示。
1.2 函数的性质•定义域:函数的输入值可能取的所有实数的集合•值域:函数的输出值可能取的所有实数的集合•单调性:函数的增减特性•奇偶性:函数在自身关于原点对称时,称为奇函数;否则称为偶函数2. 数学符号的应用2.1 函数的表示法•映射法:使用箭头表示函数的对应关系•例子:f(x) = x^2,表示函数f的定义域为实数集,值域为非负实数集。
2.2 函数的性质表示法•表格法:将函数的定义域和值域以表格的形式表示•例子:x -2 -1 0 1 2f(x) 4 1 0 1 43. 函数的图像与图象3.1 函数的图像函数的图像是函数在坐标系中的几何表现形式,可以通过作图得到。
作图时,横轴表示自变量,纵轴表示因变量。
3.2 函数的图象函数的图象是函数在平面直角坐标系中的全体点的集合。
图象的特点有: - 函数左右对称:奇函数的图象关于y轴对称,偶函数的图象关于原点对称 - 函数上下对称:在平面直角坐标系中,函数的图象上的每一点M关于x轴都有对称点N(x,-y)4. 特殊函数4.1 常数函数常数函数是定义域为全体实数的函数,且对应的函数值都相等。
4.2 一次函数一次函数表示为f(x) = ax + b,其中a和b为常数,a不等于0。
一次函数的图象是一条直线。
4.3 二次函数二次函数表示为f(x) = ax^2 + bx + c,其中a、b和c为常数,a不等于0。
二次函数的图象是一条抛物线。
4.4 幂函数幂函数表示为f(x) = ax^n,其中a和n为常数,a不等于0。
幂函数的图象随着指数n的增大而变成越来越陡峭或平缓的曲线。
4.5 指数函数指数函数表示为f(x) = a^x,其中a为常数,a大于0且不等于1。
指数函数的图象呈现指数增长或指数衰减的趋势。
4.6 对数函数对数函数表示为f(x) = log(a, x),其中a为常数,a大于0且不等于1。
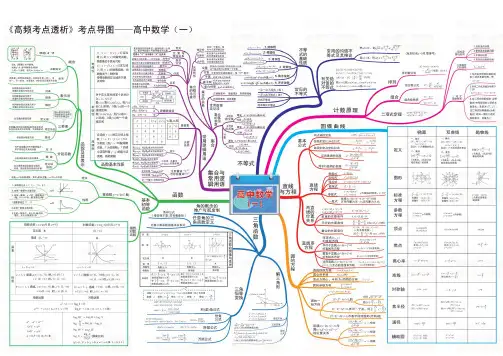

高中数学最全的思维导图
中国教育在线· 2015-11-09 06:43温馨提示商务合作QQ:1927876294小编推荐两个优秀的微信公众号:美丽的旅游(ID:mldly520)中国养生在线(ID:zg-yszx)很多同学又到一轮复习了,不知道该怎么总结,教育君给大家提个建议,要想总结,主要还是首先梳理出脉络来,提到某个知识点,那么关于这个知识点相关的所有知识你都要弄明白,这样你就成功了一半!下面是8张思维导图,先研究下看看吧!请点击标题下面:“中国教育在线”关注规则(关注后输
入数字或者汉字)我们会把相关的内容发送给您!主要不要有空格或者错误【1.正能量教育】【2.德行教育】【4.教育思维】【6.名家教育】【7.故事育人】【8.名校教育】【9.贵族教育】【14.学习行为】【15.健康心理】【16.行为教育】【17.亲情教育】【19.教育技巧】【20.教育误区】【21.名师经验】【22.明
星分享】【23.母爱】【25.教育技巧2】【28.文化教育】【29.
教育思考】【31.智慧分享】【32.开心一刻】【33.古代教育】【34.感动瞬间】【38.英语指导】【39.名家教育2】【41.生活点滴】【50.课外读物】【51.学习思维】【52.孩子叛逆】【53.名家教育3】【54.感动美文】【55.性教育】【61.单亲家庭】......更多专题,请点击菜单栏,“教育导航”微信原文微信文章为作者
独立观点,不代表微头条立场。


高一数学必修1知识网络集合123412n x A x B A B A B A n A ∈∉⎧⎪⎪⎨⎪⎪⎩∈⇒∈⊆()元素与集合的关系:属于()和不属于()()集合中元素的特性:确定性、互异性、无序性集合与元素()集合的分类:按集合中元素的个数多少分为:有限集、无限集、空集()集合的表示方法:列举法、描述法(自然语言描述、特征性质描述)、图示法、区间法子集:若 ,则,即是的子集。
、若集合中有个元素,则集合的子集有个, 注关系集合集合与集合{}00(2-1)23,,,,.4/nA A ABC A B B C A C A B A B x B x A A B A B A B A B A B x x A x B A A A A A B B A A B ⎧⎪⎧⎪⎪⎪⊆⎪⎪⎨⎪⊆⊆⊆⎨⎪⎪⎪⎩⎪⎪⊆≠∈∉⎪⊆⊇⇔=⎪⎩⋂=∈∈⋂=⋂∅=∅⋂=⋂⋂⊆真子集有个。
、任何一个集合是它本身的子集,即 、对于集合如果,且那么、空集是任何集合的(真)子集。
真子集:若且(即至少存在但),则是的真子集。
集合相等:且 定义:且交集性质:,,,运算{}{},/()()()-()/()()()()()()U U U U U U U U A A B B A B A B A A B x x A x B A A A A A A B B A A B A A B B A B A B B Card A B Card A Card B Card A B C A x x U x A A C A A C A A U C C A A C A B C A C B ⎧⎪⎨⋂⊆⊆⇔⋂=⎪⎩⎧⋃=∈∈⎪⎨⋃=⋃∅=⋃=⋃⋃⊇⋃⊇⊆⇔⋃=⎪⎩⋃=+⋂=∈∉=⋂=∅⋃==⋂=⋃,定义:或并集性质:,,,,, 定义:且补集性质:,,,, ()()()U U U C A B C A C B ⎧⎪⎪⎪⎪⎪⎪⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎧⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎧⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⋃=⋂⎪⎪⎩⎩⎩⎩函数,,,A B A x B y f B A B x y x f y y x y →映射定义:设,是两个非空的集合,如果按某一个确定的对应关系,使对于集合中的任意一个元素, 在集合中都有唯一确定的元素与之对应,那么就称对应:为从集合到集合的一个映射传统定义:如果在某变化中有两个变量并且对于在某个范围内的每一个确定的值,定义 按照某个对应关系都有唯一确定的值和它对应。