求下列函数的拉氏变换

拉普拉斯变换、复频域分析习题课1. 求下列函数的拉氏变换。

（1）1at e-- （2）sin 2cos t t + （3）2t te - （4）sin(2)t e t -（5）(12)t t e -+ （11）1()t t e e αββα---- （13）(2)(1)t te u t --- （15）()ta t e f a-，设已知[()]()L f t F s = 解：（1）11[1]()at a L e s s a s s a --=-=++ （2）2221221[sin 2cos ]111s s L t t s s s ++=+=+++ （3）221[](2)t L te s -=+ （4）22[sin(2)](1)4t L e t s -=++ （5）23[(12)](1)ts L t e s -++=+ （11）11111[()]()()()t t L e e s s s s αββαβααβαβ---=+=--++++ （13）由于(2)(1)(1)(1)[(1)](1)t t t teu t e t e e u t -------=-+- （15）[()](1)ta t L e f aF as a-=+2求下列函数的拉氏变换，注意阶跃函数的跳变时间。

（1）()(2)tf t e u t -=- （2）(2)()(2)t f t e u t --=- （3）(2)()()t f t e u t --= （4）()sin(2)(1)f t t u t =-（5）()(1)[(1)(2)]f t t u t u t =----解：（1）因为(2)2()(2)t f t ee u t ---=-，所以 222(1)11[()]11s s L f t e e e s s ---+==++ （2）21[()]1s L f t e s -=+ （3）因为2()()t f t e e u t -=，所以2[()]1e Lf t s =+ （4） ()sin[2(1)2](1) {sin[2(1)]cos 2cos[2(1)]sin 2}(1)f t t u t t t u t =-+-=-+-- 2222cos 2sin 22cos 2sin 2[()]()444s s s s L f t e e s s s --+=+=+++ （5）()(1)(1)(2)(2)(2)f t t u t t u t u t =-------222221111[()][1(1)]s s s s s L f t e e e s e e s s s s-----=--=-+ 3求下列函数的拉普拉斯逆变换。

第二章习题解题过程和参考答案第二章习题解题过程和参考答案2-1 试建立题2-1图所示各系统的微分方程 [其中外力)(t f ，位移)(t x 和电压)(t u r为输入量；位移)(t y 和电压)(t u c为输出量；k （弹性系数），μ（阻尼系数），R （电阻），C （电容）和m （质量）均为常数]。

解：2-1(a) 取质量m 为受力对象，如图，取向下为力和位移的正方向。

作用在质量块m 上的力有外力f(t)，重力mg ，这两个力向下，为正。

有弹簧恢复力[]0)(y t y k +和阻尼力()dy t dtμ，这两个力向上，为负。

其中，0y 为0)(=t f 、物体处于静平衡位置时弹簧的预伸长量。

根据牛顿第二定理F ma ∑=，有[]22()()()()dy t d y t f t mg k y t y m dt dtμ+-+-= 其中：0ky mg =代入上式得22)()()()(dt t y d mdt t dy t ky t f =--μ整理成标准式：22()()()()d y t dy t m ky t f t dt dtμ++=μμ()f t[()k y t +()dy t dt或也可写成：22()()1()()d y t dy t k y t f t dt m dt m mμ++=它是一个二阶线性定常微分方程。

2-1(b) 如图，取A 点为辅助质点，设该点位移为()Ax t ，方向如图。

再取B 点也为辅助质点，则该点位移即为输出量()y t ，方向如图A 点力平衡方程：1()()[()()][]AAdx t dy t k x t x t dt dtμ-=- ① B 点力平衡方程：2()()()[]Adx t dy t k y t dt dtμ=- ②由①和②:12[()()]()A k x t x t k y t -= 得：21()()()Akx t x t y t k=-二边微分：21()()()Adx t k dx t dy t dt dt k dt=-③将③代入②：221()()()()[]k dx t dy t dy t k y t dt k dt dtμ=--整理成标准式：1221()()()k k k dy t dx t y t k dt dtμ++=或也可写成：()A t AB1211212()()()()k k k dy t dx t y t dt k k k k dtμ+=++它是一个一阶线性定常微分方程。

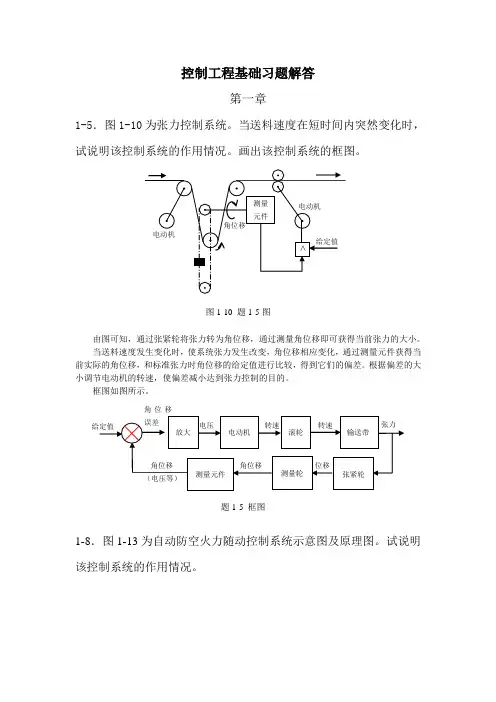
控制工程基础习题解答第一章1-5．图1-10为张力控制系统。

当送料速度在短时间内突然变化时，试说明该控制系统的作用情况。

画出该控制系统的框图。

由图可知，通过张紧轮将张力转为角位移，通过测量角位移即可获得当前张力的大小。

当送料速度发生变化时，使系统张力发生改变，角位移相应变化，通过测量元件获得当前实际的角位移，和标准张力时角位移的给定值进行比较，得到它们的偏差。

根据偏差的大小调节电动机的转速，使偏差减小达到张力控制的目的。

框图如图所示。

1-8．图1-13为自动防空火力随动控制系统示意图及原理图。

试说明该控制系统的作用情况。

题1-5 框图电动机给定值角位移误差张力-转速位移张紧轮滚轮输送带转速测量轮测量元件角位移角位移（电压等）放大电压测量 元件>电动机角位移给定值电动机图1-10 题1-5图该系统由两个自动控制系统串联而成：跟踪控制系统和瞄准控制系统，由跟踪控制系统获得目标的方位角和仰角，经过计算机进行弹道计算后给出火炮瞄准命令作为瞄准系统的给定值，瞄准系统控制火炮的水平旋转和垂直旋转实现瞄准。

跟踪控制系统根据敏感元件的输出获得对目标的跟踪误差，由此调整视线方向，保持敏感元件的最大输出，使视线始终对准目标，实现自动跟踪的功能。

瞄准系统分别由仰角伺服控制系统和方向角伺服控制系统并联组成，根据计算机给出的火炮瞄准命令，和仰角测量装置或水平方向角测量装置获得的火炮实际方位角比较，获得瞄准误差，通过定位伺服机构调整火炮瞄准的角度，实现火炮自动瞄准的功能。

控制工程基础习题解答第二章2-2．试求下列函数的拉氏变换，假定当t<0时，f(t)=0。

(3). ()t et f t10cos 5.0-=解：()[][]()1005.05.010cos 25.0+++==-s s t e L t f L t(5). ()⎪⎭⎫⎝⎛+=35sin πt t f 图1-13 题1-8图敏感 元件定位伺服机构 （方位和仰角）计算机指挥仪目标 方向跟踪环路跟踪 误差瞄准环路火炮方向火炮瞄准命令--视线瞄准 误差伺服机构（控制绕垂直轴转动）伺服机构（控制仰角）视线敏感元件计算机指挥仪解：()[]()252355cos 235sin 2135sin 2++=⎥⎦⎤⎢⎣⎡+=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+=s s t t L t L t f L π2-6．试求下列函数的拉氏反变换。

信号与系统题目部分，(卷面共有200题,0.0分,各大题标有题量和总分) 一、选择题(7小题,共0.0分)[1]题图中，若h '（0）=1，且该系统为稳定的因果系统，则该系统的冲激响应()h t 为。

A 、231()(3)()5tt h t e e t ε-=+- B 、32()()()tt h t e e t ε--=+C 、3232()()55tt e t e t εε--+D 、3232()()55tt e t e t εε--+-[2]已知信号x[n]如下图所示，则x[n]的偶分量[]e x n 是。

[3]波形如图示，通过一截止角频率为50rad sπ，通带内传输值为1，相移为零的理想低通滤波器，则输出的频率分量为（） A 、012cos 20cos 40C C t C t ππ++ B 、012sin 20sin 40C C t C t ππ++ C 、01cos 20C C t π+ D 、01sin 20C C t π+[4]已知周期性冲激序列()()T k t t kT δδ+∞=-∞=-∑的傅里叶变换为()δωΩΩ，其中2TπΩ=；又知111()2(),()()2T T f t t f t f t f t δ⎛⎫==++⎪⎝⎭；则()f t 的傅里叶变换为________。

A 、2()δωΩΩ B 、24()δωΩΩ C 、2()δωΩΩ D 、22()δωΩΩ[5]某线性时不变离散时间系统的单位函数响应为()3(1)2()kkh k k k εε-=--+，则该系统是________系统。

A 、因果稳定B 、因果不稳定C 、非因果稳定D 、非因果不稳定 [6]一线性系统的零输入响应为（23kk --+）u(k), 零状态响应为(1)2()k k u k -+,则该系统的阶数A 、肯定是二阶B 、肯定是三阶C 、至少是二阶D 、至少是三阶 [7]已知某系统的冲激响应如图所示则当系统的阶跃响应为。

Laplace拉氏变换公式表1. 常数变换：对于常数C，其拉普拉斯变换为C/s，其中s是复数频率。

2. 幂函数变换：对于幂函数t^n，其中n为实数，其拉普拉斯变换为n!/s^(n+1)。

3. 指数函数变换：对于指数函数e^(at)，其中a为实数，其拉普拉斯变换为1/(sa)。

4. 正弦函数变换：对于正弦函数sin(at)，其中a为实数，其拉普拉斯变换为a/(s^2+a^2)。

5. 余弦函数变换：对于余弦函数cos(at)，其中a为实数，其拉普拉斯变换为s/(s^2+a^2)。

6. 双曲正弦函数变换：对于双曲正弦函数sinh(at)，其中a为实数，其拉普拉斯变换为a/(s^2a^2)。

7. 双曲余弦函数变换：对于双曲余弦函数cosh(at)，其中a为实数，其拉普拉斯变换为s/(s^2a^2)。

8. 指数衰减正弦函数变换：对于指数衰减正弦函数e^(at)sin(bt)，其中a和b为实数，其拉普拉斯变换为b/(s+a)^2+b^2。

9. 指数衰减余弦函数变换：对于指数衰减余弦函数e^(at)cos(bt)，其中a和b为实数，其拉普拉斯变换为s+a)/(s+a)^2+b^2。

10. 指数增长正弦函数变换：对于指数增长正弦函数e^(at)sin(bt)，其中a和b为实数，其拉普拉斯变换为b/(sa)^2+b^2。

Laplace拉氏变换公式表11. 幂函数与指数函数的乘积变换：对于函数t^n e^(at)，其中n为实数，a为实数，其拉普拉斯变换为n!/(sa)^(n+1)。

12. 幂函数与正弦函数的乘积变换：对于函数t^n sin(at)，其中n为实数，a为实数，其拉普拉斯变换可以通过分部积分法得到。

13. 幂函数与余弦函数的乘积变换：对于函数t^n cos(at)，其中n为实数，a为实数，其拉普拉斯变换可以通过分部积分法得到。

14. 指数函数与正弦函数的乘积变换：对于函数e^(at) sin(bt)，其中a和b为实数，其拉普拉斯变换为b/(sa)^2+b^2。

第14 章 Laplace 变换1． 求下列函数的拉氏变换 （1）1cos wtw- （2）chwt 解 （1）{}{}220sin 1cos sin ()tL wt wt wL Lwzdz w p p p w -⎧⎫===⎨⎬+⎩⎭⎰（2）{}{}22111122wt wt pL chwt L e e p w p w p w-⎧⎫=+=+=⎨⎬-+-⎩⎭ 2．求下列函数的逆拉氏变换 （1）2845p p p +++； （2）222()p p a + 其中a ＞0。

解 （1）111222821645(2)1(2)1p p L L L p p p p ---⎧⎫⎧⎫⎧⎫++=+⎨⎬⎨⎬⎨⎬++++++⎩⎭⎩⎭⎩⎭22cos 6sin tt et e t --=+（2）1222sin ()2pt at L p a a -⎧⎫=⎨⎬+⎩⎭3. 设11()sin f t wt w=，2()f t chwt =，其中w ≠0,求12()()f t f t *。

解法1 由于{}{}{}1212L f f L f L f *=⋅ {}12211()sin L f t L wt w p w⎧⎫==⎨⎬+⎩⎭ {}{}222()pL f t L chwt p w ==-所以 {}1222221pL f f p w p w*=⋅+- 2222222()2()p pw p w w p w =--+2211cos 22L chwt L wt w w ⎧⎫⎧⎫=-⎨⎬⎨⎬⎩⎭⎩⎭2211cos 22L chwt wt w w ⎧⎫=-⎨⎬⎩⎭1221(cos )2f f chwt wt w *=- 解法2 由卷积定义求1201()()sin ()tf t f t w chw t d wτττ*=-⎰()()01sin 2w t w t te e w d w ττττ---+=⎰ ()()0011sin sin 22t t w t w t e w d e w d w w ττττττ---=+⎰⎰ 22221111sin cos sin 4444wt wt wt e wt w w w w =--++-2211cos 44wtt e w w -+ 2211cos 222wt wt e e wt w w -+=-21(cos )2chwt wt w =- 4．求解'1(0)0x x x +=⎧⎨=⎩解 对方程施行Laplace 变换，并注意初始条件：x(0)=0,我们有 [][][]'1L x L x L +=[][]1pL x L x p+=[]11111(1)1(1)L x p p p p p p ==-=-++--[]11111(1)tx L L x L e p p ---⎡⎤==-=-⎢⎥--⎣⎦5. 求解2'3(0)2tx x e x -⎧-=-⎨=⎩解 对方程两边施以Laplace 变换，并注意初始条件x(0)=0,则有[][]2'3tL x L x L e -⎡⎤-=-⎣⎦[][]3(0)2pL x x L x p ---=+ []311(1)(2)21L x p p p p -==--++-11211()()21t tx t L x L e e p p ---⎡⎤==-=-⎢⎥+-⎣⎦6. 求解01"(0),'(0)tx x e x x x x ⎧+=⎨==⎩解 对方程两边施以Laplace 变换得[][]"tL x L x L e ⎡⎤+=⎣⎦[][]20111p L x px x L x p --+=- 解得 []0122221111121212111x p x p L x p p p p p =--++-++++ 所以 101222211111()21212111x p x p x t L p p p p p -⎡⎤=--++⎢⎥-++++⎣⎦01111()cos ()sin 222t e x t x t =+-+- 7. 求解01"(0),'(0)tx x e x x x x ⎧-=⎨==⎩解 对方程两边施以Laplace 变换得 [][]"t L x L x L e ⎡⎤-=⎣⎦[][]201'(0)1p L x p xx L x p ---=- []201111p L x px x p ⎡⎤-=++⎣⎦- 解得 []2111()2(1)4(1)4(1)L x t p p p =-+--+ 012211x p x p p ++-- []101111()(())244t t t x t L L x t te e e x cht x sht --==-+++8. 求解"'2"'4(0)1,'(0)2,"(0)2x x x x x x --=⎧⎨===-⎩解 对方程两边施行Laplace 变换，并注三个初始条件，则有[][][][]"'2"'4L x L x L x L -+=[][]322(0)'()"(0)2(0)'(0)p x p x px x x p L x px x ⎡⎤------+⎣⎦[]4(0)L x x p-=[][][]3224222241p L x p p p L x p pL x p--+-+++-=[]224(1)5p p L x p p-=+- 解得 []222254()(1)(1)(1)p L x t p p p p p =-+--- 23421p p p =+-- 所以 []1()()342tx t L L x t t e -==+-9. 求解21"'2(0)'(0)"(0)0t x x t e x x x ⎧+=⎪⎨⎪===⎩ 解 对方程两边施以Laplace 变换并利用初始条件有 [][]21"'2tL x L x L t e ⎡⎤+=⎢⎥⎣⎦[][]3221(0)'(0)"(0)(1)p L x p x px x L x p ---+=-解得 []331()(1)(1)L x t p p =-+- 当331231,,ii p p e p e ππ-=-==是一阶极点，p=1是三阶极点，由留数计算公式：22331111Re ()lim 2(1)(1)ptpt p p d s F p e e dp p p →=⎡⎤⎡⎤=⎢⎥⎣⎦!+-⎣⎦2133448t t tt e te e =-+31311(1)Re ()|(1)24ptptt p p e p s F p e e p -=-=--⎡⎤==-⎣⎦+3332(1)Re ()|3i i pt ptp e p e e p s F p e p ππ==-⎡⎤==⎣⎦3Re ()iptp es F p e π-=⎡⎤=⎣⎦所以221331()44824t t t t t x t t e te e e -=-+--21cos 32te10. 求解3''21'4'30(0)(0)0x y x x y y x y ++=⎧⎪++=⎨⎪==⎩解 对方程组两边施行Laplace 变换，并设[][](),(),X L x t Y L y t ==得 1(32)(43)0p X pY p pX p Y ⎧++=⎪⎨⎪++=⎩解得 221111111765(116)5(1)431133(11176)25(1)10(116)Y p p p p p X p p p p p p --⎧==+⎪++++⎪⎨+⎪==--⎪++++⎩所以 [][]61116111113()251011()55t t t tx t L X e e y t L Y e e ------⎧==--⎪⎪⎨⎪==-+⎪⎩11. 求解0sin ()sin()()ta t G t t z G z dz =--⎰，a 为常数。

例4-1求下列函数的拉氏变换拉氏变换有单边和双边拉氏变换,为了区别起见,本书以表示 单边拉氏变换,以 表示 双边拉氏变换.若文字中未作说明,则 指单边拉氏变换.单边拉氏变换只研究 的时间函数,因此,它和傅里叶变换 之间有一些差异,例如在时移定理,微分定理和初值定理等方面.本例只讨论时移 定理.请注意本例各函数间的差异和时移定理的正确应用。

例4-2求三角脉冲函数 如图4-2（a ）所示的象函数和傅里叶变换类似，求拉氏变换的时，往往要借助基本信号的拉氏变换和拉氏变换的性质，这比按拉氏变换的定义式积分简单，为比较起见，本例用多种方法求解。

方法一：按定义式求解方法二：利用线性叠加和时移性质求解 方法三：利用微分性质求解 方法四：利用卷积性质求解方法一：按定义式求解()()1-=t tu t f ()s F ()t f ()s F B ()t f 0≥t ()()[]()()()[]se s s t u t u t L t tu L s F -⎪⎭⎫ ⎝⎛+=-+--=-=1111112()tf ()⎪⎩⎪⎨⎧<<-<<=其它 02t 1 21t 0t t tf ()()()()222222221101010102101112221112112sss s s s s st st st st st st ste se s e s e s e s s e s e s dtte dt e dt e s e s t dt e t dt te dt e t f s F -------------∞--=-++-+--=-++⎪⎭⎫ ⎝⎛-=-+==⎰⎰⎰⎰⎰⎰-----方法二：利用线性叠加和时移性质求解由于于是方法三：利用微分性质求解信号的波形仅由直线组成，信号导数的象函数容易求得，或者信号经过几次微分后出现原信号，这时利用微分性质比较简单。

将 微分两次，所得波形如图4-2（b ）所示显然根据微分性质由图4-2（b ）可以看出于是方法四：利用卷积性质求解 可看作是图4-2(c ）所示的矩形脉冲 自身的卷积 于是，根据卷积性质 而所以()()()()()()22112--+---=t u t t u t t tu t f ()[]()[]()0021st e s F t t f L s t tu L -=-=()()()222211211s s s ese e s s F ----=+-=()t f2()()()()[]()2221212s e t t t L dt t f d L --=-+--=⎥⎦⎤⎢⎣⎡δδδ()()()()---'-=⎥⎦⎤⎢⎣⎡00222sf f s F s dt t f d L (),00=-f ()00='-f ()()221s e s F s --=()()2211s es s F --=()()()t f t f t f 11*=()t f ()t f 1()()()s F s F s F 11=()()s e s s F --=111()()2211s e s s F --=例4-3应用微分性质求图4-3（a ）中的象函数下面说明应用微分性质应注意的问题，图4-3（b ）是 的导数 的波形。