函数的概念及相关典型例题

函数定义域的求法及常见题型一、函数定义域求法(一)常规函数函数解析式确定且已知，求函数定义域。

其解法是根据解析式有意义所需条件，列出关于自变量的不等式或不等式组，解此不等式(或组)，即得函数定义域。

例1.求函数y=-2—2x T5的定义域。

lx+31—8(二)抽象函数1.有关概念定义域：函数y=f(x的自变量x的取值范围，可以理解为函数f(x图象向x轴投影的区间；凡是函数的定义域，永远是指自变谶取值范围；2.四种类型题型一：已知抽象函数y=f(x)的定义域为［m,n］，如何求复合抽象函数y=f(g(x))的定义域？例题2.已知函数y=f(x)的定义域［0,3］，求函数y=f(3+2x)的定义域强化训练：1.已知函数y=f(x)的定义域［-1,5］，求函数y=f(3x-5)的定义域；2.已知函数y=f(x)的定义域［1/2,2］，求函数y=f(log2x)的定义域；3.已知f(x)的定义域为［—2,2］,求f(x2—1)的定义域。

题型二：已知复合抽象函数y=f(g(x))定义域［m,n］,如何求抽象函数y=f(x)的的定义域? 例题4.已知函数y=f(2x-1)的定义域［0,3］,求函数y=f(x)的定义域.强化训练：1.已知函数y=f(x2-2x+2)的定义域［0,3］,求函数y=f(x)的定义域.2.已知函数y=f［lg(x+1)］的定义域［0,9］,求函数y=f(x)的定义域.题型三：已知复合抽象函数y=f(g(x))定义域［m,n］,如何求复合抽象函数y=f(h(x))定义域的定义域？例题5.已知函数y=f(2x-1)的定义域［0,函，求函数y=f(3+x)的定义域.强化训练：1.已知函数y=f(x+1)的定义域［-2,3］，求函数y=f(2x-1)的定义域.2.已知函数y=f(2x)的定义域［-1,1］，求函数y=f(logx)的定义域.23.已知f(x+1)的定义域为［-1/2,2］,求f(x2)定义域。

初二关于函数的10题典型例题初二数学中关于函数的典型例题有很多，下面列举了其中的10题，并进行了解答。

1. 已知函数 f(x) = 2x + 1，求 f(3) 的值。

解答：将 x 替换为 3，计算得 f(3) = 2 * 3 + 1 = 7。

2. 已知函数 g(x) = x^2 + 3x，求 g(-2) 的值。

解答：将 x 替换为 -2，计算得 g(-2) = (-2)^2 + 3 * (-2) = 4 - 6 = -2。

3. 已知函数 h(x) = 4x^3 + 2x^2 + x，求 h(0) 的值。

解答：将 x 替换为 0，计算得 h(0) = 4 * 0^3 + 2 * 0^2 + 0 = 0。

4. 已知函数 f(x) = 3x - 2，求 f(1/2) 的值。

解答：将 x 替换为 1/2，计算得 f(1/2) = 3 * (1/2) - 2 = 1/2 - 2 = -3/2。

5. 已知函数 g(x) = 2x + 3，求使得 g(x) = 7 的 x 的值。

解答：将 g(x) = 7，解方程得 2x + 3 = 7，即 2x = 4，x = 2。

6. 已知函数 h(x) = 5x^2 + 4x + 1，求使得 h(x) = 0 的 x 的值。

解答：将 h(x) = 0，解方程得 5x^2 + 4x + 1 = 0，该方程可以因式分解为 (5x + 1)(x + 1) = 0，得到 x = -1 或 x = -1/5。

7. 已知函数 f(x) = 2x^2 + 5x + 3，求 f(-1) 的值。

解答：将 x 替换为 -1，计算得 f(-1) = 2 * (-1)^2 + 5 * (-1) + 3 = 2 - 5 + 3 = 0。

8. 已知函数 g(x) = 3x^2 + 2x + 1，求 g(2) 的值。

解答：将 x 替换为 2，计算得 g(2) = 3 * 2^2 + 2 * 2 + 1 = 12 + 4 + 1 = 17。

二次函数一．复习1.函数的概念：一般地，在一个变化过程中，如果有两个变量x，y，对于自变量x在某一范围内的每一个确定值，y都有惟一确定的值与它对应，那么就说y是x的函数.对于自变量x在可以取值范围内的一个确定的值a，函数y有惟一确定的对应值，这个对应值叫做当x=a时函数的值，简称函数值. 要点诠释：对于函数的概念，应从以下几个方面去理解：（1）函数的实质，揭示了两个变量之间的对应关系；（2）判断两个变量之间是否有函数关系，要看对于x允许取的每一个值，y是否都有惟一确定的值与它相对应；（3）函数自变量的取值范围，应要使函数表达式有意义，在解决实际问题时，还必须考虑使实际问题有意义.2.函数的三种表示方法表示函数的方法，常见的有以下三种：（1）解析法：用来表示函数关系的数学式子叫做函数的表达式，（或解析式），用数学式子表示函数的方法称为解析法.（2）列表法：用一个表格表达函数关系的方法.（3）图象法：用图象表达两个变量之间的关系的方法.要点诠释：函数的三种表示方法各有不同的长处.解析式法能揭示出变量之间的内在联系，但较抽象，不是所有的函数都能列出解析式；列表法可以清楚地列出一些自变量和函数值的对应值，这会对某些特定的数值带来一目了然的效果，例如火车的时刻表，平方表等；图象法可以直观形象地反映函数的变化趋势，而且对于一些无法用解析式表达的函数，图象可以充当重要角色.对照表如下：二．二次函数的概念一般地，形如y=ax2+bx+c（a, b, c是常数，a≠0）的函数叫做x的二次函数.若b=0，则y=ax2+c；若c=0，则y=ax2+bx；若b=c=0，则y=ax2.以上三种形式都是二次函数的特殊形式，而y=ax2+bx+c（a≠0）是二次函数的一般式.要点诠释：如果y=ax2+bx+c(a,b,c是常数，a≠0)，那么y叫做x的二次函数．这里，当a=0时就不是二次函数了，但b、c可分别为零，也可以同时都为零．例1.下列函数一定是二次函数的是__________.①；②；③；④；⑤y=(x-3)2-x 2 例2.若是221(3)2a a y a x --=--二次函数，则a=__________例 3.中的二次项系数=__________,一次项系数=__________,常数项=__________.例4.边长为12 cm 的正方形铁片，中间剪去一个边长x cm 的小正方形铁片，剩下的四方框铁片的面积y(cm 2)与x(cm)之间的函数关系式为_______________．例 6.某地绿色、富硒产品和特色农产品在国际市场上颇具竞争力，其中香菇远销日本和韩国等地．上市时，外商李经理按市场价格10元/千克在当地收购了2000千克香菇存放入冷库中．据预测，香菇的市场价格每天每千克将上涨0.5元，但冷库存放这批香菇时每天需要支出各种费用合计340元，而且香菇在冷库中最多保存110天，同时，平均每天有6千克的香菇损坏不能出售．（1）若存放x 天后，将这批香菇一次性出售，设这批香菇的销售总金额为y 元，试写出y 与x 之间的函数关系式．（2）李经理想获得利润22500元，需将这批香菇存放多少天后出售？（利润＝销售总金额－收购成本－各种费用）c bx ax y ++=2xy 3-=1342+-=x x y c bx x m y ++-=2)1(2y =(2x -1)-6a b c练习：1.下列函数中是二次函数的有（ ）个.（1）1y x x=+；（2)y=3(x-1)2＋2；（3)y=(x+3)2-2x 2；（4) 21y x x =+ A.4 B.3 C.2 D.1 2．当m= 时，函数y=（m ﹣1）x |m|+1是二次函数．3.若267(1)m m y m x-+=-是二次函数，则m 的值是( )．A.5B.1C.1或5D.以上都不对.4.将化成二次函数的一般式是：________________.5.一个圆柱的高与底面直径相等，试写出它的表面积S 与底面半径r 之间的函数关系式___________________.6.（2014秋·温岭市校级月考） 已知某商品的进价为每件40元，售价是每件60元，每周可卖出300件.市场调查反映：如调整价格，每涨价1元，每周要少卖出10件.假设涨价x 元，求每周的利润y （元）与涨价x 之间的函数关系式，并写出自变量的取值范围.(23)(1)3y x x =+--三．二次函数的图像及性质：二次函数y=ax2（a≠0）的图象与性质二次函数y=ax2(a≠0)的图象：二次函数y=ax2的图象（如图），是一条关于y轴对称的曲线，这样的曲线叫做抛物线.抛物线y=ax2（a≠0）的对称轴是y轴，它的顶点是坐标原点.当a＞ 0时，抛物线的开口向上，顶点是它的最低点；当a＜0时，抛物线的开口向下，顶点是它的最高点.二次函数y=ax2(a≠0)的图象的画法——描点法描点法画图的基本步骤：列表、描点、连线.（1）列表：选择自变量取值范围内的一些适当的x的值，求出相应的y值，填入表中.（自变量x的值写在第一行，其值从左到右，从小到大.）（2）描点：以表中每对x和y的值为坐标，在坐标平面内准确描出相应的点.一般地，点取的越多，图象就越准确.（3）连线：按照自变量的值由小到大的顺序，把所描的点用平滑的曲线连结起来. 要点诠释：（1）用描点法画二次函数y=ax 2（a≠0）的图象时，应在顶点的左、右两侧对称地选取自变量x 的值，然后计算出对应的y 值. （2）二次函数y=ax 2(a≠0)的图象，是轴对称图形，对称轴是y 轴．y=ax 2(a≠0)是最简单的二次函数.（3）画草图时应抓住以下几点：开口方向，对称轴，顶点，与轴的交点，与轴的交点.二次函数y=ax 2(a ≠0)的图象的性质x y要点诠释：顶点决定抛物线的位置.几个不同的二次函数，如果二次项系数相同，那么抛物线的开口方向、开口大小完全相同，只是顶点的位置不同. │a │相同，抛物线的开口大小、形状相同.│a │越大，开口越小，图象两边越靠近y 轴，│a │越小，开口越大，图象两边越靠近x 轴二次函数y=ax 2+c(a ≠0)的图象关于二次函数的性质，主要从抛物线的开口方向、顶点、对称轴、函数值的增减性以及函数的最大值或最小值等方面来研究．下面结合图象，将其性质列表归纳如下：a 2(0)y ax c a =+≠例1．二次函数y=ax2与直线y=2x﹣1的图象交于点P（1，m）（1）求a，m的值；（2）写出二次函数的表达式，并指出x取何值时该表达式y随x的增大而增大？（3）写出该抛物线的顶点坐标和对称轴．例2．已知y=(m+1)x 2m m +是二次函数且其图象开口向上,求m 的值和函数解析式例3．求下列抛物线的解析式：（1）与抛物线形状相同，开口方向相反，顶点坐标是（0，-5）的抛物线；（2）顶点为（0，1），经过点（3，-2）并且关于y 轴对称的抛物线．例4．在同一直角坐标系中，画出和的图象，并根据图象回答下列问题．2132y x =-+2y x =-21y x =-+(1)抛物线向________平移________个单位得到抛物线；(2)抛物线开口方向是________，对称轴为________，顶点坐标为________；(3)抛物线，当x________时，随x 的增大而减小；当x________时，函数y 有最________值，其最________值是________． 练习：1.下列函数中，当x ＜0时，y 值随x 值的增大而增大的是（ ） A. B. C. D.2.在同一坐标系中，作出，，的图象，它们的共同点是（ ）．A ．关于y 轴对称，抛物线的开口向上B ．关于y 轴对称，抛物线的开口向下21y x =-+2y x =-21y x =-+21y x =-+25y x =212y x =-2y x =213y x =22y x =22y x =-212y x =C ．关于y 轴对称，抛物线的顶点都是原点D ．关于原点对称，抛物线的顶点都是原点3.抛物线y=2x 2+1的对称轴是（ ） A ．直线x=B.直线x=﹣ C ．y 轴 D ． x轴4.已知抛物线的解析式为y ＝-3x 2，它的开口向________，对称轴为________，顶点坐标是________，当x ＞0时，y 随x 的增大而________．5.函数，、的图象大致如图所示，则图中从里向外的三条抛物线对应的函数关系式是_____________________．6.抛物线与的形状相同，其顶点坐标为（0，1），则其解析式为 ．7.已知直线与x 轴交于点A ，抛物线的顶点平移后与点A 重合．(1)求平移后的抛物线C 的解析式；2y x =212y x =23y x=2y ax c =+23y x =1y x =+22y x =-(2)若点B(，)，C(，)在抛物线C 上，且，试比较，的大小．8．（2014春·牙克石市校级月考）函数y=ax 2 (a ≠0)的图象与直线y=2x-3交于点(1，b)． (1)求a 和b 的值；(2)求抛物线y=ax 2的解析式，并求顶点坐标和对称轴； (3)x 取何值时，y 随x 的增大而增大?(4)求抛物线与直线y=-2的两个交点及其顶点所构成的三角形的面积．函数2()(0)y a x h a =-≠与函数2()(0)y a x h k a =-+≠的图象与性质 1.函数2()(0)y a x h a =-≠的图象与性质1x 1y 2x 2y 1212x x -<<1y 2y2.函数2()(0)y a x h k a =-+≠的图象与性质要点诠释：二次函数的图象常与直线、三角形、面积问题结合在一起，借助它的图象与性质．运用数形结合、函数、方程思想解决问题．要点二、二次函数的平移 1.平移步骤：2()+(0y a x h k a =-≠）⑴ 将抛物线解析式转化成顶点式，确定其顶点坐标；⑵ 保持抛物线的形状不变，将其顶点平移到处，具体平移方法如下：2.平移规律：在原有函数的基础上“值正右移，负左移；值正上移，负下移”．概括成八个字“左加右减，上加下减”． 要点诠释：⑴沿轴平移:向上（下）平移个单位，变成（或）⑵沿x 轴平移：向左（右）平移个单位，变成（或例1．将抛物线作下列移动，求得到的新抛物线的解析式．(1)向左平移2个单位，再向下平移3个单位；()2y a x h k =-+()h k ，2y ax =()h k，h k c bx ax y ++=2y m c bx ax y ++=2m c bx ax y +++=2m c bx ax y -++=2c bx ax y ++=2m c bx ax y ++=2c m x b m x a y ++++=)()(2c m x b m x a y +-+-=)()(222(1)3y x =-+(2)顶点不动，将原抛物线开口方向反向； (3)以x 轴为对称轴，将原抛物线开口方向反向．例2.二次函数的图象可以看作是二次函数的图象向 平移4个单位，再向 平移3个单位得到的．例3．将抛物线y=x 2﹣6x+5向上平移2个单位长度，再向右平移1个单位长度后，抛物线解析式为______________.例4．已知抛物线向上平移2个单位长度，再向右平移1个单位长度得到抛物线； （1）求出a ，h ，k 的值；（2）在同一直角坐标系中，画出与的图象； （3）观察的图象，当________时，y 随x 的增大而增大；当________时，函数y 有最________值，最________值是________；（4）观察的图象，你能说出对于一切的值，函数y 的取值范围吗？21(3)42y x =-+212y x=212y x =-2()y a x h k =-+2()y a x h k =-+212y x =-2()y a x h k =-+x x y =2()y a x h k =-+x例5．二次函数y 1=a （x ﹣2）2的图象与直线y 2交于A （0，﹣1），B （2，0）两点．（1）确定二次函数与直线AB 的解析式．（2）如图，分别确定当y 1＜y 2，y 1=y 2，y 1＞y 2时，自变量x 的取值范围．练习：1.抛物线的顶点坐标是（ ）A ．(2，-3)B ．(-2，3)C ．(2，3)D ．(-2，-3) 2.函数y=x 2+2x+1写成y=a(x －h)2+k 的形式是（ ）A.y=(x －1)2+2 B.y=(x －1)2+ C.y=(x －1)2－3 D.y=(x+2)2－1 3．抛物线y=x 2向左平移3个单位，再向下平移2个单位后，所得的抛物线表达式是( )2(2)3y x =-+-21212121212121A.y=(x+3)2－2 B.y=(x －3)2+2 C.y=(x －3)2－2 D.y=(x+3)2+2 4．把二次函数配方成顶点式为（ ）A ．B ．C ．D ．5．由二次函数，可知（ ）A ．其图象的开口向下B ．其图象的对称轴为直线C ．其最小值为1D ．当时，y 随x 的增大而增大6．（2015•泰安）在同一坐标系中，一次函数y=﹣mx+n 2与二次函数y=x 2+m 的图象可能是（ ）.A. B. C. D.7. 把二次函数的图象先向左平移2个单位，再向上平移4个单位，得到二次函数的图象．（1）试确定a 、h 、k 的值；（2）指出二次函数的开口方向，对称轴和顶点坐标，分析函数的增减性．21212121122--=x x y 2)1(-=x y 2)1(2--=x y 1)1(2++=x y 2)1(2-+=x y 22(3)1y x =-+3x =-3x <2()y a x h k =-+21(1)12y x =-+-2()y a x h k =-+二次函数与之间的相互关系：1.顶点式化成一般式从函数解析式我们可以直接得到抛物线的顶点(h ，k)，所以我们称为顶点式，将顶点式去括号，合并同类项就可化成一般式． 2.一般式化成顶点式．对照，可知，．∴ 抛物线的对称轴是直线，顶点坐标是． 要点诠释：1．抛物线的对称轴是直线，顶点坐标是2(0)y ax bx c a =++≠=-+≠2()(0)y a x h k a 2()y a x h k =-+2()y a x h k =-+2()y a x h k =-+2y ax bx c =++2222222b b b b y ax bx c a x x c a x x c a a a a ⎡⎤⎛⎫⎛⎫⎛⎫=++=++=++-+⎢⎥ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦22424b ac b a x a a -⎛⎫=++ ⎪⎝⎭2()y a x h k =-+2b h a=-244ac b k a -=2y ax bx c =++2bx a=-24,24b ac b a a ⎛⎫-- ⎪⎝⎭2y ax bx c =++2bx a=-，可以当作公式加以记忆和运用． 2．求抛物线的对称轴和顶点坐标通常用三种方法：配方法、公式法、代入法，这三种方法都有各自的优缺点，应根据实际灵活选择和运用．二次函数的图象的画法1.一般方法：列表、描点、连线；2.简易画法：五点定形法. 其步骤为：(1)先根据函数解析式，求出顶点坐标和对称轴，在直角坐标系中描出顶点M ，并用虚线画出对称轴．(2)求抛物线与坐标轴的交点，当抛物线与x 轴有两个交点时，描出这两个交点A 、B 及抛物线与y 轴的交点C ，再找到点C 关于对称轴的对称点D ，将A 、B 、C 、D 及M 这五个点按从左到右的顺序用平滑曲线连结起来． 要点诠释：当抛物线与x 轴只有一个交点或无交点时，描出抛物线与y 轴的交点C 及对称点D ，由C 、M 、D 三点可粗略地画出二次函数图象的草图；如果需要画出比较精确的图象，可再描出一对对称点A 、B ，然后顺次用平滑曲线连结五点，画出二次函数的图象，24,24b ac b a a ⎛⎫-- ⎪⎝⎭2y ax bx c =++2(0)y ax bx c a =++≠2y ax bx c =++二次函数的图象与性质2(0)=++≠y ax bx c aa<a>02.二次函数图象的特征与a 、b 、c 及b 2-4ac 的符号之间的关系20()y ax bx c a =++≠要点四、求二次函数的最大（小）值的方法如果自变量的取值范围是全体实数，那么函数在顶点处取得最大（或最小）值，即当时，．要点诠释：如果自变量的取值范围是x 1≤x ≤x 2，那么首先要看是否在自变量的取值范围x 1≤x ≤x 2内，若在此范围内，则当时，，若不在此范围内，则需要考虑函数在x 1≤x ≤x 2范围内的增减性，如果在此范围内，y 随x 的增大而增大，则当x ＝x 2时，；当x ＝x 1时，，如果在此范围内，y 随x 的增大而减小，则当x ＝x 1时，211=ax +bx +y c 最大值；当x ＝x 2时，222=ax +bx +y c 最小值，如果在此范围内，y 值有增有减，则需考察x ＝x 1，x ＝x 2，时y 值的情况．例1．求抛物线的对称轴和顶点坐标．例2.把一般式化为顶点式．2(0)y ax bx c a =++≠2b x a =-244ac b y a-=最值2ba-2bx a=-244ac b y a-=最值222y ax bx c =++最大值211y ax bx c =++最小值2bx a=-2142y x x =-+-2286y x x =-+-（1）写出其开口方向、对称轴和顶点D 的坐标；（2）分别求出它与y 轴的交点C ，与x 轴的交点A 、B 的坐标.例3．二次函数y=ax 2+bx+c （a≠0）的图象如图所示，下列结论：①2a+b=0；②a+c＞b ；③抛物线与x 轴的另一个交点为（3，0）；④abc ＞0．其中正确的结论是 （填写序号）．例4．求二次函数的最小值.例5.已知二次函数的图象过点P(2，1)．（1）求证：； （2）求bc 的最大值．例6. 抛物线与y 轴交于(0，3)点：211322y x x =++21y x bx c =+++24c b =--2(1)y x m x m =-+-+(1)求出m 的值并画出这条抛物线； (2)求它与x 轴的交点和抛物线顶点的坐标； (3)x 取什么值时，抛物线在x 轴上方？ (4)x 取什么值时，y 的值随x 值的增大而减小练习：1. 将二次函数化为的形式，结果为（ ）．A ．B ．C ．D ． 2．已知二次函数的图象，如图所示，则下列结论正确的是（ ）．A ．B ．C ．D ． 3．若二次函数配方后为，则b 、k 的值分别为（ ）．A ．0，5B ．0，1C ．-4，5D ．-4，14．抛物线的图象向右平移2个单位长度，再向下平移3个单位长度，所得图象的解析式为，则b 、c 的值为（ ）． A .b=2，c=2 B . b=2，c=0 C . b= -2，c= -1 D . b= -3，c=25.已知抛物线y=ax 2+bx+c 的对称轴为x=2，且经过点(3，0)，则a+b+223y x x =-+2()y x h k =-+2(1)4y x =++2(1)4y x =-+2(1)2y x =++2(1)2y x =-+2y ax bx c =++0a >0c <240b ac -<0a b c ++>25y x bx =++2(2)y x k =-+2y x bx c =++223y x x =--的值( )A. 等于0B.等于1C. 等于-1D. 不能确定6．如图，一次函数y1=x与二次函数y2=ax2+bx+c图象相交于P、Q 两点，则函数y=ax2+（b﹣1）x+c的图象可能是（）A. B. C. D.7.如图二次函数y=ax2+bx+c的图象开口向上，图象经过点(-1，2)和(1，0)且与y轴交于负半轴.第①问：给出四个结论：①a>0；②b>0；③c>0；④a+b+c=0其中正确的结论的序号是__________第②问：给出四个结论：①abc<0；②2a+b>0；③a+c=1；④a>1，其中正确的结论的序号是_________8．如图，在平面直角坐标系中，正方形OABC 的边长为4，顶点A 、C 分别在x 轴、y 轴的正半轴，抛物线y=﹣x 2+bx+c 经过B 、C 两点，点D 为抛物线的顶点，连接AC 、BD 、CD ． （1）求此抛物线的解析式．（2）求此抛物线顶点D 的坐标和四边形ABCD 的面积．用待定系数法求二次函数解析式1.二次函数解析式常见有以下几种形式 ：(1)一般式：2y ax bx c =++(a ，b ，c 为常数，a ≠0)；(2)顶点式：2()y a x h k =-+(a ，h ，k 为常数，a ≠0)； (3)交点式：12()()y a x x x x =--(1x ，2x 为抛物线与x 轴交点的横坐标，a ≠0)．2.确定二次函数解析式常用待定系数法，用待定系数法求二次函数解析式的步骤如下第一步，设：先设出二次函数的解析式，如2y ax bx c =++或2()y a x h k =-+，或12()()y a x x x x =--，其中a ≠0；第二步，代：根据题中所给条件，代入二次函数的解析式中，得到关于解析式中待定系数的方程(组)；第三步，解：解此方程或方程组，求待定系数； 第四步，还原：将求出的待定系数还原到解析式中． 要点诠释：在设函数的解析式时，一定要根据题中所给条件选择合适的形式：①当已知抛物线上的三点坐标时，可设函数的解析式为2y ax bx c =++；②当已知抛物线的顶点坐标或对称轴或最大值、最小值时．可设函数的解析式为2()y a x h k =-+；③当已知抛物线与x 轴的两个交点(x 1，0)，(x 2，0)时，可设函数的解析式为12()()y a x x x x =--．例1. 已知抛物线c bx ax y 2++=经过A ，B ，C 三点，当x ≥0时，其图象如图所示.求抛物线的解析式，写出顶点坐标.例2. 形状与抛物线y=2x 2﹣3x +1的图象形状相同，但开口方向不同，顶点坐标是（0，﹣5）的抛物线的关系式为 ． 例3. 已知抛物线c bx ax y 2++=的顶点坐标为（－1，4），与x 轴两交点间的距离为6，求此抛物线的函数关系式.例4.已知二次函数的图象如图所示，根据图中的数据，（1）求二次函数的解析式；（2）设此二次函数的顶点为P，求△ABP的面积．练习：1．已知二次函数的图象过（－1，－9）、（1，－3）和（3，－5）三点，求此二次函数的解析式.2．已知抛物线的顶点坐标为M（1，﹣2），且经过点N（2，3），求此二次函数的解析式．3．（2016•丹阳市校级模拟）抛物线的图象如图，则它的函数表达式是．当x时，y＞0．4．已知抛物线经过(3，5)，A(4，0)，B(-2，0)，且与y轴交于点C．(1)求二次函数解析式；(2)求△ABC的面积．5．如图，抛物线y=x2+bx+c与x轴交于A（﹣1，0），B（3，0）两点．（1）求该抛物线的解析式；（2）求该抛物线的对称轴以及顶点坐标；（3）设（1）中的抛物线上有一个动点P，当点P在该抛物线上滑动到什么位置时，满足S△PAB=8，并求出此时P点的坐标．。

第三章 函数的概念与性质典型易错题集易错点1．忽视定义域表示的是谁的范围【典型例题1】（2022·黑龙江让胡路·大庆中学高一月考）已知函数()y f x =的定义域为[)1,2-，则函数()2y f x =+的定义域为（ ）A ．[]3,0-B ．[)1,4C ．[)3,0-D ．(]1,4【错解D 】因为函数()y f x =的定义域为[)1,2-，即12x -≤<，对于()2y f x =+有124x ≤+<。

点评：本题错解在于将()y f x =中的“x ”与()2y f x =+中的“x ”当成同一个量，其次就是没有理解函数定义域的定义，表示的是“x ”的取值范围，本题错解反而求()2y f x =+中2x +的取值范围当做定义域。

【正解】C 【详解】因为函数()y f x =的定义域为[)1,2-， 所以122x -≤+<，解得30x -≤< 所以函数(2)y f x =+的定义域为[)3,0-. 故选：C.易错点2．解不等式问题时忽略讨论最高项系数是否为0【典型例题2】（2022·黑龙江让胡路·大庆中学高一月考）若函数()f x =的定义域为R ，则实数m 的取值范围是（ ） A ．()0,4 B ．[)0,4C ．[]0,4D ．(](),04,-∞+∞【错解A 】函数的定义域为R ，即不等式224mx mx ++>0的解集为R2416004m m m m >⎧⇒<<⎨⎩∆=-<点评：在解不等式问题时，本题错解漏了考虑最高项系数为0的情况，在解不等式问题时，需要特别注意最高项系数为0的情况。

【正解】B 【详解】函数的定义域为R ，即不等式224mx mx ++>0的解集为R（1）当0m =时，得到40>，显然不等式的解集为R ；（2）当0m <时，二次函数224y mx mx =++开口向下，函数值y 不恒大于0，故解集为R 不可能． （3）当0m >时，二次函数224y mx max =++开口向上，由不等式的解集为R ， 得到二次函数与x 轴没有交点，即24160m m ∆=-<，即(4)0m m -<，解得04m <<； 综上，a 的取值范围为[)0,4 故选：B易错点3．忽视函数的定义域【典型例题3】（2022·全国高一单元测试）若1)f x =+()f x 的解析式为（ ） A ．2()f x x x =-B ．2()(0)f x x x x =+≥C ．()2()1f x x x x =-≥D ．2()f x x x =+【错解A 】1)f x =+1t =，则2(1)x t =-， ∴22()(1)1f t t t t t =-+-=-，， ∴函数()f x 的解析式为2()f x x x =-．点评：本题错解在换元时没有考虑变量的取值范围，换元必换范围。

函数的单调性及典型习题一、函数的单调性1、定义：（1）设函数)(x f y =的定义域为A ，区间M ⊆A ，如果取区间M 中的任意两个值21,x x ,当改变量012>-=x x 时，都有0)()(12>-=x f x f ，那么就称函数)(x f y =在区间M 上是增函数，如图（1）当改变量012>-=x x 时，都有0)()(12<-=x f x f ，那么就称函数)(x f y =在区间M 上是减函数，如图（2）注意：函数单调性定义中的x 1,x 2有三个特征,一是任意性，二是有大小，三是同属于一个单调区间．2、巩固概念：1、定义的另一种表示方法如果对于定义域I 内某个区间D 上的任意两个自变量x 1,x 2,若0)()(2121>--x x x f x f 即0>∆∆x y ，则函数y=f(x)是增函数，若0)()(2121<--x x x f x f 即0<∆∆x y ，则函数y=f(x)为减函数。

判断题： ①已知1()f x x=因为(1)(2)f f -<，所以函数()f x 是增函数． ②若函数()f x 满足(2)(3)f f <则函数()f x 在区间[]2,3上为增函数．③若函数()f x 在区间(1,2]和(2,3)上均为增函数，则函数()f x 在区间(1,3)上为增函数．④因为函数1()f x x =在区间(,0),(0,)-∞+∞上都是减函数，所以1()f x x=在(,0)(0,)-∞⋃+∞上是减函数.通过判断题，强调几点：①单调性是对定义域内某个区间而言的，离开了定义域和相应区间就谈不上单调性．②对于某个具体函数的单调区间，可以是整个定义域(如一次函数)，可以是定义域内某个区间(如二次函数)，也可以根本不单调(如常函数)．③单调性是对定义域的某个区间上的整体性质，不能用特殊值说明问题。

④函数在定义域内的两个区间A ,B 上都是增（或减）函数，一般不能认为函数在A B ⋃上是增（或减）函数．熟记以下结论，可迅速判断函数的单调性．1．函数y ＝－f （x ）与函数y ＝f （x ）的单调性相反．2．当f （x ）恒为正或恒为负时，函数y ＝)(1x f 与y ＝f （x ）的单调性相反．3．在公共区间内，增函数＋增函数＝增函数，增函数－减函数＝增函数等3．判断函数单调性的方法（1）定义法．（2）直接法．运用已知的结论，直接得到函数的单调性，如一次函数，二次函数的单调性均可直接说出．（3）图象法．例1、证明函数x x f 1)(=在（0，+∞）是减函数．练习1：证明函数()f x =在()0,+∞上是增函数．例2、设函数f （x ）＝21+x ＋lg x x+-11,试判断f （x ）的单调性，并给出证明．例3、求下列函数的增区间与减区间(1)y ＝|x 2＋2x －3|(2)y (3)y ＝＝x xx x x 2221123-----+||例4、函数f(x)＝ax 2－(3a －1)x ＋a 2在[－1，＋∞]上是增函数，求实数a 的取值范围．例5、已知二次函数y ＝f(x)(x ∈R )的图像是一条开口向下且对称轴为x ＝3的抛物线，试比较大小：(1)f(6)与f(4)(2)f(2)f(15)与例6、 函数f (x)＝| x | 和g (x)＝x (2－x )的递增区间依次是 ( )A.] ,( ], ,(10-∞-∞B.) ,[ ], ,(∞+-∞10C.] ,( ), ,[10-∞∞+D.) ,[ ), ,[∞+∞+10例7、已知a 、b 是常数且a ≠0, f (x)bx ax +=2, 且0)2(f =, 并使方程x )x (f =有等根.(1) 求f (x )的解析式;(2) 是否存在实数m 、n )n m (<, 使f (x )的定义域和值域分别为]n ,m [和]n 2 ,m [2同步训练：一、选择题1．下列函数中，在区间（0，1）上为增函数的是A ．y ＝|x 2－1|B ．y ＝x 2C ．y ＝2x 2－x ＋1D ．y ＝|x |＋12．如果奇函数f （x ）在区间［3，7］上是增函数且最小值为5，那么f （x ）在区间［－7，－3］上是A.增函数且最小值为－5 B ．增函数且最大值为－5C ．减函数且最小值为－5D ．减函数且最大值为－53．若函数解析式为y ＝f （x ），则下列判断正确的是A 、若f （x ）在（－∞,0）和（0，＋∞）上均是增函数，则f （x ）在（－∞,0）∪（0,＋∞）上也是增函数B 、若f （x ）在（－∞,0）和（0，＋∞）上均是减函数，则f （x ）在（－∞，0）∪（0，＋∞）上也是减函数C 、若f （x ）是偶函数，且在（0，＋∞）上是增函数，则f （x ）在（－∞，0）上也是增函数D 、若f （x ）是奇函数，且在（0，＋∞）上是增函数，则f （x ）在（－∞,0）上是增函数二、填空题4．已知函数y ＝－x 2＋2x ＋1在区间［－3，a ］上是增函数，则a 的取值范围是______________5．设函数y ＝f （x ）是定义在（－1，1）上的增函数，则函数y ＝f （x 2－1）的单调递减区间是______________ 6．若函数y ＝ax ,y ＝－x b在（0，＋∞）上都是减函数，则函数y ＝ax 2＋bx 在（0,＋∞）上是________（填单调性）．三、解答题已知函数f （x ）的定义域为R ，且满足f （－x ）＝)(1x f ＞0，又g （x ）＝f （x ）＋ c （c 为常数）在［a ,b ］（a ＜b ＝上是单调递减函数，判断并证明g （x ）在［－b ,－a ］上的增减性．课后巩固：1、利用函数单调性定义证明函数f(x)＝－x 3＋1在(－∞，＋∞)上是减函数．2、.设)(x f 是定义在R 上的函数，对m 、R n ∈恒有)()()(n f m f n m f ⋅=+，且当0>x 时，1)(0<<x f 。

1．函数与映射(1)函数的定义域、值域在函数y＝f(x)，x∈A中，其中所有x组成的集合A称为函数y＝f(x)的定义域；将所有y组成的集合叫做函数y＝f(x)的值域．(2)函数的三要素：定义域、对应关系和值域．(3)函数的表示法表示函数的常用方法有解析法、图象法和列表法．3．分段函数若函数在其定义域的不同子集上，因对应关系不同而分别用几个不同的式子来表示，这种函数称为分段函数．分段函数的定义域等于各段函数的定义域的并集，其值域等于各段函数的值域的并集，分段函数虽由几个部分组成，但它表示的是一个函数．4．常见函数定义域的求法【思考辨析】判断下面结论是否正确(请在括号中打“√”或“×”)(1)对于函数f ：A →B ，其值域是集合B .( × )(2)若两个函数的定义域与值域相同，则这两个函数是相等函数．( × ) (3)映射是特殊的函数．( × )(4)若A ＝R ，B ＝{x |x >0}，f ：x →y ＝|x |，其对应是从A 到B 的映射．( × ) (5)分段函数是由两个或几个函数组成的．( × )1．下列函数中，不满足．．．f (2x )＝2f (x )的是( ) A ．f (x )＝|x | B ．f (x )＝x －|x | C ．f (x )＝x ＋1 D ．f (x )＝－x答案 C解析 将f (2x )表示出来，看与2f (x )是否相等． 对于A ，f (2x )＝|2x |＝2|x |＝2f (x )； 对于B ，f (2x )＝2x －|2x |＝2(x －|x |)＝2f (x )； 对于C ，f (2x )＝2x ＋1≠2f (x )； 对于D ，f (2x )＝－2x ＝2f (x )，故只有C 不满足f (2x )＝2f (x )，所以选C. 2．函数f (x )＝1(log 2x )2－1的定义域为( )A.⎝⎛⎭⎫0，12 B ．(2，＋∞) C.⎝⎛⎭⎫0，12∪(2，＋∞) D.⎝⎛⎦⎤0，12∪[2，＋∞) 答案 C解析 要使函数f (x )有意义，需使⎩⎪⎨⎪⎧x >0，(log 2x )2－1>0，解得x >2或0<x <12.故f (x )的定义域为⎝⎛⎭⎫0，12∪(2，＋∞)． 3．(2015·课标全国Ⅱ)设函数f (x )＝⎩⎪⎨⎪⎧1＋log 2(2－x )，x ＜1，2x －1， x ≥1，则f (－2)＋f (log 212)等于( )A ．3B ．6C ．9D ．12 答案 C解析 因为－2＜1，log 212＞log 28＝3＞1，所以f (－2)＝1＋log 2[2－(－2)]＝1＋log 24＝3，f (log 212)＝22log 121－＝22log 12×2－1＝12×12＝6，故f (－2)＋f (log 212)＝3＋6＝9，故选C.4．(教材改编)若函数y ＝f (x )的定义域为M ＝{x |－2≤x ≤2}，值域为N ＝{y |0≤y ≤2}，则函数y ＝f (x )的图象可能是( )答案 B解析 A 中函数定义域不是[－2,2]，C 中图象不表示函数，D 中函数值域不是[0,2]，故选B. 5．给出下列四个命题：①函数是其定义域到值域的映射；②f (x )＝x －2＋2－x 是函数；③函数y ＝2x (x ∈N )的图象是一条直线；④函数的定义域和值域一定是无限集合． 其中真命题的序号有________． 答案 ①②解析 对于①函数是映射，但映射不一定是函数；对于②f (x )是定义域为{2}，值域为{0}的函数；对于③函数y ＝2x (x ∈N )的图象不是一条直线；对于④函数的定义域和值域不一定是无限集合.题型一 函数的概念例1 有以下判断：①f (x )＝|x |x 与g (x )＝⎩⎪⎨⎪⎧1 (x ≥0)－1 (x <0)表示同一函数；②函数y ＝f (x )的图象与直线x ＝1的交点最多有1个； ③f (x )＝x 2－2x ＋1与g (t )＝t 2－2t ＋1是同一函数；④若f (x )＝|x －1|－|x |，则f ⎝⎛⎭⎫f ⎝⎛⎭⎫12＝0. 其中正确判断的序号是________． 答案 ②③解析 对于①，由于函数f (x )＝|x |x 的定义域为{x |x ∈R 且x ≠0}，而函数g (x )＝⎩⎨⎧1 (x ≥0)－1 (x <0)的定义域是R ，所以二者不是同一函数；对于②，若x ＝1不是y ＝f (x )定义域内的值，则直线x ＝1与y ＝f (x )的图象没有交点，如果x ＝1是y ＝f (x )定义域内的值，由函数定义可知，直线x ＝1与y ＝f (x )的图象只有一个交点，即y ＝f (x )的图象与直线x ＝1最多有一个交点；对于③，f (x )与g (t )的定义域、值域和对应关系均相同，所以f (x )和g (t )表示同一函数；对于④，由于f ⎝⎛⎭⎫12＝⎪⎪⎪⎪12－1－⎪⎪⎪⎪12＝0，所以f ⎝⎛⎭⎫f ⎝⎛⎭⎫12＝f (0)＝1. 综上可知，正确的判断是②③.思维升华函数的值域可由定义域和对应关系唯一确定；当且仅当定义域和对应关系都相同的函数才是同一函数．值得注意的是，函数的对应关系是就结果而言的(判断两个函数的对应关系是否相同，只要看对于函数定义域中的任意一个相同的自变量的值，按照这两个对应关系算出的函数值是否相同)．(1)下列四组函数中，表示同一函数的是()A．y＝x－1与y＝(x－1)2B．y＝x－1与y＝x－1 x－1C．y＝4lg x与y＝2lg x2D．y＝lg x－2与y＝lg x100(2)下列所给图象是函数图象的个数为()A ．1B ．2C ．3D ．4答案 (1)D (2)B解析 (1)A 中两函数对应关系不同；B 、C 中的函数定义域不同，答案选D.(2)①中当x >0时，每一个x 的值对应两个不同的y 值，因此不是函数图象，②中当x ＝x 0时，y 的值有两个，因此不是函数图象，③④中每一个x 的值对应唯一的y 值，因此是函数图象，故选B.题型二 函数的定义域命题点1 求给定函数解析式的定义域 例2 (1)函数f (x )＝1－2x ＋1x ＋3的定义域为( ) A ．(－3,0] B ．(－3,1]C ．(－∞，－3)∪(－3,0]D ．(－∞，－3)∪(－3,1](2)函数f (x )＝lg (x ＋1)x －1的定义域是( )A ．(－1，＋∞)B ．[－1，＋∞)C ．(－1,1)∪(1，＋∞)D ．[－1,1)∪(1，＋∞)答案 (1)A (2)C解析 (1)由题意知⎩⎪⎨⎪⎧1－2x≥0，x ＋3>0，解得－3<x ≤0，所以函数f (x )的定义域为(－3,0]，故选A.(2)要使函数f (x )＝lg (x ＋1)x －1有意义，需满足x ＋1>0且x －1≠0，得x >－1，且x ≠1，故选C.命题点2 求抽象函数的定义域例3 (1)若函数y ＝f (x )的定义域是[1,2 016]，则函数g (x )＝f (x ＋1)x －1的定义域是( )A ．[0,2 015]B ．[0,1)∪(1,2 015]C ．(1,2 016]D ．[－1,1)∪(1,2 015](2)若函数f (x 2＋1)的定义域为[－1,1]，则f (lg x )的定义域为( ) A ．[－1,1] B ．[1,2] C ．[10,100] D ．[0，lg 2]答案 (1)B (2)C解析 (1)令t ＝x ＋1，则由已知函数的定义域为[1，2 016]，可知1≤t ≤2 016.要使函数f (x ＋1)有意义，则有1≤x ＋1≤2 016，解得0≤x ≤2 015，故函数f (x ＋1)的定义域为[0,2 015]．所以使函数g (x )有意义的条件是⎩⎪⎨⎪⎧0≤x ≤2 015，x －1≠0，解得0≤x <1或1<x ≤2 015.故函数g (x )的定义域为[0,1)∪(1,2 015]．故选B.(2)因为f (x 2＋1)的定义域为[－1,1]，则－1≤x ≤1，故0≤x 2≤1，所以1≤x 2＋1≤2.因为f (x 2＋1)与f (lg x )是同一个对应关系，所以1≤lg x ≤2，即10≤x ≤100，所以函数f (lg x )的定义域为[10,100]．故选C.命题点3 已知定义域求参数范围例4 若函数f (x )R ，则a 的取值范围为________． 答案 [－1,0]解析 因为函数f (x )的定义域为R ，所以222＋－x ax a－1≥0对x ∈R 恒成立，即222＋－x ax a≥20，x 2＋2ax －a ≥0恒成立，因此有Δ＝(2a )2＋4a ≤0，解得－1≤a ≤0. 思维升华 简单函数定义域的类型及求法(1)已知函数的解析式，则构造使解析式有意义的不等式(组)求解． (2)抽象函数：①无论是已知定义域还是求定义域，均是指其中的自变量x 的取值集合； ②对应f 下的范围一致．(3)已知定义域求参数范围，可将问题转化，列出含参数的不等式(组)，进而求范围．(1)已知函数f (x )的定义域是[0,2]，则函数g (x )＝f (x ＋12)＋f (x －12)的定义域是________．(2)函数y ＝ln (x ＋1)－x 2－3x ＋4的定义域为___________________________．答案 (1)[12，32] (2)(－1,1)解析 (1)因为函数f (x )的定义域是[0,2]，所以函数g (x )＝f (x ＋12)＋f (x －12)中的自变量x 需要满足⎩⎨⎧0≤x ＋12≤2，0≤x －12≤2，解得：12≤x ≤32，所以函数g (x )的定义域是[12，32]．(2)由⎩⎪⎨⎪⎧x ＋1>0，－x 2－3x ＋4>0，得－1<x <1.题型三 求函数解析式例5 (1)已知f (2x＋1)＝lg x ，则f (x )＝________.(2)已知f (x )是一次函数，且满足3f (x ＋1)－2f (x －1)＝2x ＋17，则f (x )＝________. (3)已知函数f (x )的定义域为(0，＋∞)，且f (x )＝2f (1x )·x －1，则f (x )＝________.答案 (1)lg2x －1(x >1) (2)2x ＋7 (3)23x ＋13解析 (1)(换元法)令t ＝2x ＋1(t >1)，则x ＝2t －1，∴f (t )＝lg2t －1，即f (x )＝lg 2x －1(x >1)． (2)(待定系数法) 设f (x )＝ax ＋b (a ≠0)，则3f (x ＋1)－2f (x －1)＝3ax ＋3a ＋3b －2ax ＋2a －2b ＝ax ＋5a ＋b ， 即ax ＋5a ＋b ＝2x ＋17不论x 为何值都成立，∴⎩⎪⎨⎪⎧ a ＝2，b ＋5a ＝17，解得⎩⎪⎨⎪⎧a ＝2，b ＝7，∴f (x )＝2x ＋7. (3)(消去法)在f (x )＝2f (1x )x －1中，用1x 代替x ，得f (1x )＝2f (x )1x－1，将f (1x )＝2f (x )x －1代入f (x )＝2f (1x )x －1中，可求得f (x )＝23x ＋13.思维升华 函数解析式的求法(1)待定系数法：若已知函数的类型(如一次函数、二次函数)，可用待定系数法； (2)换元法：已知复合函数f (g (x ))的解析式，可用换元法，此时要注意新元的取值范围； (3)配凑法：由已知条件f (g (x ))＝F (x )，可将F (x )改写成关于g (x )的表达式，然后以x 替代g (x )，便得f (x )的解析式；(4)消去法：已知f (x )与f ⎝⎛⎭⎫1x 或f (－x )之间的关系式，可根据已知条件再构造出另外一个等式组成方程组，通过解方程组求出f (x )．(1)已知f (x ＋1)＝x ＋2x ，则f (x )＝________.(2)定义在R 上的函数f (x )满足f (x ＋1)＝2f (x )．若当0≤x ≤1时，f (x )＝x (1－x )，则当－1≤x ≤0时，f (x )＝________.(3)定义在(－1,1)内的函数f (x )满足2f (x )－f (－x )＝lg(x ＋1)，则f (x )＝__________________. 答案 (1)x 2－1(x ≥1) (2)－12x (x ＋1)(3)23lg(x ＋1)＋13lg(1－x ) (－1<x <1) 解析 (1)设x ＋1＝t (t ≥1)，则x ＝t －1. 代入f (x ＋1)＝x ＋2x ， 得f (t )＝t 2－1(t ≥1)， ∴f (x )＝x 2－1(x ≥1)．(2)当－1≤x ≤0时，0≤x ＋1≤1， 由已知f (x )＝12f (x ＋1)＝－12x (x ＋1)．(3)当x ∈(－1,1)时，有2f (x )－f (－x )＝lg(x ＋1)．① 以－x 代替x 得，2f (－x )－f (x )＝lg(－x ＋1)．② 由①②消去f (－x )得，f (x )＝23lg(x ＋1)＋13lg(1－x )，x ∈(－1,1)．2．分类讨论思想在函数中的应用典例 (1)(2014·课标全国Ⅰ)设函数f (x )＝⎩⎪⎨⎪⎧e x －1，x <1，13x ，x ≥1，则使得f (x )≤2成立的x 的取值范围是________．(2)(2015·山东)设函数f (x )＝⎩⎪⎨⎪⎧3x －1，x ＜1，2x ，x ≥1，则满足f (f (a ))＝2f (a )的a 的取值范围是( )A.⎣⎡⎦⎤23，1 B ．[0,1] C.⎣⎡⎭⎫23，＋∞D ．[1, ＋∞)解析 (1)当x <1时，e x －1≤2，解得x ≤1＋ln 2， ∴x <1.当x ≥1时，13x ≤2，解得x ≤8，∴1≤x ≤8. 综上可知x ∈(－∞，8]． (2)由f (f (a ))＝2f (a )得，f (a )≥1.当a <1时，有3a －1≥1，∴a ≥23，∴23≤a <1.当a ≥1时，有2a ≥1，∴a ≥0，∴a ≥1. 综上，a ≥23，故选C.答案 (1)(－∞，8] (2)C温馨提醒 (1)求分段函数的函数值，首先要确定自变量的范围，然后选定相应关系式代入求解．(2)当给出函数值或函数值的取值范围求自变量的值或自变量的取值范围时，应根据每一段解析式分别求解，但要注意检验所求自变量的值或取值范围是否符合相应段的自变量的值或取值范围．(3)当自变量含参数或范围不确定时，要根据定义域分成的不同子集进行分类讨论．[方法与技巧]1．在判断两个函数是否为同一函数时，要紧扣两点：一是定义域是否相同；二是对应关系是否相同．2．定义域优先原则：函数定义域是研究函数的基础依据，对函数性质的讨论，必须在定义域上进行．3．函数解析式的几种常用求法：待定系数法、换元法、配凑法、消去法．4．分段函数问题要分段求解．[失误与防范]1．复合函数f[g(x)]的定义域也是解析式中x的范围，不要和f(x)的定义域相混．2．分段函数无论分成几段，都是一个函数，求分段函数的函数值，如果自变量的范围不确定，要分类讨论．A组专项基础训练(时间：30分钟)1．下列各组函数中，表示同一函数的是()A．f(x)＝x，g(x)＝(x)2B．f(x)＝x2，g(x)＝(x＋1)2C．f(x)＝x2，g(x)＝|x|D．f(x)＝0，g(x)＝x－1＋1－x答案C解析在A中，定义域不同，在B中，解析式不同，在D中，定义域不同．2．已知函数f(x)＝11－x2的定义域为M，g(x)＝ln(1＋x)的定义域为N，则M∪(∁R N)等于()A ．{x |x <1}B ．{x |x ≥1}C ．∅D ．{x |－1≤x <1}答案 A解析 M ＝(－1,1)，N ＝(－1，＋∞)，故M ∪(∁R N )＝{x |x <1}，故选A.3．已知f (x )为偶函数，且当x ∈[0,2)时，f (x )＝2sin x ，当x ∈[2，＋∞)时，f (x )＝log 2x ，则f ⎝⎛⎭⎫－π3＋f (4)等于( )A ．－3＋2B ．1C ．3 D.3＋2 答案 D解析 因为f ⎝⎛⎭⎫－π3＝f ⎝⎛⎭⎫π3＝2sin π3＝3， f (4)＝log 24＝2，所以f ⎝⎛⎭⎫－π3＋f (4)＝3＋2. 4．若二次函数g (x )满足g (1)＝1，g (－1)＝5，且图象过原点，则g (x )的解析式为( ) A ．g (x )＝2x 2－3x B ．g (x )＝3x 2－2x C ．g (x )＝3x 2＋2x D ．g (x )＝－3x 2－2x答案 B解析 (待定系数法)设g (x )＝ax 2＋bx ＋c (a ≠0)， ∵g (1)＝1，g (－1)＝5，且图象过原点， ∴⎩⎪⎨⎪⎧a ＋b ＋c ＝1，a －b ＋c ＝5，c ＝0，解得⎩⎪⎨⎪⎧a ＝3，b ＝－2，c ＝0，∴g (x )＝3x 2－2x ，选B.5．已知函数f (x )满足f (2x ＋|x |)＝log 2x |x |，则f (x )的解析式是( )A ．f (x )＝log 2xB ．f (x )＝－log 2xC ．f (x )＝2－x D ．f (x )＝x －2答案 B解析 根据题意知x >0，所以f (1x )＝log 2x ，则f (x )＝log 21x ＝－log 2x .6．已知函数f (x )＝log 21x ＋1，f (a )＝3，则a ＝________.答案 －78解析 由题意可得log 21a ＋1＝3，所以1a ＋1＝23，解得a ＝－78.7．已知函数y ＝f (2x )的定义域为[－1,1]，则y ＝f (log 2x )的定义域是________． 答案 [2，4]解析 ∵函数f (2x )的定义域为[－1,1]， ∴－1≤x ≤1，∴12≤2x ≤2.∴在函数y ＝f (log 2x )中，12≤log 2x ≤2，∴2≤x ≤4.8．(2015·浙江)已知函数f (x )＝⎩⎪⎨⎪⎧x ＋2x －3，x ≥1，lg (x 2＋1)，x ＜1，则f (f (－3))＝________，f (x )的最小值是________． 答案 0 22－3解析 ∵f (－3)＝lg [(－3)2＋1]＝lg 10＝1， ∴f (f (－3))＝f (1)＝0，当x ≥1时，f (x )＝x ＋2x －3≥22－3，当且仅当x ＝2时，取等号，此时f (x )min ＝22－3<0；当x ＜1时，f (x )＝lg(x 2＋1)≥lg 1＝0，当且仅当x ＝0时，取等号，此时f (x )min ＝0.∴f (x )的最小值为22－3.9．已知f (x )是二次函数，若f (0)＝0，且f (x ＋1)＝f (x )＋x ＋1，求函数f (x )的解析式． 解 设f (x )＝ax 2＋bx ＋c (a ≠0)，又f (0)＝0， ∴c ＝0，即f (x )＝ax 2＋bx . 又∵f (x ＋1)＝f (x )＋x ＋1.∴a (x ＋1)2＋b (x ＋1)＝ax 2＋bx ＋x ＋1. ∴(2a ＋b )x ＋a ＋b ＝(b ＋1)x ＋1，∴⎩⎪⎨⎪⎧2a ＋b ＝b ＋1，a ＋b ＝1，解得⎩⎨⎧a ＝12，b ＝12.∴f (x )＝12x 2＋12x .10．根据如图所示的函数y ＝f (x )的图象，写出函数的解析式．解 当－3≤x <－1时，函数y ＝f (x )的图象是一条线段(右端点除外)，设f (x )＝ax ＋b (a ≠0)，将点(－3,1)，(－1，－2)代入，可得f (x )＝－32x －72；当－1≤x <1时，同理可设f (x )＝cx ＋d (c ≠0)， 将点(－1，－2)，(1,1)代入，可得f (x )＝32x －12；当1≤x <2时，f (x )＝1.所以f (x )＝⎩⎨⎧－32x －72，－3≤x <－1，32x －12，－1≤x <1，1，1≤x <2.B 组 专项能力提升 (时间：20分钟)11．若函数y ＝ax ＋1ax 2＋2ax ＋3的定义域为R ，则实数a 的取值范围是________．答案 [0,3)解析 因为函数y ＝ax ＋1ax 2＋2ax ＋3的定义域为R ，所以ax 2＋2ax ＋3＝0无实数解，即函数y ＝ax 2＋2ax ＋3的图象与x 轴无交点．当a ＝0时，函数y ＝13的图象与x 轴无交点；当a ≠0时，则Δ＝(2a )2－4·3a <0，解得0<a <3. 综上所述，a 的取值范围是[0,3)． 12．若函数f (x )＝x 2－1x 2＋1，则(1)f (2)f (12)＝________；(2)f (3)＋f (4)＋…＋f (2 017)＋f (13)＋f (14)＋…＋f (12 017)＝________.答案 (1)－1 (2)0解析 (1)∵f (x )＋f (1x )＝x 2－1x 2＋1＋1－x21＋x 2＝0，∴f (x )f (1x )＝－1(x ≠±1)，∴f (2)f (12)＝－1. (2)∵f (3)＋f (13)＝0，f (4)＋f (14)＝0，…，f (2 017)＋f (12 017)＝0，∴f (3)＋f (4)＋…＋f (2 017)＋f (13)＋…＋f (12 017)＝0.13．已知函数f (x )＝4|x |＋2－1的定义域是[a ，b ]，(a ，b ∈Z )，值域是[0,1]，则满足条件的整数数对(a ，b )共有________个． 答案 5解析 由0≤4|x |＋2－1≤1，即1≤4|x |＋2≤2，得0≤|x |≤2，满足条件的整数数对有(－2,0)，(－2,1)，(－2,2)，(0,2)，(－1,2)，共5个．14．具有性质：f ⎝⎛⎭⎫1x ＝－f (x )的函数，我们称为满足“倒负”变换的函数，下列函数：①y ＝x －1x ；②y ＝x ＋1x ；③y ＝⎩⎪⎨⎪⎧x ，0<x <1，0，x ＝1，－1x，x >1.其中满足“倒负”变换的函数是________．答案 ①③解析 对于①，f (x )＝x －1x ，f ⎝⎛⎭⎫1x ＝1x －x ＝－f (x )，满足；对于②，f ⎝⎛⎭⎫1x ＝1x ＋x ＝f (x )，不满足；对于③，f ⎝⎛⎭⎫1x ＝⎩⎪⎨⎪⎧1x ，0<1x<1，0，1x＝1，－x ，1x>1，即f ⎝⎛⎭⎫1x ＝⎩⎪⎨⎪⎧1x，x >1，0，x ＝1，－x ，0<x <1，故f ⎝⎛⎭⎫1x ＝－f (x )，满足．综上可知，满足“倒负”变换的函数是①③.15．如图1是某公共汽车线路收支差额y 元与乘客量x 的图象．(1)试说明图1上点A 、点B 以及射线AB 上的点的实际意义；(2)由于目前本条线路亏损，公司有关人员提出了两种扭亏为赢的建议，如图2、3所示．你能根据图象，说明这两种建议的意义吗？ (3)此问题中直线斜率的实际意义是什么？ (4)图1、图2、图3中的票价分别是多少元？解(1)点A表示无人乘车时收支差额为－20元，点B表示有10人乘车时收支差额为0元，线段AB上的点表示亏损，AB延长线上的点表示赢利．(2)图2的建议是降低成本，票价不变，图3的建议是提高票价．(3)斜率表示票价．(4)图1、2中的票价是2元．图3中的票价是4元．。

专题19 函数、一次函数、正比例函数之十大考点【考点导航】目录【典型例题】 (1)【考点一函数的概念】 (1)【考点二用表格表示变量间的关系】 (2)【考点三用关系式表示变量间的关系】 (3)【考点四用图象表示变量间的关系】 (4)【考点五动点问题的函数图象】 (6)【考点六一次函数的识别】 (7)【考点七根据一次函数的定义求参数】 (7)【考点八求一次函数自变量或函数值】 (8)【考点九根据正比例函数的定义求函数的表达式】 (8)【考点十列一次函数解析式并求值】 (9)【过关检测】 (10)【典型例题】【考点一函数的概念】例题：（23·24上·合肥·阶段练习）下列各曲线中，能表示y是x的函数的是（）A．B．C．D．【变式训练】1．（23·24上·蚌埠·阶段练习）下列图象中，表示y是x的函数的是（）A．B．C．D．2．（22·23上·长沙·开学考试）下列曲线中不能表示y是x的函数的是（）A．B．C．D．【考点二用表格表示变量间的关系】例题：小颖在网上获取了声音在空气中传播的速度y与空气温度x的关系的一些数据并制成如下表格，则下A．在这个变化中，自变量是温度，因变量是声速-︒︒范围内，温度越高，声速越快B．在20C~30CC．温度每开高10C︒，声速提高8m/sD．当空气温度为10C︒时，声音在5s内可传传1680m【变式训练】下列说法一定错误的是（）A．x与y都是变量，且x是自变量，y是x的函数B．弹簧不挂重物时的长度为0cmC．物体质量每增加1kg，弹簧长度y增加0.5cmD ．所挂物体质量为7kg 时，弹簧长度为13.5cm2．甲、乙两地打 需付的 费y （元）随通话时间t （分）的变化而变化，试根据下表列出的几组数据回(1)直接写出 费y （元）与通话时间t （分）之间的关系式； (2)若小明通话10分，则需付 费多少元？ (3)若小明某次通话后，需付 费 4.8元，则小明通话多少分？【考点三 用关系式表示变量间的关系】例题：（23·24八年级上·广西崇左·阶段练习）在一次实验中，小明把一根弹簧的上端固定，在其下端悬挂物(1)上表反映了哪两个变量之间的关系？哪个是自变量？哪个是因变量？ (2)当所挂物体重量为4kg 时，弹簧的长度是多少？不挂重物呢？ (3)直接写出长度y 与所挂物体的质量x 的函数关系式； (4)当弹簧的长度是30cm 时，所挂物体的质量是多少？【变式训练】1．（23·24八年级上·安徽合肥·期中）已知等腰三角形的周长为12cm ，若底边长为cm y ，一腰长为cm x ． (1)写出y 与x 的函数关系式．（不要求写出自变量的取值范围） (2)求出当5x 时y 的值．若这批水果在运输（包括装卸）过程中的损耗为2000元/时，设A ，B 两市间的距离为x 千米．(1)如果用123W W W ，，分别表示使用飞机、火车、汽车运输时的总支出费用（包括损耗），分别求出123W W W ，，与x 间的关系式．(2)当1000x 千米时，采用哪种运输方式能使运输时的总支出费用最小？【考点四 用图象表示变量间的关系】例题：以下四种情境分别描述了两个变量之间的关系：甲：运动员推铅球时，铅球的高度与水平距离的关系； 乙：食堂需购买一批餐具，支付费用与购餐具的数量的关系；丙：一长方形水池里原有部分水，再匀速往里注水，水池中水面的高度与注水时间的关系； 丁：小明周末离家去看电影，结束后，原速度原路返回，小明离家的距离与时间的关系． 用下面的图象刻画上述情境，排序正确的是（ ） A ．③①④② B ．④③①②C ．④①③②D ．③①②④【变式训练】1．某车间的甲、乙两名工人分别同时生产同一种零件，他们一天生产零件的个数y 与生产时间t 的关系如图所示．(1)根据图象填空：①甲、乙两人中，先完成一天的生产任务;在生产过程中，因机器故障停止生产小时;②当t 时，甲、乙生产的零件个数相等;(2)谁在哪一段时间内的生产速度最快，求该段时间内，他每小时生产零件的个数．2．风是地球上的一种空气流动现象，一般是由太阳辐射热引起的．风的测量多用电接风向风速计、轻便风速表、达因式风向风速计，以及用于测量农田中微风的热球微风仪等仪器进行．小力同学使用轻便风速表观测了某天连续12个小时风力变化的情况，并绘制下图(1)上图反映了哪两个变量之间的关系？自变量是什么？因变量是什么？(2)A，B两点表示什么？(3)什么时间范围内风力最大？此时风力为多少？(4)简要描述8—12时风力变化的情况．【考点五 动点问题的函数图象】例题：（22·23下·宜春·期末）如图1，四边形ABCD 中，AB CD ∥，90B ，AC AD =．动点Ｐ从点Ｂ出发沿折线B A D C ---方向以1单位/秒的速度匀速运动，在整个运动过程中，BCP 的面积S 与运动时间t （秒）的函数图象如图2所示，则AC 等于（ ）【变式训练】1．（22·23上·榆林·期中）如图1，在矩形ABCD 中，动点R 从点B 出发，沿B C D A →→→方向运动至点A 处停止．设点R 运动的路程为x ，ABR △的面积为y ，如果y 关于x 的函数图像如图2所示，则矩形ABCD 的面积是（ ）A ．35B ．24C ．60D ．842．（23·24上·崇左·阶段练习）如图，正方形ABCD 的边长为4，P 为正方形边上一动点，运动路线是A B C D A →→→→，设P 点经过的路程为x ，以点A 、P 、B 为顶点的三角形的面积是y ，则下列图象能大致反映y 与x 的函数关系的是（）A ．B ．C ．D ．【考点六 一次函数的识别】21yx【变式训练】；③41y x =-+⑤y kx b =+（,k b 为常数）， 其中一次函数的个数是（ ）221y x x =-+．是一次函数的有（ ）A ．1个B ．2个C ．3个D ．4个【考点七 根据一次函数的定义求参数】【变式训练】例题：（23·24上·合肥·阶段练习）若点(m ，)n 在一次函数35y x =-的图象上，则代数式1023m n +-的值【变式训练】【考点九 根据正比例函数的定义求函数的表达式】例题：（2023春·甘肃庆阳·八年级校考阶段练习）已知y 与2x +成正比例，且当1x =时，6y =． (1)求y 与x 之间的函数关系式； (2)若点(1)m ，在这个函数图象上，求m ．【变式训练】例题：（22·23八年级上·广东·单元测试）某公交公司的16路公交车每月的支出费用为4000元，每月的乘车人数x （人)与这趟公交车每月的利润（利润=收入费用-支出费用）y （元)的变化关系如表所示（每位乘请回答下列问题：(1)自变量为 ，因变量为 ； (2)y 与x 之间的关系式是 ；(3)当每月乘车人数为4000人时，每月利润为多少元？【变式训练】1．（21·22八年级·全国·假期作业）“五一”假期，小明一家将随团到某风景区旅游，集体门票的收费标准是：25人以内（含25人），每人30元；超过25人时，超过部分每人20元． (1)写出应收门票费y （元）与游览人数x （人）之间的关系式；(2)若小明一家所在的旅游团购门票花了1250元，则该旅游团共有多少人．2．（21·22八年级上·全国·课时练习）如图，甲、乙两地相距100km ，现有一列火车从乙地出发，以80km/h 的速度向丙地行驶．设()h x 表示火车行驶的时间，()km y 表示火车与甲地的距离．（1）写出y与x之间的关系式，并判断y是否为x的一次函数；x=时，求y的值．（2）当0.5【过关检测】一、单选题1．（23·24八年级上·甘肃白银·期中）下列函数中是一次函数的是（）2y x23七年级下3．（23·24八年级上·安徽合肥·期中）下列表示的图象，y是x的函数的是（）A．B．C．D．若施工队每天完成的施工量都相同，则下列说法错误的是（）A ．随着施工时间的逐渐增大，累计完成施工量也逐渐增大B ．若累计完成施工量为330米，则施工时间为10天C ．当施工时间为9天时，累计完成施工量为270米D ．施工时间每增加1天，累完成施工量就增加30米5．（21·22下·荆州·期末）若点(,)P a b 在函数34y x =-的图象上，则代数式625a b --的值等于（ ） A ．13- B ．3 C ．9- D ．1-6．（23·24八年级上·广东深圳·期中）小强所在学校离家距离为2千米，某天他放学后骑自行车回家，先骑了5分钟后，因故停留10分钟，再继续骑了5分钟到家，下面哪一个图象能大致描述他回家过程中离家的距离s (千米)与所用时间t (分)之间的关系( ) A ．B ． C ． D ．二、填空题请写出y 与x 的函数关系式为 ．（不需要考虑自变量x 的取值范围）11．（22·23八年级下·安徽马鞍山·期末）新定义：函数图象上任意一点(),P x y ，y x -称为该点的“坐标差”，函数图像上所有点的“坐标差”的最大值称为该函数的“特征值”，一次函数23y x =+（21x -≤≤）的“特征值”是 ．12．（19·20七年级下·全国·课时练习）水池有两个进水口，一个出水口，一个水口在单位时间内的进、出水量如图（a ）、（b ）所示，某天从0点到6点，该水池的蓄水量如图（c ）所示，给出以下3个论断：①0点到3点只进水不出水；②3点到4点不进水只出水；③4点到6点一定不进水不出水．则正确的论断是 ．（填上所有正确论断的序号）三、解答题13．（20·21八年级下·广东东莞·期中）已知函数()()224y k x k =-+-．(1)若该函数是一次函数，求k 的取值范围．(2)若该函数是正比例函数，求k 的值．14．（23·24八年级上·广西崇左·阶段练习）已知4y +与3x -成正比例，且1x =时，0y =(1)求y 与x 的函数表达式；(2)点(1,2)M m m +在该函数图象上，求点M 的坐标．15．（22·23六年级下·山东威海·期末）某车间的甲、乙两名工人分别同时生产同一种零件，他们一天生产零件的个数y 与生产时间t (时)的关系如图所示．(1)上表中自变量是，因变量是；(2)该型号电动汽车的电池容量为度；～时充电最佳．请根据上表直接写出该电动汽车剩余电量y（度）与行驶里(3)电动汽车在电量剩余20%30%程x（千米）之间的关系式，并求剩余电量为30%时的已行驶里程．17．（22·23七年级下·山东青岛·期末）如图所示，梯形ABCD上底的长是x，下底的长是14，高是6(1)求梯形面积y 与上底长x 之间的关系式；(2)用表格表示当x 每次增加1，从4变到13时，y 的相应值；(3)当x 每增加1时，y 如何变化？说说你的理由；(4)当0x =时，y 等于什么？此时它表示的是什么？18．（23·24八年级上·上海松江·期中）定义：对于给定的两个函数，当0x ≥时，它们对应函数值相等；当0x <时，它们对应的函数值互为相反数．我们称这样的两个函数互为相关函数．例如：正比例函数y x =-，它的相关函数为()()00x x y x x ⎧-≥⎪=⎨<⎪⎩(1)已知点()1,M m -在正比例函数y x =-的相关函数的图象上，则m 的值为______；(2)已知正比例函数2y x =①这个函数的相关函数为______；②若点(),3N n 在这个函数的相关函数的图象上，求n 的值．。

函数的基本概念与表示模块一、函数与映射要点一、映射1．映射：设A 、B 是两个集合，如果按照某种对应关系f ，对于集合A 中的 元素，在集合B 中都有 元素和它对应，这样的对应叫做 到 的映射，记作 .2．象与原象：如果f :A→B 是一个A 到B 的映射，那么和A 中的元素a 对应的 叫做象， 叫做原象。

要点二、函数1．定义：设A 、B 是 ，f :A→B 是从A 到B 的一个映射，则映射f :A→B 叫做A 到B 的 ，记作 。

2．函数的三要素为 、 、 ，两个函数当且仅当 分别相同时，二者才能称为同一函数。

3．函数的表示法有 、 、 。

要点三、函数相等只有当两个函数的 和 都分别相同时，这两个函数才是相等函数（或称为同一个函数）。

考点一、同一函数的判断 例1.下列各组函数中，表示同一函数的是（ ）.A. B. C. D. 变式训练1：下列函数中，与函数y=x 相同的函数是 （ ）A.y= B.y=()2 C.y=lg10x D.y=考点二、已知函数解析式求函数值例2-1. 已知f(x)= 12−x (x ∈R,x≠2),g(x)=x+4(x ∈R).⑴求f (1),g (1)的值.⑵求f [g (1)],g [f (1)]的值.⑶求f [g (x)],g [f (x)]的表达式.例2-2. 设f (x )={1−√x ，x ≥0，2x ，x <0，则f(f (−2))=（ ） A. -1 B. 14 C. 12 D. 32变式训练2：函数f (x )={x 2+2（x ≤2），2x （x >2）则f (−4)=（ ），若f (x 0)=8，则x 0=（ ）。

1,x y y x==211,1y x x y x =-+=-33,y x y x ==2||,()y x y x ==x x 2x x 2log 2模块二、函数的三要素要点四、函数的定义域1. 函数的定义域就是使函数式 的集合.2.常见函数：使式子有意义(1)整式：定义域为R（2）一次函数：，定义域是R 。

函数知识点一.图像及性质 1.一次函数 ①图像：y=kx+b(k≠0) y=kx(k ≠0,b=0)①k>0 增 k<0 减 ②b ≠0一次函数，b=0正比例函数 2.二次函数 ①图像：②a>0 开口向上，a<0开口向下 ③a>0最小值，a<0最大值 ④X 对称=-b2a⑤顶点坐标：（-b2a，244ac a b -）⑥三种表达形式222(1)(2)4()24y a x x x x b ac b y a x a a y ax bx c =--⎧⎫⎪⎪-⎪⎪=++⎨⎬⎪⎪⎪⎪=++⎩⎭两点式顶点式一般式3指数函数①图像：y=x a （a>0且a ≠1）②0<a<1 增函数,a 越小越靠近y 轴，a>1 减函数，a 越大越靠近y 轴,0a =1（a ≠0）③必过（0,1）④y>04对数函数①图像：y=lo x a g （a>0且a ≠1）②0<a<1 增函数，a 越小越靠近x 轴，a>1 减函数，a 越大越靠近x 轴 ③必过（1,0）④x>0 5幂函数①图像：y=a x （a ∈R ）②a<0 减函数，a>0 增函数 ③0<a<1下凸，a>1上凸 ④必过（1,1）6对勾函数①图像:y=x+ px(p>0)②顶点坐标-二.定义域1.给定解析式（1）12x-（2）2()x xy-=（3）cosl xy g=2.已知f（x）定义域，求f（g（x））定义域（1）已知f（x）定义域为[-12,12],求y=f(2x-x-12)定义域3.已知f(g(x))的定义域。

求f(x)的定义域（1）若f(2x)的定义域为[-1,1],求f(x)的定义域（一）求函数定义域例：(21)f x-的定义域为[]0,1,求(13)f x-的定义域1.求下列函数定义域①xxxy--+=2)1(2②)45(log)1(xxy-=+2.已知6lg)3(222-=-xxxf，则()f x的定义域是3．（2013陕西理1）设全集为R，函数21)(xxf-=的定义域为M，则MCR为( ).A]1,1[-.B)1,1(-.C),1[]1,(+∞--∞.D),1()1,(+∞--∞4．（2013江西理2）函数)1ln(xxy-=的定义域为( ).A)1,0(.B)1,0[.C ]1,0( .D ]1,0[5.（2013山东文5）函数3121)(++-=x x f x的定义域为( ).A ]0,3(-.B ]1,3(-.C ]0,3()3,(---∞ .D ]1,3()3,(---∞6.（2013重庆文3）函数)2(log 12-=x y 的定义域为( ).A )2,(-∞ .B ),2(+∞ .C ),3()3,2(+∞ .D ),4()4,2(+∞7.（2013安徽文11）函数1l n (11y x=++的定义域为_____________.（二）利用定义域求参数范围例.)1lg(2++=ax x y 的定义域为R ，求a 的范围？练1.82)(2--=x x x f 的定义域为A ,mx x g --=11)(的定义域为B ，Φ=⋂B A ,求m 的取值范围？练2.341)(2++=ax ax x f 的定义域为R ，求a 的范围练3.2(1),1()41x x f x x +<⎧⎪=⎨≥⎪⎩ ；使1)(≥x f 的x取值范围？三.求函数的解析式1.拼凑法:例1.已知f(x+1x )=3x +31x ,求f(x)例2：2(1)()f x x f x -=,求例3：，求2换元法：例1：已知f （2x+1）=lgx,求f(x)的解析式564)12(2+-=+x x x f )(x f例2：2)1(x x f =-，求f （x ）例3：，求例4：x x x f 2)1(-=-3.待定系数法：例1:已知二次函数f(x)满足f （2+x ）=f(2-x),且f(x)=0的两实根平方和为10，f(x)的图像过点（0,3），求f(x)例2：若()[]12-=x x f f ，则一次函数=例3：二次函数满足，且。

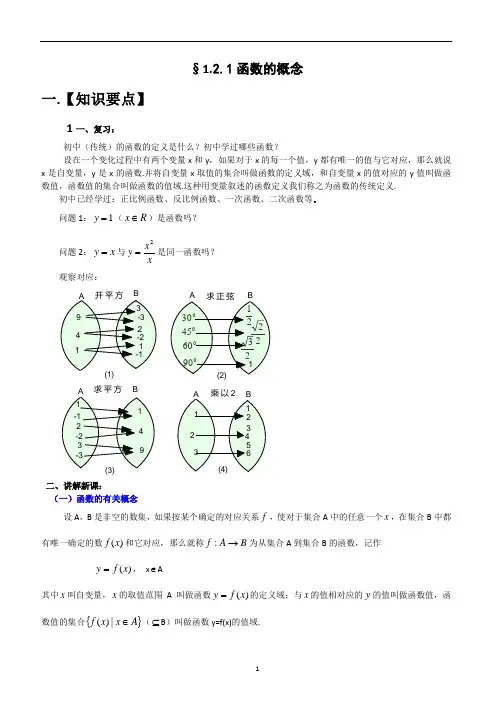
§1.2.1函数的概念一.【知识要点】1一、复习：初中（传统）的函数的定义是什么？初中学过哪些函数？设在一个变化过程中有两个变量x 和y ，如果对于x 的每一个值，y 都有唯一的值与它对应，那么就说x 是自变量，y 是x 的函数.并将自变量x 取值的集合叫做函数的定义域，和自变量x 的值对应的y 值叫做函数值，函数值的集合叫做函数的值域.这种用变量叙述的函数定义我们称之为函数的传统定义.问题1：1=y （R x ∈）是函数吗？问题2：x y =与xx y 2=是同一函数吗？观察对应：二、讲解新课：（一）函数的有关概念设A ，B 是非空的数集，如果按某个确定的对应关系f ，使对于集合A 中的任意一个x ，在集合B 中都有唯一确定的数)(x f 和它对应，那么就称B A f →:为从集合A 到集合B 的函数，记作)(x f y =， x ∈A其中x 叫自变量，x 的取值范围A 叫做函数)(x f y =的定义域；与x 的值相对应的y 的值叫做函数值，函数值的集合{}A x x f ∈|)(（⊆B ）叫做函数y=f(x)的值域.求平方B B函数符号)(x f y =表示“y 是x 的函数”，有时简记作函数)(x f . (1)函数实际上就是集合A 到集合B 的一个特殊对应 B A f →:这里 A, B 为非空的数集.（2）A ：定义域，原象的集合；{}A x x f ∈|)(：值域，象的集合,其中{}A x x f ∈|)( ⊆ B ；f ：对应法则 ， x ∈A ， y ∈B（3）函数符号：)(x f y = ↔y 是 x 的函数，简记 )(x f （二）已学函数的定义域和值域1．一次函数b ax x f +=)()0(≠a :定义域R, 值域R; 2．反比例函xkx f =)()0(≠k :定义域{}0|≠x x , 值域{}0|≠x x ; 3．二次函数c bx ax x f ++=2)()0(≠a :定义域R值域：当0>a 时，⎭⎬⎫⎩⎨⎧-≥a b ac y y 44|2；当0<a 时，⎭⎬⎫⎩⎨⎧-≤a b ac y y 44|2 4求函数的定义域时，一般应考虑:（1）偶次方根的被开方数不小于零； （2）分母不等于零；（3）零的零次幂没有意义. (4)实际问题的背景所允许的取值范围.例如：2r S ⋅=π表示圆的面积时，r 的取值范围应是()+∞∈,0r .（三）函数的值：关于函数值 )(a f例：)(x f =2x +3x+1 则 f(2)=22+3×2+1=11注意：1︒在)(x f y =中f 2︒)(x f 不一定是解析式，有时可能是“列表” 3︒)(x f 与)(a f （四）函数的三要素： 对应法则f 、定义域A 、值域{}A x x f ∈|)( （五）了解区间的概念①设a 、b 是两个实数，且a<b ，则：{x|a ≤x ≤b}＝[a,b] 叫闭区间； {x|a<x<b}＝(a,b) 叫开区间； {x|a ≤x<b}＝[a,b) ； {x|a<x ≤b}＝(a,b] ；都叫半开半闭区间。

2．函数的概念与基本初等函数 2．1 函数的概念与表示法【知识网络】1．函数的概念；2．函数的表示法：解析法、列表法、图象法；3．分段函数；4．函数值．【典型例题】例1．（1）下列函数中哪个与函数y x =(0)x ≥是同一个函数（ A ）A ．y=(x )2B ．y=xx 2C ．y=33xD ．y=2x提示：当两个函数的解析式和定义域完全相同时，这两个函数为同一函数．同时满足这两个条件的只有B 中的函数． (2) 函数||)(x xx f =的图象是（ C ）提示：所给函数可化为：1(0)()1(0)x f x x >⎧=⎨-<⎩，故答案为C ．也可以根据函数的的定义域为{|0}x x ≠而作出判断．（3）已知)(x f 的图象恒过（1，1）点，则)4(-x f 的图象恒过（ ） A ．（－3，1） B ．（5，1） C ．（1，－3）D ．（1，5）提示：法一：由)(x f 的图象恒过（1，1）知(1)1f =，即(54)1f -=，故函数)4(-x f 的图像过点（5，1）．法二：)4(-x f 的图象可由)(x f 的图象向右平移4个单位而得到，（1，1）向右平移4个单位后变为（5，1）,答案为B ．（4）已知2()1f x x x =++，则[f f =提示：213f =+=，2[(3(3115f f =++=+ （5）函数2)1(+=x y -2的图象可由函数2x y =的图象经过 ③ 得到.①先向右平移1个单位，再向下平移2个单位；②先向右平移1个单位，再向上平移2个单位；③先向左平移1个单位，再向下平移2个单位；④先向左平移1个单位，再向上平移2个单位． 提示：由“左加右减”，“上加下减”的方法可得．例2．（1）已知1)f x +=+()f x 及2()f x ；（2）已知12)(3)(+=-+x x f x f ，求)(x f .解：（1）令1t =，则1t ≥1t =-，2(1)x t =-，22()(1)2(1)1f t t t t =-+-=- ∴ 2()1(1)f x x x =-≥，2224()()11(1)f x x x x =-=-≥． （2）12)(3)(+=-+x x f x f ………………①把①中的x 换成x -得：()3()21f x f x x -+=-+………………② 由①②解得：1()4f x x =-+． 例3．画出下列函数的图象．（1）y ＝x 2－2，x ∈Z 且｜x ｜2≤；（2）y ＝－22x ＋3x ，x ∈（0，2］； （3）y ＝x ｜2－x ｜；（4）3232232x y xx x ⎧⎪⎨⎪⎩≤≥＜－，＝－－＜－．． 解：四个函数的图象如下例4．如图，动点P 从单位正方形ABCD 顶点A 开始，顺次经C 、D 绕边界一周，当x 表示点P 的行程，y 表示PA 之长时，求y 关于x 的解析式，并求f(25)的值． 解：当P 在AB 上运动时， (01)y x x =≤≤； 当P 在BC 上运动时，y=2)1(1-+x (12)x <≤ 当P 在CD 上运动时，y=2)3(1x -+(23)x <≤ 当P 在DA 上运动时，y=4－x (34)x <≤∴y= (01)2)3)4 (34)x x x x x x ≤≤⎧<≤<≤-<≤⎩ ∴f (25)=25 【课内练习】 1．与曲线11-=x y 关于原点对称的曲线为 （ A ）A ．x y +=11 B ．x y +-=11 C ．xy -=11D ．xy --=11 提示：用,x y --代替方程11-=x y 中的,x y 得：11y x -=--,即x y +=11．答案为A ．2．已知函数)(x f y =,[,]x a b ∈,那么集合}2|),{(]},[),(|),{(=∈=x y x b a x x f y y x 中所含元素的个数是 A ．0个 B ．1个 C ． 0或1个 D ．0或1或无数个 提示：垂直于x 轴的直线与函数的图象最多只有一个交点．答案为C ． 3．下列说法中，正确的有（ ）个①函数)(x f y =与函数)(x f y -=的图象关于直线x =0对称； ②函数)(x f y =与函数)(x f y -=的图象关于直线y=0对称； ③函数)(x f y =与函数)(x f y --=的图象关于坐标原点对；④如果函数)(x f y =对于一切,R x ∈都有()f a x +=()f a x -，那么)(x f y =的图象关于直线a x =对称．A ．1B ．2C ．3D ．4提示：①把函数)(x f y =中的x 换成x -，y 保持不变，得到的函数的图象与原函数的图象关于y 轴对称；②把函数)(x f y =中的y 换成y -，x 保持不变，得到的函数的图象与原函数的图象关于x 轴对称；③把函数)(x f y =中的x 换成x -，y 换成y -，得到的函数的图象与原函数的图象关于原点轴对称；④若对于一切,R x ∈都有()f a x +=()f a x -，则()f x 的图象关于直线()()2a x a x x ++-=对称．答案为D ．4．设函数10221,0,()()1,0x x f x f x x x -⎧-≤⎪=>⎨⎪>⎩若，则0x 的取值范围是 （ D ）A ．（－1，1）B ．（－1，+∞）C ．（－∞，－2）∪（0，+∞）D ．（－∞，－1）∪（1，+∞）5．已知⎩⎨⎧>-<+=0404)(x x x x x f ，则)3([-f f ]的值为－3解析：(3)341,((3))(1)143f f f f -=-+=-==-=-．6．已知f （x ）＝x 5＋ax 3＋bx －8，f （－2）＝10，则f （2）＝－26__． 提示：f （－2）＝（－2）5＋a （－2）3－2b －8＝10， ∴ 8a ＋2b ＝－50，f （2）＝25＋23a ＋2b －8＝24＋82a b +＝－26．7．已知函数22()1x f x x=＋，那么111(1)(2)()(3)()(4)()234f f f f f f f ++++++＝27 提示：()f x ＝221xx ＋，)1(x f ＝112＋x ，()f x ＋)1(x f ＝1． ∴ 111(1)(2)()(3)()(4)()234f f f f f f f ++++++＝21＋1＋1＋1＝27．8．作出下列函数的图象：(1)⎩⎨⎧---=14)(22x x x f )20()02(≤<≤≤-x x ； (2)322-+=x x y ；01()2(3)||x y x x+=-解：（1）函数图象如下：第（1）题 第（2）题 第（3）题（2）2223(02)23(20)x x x x y x x x ⎧+-≥≤-⎪=⎨----<<⎪⎩或22(1)4(02)(1)2(20)x x x x x ⎧+-≥≤-⎪=⎨-+--<<⎪⎩或 函数的图象如右上． （3）11(0)22y x x x =-<≠-且，图象如右上．9．设二次函数()f x 满足f (x +2)=f (2-x )，且方程()0f x =的两实根的平方和为10，)(x f 的图象过点(0,3)，求f (x )的解析式. 解：设2()(0)f x ax bx c a =++≠∵ f (x +2)=f (2-x )，∴()f x 的图像有对称轴2x =， ∴ 22ba-=,4b a =-． ∵ )(x f 的图象过点(0,3)，∴ 3c =，∴ 2()43(0)f x ax ax a =-+≠ 设方程2430ax ax -+=的两根为12,x x ，则：121243x x x x a +=⎧⎪⎨=⎪⎩，由221210x x +=，得：21212()210x x x x +-=，∴ 234210a-⋅=，解得：1a =． ∴ 2()43f x x x =-+．10．设2()32f x ax bx c =++，若0,(0)0,(1)0a b c f f ++=>>，求证： （1）0a >且21ba-<<-； （2）方程()0f x =在（0，1）内有两个实根。

"Pocket" members 1037, find there ar e 640 "lost" party members are not conta cted 148 "Pocket" party members a nd impl ementati on of orga nizati onal rel ationshi ps. E ducational manageme nt of party member s into t he Orga nizati on, t here is a l ot of work to do. Weak a nd lax party continued re organization as a n importa nt task, finish perfe ct organization, with a g ood team, Good system. Spe cial highlight s of grass -roots party organizations, to be dealt wit h first in pl ace, furt her educati on, r eorganization, transformation and educati onal i nteracti on. In short, thr oug h soli d and effective w ork initiatives函数的概念,三要素的求法一、函数的概念：1． 函数的概念：函数概念：设A 、B 是非空的数集，如果按照某种确定的对应关系f ，使对于集合A 中的任意一个数x ，在集合B 中都有唯一确定的数f (x )和它对应，那么就称f ：A →B 为从集合A 到集合B 的一个函数 记作：y = f (x )，x ∈A .其中，x 叫做自变量，x 的取值范围A 叫做函数的定义域；与x 的值相对应的y 值叫做函数值，函数值的集合{f (x ) | x ∈A }叫做函数的值域. 显然，值域是集合B 的子集.（2）函数的表示方法1．解析式：把常量和表示自变量的字母用一系列运算符号连接起来，得到的式子叫做解析式. 2．列表法：列出表格来表示两个变量之间的对应关系.3．图象法：用图象表示两个变量之间的对应关系.（3）典型例题：1. 函数y = f (x )表示（ ） A ．y 等于f 与x 的乘积 B ．f (x )一定是解析式 C ．y 是x 的函数 D ．对于不同的x ，y 值也不同2.下列各图中，可表示函数y =f (x )的图象的只可能是A B C D3. 下列四种说法中，不正确的是（ ）A ．函数值域中每一个数都有定义域中的一个数与之对应B ．函数的定义域和值域一定是无限集合C ．定义域和对应关系确定后，函数的值域也就确定了D ．若函数的定义域只含有一个元素，则值域也只含有一个元素4. 已知f (x ) = x 2 + 4x + 5，则f (2) = __ ，f (–1) = __ .5. 已知f (x ) = x 2 (x ∈R )，表明的“对应关系”是______，它是____→_____的函数.x y o x y o x y o xy o"Pocket" members 1037, find there ar e 640 "lost" party members are not conta cted 148 "Pocket" party members a nd impl ementati on of orga nizati onal rel ationshi ps. E ducational manageme nt of party member s into t he Orga nizati on, t here is a l ot of work to do. Weak a nd lax party continued re organization as a n importa nt task, finish perfe ct organization, with a g ood team, Good system. Spe cial highlight s of grass-roots party organizations, to be dealt wit h first in pl ace, furt her educati on, r eorganization, transformation and educati onal i nteracti on. In short, thr oug h soli d and effective w ork initiatives2.映射映射的定义：设A，B是两个非空的集合，如果按某一个确定的对应关系f，使对于集合A中的任意一个元素x，在集合B中都有惟一确定的元素y与之对应，那么这样的对应(包括集合A，B以及A到B的对应法则f)叫做集合A到集合B的映射，记作f:A→B.其中与A中的元素a对应的B中的元素b叫做a的象，a叫做b的原象.看下面的例子：设A，B分别是两个集合，为简明起见，设A，B分别是两个有限集说明：（2）（3）（4）这三个对应的共同特点是：对于左边集合A中的任何一个元素，在右边集合B中都有唯一的元素和它对应①“A到B”：映射是有方向的，A到B的映射与B到A的映射往往不是同一个映射,A到B是求平方，B到A则是开平方，因此映射是有序的；②“任一”：就是说对集合A中任何一个元素，集合B中都有元素和它对应，这是映射的存在性；③“唯一”：对于集合A中的任何一个元素，集合B中都是唯一的元素和它对应，这是映射的唯一性；④“在集合B中”：也就是说A中元素的象必在集合B中，这是映射的封闭性.指出：根据定义，（2）（3）（4）这三个对应都是集合A到集合B的映射；注意到其中（2）（4）是一对一，（3）是多对一一对一，多对一是映射但一对多显然不是映射辨析：①任意性：映射中的两个集合A,B可以是数集、点集或由图形组成的集合等；②有序性：映射是有方向的，A到B的映射与B到A的映射往往不是同一个映射；③存在性：映射中集合A的每一个元素在集合B中都有它的象；"Pocket" members 1037, find there ar e 640 "lost" party members are not conta cted 148 "Pocket" party members a nd impl ementati on of orga nizati onal rel ationshi ps. E ducational manageme nt of party member s into t he Orga nizati on, t here is a l ot of work to do. Weak a nd lax party co ntinued re organization as a n importa nt task, finish perfe ct organization, with a g ood team, Good system. Spe cial highlight s of grass-roots party organizations, to be dealt wit h first in pl ace, furt her educati on, r eorganization, transformation and educati onal i nteracti on. In short, thr oug h soli d and effective w ork initiatives④唯一性：映射中集合A的任一元素在集合B中的象是唯一的；⑤封闭性：映射中集合A的任一元素的象都必须是B中的元素，不要求B中的每一个元素都有原象，即A中元素的象集是B的子集.映射三要素：集合A、B以及对应法则f，缺一不可；映射观点下的函数概念如果A，B都是非空的数集，那么A到B的映射f：A→B就叫做A到B的函数，记作y=f(x)，其中x∈A，y ∈B.原象的集合A叫做函数y=f(x)的定义域，象的集合C（C B）叫做函数y=f(x)的值域.函数符号y=f(x)表示“y是x的函数”，有时简记作函数f(x).例以下给出的对应是不是从集合A到B的映射？（1）集合A = {P | P是数轴上的点}，集合B = R，对应关系f：数轴上的点与它所代表的实数对应；（2）集合A = {P | P是平面直角坐标系中的点，集合B = {(x | y) | x∈R，y∈R}，对应关系f：平面直角坐标系中的点与它的坐标对应；（3）集合A = {x | x是三角形}，集合B = {x | x是圆}，对应关系f：每一个三角形都对应它的内切圆；（4）集合A = {x | x是新华中学的班级}，集合B = {x | x是新华中学的学生}，对应关系f：每一个班级都对应班里的学生.（1）按照建立数轴的方法可知，数轴上的任意一个点，都有惟一的实数与之对应，所以这个对应f：A→B是从集合A到B的一个映射.（2）按照建立平面直角坐标系的方法可知，平面直角坐标系中的任意一个点，都有惟一的一个实数对与之对应，所以这个对应f：A→B是从集合A到B的一个映射.（3）由于每一个三角形只有一个内切圆与之对应，所以这个对应f：A→B是从集合A到B的一个映射.（4）新华中学的每一个班级里的学生都不止一个，即与一个班级对应的学生不止一个，所以这个对应f：A→B 不是从集合A到B的一上映射.1.图1-2-2-21(1),(2),(3),(4)用箭头所标明的A中元素与B中元素的对应法则,是不是映射？图1-2-2-21“一对一”或“多对一”的对应,即集合A中的任意一个元素,在集合B中都有唯一确定的元素与之对应."Pocket" members 1037, find there ar e 640 "lost" party members are not conta cted 148 "Pocket" party members a nd impl ementati on of orga nizati onal rel ationshi ps. E ducational manageme nt of party member s into t he Orga nizati on, t here is a l ot of work to do. Weak a nd lax party continued re organization as a n importa nt task, finish perfe ct organization, with a g ood team, Good system. Spe cial highlight s of grass-roots party organizations, to be dealt wit h first in pl ace, furt her educati on, r eorganization, transformation and educati onal i nteracti on. In short, thr oug h soli d and effective w ork initiatives例1，已知下列集合A 到B 的对应，请判断哪些是A 到B 的映射？并说明理由：⑴ A=N ，B=Z ，对应法则：“取相反数”；⑵A={-1，0，2}，B={-1，0，1/2}，对应法则：“取倒数”； ⑶A={1，2，3，4，5}，B=R ，对应法则：“求平方根”； ⑷A={α|00≤α≤900}，B={x|0≤x ≤1}，对应法则：“取正弦”.二、函数的三要素——定义域、值域、对应法则（a ）函数定义的理解.由函数的定义可知，一个函数的构成要素为：定义域、对应关系和值域. 由于值域是由定义域和对应关系决定的，所以，如果两个函数的定义域相同，并且对应关系完全一致，我们就称这两个函数相等.(b) 区间的概念（1）不等式a ≤x ≤b ，用闭区间[a ，b ]表示；（2）不等式a ＜x ＜b ，用开区间(a , b )表示；（3）不等式a ≤x ＜b (或a ＜x ≤b )用半开半闭区间[a ，b ](或(a ，b ])表示；（4）x ≥a ，x ＞a ，x ≤b ，x ＜b 分别表示为[a ，+∞)，(a , +∞)，(–∞, b ]，(–∞, b ).1.定义域的求法：例1：列函数中哪个与函数y = x 相等？（1）1()2f x x =-；（2）()32f x x =+；（3）1()12f x x x=++-.（4）3212+=x y（5）1||142-+-=x x y（6）||13x x x y +-=求函数的定义域的类型： 一、 含分式的函数在求含分式的函数的定义域时，要注意两点：（1）分式的分母一定不能为0；（2）绝对不能先化简后求函数定义域。

专题09函数的概念及其表示1．函数的概念定义设A、B是非空的数集，如果按照某种确定的对应关系f，使对于集合A中的任意一个数x，在集合B中都有唯一确定的数f(x)和它对应，那么就称f：A→B为从集合A到集合B的一个函数三要素对应关系y＝f(x)，x∈A定义域x的取值集合值域与x的值相对应的y的值的集合{f(x)|x∈A}.[知识点拨](1)对数集的要求：集合A、B为非空数集．(2)任意性和唯一性：集合A中的数具有任意性，集合B中的数具有唯一性．(3)对符号“f”的认识：它表示对应关系，在不同的函数中f的具体含义不一样．(4)一个区别：f(x)是一个符号，不表示f与x的乘积，而f(a)表示函数f(x)当自变量x取a时的一个函数值．(5)函数三要素：定义域、对应关系和值域是函数的三要素，三者缺一不可．2．区间及有关概念(1)一般区间的表示．设a，b∈R，且a<b，规定如下：定义名称符号数轴表示{x|a≤x≤b}闭区间[a，b]{x|a＜x＜b}开区间(a，b){x|a≤x＜b}半开半闭区间[a，b){x|a＜x≤b}半开半闭区间(a，b](2)定义R{x|x≥a}{x|x>a}{x|x≤a}{x|x<a}符号(－∞，＋∞)[a，＋∞)(a，＋∞)(－∞，a](－∞，a)[知识点拨](1)关注实心点、空心圈：用数轴表示区间时，用实心点表示包括在区间内的端点，用空心圈表示不包括在区间内的端点．(2)区分开和闭：在用区间表示集合时，开和闭不能混淆．(3)正确理解“∞”：“∞”是一个趋向符号，不是一个数，它表示数的变化趋势．以“－∞”和“＋∞”为区间的一端时，这一端点必须用小括号．3.函数的表示法[4. 所谓分段函数，是指在定义域的不同部分，有不同的对应关系的函数．[知识点拨] 分段函数是一个函数，不要把它误认为是几个函数．分段函数的定义域是各段定义域的并集，值域是各段值域的并集．重要考点一：函数概念的理解【典型例题】函数()y f x =的图象与直线1x =的公共点有（ ）A ．0个B ．1个C ．至多1个D ．至少1个【答案】C 【解析】 若函数()y f x =在1x =处有定义，则函数()y f x =的图象与直线1x =的公共点个数是1； 若函数()y f x =在1x =处没有定义，则函数()y f x =的图象与直线1x =没有公共点，因此，函数()y f x =的图象与直线1x =的公共点至多1个.故选：C.【题型强化】1.可作为函数()y f x =的图象的是（ ）A ．B ．C ．D ．【答案】D 【解析】A,B,C 不可作为函数图像；因为在图像对应的自变量x 的取值范围内存在自变量0x ，有两个y 值与之对应，不符合函数的概念；D 符合函数概念；故选D 2.下列四组函数中，表示同一函数的是（ ） A ．f （x ）=1与g （x ）=x 0B ．()f x x =与()2g x x =C ．f （x ）=x 与g （x ）=2x xD ．()21f x x =-与()11g x x x =+-【答案】B【解析】A 选项：两个函数定义与不同：f(x)定义域为R ，g(x)定义域00-∞⋃+∞（，）（，），排除A C 选项：f(x)定义域为R ，g(x)定义域00-∞⋃+∞（，）（，），定义域不同，故排除C D 选项：：f(x)定义域为11-∞-⋃+∞（，）（，），g(x)定义域1（，）+∞，故排除D ， 故选：B 【名师点睛】1．判断一个对应关系是否是函数，要从以下三个方面去判断，即A ，B 必须是非空数集；A 中任何一个元素在B 中必须有元素与其对应；A 中任一元素在B 中必有唯一元素与其对应．2．函数的定义中“任一x ”与“有唯一确定的y ”说明函数中两变量x ，y 的对应关系是“一对一”或者是“多对一”而不能是“一对多”．重要考点二：求函数的定义域【典型例题】函数0()(2)f x x =-+ ） A ．(2,)+∞ B ．(1,)-+∞C ．(1,2)(2,)-+∞ D ．R【答案】C【解析】由已知，20101x x -≠⎧⎪⎨≥⎪+⎩，解得1x >-且2x ≠，所以()f x 的定义域为(1,2)(2,)-+∞.故选：C.【题型强化】1.函数y =的定义域为（ ） A ．()1,2- B ．()0,2 C ．[)1,2- D ．(]1,2-【答案】D 【解析】 由题意可得1020x x +>⎧⎨-≥⎩，解得12x -<≤，所以，函数y =的定义域为(]1,2-. 故选：D. 2.已知函数()21f x +的定义域为()2,0-，则()f x 的定义域为（ ）A ．()2,0-B ．()4,0-C ．()3,1-D ．1,12⎛⎫-⎪⎝⎭【答案】C 【解析】()21f x +的定义域为()2,0-，即20x -<<，3211x ∴-<+<，所以，函数()f x 的定义域为()3,1-，故选C. 【名师点睛】 求函数的定义域：(1)要明确使各函数表达式有意义的条件是什么，函数有意义的准则一般有：①分式的分母不为0；②偶次根式的被开方数非负；③y ＝x 0要求x ≠0.(2)当一个函数由两个或两个以上代数式的和、差、积、商的形式构成时，定义域是使得各式子都有意义的公共部分的集合．(3)定义域是一个集合，要用集合或区间表示，若用区间表示数集，不能用“或”连接，而应该用并集符号“∪”连接．重要考点三：求函数值【典型例题】若()22f x x x =-，则()()()1ff f =（ ）A ．1B ．2C ．3D ．4【答案】C 【解析】由()22f x x x =-，可得()1121f =-=-；所以()()()11123f f f =-=+=；()()()()13963f f f f ==-=.故选C.【题型强化】1.已知函数f(x －1)＝x 2－3，则f(2)的值为( ) A ．－2 B ．6 C ．1 D ．0【答案】B【解析】令1x t -=，则1x t =+,()()213f t t ∴=+-,()()213f x x ∴=+-()()222136f ∴=+-=,故选B.2.若()f x 满足关系式()12()3f x f x x+=，则()2f 的值为 A ．1 B ．1-C ．32-D ．32【答案】B【解析】∵f （x ）满足关系式f （x ）+2f （1x）=3x ， ∴()()12262132222f f f f ⎧⎛⎫+= ⎪⎪⎪⎝⎭⎨⎛⎫⎪+= ⎪⎪⎝⎭⎩，①，②， ①﹣②×2得﹣3f （2）=3，∴f （2）=﹣1，故选B ． 【名师点睛】解题时，(一)要注意审题，观察分析、发现规律．(二)要注意一题多问时，有时前面问题的结论可作为后面问题的条件使用．重要考点四：求函数定义域时非等价化简解析式而致误【典型例题】已知函数()f x 的定义域为()0,∞+，且()1f x 2f 1x ⎛= ⎝，则()f x =______．13【解析】在()1f x 2f 1x ⎛=⎝，用1x 代替x ，得(1f 2f x 1x ⎛⎫=- ⎪⎝⎭，联立得 ()(1f x =2f x 1f =2f x x ⎧⎛ ⎪⎪⎝⎨⎛⎫⎪ ⎪⎪⎝⎭⎩ ， 将2f x 1f 1x ⎛⎫=- ⎪⎝⎭代入()1f x 2f 1x ⎛= ⎝中，可求得()1f x 3=． 13+【题型强化】1.若()f x 对于任意实数x 都有12()21f x f x x ⎛⎫-=+ ⎪⎝⎭，则12f ⎛⎫= ⎪⎝⎭__________. 【答案】3 【解析】()f x 对于任意实数x 都有12()21f x f x x ⎛⎫-=+ ⎪⎝⎭，∴12()21122()1f x f x x f f x x x ⎧⎛⎫-=+ ⎪⎪⎪⎝⎭⎨⎛⎫⎪-=+ ⎪⎪⎝⎭⎩，解得42()133f x x x =++，∴141213123232f ⎛⎫=⨯++= ⎪⎝⎭⨯． 故答案为：3．2.已知()2212f x x x +=-，则()9f =______________.【答案】8【解析】21x t +=，则12t x -=，代入()2212f x x x +=-得： 22111()()2(65)224t t f t t t --=-⨯=-+，∴2135()424f x x x =-+， ∴2135(9)998424f =⨯-⨯+=．故答案为：8．重要考点五：求函数值域的方法（分离常数法）【典型例题】函数11x y x -=+()0x ≥的值域为（ ） A ．[)1,1- B ．[]1,1-C ．[)1,-+∞D ．[)0,+∞【答案】A 【解析】()112210111x x y x x x x -+-===-≥+++ 0x ≥ 11x ∴+≥ 2021x ∴<≤+ 2201x ∴-≤-<+ 21111x ∴-≤-<+，即()101x y x x -=≥+的值域为[)1,1-故选：A 【题型强化】1.函数()3452xf x x-+=-的值域是（ ）A ．()(),22,-∞+∞B ．()(),22,-∞--+∞C ．55,,22⎛⎫⎛⎫-∞⋃+∞ ⎪ ⎪⎝⎭⎝⎭D ．R【答案】B 【解析】()344341077252252525x x x f x x x x x -+--+==-=-=-+----，()2f x ∴≠-，值域为()(),22,-∞-⋃-+∞．2.函数222231x x y x x ++=+-的值域为________．【答案】(,2](2,)-∞-⋃+∞【解析】2222235211x x y x x x x ++==++-+-， 因为221551244x x x ⎛⎫+-=+-- ⎪⎝⎭，所以21415x x ≤-+-或2101x x >+-， 则25221x x +≤-+-或25221x x +>+-，即(,2](2,)y ∈-∞-⋃+∞. 故答案为：(,2](2,)-∞-⋃+∞【名师点睛】求y ＝ax ＋c x ＋b 这种类型的函数的值域，应采用分离常数法，将函数化简为y ＝d ＋n x ＋m的形式．重要考点六：求函数值域的方法（配方法）【典型例题】求下列函数的值域221y x x =--+，[)2,1x ∈-；【答案】(]2,2-；【解析】（3）因为2(1)2y x =-++，[)2,1x ∈-，画出其图象如图：观察图象可知值域为(]2,2-.【题型强化】1.作出下列函数图象，并指出其值域. （1）y ＝x 2＋x (－1≤x ≤1)； （2）y ＝2x(－2≤x ＜1且x ≠0). 【答案】（1）图象见解析，值域为1,24⎡⎤-⎢⎥⎣⎦；（2）图象见解析，值域为(](),12,-∞-+∞.【解析】（1）由题意()2211,1124y x x x x ⎛⎫=+=+--≤≤ ⎪⎝⎭，当1x =-时，211024y x ⎛⎫=+-= ⎪⎝⎭；当12x =-时，2111244y x ⎛⎫=+-=- ⎪⎝⎭； 当1x =时，211224y x ⎛⎫=+-= ⎪⎝⎭；函数2y x x =+的图象为抛物线的一部分，如图：由图象可知，函数()2,11y x x x =+-≤≤的值域为1,24⎡⎤-⎢⎥⎣⎦； （2）由题意函数2y x = (－2≤x ＜1且x ≠0)的图象为反比例函数图象的一部分， 当2x =-时，21y x ==-；当1x =时，22y x==；所以该函数图象如图：由图象可知，函数2y x= (－2≤x ＜1且x ≠0)的值域为(](),12,-∞-+∞.2.求下列函数值域：（1）y ＝2x 2－2x ＋3； （2）y ＝372x x ++； （3）y ＝2x 1x - （4）y ＝224x x -+.【答案】（1）5,2⎡⎫+∞⎪⎢⎣⎭；（2）()(),33,-∞+∞；（3）15,8⎡⎫+∞⎪⎢⎣⎭；（4）[]0,2. 【解析】（1）由题意2215223222y x x x ⎛⎫=-+=-+ ⎪⎝⎭，所以函数2223y x x =-+的值域为5,2⎡⎫+∞⎪⎢⎣⎭；（2）由题意()3213713222x x y x x x +++===++++， 由102x ≠+可得函数372x y x +=+的值域为()(),33,-∞+∞；（3）令10t x =-≥，则21x t =+，所以()()2211521212,048y x x t t t t ⎛⎫=-=+-=-+≥ ⎪⎝⎭，所以当14t =时，函数取最小值158， 所以函数21y x x =-15,8⎡⎫+∞⎪⎢⎣⎭；（4）由题意()22424x x x -+=--+，所以2044x x ≤-+≤， 所以2042x x -+≤，20242x x ≤-+≤， 所以函数224y x x =-+[]0,2.【名师点睛】遇到求解一般二次函数y ＝ax 2＋bx ＋c (a ≠0)的值域时，应采用配方法，将函数化简为y ＝m (x ＋n )2＋d 的形式，从而求得函数的值域．重要考点七：求函数值域的方法（换元法）【典型例题】已知1x >-，则函数27101x x y x ++=+的值域为________． 【答案】[9,)+∞【解析】设1t x =+由1x >-知，0t >，1x t =-，故22710(1)7(1)10451x x t t y t x t t++-+-+===+++， ∵44t t +≥ （当且仅当2t =时，等号成立）．∴函数2710(1)1x x y x x ++=>-+的值域为[9,)+∞．【题型强化】1.函数23y x =-的值域是__________ 【答案】7,2⎛⎤-∞ ⎥⎝⎦t =，则()21304t x t -=≥， ∴原函数化为213234t y t -=⨯--21722t t =--+()21142t =-++ ∵0t ≥，∴72y ≤，故答案为：7,2⎛⎤-∞ ⎥⎝⎦．2.函数y x =_______. 【答案】74⎡⎫+∞⎪⎢⎣⎭，【解析】令a =0a ≥，22x a =+，2217224y a a a ⎛⎫∴=+-=-+ ⎪⎝⎭0a ≥,12a ∴=，74min y =，∴函数y x =74⎡⎫+∞⎪⎢⎣⎭， 【名师点睛】 求解带根号且被开方式为一次式的函数的值域，直接求解很困难，既费时又费力，所以遇到这样的问题，我们要想到用一个字母代换掉带根号的式子．值得注意的是，在代换过程中，要注意根号下变量的取值范围．重要考点八：求函数解析式的常用方法（待定系数法）【典型例题】已知()y f x =是一次函数，且有[()]1615f f x x =-，则()f x 的解析式为______．【答案】()43f x x =-或()45f x x =-+【解析】由题意设()(0)f x ax b a =+≠，2(())()1615f f x a ax b b a x ab b x ∴=++=++=-，则21615a ab b ⎧=⎨+=-⎩，解得45a b =-⎧⎨=⎩或43a b =⎧⎨=-⎩，()43f x x ∴=-或()45f x x =-+， 故答案为：()43f x x =-或()45f x x =-+．【题型强化】1.已知函数()(0)f x ax b a =->，(())43f f x x =-，则(2)f =_______．【答案】3【解析】由题意，得2(())()()()43f f x f ax b a ax b b a x ab b x =-=⋅--=-+=-，即2430a ab b a ⎧=⎪+=⎨⎪>⎩，解得21a b =⎧⎨=⎩，()21f x x ∴=-，因此(2)3f =， 故答案为3.2.已知二次函数()()20f x ax bx c a =++≠，其图象过点()1,1-，且满足()()244f x f x x +=++，则()f x 的解析式为______.【答案】22f x x【解析】根据题意可知1a b c ++=-，又()()222244a x b x c ax bx c x ++++=++++恒相等，化简得到()()44244a b x a b c b x c ++++=+++恒相等， 所以444241a b b a b c c a b c +=+⎧⎪++=+⎨⎪++=-⎩，故1a =，0b =，2c =-，所以()f x 的解析式为22f x x .故答案为：22f x x .【名师点睛】 (1)一次函数可设为y ＝kx ＋b (k ≠0)，正比例函数可设为y ＝kx (k ≠0)；反比例函数可设为y ＝k x(k ≠0)；已知二次函数f (x )的顶点或对称轴、最值时，可设顶点式f (x )＝a (x ＋m )2＋n ；已知二次函数与x 轴两交点坐标时，常设分解(标根)式f (x )＝a (x －x 1)(x －x 2)．已知f (x )的图象过某三点时，常设一般式f (x )＝ax 2＋bx ＋c ；(2)凡是已知函数(或方程、不等式等)的形式时，常用待定系数法求解．重要考点九：恒成立的应用【典型例题】不等式210x kx -+>对任意实数x 都成立，则实数k 的取值范围是__________．【答案】(2,2)-【解析】∵不等式210x kx -+>对任意实数x 都成立，∴240k =-＜。

高一数学函数的定义一、考点、热点回顾1、判断函数2、求函数值3、求函数的定义域和值域二、典型例题1、函数的概念设A、B是非空的数集，如果按照某个确定的对应关系f，使对于集合A中的任意一个数x，在集合B中都有唯一确定的数f(x)和它对应，那么就称f：A→B为从集合A到集合B的一个函数．记作：y=f(x)，x∈A．其中，x叫做自变量，x的取值范围A叫做函数的定义域；与x的值相对应的y值叫做函数值，函数值的集合{f(x)| x∈A }叫做函数的值域．函数的判断方法：1、A和B必须是非空数集2、每个x必须有所对应3、一个x只能对应一个y (一个y却可以对应多哥x)注意：1、“y=f(x)”是函数符号，可以用任意的字母表示，如“y=g(x)”；2、f(x)表示一个整体，是一个函数；记号“f”可以看做是对x施加的某种运算法则；f(x)表示与x对应的函数值，是一个数，而不是f乘x3、A一定是定义域而B不一定是值域，值域是{f(x)| x∈A }【例一】判断下列对应关系是不是函数x1、A={ x| x∈Z }，B={ y| y∈Z },对应法则：y=32、A={ x|x>0, x∈R}，B={ y| y∈R },对应法则：2y =3x3、A={ x| x∈R }，B={ y| y∈R },对应法则：2y+2x =254、A=R,B=R, 对应法则：y=2x5、A={ x|-1<X<1, x∈R },B={0 },对应法则：y=0练习：判断下列图形表示的是不是函数【例二】求函数值：1、已知f(x)=x+4,求：f(x-1)，f(1/x), f(-a)2、定义在R上的函数f(x)满足f(x+y)= f(x)+ f(y)+2xy (x,y∈R)，f(1)=2，则f(-3)等于多少？练习：若f(x)满足f(ab)= f(a) +f(b),且f(2)=p, f(3)=q,则f(72)等于多少？2、函数的定义域函数的定义域是自变量x的取值范围，它是构成函数的重要组成部分，如果没有标明定义域，则认为是使函数解析式有意义的所有x的集合，但是要注意，在实际问题中定义域收到实际意义的制约。