牛顿冷却定律的表达式

牛顿冷却定律牛顿冷却定律（Newton's law of cooling)：温度高于周围环境的物体向周围媒质传递热量逐渐冷却时所遵循的规律。

当物体表面与周围存在温度差时，单位时间从单位面积散失的热量与温度差成正比，比例系数称为热传递系数。

牛顿冷却定律是牛顿在1701年用实验确定的，在强制对流时与实际符合较好，在自然对流时只在温度差不太大时才成立。

是传热学的基本定律之一，用于计算对流热量的多少。

如图所示：温差Δt＝|tw-tf|q＝hΔtΦ＝qA＝AhΔt＝Δt/(1/hA)其中的1/hA 称为对流传热热阻字母代码：q为热流密度h为物质的对流传热系数Φ为传热量A为传热面积冷却定律对于同一物体温度下降的速率,牛顿做过研究,并发现同一物体在外部介质性质及温度相同,本身性质及表面积相同时,物体冷却的速率只与外部与物体的温差有关.一个较周围热的物体温度为T,忽略表面积以及外部介质性质和温度的变化.它的冷却速率(dT/dt)与该物体的温度与周围环境的温度C的差(T-C)成正比.即dT/dt=-k(T-C).其中,t为时间,k为一个常数.计算方法是:对dT/dt=-k(T-C) 进行积分,得ln(T-C)=-kt+B(B为积分常数)(T-C)=e^(-kt+B) (1)设t=0,也就是物体的初温,(1)变成(T0-C)=e^B然后代入(1) 得T=C+(T0-C)^(-kt)算出B与k,代入t的值,就可以算出某个时间物体的温度.冷却定律推导出来,在忽略表面积以及外部介质性质和温度的变化,物体温度变化是越来越慢的.一、对权威的牛顿冷却定律提出挑战中学生姆潘巴的精心观察对权威的牛顿冷却定律提出挑战我（姆潘巴）在坦桑尼亚的马干巴中学读三年级时，校中的孩子们做冰淇淋总是先煮沸牛奶，待到冷却后再倒入冰盘，放进电冰箱。

为了争得电冰箱的最后一只冰盘，我决心冒着弄坏电冰箱的风险而把热牛奶放进去了。

一个多小时以后，我们打开电冰箱，里面出现了惊人的奇迹：我的冰盘里的热牛奶已结成坚硬的冰块，而他们的冰里还是稠稠的液体。

牛顿冷却定律牛顿冷却定律牛顿冷却定律（Newton's law of cooling)：温度高于周围环境的物体向周围媒质传递热量逐渐冷却时所遵循的规律。

当物体表面与周围存在温度差时，单位时间从单位面积散失的热量与温度差成正比，比例系数称为热传递系数。

牛顿冷却定律是牛顿在1701年用实验确定的，在强制对流时与实际符合较好，在自然对流时只在温度差不太大时才成立。

是传热学的基本定律之一，用于计算对流热量的多少。

如图所示：温差Δt＝|tw-tf|q＝hΔtΦ＝qA＝AhΔt＝Δt/(1/hA)其中的1/hA 称为对流传热热阻字母代码：q为热流密度h为物质的对流传热系数Φ为传热量A为传热面积冷却定律对于同一物体温度下降的速率,牛顿做过研究,并发现同一物体在外部介质性质及温度相同,本身性质及表面积相同时,物体冷却的速率只与外部与物体的温差有关.一个较周围热的物体温度为T,忽略表面积以及外部介质性质和温度的变化.它的冷却速率(dT/dt)与该物体的温度与周围环境的温度C的差(T-C)成正比.即dT/dt=-k(T-C).其中,t为时间,k为一个常数.计算方法是:对 dT/dt=-k(T-C) 进行积分,得ln(T-C)=-kt+B(B为积分常数)(T-C)=e^(-kt+B) (1)设t=0,也就是物体的初温,(1)变成(T0-C)=e^B然后代入 (1) 得T=C+(T0-C)^(-kt)算出B与k,代入t的值,就可以算出某个时间物体的温度.冷却定律推导出来,在忽略表面积以及外部介质性质和温度的变化,物体温度变化是越来越慢的.一、对权威的牛顿冷却定律提出挑战中学生姆潘巴的精心观察对权威的牛顿冷却定律提出挑战我（姆潘巴）在坦桑尼亚的马干巴中学读三年级时，校中的孩子们做冰淇淋总是先煮沸牛奶，待到冷却后再倒入冰盘，放进电冰箱。

为了争得电冰箱的最后一只冰盘，我决心冒着弄坏电冰箱的风险而把热牛奶放进去了。

一个多小时以后，我们打开电冰箱，里面出现了惊人的奇迹：我的冰盘里的热牛奶已结成坚硬的冰块，而他们的冰里还是稠稠的液体。

传热学三大基本公式Nu = 2+0.6(Re^1/2)(Pr^1/3) 。

F=Q/kK*△tm F 是换热器的有效换热面积。

Q 是总的换热量。

k 是污垢系数一般取0.8-0.9K。

是传热系数。

△tm 是对数平均温差。

传热学三种传热方式可以分开学。

传热学相较于理论力学，工程热力学，流体力学而言还是比较简单的，一般大学生掌握了高等数学完全可以自学的。

学习传热学必须有耐心，了解几种换热方式和常见的几个常数公式（努谢尔特数、格拉晓夫数、伯努利常数，傅里叶常数，而且常常推导下几个常用常数公式间的关系，你会惊奇地发现他们其实不少是远亲的），其实解决传热学问题绝大多数都是在和导热系数较劲，有时候是直接涉及。

扩展资料：在热对流方面，英国科学家牛顿于1701年在估算烧红铁棒的温度时，提出了被后人称为牛顿冷却定律的数学表达式，不过它并没有揭示出对流换热的机理。

传热学作为学科形成于19世纪。

1804年，法国物理学家毕奥在热传导方面得出的平壁导热实验结果是导热定律的最早表述。

稍后，法国的傅里叶运用数理方法，更准确地把它表述为后来称为傅里叶定律的微分形式。

1860年，基尔霍夫通过人造空腔模拟绝对黑体，论证了在相同温度下以黑体的辐射率(黑度)为最大，并指出物体的辐射率与同温度下该物体的吸收率相等，被后人称为基尔霍夫定律。

传热的三种方式：热的传递是由于物体内部或物体之间的温度差引起的。

若无外功输入，根据热力学第二定律，热量总是自动地从温度高的地方传递至温度较低的地方。

热能的传递有三种基本方式：热传导、热对流、热辐射，下面分别介绍这三种传热方式（一）热传导物体各部分之间不发生相对位移时，依靠分子，原子及自由电子等微观粒子的热运动而产生的热能传递成为热传导。

热传导的基本计算公式是傅立叶定律：在单位时间内热传导方式传递的热量与垂直于热流的截面积成正比，与温度梯度成正比，负号表示导热方向与温度梯度方向相反。

其中Q表示热流率，单位为W; dT/dx为温度梯度，单位为°C/m ;A为导热面积，单位为m2；λ为材料的导热系数，又称热导率，单位为W/(m°C) ，也可以为W/(mK) 。

对流传热公式
对于对流传热公式，其本质是牛顿冷却定律，即对流传热率与温
度差成正比，与传热面积、传热系数成正比。

其数学表达式为：Q = hAΔT
其中，Q为传热速率，单位为W或J/s；h为对流传热系数，单位
为W/(m²·K)；A为传热面积，单位为m²；ΔT为传热的温度差，单位
为K或℃。

需要注意的是，对流传热系数是由传热流体的性质、流速、传热
面的特性等因素决定的，而其解析式一般是无法给出的，需要通过实
验测定或经验公式来获得。

同时，在实际应用中，涉及较复杂的情况时，如自然对流、强迫对流、辐射对流等，对流传热公式需要结合其
他传热模型和理论来计算。

此外，对流传热过程中还会出现边界层效应、湍流效应等，这些
都需要进行特殊考虑。

还有一些特殊技术和装置，如换热器、冷却塔、空气调节装置等，则需要运用更为复杂的传热理论和模型。

综上所述，对流传热公式是传热学中最常见且基础的一种模型，但在实际应用中需要注意各种特殊因素，并采用合适的传热模型和理论进行分析和计算。

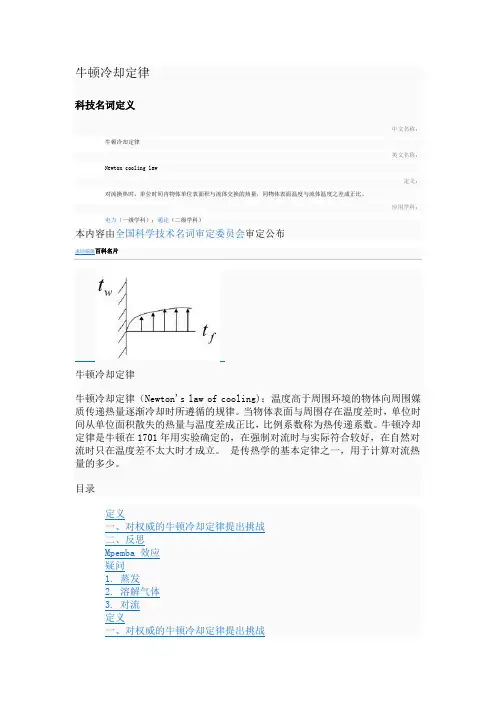
牛顿冷却定律科技名词定义中文名称：牛顿冷却定律英文名称：Newton cooling law定义：对流换热时，单位时间内物体单位表面积与流体交换的热量，同物体表面温度与流体温度之差成正比。

应用学科：电力（一级学科）；通论（二级学科）本内容由全国科学技术名词审定委员会审定公布牛顿冷却定律牛顿冷却定律（Newton's law of cooling)：温度高于周围环境的物体向周围媒质传递热量逐渐冷却时所遵循的规律。

当物体表面与周围存在温度差时，单位时间从单位面积散失的热量与温度差成正比，比例系数称为热传递系数。

牛顿冷却定律是牛顿在1701年用实验确定的，在强制对流时与实际符合较好，在自然对流时只在温度差不太大时才成立。

是传热学的基本定律之一，用于计算对流热量的多少。

目录展开编辑本段定义如图所示：温差Δt＝|tw-tf|q＝hΔtΦ＝qA＝AhΔt＝Δt/(1/hA)其中的1/hA 称为对流传热热阻字母代码：q为热流密度h为物质的对流传热系数Φ为传热量A为传热面积一个热的物体的冷却速度与该物体和周围环境的温度差成正比。

分析即 -dT/dt=(T-Tc)/τ式中，-dT/dt——物体的温度随时间下降的速度，负号表示物体的温度是下降的τ——物体的温度从T 下降到环境温度Tc实际所需要的弛豫时间在微分条件下，-dT/dt和(T-Tc)/τ是微线性关系。

这是微线性思维的典范之一。

牛顿冷却定律的这个微分方程没有考虑物体的性质，所以这不是物性方程式。

它只是关于一个假想物体，其温度随时间单纯下降的一个数学微分方程。

与其叫“牛顿冷却定律”，毋宁叫“牛顿冷却定理”更准确。

不过，这个明显的缺点，反而是最大的优点。

它的无比抽象性在宣告：“这是任何物体冷却的共同遵守的数学规律！”。

实验表明物体的温度随时间下降的速度和物体的结构以及理化性质并非完全无关。

尤其是急速冷却的条件下，我们可以修改线性“牛顿冷却定理”，给它添加若干个非线性的项就可以了解决实际问题了。

牛顿与冷却公式牛顿与冷却公式是物理学中两个重要的概念和公式。

牛顿是英国伟大的科学家和数学家，他对力学和光学的研究有着深远的影响。

而冷却公式则是描述物体在冷却过程中温度变化的数学模型。

本文将分别介绍牛顿和冷却公式的背景、原理和应用。

牛顿是17世纪的科学巨人，他的研究成果对于现代科学的发展起到了重要的推动作用。

在力学方面，他提出了三大运动定律，即惯性定律、动量定律和作用-反作用定律。

这些定律为后来的科学家们提供了研究物体运动和力学系统的基本原理。

而在光学方面，牛顿的研究成果主要体现在他的《自然哲学的数学原理》一书中。

他通过实验证明了白光是由多种颜色的光组成的，提出了色散理论，并发明了反射式望远镜和分光镜等仪器。

牛顿的成就使他被誉为科学史上最伟大的科学家之一。

冷却公式是描述物体在冷却过程中温度变化的数学模型。

根据热学定律，物体的温度会随着时间的推移而发生变化。

冷却公式可以用来计算物体在特定时间内的温度变化情况。

其中最常用的冷却公式是牛顿冷却定律，它表达了物体的冷却速率与物体表面积、温度差和环境温度之间的关系。

牛顿冷却定律的数学表达式为：q = h * A * ΔT其中，q表示冷却速率，h表示传热系数，A表示物体表面积，ΔT 表示物体温度与环境温度之差。

牛顿冷却定律的应用非常广泛，例如在工程领域中用于设计散热器、在天气预报中用于预测气温变化等。

牛顿与冷却公式在物理学和工程学中有着重要的应用。

牛顿的力学定律被广泛应用于各个领域，从天体运动到机械设计，都离不开这些基本定律的指导。

例如，火箭的发射过程中需要考虑到牛顿的第三定律，即推力和重力之间的平衡关系。

而冷却公式的应用则更加注重于热传导和温度变化方面。

在工程设计中，合理地利用冷却公式可以帮助我们设计出更高效的散热系统，提高设备的稳定性和寿命。

此外，在气象学中，冷却公式也被用来分析大气中的温度变化，从而预测天气情况和气温变化。

牛顿与冷却公式是物理学中两个重要的概念和公式。

牛顿冷却定律例题牛顿冷却定律是一个经典的物理学定律，用于描述物体受热或冷却过程中温度的变化规律。

这一定律在实际应用中非常广泛，如在医学中用于测量人体温度、在食品冷藏过程中控制温度等等。

本文将结合例题来详细介绍牛顿冷却定律的相关概念及应用。

1. 牛顿冷却定律的概念牛顿冷却定律是指一个物体受到周围介质的热交换时，它的温度变化与周围介质的温度差成正比，与物体的温度差成反比。

具体来说，设T为物体的温度，T0为周围介质的温度，t为时间，k为比例常数，则牛顿冷却定律可以表述为：dT/dt = -k(T - T0)其中，-k为物体的冷却速率，d(T - T0)为物体温度和周围介质温度之差的微小变化。

2. 牛顿冷却定律的应用下面我们结合一个具体的例题来探讨牛顿冷却定律在实际应用中的作用。

【例题】某医院使用一种新型温度计来测量患者体温。

这种温度计可以在药物中使用，可以测量口腔、肛门和腋下的体温。

假设一名患者在用完药物后，温度计放置在其腋下测量，初始温度为38.5℃，经过5分钟，温度下降至37.5℃。

已知室温为25℃，温度计的初始温度与室温相差10℃，试求出该患者的冷却速率和相对温度变化率。

（1）冷却速率的计算：根据牛顿冷却定律可得：ΔT/Δt = k(T - T0)代入已知数据可得：(38.5℃ - 25℃)/(5min) = k(38.5℃ - 25℃ - 10℃)解得 k = 0.0273 ℃/min因此，该患者的冷却速率为0.0273 ℃/min。

（2）相对温度变化率的计算：相对温度变化率也称为衰减系数，表示物体温度经过Δt时间后的相对变化程度，可以用指数函数来表示。

具体来说：ΔT/ΔT0 = e^(-kΔt)代入已知数据可得：ΔT/ΔT0 = e^(-0.0273*5) ≈ 0.755因此，该患者的相对温度变化率为0.755。

3. 总结牛顿冷却定律是物理学中的一个重要定律，在实际应用中具有非常广泛的应用。

牛顿冷却定律指数函数是什么牛顿冷却定律指数函数的标题：牛顿冷却定律与指数函数的关系牛顿冷却定律是描述物体温度变化的经典定律之一，它与指数函数有着密切的关系。

本文将探讨牛顿冷却定律与指数函数之间的联系以及如何利用指数函数来描述物体的温度变化。

让我们回顾一下牛顿冷却定律的表述：如果一个物体的温度远高于周围环境的温度，那么它的温度变化率与其与环境的温差成正比。

具体来说，牛顿冷却定律可以用以下公式表示：dT/dt = -k(T - Ta)其中，dT/dt表示温度变化率，k是一个正比例常数，T是物体的温度，Ta是环境的温度。

现在，我们来看看指数函数与牛顿冷却定律之间的关系。

指数函数是一种特殊的函数形式，可以用以下公式表示：f(x) = a * e^(bx)其中，a和b是常数，e是自然对数的底数。

指数函数的特点是随着自变量x的增加或减小，函数值呈指数级别的变化。

将牛顿冷却定律的温度变化率dT/dt与指数函数中的自变量x对应起来，我们可以发现它们之间存在着一定的对应关系。

在牛顿冷却定律中，温度变化率dT/dt与温度差(T - Ta)成正比；而在指数函数中，函数值f(x)与自变量x成指数关系。

这两者可以通过适当的变换联系起来。

假设我们令x = -kt，其中t表示时间，那么牛顿冷却定律可以改写为：dT/dx = -k(T - Ta)这与指数函数的形式相似，只是自变量的符号发生了变化。

我们可以将牛顿冷却定律的温度变化率dT/dx看作是指数函数f(x)关于自变量x的导数。

这意味着，物体的温度变化可以用指数函数来描述。

通过对指数函数的研究，我们可以了解物体温度随时间的变化趋势。

指数函数具有指数增长或指数衰减的特点，这取决于指数函数中常数b的值。

如果b大于零，指数函数将呈现指数增长的趋势；如果b小于零，指数函数将呈现指数衰减的趋势。

在牛顿冷却定律中，常数b与常数k有一定的关系。

根据牛顿冷却定律的表述，温度变化率dT/dt与温度差(T - Ta)成正比，而指数函数的导数f'(x)与指数函数的函数值f(x)成正比。

“化学工程基础”第三章热量传递复习题及答案一、填空题1. 牛顿冷却定律的表达式为_________，给热系数（或对流传热系数）α的单位是_______。

***答案*** q=αA△t ；W/（m2.K）2. 在列管式换热器中,用饱和蒸气加热空气,此时传热管的壁温接近________流体的温度,总传热系数K接近______流体的对流给热系数. ***答案*** 蒸气；空气3. 热量传递的方式主要有三种:_____、_______、__________.***答案*** 热传导；热对流；热辐射。

4．强化传热的方法之一是提高K值. 而要提高K值,则应提高对流传热系数_______________________. ***答案***较小一侧的给热系数。

5. 影响给热系数α的因素有＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿。

***答案*** 流体种类、流体性质、流体流动状态和传热壁面的几何尺寸6. 厚度不同的三种材料构成三层平壁,各层接触良好,已知b1>b2>b3;导热系数λ1<λ2<λ3。

在稳定传热过程中，各层的热阻R1______R2______R3;各层导热速率Q___Q___Q。

***答案*** R1>R2>R3；Q1=Q2=Q37. 一包有石棉泥保温层的蒸汽管道，当石棉泥受潮后，其保温效果应＿＿＿＿＿＿，主要原因是＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿。

***答案*** 降低；因水的导热系数大于保温材料的导热系数，受潮后，使保温层材料导热系数增大，保温效果降低。

8. 用冷却水将一定量的热流体由100℃冷却到40℃，冷却水初温为15℃，在设计列管式换热器时，采用两种方案比较，方案Ⅰ是令冷却水终温为30℃，方案Ⅱ是令冷却水终温为35℃，则用水量W1＿＿W2，所需传热面积A1＿＿＿A2。

***答案*** 大于；小于9. 列管式换热器的壳程内设置折流挡板的作用在于___________________，折流挡板的形状有____________________，____________________等。