2020年全国1卷省份高考模拟理科数学分类---三角函数
- 格式:docx
- 大小:1.53 MB
- 文档页数:39
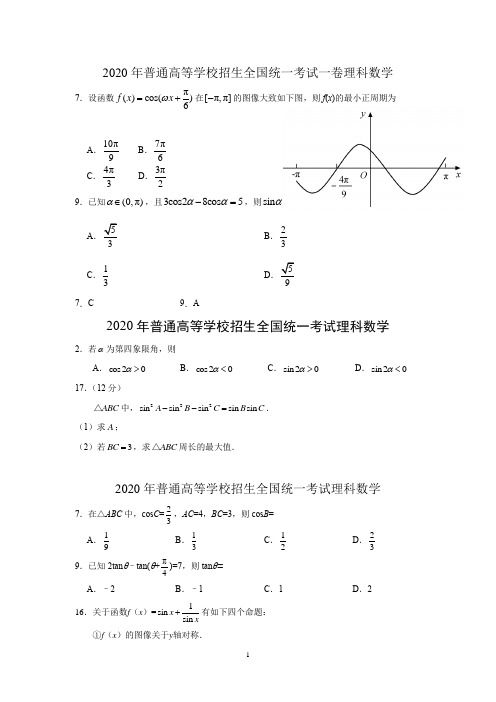
2020年普通高等学校招生全国统一考试一卷理科数学7.设函数()cos π()6f x x ω=+在[]π,π-的图像大致如下图,则f (x )的最小正周期为A .10π9 B .7π6C .4π3D .3π29.已知 π()0,α∈,且3cos28cos 5αα-=,则sin α=A .53B .23 C .13D .597.C9.A2020年普通高等学校招生全国统一考试理科数学2.若α为第四象限角,则A .02cos >αB .02cos <αC .02sin >αD .02sin <α17.(12分)ABC △中,222sin sin sin sin sin A B C B C --=.(1)求A ;(2)若3BC =,求ABC △周长的最大值.2020年普通高等学校招生全国统一考试理科数学7.在△ABC 中,cos C =23,AC =4,BC =3,则cos B = A .19B .13C .12D .239.已知2tan θ–tan(θ+π4)=7,则tan θ= A .–2B .–1C .1D .216.关于函数f (x )=1sin sin x x+有如下四个命题: ①f (x )的图像关于y 轴对称.②f (x )的图像关于原点对称. ③f (x )的图像关于直线x =2π对称. ④f (x )的最小值为2.其中所有真命题的序号是__________. 7.A9.D16.②③2020年普通高等学校招生全国统一考试文科数学7.设函数π()cos()6f x x ω=+在[−π,π]的图像大致如下图,则f (x )的最小正周期为A .10π9 B .7π6 C .4π3D .3π218.(12分)ABC △的内角A ,B ,C 的对边分别为a ,b ,c .已知B =150°.(1)若a 3,b 7ABC △的面积; (2)若sin A 3C 2,求C . 7.C18.解:(1)由题设及余弦定理得22228323cos150c c c =+-⨯︒,解得2c =-(舍去),2c =,从而23a =ABC △的面积为1232sin15032⨯⨯︒=(2)在ABC △中,18030A B C C =︒--=︒-,所以sin 3sin(30)3sin(30)A C C C C =︒-=︒+,故2sin(30)2C ︒+=而030C <<︒,所以3045C ︒+=︒,故15C =︒.2020年普通高等学校招生全国统一考试文科数学13.若2sin 3x =-,则cos2x =__________. 17.(12分)△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知25cos ()cos 24A A π++=. (1)求A ;(2)若b c -=,证明:△ABC 是直角三角形. 13.1917.解:(1)由已知得25sin cos 4A A +=,即21cos cos 04A A -+=. 所以21(cos )02A -=,1cos 2A =.由于0A <<π,故3A π=.(2)由正弦定理及已知条件可得sin sin B C A -=.由(1)知23B C π+=,所以2sin sin()33B B ππ--=.即11sin 22B B =,1sin()32B π-=.由于03B 2π<<,故2B π=.从而ABC △是直角三角形. 2020年普通高等学校招生全国统一考试文科数学5.已知πsin sin=3θθ++()1,则πsin =6θ+()A .12BC .23D11.在△ABC 中,cos C =23,AC =4,BC =3,则tan B = AB .C .D .12.已知函数f (x )=sin x +1sin x,则 A .f (x )的最小值为2 B .f (x )的图像关于y 轴对称 C .f (x )的图像关于直线x =π对称D .f (x )的图像关于直线2x π=对称 5.B11.C12.D2020年普通高等学校招生全国统一考试(北京卷)(9)已知αβ∈R ,,则“存在k ∈Z ,使得π(1)kk αβ=+-”是“βαsin sin =”的(A )充分而不必要条件 (B )必要而不充分条件 (C )充分必要条件(D )既不充分也不必要条件(10)2020年3月14日是全球首个国际圆周率日(πay)D 。

2020全国高考数学1卷三角
2020年全国高考数学一卷的试题涉及到了一道关于三角函数的题目,让考生
们在短时间内展示出对三角函数的理解和运用能力。
三角函数作为数学中的一个重要分支,在几何学和物理学中起着重要的作用,因此掌握好三角函数的知识是非常重要的。
这道题目要求考生证明一个不等式,其中涉及到了三角函数的性质和运算规律。
在解这类题目时,首先要明确三角函数的定义和基本性质,例如正弦函数和余弦函数的周期性、奇偶性等。
这样才能在解题过程中正确地运用三角函数的相关性质,从而得出正确的结论。
另外,解这类题目还需要考生具备一定的逻辑推理能力和数学思维,能够灵活运用已有的知识来解决新的问题。
在解题过程中,考生需要不断地分析题目的要求,找出其中隐藏的规律和线索,从而有针对性地展开解题思路,最终得出正确的结论。
此外,解这类题目还需要考生具备一定的数学运算技巧,能够熟练地运用三角函数的性质和运算规律,灵活地变换和简化复杂的表达式。
只有在掌握了基本的数学运算技巧的基础上,才能在解题过程中高效地进行推理和计算,从而顺利地解出题目。
综上所述,三角函数作为数学中的一个重要分支,在高考数学试题中往往扮演着重要的角色。
掌握好三角函数的基本知识和运用技巧,对于考生来说至关重要。
只有在不断地学习和实践中提升自己的数学能力,才能在高考中取得优异的成绩。
希望广大考生能够认真学习三角函数的相关知识,不断提升自己的数学水平,为高考取得好成绩打下坚实的基础。


2020年高考试题分类汇编(三角函数)考点1三角函数的图像和性质1.(2020·全国卷Ⅰ·文理科)设函数()cos()f x x πω=+在[,]ππ-的图像大致如下图,则()fx 的最小正周期为 A .109πB .76π C 2.(2020·山东卷)如图是函数sin()y x ωϕ=+的部分图像,则sin()x ωϕ+=A.sin()3x π+ B .sin(2)3x π- C.cos(2)6x π+ D .5cos(2)6x π-3.(2020·浙江卷)函数cos sin y x x x =+在区间[,]ππ-的图象大致为4.(2020·全国卷Ⅲ·理科)关于函数1()sin sin f x x x=+有如下四个命题: ①()f x 的图像关于y 轴对称; ②()f x 的图像关于原点对称; ③()f x 的图像关于2x π=轴对称; ④()f x 的最小值为2.其中所有真命题的序号是 .5.(2020·全国卷Ⅲ·文科)设函数1()sin sin f x x x=+,则 A .()f x 有最小值为2 B .()f x 的图像关于y 轴对称 C .()f x 的图像关于x π=轴对称 D .()f x 的图像关于2x π=轴对称6.(2020·上海卷)已知()sin f x x ω=(0ω>). (Ⅰ)若()f x 的周期是4π,求ω,并求此时1()2f x =的解集;(Ⅱ)已知1ω=,2()()()()2g x f x x f x π=--,[0,]4x π∈,求()g x的值域.7.(2020·天津卷)已知函数()sin()3f x x π=+.给出下列结论: ①()f x 的最小正周期为2π; ②()2f π是()f x 的最大值;③把函数sin y x =的图象上所有点向左平移3π个单位长度,可得到函数()y f x =的图象.其中所有正确结论的序号是A.①B.①③C.②③D.①②③ 8.(2020·北京卷)若函数()sin()cos f x x x ϕ=++的最大值为2,则常数ϕ的一个取值为 .9.(2020·全国卷Ⅱ·理科)已知函数2()sin sin 2f x x x =. (Ⅰ)讨论()f x 在区间(0,)π的单调性;(Ⅱ)证明:()f x ≤;(Ⅲ)设n N *∈,证明:22223sin sin 2sin 4sin 24nnn x x xx ≤.考点2恒等变换1.(2020·全国卷Ⅰ·理科)已知(0,)απ∈,且3cos28cos 5αα-=,则sin α=A .23 C .13D 2.(2020·全国卷Ⅱ·理科)若α为第四象限的角,则A .cos20α>B .cos20α<C .sin 20α>D .sin 20α<3.(2020·全国卷Ⅱ·文科)2sin 3x =-,则cos2x = .4.(2020·全国卷Ⅲ·理科)已知2tan tan()74πθθ-+=,则tan θ=A .2-B .1-C .1D .2 5.(2020·全国卷Ⅲ·文科)sin sin()13πθθ++=,则sin()6πθ+=A .12BC .23D6.(2020·浙江卷)已知tan 2θ=,则cos2θ= ;tan()4πθ-= .考点3解三角形1.(2020·全国卷Ⅲ·理科)在ABC ∆中,2cos 3C =,4AC =,3BC =,则cos B = A .19 B .13 C .12 D .232.(2020·全国卷Ⅲ·文科)在ABC ∆中,2cos 3C =,4AC =,3BC =,则tan B =A B ... 3.(2020·全国卷Ⅰ·文科)ABC ∆的内角A ,B ,C 所对的边分别为a ,b ,c .已知150B =.(Ⅰ)若a =,b =ABC ∆的面积;(Ⅱ)若sin 2A C =,求C . 4.(2020·全国卷Ⅱ·理科)ABC ∆中,222sin sin sin sin sin A B C B C --=.(Ⅰ)求A ;(Ⅱ)若3BC =,求ABC ∆周长的最大值.5.(2020·全国卷Ⅱ·文科)ABC ∆的内角A ,B ,C 所对的边分别为a ,b ,c ,已知25cos ()cos 24A A π++=.(Ⅰ)求A ;(Ⅱ)若b c -=,证明:ABC ∆是直角三角形.6.(2020·山东卷)在①ac =,②sin 3c A =,③c =这三个条件中任选一个,补充在下面问题中,若问题中的三角形存在,求c 的值;若问题中的三角形不存在,说明理由.问题:是否存在ABC ∆,它的内角A ,B ,C 所对的边分别为a ,b ,c .且sin AB ,6C π=, ?7.(2020·北京卷)在ABC ∆中,11a b +=,再从条件①、条件②这两个条件中选择一个作为己知,求: (Ⅰ)a 的值:(Ⅱ)sin C 和ABC ∆的面积.条件①:7c =,1cos 7A =-;条件②:1cos 8A =,9cos 16B =.注:如果选择条件①和条件②分别解答,按第一个解答计分.8.(2020·天津卷)在ABC ∆中,角A ,B ,C 所对的边分别为a ,b ,c .已知a =5b =,c =. (Ⅰ)求角C 的大小; (Ⅱ)求sin A 的值; (Ⅲ)求sin(2)4A π+的值. 9.(2020·浙江卷)在锐角ABC ∆中,角A ,B ,C 所对的边分别为a ,b ,c ,且2sin b A =. (Ⅰ)求角B ;(Ⅱ)求cos cos cos A B C ++的取值范围.。

2020年高考全国一卷理科数学答案及解析2020-12-12【关键字】情况、条件、问题、焦点、建设、建立、了解、研究、位置、关系、检验、倾斜、满足、规划、实现参考答案与解析一、选择题:本题有12小题,每小题5分,共60分。
1、设z=,则|z|=A 、0B 、C 、1D 、【答案】C【解析】由题可得i z =+=2i )i -(,所以|z|=1【考点定位】复数2、已知集合A={x|x 2-x-2>0},则A =A 、{x|-1<x<2}B 、{x|-1x 2}C 、{x|x<-1}∪{x|x>2}D 、{x|x -1}∪{x|x 2} 【答案】B【解析】由题可得C R A={x|x 2-x-2≤0},所以{x|-1x 2}【考点定位】集合3、某地区经过一年的新农村建设,农村的经济收入增加了一倍,实现翻番,为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例,得到如下饼图:则下面结论中不正确的是:A 、新农村建设后,种植收入减少。
B 、新农村建设后,其他收入增加了一倍以上。
C 、新农村建设后,养殖收入增加了一倍。
D 、新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半。
【答案】A【解析】由题可得新农村建设后,种植收入37%*200%=74%>60%, 【考点定位】简单统计4、记S n 为等差数列{a n }的前n 项和,若3S 3=S 2+S 4,a 1=2,则a 5= A 、-12 B 、-10C 、10D 、12 【答案】B【解析】3*(a 1+a 1+d+a 1+2d)=( a 1+a 1+d) (a 1+a 1+d+a 1+2d+a 1+3d),整理得: 2d+3a 1=0 ; d=-3 ∴a 5=2+(5-1)*(-3)=-10 【考点定位】等差数列 求和5、设函数f (x )=x 3+(a-1)x 2+ax ,若f (x )为奇函数,则曲线y=f (x )在点(0,0)处的切线方程为: A 、y=-2x B 、y=-x C 、y=2x D 、y=x 【答案】D【解析】f (x )为奇函数,有f (x )+f (-x )=0整理得: f (x )+f (-x )=2*(a-1)x 2=0 ∴a=1 f (x )=x 3+x 求导f ‘(x )=3x 2+1 f ‘(0)=1 所以选D【考点定位】函数性质:奇偶性;函数的导数 6、在ABC 中,AD 为BC 边上的中线,E 为AD 的中点,则=A 、--B 、--C 、-+D 、- 【答案】A【解析】AD 为BC 边∴上的中线 AD=AC 21AB 21+ E 为AD 的中点∴AE=AC 41AB 41AD 21+= EB=AB-AE=AC 41AB 43)AC 41AB 41(-AB -=+= 【考点定位】向量的加减法、线段的中点7、某圆柱的高为2,底面周长为16,其三视图如右图,圆柱表面上的点M 在正视图上的对应点为11A ,圆柱表面上的点N 在左视图上的对应点为B ,则在此圆柱侧面上,从M 到N的路径中,最短路径的长度为 A 、B 、C 、3D 、2 【答案】B【解析】将圆柱体的侧面从A 点展开:注意到B 点在41圆周处。

专题6三角函数研究发现,课标全国卷的试卷结构和题型具有一定的稳定性和延续性,每个题型考查的知识点、考查方法、考查角度、思维方法等相对固定,掌握了全国卷的各种题型,就把握了全国卷命题的灵魂,基于此,潜心研究全国Ⅰ、Ⅱ、Ⅲ卷及高考数学考试说明,精心分类汇总至少最近三年全国卷的所有题型(按年份先理后文排列),对把握全国卷命题的方向,指导我们的高考有效复习,走出题海,快速提升成绩,会起到事半功倍的效果。
三角函数——近3年三角函数考了45道,每年理科1-3道小题,文科2-4道小题,当考3-4道小题时,当年就不在考三角函数大题了,题目多数难度较小,主要考查公式熟练运用、平移、图像性质、化简求值、解三角形等问题(含应用问题),多数属于“中档题”,小心平移(重点,难点,几乎年年考),也会有难题,如2016年全国1卷12题和2018年全国1卷16题的考法是比较难的,所以当了压轴题。
1.(2018年普通高等学校招生统一考试新课标Ⅰ卷数学(理16))已知函数f(x)=2sinx+sin2x,则f(x)的最小值是.【答案】见解析。
【考点】利用导数研究函数的最值;三角函数的最值.【专题】11:计算题;34:方程思想;49:综合法;53:导数的综合应用;56:三角函数的求值.【分析】由题意可得T=2π是f(x)的一个周期,问题转化为f(x)在[0,2π)上的最小值,求导数计算极值和端点值,比较可得.【解答】解:由题意可得T=2π是f(x)=2sinx+sin2x的一个周期,故只需考虑f(x)=2sinx+sin2x在[0,2π)上的值域,先来求该函数在[0,2π)上的极值点,求导数可得f′(x)=2cosx+2cos2x=2cosx+2(2cos2x﹣1)=2(2cosx﹣1)(cosx+1),令f′(x)=0可解得cosx=或cosx=﹣1,可得此时x=,π或;∴y=2sinx+sin2x的最小值只能在点x=,π或和边界点x=0中取到,计算可得f()=,f(π)=0,f()=﹣,f(0)=0,∴函数的最小值为﹣,故答案为:.【点评】本题考查三角函数恒等变换,涉及导数法求函数区间的最值,属中档题.2.(2017年普通高等学校招生统一考试新课标Ⅰ卷数学(理9))已知曲线C1:y=cosx,C2:y=sin(2x+),则下面结论正确的是()A.把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移个单位长度,得到曲线C2B.把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移个单位长度,得到曲线C2C.把C1上各点的横坐标缩短到原来的倍,纵坐标不变,再把得到的曲线向右平移个单位长度,得到曲线C2D.把C1上各点的横坐标缩短到原来的倍,纵坐标不变,再把得到的曲线向左平移个单位长度,得到曲线C2【考点】:函数y=Asin(ωx+φ)的图象变换.【专题】计算题;35:转化思想;57:三角函数的图像与性质.【分析】利用三角函数的伸缩变换以及平移变换转化求解即可.【解答】解:把C1上各点的横坐标缩短到原来的倍,纵坐标不变,得到函数y=cos2x图象,再把得到的曲线向左平移个单位长度,得到函数y=cos2(x+)=cos(2x+)=sin(2x+)的图象,即曲线C2,故选:D.【点评】本题考查三角函数的图象变换,诱导公式的应用,考查计算能力.3.(2016年普通高等学校招生统一考试新课标Ⅰ卷数学(理12))已知函数f(x)=sin(ωx+φ)(ω>0,|φ|≤),x=﹣为f(x)的零点,x=为y=f(x)图象的对称轴,且f(x)在(,)上单调,则ω的最大值为()A.11 B.9 C.7 D.5【考点】H6:正弦函数的奇偶性和对称性.【专题】35:转化思想;4R:转化法;57:三角函数的图像与性质.【分析】根据已知可得ω为正奇数,且ω≤12,结合x=﹣为f(x)的零点,x=为y=f(x)图象的对称轴,求出满足条件的解析式,并结合f(x)在(,)上单调,可得ω的最大值.【解答】解:∵x=﹣为f(x)的零点,x=为y=f(x)图象的对称轴,∴,即,(n∈N)即ω=2n+1,(n∈N)即ω为正奇数,∵f(x)在(,)上单调,则﹣=≤,即T=≥,解得:ω≤12,当ω=11时,﹣+φ=kπ,k∈Z,∵|φ|≤,∴φ=﹣,此时f(x)在(,)不单调,不满足题意;当ω=9时,﹣+φ=kπ,k∈Z,∵|φ|≤,∴φ=,此时f(x)在(,)单调,满足题意;故ω的最大值为9,故选:B.【点评】本题考查的知识点是正弦型函数的图象和性质,本题转化困难,难度较大.4.(2018年普通高等学校招生统一考试新课标Ⅱ卷数学(理6))在△ABC中,cos=,BC=1,AC=5,则AB=()A.4B.C.D.2【考点】HR:余弦定理.【专题】11:计算题;35:转化思想;49:综合法;58:解三角形.【分析】利用二倍角公式求出C的余弦函数值,利用余弦定理转化求解即可.【解答】解:在△ABC中,cos=,cosC=2×=﹣,BC=1,AC=5,则AB====4.故选:A.【点评】本题考查余弦定理的应用,考查三角形的解法以及计算能力.5.(2018年普通高等学校招生统一考试新课标Ⅱ卷数学(理10))若f(x)=cosx﹣sinx在[﹣a,a]是减函数,则a的最大值是()A.B.C.D.π【考点】GP:两角和与差的三角函数;H5:正弦函数的单调性.【专题】33:函数思想;4R:转化法;56:三角函数的求值.【分析】利用两角和差的正弦公式化简f(x),由,k∈Z,得,k∈Z,取k=0,得f(x)的一个减区间为[,],结合已知条件即可求出a的最大值.【解答】解:f(x)=cosx﹣sinx=﹣(sinx﹣cosx)=,由,k∈Z,得,k∈Z,取k=0,得f(x)的一个减区间为[,],由f(x)在[﹣a,a]是减函数,得,∴.则a的最大值是.故选:A.【点评】本题考查了两角和与差的正弦函数公式的应用,三角函数的求值,属于基本知识的考查,是基础题.6.(2018年普通高等学校招生统一考试新课标Ⅱ卷数学(理15))已知sinα+cosβ=1,cosα+sinβ=0,则sin(α+β)=.【答案】见解析。
专题06三角函数及解三角形2020年高考真题1. [2020年高考全国I卷理数】设函数f(x) = cos(®x + -)在[-”,兀]的图像大致如下图,则/(%)的最小正6周期为9 64兀3兀C. —D.兰3 2【答案】C【解析】由图可得:函数图象过点( 4 兀1T \将它代入函数/(兀)可得:cosl一- •<« + —1 = 0,又[-普,o]是函数/(兀)图象与x轴负半轴的第一个交点,十.I 4兀兀兀5 e 3所以-亍0+丁丐,解得r •2K _ 2兀_ 4兀所以函数/(%)最小正周期为=T=T=T2故选C.【点睛】本题主要考查了三角函数的性质及转化能力,还考查了三角函数周期公式,属于中档题.2. [2020 年高考全国I 卷理数】已知cc G (0,7i),且3COS2Q-8COSQ =5 ,贝0 sin^z =A. B.【答案】A又 a e (0, n),.'. sin a = Jl-cos? a =•故选:A. 【点睛】本题考查三角恒等变换和同角间的三角函数关系求值,熟记公式是解题的关键,考查计算求解 能力,属于基础题.3.【2020年高考全国II 卷理数】若a 为第四象限角,则B. cos2a<0D. sin2a<0 【答案】D【解析】方法-:由。
为第四象限角,可得亍2炽“<2卄2炽从Z,所以 3兀 + 4k 兀 < 2a < 4兀 + 4-kn, e Z此时2a 的终边落在第三、四象限及V 轴的非正半轴上,所以sin2a<0,故选:D.兀方法二:当& =——时,cos 2a = cos 由a 在第四象限可得:sin a <0, cos a > 0 ,则由2 a 蕃1 aaz Qz < ,选项C 错误,选项D 正确; 故选:D.【点睛】本题主要考查三角函数的符号,二倍角公式,特殊角的三角函数值等知识,意在考查学生的转 化能力和计算求解能力.C. sin2a>0>0,选项B 错误;<0,选项A 错误;【解析】3cos2a-8cosa = 5 ,得6cos 2tz-8coscr-8 = 0 -【答案】A2【解析】在ABC中,cosC = —, AC = 4, BC = 3, 3根据余弦定理:AB2 =AC2+BC2-2AC BC COS C,7AB- =42+32-2X4X3X-,3可得AB2 = 9,即AB — 3 ,… AB2+BC2-AC2 9 + 9-16 1由cos B = ------------------------- = ------------ =—,2ABBC2x3x3 9故cos B =—.9故选:A.5. [2020年高考全国III卷理数】已知2tan^-tan(0+ —)=7,则tan^=A. -2B. -1【答案】D【解析】2 tan - tan | ^ + — | = 7 , z. 2tan^~ tan^ + ^ =7 ,I 4 丿 1 - tan令/ = tan&,/Hl,则2/—土 = 7,整理得严_4/ + 4 = 0,解得t = 2,即tan6» = 2.故选:D.【点睛】本题主要考查了利用两角和的正切公式化简求值,属于中档题.6.【2020年高考北京】2020年3月14日是全球首个国际圆周率日(兀Day).历史上,求圆周率兀的方法有多种,与中国传统数学中的“割圆术”相似.数学家阿尔•卡西的方法是:当正整数"充分大时,计算单位圆的内接正6“边形的周长和外切正6“边形(各边均与圆相切的正6“边形)的周长,将它们的算术平均数作为2兀的近似值.按照阿尔•卡西的方法,兀的近似值的表达式是2 71 、[/ — 71 -- 当“一 2571 6 _ 时,y = —1 二 2x^ + ^ = —+ 2^(^ e Z),3n < .30° 30°) 6n < .30° 30°) A. sin —— + tan ----- B. sin —— + tan ----- 1 n n 丿 I n n ) 3n (.60° 60°) 6n (.60° < 60°) c. sin ---- + tan ----- D. sin ----- + tan ----- I nn 丿 I nn ) 【答案】A 360° 60° 30° 【解析】单位圆内接正6〃边形的每条边所对应的圆周角为一 =——,每条边长为2sin —, nx6 n n 30° 所以,单位圆的内接正6〃边形的周长为12nsin ——, n30° 30° 单位圆的外切正6n 边形的每条边长为2tan —,其周长为12〃tan —, n n30° 30° 12nsin ----- 12ntan ---------.・.* 二 ----- n --------------- n _ 2( 30° 30°则 7i = 3n\ sin------ + tan --- I n n故选:A.【点睛】本题考查圆周率兀的近似值的计算,根据题意计算出单位圆内接正6〃边形和外切正6〃边形的 周长是解答的关键,考查计算能力,属于中等题.7. [2020年新高考全国I 卷】下图是函数y 二sin (亦+卩)的部分图像,贝!j sin (亦+卩)=【答案】BC=6“ sin 竺+ tan 竺, I n n ) A. sin(x + f)¥亠)【解析】由函数图像可知:- = -7T —— 2 3 71 _71 6~2 27T 则血=—=—=2,所以不选A, T 71 B.解得:cp 二 Ikn + 彳兀(£ e Z ),即函数的解析式为:y = sin| 2x + —TT + 2A ;7Z - | = sin| 2x + —+ —| = cos| 2x + — | = sin| — -2x I 3 丿(6 2丿(6丿(3 (\5/r而 cos I 2x + — I — - cos( — 2x) 故选:BC.【点睛】已知fix) =Asin(a}x +^)(A>0, e>0)的部分图象求其解析式时,A 比较容易看图得出,困难的 是求待定系数e 和0常用如下两种方法:竺即可求出e ;确定y 时,若能求出离原点最近的右侧图象上升(或下降)的“零点”横坐标xo,则令 exo+0 = O(或 a )xo+<p=7t'),即可求出 <p.(2)代入点的坐标,利用一些已知点(最高点、最低点或“零点”)坐标代入解析式,再结合图形解出co 和<p, 若对A, e 的符号或对°的范围有要求,则可用诱导公式变换使其符合要求.&【2020年高考全国I 卷理数】如图,在三棱锥P ABC 的平面展开图中,AC=1, AB = AD =也,佔丄AC, AB±AD, ZCAE=30°,贝0 cosZFCB= _______________ .【答案】4【解析】 AB 丄AC, AB = j3, AC = E由勾股定理得BC = V A B 2+AC 2 = 2 ‘71 F(P)同理得 BD =品,:.BF = BD = ^,在△4CE 中,AC = 1, AE = AD =运,ZCAE = 30 ,由余弦定理得 CF = 3+^2—240 AEcos30 =l + 3-2xlxV3x —= 1, 2:.CF = CE = 1,在 BCF 中,BC = 2, BF =愿,CF = 1,CF~ + BC 2 -BF 2由余弦定理得cos ZFCB = 七——2CFBC故答案为:—. 4【点睛】本题考查利用余弦定理解三角形,考查计算能力,属于中等题.9.【2020年高考全国III 卷理数】16.关于函数f (x) =sinx ——-—有如下四个命题: sinx®f (%)的图像关于y 轴对称.®f (x)的图像关于原点对称.1T®f (X )的图像关于直线x=3对称.®f (X )的最小值为2.其中所有真命题的序号是 __________ .【答案】②③所以,函数/(x)的图象不关于y 轴对称,命题①错误;对于命题②,函数/(X )的定义域为[x\x^kn,k^Z^ ,定义域关于原点对称, / ( -x) = sin (-%) + —r = - sin x - -— = -fsinx + -^―] = -/(%),sin (—兀) sinx I sinx)所以,函数/(x)的图象关于原点对称,命题②正确;1 + 4-6 2x1x2 【解析】对于命题①,A 7C \ . (7C ] 1(2 丿(2 ) .(7i' 7' 7 sm —+ x12所以,函数/(x)的图象关于直线x = |对称,命题③正确;对于命题④,当一7i<x<0时,sinx<0,贝J f(x} = sinx + — <0< 2 , sinx命题④错误.故答案为:②③.【点睛】本题考查正弦型函数的奇偶性、对称性以及最值的求解,考查推理能力与计算能力,属于中等题.JT 210.【2020年高考江苏】已知sin2(-+ <?) = -,则sin2a 的值是▲.4 3【解析】Qsin2(—+ cr) = (-^cosa-\——sin a)2 = —(1 + sin 2a)4 2 2 21 2 1— (1 + sin 2a) = —sin 2a =—2 3 3故答案为:-3【点睛】本题考查两角和正弦公式、二倍角正弦公式,考查基本分析求解能力,属基础题.11.【2020年高考北京】若函数/(x) = sin(x+^) + cosx的最大值为2,则常数0的一个取值为 _______________IT TT【答案辽(2唸+亍心均可)【解析】因为 (兀)=cos ©sin 兀 +(sin 0 + 1)cos 兀=Jcos? 0 +(sin 0 + 1)2 sin (兀+ 0), 所以Jcos?(p + (sin(p +1『=2,解得sin0 = l,故可取^ = ~-7T7T故答案为:-(2^ + -,^eZ 均可). 2 2【点睛】本题主要考查两角和的正弦公式,辅助角公式的应用,以及平方关系的应用,考查学生的数 学运算能力,属于基础题.1T12. [2020 年高考浙江】已知 tan& = 2,则 cos2& = _______ , tan(6>-一) = ______ .3 1【答案】V 巧cos 2 0-sin 2 0 _ 1-tan 2 _ 1 -22cos 2 ^ + sin 2 0 1 + tan 2 0 1 + 223 1故答案为: 【点睛】本题考查二倍角余弦公式以及弦化切、两角差正切公式,考查基本分析求解能力,属基础题.13. [2020年高考江苏】将函数y = 3sin(2x +^)的图象向右平移夕个单位长度,则平移后的图象中与y 轴最 4 6近的对称轴的方程是▲ • 【答案】2-峯 24V/ 'j I r jl【解析】y — 3sin[2(x ---- ) —] = 3 sin(2x ------ ) 6 4 12小 TC TC , , x 7 TT k/C 7 x2x ------ — —F k 兀G Z)x — ----------- 1 ---- (k G Z) 12 2 24 2当k = -1时兀=——• 24故答案为:x =———24 【点睛】本题考查三角函数图象变换、正弦函数对称轴,考查基本分析求解能力,属基础题.14. [2020年新高考全国I 卷】某中学开展劳动实习,学生加工制作零件,零件的截面如图所示.O 为圆孔 及轮廓圆弧AB 所在圆的圆心,A 是圆弧AB 与直线AG 的切点,B 是圆弧与直线BC 的切点,四边 形 DEFG 为矩形,BC 丄DG,垂足为 C, tanZODC= - , BH//DG , EF=12 cm, DE=2 cm, A 到直线5DE 和EF 的距离均为7 cm,圆孔半径为1 cm,则图中阴影部分的面积为 ___________ cm 2.【解析】cos 20 = cos 2 0 - sin 2 0 = tan <9-1 l + tan& 2-11 + 2【答案】4 + »兀 2【解析】设05 = OA=r,由题意AM = AN = 1, EF = \2,所以NF = 5,因为 AP = 5,所以 ZAGP = 45\因为 BH//DG,所以 ZAH0 = 45°,因为AG 与圆弧4B 相切于A 点,所以Q4丄4G,即AOAH 为等腰直角三角形;在直角△0QD 中,0Q = 5_^r ,DQ = l-—r ,2 2因为 tanZ0DC = -^ = |,所以 21- —r = 25-^r , DQ 5 22 解得 r = 2A /2 ;等腰直角MAH 的面积为恥》2屈2尽4;I 所以阴影部分的面积为S] + S?—㊁兀=4 +三-•故答案为:4 + T.扇形A0B 的面积S 2 = =3乃,【点睛】本题主要考查三角函数在实际中应用,把阴影部分合理分割是求解的关键,以劳动实习为背景,体现了五育并举的育人方针.15.【2020 年高考全国II 卷理数】/XABC 中,sin2A —sin2B—sin2C= sinBsinC.(1)求A;(2)若BC=3,求zMBC周长的最大值.【解析】(1)由正弦定理和已知条件得BC2-AC2-AB2^AC AB,①由余弦定理得BC2 = AC2 +AB2- 2AC AB cos A,②由①,②得cos A =—.22兀因为0<4<兀,所以A =—.3(2)由正弦定理及(1)得上匕=少-=-?£ = 2巧,sin B sin C sin A从而AC = 2A/3 sin B , AB = 2^3 sin(兀一A - B) = 3 cos B一A/3 sin B.故BC + 4C + AB = 3 + 7^sinB + 3cosB = 3 + 2V^sin(B + ¥).X0<B<-,所以当B =-时,AABC周长取得最大值3 + 2^3-3 616.[2020年高考江苏】在A ABC中,角A, B, C的对边分别为°, b, c,已知a = 3,c =迈,B = 45。
历年(2020‐2023)全国高考数学真题分类(三角函数)汇编【2023年真题】1. (2023ꞏ新课标I 卷 第8题)已知1sin()3αβ-=,1cos sin 6αβ=,则cos(22)αβ+=( ) A.79B.19C. 19-D. 79-2. (2023ꞏ新课标II 卷 第7题) 已知α为锐角,1cos 4α+=,则sin 2α=( )A. 38B. 18-C. 34D. 14-+3. (2023ꞏ新课标I 卷 第15题)已知函数()cos 1(0)f x x ωω=->在区间[0,2]π有且仅有3个零点,则ω的取值范围是__________.4. (2023ꞏ新课标II 卷 第16题)已知函数()sin()f x x ωϕ=+,如图,A ,B 是直线12y =与曲线()y f x =的两个交点,若||6AB π=,则()f π= .【2022年真题】5.(2022·新高考I 卷 第6题)记函数()sin()(0)4f x x b πωω=++>的最小正周期为.T 若23T ππ<<,且()y f x =的图像关于点3(,2)2π中心对称,则(2f π=( ) A. 1B.32C.52D. 36.(2022·新高考II 卷 第6题)若sin()cos()4παβαβαβ+++=+,则( )A. tan()1αβ+=-B. tan()1αβ+=C. tan()1αβ-=-D. tan()1αβ-=7.(2022·新高考II 卷 第9题)(多选)已知函数()sin(2)(0)f x x ϕϕπ=+<<的图象关于点2(,0)3π对称,则( ) A. ()f x 在5(0,)12π单调递减 B. ()f x 在11(,)1212ππ-有两个极值点 C. 直线76x π=是曲线()y f x =的一条对称轴D. 直线2y x =-是曲线()y f x =的一条切线【2021年真题】8.(2021·新高考I 卷 第4题)下列区间中,函数()7sin ()6f x x π=-单调递增的区间是( )A.0,2π⎛⎫⎪⎝⎭B. ,2ππ⎛⎫⎪⎝⎭C. 3,2ππ⎛⎫ ⎪⎝⎭D. 3,22ππ⎛⎫⎪⎝⎭9.(2021·新高考I 卷 第6题)若tan 2θ=-,则sin (1sin 2)sin cos θθθθ+=+( )A. 65-B. 25-C.25 D.65【2020年真题】10.(2020·新高考I 卷 第10题 、II 卷 第11题)(多选)如图是函数()sin y x ωϕ=+的部分图象,则()sin x ωϕ+( )A. sin ()3x π+B. sin (2)3x π- C. cos (2)6x π+D. 5cos (2)6x π- 11.(2020·新高考I 卷 第15题、II 卷 第16题))某中学开展劳动实习,学生加工制作零件,零件的截面如图所示,O 为圆孔及轮廓圆弧AB 所在圆的圆心,A 是圆弧AB 与直线AG 的切点,B 是圆弧AB 与直线BC的切点,四边形DEFG 为矩形,BC DG ⊥,垂足为C ,3tan 5ODC ∠=,//BH DG ,12EF cm =,2DE cm =,A 到直线DE 和EF 的距离均为7cm ,圆孔半径为1cm ,则图中阴影部分的面积为__________2.cm参考答案1. (2023ꞏ新课标I 卷 第8题)解:因为1sin()sin cos cos sin 3αβαβαβ-=-=,1cos sin 6αβ=,则1sin cos .2αβ=故112sin()sin cos cos sin .263αβαβαβ+=+=+= 即2221cos(22)12sin ()12().39αβαβ+=-+=-⨯=故选B.2. (2023ꞏ新课标II 卷 第7题)解:22111cos 36114sin ()sin 222816424ααα+-----=====⇒=故选:.D3. (2023ꞏ新课标I 卷 第15题)解:令()cos 10f x x ω=-=,得cos 1x ω=,又[0,2]x π∈,则[0,2]x ωωπ∈,所以426πωππ<…,得2 3.ω<… 故答案为:[2,3).4. (2023ꞏ新课标II 卷 第16题)解: 设相邻的两个交点A ,B 的横坐标为1 t ,2 t ,则21 - 6t t π=又1sin()2x ωϕ+=,522,.0,66x k k k Z k ππωϕππ+=++∈=或当时 16t πωϕ+=,256t πωϕ+=,212( - )3t t πω=,故 4.ω=函数图象过点2(,0)3π,8sin ()03πϕ+=,故8 ,.3k k Z πϕπ=-∈ 2k =时满足图片条件,故2.3πϕ=-2()sin(4.32f πππ=-=- 5.(2022·新高考I 卷 第6题)解:由题可知:22(,)3T πππω=∈,所以(2,3).ω∈ 又因为()y f x =的图像关于点3(,2)2π中心对称,所以2b =,且33()sin() 2.224f b πππω=⨯++= 所以21(34k ω=-,k Z ∈,所以5.2ω=所以5()sin() 2.24f x x π=++所以() 1.2f π=6.(2022·新高考II 卷 第6题)解:解法一:设0β=则sin cos 0αα+=,取34απ=,排除B ,D 再取0α=则sin cos 2sin βββ+=,取4πβ=,排除;A 选.C解法二:由sin()cos())]44ππαβαβαβαβ+++=++=++)cos 44ππαβαβ=++,cos )sin 44ππαβαβ+=+ 故sin()cos cos(044ππαβαβ+-+=,即sin()04παβ+-=,故sin(sin()cos()0422παβαβαβ-+=-+-=, 故sin()cos()αβαβ-=--,故tan() 1.αβ-=- 7.(2022·新高考II 卷 第9题)(多选) 解:由题意得:24(sin()033f ππϕ=+=, 所以43k πϕπ+=,即43k πϕπ=-+,k Z ∈, 又0ϕπ<<,所以2k =时,23πϕ=,故2()sin(2).3f x x π=+ 选项5:(0,)12A x π∈时,2232(,)332x πππ+∈,由sin y u =图象知()f x 在5(0,)12π单调递减; 选项11:(,1212B x ππ∈-时,252(,)322x πππ+∈,由sin y u =图象知()f x 在11(,1212ππ-有1个极值点; 选项:C 由于,故直线76x π=不是()f x 的对称轴;选项:D 令,得21cos(232x π+=-, 解得222233x k πππ+=+或242233x k πππ+=+,k Z ∈,从而得x k π=或3x k ππ=+,k Z ∈,令0k =,则是斜率为1-的直线与曲线的切点,从而切线方程为(0)2y x -=--,即.2y x =- 8.(2021·新高考I 卷 第4题) 解:由22262k x k πππππ-+-+剟,得222,33k x k k Z ππππ-++∈剟, 所以()7sin ()6f x x π=-的单调递增区间为22,2,33k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦, 当0k =时,一个单调递增区间为2,33ππ⎡⎤-⎢⎥⎣⎦,可知20,,233πππ⎛⎫⎡⎤⊆- ⎪⎢⎥⎝⎭⎣⎦, 故选:.A9.(2021·新高考I 卷 第6题)解:原式22sin (sin cos 2sin cos )sin cos θθθθθθθ++=+ 22sin (sin cos )sin sin cos sin cos θθθθθθθθ+==++22222sin sin cos tan tan 422sin cos tan 1415θθθθθθθθ++-====+++, 故选:.C10.(2020·新高考I 卷 第10题 、II 卷 第11题)(多选) 解:由图象可知222()||36T ππππω==-=,故A 错误; 解得2ω=±, 点5(,1)12π-在函数图象上, 当2ω=时,522,k Z 122k ππϕπ⨯+=-+∈, 解得42,k Z 3k πϕπ=-+∈,故44sin 2sin 2sin 2333y x x x ππππ⎛⎫⎛⎫⎛⎫=-=-+-=-+ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭,当2ω=-时,522,k Z 122k ππϕπ-⨯+=-+∈ 解得2,k Z 3k πϕπ=+∈,故函数解析式为sin 23y x π⎛⎫=-+ ⎪⎝⎭,又cos 2sin 2sin 26263x x x ππππ⎡⎤⎛⎫⎛⎫⎛⎫+=-+=- ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦,故选.BC11.(2020·新高考I 卷 第15题、II 卷 第16题) 解:设上面的大圆弧的半径为x ,连接OA ,过A 作AI BH ⊥交BH 于J ,交DG 于K ,交EF 于I ,过O 作OL DG ⊥于L ,记扇形OAB 的面积为S 扇形,由题中的长度关系易知45AGD ︒∠=,所以45AHO ︒∠=, 又90OAH ︒∠=,可得AOH 为等腰直角三角形,可得2OJ AJ x ==,52OL JK x ==-, 72DL DK LK DK OJ x=-=-=-,3tan 5OL ODC DL ∠==, 5352x-=,解得x =,12AOH O S S S S =+- 阴影圆扇形222131154()24222cm πππ=⨯⨯+⨯-=+,故答案为54.2π+。
2020年普通高等学校招生全国统一考试理科数学(I 卷)试题及解析一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 若1z i =+,则22z z -= ( )D.2 解析:把Z=1+i ,代入计算222(1)2(1)(1)(12)(1)(1)112z z i i i i i i -=+-+=++-=+-+=--=正解答案为D或者 22222211(1)1(11)12z z z z z i -=-+-=--=+--=这里是凑好了一个完成平方的形式,正好抵消了1点评:这是复数的计算题,掌握复数的运算法则就可以,属于送分题。
2.设集合{}240A x x =-≤,{}20B x x a =+≤,且{}21A B x x =-≤≤,则a =( )A.-4B.-2C.2D.4解析:解不等式,集合{|22}A x x =-≤≤集合{|/2}B x x a =≤-而 {}21A B x x =-≤≤,由此可以看出交集的下限是A 集合的-2,上眼1应该是B 集合的,也集12a -= ,解得a=-2。
正确答案为B3. 埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥,以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与底面正方形的边长的比值为( )A. 514-B. 512-C. 514+D.512+ 解析:设正四棱锥的顶点为H ,底面正方形为ABCD ,中心为O ,AB 的中点F ,则求x=HF/AB 的值,示意图。
面积关系:21*2HAB OH S AB HF ∆==, 三角形HOF 为直角三形,由勾股定理:22214HF OH AB =+则,2211*24HF AB HF AB =+ 把x=HF/AB 代入式中 24210x x --=解得154x += 点评:不要被金子塔吓着,其实题目和它没什么关系,就是考查正四棱锥的几何关系,不题不算难,但过程还是有点复杂,对四棱锥的结构一定要非常熟悉,思路一定要清晰。
2020年高考全国1卷省份高考模拟理科数学分类----三角函数一、选填问题:1.(2020深圳模拟)已知函数()()sin f x x ωϕ=+0,2πωϕ⎛⎫>< ⎪⎝⎭的最小正周期是π,把它图象向右平移3π个单位后得到的图象所对应的函数为奇函数.现有下列结论: ①函数()f x 的图象关于直线512x π=对称②函数()f x 的图象关于点,012π⎛⎫⎪⎝⎭对称 ③函数()f x 在区间,212ππ⎡⎤--⎢⎥⎣⎦上单调递减④函数()f x 在3,42ππ⎡⎤⎢⎥⎣⎦上有3个零点 其中所有正确结论的编号是( ) A. ①② B. ③④C. ②③D. ①③【答案】D 【分析】利用函数最小正周期和平移后的对称性可得()sin 23πf x x ⎛⎫=- ⎪⎝⎭;代入512x π=即可判断①;代入12x π=即可判断②;由,212x ππ⎡⎤∈--⎢⎥⎣⎦,42,332x πππ⎡⎤-∈--⎢⎥⎣⎦即可判断③;由3,42x ππ⎡⎤∈⎢⎥⎣⎦,82,363x πππ⎡⎤-∈⎢⎥⎣⎦即可判断④;即可得解. 【详解】函数()f x 的最小正周期是T π=,∴222T ππωπ===, 函数()f x 的图象向右平移3π个单位后得到的图象所对应的函数为奇函数, ∴函数()f x 的图象过点,03π⎛-⎫⎪⎝⎭即2sin 03πϕ⎛⎫-+= ⎪⎝⎭, ∴()23k k Z πϕ=π-+∈即()23k k Z πϕπ=+∈,由2πϕ<可得3πϕ=-,∴()sin 23πf x x ⎛⎫=- ⎪⎝⎭; 当512x π=时,()5sin 2sin 11232f x πππ⎛⎫=⨯-== ⎪⎝⎭,故①正确;当12x π=时,()1sin 2sin 12362f x πππ⎛⎫⎛⎫=⨯-=-=- ⎪ ⎪⎝⎭⎝⎭,故②错误; 当,212x ππ⎡⎤∈--⎢⎥⎣⎦时, 432,,33222x πππππ⎡⎤⎡⎤-∈--⊆--⎢⎥⎢⎥⎣⎦⎣⎦,故③正确; 当3,42x ππ⎡⎤∈⎢⎥⎣⎦时,82,363x πππ⎡⎤-∈⎢⎥⎣⎦,故函数()f x 在3,42ππ⎡⎤⎢⎥⎣⎦上有2个零点,故④错误.故选:D.【点睛】本题考查了三角函数图象的综合应用,考查了整体法的应用,属于中档题.2.(2020福建模拟)上世纪末河南出土的以鹤的尺骨(翅骨)制成的“骨笛”(图1),充分展示了我国古代高超的音律艺术及先进的数学水平,也印证了我国古代音律与历法的密切联系.图2为骨笛测量“春(秋)分”,“夏(冬)至”的示意图,图3是某骨笛的部分测量数据(骨笛的弯曲忽略不计),夏至(或冬至)日光(当日正午太阳光线)与春秋分日光(当日正午太阳光线)的夹角等于黄赤交角.由历法理论知,黄赤交角近1万年持续减小,其正切值及对应的年代如下表:根据以上信息,通过计算黄赤交角,可估计该骨笛的大致年代是( ) A. 公元前2000年到公元元年 B. 公元前4000年到公元前2000年 C. 公元前6000年到公元前4000年 D. 早于公元前6000年【答案】D 【解析】 【分析】先理解题意,然后根据题意建立平面几何图形,在利用三角函数的知识计算出冬至日光与春秋分日光的夹角,即黄赤交角,即可得到正确选项.【详解】解:由题意,可设冬至日光与垂直线夹角为α,春秋分日光与垂直线夹角为β, 则αβ-即为冬至日光与春秋分日光的夹角,即黄赤交角, 将图3近似画出如下平面几何图形:则16tan 1.610α==,169.4tan 0.6610β-==, tan tan 1.60.66tan()0.4571tan tan 1 1.60.66αβαβαβ---==≈++⨯.0.4550.4570.461<<,∴估计该骨笛的大致年代早于公元前6000年.故选:D .【点睛】本题考查利用三角函数解决实际问题的能力,运用了两角和与差的正切公式,考查了转化思想,数学建模思想,以及数学运算能力,属中档题.3.(2020山西运城模拟)已知tan 3α=,则2cos sin 2αα+=( )A.B.710C. D. 710-【答案】B 【分析】利用“1”的变换,所求式子化为关于sin ,cos αα的齐次分式,化弦为切,即可求解.【详解】22222cos 2sin cos 12tan 7cos sin 2cos sin 1tan 10ααααααααα+++===++. 故选:B【点睛】本题考查同角间三角函关系,弦切互化是解题的关键,属于基础题.4.(2020山西运城模拟)已知函数()()()2sin 0,0f x x ωϕωϕπ=+><<,8f π⎛⎫= ⎪⎝⎭02f ⎛⎫= ⎪⎝⎭π且在()0,π上是单调函数,则下列说法正确的是( )A. 12ω=B. 82f π⎛⎫-= ⎪⎝⎭C. 函数()f x 在,2ππ⎡⎤--⎢⎥⎣⎦上单调递减D. 函数()f x 的图像关于点5,04π⎛⎫⎪⎝⎭对称 【答案】B 【分析】根据函数()f x ,在()0,π上是单调函数,确定 01ω<≤,然后一一验证, A.若12ω=,则()12sin 2ϕ⎛⎫=+ ⎪⎝⎭f x x ,由02f π⎛⎫= ⎪⎝⎭,得34πϕ=,但13sin 84822πππ⎛⎫⨯+≠ ⎛⎫= ⎪⎭⎪⎝⎭⎝f .B.由8f π⎛⎫= ⎪⎝⎭02f π⎛⎫= ⎪⎝⎭,确定()222sin 33π⎛⎫=+⎪⎝⎭f x x ,再求解8f π⎛⎫-⎪⎝⎭验证.C.利用整体法根据正弦函数的单调性判断.D.计算54f π⎛⎫⎪⎝⎭是否为0. 【详解】因为函数()f x ,在()0,π上是单调函数,所以2T ≥π ,即22ππω≥,所以 01ω<≤ , 若12ω=,则()12sin 2ϕ⎛⎫=+ ⎪⎝⎭f x x ,又因为02f π⎛⎫= ⎪⎝⎭,即1sin 0222ππϕ⎛⎫⎛⎫⨯+= ⎪⎝=⎪⎝⎭⎭f ,解得34πϕ=, 而13sin 84822πππ⎛⎫⨯+≠ ⎛⎫= ⎪⎭⎪⎝⎭⎝f ,故A 错误. 由2sin 022πωπϕ⎛⎫⎛⎫=+=⎪ ⎪⎝⎭⎝⎭f ,不妨令2ωπϕπ+= ,得2πωϕπ=-由sin 882ππωϕ⎛⎫⎛⎫=⨯+=⎪ ⎪⎝⎭⎝⎭f ,得 2+84ππωϕπ⨯+=k 或32+84ππωϕπ⨯+=k 当2+84ππωϕπ⨯+=k 时,2=23k πω+,不合题意. 当32+84ππωϕπ⨯+=k 时,22=33k πω+,此时()222sin 33π⎛⎫=+⎪⎝⎭f x x所以222272sin 2sin 2sin 8383383122ππππππ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫-=⨯-+=⨯-+== ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭f ,故B 正确. 因为22,,0,2333ππππ⎡⎤⎡⎤∈--+∈⎢⎥⎢⎥⎣⎦⎣⎦x x ,函数()f x ,在0,3π⎛⎫⎪⎝⎭上单调递增,故C 错误.525232sin 2sin 043432f ππππ⎛⎫⎛⎫=⨯+==≠ ⎪ ⎪⎝⎭⎝⎭,故D 错误. 故选:B【点睛】本题主要考查三角函数的性质及其应用,还考查了运算求解的能力,属于较难的题.5.(2020山西运城模拟)已知ABC ∆中,AB BC =,点D 是边BC 的中点,ABC ∆的面积为2,则线段AD 的取值范围是__________.【答案】)+∞ 【分析】设,===AB BC t AD m ,利用正弦定理,根据21sin 22ABCSt B ==,得到2sin 4t B =①,再利用余弦定理得2225cos 4t B t m =-②,①②平方相加得:24225164t t m ⎛⎫=-+ ⎪⎝⎭,转化为4224940162560t m t m -++= 有解问题求解.【详解】设,===AB BC t AD m ,所以21sin 22ABCSt B ==, 即2sin 4t B =① 由余弦定理得2222cos 22t tmt t B ⎛⎫=+-⋅⋅ ⎪⎝⎭,即 2225cos 4t B t m =-②,①②平方相加得:24225164t t m ⎛⎫=-+ ⎪⎝⎭,即4224940162560t m t m -++= , 令20t x =>,设 ()22494016256gx x m x m =-++,在()0,∞+上有解,所以 222224202020940162560999m m m g m m ⎛⎫⎛⎫=-⨯++≤ ⎪ ⎪⎝⎭⎝⎭, 解得49m ≥,即m ≥,故答案为:)+∞【点睛】本题主要考查正弦定理和余弦定理在平面几何中的应用,还考查了运算求解的能力,属于难题.是6.(2020福建泉州二模)我国南宋著名数学家秦九韶发现了由三角形三边求三角形面积的“三斜求积”公式:设ABC 三个内角,,A B C 所对的边分别为,,a b c ,面积为S ,则“三斜求积”公式为S =.若2sin sin 5C c A =,且()()40,a b c a b c +---+=则利用“三斜求积”公式可得ABC 的面积S =( )A.B. 2C. 4D.【答案】B 【分析】根据正弦定理可得5ac =,代入()()40,a b c a b c +---+=可得2226a c b +-=,再由三斜求体即可解答.【详解】因为2sin sin 5C c A =,由正弦定理得25c c a =,5ac =,又因为()2240a c b --+=,所以222246a c b ac +-=-=,代入2S ==.故选:B 【点睛】本题考查了正弦定理以及新定义,需熟记定理的内容,属于基础题.7.(2020福建泉州二模)如图,一个水轮的半径为6m ,水轮轴心O 距离水面的高度为3m ,已知水轮按逆时针匀速转动,每分钟转动5圈,当水轮上点P 从水中浮现时的起始(图中点P )开始计时,记()f t 为点P 距离水面的高度关于时间()t s 的函数,则下列结论正确的是( )A. ()39f =B. ()()71f =C. 若()6f t ≥,则[]212,512 N ()t k k k ∈++∈D. 不论t 为何值,()()()4f 8f t f t t ++++是定值 【答案】BD【解析】 【分析】以水轮所在面为坐标平面,以水轮的轴心O 为坐标原点,x 轴和y 轴分别平行和垂直于水面建立平面直角坐标系,从而点P 的纵坐标为6sin 66y t ππ⎛⎫=- ⎪⎝⎭,逐一判断选项即可求解.【详解】如图,以水轮所在面为坐标平面,以水轮的轴心O 为坐标原点,x 轴和y 轴分别平行和垂直于水面建立平面直角坐标系,依题意得OP 在()t s 内所转过的角度为t ,则66POx t ππ∠=-.则点P 的纵坐标为6sin 66y t ππ⎛⎫=- ⎪⎝⎭,点P 距离水面的高度关于时间()t s 的函数()6sin 366f t t ππ⎛⎫=-+ ⎪⎝⎭;()36sin 3326f ππ⎛⎫=-+= ⎪⎝⎭,选项A 错误;()16sin 3366f ππ⎛⎫=-+= ⎪⎝⎭,()776sin 3366f ππ⎛⎫=-+= ⎪⎝⎭,()()17f f =,选项B 正确;由()6f t ≥得,1sin 662t ππ⎛⎫-≥ ⎪⎝⎭解得[]()212,612t k k k N ∈++∈,选项C 错误;由()()()37486sin()36sin 36sin 3666666f t f t f t t t t ππππππ⎛⎫⎛⎫++++=-+++++++ ⎪⎪⎝⎭⎝⎭展开整理得()()()489f t f t f t ++++=为定值,选项D 正确;故答案为:BD.【点睛】本题考查了三角函数的应用、解三角不等式,两角和与差的正弦公式,属于基础题.8.(2020江西南昌市模拟)台球是一项国际上广泛流行的高雅室内体育运动,也叫桌球(中国粤港澳地区的叫法)、撞球(中国台湾地区的叫法)控制撞球点、球的旋转等控制母球走位是击球的一项重要技术,一次台球技术表演节目中,在台球桌上,画出如图正方形ABCD ,在点E ,F 处各放一个目标球,表演者先将母球放在点A 处,通过击打母球,使其依次撞击点E ,F 处的目标球,最后停在点C 处,若AE =50cm .EF =40cm .FC =30cm ,∠AEF =∠CFE =60°,则该正方形的边长为( )cm cmC. 50cmcm【答案】D 【分析】过点,E F 做正方形边的垂线,如图,设AEM α∠=,利用直线三角形中的边角关系,将,AB BC 用α表示出来,根据AB BC =,列方程求出α,进而可得正方形的边长. 【详解】过点,E F 做正方形边的垂线,如图,设AEM α∠=,则CFQ α∠=,60MEF QFE α∠=∠=-,则()sin sin 60sin AB AM MN NB AE EF FC ααα=++=+-+()350sin 40sin 6030sin 40sin 22ααααα⎛⎫=+-+=+ ⎪ ⎪⎝⎭, ()cos cos cos 60CB BP PC AE FC EF ααα=+=+--()350cos 30cos 40cos 6040cos 22ααααα⎛⎫=+--=- ⎪ ⎪⎝⎭因为AB CB =,则3340sin 40cos 22αααα⎛⎫⎛⎫+=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭,整理化简得sin 2cos αα=,又22sin cos 1αα+=,得sin α=,cos α=3340sin 4022AB αα⎛⎫⎛∴==⨯= ⎪ ⎪ ⎝⎭⎝即该正方形的边长为. 故选:D.【点睛】本题考查直角三角形中的边角关系,关键是要构造直角三角形,是中档题. 9.(2020江西南昌市模拟)已知函数()sin()(0,0)3f x x πωφωφ=+><<满足()(),()12f x f x f ππ+==1,则()12f π-等于( )B.C. -12D.12【答案】C 【分析】设()f x 的最小正周期为T ,可得,nT n N π*=∈,则*2,n n ω=∈N ,再根据112f π⎛⎫=⎪⎝⎭得*2,,26k n k Z n N ππφπ=+-⋅∈∈,又03πφ<<,则可求出122n k -=,进而可得()12f π-.【详解】解:设()f x 的最小正周期为T ,因为()()f x f x π+=,所以,nT n N π*=∈,所以*2,T n nππω==∈N ,所以*2,n n ω=∈N ,又112f π⎛⎫=⎪⎝⎭,所以当12x π=时,262x n k ππωϕφπ+=⋅+=+, *2,,26k n k Z n N ππφπ∴=+-⋅∈∈,因为03πφ<<,02263k n ππππ∴<+-⋅<,整理得1123n k <-<,因为12n k Z -∈,122n k ∴-=,()2212266k k πππφπ∴=+-+⋅=,则2662n k ππππ⋅+=+,263n k πππ∴=+ 所以()sin 212126sin 66f n n πππππ⎛⎫--- ⎪⎝⎡⎤⎛⎫=⋅+=+ ⎪⎢⎥⎝⎭⎣⎦⎭1sin 2sin 3662k ππππ⎛⎫⎛⎫=--+=-=- ⎪ ⎪⎝⎭⎝⎭.故选:C.【点睛】本题考查三角形函数的周期性和对称性,考查学生分析能力和计算能力,是一道难度较大的题目. 10.(2020江西赣州模拟)如图所示,直线12//l l ,点A 是1l 、2l 之间的一定点,并且点A 到1l 、2l 的距离分别为2、4,过点A 且夹角为3π的两条射线分别与1l 、2l 相交于B 、C 两点,则ABC 面积的最小值是( )A.B.C.D. 【答案】C【分析】设AB 与垂线的夹角为02πθθ⎛⎫<<⎪⎝⎭,用θ表示,AB AC ,则ABC 的面积1sin 23S AB AC π=⋅,根据两角差的余弦公式和辅助角公式可求面积的最小值.【详解】设AB 与垂线的夹角为02πθθ⎛⎫<<⎪⎝⎭,则2cos AB θ=,42cos 3AC πθ=⎛⎫- ⎪⎝⎭, ∴面积1sin 23cos cos 2sin 2136S AB AC πθθθ=⋅===--- ⎪ ⎪⎝⎭⎝⎭所以当262ππθ-=,即当3πθ=时,面积最小,最小值是故选:C .【点睛】本题考查三角形面积公式、两角差的余弦公式和辅助角公式,属于中档题. 11.(2020江西赣州模拟)设向量()2cos ,sin a θθ=,向量()1,6b =-,且0a b ⋅=,则2cos 3sin cos 3sin θθθθ++等于______. 【答案】32【分析】由0a b ⋅=,得1tan 3θ=.又2cos 3sin 23tan cos 3sin 13tan θθθθθθ++=++,把1tan 3θ=代入即得答案.【详解】0a b ⋅=,2cos 6sin 0θθ∴-=,1tan 3θ∴=.2cos 3sin 23tan 213cos 3sin 13tan 211θθθθθθ+++∴==+=++.故答案为:32.【点睛】本题考查向量数量积的坐标表示,考查三角函数式的求值,属于基础题.12.(2020湖南师大附中模拟)已知α为锐角,且()cos 11α+︒=,则α的值为( ) A. 20︒ B. 40︒ C. 50︒ D. 70︒【答案】B【分析】直接利用三角函数关系式的恒等变换和角公式的应用求出结果.【详解】解:由()cos 11α︒=可得cos 1α=,即2sin 40cos 1cos10α︒=︒, 所以cos10sin80cos 2sin 402sin 40α︒︒==︒︒2sin 40cos 40cos 402sin 40︒︒==︒︒,又α为锐角,故40α=︒,故选:B.【点睛】本题考查的知识要点:三角函数关系式的恒等变换,和角公式的运用,主要考查学生的运算能力和转换能力及思维能力,属于基础题.13.(2020湖南师大附中模拟)若()()()2sin 20f x x ϕϕ=+>的图象关于直线12x π=对称,且当ϕ取最小值时,00,2x π⎛⎫∃∈ ⎪⎝⎭,使得()0f x a =,则a 的取值范围是______.【答案】(2⎤⎦ 【分析】直接利用正弦型函数的性质的应用和函数的定义域的应用求出结果. 【详解】解:∵函数()()()2sin 20f x x ϕω=+>的图象关于直线12x π=对称,62k ππϕπ+=+,()3k k Z πϕπ=+∈,当ϕ取最小值是3πϕ=,()2sin 23f x x π⎛⎫=+ ⎪⎝⎭,∵00,2x π⎛⎫∈ ⎪⎝⎭,∴042,333x πππ⎛⎫+∈ ⎪⎝⎭,2sin 223x π⎛⎫<+≤ ⎪⎝⎭,即a 的取值范围是(2⎤⎦.故答案为:(2⎤⎦【点睛】本题考查的知识要点:三角函数关系式的恒等变换,正弦型函数的性质的应用,主要考查学生的运算能力和转换能力及思维能力,属于基础题.14.(2020湖南长郡中学模拟)已知()cos()0,||,2f x x x πωϕωϕ⎛⎫=+><∈ ⎪⎝⎭R 两个相邻极值点的横坐标差的绝对值等于2π,当23x π=时,函数()f x 取得最小值,将()f x 的图象向左平移m 个单位得到一个奇函数,则m 的最小正值是( ) A12πB.2πC.3π D.512π 【答案】D【分析】由题可知22T π= 从而求出,T ω 再将最小值代入解析式求出ϕ 从而得到()f x 进而根据平移变换得到平移后的解析式 再利用奇偶性求出m 即可得出结论.【详解】因为()cos()f x x =+ωϕ两个相邻极值点的横坐标差的绝对值等于2π所以22T T ππ=⇒=所以22T πω== 即()cos(2)f x x ϕ=+,又当23x π=时 函数()f x 取得最小值 所以24()cos()133f ππϕ=+=- 则42()2()33k k Z k k Z ππϕππϕπ+=+∈⇒=-+∈ 又||2ϕπ< 所以3πϕ=- 所以()cos(2)3f x x π=-设将()f x 的图象向左平移m 个单位得到()g x 则()cos(22)3g x x m π=+- 因为()g x 是一个奇函数所以2(21)()32m k k Z ππ-=-∈ 即()212k m k Z ππ=-∈ 所以当1k =时 m 的最小正值是512π故选:D.【点睛】本题综合考查了三角函数的图象性质及平移变换 需要学生对基础知识掌握牢固且灵活运用 属于中档题.15.(2020湖北宜昌市模拟)已知函数()sin f x x x =,下列命题:①()f x 关于点,03π⎛⎫⎪⎝⎭对称;②()f x 的最大值为2;③()f x 的最小正周期为2π;④()f x 在区间()0,π上递增.其中正确命题的个数是( ).A. 0B. 1C. 2D. 3【答案】C【分析】把函数化为一个角的一个三角函数,然后结合正弦函数性质判断.【详解】1()sin2(sin cos)2sin()223f x x x x x xπ=-=-=-,()03fπ=,①正确;最大值是2,②正确;周期为2π,③错;函数在5(0,)6π上递增,在5(,)6ππ上递减,④错.正确的命题有2个.故选:C.【点睛】本题考查三角函数的图象与性质,解题时必须把函数化为一个角的一个三角函数形式,掌握正弦函数性质是解题关键.16.(2020湖北武汉市模拟)已知函数f(x)=sin2x+sin2(x3π+),则f(x)的最小值为()A.12B.14C.4D.2【答案】A【分析】先通过降幂公式和辅助角法将函数转化为()11cos223f x xπ⎛⎫=-+⎪⎝⎭,再求最值.【详解】已知函数f(x)=sin2x+sin2(x3π+)=21cos21cos2322xxπ⎛⎫-+⎪-⎝⎭+,=1cos2111cos22223xxπ⎛⎛⎫-=-+⎪⎝⎭⎝⎭,因为[]cos21,13xπ⎛⎫+∈-⎪⎝⎭,所以f(x)的最小值为12.故选:A【点睛】本题主要考查倍角公式及两角和与差的三角函数的逆用,还考查了运算求解的能力,属于中档题.17.(2020湖北武汉市模拟).根据气象部门预报,在距离某个码头A南偏东45°方向的600km处的热带风暴中心B正以30km/h的速度向正北方向移动,距离风暴中心450km以内的地区都将受到影响,从现在起经过___小时后该码头A将受到热带风暴的影响(精确到0.01).【答案】9.14h.【分析】先建立坐标系,设风暴中心最初在B处,经th后到达C处.自B向x轴作垂线,垂足为D.若在点C处受到热带风暴的影响,则A C =450,则有22AD DC +=450,即22(60045)(6004530)cos sin t ︒+︒-=450;两边平方并化简、整理求解. 【详解】建立如图所示直角坐标系:设风暴中心最初在B 处,经th 后到达C 处.自B 向x 轴作垂线,垂足为D .若在点C 处受到热带风暴的影响,则OC =450, 即22AD DC +=450,即22(60045)(6004530)cos sin t ︒+︒-=450; 两边平方并化简、整理得t 2﹣202t +175=0 ∴t 1025=+或1025-,1024159.≈-所以9.14时后码头将受到热带风暴的影响.【点睛】本题主要考查了三角函数的实际应用,还考查了运算求解的能力,属于中档题. 18.(2020河南郑州市模拟)若,2παπ⎛⎫∈ ⎪⎝⎭,2cos2sin 4παα⎛⎫=- ⎪⎝⎭,则sin 2α的值为( )A. 78-B.78 C. 18-D.18【答案】A【分析】利用二倍角公式及两角差的正弦公式化简得到2cos sin 4αα+=,再将两边平方利用二倍角正弦公式计算可得;【详解】解:因为2cos2sin 4παα⎛⎫=- ⎪⎝⎭,所以()222cos sin sin cos cos sin 44ππαααα-=-所以()()()22cos sin cos sin cos sin 2αααααα-+=-,,cos sin 02παπαα⎛⎫∈-≠ ⎪⎝⎭, 所以2cos sin 4αα+=所以()21cos sin 8αα+=,即221cos 2cos sin sin 8αααα++=,11sin 28α+= 所以7sin 28α=-,故选:A 【点睛】本题考查两角和差的正弦公式、二倍角公式的应用,属于中档题;19.(2020河南南阳市模拟)方程2(1)sin 10x x π-+=在区间[]2,4-内的所有解之和等于( ) A. 4 B. 6C. 8D. 10【答案】C【分析】画出函数sin y x =π和12(1)y x =--的图像,sin y x =π和12(1)y x =--均关于点()1,0中心对称,计算得到答案.【详解】2(1)sin 10x x π-+=,验证知1x =不成立,故1sin 2(1)x x π=--,画出函数sin y x =π和12(1)y x =--的图像,易知:sin y x =π和12(1)y x =--均关于点()1,0中心对称,图像共有8个交点,故所有解之和等于428⨯=.故选:C .【点睛】本题考查了方程解的问题,意在考查学生的计算能力和应用能力,确定函数关于点()1,0中心对称是解题的关键.20.(2020河南省理科模拟)已知()1,0A x ,()2,0B x 两点是()2sin()1(0,(0,))f x x ωϕωϕπ=++>∈与x 轴的两个交点,且满足12min3x x π-=现将函数()f x 的图像向左平移6π个单位,得到的新函数图像关于y 轴对称,则ϕ的可能取值为( ) A.6π B.3π C.23π D.56π 【答案】A【分析】根据12min3x x π-=,即可求得ω,再根据平移后函数为偶函数,即可求得ϕ.【详解】令()2sin 10x ωϕ++=,解得()1sin 2x ωϕ+=-, 因为12min3x x π-=,故令21x x >,并取12711,66x x ππωϕωϕ+=+=, 则()2123x x πω-=,即可求得2ω=.此时()()2sin 21f x x ϕ=++, 向左平移6π个单位得到2sin 213y x πϕ⎛⎫=+++ ⎪⎝⎭,若其为偶函数,则2,32k k Z ππϕπ+=+∈, 解得26k πϕπ=+.当0k =时,6π=ϕ.故选:A . 【点睛】本题考查由三角函数的性质求参数值,属综合中档题.21.(2020河北保定市理科模拟)在ABC ∆中,内角A ,B ,C 所对的边分别是a ,b ,c ,且cos a C ,cos b B ,cos c A 成等差数列,若ABC ∆外接圆的半径为1,则b =( )A.32B. 2【答案】C【分析】由等差中项的定义得2cos cos cos b B a C c A =+,由正弦定理化角计算得3B π=,再由正弦定理得2sin b r B =算出结果.【详解】在ABC ∆中,cos a C ,cos b B ,cos c A 成等差数列,2cos cos cos b B a C c A ∴=+,由正弦定理得2sin cos sin cos sin cos B B A C C A =+,即()12sin cos sin sin ,cos 2B B AC B B =+=∴=,则3B π=,又ABC ∆外接圆的半径为1,2sin b r B ∴==故选:C 【点睛】本题主要考查了正弦定理的应用,等差中项的定义. 22.(2020河北保定市理科模拟)设函数()2sin sin 3f x x x πϕ⎛⎫=++ ⎪⎝⎭是奇函数,其中(0,)ϕπ∈,则ϕ=____【答案】6π; 【分析】函数()f x 为定义在R 上的奇函数,而sin y x =是奇函数,故sin 3y x ⎛⎫=++ ⎪⎝⎭πϕ为偶函数,再利用其对称轴为0x =,即可得到答案.【详解】因为函数()f x 为定义在R 上的奇函数,而sin y x =是奇函数, 故sin 3y x ⎛⎫=++ ⎪⎝⎭πϕ为偶函数,所以,32ππφk πk Z +=+∈,又(0,)ϕπ∈,所以6π=ϕ. 故答案为:6π 【点睛】本题主要考查利用奇偶性求参数值,同时考查函数奇偶性的运算性质. 23.(2020河北保定市理科模拟).Rt ABC ∆中,2A π∠=,6BC =,以BC 的中点为圆心,以1为半径的圆,分别交BC 于点P 、Q ,则2222||||||||AB AP AQ AC +++=________.【答案】56 【分析】设BC 的中点为圆心O ,利用余弦定理求出22,AP AQ 结合AOP AOQ π∠+∠=,222AB AC BC +=,即可求2222||||||||AB AP AQ AC +++的值.【详解】设BC 的中点为圆心O ,由题得,3,1OA OP OQ ===, 在AOP ∆中,由余弦定理得,2222cos 106cos AP OA OP OA OP AOP AOP =+-⋅⋅∠=-∠,在AOQ ∆中,由余弦定理得,2222cos 106cos AQ OA OQ OA OQ AOQ AOQ =+-⋅⋅∠=-∠,又AOP AOQ π∠+∠=,cos cos 0AOP AOQ ∠+∠=, 又222AB AC BC +=,22222225||||||||||||6AB AP AQ AC AP AQ BC ∴=+++=++.故答案为:56【点睛】本题主要考查了余弦定理的应用,勾股定理,考查了学生的运算求解能力. 24.(2020厦门市理科模拟)关于函数()cos sin f x x x =+有下述四个结论: ①()f x 是偶函数;②()f x 在区间0,2π⎛⎫⎪⎝⎭上是增函数;③()f x 的最大值为2;④()f x 的周期为2π. 其中所有正确结论的编号是( ) A. ①② B. ①④C. ①③④D. ②③④【答案】B 【分析】对①,根据偶函数定义可判断;对②,去绝对值并利用导数判断;对③,直接根据同角三角函数的基本关系判断;对④,利用排除法可排除选项. 【详解】对①,函数的定义域为R 关于原点对称,且()()f x f x -=,∴()f x 为偶函数,故①正确;对②,当0,2x π⎛⎫∈ ⎪⎝⎭时,()sin cos f x x x =+,则'()cos sin f x x x =-,'()0f x ≥在0,2x π⎛⎫∈ ⎪⎝⎭不恒成立,∴()f x 在区间0,2π⎛⎫⎪⎝⎭上是增函数错误,故②错误; 对③,若()f x 的最大值为2,则cos 1,sin 1x x ==,显然不可能同时取到,故③错误; 利用排除法,可选排除选项ACD. 故选:B.【点睛】本题考查三角函数的图象与性质运用,考查函数与方程思想、转化与化归思想,考查逻辑推理能力、运算求解能力,求解时注意排除法的运用.25.(2020安徽淮北市理科模拟)关于函数22()cos sin 1f x x x =-+,下列说法正确的是( ) A. 函数()f x 以π为周期且在()2k x k Z π=∈处取得最大值 B. 函数()f x 以2π为周期且在区间,42ππ⎛⎫⎪⎝⎭单调递增 C. 函数()f x 是偶函数且在区间,42ππ⎛⎫⎪⎝⎭单调递减 D. 将()f x 的图像向右平移1个单位得到()|cos(21)|1g x x =-+的【答案】AB 【分析】利用二倍角公式化简函数的解析式,然后根据余弦函数的性质和绝对值的性质逐一判断即可. 【详解】22()cos sin 1cos 21f x x x x =-+=+.A :()cos2()1cos21()f x x x f x ππ+=++=+=,所以函数()f x 的周期为π.当()2k x k Z π=∈时,()cos 21cos 1222k k f k πππ=+=+=,所以函数()f x 在()2k x k Z π=∈处取得最大值,故本选项是正确的; B :()cos 2()1cos 21()22f x x x f x ππ+=++=+=,所以函数()f x 的周期为2π.当,42x ππ⎛⎫∈⎪⎝⎭时,2,2x ππ⎛⎫∈ ⎪⎝⎭,所以()cos21cos21f x x x =+=-+,故函数是单调递增函数,因此本选项是正确的;C :()cos[2()]1cos2+1=()f x x x f x -=-+=,所以函数是偶函数,由上分析,函数在区间,42ππ⎛⎫⎪⎝⎭单调递减是不正确的,故本选项是错误的;D :将()f x 的图像向右平移1个单位得到()|cos[2(1)]|1cos(22)1g x x x =-+=-+,故本选项是错误, 故选:AB【点睛】本题考查了余弦型函数的性质,考查了二倍角的余弦公式,考查了绝对值的性质,考查了余弦的诱导公式.26.(2020安徽淮北市理科模拟)已知锐角α满足sin 23πα⎛⎫+= ⎪⎝⎭,则tan2α=( )A. B. -C. D.【答案】B 【分析】根据正弦的诱导公式化简等式,再利用同角的三角函数关系式,求出tan α的值,最后利用二倍角的正切公式求值即可.【详解】sin cos 2παα⎛⎫+=⇒= ⎪⎝⎭,因为α是锐角,所以有2sin 2tan sin tan tan 23cos 1tan ααααααα==⇒====--故选:B【点睛】本题考查了正弦诱导公式,考查了同角的三角函数关系式,考查了二倍角的正切公式. 27.(2020安徽合肥市理科模拟)若函数()sin 2f x x =的图象向右平移116π个单位得到的图象对应的函数为()g x ,则下列说法正确的是( ) A. ()g x 的图象关于12x π=-对称B. ()g x 在[]0π,上有2个零点C. ()g x 在区间5 36ππ⎛⎫⎪⎝⎭,上单调递减 D. ()g x 在 02π⎡⎤-⎢⎥⎣⎦,上的值域为 0⎡⎤⎢⎥⎣⎦【答案】B 【分析】求出()g x 的解析式,并整理后,根据正弦函数性质判断.【详解】由题意1111()sin 2()sin(2)sin(2)633g x x x x πππ=-=-=+, 1()sin()12632g πππ-=-+=不是函数的最值,12x π=-不是对称轴,A 错;由()sin(2)03g x x π=+=,2()3x k k Z ππ+=∈,26k x ππ=-,其中5,36ππ是[0,]π上的零点,B 正确; 由3222232k x k πππππ+≤+≤+得71212k x k ππππ+≤≤+,k Z ∈,因此()g x 在7(,)312ππ是递减,在75(,)126ππ上递增,C 错;[,0]2x π∈-时,22[,]333x πππ+∈-,()[g x ∈-,D 错.故选:B .【点睛】本题考查三角函数图象变换,考查三角函数的性质.掌握正弦函数性质是解题关键.28.(2020河北省理科模拟)函数f (x )=12(x 2+cos x ﹣|x 2﹣cos x |)的大致图象是( )A .B .C .D .将函数化为分段函数的形式,再结合选项直接判断即可. 因为f(x)=12(x 2+cosx −|x 2−cosx|)={cosx ,x 2≥cosx x 2,x 2<cosx ,故选:B .本题考查函数的图象,考查识图能力与推理论证能力,属于基础题. 29.(2020河北省理科模拟)已知函数f (x )=√3sinπx ω+cosπx ω(ω>0),如果存在实数x 0,使得对任意的实数x ,都有f (x 0﹣2020)≤f (x )≤f (x 0)成立,则ω的最大值为( ) A .2020B .4040C .1010D .20203利用辅助角公式对函数化解可得f (x )=√3sin πx ω+cosπxω=2sin (πωx +π6),由对任意的实数x ,都有f (x 0﹣2020)≤f (x )≤f (x 0)成立可得,两端点值分别为函数的最小值和最大值,要使得ω 最大,只要周期T =2ππω=2ω最大,当T 2=2020,周期最大,代入可求得结果.利用辅助角公式对函数化解可得f (x )=√3sin πx ω+cosπxω=2sin (πωx +π6), 由对任意的实数x ,对任意的实数x ,都有f (x 0﹣2020)≤f (x )≤f (x 0)成立; 可得f (x 0),f (x 0﹣2020),分别为函数的最大值和最小值, 要使得ω最大,只要周期T =2ππω=2ω最大,当T 2=2020即T =4040=2ω,周期最大,此时ω=2020;故选:A .本题目主要考查了三角函数的辅助角公式的应用,三角函数的性质的应用,周期公式的应用,解题的关键是根据条件求得函数的最小值和最大值,属于中档题.30.(2020华南师大附中理科模拟)△ABC中,a=x,b=2,∠B=60°,则当△ABC有两个解时,x的取值范围是()A.x>B.x<2或x>C.x<2D.2<x<【分析】根据三角形有两个解的条件列出不等式,求出x的范围.【解答】解:当△ABC有两个解时,有a sin B<b<a,∵a=x,b=2,∠B=60°,∴x sin60°<2<x,解得2<x<,故选:D.【点评】本题考查了已知两边和其中一边的对角时,三角形解的个数对应的条件应用,属于中档题.31.(2020华南师大附中理科模拟)函数在1<x<7上的图象与x轴交于点A,过点A的直线l与函数的图象交于点B、C两点,则=()A.B.C.32D.【分析】求出A的坐标,结合三角函数的对称性得到B,C关于点A对称,利用向量加法以及向量数量积进行计算即可.【解答】解:由f(x)=2sin(x+)=0可得x+=kπ,∴x=6k﹣2,k∈Z∵1<x<7∴x=1即A(4,0),过点A的直线l与函数的图象交于点B、C两点,则B,C关于点A对称,则A是B,C的中点,则=2=2||2=2×4×4=32,故选:C.【点评】本题主要考查向量数量积的应用,利用数形结合以及向量中点公式进行转化是解决本题的关键.32.(2020华南师大附中理科模拟)已知函数的图象在区间上有且只有9个交点,记为(x i,y i)(i=1,2,…,9),则=()A.B.8C.D.【分析】直接利用三角函数的关系式求出函数的对称中心,进一步求出函数的值.【解答】解:由,可知g(x)的图象关于点对称,由,可得,所以f(x)的图象关于点对称,所以=,故选:D.【点评】本题考查的知识要点:三角函数关系式的恒等变变换,正弦型函数的性质的应用,主要考查学生的运算能力和转化能力,属于基础题型.33.(2020华南师大附中理科模拟)已知函数f(x)=A sin(ωx+φ)(A>0,ω>0,|φ|<)的部分图象如图所示,则f(x)的解析式是f(x)=2sin(2x﹣).【分析】由图象可知A=2,可求周期T,利用周期公式可求ω,从而可求f(x)=2sin(2x+φ),代入点(,2),结合范围|φ|<,可求φ,即可得解解析式.【解答】(本小题12分)解:(1)由图象可知,A=2,周期T=[﹣(﹣)]=π,∴=π,ω>0,则ω=2,…(3分)从而f (x )=2sin (2x +φ),代入点(,2),得sin (+φ)=1,则+φ=+2k π,k ∈Z ,即φ=﹣+2k π,k ∈Z ,又|φ|<,则φ=﹣,∴f (x )=2sin (2x ﹣),…(6分)故答案为:f (x )=2sin (2x ﹣). 【点评】本题主要考查了函数y =A sin (ωx +φ)的图象变换,考查了正弦函数的图象和性质的应用,考查了数形结合思想,属于基础题.二、解答题部分:34.(2020深圳模拟)在ABC ∆中,内角A 、B 、C 对边分别是a 、b 、c ,已知2sin sin sin B A C =. (1)求证:03B π<≤;(2)求222sinsin 1A CB +-+的取值范围.【答案】(1)证明见解析(2)(【分析】(1)由正弦定理结合条件得2b ac =,再由余弦定理结合基本不等式可得1cos 2B ≥,由三角函数的性质即可得证;(2)由三角函数的性质化简得22sinsin 124A C B B π+⎛⎫++= ⎝-⎪⎭,结合(1)中03B π<≤即可得74412B πππ<+≤,即可得解. 【详解】(1)证明:由正弦定理可得2b ac =,∴22221cos 222a cb ac ac B ac ac +--=≥=,0B π<<,03B π∴<≤.(2)由题意222sin sin 1A C B +-+()cos sin A C B =-++cos sin 4B B B π⎛⎫=+=+ ⎪⎝⎭,由(1)知03B π<≤,∴74412B πππ<+≤,∴14B π⎛⎫<+≤ ⎪⎝⎭,即222sinsin 1A CB +-+的取值范围是(.【点睛】本题考查了正弦定理、余弦定理和三角函数的综合问题,考查了基本不等式的应用,属于中档题. 35.(2020福建模拟)已知ABC ∆的内角A ,B ,C 的对边分别为a ,b ,c ,且2222c a b ab +-=.(1)若sin 3C =,求B ; (2)若D 为AC 中点,且BD BC =,求a b. 【答案】(1)6π;(212. 【分析】(1)直接利用已知条件结合余弦定理,得出cos c B b =,再利用正弦定理得tan 3B =,即可求出结果;(2)已知BD BC =,则BD a =,在ABD ∆和BCD ∆中,BD a =,由余弦定理可得出cos ADB ∠和cos CDB ∠,由于cos ADB cos DB 0∠+∠=C ,化简得2222b c a =+,再结合题给条件即可算出a b. 【详解】(1)由余弦定理得,2222cos c a b ac B +-=, 又2222c a b ab +-=,所以2cos 2ac B ab =,即cos c B b =,由正弦定理得,sin cos sin C B B =,显然cos 0B ≠,所以tan sin B C =,因为sin 3C =,所以tan 3B =,又因为0B π<<,所以6B π=.(2)如图所示:在ABD ∆和BCD ∆中,BD a =,由余弦定理可得2222222cos 222b a c BD AD AB ADB b BD AD a ⎛⎫+- ⎪+-⎝⎭∠==⋅⎛⎫⋅ ⎪⎝⎭, 2222222cos 222b a a BD CD BC CDB b BD CD a ⎛⎫+- ⎪+-⎝⎭∠==⋅⎛⎫⋅ ⎪⎝⎭, 因cos ADB cos DB 0∠+∠=C ,所以2222b c a =+,又因为2222c a b ab +-=,所以22440a ab b --=,即24410a a b b ⎛⎫-⋅-= ⎪⎝⎭,解得a b =因为0a >,0b >,所以12a b +=. 【点睛】本题考查正弦定理和余弦定理以及三角形面积公式的应用,考查学生的运算能力和转换能力及思维能力,属于中档题.36.(2020福建泉州模拟)如图,已知在平面四边形ABCD 中,,CAB a ABC ACB βγ∠=∠=∠=,,且()()2cos sina sin sin cosa cos γβγβ+=--.(1)证明:2CA CB AB +=;(2)若21CA CB DA DC ===,,求四边形ABCD 的面积的取值范围.【答案】(1)证明见解析;(2)81616⎛+ ⎦⎝. 【分析】(1)根据题意可得()()cos sin sin cos cos sin sin cos 2sin γαγαγβγβγ+++=,然后再利用两角和的正弦公式的逆应用可得()()sin sin 2sin αγβγγ+++=,从而可得sin sin 2sin βαγ+=,再利用正弦定理即可求解. (2)由(1)可得ABC ∆为是等边三角形,设(),0,ADC ϕϕπ∠=∈,利用三角形的面积公式可得21sin 4ABCD S ϕ=,在ADC 中,由余弦定理求出AC ,然后利用辅助角公式以及三角函数的性质即可求解.【详解】(1)由cos (sin sin )sin (2cos cos )γαβγαβ+=--得 cos sin cos sin 2sin sin cos sin cos γαγβγγαγβ+=--.整理得()()cos sin sin cos cos sin sin cos 2sin γαγαγβγβγ+++=,即得()()sin sin 2sin αγβγγ+++=. 因为在ABC 中,αβγπ++=,所以()()()sin sin sin ,sin sin αγπβββγα+=-=+=, 所以sin sin 2sin βαγ+=.由正弦定理得2CA CB AB +=.(2)因为CA CB =,2CA CB AB +=,所以CA CB AB ==,ABC 为是等边三角形.设(),0,ADC ϕϕπ∠=∈,则ABCD ACD ABC S S S =+△△211sin sin 6022DA DC AC ϕ=⋅⋅+゚21sin 4AC ϕ=+ 在ADC 中,由余弦定理得22252cos cos 4AC DA DC DA DC ADC ϕ=+-⋅∠=-.15sin cos 44ABCD S ϕϕ⎫=-⎪⎝⎭()1sin 4ϕϕ=+1sin 23πϕ⎛⎫=-+⎪⎝⎭ 因为0ϕπ<<,所以2333πππϕ-<-<,所以sin 13πϕ⎛⎫<-≤ ⎪⎝⎭,得11sin 232πϕ⎛⎫<-≤ ⎪⎝⎭.1sin 23πϕ⎛⎫<-≤ ⎪⎝⎭.因此,四边形ABCD 面积的取值范围为⎦⎝. 【点睛】本题考查了正弦定理、余弦定理解三角形,同时考查了辅助角公式以及三角函数的性质,综合性比较强,属于中档题.37.如图,D 是在△ABC 边AC 上的一点,△BCD 面积是△ABD 面积的2倍,∠CBD =2∠ABD =2θ.(Ⅰ)若θ=6π,求sin sin A C的值;(Ⅱ)若BC =4,AB ,求边AC 的长.【答案】(Ⅰ)sin sin 3A C =;(Ⅱ)AC =【分析】(Ⅰ)利用三角形面积公式以及2BCD ABD S S ∆∆=并结合正弦定理sin sin AB BCC A=,可得结果. (Ⅱ)根据2BCD ABD S S ∆∆=,可得θ,然后使用余弦定理2222sin AC AB BC AB BC ABC =+-⋅∠,可得结果.【详解】(Ⅰ)23CBD ABD π∠=∠=,所以11sin 2sin 2326BC BD AB BD ππ⋅=⨯⋅所以sinsin 3BC A AB C =⇒==;(Ⅱ)11sin 22sin 22BC BD AB BD θθ⋅=⨯⋅,所以42sin cos 2cos 2θθθθ⨯=⨯⇒=,所以4πθ=,334ABC πθ∠==,所以21682440AC ⎛=+-⨯⨯= ⎝⎭,所以边AC =【点睛】本题考查三角形面积公式,正弦定理以及余弦定理的应用,关键在于识记公式,属中档题.38.(2020江西赣州模拟)已知点O 是ABC 的外接圆的圆心,3AB =,AC =4BAC π∠=.(1)求外接圆O 的面积.(2)求BO BC ⋅ 【答案】(1)52π;(2)52. 【分析】(1)根据余弦定理求出BC .设外接圆的半径为r ,由正弦定理得2sin BCr BAC=∠,即求外接圆O 的面积;(2)设BC 的中点为E ,则EO BC ⊥,则()BO BC BE EO BC ⋅=+⋅,即可求出数量积. 【详解】(1)由余弦定理得(222222cos323542BC AB AC AB AC π=+-⋅=+-⨯⨯=,BC ∴=设外接圆的半径为r,由正弦定理得2sin BCr BAC===∠所以外接圆的面积为2252S r πππ===⎝⎭. (2)设BC 的中点为E ,则EO BC ⊥,()21522BO BC BE EO BC BE BC EO BC BC ∴⋅=+⋅=⋅+⋅==.【点睛】本题考查正、余弦定理和向量的数量积,属于基础题.39.(2020湖南师大附中模拟)已知ABC ∆的内角A ,B ,C 的对边分别为a ,b ,c ,且()()sin sin a A B C c B C +-=+.(1)求角C 的值;(2)若26a b +=,且ABC ∆ABC ∆的周长. 【答案】(1)3π;(2)6或5+ 【分析】(1)结合三角形内角和及诱导公式对已知进行化简可求cos C ,进而可求C ,(2)由已知,结合三角形的面积公式可求,a ,b 然后结合C 的值及余弦定理可求c ,进而可求周长.。