2016年寒假学习效果监测数学试卷
- 格式:doc
- 大小:288.50 KB
- 文档页数:2

【KS5U】新课标2016年高三数学寒假作业6一、选择题.1.设集合A={x|﹣1≤x≤2,x∈N},集合B={2,3},则A∪B=( )A.{1,2,3} B.{0,1,2,3} C.{2} D.{﹣1,0,1,2,3}2.已知a0=20.5,b=log32,c=log20.1,则( )A.a<b<c B.c<a<b C.c<b<a D.b<c<a3.已知函数f(n)=n2cos(nπ),且a n=f(n),则a1+a2+a3+…+a100=( )A.0 B.100 C.5050 D.102004.已知函数y=Asin(ωx+∅)(A>0,ω>0,﹣π≤∅≤π)一个周期的图象(如图),则这个函数的一个解析式为( )A.B.C.D.5.已知向量=(0,sinx),=(1,2cosx),函数f(x)=•,g(x)=2+2﹣,则f(x)的图象可由g(x)的图象经过怎样的变换得到( )A.向左平移个单位长度B.向右平移个单位长度C.向左平移个单位长度D.向右平移个单位长度6.已知a>0,b>0满足a+b=1,则的最小值为( )A.12 B.16 C.20 D.257.已知a,b是两条不同的直线,α是一个平面,则下列说法正确的是( )A.若a∥b,b⊂α,则a∥αB.若a∥α,b⊂α,则a∥bC.若a⊥α,b⊥α,则a∥b D.若a⊥b,b⊥α,则a∥α8.某程序框图如图所示,若输出的S=57,则判断框内为( )A.k>4?B.k>5?C.k>6?D.k>7?9.f(x)=x3﹣x2+ax﹣1己知曲线存在两条斜率为3的切线,且切点的横坐标都大于零,则实数a的取值范围为( )A.(3,+∞)B.(3,)C.(﹣∞,] D.(0,3)10.若焦点在x轴上的双曲线的离心率为,则该双曲线的渐近线方程为( )A.B.y=±2x C.D.二.填空题.11.已知条件p:x2﹣3x﹣4≤0;条件q:x2﹣6x+9﹣m2≤0,若¬q是¬p的充分不必要条件,则实数m的取值范围是.12.已知数列{a n}的通项公式为a n=19﹣2n(n∈N*),则S n最大时,n= .13.在△ABC中,已知a、b、c成等比数列,且,则= .14.若a>1,设函数f(x)=a x+x﹣4的零点为m,g(x)=log a x+x﹣4的零点为n,则+的最小值为.三、解答题.15.已知{a n}是等差数列,满足a1=3,a4=12,等比数列{b n}满足b1=4,b4=20.(1)求数列{a n}和{b n}的通项公式;(2)求数列{b n}的前n项和.16.已知向量,函数f(x)=图象的对称中心与对称轴之间的最小距离为.(1)求ω的值,并求函数f(x)在区间[0,π]上的单调递增区间;(2)△ABC中,角A,B,C的对边分别为a,b,c,f(A)=1,cosC=,a=5,求b.17.已知:集合A={x|≥1},B={x|3+2x﹣x2<0},U=R,求:A∩B,A∩(∁U B).【KS5U】新课标2016年高三数学寒假作业61.B【考点】并集及其运算.【专题】计算题.【分析】把集合A的所有元素和集合B的所有元素合并到一起,得到集合A∪B.由此根据集合A={x|﹣1≤x≤2,x∈N},集合B={2,3},能求出A∪B.【解答】解:∵集合A={x|﹣1≤x≤2,x∈N}={0,1,2},集合B={2,3},∴A∪B={0,1,2,3}.故选B.【点评】本题考查集合的并集的定义及其运算,解题时要认真审题,仔细解答,注意并集中相同的元素只写一个.2.C【考点】对数值大小的比较.【专题】函数的性质及应用.【分析】利用指数函数和对数函数的单调性即可得出.【解答】解:∵a=20.5>20=1,0<b=log32<log33=1,c=log20.1<log21=0.∴c<b<a.故选:C.【点评】本题考查了指数函数和对数函数的单调性,属于基础题.3.C【考点】数列的求和.【分析】先求出分段函数f(n)的解析式,进一步给出数列的通项公式,再使用分组求和法,求解.【解答】解:∵f(n)=n2cos(nπ)==(﹣1)n•n2,且a n=f(n),∴a1+a2+a3+…+a100=22﹣12+42﹣32+62﹣52+…+1002﹣992=1+2+3+4+5+6+…+99+100==5050.故选C.【点评】本小题是一道分段数列的求和问题,综合三角知识,主要考查分析问题和解决问题的能力.4.D【考点】由y=Asin(ωx+φ)的部分图象确定其解析式.【专题】数形结合.【分析】由已知中函数y=Asin(ωx+∅)(A>0,ω>0,﹣π≤∅≤π)的图象,我们分别求出函数的最大值,最小值及周期,进而求出A值和ω值,将最大值点代入结合正弦函数的性质求出φ值,即可得到函数的解析式.【解答】解:由函数的图象可得函数的最大值为2,最小值为﹣2,结合A>0,可得A=2又∵函数的图象过(,2)点和(,0)点,则T=,结合ω>0,可得ω=3则函数的解析式为y=2sin(3x+∅)将(,2)代入得π+φ=,k∈Z当k=0时,φ=﹣故函数的解析式为故选D【点评】本题考查的知识点是由函数y=Asin(ωx+∅)的图象确定函数的解析式,其中根据函数的图象分析出函数的最大值,最小值,周期,向左平移量,特殊点等是解答本题的关键.5.B【考点】函数y=Asin(ωx+φ)的图象变换;平面向量数量积的运算.【专题】平面向量及应用.【分析】由题意利用两个向量的数量积公式、诱导公式可得函数f(x)=sin2x,g(x)=sin2(x+),再根据函数y=Asin(ωx+φ)的图象变换规律,可得结论.【解答】解:由题意可得函数f(x)=•=(2sinxcosx)=sin2x,g(x)=2+2﹣=sin2x+1+4cos2x﹣=3cos2x﹣=cos2x=sin(2x+)=sin2(x+),故把g(x)的图象向右平移个单位长度,可得f(x)的图象,故选:B.【点评】本题主要考查诱导公式的应用,函数y=Asin(ωx+φ)的图象变换规律,统一这两个三角函数的名称,是解题的关键,属于基础题.6.B【考点】基本不等式.【专题】计算题;转化思想;不等式的解法及应用.【分析】通过“1”的代换,化简所求表达式,利用基本不等式求出它的最小值.【解答】解:∵a>0,b>0,且满足a+b=1,则==10+≥10+2=16,当且仅当,即a=,时,等号成立.故的最小值为16,故选:B.【点评】本题主要考查基本不等式的应用,注意基本不等式的使用条件,并注意检验等号成立的条件,式子的变形是解题的关键,属于基础题.7.C【考点】空间中直线与平面之间的位置关系.【专题】探究型;空间位置关系与距离.【分析】根据有关定理中的诸多条件,对每一个命题进行逐一进行是否符合定理条件去判定即可.【解答】解:若a∥b、b⊂α,则a∥α或a⊂α,故A错误;若a∥α、b⊂α,则a∥b或a,b异面,故B错误;若a⊥α,b⊥α,则a∥b,满足线面垂直的性质定理,故正确若b⊥α,a⊥b,则a∥α或a⊂α,故D错误;故选:C【点评】本题考查空间中直线与直线、直线与平面、平面与平面的位置关系,是基础题.解题时要认真审题,仔细解答,注意空间想象能力的培养.8.A【考点】程序框图.【专题】算法和程序框图.【分析】分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是累加并输入S的值,条件框内的语句是决定是否结束循环,模拟执行程序即可得到答案.【解答】解:程序在运行过程中各变量值变化如下表:K S 是否继续循环循环前 1 1/第一圈 2 4 是第二圈 3 11 是第三圈 4 26 是第四圈 5 57 否故退出循环的条件应为k>4故答案选A.【点评】算法是新课程中的新增加的内容,也必然是新高考中的一个热点,应高度重视.程序填空也是重要的考试题型,这种题考试的重点有:①分支的条件②循环的条件③变量的赋值④变量的输出.其中前两点考试的概率更大.此种题型的易忽略点是:不能准确理解流程图的含义而导致错误.9.B【考点】利用导数研究曲线上某点切线方程.【专题】转化思想;转化法;导数的概念及应用.【分析】求得f(x)的导数,由题意可得2x2﹣2x+a﹣3=0有两个不等的正根,运用判别式大于0,两根之和大于0,两根之积大于0,解不等式即可得到a的范围.【解答】解:f(x)=x3﹣x2+ax﹣1的导数为f′(x)=2x2﹣2x+a,由题意可得2x2﹣2x+a=3,即2x2﹣2x+a﹣3=0有两个不等的正根,则△=4﹣8(a﹣3)>0,x1+x2=1>0,x1x2=(a﹣3)>0,解得3<a<.故选B.【点评】本题考查导数的几何意义,考查二次方程实根的分布,以及韦达定理的运用,考查运算能力,属于中档题.10.A【考点】双曲线的简单性质.【专题】计算题.【分析】由离心率可得关于m的方程,解之代入可得双曲线方程,可得渐近线方程.【解答】解:由题意可得离心率e==,解之可得m=1,故方程为,故渐近线方程为y==,故选A【点评】本题考查双曲线的简单性质,涉及渐近线和离心率,属中档题.11.m≥4考点:必要条件、充分条件与充要条件的判断.专题:简易逻辑.分析:分别解关于p,q的不等式,求出¬q,¬p的关于x的取值范围,从而求出m的范围.解答:解:∵条件p:x2﹣3x﹣4≤0;∴p:﹣1≤x≤4,∴¬p:x>4或x<﹣1,∵条件q:x2﹣6x+9﹣m2≤0,∴q:3﹣m≤x≤3+m,∴¬q:x>3+m或x<3﹣m,若¬q是¬p的充分不必要条件,则,解得:m≥4,故答案为:m≥4.点评:本题考察了充分必要条件,考察集合的包含关系,是一道基础题.12.9【考点】等差数列的前n项和.【专题】等差数列与等比数列.【分析】由已知得a1=19﹣2=17,从而S n==﹣(n2﹣18n)=﹣(n﹣9)2+81.由此能求出n=9时,S n取最大值81.【解答】解:∵数列{a n}的通项公式为a n=19﹣2n(n∈N*),∴a1=19﹣2=17,S n==﹣(n2﹣18n)=﹣(n﹣9)2+81.∴n=9时,S n取最大值81.故答案为:9.【点评】本题考查等差数列的前n项和取最大值时项数n的求法,解题时要认真审题,注意配方法的合理运用.13.【考点】余弦定理;平面向量数量积的运算.【专题】计算题;解三角形.【分析】先求a+c的平方,利用a、b、c成等比数列,结合余弦定理,求解ac的值,然后求解.【解答】解:∵a+c=3,∴a2+c2+2ac=9…①∵a、b、c成等比数列:∴b2=ac…②又cosB=,由余弦定理:b2=a2+c2﹣2accosB可得b2=a2+c2﹣ac…③解①代入③得b2=9﹣2ac﹣ac,又b2=ac,∴ac=2,=accos(π﹣B)=﹣accosB=﹣.故答案为:.【点评】本题考查平面向量数量积的运算,等比数列的性质,余弦定理,考查学生分析问题解决问题的能力.14.1【考点】函数零点的判定定理;基本不等式.【专题】函数的性质及应用.【分析】构建函数F(x)=a x,G(x)=log a x,h(x)=4﹣x,则h(x)与F(x),G(x)的交点A,B的横坐标分别为m、n,注意到F(x)=a x,G(x)=log a x,关于直线y=x对称,可得m+n=4,再用“1”的代换,利用基本不等式,即可得出结论.【解答】解:由题意,构建函数F(x)=a x,G(x)=log a x,h(x)=4﹣x,则h(x)与F(x),G(x)的交点A,B的横坐标分别为m、n.注意到F(x)=a x,G(x)=log a x,关于直线y=x对称,可以知道A,B关于y=x对称,由于y=x与y=4﹣x交点的横坐标为2,∴m+n=4.则+=(+)(m+n)=(2++)≥(2+2)=1,当且仅当m=n=2时,等号成立,故+的最小值为1,故答案为:1.【点评】本题考查函数的零点,考查基本不等式的运用,考查学生分析转化问题的能力,求出m+n=4,正确运用基本不等式是关键,属于基础题.15.【考点】数列的求和.【专题】计算题;转化思想;综合法;等差数列与等比数列.【分析】(1)由等差数列的通项公式求出公差,由此能求出数列{a n}的通项公式;由等比数列{b n}通项公式求出公比q,由此能求出数列{b n}的通项公式.(2)由等比数列{b n}的首项和公比能求出数列{b n}的前n项和.【解答】解:(1)∵{a n}是等差数列,满足a1=3,a4=12,∴3+3d=12,解得d=3,∴a n=3+(n﹣1)×3=3n.∵等比数列{b n}满足b1=4,b4=20,∴4q3=20,解得q=,∴b n=4×()n﹣1.(2)∵等比数列{b n}中,,∴数列{b n}的前n项和S n==.【点评】本题考查数列的通项公式和前n项和的求法,是中档题,解题时要认真审题,注意等差数列和等比数列的性质的合理运用.16.【考点】平面向量数量积的运算;三角函数中的恒等变换应用;正弦定理.【专题】解三角形;平面向量及应用.【分析】(1)先求出f(x)=2sin(ωx+),而f(x)图象的对称中心与对称轴之间的最小距离为其周期的四分之一,这样即可求得ω=2,从而f(x)=2sin(2x+),写出f(x)的单调增区间,然后再找出[0,π]上的单调递增区间即可;(2)由f(A)=1,能够求出A=,由cosC=求出sinC,而由sinB=sin()即可求出sinB,而由正弦定理:,即可求出b.【解答】解:(1);由于图象的对称中心与对称轴的最小距离为,所以;令,解得,k∈Z;又x∈[0,π],所以所求单调增区间为;(2)或;∴A=kπ或,(k∈Z),又A∈(0,π);故;∵;∴;由正弦定理得;∴.【点评】考查求函数Asin(ωx+φ)的周期的公式,并且知道该函数的对称轴与对称中心,以及能写出该函数的单调区间,数量积的坐标运算,已知三角函数值求角,两角和的正弦公式,正弦定理.17.【考点】交、并、补集的混合运算.【专题】集合.【分析】分别求解分式不等式与一元二次不等式化简集合A,B,然后利用交、并、补集的混合运算得答案.【解答】解:由≥1,得,解得.∴A={x|≥1}={x|<x≤1}.由3+2x﹣x2<0,得x2﹣2x﹣3>0,解得x<﹣1或x>3.∴B={x|3+2x﹣x2<0}={x|x<﹣1或x>3}.则A∩B=∅;又U=R,∴∁U B={x|﹣1≤x≤3}.∴A∩(∁U B)={x|<x≤1}.【点评】本题考查交、并、补集的混合运算,考查了分式不等式与一元二次不等式的解法,是基础题.。

山东省2016年冬季普通高中学业水平考试数学试题第I 卷(共60分)一、选择题(本大题共20个小题,每小题3分,共60分) 1.已知全集{}c b a U ,,=,集合{}a A =,则=A C U ( )A. {}b a ,B. {}c a ,C. {}c b ,D. {}c b a ,, 2.已知0sin <θ,0cos >θ,那么θ的终边在( )A.第一象限B. 第二象限C. 第三象限D.第四象限 3.若实数第3,a ,5成等差数列,则a 的值是( )A. 2B. 3C. 4D. 15 4.图像不经过第二象限的函数是( )A. xy 2= B.x y -= C. 2x y = D. x y ln = 5.数列1,32,53,74,95,…的一个通项公式是=n a ( ) A. 12+n n B. 12-n n C. 32+n n D. 32-n n6.已知点)4,3(A ,)1,1(-B ,则线段AB 的长度是( )A. 5B. 25C. 29D. 29 7.在区间]4,2[-内随机取一个实数,则该实数为负数的概率是( ) A.32B. 21C. 31D. 41 8.过点)2,0(A ,且斜率为1-的直线方程式( )A.02=++y xB.02=-+y xC.02=+-y xD.02=--y x 9.不等式0)1(<+x x 的解集是( )A.{}01|<<-x xB.{}0,1|>-<x x x 或C. {}10|<<x xD.{}1,0|><x x x 或 10.已知圆C :036422=-+-+y x y x ,则圆C 的圆心坐标和半径分别为( )A. )(3,2-,16B. )(3,2-,16C. )(3,2-,4D. )(3,2-,411.在不等式22<+y x 表示的平面区域内的点是( )A. )(0,0B. )(1,1C. )(2,0D. )(0,2 12.某工厂生产了A 类产品2000件,B 类产品3000件,用分层抽样法从中抽取50件进行产品质量检验,则应抽取B 类产品的件数为( )A. 20B. 30C. 40D. 50 13.已知3tan -=α,1tan =β,则)tan(βα-的值为( )A. 2-B. 21-C. 2D. 2114.在ABC ∆中,角A ,B ,C 所对的边分别是a ,b ,c ,若1=a ,2=b ,41sin =A ,则B sin 的值是( ) A.41 B. 21C. 43 D. 4215.已知偶函数)(x f 在区间),0[+∞上的解析式为1)(+=x x f ,下列大小关系正确的是( ) A. )2()1(f f > B. )2()1(->f f C. )2()1(->-f f D. )2()1(f f <-16.从集合{}2,1中随机选取一个元素a ,{}3,2,1中随机选取一个元素b ,则事件“b a <”的概率是( ) A.61 B. 31 C. 21 D. 3217.要得到)42sin(π+=x y 的图像,只需将x y 2sin =的图像( )A. 向左平移8π个单位 B.向右平移 8π个单位 C.向左平移4π个单位 D.向右平移 4π个单位 18.在ABC ∆中,角A ,B ,C 所对的边分别是a ,b ,c ,若1=a ,2=b ,60=C ,则边c 等于( ) A. 2 B. 3 C. 2 D. 319.从一批产品中随机取出3件,记事件A 为“3件产品全是正品”,事件B 为“3件产品全是次品”,事件C 为“3件产品中至少有1件事次品”,则下列结论正确的是( ) A.A 与C 对立 B.A 与C 互斥但不对立 C.B 与C 对立 D.B 与C 互斥但不对立20.执行如图所示的程序框图(其中[]x 表示不超过x 的最大整数),则输出的S 的值为( )A. 1B. 2C. 3D. 4二、填空题(本大题共5个小题,每小题3分,共15分)21. 2log 2的值为 .22.在各项均为正数的等比数列{}n a 中,971=⋅a a , 则=4a .23.已知向量)2,1(=a ,)1,(x b =,若b a ⊥,则实数x 的值是 . 24.样本5,8,11的标准差是 .25.已知一个圆锥的母线长为20,母线与轴的夹角为60,则该圆锥的高是 . 三、解答题(本大题共3个小题,共25分)26.(本小题满分8分)如图,在三棱锥BCD A -中,E ,F 分别是棱AB ,AC 的中点.求证://EF 平面BCD .27.(本小题满分8分)已知函数x x x f 22sin cos )(-=.求:⑵ )12(πf 的值; ⑵)(x f 的单调递增区间.28.(本小题满分9分)已知函数41)(2++=ax x x f )(R a ∈ ⑴当函数)(x f 存在零点时,求a 的取值范围; ⑵讨论函数)(x f 在区间)1,0(内零点的个数.题号 1 2 3 4 5 6 7 8 9 10 答案 题号 11 12 13 14 15 16 17 18 19 20 答案2016冬季学业水平数学试题参考答案1-5:CDCDB 6-10:ACBAD 11-15:ABCBD 16-20: CABAC 21.2122. 3 23. 2- 24.6 25. 10 26.证明:在ABC ∆中,因为E ,F 分别是棱AB ,AC 的中点,所以EF 是ABC ∆的中位线, ……………………………………………1分所以BC EF //………………………………………………………………4分又因为⊂/EF 平面BCD ……………………………………………………5分 ⊂BC 平面BCD ……………………………………………………………6分 所以//EF 平面BCD ………………………………………………………8分 27.解:x x x x f 2cos sin cos )(22=-=……………………………………………2分⑴236cos)122cos()12(==⨯=πππf ……………………………………5分 ⑵由πππk x k 222≤≤-,Z k ∈, 得πππk x k ≤≤-2,Z k ∈.………………………………………………7分所以)(x f 的单调递增区间为],2[πππk k -,Z k ∈.……………………8分28.解⑴因为函数)(x f 有零点, 所以方程0412=++ax x 有实数根. 所以012≥-=∆a ,解得1-≤a ,或1≥a因此,所求a 的取值范围是1-≤a ,或1≥a .………………………………2分 ⑵综上,当1->a 时,)(x f 在区间)1,0(内没有零点; 当1-=a ,或45-≤a 时,)(x f 在区间)1,0(内有1个零点; 当145-<<-a 时,)(x f 在区间)1,0(内有2个零点.2017年山东省普通高中学业水平考试数学试题一、选择题(本大题共20个小题,每小题3分,共60分)1.已知集合{}4,2,1=A ,{}84,2,=B ,则=B A ( ) A .{4} B .{2} C .{2,4} D .{1,2,4,8}2.周期为π的函数是( )A .y =sinxB .y =cosxC .y =tan 2xD .y =sin 2x3.在区间()∞+,0上为减函数的是( ) A .2x y = B .21x y = C .xy ⎪⎭⎫⎝⎛=21 D .x y ln =4.若角α的终边经过点()2,1-,则=αcos ( ) A .55-B .55C .552-D .552 5.把红、黄两张纸牌随机分给甲、乙两个人,每人分得一张,设事件P 为“甲分得黄牌”,设事件Q为“乙分得黄牌”,则( )A .P 是必然事件B .Q 是不可能事件C .P 与Q 是互斥但是不对立事件D .P 与Q 是互斥且对立事件 6.在数列{}n a 中,若n n a a 31=+,21=a ,则=4a ( )A .108B .54C .36D .187.采用系统抽样的方法,从编号为1~50的50件产品中随机抽取5件进行检验,则所选取的5件产品的编号可以是( )A .1,2,3,4,5B .2,4,8,16,32C .3,13,23,33,43D .5,10,15,20,25 8.已知()+∞∈,0,y x ,1=+y x ,则xy 的最大值为( ) A .1 B .21 C .31 D .419.在等差数列{}n a 中,若95=a ,则=+64a a ( )A .9B .10C .18D .2010.在ABC ∆中,角A ,B ,C 的对边分别是a ,b ,c ,若︒=60A ,︒=30B ,3=a ,则=b ( ) A .3 B .233 C .32 D .33 11.已知向量()3,2-=a ,()6,4-=b ,则a 与b ( )A .垂直B .平行且同向C .平行且反向D .不垂直也不平行 12.直线012=+-y ax 与直线012=-+y x 垂直,则=a ( ) A .1 B .-1 C .2 D .-213.在△ABC 中,角A ,B ,C 的对边分别是a ,b ,c ,若222c bc b a +-=,则角A 为( ) A .6π B .3π C .32π D .3π或32π 14.在学校组织的一次知识竞赛中,某班学生考试成绩的频率分布直方图如图所示,若低于60分的有12人,则该班学生人数是( )A .35B .40C .45D .5015.已知△ABC 的面积为1,在边AB 上任取一点P ,则△PBC 的面积大于41的概率是( ) A .41 B .21 C .43 D .32 16.设x ,y 满足约束条件⎪⎩⎪⎨⎧≥≥≤+1142y x y x ,则y x z -=的最小值是( )A .-1B .21-C .0D .1 17.下列结论正确的是( )A .平行于同一个平面的两条直线平行B .一条直线与一个平面平行,它就和这个平面内的任意一条直线平行C .与两个相交平面的交线平行的直线,必平行于这两个平面D .平面外两条平行直线中的一条与这个平面平行,则另一条也与这个平面平行18.若圆柱的底面半径是1,其侧面展开是一个正方形,则这个圆柱的侧面积是( ) A .24π B .23π C .22π D .2π 19.方程x x -=33的根所在区间是( )A .(-1,0)B .(0,1C .(1,2D .(2,3)20.运行如图所示的程序框图,如果输入的x 值是-5,那么输出的结果是( ) A .-5 B .0 C .1 D .2二、填空题(本大题共5个小题,每题3分,共15分) 21.函数)1lg()(-=x x f 的定义域为 .22.已知向量,2=a ,与的夹角θ为32π,若1-=⋅,则=b .23.从集合{}3,2=A ,{}3,21,=B 中各任取一个数,则这两个数之和等于4的概率是 .24.已知数列{n a }的前n 项和为n n S n 22+=,则该数列的通项公式=n a .25.已知三棱锥P -ABC 的底面是直角三角形,侧棱⊥PA 底面ABC ,P A =AB =AC =1,D 是BC 的中点,PD 的长度为 .三、解答题(本大题共3个小题,共25分)26.(本小题满分8分)已知函数1cos sin )(+=x x x f .求: (1))4(πf 的值; (2)函数)(x f 的最大值.27.(本小题满分8分)已知n mx x x f ++=22)((m ,n 为常数)是偶函数,且f (1)=4. (1)求)(x f 的解析式;(2)若关于x 的方程kx x f =)(有两个不相等的实数根,求实数k 的取值范围.28.(本小题满分9分)已知直线l :y =kx +b ,(0<b <1)和圆O :122=+y x 相交于A ,B 两点. (1)当k =0时,过点A ,B 分别作圆O 的两条切线,求两条切线的交点坐标;(2)对于任意的实数k ,在y 轴上是否存在一点N ,满足ONB ONA ∠=∠?若存在,请求出此点坐标;若不存在,说明理由.山东省2017年普通高中学业水平考试参考答案1-5: CDCAD 6-10:BCDCA 11-15:CABBC 16-20:BDABC21、()∞+,1 22、1 23、3124、2n+1 25、2626、(1)23;(2)最大值为23. 27、(1)22)(2+=x x f ; (2)4>k 或4-<k . 28、(1)⎪⎭⎫ ⎝⎛b 10,;(2)存在;⎪⎭⎫ ⎝⎛b 10,.。

2016年寒假学习成果检测(数学)试卷试卷满分120分,时间150分钟。
一、选择题(每题4分,共48分)1. PM2.5是指大气中直径小于或等于2.5μm (1μm =0.000001m )的颗粒物,也称为可入肺颗粒物,它们含有大量的有毒、有害物质,对人体健康和大气环境质量有很大危害.2.5μm 用科学记数法可表示为( )A . 2.5×10﹣5mB . 0.25×10﹣7mC . 2.5×10﹣6mD . 25×10﹣5m 2. 已知等腰三角形的两边长分別为a 、b ,且a 、b 满足+(2a +3b ﹣13)2=0,则此等腰三角形的周长为( )A . 7或8B . 6或1OC . 6或7D . 7或103. 如图1所示是某公园为迎接“中国﹣﹣南亚博览会”设置的一休闲区.∠AOB=90°,弧AB 的半径OA 长是6米,C 是OA 的中点,点D 在弧AB 上,CD ∥OB ,则图中休闲区(阴影部分)的面积是( )A .米2B .米2C .米2D .米2(图1) (图2) (图4) (图5)4. 如图2所示,在直角坐标系中放置一个边长为1的正方形ABCD ,将正方形ABCD 沿x 轴的正方向无滑动的在x 轴上滚动,当点A 离开原点后第一次落在x 轴上时,点A 运动的路径线与x 轴围成的面积为( )A. B. C . D .5.已知反比例函数k y x =的图像如图3所示,则二次函数2224y kx x k =-+的图像大致为( ).A. B. C. D. 图36. 如图4,在△ABC 中,∠ACB =90º,AC =BC =1,E 、F 为线段AB 上两动点,且∠ECF =45°,过点E 、F 分别作BC 、AC 的垂线相交于点M ,垂足分别为H 、G .现有以下结论:①AB②当点E 与点B 重合时,MH =12;③AF+BE=EF ;④MG•MH =12,其中正确结论为( )A .①②③B .①③④C .①②④D .①②③④7. 如图5,AB =4,射线BM 和AB 互相垂直,点D 是AB 上的一个动点,点E 在射线BM 上,BE =DB ,作EF ⊥DE﹣(图6) (图7) (图8) (图9)8. 已知:如图6,在△ABC 中,BC =10,BC 边上的高h =5,点E 在边AB 上,过点E 作EF ∥BC ,交AC 边于点F .点 C9. 某种花卉每盆的盈利与每盆的株数有一定的关系,每盆植3株时,平均每株盈利4元;若每盆增加1株,平均每株盈利减少0.5元,要使每盆的盈利达到15元,每盆应多植多少株?设每盆多植x 株,则可以列出的方程是( )A.(3+x)(4-0.5x)=15B.(x+3)(4+0.5x)=15C.(x+4)(3-0.5x)=15D.(x+1)(4-0.5x)=1510. 如图7所示,顶角为36°的等腰三角形,其底边长与腰长之比等于k(k 值等于黄金比),这样的三角形叫黄金三角形.已知腰长AB=1,△ABC 为第一个黄金三角形,△BCD 为第二个黄金三角形,△CDE 为第三个黄金三角形,以此类推,第 2 014 个黄金三角形的周长为( )A.k 2 013B.k 2 012C.D.k 2 013(2+k)11. 如图8,在Rt △ABC 中,∠ABC =90°,AB =B C .点D 是线段AB 上的一点,连结CD ,过点B 作BG ⊥CD ,分别交CD 、CA 于点E 、F ,与过点A 且垂直于AB 的直线相交于点G ,连结DF .给出以下四个结论:①;②若点D 是AB 的中点,则AF =AB ;③当B 、C 、F 、D 四点在同一个圆上时,DF =DB ;④若,则.其中正确的结论序号是( )A .①②B .③④C .①②③D .①②③④ .12. 如图9,在第1个△A 1BC 中,∠B =30°,A 1B =CB ;在边A 1B 上任取一点D ,延长CA 1到A 2,使A 1A 2=A 1D ,得到第2个△A 1A 2D ;在边A 2D 上任取一点E ,延长A 1A 2到A 3,使A 2A 3=A 2E ,得到第3个△A 2A 3E ,…按此做法继续下去,则第n 个三角形中以A n 为顶点的内角度数是( )A .()n •75°B . ()n ﹣1•65°C . ()n ﹣1•75°D . ()n •85°二、填空题(每小题3分,共12分)13. 如图10.在正方形ABCD的边长为3,以A为圆心,2为半径作圆弧.以D为圆心,3为半径作圆弧.若图中阴影部分的面积分为S1、S2.则S1﹣S2=.14. 如图11,正方形ABCD的边长为6,点O是对角线AC、BD的交点,点E在CD上,且DE=2CE,过点C作CF ⊥BE,垂足为F,连接OF,则OF的长为.(图10)(图11)(图12)(图13)15. 如图12,矩形ABCD中,OA在x轴上,OC在y轴上,且OA=2,AB=5,把△ABC沿着AC对折得到△AB′C,AB′交y轴于D点,则B′点的坐标为(,).16. 一走廊拐角的横截面积如图13 ,已知AB⊥BC,AB∥DE,BC∥FG,且两组平行墙壁间的走廊宽度都是1m,的圆心为O,半径为1m,且∠EOF=90°,DE、FG分别与⊙O相切于E、F两点.若水平放置的木棒MN的两个端点M、N分别在AB和BC上,且MN与⊙O相切于点P,P是的中点,则木棒MN的长度为______三、解答题(共60分)17. 阳光中学九(1)班同学在一次综合实践活动中,对本县居民参加“全民医保”情况进行了调查,同学们利用节假日随机调查了2 000人,对调查结果进行了统计分析,绘制出两幅不完整的统计图,如图14所示:(8分)(图14)(1)补全条形统计图;(2分)(2)在本次调查中,B类人数占被调查人数的百分比为________;(2分)(3)据了解,国家对B类人员每人每年补助155元.已知该县人口数约80万人,请估计该县B类人员每年享受国家补助共多少万元.(4分)18. 为落实国务院房地产调控政策,使“居者有其屋”,某市加快了廉租房的建设力度.2010年市政府共投资2亿元人民币建设了廉租房8万平方米,预计到2012年底三年共投资9.5亿元人民币建设廉租房,若在这两年内每年投资的增长率相同.(8分)(1)求每年市政府投资的增长率;(4分)(2)若这两年内的建设成本不变,求到2012年底共建设多少万平方米廉租房?(4分)19. 在数学学习的过程中,常常需要知识迁移,使用特殊方法....求解。
2016年寒假学习效果监测九年级数学试题一、选择题1. .△ABC 中,a 、b 、c 分别是∠A 、∠B 、∠C 的对边,如果222c b a =+,那么下列结论正确的是( ) A .c sinA =a B .b cosB =c C .a tanA =b D .c tanB =b 2.如图,点P 是ABC ∆的边AC 上一点,连结BP ,以下条件中,不能判定ABP ∆∽ACB ∆的是( )A .AB AC AP AB = B .AB ACBP BC = C .C ABP ∠=∠ D .ABC APB ∠=∠3.用配方法解方程x 2-4x +2=0,下列配方正确的是( ) A .(x -2)2=2 B ..(x +2)2=2 C ..(x -2)2=-2 D ..(x -2)2=6 4.如图2,已知ABC ∆的三个顶点均在格点上,则cos A 的值为ABCD5.在一个不透明的袋中装着3个红球和1个黄球,它们只有颜色上的区别,随机从袋中摸出2个小球,两球恰好是一个黄球和一个红球的概率为( )A .12B .13C .14D .166.在平面直角坐标系中,如果抛物线y =2x 2分别向上、向右平移2个单位,那么新抛物线的解析式是( )A .y =2(x + 2)2-2B .y =2(x -2)2 + 2C .y =2(x -2)2-2D .y =2(x + 2)2 + 2 7.在同一直角坐标系中,函数y =kx -k 与(k ≠0)的图像大致是( )8.⊙O 的直径AB =10cm ,弦CD ⊥AB ,垂足为P .若OP :OB =3:5,则CD 的长为( ) A .6cm B .4cm C .8 cm D .91 cm9.如图,斜面AC 的坡度(CD 与AD 的比)为1:2,AC =3米,坡顶有旗杆BC ,旗杆顶端B 点与A 点有一条彩带相连.若AB =10米,则旗杆BC 的高度为( ) A .5米 B .6米 C .8米 D .(3+)米10. 下列四个几何体中,主视图是圆的是( )AB .C .D .11. 如图,⊙O 是△ABC 的内切圆,切点分别是D 、E 、F ,已知∠A =100°,∠C =30°,则∠DFE 的度数是( )A .55°B .60°C .65°D .70°12. 已知直线l 1∥l 2∥l 3∥l 4,相邻的两条平行直线间的距离均为h ,矩形ABCD 的四个顶点分别在这四条直线上,放置方式如图所示,AB =4,BC =6,则tanα的值等于( ) A .23 B . 34 C . 43 D . 32二、填空题: 13.函数y =x 的取值范围是 . 14△ABC 中,DE 是BC 的垂直平分线,DE 交AC 于点E ,连接BE ,若BE =9,BC =12,则cosC = . 15. 如图,AB 是⊙O 的直径,点C 在AB 的延长线上,CD 与⊙O 相切于点D .若∠C=20°,则∠CDA = °.A16. 如右图抛物线y =-x 2+bx +c 的图像与x 轴的一个交点(1,0),则抛物线与x 轴的另一个交点坐标是___________。

2016-2017学年初三数学寒假训练题(1)答案一、选择题(每小题3分,共30分):CABBB DCDAC二、填空题(每小题3分,共30分): 11.2-x x 12.4113.>14. -8. 16. 39217. 4-. 18.()12-n 19.1225三、解答题:21.(1)原式 =–2 + 1 + 2 + 2×1 = 3 (2).解:方程两边同乘以(x –4),约去分母得:()143-=-++x x解得:x = 0经检验,x = 0是原方程的根。
22.(1)240;(2)如右图;(3)135º;(4)5523. 【答案】(1)y =-x ,4y x=-;(2)点C 的坐标为(4,-1),6.月某品牌手机今年1~4月份销量条形月月月解法二:如图2,连接OC .∵ OA ∥BC ,∴S △ABC =S △BOC =12OBx c =12×3×4=6. 试题解析:(1) ∵ 正比例函数y kx =的图象与反比例函数直线m y x =的图象都经过点A (2,-2).,∴ 2222k m =-⎧⎪⎨=-⎪⎩解得:14k m =-⎧⎨=-⎩ ∴ y =-x ,4y x =-;(2) ∵ 直线BC 由直线OA 向上平移3个单位所得,∴ B (0,3),k bc = k oa =-1,∴ 设直线BC 的表达式为 y =-x +3, 由 43y x y x ⎧=-⎪⎨⎪=-+⎩,解得1141x y =⎧⎨=-⎩,2214x y =-⎧⎨=⎩.∵ 因为点C 在第四象限 ∴ 点C 的坐标为(4,-1).24.(1)解:设A 型花每枝x 元,B 型花每枝y元,根据题意得: …………………1分⎩⎨⎧=+=+2552232y x y x …………………………2分 解得:⎩⎨⎧==45y x …………………………3分答:A 型花每枝5元,B 型花每枝4元。
………4分(2)解:设当按甲方案绿化道路的总长度为a 米时,总成本为w 元,由题意得:()37500315002522+-=-+=a a a w ……………………………… 5分由a a -≤15002得:500≤a ……………………………………………6分 ∵–3 < 0,∴当a 增大时,w 减小∴当a=500时,w 取得最小值,此时w=–3500+37500=36000 ………………7分故当按甲方案绿化道路的总长度为500米时,所需总成本最少。

【KS5U 】新课标2016年高二数学寒假作业10一、选择题.1.数列}{n a 的前n 项和n n S n +=22,那么它的通项公式是 ( )A 、 12-=n a nB 、 12+=n a nC 、 14-=n a nD 、 14+=n a n2.数列 ,513,57,0-的一个通项公式是 ( ) A .11)1(231+--+n n n B . 11)1(23+--n n n C .11)1(231+---n n n D . 11)1(33+--n n n 3.等差数列{}n a 满足1234345661525=a a a a a a a a S +++=+++=,,则A.12B.30C.40D.254.已知数列{}n a ,若点()()*,n n a n N ∈在经过点()8,4的定直线l 上,则数列{}n a 的前15项和15S 为( )A.12B.32C.60D.120 5.已知双曲线﹣=1(a >)的两条渐近线的夹角为,则双曲线的离心率为( ) A . B . C . D .26.双曲线=1的渐近线方程是( ) A .y=±x B .y=±x C .y=±x D .y=±2x7.已知椭圆E 的中心在坐标原点,离心率为,E 的右焦点与抛物线C :y 2=8x 的焦点重合,A ,B 是C 的准线与E 的两个交点,则|AB|=( )A .3B .6C .9D .128.已知抛物线y 2=2px (p >0)的准线与圆x 2+y 2﹣4x ﹣5=0相切,则p 的值为( )A .10B .6C .4D .29.如图,已知直线l :y =k(x +1)(k>0)与抛物线C :y 2=4x 相交于A 、B 两点,且A 、B 两点在抛物线C准线上的射影分别是M 、N ,若|AM|=2|BN|,则k 的值是(A) 13 (B) (C) (D)10.已知动点(,)P x y 在椭圆2212516x y +=上,若A 点坐标为(3,0),||1AM =,且0PM AM ⋅=则||PM 的最小值是( )A B C .2 D .3二.填空题.11.若数列{a n }的前n 项和S n =n 2+n ,则数列{a n }的通项公式a n = .12.已知等比数列{a n }的各项均为正数,若a 1=3,前三项的和为21,则a 4+a 5+a 6= .13.若等差数列}{n a 的前n 项和为n S ,1442=+a a ,770S =,则数列}{n a 的通项公式 为 .14.已知数列}{n a 的首项)(1,1*11N n a a a a nn n ∈+==+,数列}{n a .的通项公式_______________ 三、解答题.15.(本小题满分12分)设ABC ∆是锐角三角形,三个内角A ,B ,C 所对的边分别记为a ,b ,c ,并且 )3sin()3sin()sin )(sin sin (sin B B B A B A +-=+-ππ.(Ⅰ)求角A 的值; (Ⅱ)若12=⋅AC AB ,72=a ,求b ,c (其中c b <).16.(本小题满分13分)已知点()0,2H -,椭圆()2222:10x y E a b a b+=>>F 是椭圆E 的右焦点,直线HF. (I )求椭圆E 的方程;(II )点A 为椭圆E 的右顶点,过B (1,0)作直线l 与椭圆E 相交于S,T 两点,直线AS,AT 与直线3x =分别交于不同的两点M,N ,求MN 的取值范围.17.已知数列{a n }满足a 1=1,a n+1=3a n +1.(Ⅰ)证明{a n +}是等比数列,并求{a n }的通项公式;(Ⅱ)证明:++…+<.【KS5U】新课标2016年高二数学寒假作业10参考答案1.C2.B3.B4.C5.A【考点】双曲线的简单性质.【专题】圆锥曲线的定义、性质与方程.【分析】由题意可得斜率为的渐近线的倾斜角为,由tan=,求得a的值,可得双曲线的离心率.【解答】解:双曲线﹣=1(a>)的两条渐近线的夹角为,可得斜率为的渐近线的倾斜角为,∴tan==,求得a=,∴双曲线的离心率为==,故选:A.【点评】本题主要考查双曲线的标准方程和简单性质,属于基础题.6.B【考点】双曲线的简单性质.【专题】圆锥曲线的定义、性质与方程.【分析】直接利用双曲线方程求渐近线方程即可.【解答】解:双曲线=1可得,所以双曲线的渐近线方程为:y=±x.故选:B.【点评】本题考查双曲线的渐近线方程的求法,基本知识的考查.7.B【考点】圆锥曲线的综合;直线与圆锥曲线的关系.【专题】圆锥曲线的定义、性质与方程.【分析】利用椭圆的离心率以及抛物线的焦点坐标,求出椭圆的半长轴,然后求解抛物线的准线方程,求出A,B坐标,即可求解所求结果.【解答】解:椭圆E的中心在坐标原点,离心率为,E的右焦点(c,0)与抛物线C:y2=8x的焦点(2,0)重合,可得c=2,a=4,b2=12,椭圆的标准方程为:,抛物线的准线方程为:x=﹣2,由,解得y=±3,所以a(﹣2,3),B(﹣2,﹣3).|AB|=6.故选:B.【点评】本题考查抛物线以及椭圆的简单性质的应用,考查计算能力.8.D【考点】圆与圆锥曲线的综合;直线与圆的位置关系;抛物线的简单性质.【专题】直线与圆;圆锥曲线的定义、性质与方程.【分析】将圆化成标准方程,得到圆心为C(2,0),半径r=3.再将抛物线化成标准方程,得到抛物线的准线为x=﹣,根据准线与圆相切建立关于p的等式,解之即可得到p的值.【解答】解:圆x2+y2﹣4x﹣5=0化成标准方程,得(x﹣2)2+y2=9,∴圆心为C(0,2),半径r=3,又∵抛物线y2=2px(p>0),∴抛物线的准线为x=﹣,∵抛物线的准线与圆相切,∴准线到圆心C的距离等于半径,得|2﹣(﹣)|=3,解之得p=2(舍负).故选:D.【点评】本题给出抛物线的准线与已知圆相切,求p的值.着重考查了圆的标准方程、直线与圆的位置关系和抛物线的标准方程与简单性质等知识,属于中档题.9.C10.BAM 可知点M的轨迹为以点A为圆心,1为半径的圆,试题分析:由||1过点P作该圆的切线PM,则|PA|2=|PM|2+|AM|2,得|PM|2=|PA|2-1,PM的值最小,则要PA的值最小,而PA的最小值为a-c=2,∴要使得||PM=3B.此时||考点:椭圆的定义.11.2n考点:数列递推式.专题:等差数列与等比数列.分析:由已知条件利用公式,能求出a n.解答:解:∵数列{a n}的前n项和S n=n2+n,∴a1=S1=1+1=2,a n=S n﹣S n﹣1=(n2+n)﹣[(n﹣1)2+(n﹣1)]=2n,当n=1时,上式成立,∴a n=2n.故答案为:2n.点评:本题考查数列的通项公式的求法,是基础题,解题时要认真审题,注意公式的合理运用.12.168【考点】等比数列的性质.【专题】计算题;等差数列与等比数列.【分析】由题意可得公比,而a 4+a 5+a 6=(a 1+a 2+a 3)•q 3,代入求解可得.【解答】解:可设等比数列{a n }的公比为q ,(q >0)由题意可得a 1+a 2+a 3=3+3q+3q 2=21,解之可得q=2,或q=﹣3(舍去)故a 4+a 5+a 6=(a 1+a 2+a 3)•q 3=21×8=168故答案为:168【点评】本题考查等比数列的性质,整体法是解决问题的关键,属中档题.13.32n a n =-(*N n ∈)在等差数列中,设公差为d ,则由2414a a +=,770S =得12414a d +=,71767702S a d ⨯=+=,即1310a d +=,解得11,3a d ==,所以13(1)32,n a n n =+-=-*N n ∈。
2016年秋高一年数学寒假作业二本试卷满分为150分,考试时间为120分钟.一、选择题:本大题共12个小题,每小题5分,共60分.1.已知函数()()221f x m x mx =+++为偶函数,则()f x 在区间()1,+∞上是( )A .先增后减B .先减后增C .减函数D .增函数2.已知全集{}1,0,1,2,3,4M =-,且{}{}1,2,3,4,2,3A B A ==U ,则()B C A =U I ()A .{}1,4B .{}1C .{}4D .φ3.有3个兴趣小组,甲、乙两位同学各自参加其中一个小组,每位同学参加各个小组的可能性相同,则这两位同学不在同一个兴趣小组的概率为( )A .13 B .12 C .23 D .344.一个水平放置的图形的斜二测直观图是一个底角为45︒,腰和上底均为1的等腰梯形,那么原平面图形的面积是( )A . 2B D .1+5.圆221:2610C x y x y +--+=与圆222:4210C x y x y ++++=的公切线有且仅有()A .1条B .2条 C.3条 D .4条6.如图,在正方体1111ABCD A B C D -中,M 、N 分别为棱BC 和棱1CC 的中点,则异面直线AC 和MN 所成的角为( )A .30︒B .45︒ C.60︒ D .90︒7.已知,m n 是两条不重合的直线,,αβ是不重合的平面,下面四个命题中正确的是( ) A .若,,m n m n αβ⊂⊂⊥,则αβ⊥ B .若//,m m n α⊥,则n α⊥ C.若,m m αβ⊥⊥,则//αβ D .若,m n m β⊥⊥,则//n β8.已知三棱锥的正视图与俯视图如图所示,俯视图是边长为2的正三角形,则该三棱锥的侧视图可能为( )A.B. C.D .9.直线l 过点()1,2P -且与以点()3,2M --、()4,0N 为端点的线段恒相交,则l 的斜率取值范围是( ) A .2,55⎡⎤-⎢⎥⎣⎦B .(]2,00,25⎡⎫-⋃⎪⎢⎣⎭ C.[)2,5,5⎛⎤-∞-⋃+∞ ⎥⎝⎦D .[)2,2,5⎛⎤-∞-⋃+∞ ⎥⎝⎦10.直线1y kx =+与圆()()22214x y -+-=相交于P 、Q 两点.若PQ ≥k 的取值范围是( )A .3,04⎡⎤-⎢⎥⎣⎦ B .,33⎡-⎢⎣⎦ C. []1,1- D .⎡⎣ 11.如图,直三棱柱111ABC A B C -的六个顶点都在半径为2的半球面上,AB AC =,侧面11BCC B 是半球底面圆的内接正方形,则侧面11ABB A 的面积为( )A .B . C. 2 D12.已知平面上两点()()(),0,,00A a B a a ->,若圆()()22344x y -+-=上存在点P ,使得90APB ∠=︒,则a 的取值范围是( )A .[]3,6B .[]3,7 C.[]4,6 D .0,7 二、填空题:(每题4分,满分16分)13.已知直线21y kx k =++.则直线恒经过的定点 .14.设O 为原点,点M 在圆()()22:341C x y -+-=上运动,则OM 的最大值为 .15.某空间几何体的三视图如右图所示,则该几何体的体积为 .16.如图,ABC ∆为等腰直角三角形,90,2,1BAC AB BD ∠=︒==,一束光线从点D 射入,先后经过斜边BC 与直角边AC 反射后,恰好从点D 射出,则该光线在三角形内部所走的路程是 .三、解答题:(共70分)17.已知平面内两点()()2,2,4,4M N -. (Ⅰ)求MN 的中垂线方程;(Ⅱ)求过点()2,3P -且与直线MN 平行的直线l 的方程. 18.如图,在三棱锥P ABC -中,E 、F 分别为AC 、BC 的中点. (Ⅰ)求证://EF 平面PAB ;(Ⅱ)若平面PAC ⊥平面ABC ,且,90PA PC ABC =∠=︒,求证:BC ⊥平面PEF19. 如图,在四棱锥P ABCD -中,底面ABCD 是正方形,侧棱PD ⊥底面,,ABCD PD DC E =是PC 中点,(Ⅰ)证明://PA 平面EDB (Ⅱ)证明:平面BDE ⊥平面PCB20.如图是某圆拱桥的示意图.这个圆拱桥的水面跨度24AB m =,拱高8OP m =.现在一船;宽10m ,水面上高6m ,这条船能从桥下通过吗?为什么?21.如图,在四棱锥P ABCD-中,PA ⊥底面,,60,,ABCD AC CD ABC PA AB BC E ⊥∠=︒==是PC 的中点.(Ⅰ)证明:AE ⊥平面PCD ;(Ⅱ)求PB 和平面PAC 所成的角的正切值.22.已知圆22:430C x y x +-+=,过原点的直线l 与其交于不同的两点,A B . (Ⅰ)求直线l 斜率k 的取值范围;(Ⅱ)求线段AB 的中点P 的轨迹Γ的方程;(Ⅲ)若直线:4m y ax =+与曲线Γ只有一个公共点,求a 的取值范围.2016年秋高一年数学寒假作业二试卷答案一、选择题:1-12:BBDACC CBDCAB 二、填空题:13.()2,1- 14. 6 15.264 16.10 三、解答题:17.解(1)易求得MN 的中点坐标为()3,1…………(2分) 又()42342MN k --==-,所以MN 的中垂线的斜率为13-,…………(6分)18.证明:(1)∵,E F 分别是,AC BC 的中点,∴//EF AB . 又EF ⊄平面,PAB AB ⊂平面PAB , ∴//EF 平面PAB .…………(6分)(2)在三角形PAC 中,∵,PA PC E =为AC 中点, ∴PE AC ⊥∵平面PAC ⊥平面ABC ,平面PAC ⋂平面ABC AC =, ∴PE ⊥平面ABC . ∴PE BC ⊥又//,90EF AB ABC ∠=︒, ∴EF BC ⊥,又EF PE E ⋂=, ∴BC ⊥平面PEF …………(12分)19.(1)连接AC 交BD 于O ,连接OE∵底面ABCD 是正方形,∴O 为AC 中点,∵在PAC V 中,E 是PC 的中点, ∴//OE PA …………(3分)∵OE ⊂平面,EDB PA ⊄平面EDB ,∴在//PA 平面EDB …………(5分) (2)∵侧棱PD ⊥底面,ABCD BC ⊂底面ABCD ,∴PD BC ⊥ ∵底面ABCD 是正方形,∴DC BC P∵PD 与DC 为平面PCD 内两条相交直线,∴BC ⊥平面PCD …………(8分) ∵DE ⊂平面PCD ,∴BC DE ⊥∵,PD CD E =是PC 的中点,∴DE PC ⊥∵PC 与BC 为平面PBC 内两条相交直线,∴DE ⊥平面PBC …………(11分) ∵DE ⊂平面BDE ,∴平面BDE ⊥平面PBC …………(12分)20.解:建立如图所示的坐标系,依题意,有()()()()()12,0,12,0,0,8,5,0,5,0A B P D E --…………(2分)设所求圆的方程是()()222x a y b r -+-=.于是有 ()()()22222222212128a b r a b r a b r ⎧++=⎪⎪-+=⎨⎪+-=⎪⎩,解此方程组得0,5,13a b r ==-=所以这座圆拱桥的拱圆的方程是()()22516908x y y ++=≤≤…………(8分) 把点D 的横坐标5x =-代入上式,得7y =,…………(10分)由于船在水面以上高6,67m <,所以该船可以从桥下通过,…………(12分)21.解:(1)∵在ABC V 中,60,ABC PA AB BC ∠=︒==,∴ABC V 为等边三角形,∴PA AC =…………(1分)∵在PAC V 中,E 是PC 的中点,∴AE PC ⊥∵,AC CD PA ⊥与AC 为平面PAC 内两条相交直线,∴CD ⊥平面PAC …………(4分) ∵AE ⊂平面PAC ,∴CD AE ⊥∵,AE PC PC ⊥与CD 为平面PCD 内两条相交直线,∴AE ⊥平面PCD …………(6分)(2)取AC 中点F ,连接BF 、PF ,设2PA AB BC AC a ====∵在ABC V 中,,AB BC F =为AC 中点,∴BF AC ⊥∵PA ⊥底面,ABCD BF ⊂底面ABCD ,∴PA BF ⊥∵PA 与AC 为平面PAC 内两条相交直线,∴BF ⊥平面PAC∴PF 为PB 在平面PAC 内的射影,∴BPF ∠为PB 和平面PAC 所成的角…………(9分)∵PA ⊥底面,ABCD AC ⊂底面ABCD ,∴PA AC ⊥∵2PA AB BC AC a ====,∴,PF BF ==∴在Rt PBF V 中,tan BPF ∠==∴PB 和平面PAC 所成的角的正切值为5…………(12分)22.(1)由22430x y x +-+=得()2221x y -+= 直线l 过原点,可设其方程:y kx =∵直线l 与其将于不同的两点,A B1<∴k << (2)设点(),P x y ,∵点P 为线段AB 的中点,而曲线C 是圆心为()2,0C ,半径1r =的圆,∴CP OP ⊥ ∴012CP OP y y k k x x-⋅=⋅=--(2x ≠且0x ≠)化简得2220x y x +-=① 由222243020x y x x y x ⎧+-+=⎪⎨+-=⎪⎩得3,2x y == ,A B 是不同的两点,且点()2,0的坐标满足①因此点(),P x y 满足2232022x y x x ⎛⎫+-=<≤ ⎪⎝⎭② 这是圆心为()11,0O ,半径为1的一段圆弧(不包括端点1233,,,2222M M ⎛⎫⎛⎫- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭),反之,可验证以方程②的解(),x y 为坐标的点(),P x y 是曲线Γ上的一个点,因此②是轨迹Γ的方程.(3)设直线:4m y ax =+过()0,4D设直线m 与圆221:20O x y x +-=相切于点M1=,解得158a =- 直线1M D的斜率为142302M D k -==-类似的可得2M D k =综上,若直线m 与曲线Γ只有一个公共点, 则a 的取值范围是158a =-或8833a <≤。
【KS5U 】新课标2016年高二数学寒假作业4一、选择题.1.等比数列{}n a 的前n 项和为n S ,且1234,2,a a a 成等差数列.若11a =,则4S =( )A .7B .8C .15D .162.已知等差数列{a n }满足a 6+a 10=20,则下列选项错误的是( )A .S 15=150B .a 8=10C .a 16=20D .a 4+a 12=203.已知{a n }是首项为1的等比数列,且4a 1,2a 2,a 3成等差数列,则数列{a n }的前5项的和为A .3116B .3132C .32D .314.设{}n a 是任意等比数列,它的前n 项和,前2n 项和与前3n 项和分别为,,X Y Z ,则下列等式中恒成立的是( )(A )2X Z Y +=(B )()()Y Y X Z Z X -=- (B )2Y XZ =(D )()()Y Y X X Z X -=- 5.已知抛物线C 1:y=x 2(p >0)的焦点与双曲线C 2:﹣y 2=1的右焦点的连线交C 1于第一象限的点M ,若C 1在点M 处的切线平行于C 2的一条渐近线,则p=( )A .B .C .D .6.抛物线y=上点P 的纵坐标是4,则其焦点F 到点P 的距离为( ) A .3 B .4C .5D .6 7.已知抛物线22(0)y px p =>的焦点F 恰为双曲线22221(0,0)x y a b a b-=>>的右焦点,且两曲线交点的连线过点F ,则双曲线的离心率为( )A. 22 C.1+ D. 1+8.设F 1,F 2是椭圆+=1(a >b >0)的左右焦点,过点F 1,F 2作x 轴的垂线交椭圆四点构成一个正方形,则椭圆的离心率e 为( )A .B .C .D .9.若抛物线22y px =的焦点与椭圆22162x y +=的右焦点重合,则p 的值为( ) A.-2 B.2 C.-4 D.410.设点P 是椭圆22221(0)x y a b a b+=>>上一点,12,F F 分别是椭圆的左、右焦点,I 为12PF F ∆的内心,若12122IPF IPF IF F S S S ∆∆∆+=,则该椭圆的离心率是( )A . 12B .2C .2D .14二.填空题.11.命题“∃x ∈R ,lgx=x ﹣2”的否定是 .12.数列{a n }满足a n+1=,a 8=2,则a 1=.13.在数列{}n a 中,若11a =,()121n n a a n +-=≥,则=3a _______________.14.已知{a n }为等比数列,S n 是它的前n 项和.若a 2•a 3=2a 1,且a 4与2a 7的等差中项为,则S 6= .三、解答题.15.设p :实数x 满足x 2﹣4ax+3a 2<0,q :实数x 满足|x ﹣3|<1.(1)若a=1,且p ∧q 为真,求实数x 的取值范围;(2)若其中a >0且¬p 是¬q 的充分不必要条件,求实数a 的取值范围.16.已知数列{}n a 是等差数列, 256,18a a ==;数列{}n b 的前n 项和是n T ,且112n n T b +=. (1) 求数列{}n a 的通项公式;(2) 求证:数列{}n b 是等比数列;(3) 记n n nc a b =⋅,求{}n c 的前n 项和n S . 17.已知动点M (x ,y )到直线l :x=4的距离是它到点N (1,0)的距离的2倍.(Ⅰ) 求动点M 的轨迹C 的方程;(Ⅱ) 过点P (0,3)的直线m 与轨迹C 交于A ,B 两点.若A 是PB 的中点,求直线m 的斜率.【KS5U】新课标2016年高二数学寒假作业4参考答案1.C2.C考点:等差数列的性质.专题:计算题;等差数列与等比数列.分析:利用等差数列的通项的性质,可得结论.解答:解:S15=(a1+a15)=(a6+a10)=150,即A正确;a6+a10=2a8=20,∴a8=10,即B正确;a6+a10≠a16,即C错误a4+a12=a6+a10=20,即D正确.故选:C.点评:本题考查等差数列的通项的性质,考查学生的计算能力,正确运用等差数列的通项的性质是关键.3.D4.D5.D【考点】抛物线的简单性质.【专题】综合题;圆锥曲线的定义、性质与方程.【分析】由曲线方程求出抛物线与双曲线的焦点坐标,由两点式写出过两个焦点的直线方程,求出函数y=x2(p>0)在x取直线与抛物线交点M的横坐标时的导数值,由其等于双曲线渐近线的斜率得到交点横坐标与p的关系,把M点的坐标代入直线方程即可求得p的值.【解答】解:由抛物线C1:y=x2(p>0)得x2=2py(p>0),所以抛物线的焦点坐标为F(0,).由﹣y2=1得a=,b=1,c=2.所以双曲线的右焦点为(2,0).则抛物线的焦点与双曲线的右焦点的连线所在直线方程为,即①.设该直线交抛物线于M(),则C1在点M处的切线的斜率为.由题意可知=,得x0=,代入M点得M(,)把M点代入①得:.解得p=.故选:D.【点评】本题考查了双曲线的简单几何性质,考查了利用导数研究曲线上某点的切线方程,函数在曲线上某点处的切线的斜率等于函数在该点处的导数,是中档题.6.C【考点】抛物线的简单性质;直线与圆锥曲线的关系.【专题】计算题;数形结合;函数思想;圆锥曲线的定义、性质与方程.【分析】先根据抛物线的方程求得准线的方程,进而利用点A的纵坐标求得点P到准线的距离,进而根据抛物线的定义求得答案.【解答】解:依题意可知抛物线化为抛x2=4y,抛物线的准线方程为y=﹣1,∴点P到准线的距离为4+1=5,根据抛物线的定义可知点P与抛物线焦点的距离就是点P与抛物线准线的距离,∴点A与抛物线焦点的距离为5,故选:C.【点评】本题主要考查了抛物线的定义的运用.考查了学生对抛物线基础知识的掌握.属基础题.7.D8.B【考点】椭圆的简单性质.【专题】圆锥曲线的定义、性质与方程.【分析】由题意推出椭圆上的点的坐标,代入椭圆方程,得到abc的关系,然后求解椭圆的离心率即可.【解答】解:F 1,F 2是椭圆+=1(a >b >0)的左右焦点,过点F 1,F 2作x 轴的垂线交椭圆四点构成一个正方形,所以(c ,c )是椭圆上的点,可得:, 即,a 2c 2﹣c 4+a 2c 2=a 4﹣a 2c 2,可得e 4﹣3e 2+1=0.解得e==. 故选:B .【点评】本题考查椭圆的简单性质的应用,椭圆的离心率的求法,考查计算能力.9.D选D 椭圆的右焦点为F (2,0)4,22==∴p p 即 10.A11.∀x ∈R ,lgx≠x﹣2【考点】命题的否定.【专题】计算题;规律型;对应思想;简易逻辑.【分析】利用特称命题的否定是全称命题写出结果即可.【解答】解:因为特称命题的否定是全称命题,所以命题“∃x ∈R ,lgx=x ﹣2”的否定是:∀x ∈R ,lgx≠x﹣2.故答案为:∀x ∈R ,lgx≠x﹣2.【点评】本题考查命题的否定,特称命题与全称命题的否定关系,考查计算能力. 12.考点:数列递推式.专题:计算题.分析:根据a 8=2,令n=7代入递推公式a n+1=,求得a 7,再依次求出a 6,a 5的结果,发现规律,求出a 1的值.解答:解:由题意得,a n+1=,a8=2,令n=7代入上式得,a8=,解得a7=;令n=6代入得,a7=,解得a6=﹣1;令n=5代入得,a6=,解得a5=2;…根据以上结果发现,求得结果按2,,﹣1循环,∵8÷3=2…2,故a1=故答案为:.点评:本题考查了数列递推公式的简单应用,即给n具体的值代入后求数列的项,属于基础题.13.514.【考点】等比数列的前n项和;等差数列的性质.【专题】计算题;等差数列与等比数列.【分析】设等比数列{a n}的公比为q,由已知可得q=,a1=16,代入等比数列的求和公式可得.【解答】解:设等比数列{a n}的公比为q,则可得a1q•a1q2=2a1,即a4==2又a4与2a7的等差中项为,所以a4+2a7=,即2+2×2q3=,解之可得q=,故a1=16故S6==故答案为:【点评】本题考查等比数列的求和公式,涉及等差数列的性质,属中档题.15.【考点】必要条件、充分条件与充要条件的判断.【专题】简易逻辑.【分析】(1)若a=1,根据p ∧q 为真,则p ,q 同时为真,即可求实数x 的取值范围;(2)根据¬p 是¬q 的充分不必要条件,建立条件关系即可求实数a 的取值范围.【解答】解:(1)由x 2﹣4ax+3a 2<0得(x ﹣3a )(x ﹣a )<0当a=1时,1<x <3,即p 为真时实数x 的取值范围是1<x <3.由|x ﹣3|<1,得﹣1<x ﹣3<1,得2<x <4即q 为真时实数x 的取值范围是2<x <4,若p ∧q 为真,则p 真且q 真,∴实数x 的取值范围是2<x <3.(2)由x 2﹣4ax+3a 2<0得(x ﹣3a )(x ﹣a )<0,若¬p 是¬q 的充分不必要条件,则¬p ⇒¬q ,且¬q ⇏¬p ,设A={x|¬p},B={x|¬q},则A ⊊B ,又A={x|¬p}={x|x≤a 或x≥3a},B={x|¬q}={x|x≥4或x≤2},则0<a≤2,且3a≥4∴实数a 的取值范围是. 【点评】本题主要考查复合命题的真假关系以及充分条件和必要条件的应用,考查学生的推理能力.16.解:(1)设{}n a 的公差为d ,则:21a a d =+,514a a d =+,∵26a =,518a =,∴116418a d a d +=⎧⎨+=⎩,∴12,4a d ==. ………………………2分 ∴24(1)42n a n n =+-=-. …………………………………………4分(2)当1n =时,11b T =,由11112T b +=,得123b =. …………………5分 当2n ≥时,112n n T b =-,11112n n T b --=-,∴111=() 2n n n n T T b b ----,即11()2n n n b b b -=-. …………………………7分 ∴11=3n n b b -. ……………………………………………………………8分 ∴{}n b 是以23为首项,13为公比的等比数列. …………………………………9分 (3)由(2)可知:1211()2()333n n n b -=⋅=⋅. ……………………………10分 ∴11(42)2()(84)()33n n n n n c a b n n =⋅=-⋅⋅=-⋅. …………………………………11分 ∴2112111114()12()(812)()(84)()3333n n n n n S c c c c n n --=++++=⨯+⨯++-⨯+-⨯. ∴231111114()12()(812)()(84)()33333n n n S n n +=⨯+⨯++-⨯+-⨯. ∴231121111148()8()8()(84)()3333333n n n n n S S S n +-==⨯+⨯+⨯++⨯--⨯ 21111()[1()]41338(84)()13313n n n -+⋅-=+⨯--⨯- 118114()(84)()333n n n -+=-⨯--⨯. ………………………………………13分 ∴144(1)()3n n S n =-+⋅. …………………………………………………14分 17.【考点】直线与圆锥曲线的综合问题;曲线与方程.【专题】压轴题;圆锥曲线的定义、性质与方程.【分析】(Ⅰ)直接由题目给出的条件列式化简即可得到动点M 的轨迹C 的方程;(Ⅱ)经分析当直线m 的斜率不存在时,不满足A 是PB 的中点,然后设出直线m 的斜截式方程,和椭圆方程联立后整理,利用根与系数关系写出x 1+x 2,x 1x 2,结合2x 1=x 2得到关于k 的方程,则直线m 的斜率可求.【解答】解:(Ⅰ)点M (x ,y )到直线x=4的距离是它到点N (1,0)的距离的2倍,则 |x ﹣4|=2,即(x ﹣4)2=4,整理得.所以,动点M 的轨迹是椭圆,方程为;(Ⅱ)P (0,3),设A (x 1,y 1),B (x 2,y 2),由A 是PB 的中点,得2x 1=0+x 2,2y 1=3+y 2.椭圆的上下顶点坐标分别是和,经检验直线m不经过这两点,即直线m 的斜率k存在.设直线m的方程为:y=kx+3.联立,整理得:(3+4k2)x2+24kx+24=0..因为2x1=x2.则,得,所以.即,解得.所以,直线m的斜率.【点评】本题考查了曲线方程,考查了直线与圆锥曲线的位置关系,考查了学生的计算能力,关键是看清题中给出的条件,灵活运用韦达定理,中点坐标公式进行求解,是中档题.。
【KS5U 】新课标2016年高二数学寒假作业9一、选择题.1.已知椭圆的方程为63222=+y x ,则此椭圆的离心率为( )A .31 B .33 C .22 D .21 2.已知椭圆14222=+by x (0<b<2)与y 轴交于A 、B 两点,点F 为该椭圆的一个焦点,则△ABF 面积的最大值为( )A .1B .2C .4D .83.的右顶点A 作斜率为1-的直线,该直线与双曲线的两条渐近线的交点分别为,B C .若1AB BC =,则双曲线的离心率是( )A 4.从抛物线x y 42=上一点P 引抛物线准线的垂线,垂足为M ,且|PM|=5,设抛物线的焦点为F ,则△MPF 的面积( ) A .5 B .10C .20D .155.在ABC ∆中,内角,,A B C 所对的边分别为,,a b c ,且BC 边上的高为6a ,则c bb c+取得最大值时,内角A 的值为( ) A .2π B .6π C .23π D .3π6.在ABC ∆中,角A ,B ,C 的对边分别为,,a b c ,若222a cb +-=,则角B 的值为 A.6πB.3π C.566ππ或D.233ππ或7.设等比数列{a n }的前n 项和为S n ,若S m ﹣1=5,S m =﹣11,S m+1=21,则m=( ) A .3B .4C .5D .68.在等差数列{a n }中,首项a 1=0,公差d≠0,若a k =a 1+a 2+a 3+…+a 7,则k=( ) A .22B .23C .24D .259.设为等差数列的前项和,若,公差,,则( ) A . B . C . D .10.正项等比数列{}n a 满足:3212a a a =+,若存在,m n a a ,使得2116m n a a a ⋅=,则值为( )A.2B.16C.二.填空题.11.由命题“02,2≤++∈∃m x x R x ”是假命题,求得实数m 的取值范围是),(+∞a ,则实数a 的值是 .12.已知数列{a n }满足:a 3=5,a n+1=2a n ﹣1(n ∈N *),则a 1= .13.若数列{}n a 满足:111,2()n n a a a n N *+==∈,则前6项的和6S = .(用数字作答)14.已知圆G :x 2+y 2﹣2x ﹣2y=0经过椭圆+=1(a >b >0)的右焦点及上顶点.过椭圆外一点M (m ,0)(m >a ),倾斜角为π的直线l 交椭圆于C ,D 两点,若点N (3,0)在以线段CD 为直径的圆E 的外部,则m 的取值范围是 _________ . 三、解答题.15.已知数列{a n }中,a 1=1,且点(a n ,a n+1)在函数y=x+1的图象上(n ∈N *),数列{b n }是各项都为正数的等比数列,且b 2=2,b 4=8. (Ⅰ)求数列{a n },{b n }的通项公式;(Ⅱ)若数列{c n }满足c n =(﹣1)na n +b n ,记数列{c n }的前n 项和为T n ,求T 100的值. 16.(本小题14分)如图,在ABC ∆的区域内割出一块四边形绿化区域BCED ,其中090=∠=∠D C ,3==BD BC ,1CE DE ==,现准备经过DB 上一点P 和EC 上一点Q 铺设水管PQ ,且PQ 将四边形BCED 分成面积相等的两部分. 设x DP =,y EQ =. (1)求,x y 的等量关系式; (2)求水管PQ 长的最小值.I17.(12分)已知圆的方程为x2+y2=4,过点M(2,4)作圆的两条切线,切点分别为A1、A2,直线A1A2恰好经过椭圆C1:+=1(a>b>0)的右顶点和上顶点.(1)求直线A1A2的方程及椭圆C1的方程;(2)椭圆C2以C1的长轴为短轴,且与C1有相同的离心率,求椭圆C2的方程;(3)设O为坐标原点,点A,B分别在椭圆C1和C2上,=2,求直线AB的方程.【KS5U 】新课标2016年高二数学寒假作业9参考答案1.B2.B3.C4.B5.【知识点】解三角形C8D解析:因为11sin 262a a bc A ⨯⨯=,得2sin a A =,则2222cos2cos 4sin 6c b c b a bc A A A A b c bc bc π++⎛⎫+==+=+ ⎪⎝⎭,所以当,623A A πππ+==时c bb c+取得最大值,则选D. 【思路点拨】结合已知条件利用三角形面积公式及余弦定理把c bb c+转化为关于角A 的三角函数问题,再进行解答即可. 6.A 7.C考点:等比数列的性质. 专题:等差数列与等比数列.分析:根据等比数列的通项公式和前n 项和公式,建立方程组即可解得m 的值. 解答: 解:在等比数列中, ∵S m ﹣1=5,S m =﹣11,S m+1=21,∴a m =S m ﹣S m ﹣1=﹣11﹣5=﹣16,a m+1=S m+1﹣S m =21﹣(﹣11)=32, 则公比q=,∵S m =﹣11,∴,①又,②两式联立解得m=5,a 1=﹣1,故选:C .点评:本题主要考查等比数列的通项公式和前n 项和公式的计算和应用,考查学生的计算能力. 8.A考点:等差数列的性质.分析:根据等差数列的性质,我们可将a k =a 1+a 2+a 3+…+a 7,转化为a k =7a 4,又由首项a 1=0,公差d≠0,我们易得a k =7a 4=21d ,进而求出k 值. 解答: 解:∵数列{a n }为等差数列 且首项a 1=0,公差d≠0,又∵a k =(k ﹣1)d=a 1+a 2+a 3+…+a 7=7a 4=21d 故k=22 故选A点评:本题考查的知识点是等差数列的性质,其中根据a 4是数列前7项的平均项(中间项)将a k =a 1+a 2+a 3+…+a 7,化为a k =7a 4,是解答本题的关键. 9.D 10.C【知识点】等比数列及等比数列前n 项和. D3【思路点拨】正项等比数列{}n a 满足:3212a a a =+,知q=2,由存在,m n a a ,使得2116m n a a a ⋅=,知m+n=6,由此问题得以解决. 11.1 12.2【考点】数列递推式.【专题】等差数列与等比数列.【分析】利用递推公式,结合递推思想求解.【解答】解:∵数列{a n }满足:a 3=5,a n+1=2a n ﹣1(n ∈N *), ∴a 2=×(5+1)=3. a 1==2.故答案为:2.【点评】本题考查数列的第3项的求法,是基础题,解题时要注意递推思想的合理运用. 13.63试题分析:要求数列的前n 项的和,一般先确定下这个数列是不是等差数列或者等比数列,或者是否能转化为等差(或等比)数列,例如本题中由12n n a a +=,110a =≠,故数列{}n a 是等比数列,公比2q =,因此66126312S -==-. 考点:等比数列的定义与前n 项和.14.15.考点: 数列的求和;数列递推式. 专题: 等差数列与等比数列.分析: (I )由于点(a n ,a n+1)在函数y=x+1的图象上(n ∈N *),可得a n+1=a n +1,利用等差数列的通项公式即可得出.数列{b n }为等比数列,设公比为q ,由于b 2=2, b 4=8,可得b 4=b 1q 3=8,b 1q=2.解出即可. (II )数列{c n }满足c n =(﹣1)na n +b n =(﹣1)nn+2n ﹣1,可得T 100=(﹣1+2﹣3+4+…+100)+(1+2+22+…+299),利用分组求和与等比数列的前n 项和公式即可得出. 解答: 解:(I )∵点(a n ,a n+1)在函数y=x+1的图象上(n ∈N *), ∴a n+1=a n +1,即a n+1﹣a n =1,∴数列{a n }是以1为首项,1为公差的等差数列. 故数列{a n }的通项公式为a n =n . 数列{b n }为等比数列,设公比为q , ∵b 2=2,b 4=8, ∴b 4=b 1q 3=8,b 1q=2.b n >0, ∴b 1=1,q=2. ∴b n =2n ﹣1(n ∈N *).(Ⅱ)∵数列{c n }满足c n =(﹣1)na n +b n =(﹣1)nn+2n ﹣1,∴T 100=(﹣1+2﹣3+4+…+100)+(1+2+22+…+299) =50+=50+2100﹣1 =22100+49.点评: 本题考查了“分组求和”方法、等差数列与等比数列的通项公式与前n 项和公式,考查了推理能力与计算能力,属于中档题. 16.(1)如图,AD=3,AE=2.则S △ADE = S △BDE = S △BCE∴S △APQ =3,即1(2)4x y +=∴(2)4x y +=3…………………………………7分I(2)APQ ∆中,2222cos30PQ AP AQ AP AQ =+-⋅⋅︒ =223342)334()3(22≥⨯⨯-+++x x ·12381234-=- ………………………………10分当且仅当22)334()3(+=+x x ,即时3324-=x ,33221238min -=-=PQ …………………………………………14分17.【考点】: 直线与圆锥曲线的综合问题. 【专题】: 圆锥曲线中的最值与范围问题.【分析】: (1)x=2是圆的一条切线,切点为A 1(2,0),设O 为圆心,根据圆的切线性质,MO ⊥A 1A 2,由此能求出直线A 1A 2的方程和椭圆C 1的方程. (2)设椭圆C 2的方程为,(a >2),由e=能求出椭圆C 2的方程.(3)设A (x 1,y 1),B (x 2,y 2),设直线AB 的方程为y=kx ,并分别代入和,得,,由此能求出直线AB 的方程.解:(1)观察知,x=2是圆的一条切线,切点为A 1(2,0),(1分) 设O 为圆心,根据圆的切线性质,MO ⊥A 1A 2,(2分) 所以,(3分)所以直线A 1A 2的方程为,(4分)直线A 1A 2与y 轴相交于(0,1),依题意a=2,b=1,(6分) 所求椭圆C 1的方程为.(2)依题意设椭圆C 2的方程为,(a >2),∵e=,∴,解得a 2=16,∴椭圆C 2的方程为.(8分)(3)设A (x 1,y 1),B (x 2,y 2), ∵,∴O ,A ,B 三点共线且不在y 轴上,(9分)∴设直线AB 的方程为y=kx ,并分别代入和,得:,,(11分)∵,∴,∴,解得k=±1,∴直线AB的方程为y=x或y=﹣x.【点评】:本题考查直线方程及椭圆方程的求法,解题时要认真审题,注意直线方程、圆、椭圆等知识点的合理运用.。
【KS5U 】新课标2016年高一数学寒假作业6一、选择题.1.设集合A ={5,2,3},B ={9,3,6},则A ∩B 等于 ( )A .{3}B .{1}C .{-1}D .Ø 2.设a ·b ·c >0, 二次函数f (x )=ax 2+bx +c 的图象可能是( )3.函数y =的定义域为A.[0,)+∞B.(,0]-∞C. (0,)+∞D. (,0)-∞4.函数131()2x f x x =-的零点所在区间是 A .1(0,)6B .11(,)63C .11(,)32D .1(,1)25.若函数2()2(1)2(,4)f x x a x =+-+-∞在区间上是减函数,则实数a 的取值范围是A .3a ≤-B .3a ≥-C .3a <-D .3a >-6.下列函数中既是偶函数,又在区间(0,1)上是减函数的是A .||y x =B .2y x =-C .x xy e e -=+D .cos y x =7.函数1()11f x x=+-的图象是8.已知直线l 过点(1,2),且在x 轴截距是在y 轴截距的2倍,则直线l 的方程为 A.250x y +-= B.250x y ++=C.20x y -=或250x y +-=D.20x y -=或230x y -+=9.若坐标原点在圆22()()4x m y m -++=的内部,则实数m 的取值范围是( )(A )11m -<< (B )m -<(C )m -< (D )22m -<< 10.若直线42:2:21+-=++=x y l k kx y l 与的交点在第一象限内,则实数k 的取值范围( )32.->k A 2.<k B 232.<<-k C 232.>-<k k D 或二.填空题.11.若函数()f x 满足2(1)(1)2f x f x x ---=,则(1)f -= ;12.已知幂函数()f x 的定义域为R ,且过点(2,8),则满足不等式(21)(3)f x f -<的x 的取值范围是 .13.复利是一种计算利息的方法,即把前一期的利息和本金加在一起算做本金,再计算下一期的利息.现有一种储蓄按复利计算利息,本金为a 元,每期利率为r ,设本利和为y , 存期为x ,则y 随着x 变化的函数式 .14.给出下列四个命题: ①函数1y x=-在R 上单调递增; ②若函数221y x ax =++在(,1]-∞-上单调递减,则1a ≤; ③若0.70.7log (2)log (1)m m <-,则1m >-;④若()f x 是定义在R 上的奇函数,则(1)(1)0f x f x -+-=.三、解答题.15.设定义域为R 的函数21,0,()21,0x x f x x x x ⎧+≤=⎨-+>⎩ (Ⅰ)在平面直角坐标系内作出函数()f x 的图象, 并指出()f x 的单调区间(不需证明);(Ⅱ)若方程()20f x a +=有两个解,求出a 的取值范围(只需简单说明,不需严格证明). (Ⅲ)设定义为R 的函数()g x 为奇函数,且当0x >时,()(),g x f x =求()g x 的解析式.16.如图:已知四棱锥P ABCD -中,,PD ABCD ABCD ⊥平面是正方形,E 是PA 的中点,求证:(1)//PC 平面EBD ;(2) B C ⊥P C 。
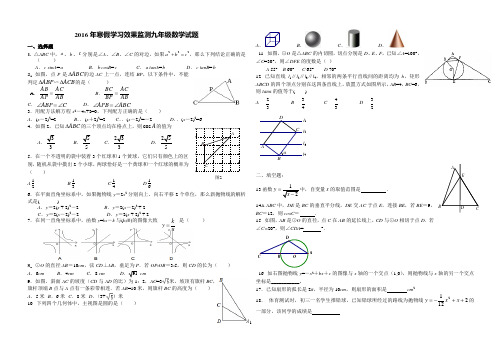
2016年寒假学习效果监测九年级数学试题
1. .△ABC 中,a 、b 、c 分别是∠A 、∠B 、∠C 的对边,如果222c b a =+,那么下列结论正确的是( ) A .c sinA =a B .b cosB =c C .a tanA =b D .c tanB =b 2.如图,点P 是ABC ∆的边AC 上一点,连结BP ,以下条件中,不能判定ABP ∆∽
ACB ∆的是( )
A .A
B AC
AP AB = B
.AB AC
BP BC = C .C ABP ∠=∠
D .ABC APB ∠=∠
3.用配方法解方程x 2-4x +2=0,下列配方正确的是( )
A .(x -2)2=2
B .(x +2)2=2
C .(x -2)2=-2
D .(x -2)2=6 4.如图2,已知ABC ∆的三个顶点均在格点上,则cos A 的值为
A B C D 5.在一个不透明的袋中装着3个红球和1个黄球,它们只有颜色上的区别,随机从袋中摸出2个小球,两球恰好是一个黄球和一个红球的概率为( )
A .12
B .13
C .14
D .16
6.在平面直角坐标系中,如果抛物线y =2x 2分别向上、向右平移2个单位,那么新抛物线的解析
式是( )
A .y =2(x + 2)2-2
B .y =2(x -2)2 + 2
C .y =2(x -2)2-2
D .y =2(x + 2)2 + 2 7.在同一直角坐标系中,函数y =kx -k 与(k ≠0)的图像大致是( )
8.⊙O 的直径
AB =10cm ,弦CD ⊥AB ,垂足为P .若OP :OB =3:5,则CD 的长为( ) A .6cm B .4cm C .8 cm D .91 cm
9.如图,斜面AC 的坡度(CD 与AD 的比)为1:2,AC =3米,坡顶有旗杆BC ,旗杆顶端B 点与A 点有一条彩带相连.若AB =10米,则旗杆BC 的高度为( ) A .5米 B .6米 C .8米 D .(3+)米
10. 下列四个几何体中,主视图是圆的是( )
A B . C
. D .
11. 如图,⊙O 是△ABC 的内切圆,切点分别是D 、E 、F ,已知∠A =100°,∠C =30°,则∠DFE 的度数是( )
A .55°
B .60°
C .65°
D .70°
12. 已知直线l 1∥l 2∥l 3∥l 4,相邻的两条平行直线间的距离均为h ,矩形ABCD 的四个顶点分别在这四条直线上,放置方式如图所示,AB =4,BC =6,则tanα的值等于( )
A . 23
B . 3
4 C . 43 D . 32
二、填空题: 13.函数y =
x 的取值范围是 . 14△ABC 中,DE 是BC 的垂直平分线,DE 交AC 于点E ,连接BE ,
若BE =9,BC =12,则cosC =
.
15. 如图,AB 是⊙O 的直径,点C 在AB 的延长线上,CD 与⊙O 相切于点D .若∠C=20°,则∠CDA = °.
A
16. 如右图抛物线y =-x 2+bx +c 的图像与x 轴的一个交点(1,0),则抛物线与x 轴的另一个交点坐标是___________。
17.已知扇形的弧长是2π,半径为10cm ,则扇形的面积是 cm 2
18. 体育测试时,初三一名学生推铅球,已知铅球所经过的路线为抛物线212
12
++-=x x y 的一部分,该同学的成绩是
k y x
=
图2
A
B
C D
α l 1
l 2
l 3 l 4
三、解答题
19.小明在热气球A 上看到正前方横跨河流两岸的大桥BC ,并测得B ,C 两点的俯角分别为45°,35°.已知大桥BC 与地面在同一水平面上,其长度为100m ,请求出热气球离地面的高度.(结果保留整数)
(参考数据:sin 35°≈
,cos 35°≈,tan 35°≈
)
20.如图四边形ABCD 为正方形,点A 的坐标为(0,2),点B 的坐标为(0,-3),反比例函数y =
x
k 的图象经过点C ,一次函数y =ax +b 的图象经过点A 、C . (1) 求反比例函数和一次函数的解析式;
(2)若点P 是反比例函数图像上的一点,△OAP 的面积恰好等于正方形ABCD 的面积,求P 点的坐标.
21.如图,在△ABC 中,AB =AC ,点O 在边AB 上,⊙O 过点B 且分别与边AB 、BC 相交于点D 、E ,EF ⊥AC ,垂足为F .求证:直线EF 是⊙O 的切线.
22、已知:如图,一次函数1
12
y x =
+的图像与x 轴交于点A ,与y 轴交于点B ,二次函数212y x bx c =++的图像与一次函数1
12
y x =+的图像相交于B 、C 两点,与x 轴
交于D 、E 两点且D 点坐标为(1,0). (1)求二次函数的解析式;
(2)求四边形BDEC 的面积S ;
A C
D y O x B。