当前位置：文档之家 › 平行四边形的判定ppt课件

平行四边形的判定ppt课件

  • 格式：ppt
  • 大小：3.05 MB
  • 文档页数：23

下载文档原格式

  / 23

合集下载

平行四边形判定PPT课件

平行四边形判定PPT课件

两组对边分别相等
四边形中，如果两组对边分别相等，则该四边形为平行四边形。
一组对边平行且相等
四边形中，如果有一组对边既平行又相等，则该四边形为平行四边 形。
角度判定法
两组对角分别相等
四边形中，如果两组对角分别相等，则该四边形为平行四边 形。
一组邻角互补
四边形中，如果有一组邻角互补（即两个角的度数之和为 180度），则该四边形为平行四边形。
在水准测量中，可以利用 平行四边形对角线互相平 分的性质进行高程传递和 计算。
05 误区提示与易错点剖析
常见误区提示
误区一
仅根据两组对边分别平行就判定为平行四边形。实际上， 还需要考虑其他条件，如对角线是否互相平分等。
误区二
忽视平行四边形的性质，仅根据图形外观判断。平行四边 形的性质包括两组对边分别平行且相等、对角线互相平分 等，需要综合考虑。
梯形判定
一组对边平行且不相等的四边形是梯形；只有一组对边平行的四边形是梯形。
其他特殊情况
01
等腰梯形判定
同一底上的两个角相等的梯形是等腰梯形；对角线相等的梯形是等腰梯
形。
02
直角梯形判定
有一个角是直角的梯形是直角梯形。
03
平行四边形与特殊四边形的转化
通过添加辅助线或改变条件，可以将平行四边形转化为矩形、正方形、
正方形
既是矩形又是菱形的四边形是正方形。 正方形具有矩形和菱形的所有性质，此 外还具有四个直角和四条相等的边。
菱形
有一组邻边相等的平行四边形是菱形。菱形 具有平行四边形的所有性质，此外还具有四 条相等的边和两条垂直且平分的对角线。
02 平行四边形判定方法
边长判定法
两组对边分别平行
四边形中，如果两组对边分别平行，则该四边形为平行四边形。
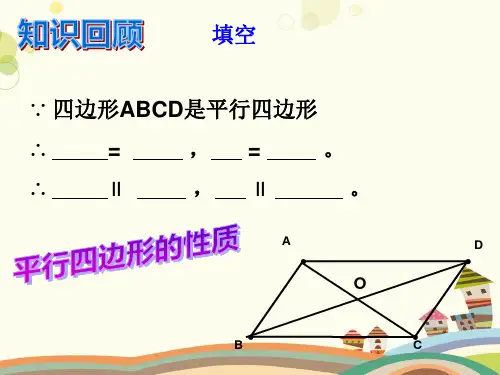
平行四边形的判定 完整版课件

平行四边形的判定 完整版课件


∵AC+CE>AE, ∴AB+AC>2AD, 即2AD<AB+AC.
例2：如图，在△ABC中，AB=14，BC=18，BO是 AC边上的中线，求BO的取值范围。
A O
B
C
平行四边形的五个判定方法
两组对边分别平行 从边看: 两组对边分别相等
的四边形是 平行四边形
一组对边平行且相等
从对角线看: 两组对角线互相平分
A
D
E
F
O
B
C
如图：在 ABCD中，E,F是对角线AC上的两个点； G,H是对角线B,D上的两点.已知AE=CF,DG=BH, 求证：四边形EHFG是平行四边形.
证明：
D
C
在 ＡＢＣＤ中， ＯＡ＝ＯＣ，ＯＢ＝ＯＤ
G
O
F
∵ＡＥ＝ＣＦ，ＤＧ＝ＢＨ
EH
∴ＯＥ＝ＯＦ，ＯＧ＝ＯＨ
A
B
∴四边形EHFG是平行四边形
A
G B
E
D
O
H
FC
如图 A 3 ( , 2 )B , 1 ( 1 , C ) 3 , ( , 2 )D , 1 ( 1 , )
四边形ABCD是不是平行四边形？请给出证明.
A ( 3, 2)与C(3, 2)关于原点O对 y 称
B1 ( 1 ,与 ) D 1 ( 1 , 关 )原 于 对 点称 O
平行四边形的性质定理和判定定理
条件
结论
性质 1
四边形是平行四边形 两组对边平行且相等
定理
2
平行四边形的对角相等、邻角互补
四边形是平行四边形
对角线互相平分
两组对边分别平行的四边形叫做平行四边形
《平行四边形的判定》课件

《平行四边形的判定》课件


学科运用
平行四边形是不可或缺的数学 形态，常用于解决几何、物理 学中的问题。
日常生活
平行四边形存在于日常生活中， 比如棋盘、车库、篮球场等都 是由平行四边形构成的。
总结和要点
1 定义
两组对边平行的四边形。
2 判定条件
3 性质
两组对边互相平行或一个 组对边长度相等，且另一 个组对边长度相等或一个 组的对边中点相连且重合。
《平行四边形的判定》 PPT课件
本课件将为你介绍平行四边形的定义，如何判定平行四边形，平行四边形的 性质，特殊平行四边形，例题，并应用几个实际问题来加深你对平行四边形 的理解。
平行四边形的定义
平行四边形是指两组对边平行的四边形
举例
矩形、菱形、正方形等都是平行 四边形。
形态
平行四边形两组对边长度相等， 两组对边都互相平行，且四个角 度的大小和为360度。
2
例题2
已知四边形EFGH是矩形，且E（-4, -3），F（2, 1），G（5, 4），求顶点H的坐标。
3
例题3
已知ABCD和CBFE是平行四边形，DE和BF相交于点G，DE=10cm，GF=8cm，求CG 的长度。
平行四边形的应用
建筑设计
平行四边形的形状具有空间感， 常用于建筑设计中的立面和室 内设计中的家具设计。
角度
相邻角积等于底边乘以高，其中高是两组对边之间 的距离。
特殊平行四边形
菱形
所有边相等的平行四边形。
矩形
正方形
所有内角都是直角的平行四边形。 所有边和内角都相等的矩形。
平行四边形的例题
1
例题1
已知四边形ABCD为平行四边形，AB=8cm，BC=10cm，求AD的长度。
《 平行四边形的判定》课件(共48张PPT)

《 平行四边形的判定》课件(共48张PPT)

【 ∵四边形 是平行四边形，∴OD=OB， 证明】 ABCD 已知：如图，四边形ABCD的对角线AC，BD相交于点O，并且 AO=CO，BO=DO。
将两长两短的四根细木条用小钉绞合在一起,做成一个四边形,使等长的木条成为对边.
OA=OC，AB∥CD （2010·怀化中考）如图，平行四边形ABCD的对角线
E，F. 于点 ∴AB＝B′C， AB＝A′C(平行四边形的对边相等)． AECF . 上两的组两 对点角，分求并别且相证等A：E的=四C四F边。形边是平形行四边形。是平行四边形
从实验结果得出什么结论？ ∵ AO=OC，BO=OD 判定一个四边形是平行四边形应具备几个条件？ 两组对角分别相等的四边形是平行四边形。 你认为下面四个条件中可选择的是（ ） 证明：连结BD，交AC于点O ∵AB CD， ∴四边形ABCD是平行四边形 两组对边分别相等的四边形是平行四边形 求证：四边形BFDE是平行四边形 ∴四边形ABCD是平行四边形
A B
证明：∵四边形ABCD是
E
D
平行四边形
∴AD∥BC AD=BC
∵ DE=1/2AD
BF=1/2BC
∴DE∥BF DE=BF
F
C
∴四边形EBFD是平
行四边形
∴EB=DF
如图，在 ABCD中，已知AE、CF分别是
∠DAB、∠BCD的角平分线，
求证：四边形AECF是平行四边形。
A
F
D
256
1
34
8 7
∵AB ﹦∥CD， ∴四边形ABCD是平行四边形
A
通过了本节课学习,
你有哪些收获?
B
D
O
C
1、两组对边分别平行的 ∵AB∥CD，AD∥BC
平行四边形的判定教学课件

平行四边形的判定教学课件

平行四边形的判定教学课件
目 录
• 平行四边形的基础知识 • 平行四边形的判定方法 • 平行四边形的应用举例 • 平行四边形的问题建模 • 平行四边形的判定教学建议
01
平行四边形的基础知 识
平行四边形的定义
两组对边分别平行的四边形是平行四边形 平行四边形属于中心对称图形
平行四边形的性质
对边平行且相等 对角相等，邻角互补
3. 根据三角形中位线定理，得出四 边形ABCD是平行四边形。
方法二：通过两组对边分别平行证明
判定定理的证明方法
1. 画出平行四边形ABCD，过点A作AE平行于 BC，交CD的延长线于点E。
3. 根据两组对边分别平行的四边形是平行四边形， 得出四边形ABCD是平行四边形。
步骤
2. 根据平行线性质，得出AE=BC，且AE平行于 BC。
03
平行四边形的应用举 例
在几何作图中的应用
总结词：基础应用
详细描述：在几何作图中，平行四边形是一个基础图形，经常用于绘制各种几何图形和证明各种几何 定理。
在证明中的应用
总结词：定理证明
详细描述：平行四边形在数学中有着广泛的应用，特别是在证明各种几何定理中，如平行线定理、垂直平分线定理等。
在求解中的应用
01
总结词：解析几何
02
详细描述：在解析几何中，平行 四边形是一种常见的图形，可以 用来求解各种问题，如面积、周 长等。
04
平行四边形的问题建 模
平行四边形的建模思路
01
定义平行四边形
02
03
04
介绍平行四边形的性质
讲解平行四边形的判定方法
总结平行四边形的建模思路
问题建模的方法
使用定义法证明平行四边形 使用反证法证明平行四边形
6.平行四边形的判定课件

6.平行四边形的判定课件


-6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 -1
X轴
（-1，-2）B -2 -3
C（3 , -2 ）
-4
-5 -6
F（0，-5）
高效上好每节课·快乐上好每天学
学习了本节课后， 你会用什么方法 来画一个平行四
边形呢？
1
2
3
4
高效上好每节课·快乐上好每天学
高效上好每节课·快乐上好每天学
高效上好每节课·快乐上好每天学
已知：在四边形ABCD中，AB＝CD， AD＝BC ， 求证：四边形ABCD是平行四边形.
A
D
分析： △ABC ≌△CDA
连结AC
B
C
角相等
AD ∥ BC或AB ∥ CD
两组对边分别平行 一组对边平行且相等 四边形ABCD是平行四边形
高效上好每节课·快乐上好每天学
已知：在四边形ABCD中，AB＝CD， AD＝BC ， 求证：四边形ABCD是平行四边形.
高效上好每节课·快乐上好每天学
已知：如图 ，在平行四边形ABCD中， E，F分别是边AD，BC的中点.
(1)求证：EB=DF．
(2)图中还有其它平行四边形吗？说明理由.
高效上好每节课·快乐上好每天学
学习目标
1.探索平行四边形的性质定理1与判定定理1互为逆命 题的关系，体验数学命题探究和发现的过程； 2.理解并掌握平行四边形的判定定理1和2——“一组 对边平行且相等的四边形是平行四边形”、“两组 对边分别相等的四边形是平行四边形”.
3
1
2
4
∵ AB ∥ CD （已知）
B
C
∴∠1＝∠2（两直线平行，内错角相等）
又∵ AB＝CD（已知） AC＝AC（公共边）
《平行四边形的判定》课件

《平行四边形的判定》课件


∵四边形ABCD是平行四边形，A ∴来自D//BC， ∠CFD=∠FCB，
FD
∴∠AEB=∠FCB ∴AE//CF.
BE
C
∵ AE//CF，AF//CE，
平行四边形的判定方法1
∴四边形AECF是平行四边形.
3.如图，已知在四边形ABCD中，AE⊥BD于点E，
CF⊥BD于点F，AE=CF，BF=DE，
D F
∴四边形ABCD是平行四边形． B
平行四边形的判定方法2
E C
课堂小结
平
判定方法1
行
四
边
形
的
判
定
判定方法2
两组对边分别平行的四 边形是平行四边形.
两组对边分别相等的四 边形是平行四边形.
拓展提升
1.如图，AD⊥AC，BC⊥AC，且AD=BC. 求证：四边形ABCD是平行四边形.
要判定该四边形是平行四边 形，已知AD=BC ，可证 AB=CD，根据已知条件，通 过证明△ABC≌△CDA可得.
一点，DE平行AC交AB于点E， DF平行AB交AC于点F.
求证：DE+DF=AC.
A
易证DE=AF ，需证DF=CF， 根据等角对等边可得.
E F
B DC
证明：∵DE//AC ，DF//AB , ∴四边形AEDF是平行四边形， ∴DE=AF . ∵AB=AC，∴∠B=∠C. ∵DF//AB ，∴∠B=∠FDC , ∴∠C=∠FDC，∴DF=CF,
∴ DE+DF=AF+CF=AC.
A
E F
B DC
求证：四边形ABCD是平行四边形.
证明：∵AE⊥BD，CF⊥BD，
∴∠AED=∠CFB=90°.
人教版数学八年级下册《 平行四边形的判定一》ppt课件

人教版数学八年级下册《 平行四边形的判定一》ppt课件

证明：在平行四边形ABCD中，∠A=∠C，AD=BC, 又∵BF=DH，∴AH=CF. 又∵AE=CG， ∴△AEH≌△CGF（SAS）. ∴EH=GF.同理得△BEF≌△DGH（SAS）. ∴GH=EF. ∴四边形EFGH是平行四边形．
课堂检测
能力提升题
如图，五边形ABCDE是正五边形，连接BD , CE，交于点P．
D
110°
70° B
110°C
A
是
B 120°
C 60°
D
不是
能判定四边形ABCD是平行四边形的条件： ∠A:∠B:∠C:∠D的值为 （ ）D
A. 1:2:3:4
B. 1:4:2:3
C. 1:2:2:1
D. 3:2:3:2
探究新知
知识点 3 平行四边形的判定定理3
如图，将两根木条AC，BD的中点重叠，用小钉绞合在一
人教版 数学 八年级 下册
18.1 平行四边形 18.1.2 平行四边形的判定
（第1课时）
导入新知
一天，八年级的李明同学在生物实验室做实验时，不小心碰碎 了实验室的一块平行四边形的实验用的玻璃片,只剩下如图所示 部分,他想去割一块赔给学校，带上玻璃剩下部分去玻璃店不安 全，于是他想把原来的平行四边形重新在纸上画出来，然后带 上图纸去就行了，可原来的平行四边形怎么画出来呢？
E
OF
B
C
∴ A∵BO=DO，
∴四边形BFDE是平行四边形.
巩固练习
根据下列条件,不能判定四边形为平行四边形的是( C )
A.两组对边分别相等 B.两条对角线互相平分
C.两条对角线相等
D.两组对边分别平行
如图，在四边形ABCD中，AC与BD交于点O.
最新平行四边形的判定第一课时PPT课件

最新平行四边形的判定第一课时PPT课件


求证：四边形ABCD是平行四边形
转，则四边形ABCD
A
就是平行四边形。你
能说出这种方法的道
O
理吗？并与同伴交流。
B
D C
判定1
对角线互相平分的四边形是平行 四边形.
探索二.将两长两短的
四根木条用钉子固定， 做成一个四边形，使等 长的木条成为对边，转 动这个四边形，使它改 变形状，在转动的过程 中，四边形ABCD一直 是一个平行四边形吗？ 与同伴交流。
交流的意识，思考习惯，发现能力几方面，及时调控教学进 程。
4.评价语言——— 及时有效地使用激励性语言评价学生
设计意图
此题具有一定的 综合性、灵活性， 能够激发学生多层 次、多角度的思维
A
D
E
O
F
B
C
方式，培养学生解 决几何问题的能力， 培养学生发散性思 维。
四 说教学过程
3
分析范例、形成体系---挑战自我
在四边形ABCD中,若 分别给出四个条件: ⑴AB∥CD ⑵AD=BC ⑶∠A=∠C ⑷AD∥BC 现在,以其中的两个为一 组,能识别四边形ABCD 为平行四边形的条件是 (只填序号)
五、 作业布置
平行四边形的性质：……
必做：
选做：
课堂练习：
二、 平行四边形的判定方法
判别 1：…………
判别 2：…………
五 教学评价 1. 评价主体——采用学生自我评价，学生互评，教师评价相
结合，实现评价主体多元化。
2. 评价方式——采用口试，课堂观察，课后作业等多种形式，
多层面了解学生。
3. 学习过程——从学生参与数学活动的程度、自信心、合作
设计意图
从实际问题引入新课, 提出具有启发性的问题, 能够调动学生的积极思 维，激起学生的学习欲 望,为下一步的探究做好 铺垫。
平行四边形的判定课件(第一课时)

平行四边形的判定课件(第一课时)


1、能判定四边形是平行四边形的题设是四边形的( B).
(A) 对角线相等.
(B)对角线互相平分.
(C) 对角线互相垂直. (D)对角线互相垂直且相等.
2、下列命题错误的是 ( D ).
(A)两组对边分别平行的四边形是平行四边形.
(B) 平行四边形的两组对边分别相等.
(C) 对角线互相平分的四边形是平行四边形.
4.对角线互相平分的四边形
4.平行四边形的对角线
是平行四边形
互相平分.
第十页，共19页。
已知：四边形ABCD, AB=CD，AD=BC
求证：四边形ABCD是平行四边形
证明：
A
D
∵ AB=CD，AD=BC （已知）
∴四边形ABCD是平行四边形 B
C
第十一页，共19页。
已知: 在四边形ABCD中,∠A=∠C,∠B=∠D.
第二页，共19页。
两组对边分别平行
的
从边考虑
四
边
两组对边分别相等
形
是
平
行
从角考虑
两组对角相等 四
边
形
从对角线考虑
两角线互相平分
第三页，共19页。
1.两组对边分别相等的四边形是平行
四边形
第四页，共19页。
已知：四边形ABCD, AB=CD，AD=BC 求证：四边形ABCD是平行四边形
证明：连结AC，
由此你得到的结论是:
对角线互相平分的四边形是平行四边形.
第九页，共19页。
性质:
判定:
1.平行四边形的对边
互 平行; 为 逆 2.平行四边形的对边
1.两组对边分别平行的 四边形是平行四边形;
2.两组对边分别相等的 四边形是平行四边形;
平行四边形的性质ppt课件

平行四边形的性质ppt课件

平行四边形的性质
目录
• 平行四边形的定义 • 平行四边形的性质 • 平行四边形的判定 • 平行四边形的面积与周长 • 平行四边形在几何中的应用
01
平行四边形的定义
定义与性质
定义
平行四边形是一个四边形，其中 相对的两边平行。
性质
平行四边形的对边相等，对角相 等，对角线互相平分。
平行四边形的分类
对角线互相平分
平行四边形的对角线互相 平分，将平行四边形分成 两个面积相等的三角形。
对角线相等
在平行四边形中，相对的 两个角是补角，因此其对 角线长度相等。
对角线与边的关系
平行四边形的对角线可以 用来计算其面积，公式为 面积 = 对角线1 × 对角线 2 ÷ 2。
对边性质
对边平行
平行四边形的定义就是两 组对边平行，这是平行四 边形的基本性质。
了矩形，其周长计算方法与矩形相同。
05
平行四边形在几何中的 应用
在几何证明中的应用
1 2
平行四边形的对角线互相平分
利用这一性质，可以证明线段的相等关系。
平行四边形的对角相等
利用这一性质，可以证明角度的相等关系。
3
平行四边形的邻角互补
利用这一性质，可以证明角度的和为90度。
在几何作图中的应用
利用平行四边形的性 质，可以方便地作出 平行线。
对边相等
在平行四边形中，相对的 两边长度相等，即对边相 等。
对边与角的关系
平行四边形的对角线与对 边之间存在角度关系，可 以通过对角线来计算其他 角度。
对角性质
对角相等
在平行四边形中，相对的两个角大小 相等，即对角相等。
邻角互补
对角与边长关系
在平行四边形中，对角的大小与边的 长度之间存在一定的关系，可以通过 对角来计算边的长度。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
平面内，不共线的三个点最多可 以画3个平行四边形。
12
如图，在平行四边形ABCD中，E、F、G、H分 别是各边上的点，且AE=CG，AH=CF，
求证：四边形EFGH是平行四边形。
A
H
D
E G
B
F
C
13
已知：E、F是平行四边形ABCD对角线AC上的 两点，并且AE=CF.
求证：四边形BFDE是平行四边形
有哪些互相平行的线段？ A 解：图中互相平行的线段有：
D E
AB//DC//EF， AD//BC， DE//CF
B
C
F 21
知识整理
平行四边形的判定方法
从边看:
两组对边分别平行 两组对边分别相等
？？？
的四边形是 平行四边形
22
23
符号语言
Ｄ
Ａ Ｄ
Ａ
Ｃ∵AB∥CD
AD∥BC
Ｂ ∴ABCD是平行四边形 Ｃ ∵AB=CD
AD= BC
Ｂ ∴ABCD是平行四边形
10
两个全等三角形纸片，在平面上把它拼在一起，使一 组对应边互相重合所得的四边形形一定是平行四边形吗？
你能拼出几个不同的平行四边形？
11
平面内，过不共线的三个点 最多可以画几个平行四边形？
证
AB∥CD, AD ∥BC
明 思 路
∠1=∠2，∠3=∠4 ⊿ABC≌⊿CDA
A
D
3
1
2
4
B
C
7
满足下列条件的四边形ABCD是不是平行四边形？
1.AB=CD，AD=BC
A
（是）
2.AB=BC，AD=DC
（不是 ）
B
3.AB ∥ CD，AD ∥ BC （ 是） A
4.AB ∥ CD，AD=BC （不是）
定 义
性质 ∵四边形ABCD是平行四边形
的
∴AB∥CD AD∥BC
双
重
作 判定 ∵ AB∥CD AD∥BC
用
∴四边形ABCD是平边形 ？？
已知：在四边形ABCD中， AB=CD , AD=BC
求证：四边形ABCD 是平行四边形
证
AB∥CD, AD ∥BC
明 思 路
改为:E、F是直线AC上两点，并且AE＝CF。
四边形BFDE是平行四边形吗？自己画图
A
E
DE A
D
F
B
C
B
C
F
E、F是对角线AC上两点 E、F是对角线AC延长线上两16 点
变式二：
若将条件:E、F是平行四边形ABCD对角线AC
上的两点，并且AE=CF.
改为:E、F是直线AC上两点，并且AE＝CF。
四边形BFDE是平行四边形吗？自己画图
A
D
E
B
CF
E点在对角线AC上，F点在AC延长线上
17
学而不思则罔
回
头 一
通过本堂课的学习
看 ，
我学会了… …
我 想
我体会到… …
说
…
18
掌握了一种方法：平行四边形的判定方法
体会了一种思想：
平行四边形的问题常转化为三角形来解决。
提升了一种认识：
解决一个数学问题，常要通过“动手实践”---“ 猜想”----“验证猜想(证明)”-----“得出结论”
A
E
B
D
F
C
14
变式一：
若将条件:E、F是平行四边形ABCD对角
线AC上的两点，并且AE=CF.
改为:E、F是平行四边形ABCD对角线AC 延长线上两点，并且AE＝CF。
四边形BFDE是平行四边形吗？
E
A
D
B
C
15
F
变式二：
若将条件:E、F是平行四边形ABCD对角线AC
上的两点，并且AE=CF.
平行四边形就在我们身边
1
B
利用手中的两组长度分别相等的细木条， 将这四根细木条首尾顺次相接，你能拼成 一个平行四边形吗？
3
大家齐动手
B
如图，拖动这个四边形，使它形状改 变，在图形变化过程中，它始终是平行四 边形吗？
猜想： 两组对边分别相等的四边形一定是
平行四边形？？
4
A
D
B
C
ABCD
有两组对边分别平行的四边形 叫做 平行四边形
D
D
C B
C
8
请你识别下列四边形哪些是平行四边形?请说明
理由？
A
D
110°
70°
B
110°
C
（1）
A
4.8㎝
7.6㎝
D
4.8㎝
B
7.6㎝ C
（2）
4.8㎝
4.8㎝
2.5㎝
2.5㎝
（3）
9
判 文字语言
定
定 两组对边分别 义 平行的四边形
是平行四边形
定 两组对边分别 理 相等的四边形
是平行四边形
图形语言
∠1=∠2，∠3=∠4 ⊿ABC≌⊿CDA
A
D
13 2 4
B
C
6
平行四边形判定定理1：
两两组组对对边边分分别别相相等等的的四四边边形形是是平平行行四四边边形形？？
几已何知语：言在：四∵边A形BA＝BCCDD中，，AADB＝=CBDC , AD=BC
求证：四边∴形A四B边CD形是A平BC行D四是边平形行四边形
19
在数学的天地里，重要的不 是我们知道什么，而是我们怎么 知道什么。
——毕达哥拉斯
20
1、在下列条件中,不能判定四边形是平行四
边形的是( C )
A
D
(A)AB∥CD,AD∥BC
B
C
(B) AB=CD,AD=BC
(C) AB∥CD,AD=BC
2、如图，AB=DC=EF，AD=BC，DE=CF，图中