“隐圆”最值问题演示教学

AB是 O 的直径，
ACB 90．
ABC 45 ， AC 5 ，
ABC 45 ，
AB AC 5 5 2 ， sin 45 2 2
MN最大
52 2
．
故答案为： 5 2 ．
6．如图，在平面直角坐标系中，已知 C(3, 4) ，以点 C 为圆心的圆与 y 轴相切．点 A 、 B 在 x 轴上，且 OA OB ．点 P 为 C 上的动点， APB 90 ，则 AB 长度的最大值为 ．
1．如图，等边 ABC 的边长为 2， A 的半径为 1，D 是 BC 上的动点，DE 与 A 相切于 E ， DE 的最小值是 ( )
A．1
B． 2
C． 3
D．2
【分析】连接 AE ， AD ，作 AH BC 于 H ，因为 DE 与 A 相切于 E ，所以 AE DE ， 可得 DE AD2 AE2 AD2 1 ，当 D 与 H 重合时， AD 最小，此时 DE 最小，求出 AH 的长，即可得出 DE 的最小值． 【解答】解：如图，连接 AE ， AD ，作 AH BC 于 H ，
若平面上 A、B、C、D 四个点满足 ABC ADC ， 则 A、B、C、D 四点共圆． 证明条件：1．四边形对角互补； 2．四边形外角等于内对角．
两条线段被一点分成（内分或外分）两段长的乘积相等，则这两条线段的四个端点共圆．
D
C
H
O
A
B
四边形 ABCD 的对角线 AC、BD 交于 H， 若 AH CH BH DH ，则 A、B、C、D 四点共圆.
作 AM⊥BP 于 M．当点 P 从点 C 运动到点 A 时，线段 BM 的中点 N 运动的路径长为（
）
A． 2 π 2

例1：如图，若AB＝OA＝OB＝OC，则∠ACB的大
小是_______
练习：如图，已知AB=AC=AD，∠CBD=2∠BDC， ∠BAC=44°，则∠CAD的度数为__________
县民政局依法行政工作计划总结 2 0 * * 年,在县委、县政府的正确领导下, 在县法制办的直接指导下, 我局认真贯彻 落 实党的十八大精神和国务院《全面推 进依法 行政实 施纲要 》, 坚持“ 以人为本, 为民 解困、为民服务” 的工作理念, 认真履行“ 解决民生、落实民 权、维 护民利” 的工作 职 责, 以服务科学发展、创新体制机制、强化执 法队伍 建设, 全面推 进依法 行政工 作, 推动民政工作制度化、规范化, 充分发挥在社 会建设 和管理 中的职 能作用, 积极 实
施社会惠民保障工程。现将全年依法 行政工 作情况 汇报如 下: 一、齐抓共管, 加强对依法行政工作的组织领 导
为使依法行政理念真正落到实处, 我局成立了“ 一把 手” 局长、党组 书记为 组长, 分管 副局长为副组长和各职能业务科室负 责人为 成员的 依法行 政工作 领导小 组, 并明确 日常工作由办公室( 法制股) 组织实施。年初对全局 的依法 行政工 作排出 计划, 狠抓 落实, 切实把本单位的依法行政工作列入重要 议事日 程。建 立领导 责任制, 做到 有 部署、有检查、有总结, 逐步形成法制工作“ 一把手” 局长亲 自抓、 分管领 导分工 抓 、职能部门牵头抓、业务科室协同抓, 全局干 部职工 积极参 与的工 作格局, 并严 格
例1：等腰直角△ABC中，∠C＝90°，AC＝BC＝ 4，D为线段AC上一动点，连接BD，过点C作 CH⊥BD于H，连接AH，则AH的最小值.
练习：1、如图，在正方形ABCD中，动点E、F分 别从D、C两点同时出发，以相同的速度在边DC、 CB上移动，连接AE和DF交于点P，由于点E、F的 移动，使得点P也随之运动.若 ，线段CP的最小值 是_____________

B
C
△BOC是等腰直角三角形,锐角顶点C的轨迹是以点A为圆
心,2为半径的圆,所以O点轨迹也是圆,以AB为斜边构造等
M
腰直角三角形,直角顶点M即为点O轨迹圆圆心.
连接AM并延长与圆M交点即为所求的点O,此时AO最大,
根据AB先求AM,再根据BC与BO的比值可得圆M的半径与圆A
O
半径的比值,得到MO,相加即得AO.
E
MN
AD
B
当堂训练---轨迹之线段篇
3.如图,∠AOB=60º,OA=OB,动点C从点O出发,沿射线OB方向移动,
D
，D是定点,E点满足EO=2,故E点
轨迹是以O为圆心,2为半径的圆.
当DE⊥DF且DE=DF,故作DM⊥DO
且DM=DO,F点轨迹是以点M为圆心
,2为半径的圆.
连接OM,与圆M交点即为F点,此 E
时OF最小.可构造三垂直全等求
线段长,再利用勾股定理求得OM,
减去MF即可得到OF的最小值. B
O
C
M F
接得到M点的轨迹长为P点轨迹长一半,即可解 C
FB
决问题.
当堂训练---轨迹之圆篇
3.如图,正方形ABCD中,AB=2 5,O是BC边的中点,点E是正方形内一
动点,OE=2,连接DE,将线段DE绕点D逆时针旋转90º得DF,连接AE、
CF.求线段OF长的最小值.5 2 - 2
【分析】E是主动点,F是从动点 A
连接DF.DF的最小值是_1___.
A
一个定点----垂线段最短
E
G
D
B
C
F
当堂训练---轨迹之线段篇
2.如图,已知等边三角形ABC的边长为8,点D为AB边上一动点,DE始

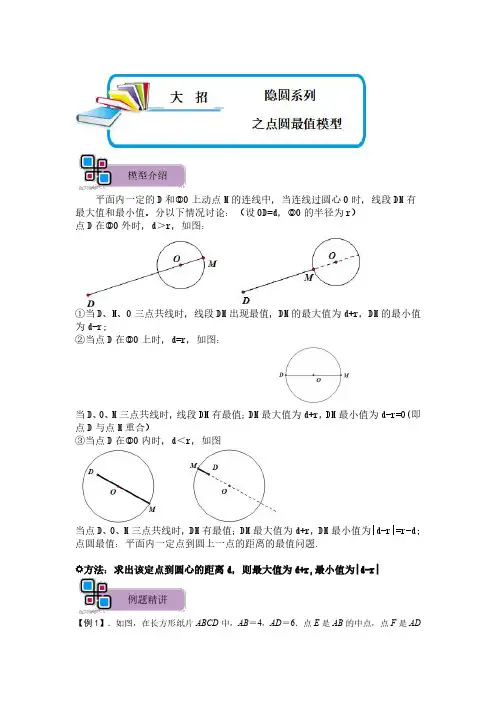
模型介绍平面内一定的D和⓪O上动点M的连线中，当连线过圆心O时，线段DM有最大值和最小值。

分以下情况讨论：（设OD=d，⓪O的半径为r）点D在⓪O外时，d＞r，如图：①当D、M、O三点共线时，线段DM出现最值，DM的最大值为d+r，DM的最小值为d-r;②当点D在⓪O上时，d=r，如图：当D、O、M三点共线时，线段DM有最值；DM最大值为d+r，DM最小值为d-r=0(即点D与点M重合）③当点D在⓪O内时，d＜r，如图当点D、O、M三点共线时，DM有最值；DM最大值为d+r，DM最小值为|d-r|=r-d;点圆最值：平面内一定点到圆上一点的距离的最值问题.方法：求出该定点到圆心的距离d，则最大值为d+r,最小值为|d-r|例题精讲【例1】．如图，在长方形纸片ABCD中，AB＝4，AD＝6．点E是AB的中点，点F是AD边上的一个动点．将△AEF沿EF所在直线翻折，得到△GEF．则GC长的最小值是（）A．B．C．2D．2解：以点E为圆心，AE长度为半径作圆，连接CE，当点G在线段CE上时，GC的长取最小值，如图所示根据折叠可知：GE＝AE＝AB＝2．在Rt△BCE中，BE＝AB＝2，BC＝6，∠B＝90°，∴CE＝＝2，∴GC的最小值＝CE﹣GE＝2﹣2．故选：A．变式训练【变式1-1】.如图，在平行四边形ABCD中，AB＝6，AD＝2，∠A＝45°，M是AD边的中点，N是AB边上的一动点，将△AMN沿MN所在直线翻折得到△A′MN，连接A′C，则A′C长度的最小值是．解：如图，连接MC；过点M作ME⊥CD，交CD的延长线于点E．∵四边形ABCD为平行四边形，∴AD∥BC，AD＝BC＝2，CD＝AB＝6，∵点M为AD的中点，∠A＝45°，∴DM＝MA＝，∠MDE＝∠A＝45°，∴ME＝DE＝DM＝1，∴CE＝CD+DE＝6+1＝7，由勾股定理得：CM2＝ME2+CE2，∴CM＝＝5；由翻折变换的性质得：MA′＝MA＝，点A′在以M为圆心，为半径的圆上显然，当折线MA′C与线段MC重合时，线段A′C的长度最短，此时A′C＝MC﹣MA′＝5﹣＝4，故答案为4．【变式1-2】．如图，矩形ABCD中，AB＝6，BC＝9，以D为圆心，3为半径作⊙D，E为⊙D上一动点，连接AE，以AE为直角边作Rt△AEF，使∠EAF＝90°，tan∠AEF＝，则点F与点C的最小距离为．解：如图取AB的中点G，连接FG．FC．GC．∵∠EAF＝90°，tan∠AEF＝，∴＝，∵AB＝6，AG＝GB，∴AG＝GB＝3，∵AD＝9，∴＝＝，∴＝，∵四边形ABCD是矩形，∴∠BAD＝∠B＝∠EAF＝90°，∴∠FAG＝∠EAD，∴△FAG∽△EAD，∴FG：DE＝AF：AE＝1：3，∵DE＝3，∴FG＝1，∴点F的运动轨迹是以G为圆心1为半径的圆，∵GC＝＝3，∴FC≥GC﹣FG，∴FC≥3﹣1，∴CF的最小值为3﹣1．故答案为3﹣1．【例2】.如图，△ABC中，AB＝AC，BC＝24，AD⊥BC于点D，AD＝5，P是半径为3的⊙A上一动点，连结PC，若E PC的中点，连结DE，则DE长的最大值为_______解：如图，连接PB，∵AB＝AC，AD⊥BC，∴CD＝DB＝BC＝12，∵点E为AC的中点，∴DE是△PBC的中位线，∴DE＝PB，∴当PB取最大值时，DE的长最∵P是半径为3的⊙A上一动点，∴当PB过圆心A时，PB最大，∵BD＝12，AD＝5，∴AB＝，∵⊙A的半径为3，∴PB的最大值为13+3＝16，∴DE长的最大值为8，故选：A．变式训练【变式2-1】.如图，在正方形ABCD中，AB＝2，F是BD边上的一个动点，连接AF，过点B作BE⊥AF于E，在点F变化的过程中，线段DE的最小值是．解：如图，∵BE⊥AF于E，∴E在以AB为直径圆心为O的圆上，∴当O、E、D三点共线的时候线段DE最小，∵AB＝2，四边形ABCD为正方形，∴AO＝1＝OE，AD＝2，∴OD＝＝，∴段DE最小值为OD﹣OF＝﹣1．故答案为：﹣1．【变式2-2】．如图，AB是⊙O的直径，点C在半圆的中点，且BC＝4cm，点D是上的一个动点，连接BD，过C点作CH⊥BD于H，连接AH，在点D的运动过程中，AH 长度的最小值是．解：连接AC，取BC的中点T，连接AT，TH．∵AB是直径，∴∠ACB＝90°，∵点C在半圆的中点，∴＝，∴AC＝CB＝4，∵CT＝TB＝2，∴AT＝＝＝2，∵CH⊥BD，∴∠CHB＝90°，∴点H在以BC为直径的圆上运动，∵CT＝TB，∴HT＝BC＝2，∵AH≥AT﹣HT＝2﹣2，∴AH的最小值为2﹣2，故答案为：2﹣2．1．如图，四边形ABCD为矩形，AB＝3，BC＝4，点P是线段BC上一动点，点M为线段AP上一点，∠ADM＝∠BAP，则BM的最小值为（）A．B．C．﹣D．﹣2解：如图，取AD的中点O，连接OB，OM．∵四边形ABCD是矩形，∴∠BAD＝90°，AD＝BC＝4，∴∠BAP+∠DAM＝90°，∵∠ADM＝∠BAP，∴∠ADM+∠DAM＝90°，∴∠AMD＝90°，∵AO＝OD＝2，∴OM＝AD＝2，∴点M在以O为圆心，2为半径的⊙O上，∵OB＝＝＝，∴BM≥OB﹣OM＝﹣2，∴BM的最小值为﹣2．故选：D．2．如图，△ABC为等边三角形，AB＝3．若P为△ABC内一动点，且满足∠PAB＝∠ACP，则线段PB长度的最小值为（）A．1.5B．C．D．2解：∵△ABC是等边三角形，∴∠ABC＝∠BAC＝60°，AC＝AB＝3，∵∠PAB＝∠ACP，∴∠PAC+∠ACP＝60°，∴∠APC＝120°，∴点P的运动轨迹是，设所在圆的圆心为O，当O、P、B共线时，PB长度最小，设OB交AC于D，如图所示：此时PA＝PC，OB⊥AC，则AD＝CD＝AC＝，∠PAC＝∠ACP＝30°，∠ABD＝∠ABC＝30°，∴PD＝，BD＝，∴PB＝BD﹣PD＝﹣＝．故选：B．3．如图，在Rt△ABC中，∠ACB＝90°，AB＝2，点D为线段AB的中点，将线段BC绕点B顺时针旋转90°，得到线段BE，连接DE，则DE最大值是．解：如图，将线段BD绕点B顺时针旋转90°，得到线段BP，连接PE，PD，则DB＝PB，∠DBP＝90°，∵将线段BC绕点B顺时针旋转90°，得到线段BE，∴BC＝BE，∠CBE＝90°，∴∠CBD＝∠EBP，∴△CBD≌△EBP（SAS），∴PE＝DC，∵在Rt△ABC中，∠ACB＝90°，AB＝2，点D为线段AB的中点，∴DB＝CD＝AB＝1，∴PE＝1，PB＝1，∴DP＝，∵PD+PE≥DE，∴DE≤+1，∴DE最大值为+1，故答案为：+1．4．如图，在边长为2的正方形ABCD中，E，F分别是边DC，CB上的动点，且始终满足DE＝CF，AE，DF交于点P，则∠APD的度数为90°；连接CP，线段CP的最小值为﹣1．解：∵四边形ABCD是正方形，∴AD＝CD，∠ADE＝∠DCF＝90°，在△ADE和△DCF中，，∴△ADE≌△DCF（SAS），∴∠DAE＝∠CDF，∵∠CDF+∠ADF＝∠ADC＝90°，∴∠ADF+∠DAE＝90°，∴∠APD＝90°，取AD的中点O，连接OP，则OP＝AD＝×2＝1（不变），根据两点之间线段最短得C、P、O三点共线时线段CP的值最小，在Rt△COD中，根据勾股定理得，CO＝＝＝，所以，CP＝CO﹣OP＝﹣1．故答案为：90°，﹣1．5．如图，在△ABC中，∠BAC＝90°，AC＝8，BC＝10，AD是BC边上的高，E、F分别为边DC，DA上的动点，且DE：DF＝4：3，射线AE与BF相交于点M，若连接CM，则线段CM的最小值为．解：如图1，连接EF，并延长EF交边AB于点G，∵在△ABC中，∠BAC＝90°，AC＝8，BC＝10，∴，∴AC：AB＝4：3，∴AC：AB＝DE：DF＝4：3，∴，∵∠BAC＝∠FDE＝90°，∴△BAC∽△FDE，∴∠GBE＝∠DFE，∵AD是BC边上的高，∴AD⊥BC，∴∠DFE+∠DEF＝90°，∴∠GBE+∠DEF＝90°，∴∠BGE＝90°，∴EG是△ABE的高，∵AD是△ABE的BE边上的高，∴BM是△ABE的AE边上的高，∴BM⊥AM，∴∠AMB＝90°，∴点M在线段AB为直径的上，如图2，作以线段AB为直径的，取圆心O，连接OC交于点N，则当点O、M、C 三点共线时，线段CM的最小值，如图3，∵AB＝6，点O是圆心，∴OA＝ON＝3，∵∠BAC＝90°，AC＝8，∴，∴线段CM的最小值即，故答案为：．6．如图，直角梯形ABCD中，AB∥DC，∠B＝90°，AB＝1，BC＝2，CD＝3，以B为圆心，半径为1的弧交BC于M，E是线段CD上一动点，EG⊥AD，垂足为G，F是弧AM 上一动点，则EG+EF的最小值为．解：作AH⊥CD于点H是矩形．DH＝CD﹣AB＝3﹣1＝2，AH＝BC＝2．则AH＝DH，△ADH是等腰直角三角形．则∠ADC＝45°．延长BC到M使CM＝BC＝2，作MN⊥AD于点N，交CD于点K．则当E到K时，EG+EF 取得最小值．∵∠ADC＝90°，MN⊥AD，∴△DNK是等腰直角三角形，∠NKD＝∠CKM＝45°，同理△CMK是等腰直角三角形．则CK＝CM＝2，KM＝CM＝2，∴DK＝CD﹣CK＝3﹣2＝1，∴NK＝DK＝．则MN＝MK+NK＝2+＝，则EG+EF的最小值是﹣1＝．故答案是：．7．如图，在△ABC中，∠ACB＝90°，AB＝4，点O是AB的中点，以BC为直角边向外作等腰Rt△BCD，连接OD，当OD取最大值时，则∠ODB的度数是．解：如图，将△ODB绕点B逆时针旋转90°，得到△ECB，连接CO，EO，∵将△ODB绕点B逆时针旋转90°，得到△ECB，∴OB＝BE，OD＝CE，∠BCE＝∠BDO，∠OBE＝90°∵CE≤OC+OE∴当点O在CE上时，CE有最大值，即OD取最大值，∵BE＝OB，∠ABE＝90°∴∠BOE＝45°∵点O是AB中点，∠ACB＝90°∴CO＝BO∴∠ECB＝∠CBO，∵∠EOB＝∠ECB+∠OBC＝45°∴∠ECB＝22.5°＝∠BDO故答案为：22.5°8．如图，正方形ABCD的边长为2，点E为正方形外一个动点，∠AED＝45°，P为AB中点，线段PE的最大值是．解：如图，若点E在正方形右侧，连接AC，BD交于点O，连接PO，EO，∵∠AED＝45°，∠ACD＝45°，∴A，C，E，D四点共圆，∵正方形ABCD的边长为2，∴OE＝OD＝BD＝，∵P为AB的中点，O是BD的中点，∴OP＝AD＝，∵PE≤OP+OE＝+，∴当点O在线段PE上时，PE＝OP+OE＝+，即线段PE的最大值为+，如图，点E在正方形ABCD上方，作斜边为AD的等腰直角△AOD，∠AOD＝90°，则点E在以O为圆心，OA为半径的圆上，∴当点P，点O，点E共线时，PE的值最大，过点O作ON⊥AB，交BA延长线于点N，∵AD＝2，AO＝DO，∠AOD＝90°∴AO＝，∠OAD＝45°，∵ON⊥AB，AD⊥AB∴∠NAO＝∠NOA＝45°∴AN＝NO＝∴PO＝＝＝∴PE最大值为+＞+，故答案为：+9．如图，在矩形ABCD中，AB＝4，BC＝6．（1）如图①，点E是AB的中点，点F是BC边上一点，将△BEF沿EF折叠，点B的对应点为点P，求CP的最小值；（2）如图②，若点P是矩形ABCD内部一点，且∠BPC＝90°，求PD取得最小值时，BP的长；（3）如图③，若点P是矩形ABCD内部一点，且∠PAD+∠PBC＝60°，求AP+BP的最大值.解：（1）如图1，∵点E是AB的中点，∴BE＝AB＝2，由折叠知，PE＝BE＝2，∴点P是在以E为圆心，2为半径的半圆上运动，当点E，P，C共线时，CP最小，∵四边形ABCD时矩形，∴∠ABC＝90°，∴CE＝＝＝2，＝CP′＝CE﹣EP′＝2﹣2；∴CP最小（2）如图2，∵∠BPC＝90°，∴点P在以BC为直径的半圆O上运动，当点D，P，O共线时，PD最小，在Rt△COD中，CD＝4，OC＝BC＝3，∴OD＝5，∴P′D＝OD﹣OP′＝5﹣3＝2，作P′Q⊥BC于Q，∵∠OQP′＝∠BCD＝90°，∠COD为公共角，∴△OQP′∽△OCD，∴，∴，∴OQ＝，QP′＝，在Rt△BQP′中，QP′＝，BQ＝OB+OQ＝3+＝，∴BP′＝＝，∴当PD取得最小值时，BP的长为：；（3）如图3，∵四边形ABCD是矩形，∴∠CAB＝∠BAD＝90°，∴∠CAB+∠BAD＝180°，∵∠PAD+∠PBC＝60°，∴（∠CAB+∠BAD）﹣（∠PAD+∠PBC）＝120°，∴∠PAB+∠PBA＝120°，在△ABP中，∠APB＝180°﹣120°＝60°，延长BP至E，使PE＝PA，∴∠E＝∠PAE，∵∠E+∠PAE＝∠APB＝60°，∴∠E＝30°，在AB的右侧作等边三角形ABO，以O为圆心，AB为半径作圆O，则点E优弧AEC上运动，当BE为直径时，即点P在点O处时，AP+BP最大，最大为直径BE′＝2AB＝8．10．如图，已知四边形ABCD为正方形，△AEF为等腰直角三角形，∠AEF＝90°，连接FC，G为FC的中点，连接GD，ED．（1）如图①，当点E在AB边上时，请直接写出DE，DG的数量关系；（2）如图②，将图①中的△AEF绕点A逆时针旋转，其他条件不变．①探究（1）中的结论是否成立？若成立，请证明；若不成立，请说明理由；②若AD＝4，AE＝1，求DG的最大值和最小值．解：（1）DE＝DG，理由如下：如图①，连接EG，延长EG交BC的延长线于M，连接DM．∵四边形ABCD是正方形，∴AD＝CD，∠B＝∠ADC＝∠DAE＝∠DCB＝∠DCM＝90°，∵∠AEF＝∠B＝90°，∴EF∥CM，∴∠CMG＝∠FEG，∵∠CGM＝∠EGF，GC＝GF，∴△CMG≌△FEG（AAS），∴EF＝CM，GM＝GE，∵AE＝EF，∴AE＝CM，∴△DCM≌△DAE（SAS），∴DE＝DM，∠ADE＝∠CDM，∴∠EDM＝∠ADC＝90°，∴DG⊥EM，DG＝GE＝GM，∴△EGD是等腰直角三角形，∴DE＝DG．（2）①结论成立，理由如下：如图②，连接EG，延长EG到M，使得GM＝GE，连接CM，DM，延长EF交CD于R．∵EG＝GM，FG＝GC，∠EGF＝∠CGM，∴△CGM≌△FGE（SAS），∴CM＝EF，∠CMG＝∠GEF，∴CM∥ER，∴∠DCM＝∠ERC，∵∠AER+∠ADR＝180°，∴∠EAD+∠ERD＝180°，∵∠ERD+∠ERC＝180°，∴∠DCM＝∠EAD，∵AE＝EF，∴AE＝CM，∴△DAE≌△DCM（SAS），∴DE＝DM，∠ADE＝∠CDM，∴∠EDM＝∠ADC＝90°，∵EG＝GM，∴DG＝EG＝GM，∴△EDG是等腰直角三角形，∴DE＝DG；②∵AE＝1，△AEF绕点A旋转，∴点E在以点A为圆心，1为半径的圆A上运动，如图③，当点A、E、D三点共线，且点E在点A的左侧时，DE最大，此时DE＝AD+AE＝4+1＝5，由①可知，DE＝DG，∴DG＝DE＝，即DG的最大值为；如图④，当点A、E、D三点共线，且点E在点A的右侧时，DE最小，此时DE＝AD﹣AE＝4﹣1＝3，由①可知，DE＝DG，∴DG＝DE＝，即DG的最小值为；综上所述，DG的最大值为，最小值为．11．（1）如图1，A、B是⨀O上的两个点，点P在⨀O上，且△APB是直角三角形，⨀O 的半径为1①请在图1中画出点P的位置；②当AB＝1时，∠APB＝30°；（2）如图2，⨀O的半径为5，A、B为⨀O外固定两点（O、A、B三点不在同一直线上），且OA＝9，P为⊙O上的一个动点（点P不在直线AB上），以PA和AB为作平行四边形PABC，求BC的最小值并确定此时点P的位置；（3）如图3，A、B是⊙O上的两个点，过A点作射线AM⊥AB，AM交⨀O于点C，若AB＝3，AC＝4，点D是平面内的一个动点，且CD＝2，E为BD的中点，在D的运动过程中，求线段AE长度的最大值与最小值．解：（1）①如图1，△APB、△AP′B是直角三角形；②在Rt△APB中，AB＝AP，∴∠APB＝30°，故答案为：30；（2）四边形PABC是平行四边形，∴BC＝AP，∴BC的最小值即AP的最小值，∵当P为OA与⊙O的交点时，AP最小，∴AP的最小值为9﹣5＝4，即BC的最小值为4；（3）连接BC，∵AM⊥AB，∴∠CAB＝90°，∴BC是⊙O的直径，∵点D是平面内的一个动点，且CD＝2，∴点D的运动路径为以C为圆心，以2为半径的圆，在直角△ABC中，BC＝＝＝5，∵O是直角△ABC斜边BC上的中点，∴AO＝BC＝，∵E是BD的中点，O是BC的中点∴OE＝CD＝1，∴AE的最小值是AO﹣OE＝，最大值是AO+OE＝．12．【问题提出】（1）如图①，四边形ABCD为正方形，以BC边为直径在BC上方作半圆O，P是上一点，若AB＝6，则DP的最小值为3﹣3；【问题探究】（2）如图②，在Rt△ABC中，∠ACB＝90°，BC＝4，AC＝3，CD是中线，将△ACD 沿CD折叠，得到△ECD，点A的对应点为E，连接AE，求AE的长；【问题解决】（3）如图③是一块矩形ABCD的场地，AB＝300m，AD＝600m，D为场地的出人口，点E在AD边上，且AE＝400m．按照规划，要在矩形内修建一个小型观光台P，且满足∠APE＝90°，在BC上修建休息亭M，并要在观光台P、休息台M以及出入口D之间规划道路PM，DM，为了节约成本，要使得线段PM，DM之和最短，试求PM+DM的最小值，并说明理由．（道路的宽度忽略不计）解：（1）如图1，连接OD，交⊙O于点P，则DP最小，∵四边形ABCD是正方形，∴∠BCD＝90°，CD＝BC＝AB＝3，在Rt△COD中，OC＝＝3，CD＝6，∴OD＝＝3，∴DP＝OD﹣OP＝3﹣3，故答案为：3﹣3；（2）设CD，AE交于点F，∵∠ACB＝90°，AC＝3，BC＝4，∴AB＝5，由折叠得：AE＝2AF，CD⊥AE，∵∠ACB＝90°，CD是中线，∴AD＝CD，∴∠ACD＝∠CAD，∵∠AFC＝∠ACB＝90°，∴△ACF∽△BAC，∴，∴＝，∴AF＝，∴AE＝2AF＝；（3）如图2，∵∠APE＝90°，∴点P在以AE为直径的⊙O上运动，作点D关于BC的对称点G，连接OG，交BC于M，交⊙O于P，则PM+DM最小，最小值为PG的长，∵四边形ABCD是矩形，∴CG＝CD＝AB＝300，∠ADC＝90°，在Rt△ODG中，DG＝CD+CG＝600，OD＝AD﹣OA＝600﹣200＝400，∴OG＝＝＝200，∴PG＝OG﹣OP＝200﹣200，∴PM+DM的最小值为：200﹣200．。

找线段，求张角； 定弦定角画隐圆 找路径，求最值； 圆的知识来帮忙
若∠ACB为锐角， 则C点在两段优弧AB上
若∠ACB为直角， 则C点在半圆AB上
C
若∠ACB为钝角， 则C点在两段劣弧AB上
如图，边长为3的等边△ABC，D、E分别为边BC、AC上 的两个动点，且BD＝CE，AD、BE交于P点，求P点的运
探 究 隐 圆
在 几 何 最 值 问 题 中 的 作 用
已知线段AB=6，平面内一点C，满足∠AC能得到什么结论？ 问题二：求C点的运动路径长？ 问题三：求△ABC面积的最大值？
C
C
A
B
A
运动路径长：6π
Smax=9
∟
O
B
已知线段AB=6，平面内一点C，满足∠ACB=600，情况又如何？
动路径长？并求CP的最小值？
A
O P’
P B D C E
如图，E、F是正方形ABCD的边AD上两个动点，满足AE=DF,连接CF 交BD与点G, 连接BE交AG与点H,若正方形的边长为2，求线段DH长 度的最小值？
C
C1
600 ∟
A
B
600
C2
已知线段AB=4，线段外一点C，满足∠ACB=900 ,
问题四：若I点为△ABC的内心，求I点的运动路径长？
P
450
C1
I1 A
I2
O
B
A
1350
B
I2
C2
方法总结：AB为定线段，线段AB外一点C与A、B两端点形成的张角 固定（即∠ACB=θ），则点C在以AB为弦的圆上运动（不与A、B重合）

“隐形圆”与圆有关问题第一讲“形”现“圆”形问题如图所示，在等腰直角三角形ABC中，AB＝BC＝2，点P为等腰直角三角形ABC所在平面内一点，且满足PA⊥PB，则PC的取值范围是__________．APB C圆是高中数学中一种简单但又非常重要的曲线，近几年高考题和高考模拟题中，经常会出现一类有关圆的题目，这类题目在条件中没有直接给出有关圆方面的信息，而是以隐性的形式出现，但我们通过分析和转化，最终都可以利用圆的知识求解．这类题目构思巧妙，综合性强,，充分考查了学生的数形结合、转化和化归等数学思想方法，处理这类题目关键在于能否把"隐形圆"找出来．圆作为几何图形，找“隐形圆”的一个角度可以从“形”的角度来发现．策略一由圆的定义（到定点的距离等于定长的点的轨迹）确定隐形圆例1（1）如果圆(x－2a)2＋(y－a－3)2＝4上总存在两个点到原点的距离为1，则实数a的取值范围是________．（2）（2016年南京二模）已知圆O ：x 2＋y 2＝1，圆M ：(x －a )2＋(y －a ＋4)2＝1．若圆M 上存在点P ，过点P 作圆O 的两条切线，切点为A ，B ，使得∠APB ＝60°，则a 的取值范围为_________．（3）（2017年苏北四市一模）已知A B 、是圆221:1C x y +=上的动点，AB P 是圆222:(3(4)1C x y -+-=）上的动点，则PA PB +u u u r u u u r的取值范围是_________．（4）若对任意α∈R ，直线l ：x cos α＋y sin α＝2sin(α＋6π)＋4与圆C ：(x －m )2＋(y －)2＝1均无公共点，则实数m 的取值范围是_________．（5）（2016年南通三模）在平面直角坐标系xOy 中，圆()221:12C x y -+=，圆()()2222:C x m y m m -++=，若圆2C 上存在点P 满足：过点P 向圆1C 作两条切线PA 、PB ，切点为A 、B ，ABP ∆的面积为1，则正数m 的取值范围是_________．策略二 由动点P 对两定点A 、B 张角是090（1PA PB k k ⋅=-，或PA PB ⋅=uu r uu r0）确定隐形圆例2 （1）已知圆C ：22(3)(4)1x y -+-=和两点(,0)A m -，(,0)B m (0)m >， 若圆上存在点P ，使得∠APB =90°，则m 的取值范围是_________．（2）（海安2016届高三上期末）在平面直角坐标系xOy 中，已知点P (−1，0)， Q (2，1)，直线l ：0ax by c ++=其中实数a ，b ，c 成等差数列，若点 P 在直线 l 上的射影为 H ，则线段 QH 的取值范围是_________．（3）设m ∈R ，直线1l ：0x my +=与直线2l ：240mx y m ---=交于点00(,)P x y ，则220002x y x ++的取值范围是_________．策略三 由圆周角的性质确定隐形圆例3 （1）已知,,a b c 分别为ABC ∆的三个内角,,A B C 的对边，2a =，(a +b )(sin A -sin B )=(c -b )sin C 则ABC ∆面积的最大值为_________．（2）（2017年常州一模）在△ABC 中，∠C ＝45o ，O 是△ABC 的外心，若OC mOA nOB =+u u u r u u u r u u u r(m ，n ∈R )，则m ＋n 的取值范围是_________．策略四 由四点共圆的定理来确定隐形圆（如一个四边形的对角互补，则该四边形四点共圆）例4 设向量a ，b ，c 满足|a |＝|b |＝1，a ·b ＝－12，若a －c 与b －c 的夹角为60°，则|c |的最大值等于 ．【同步练习】1.点A ，B 分别在x 轴与y 轴的正半轴上移动，且AB ＝2，若点A 从(3，0)移动到(2，0)，则AB 中点D 经过的路程为 ．2．已知O 为坐标原点，向量20(,)OB =uu u r，22(,)OC =uuu r,)CA αα=uu r，则OA uu r 与OB uu u r夹角的范围为 ．3．已知直线20:l x y m -+=上存在点M 满足与两点(2,0)A -,(2,0)B 连线的斜率之积为1-，则实数m 的取值范围是 ．4．已知圆C ：x 2＋y 2＝1，点P (x 0，y 0)在直线x －y －2＝0上，O 为坐标原点，若圆C 上存在一点Q ，使得∠OPQ ＝30°，则x 0的取值范围是________．5．如图，已知点A (－1,0)与点B (1,0)，C 是圆x 2＋y 2＝1上的动点(与点A ,B 不重合)，连接BC 并延长至D ，使得|CD |＝|BC |，则线段PD 的取值范围 ．题第二讲 “数”现“圆”形解析几何中，找“隐形圆”的另一个角度可以从“数”的角度（求出其方程）来发现．策略五 直接由圆（半圆）的方程确定隐形圆例1 （1）(2016年泰州一模)已知实数a ，b ，c 满足222a b c +=，0c ≠，则2b a c-的取值范围为__________．（2）若方程3x ＋b 有解，则b 的取值范围是 ．（3）已知实数x 、y 满足x y -=，则x +y 的最大值是__________．策略六 直接由圆（半圆）的参数方程确定隐形圆例2（1） 已知,t R θ∈，则22(cos 2)(sin 2)t t θθ--+-+的取值范围是__________．（2）函数f (x02x π≤≤) 的值域是________．策略七 由两定点A 、B ，动点P 满足PA PB λ⋅=uu r uu r（λ是常数）,求出动点P 的轨迹方程确定隐形圆例3 已知圆22341:()()C x y -+-=和两点00(,),(,)A m B m -0()m >．若圆C 上存在点P ，使得1PA PB ⋅=u u r u u r，则m 的取值范围是__________．策略八 由两定点A 、B ，动点P 满足22PA PB +是定值确定隐形圆例4（1）在平面直角坐标系xOy 中，已知圆C ：(x －a )2＋(y －a ＋2)2＝1，点A (0，2)，若圆C 上存在点M ，满足MA 2＋MO 2＝10，则实数a 的取值范围是__________．（2） （2017届盐城三模）已知A B C D ，，，四点共面，2BC =，2220AB AC +=，3CD CA =u u u r u u u r ，则||BD u u u r的最大值为 ．策略九 由两定点A 、B ，动点P 满足01PAPBλλλ=>≠(,)确定隐形圆（阿波罗尼斯圆）例5（1）（2016年南通一模）在平面直角坐标xOy 中，已知点(1,0),(4,0)A B ，若直线0x y m -+=上存在点P 使得12PA PB =,则实数m 的取值范围是________．（2）（2016届常州一模）在平面直角坐标系xOy 中，已知圆O ：x 2＋y 2＝1，O 1：(x －4)2＋y 2＝4，动点P 在直线0x b +-=上，过点P 作圆O ，O 1的两条切线，切点分别为A ，B ，若满足2PB PA =的点P 有且仅有两个，则b 的取值范围_________．（3）已知曲线C 的方程221x y +=，()2,0A -，存在一定点()(),02B b b ≠-和常数λ，对曲线C 上的任意一点(),M x y ，都有MA MB λ=成立，则点(),P b λ到直线()220m n x ny n m ++++=的最大距离为_________．例6（2017年南通二模）一缉私艇巡航至距领海边界线l （一条南北方向的直线）3.8海里的A 处，发现在其北偏东30°方向相距4海里的B 处有一走私船正欲逃跑，缉私艇立即追击．已知缉私艇的最大航速是走私船最大航速的3倍．假设缉私艇和走私船均按直线方向以最大航速航行．（1）若走私船沿正东方向逃离，试确定缉私艇的追击方向，使得用最短时间在领海内拦截成功；（参考数据：sin17°5.7446） （2）问：无论走私船沿何方向逃跑，缉私艇是否总能在领海内成功拦截？并说明理由．(例6)【同步练习】1．已知圆C ：(x －3)2＋(y －4)2＝1，点A (0，－1)，B (0,1)．P 是圆C 上的动点，当|P A |2＋|PB |2取最大值时，点P 的坐标是 ．2．（2016年盐城三模）已知线段AB 的长为2，动点C 满足CA CB λ⋅=u u u r u u u r（λ为常数），且点C 总不在以点B 为圆心，12为半径的圆内，则负数λ的最大值是__________．3．（2016年苏北四市一模）已知)1,0(A，)0,1(B，)0,(tC，点D是直线AC上的动点，若2≤恒成立，则最小正整数t的值为．AD BD4．在平面直角坐标系xOy中，M为直线x＝3上一动点，以M为圆心的圆记为圆M，若圆M截x轴所得的弦长恒为4．过点O作圆M的一条切线，切点为P，则点P到直线2x＋y－10＝0距离的最大值为．5．已知x y ∈R 、且满足22246x xy y ++=，则224z x y =+的取值范围是 ．第三讲 “隐圆”综合隐藏圆问题可以和很多知识点结合，在三角形、向量、圆锥曲线等背景的一些问题中看上去和圆无关，但却隐藏着圆． 一、三角形中的隐形圆例1（1）（2017年南京、盐城一模）在ABC ∆中，A ，B ，C 所对的边分别为,,a b c ，若22228a b c ++=，则ABC ∆面积的最大值为__________．（2）（2008年高考江苏卷）若=2AB AC ，，则ABC S ∆的最大值是__________．例2 （1）在ABC ∆中，BC ＝2，AC ＝1，以AB 为边作等腰直角三角形ABD (B 为直角顶点，C 、D 两点在直线AB 的两侧)．当∠C 变化时，线段CD 长的最大值为 ．（2）在ABC ∆中，点D 在边BC 上，且DC ＝2BD ，AB ∶AD ∶AC ＝3∶k ∶1，则实数k 的取值范围为 ．二、向量中的隐形圆例3 （1）已知向量a 、b 、c 满足=a ，3==⋅b a b ，若()()0--=c a c b ，则-b c 的最大值是__________．（2）在平面内，定点A ，B ，C ，D 满足DA u u u r=DB u u u r=DC u u u r，DA u u u r ⋅DB u u u r =DB u u u r ⋅DC u u u r =DC u u u r ⋅DA u u u r = -2，动点P ，M 满足AP u u u r=1，PM u u u u r =MC u u u u r ，则2BM u u u u r 的最大值是__________．例4 已知OA u u u r ，OB u u u r 为非零的不共线的向量，设111r OC OA OB r r=+++u u u r u u u r u u ur ．定义点集{|}||||KA KC KB KCM K KA KB ⋅⋅==u u u r u u u r u u u r u u u r u u u r u u u r ．当1K 、2K M ∈时，若对任意的2r ≥，不等式12||||K K c AB u u u u u r u u u r≤恒成立，则实数c 的最小值为__________．例5 （2014年常州高三期末卷）在平面直角坐标系xOy 中，已知圆2216:O x y +=，点P 12(,)，M 、N 为圆O 上两个不同的点，且0PM PN ⋅=uuu r uuu r，若PQ PM PN =+uu u r uuu r uuu r，则PQ uu u r 的最小值为__________．三、圆锥曲线中的隐形圆例6 在平面直角坐标系xOy 中，已知圆1O ，圆2O 均与x 轴相切且圆心1O ，2O 与原点O 共线，1O ，2O 两点的横坐标之积为6，设圆1O 与圆2O 相交于P ，Q 两点，直线l ：280x y --=，则点P 与直线l 上任意一点M 之间的距离的最小值为__________．例7 设椭圆E ：x 28＋y 24＝1，是否存在圆心在原点的圆，使得该圆的任意一条切线与椭圆E恒有两个交点A ，B ，且OA u u u r ⊥OB u u u r？【同步练习】1． 若a ，b ，c 均为单位向量，且a·b ＝0，(a －c )·(b －c )≤0，则|a ＋b －c |的最大值为_________．2．已知曲线C ：x ＝－4－y 2，直线l ：x ＝6，若对于点A (m ，0)，存在C 上的点P 和l 上的点Q 使得AP u u u r＋AQ u u u r ＝0，则m 的取值范围为 ．3．已知圆()22:11C x y -+=，点(3,0)D ，过动点P 作圆C 的切线PQ ，切点为Q ，若PD =，则△PCD 面积的最大值为__________．4．设点,A B 是圆224x y +=上的两点，点(1,0)C ，如果90ACB ∠=o ，则线段AB 长度的取值范围为__________．精品文档收集于网络，如有侵权请联系管理员删除5．已知ABC ∆是边长为3的等边三角形，点P 是以A 为圆心的单位圆上一动点，点Q 满足2133AQ AP AC =+u u u r u u u r u u u r ，则BQ u u u r 的最小值是__________．。

1234
解析 由题意得|OM|＝ 5－1＝2，所以点 M 在以 O 为圆心，半径为 2 的 圆上. 设 CD 的中点为 N，则 N(2 2，a＋1)，且|CD|＝2. 因为当 A，B 在圆 O 上运动时，始终有∠CMD 为锐角，所以以 O 为圆心， 半径为 2 的圆与以 N(2 2，a＋1)为圆心，半径为 1 的圆外离， 所以 2 22＋a＋12>3，整理得(a＋1)2>1，解得 a<－2 或 a>0， 所以实数a的取值范围为(－∞，－2)∪(0，＋∞).
A. 6
B. 7
√C. 10
D. 11
1234
解析 设 Q(a,0)，M(x，y)，所以|MQ|＝ x－a2＋y2， 由 P－12，0，所以|MP|＝ x＋122＋y2， 因为||MMQP||＝λ 且 λ＝2，所以 xx－＋a1222＋＋yy22＝2， 整理可得 x2＋y2＋4＋32ax＝a2－3 1， 又动点M的轨迹是x2＋y2＝1，
1234
跟踪演练
1.在平面直角坐标系 xOy 中，点 A(－12,0)，B(0,6)，点 P 在圆 O：x2＋y2＝
50 上，若P→A·P→B≤20，则点 P 的横坐标的取值范围是
A.[0， 2]
√B.[－5 2，1]
C.[－ 2， 2]
D.[－2,0]
1234
解析 设 P(x，y)，由P→A·P→B≤20 可得
解析 设M(x，y)，由|MA|2＋|MO|2＝10， 可得x2＋(y－1)2＝4， ∴M点在圆x2＋(y－1)2＝4上， 故圆x2＋(y－1)2＝4和圆(x－a)2＋(y－a＋2)2＝1相交或相切， ∴1≤ a2＋a－32≤3，∴0≤a≤3.
1234
4.已知圆 O：x2＋y2＝5，A，B 为圆 O 上的两个动点，且|AB|＝2，M 为弦 AB 的中点，C(2 2，a)，D(2 2，a＋2).当 A，B 在圆 O 上运动时，始终有 ∠CMD 为锐角，则实数 a 的取值范围为__(－__∞__，__－__2_)_∪__(_0_，__＋__∞__) _.

A
D
E O
C
B
取 CB 中点 M，所以 E 点轨迹是以 M 为圆心、CB 为直径的圆弧．
A
D
E O
CM
B
连接 AM，与圆弧交点即为所求 E 点，此时 AE 值最小， AE AM EM 102 22 2 2 26 2 ．
A
E
C
M
B
【2019 园区一模】如图，正方形 ABCD 的边长为 4，动点 E、F 分别从点 A、C 同时出发，
C
M
E
A
O
B
【寻找定边与直角】如图，在 Rt△ABC 中，∠ACB =90°，BC=4，AC=10，点 D 是 AC 上的 一个动点，以 CD 为直径作圆 O，连接 BD 交圆 O 于点 E，则 AE 的最小值为_________．
A
D
O
E
C
B
【分析】连接 CE ，由于 CD 为直径，故∠CED=90°，考虑到 CD 是动线段，故可以将此 题看成定线段 CB 对直角∠CEB ．
A
D
O
P
F
B
E
C
连接 OC，与圆的交点即为 P 点，再通过勾股定理即可求出 PC 长度． 思路概述：分析动点形 成原理，通常“ 非直即圆” （不是直线就 是圆），接下来可以 寻找与动 点相关有无定直线与定 角．
【2013 武汉中考】如图，E 、F 是正方形 ABCD 的边 AD 上的两个动点，满足 AE =DF，连 接 CF 交 BD 于点 G，连接 BE 交 AG 于点 H，若正方形边长为 2，则线段 DH 长度的最小 值是________．
A
O
B
【辅助圆+相切】如图，在 Rt△ABC 中，∠ACB =90°，∠B=30°，AB =4，D 是 BC 上一动点， CE ⊥AD 于 E ，EF⊥AB 交 BC 于点 F，则 CF 的最大值是_________．

例1：如图，若AB＝OA＝OB＝OC，则∠ACB的大 小是_______


练习：如图，已知AB=AC=AD，∠CBD=2∠BDC， ∠BAC=44°，则∠CAD的度数为__________


例1：木杆AB斜靠在墙壁上，当木杆的上端A沿墙 壁NO竖直下滑时，木杆的底端B也随 之沿着射线OM方向滑动．下列图中用虚线画出木 杆中点P随之下落的路线，其中正确的是（ ）

2、（2016· 安徽）如图，Rt△ABC中，AB⊥BC， AB=6，BC=4，P是△ABC内部的一个动点，且满 足∠PAB=∠PBC，则线段CP长的最小值为 _________.

3、如图，在平面直角坐标系xOy中，A（﹣2， 0），B（0，2），⊙O的半径为1，点C为⊙O上一 动点，过点B作BP⊥直线AC，垂足为点P，则P点纵 坐标的最大值（ ）

4、如图，矩形OABC的边OA、OC分别在x轴、y 轴上，点B的坐标为（7，3），点E在边AB上，且 AE=1，已知点P为y轴上一动点，连接EP，过点O 作直线EP的垂线段，垂足为点H，在点P从点F （0， ）运动到原点O的过程中，点H的运动路径 长为______．

5、如图，半圆的半径BC为2，O是圆心，A是半圆 上的一个动点，连接AB，M是AB的中点，连接CM 并延长交半圆于点D，连接BD，则BD的最大值为 ____________


练习、如图，AB为直径，AB=4，C、D为圆上两 个动点，N为CD中点，CM⊥AB于M，当C、D在 圆上运动时保持∠CMN=30°，则CD的长（ ） A．随C、D的运动位置而变化，且最大值为4 B．随C、D的运动位置而变化，且最小值为2 C．随C、D的运动位置长度保持不变，等于2 D．随C、D的运动位置而变化，没有最值

发现发现““隐形隐形””圆 巧求最小值在近几年的中考数学试题中，常有一些涉及到求线段最小值的问题.这些题目入手较难，得分率很低，分析其原因不难发现，学生对题目中运动变化的本质没有搞清楚.在这些蕴含运动变化的问题中，并没有显性的圆，但是仔细分析题目的条件，如果能发现某个点的运动路径是一个圆(或是一段弧)，可谓是“山重水复疑无路，柳暗花明又一村”，将会对问题的解决起着重要的作用.下面举例说明.一、翻折中的“隐形”圆例1 如图1，在Rt ABC ∆中，90,6,8C AC BC ∠=°==，点F在边AC 上，并且2CF =，点E 为边BC 上的动点，将CEF ∆沿直线EF 翻折，点C 落在点P 处，则点P 到边AB 距离的最小值是 .解 如图2，当点E 在BC 上运动时, PF 的长固定不变，即2PF CF ==.所以点P 在 以点F 为圆心，以2为半径的圆上运动.过点F 作FH AB ⊥交⊙F 于点P ，垂足为H ，此时PH 最短.由AFH ABC ∆∆:，得FH FA BC AB=.又由已知易得4,10AF AB ==.所以4810FH =，即165FH =.所以P 到AB 距离的最小值166255PH FH FP =−=−=.点评 本题关键的地方在于抓住无论点E 的位置在哪，翻折,FCE PF ∆的长度始终等 于FC 的长度，即2PF =.也就是说动点P 到定点F 的距离是定值2，所以点F 的运动路径是以点F 为圆心，2为半径的圆(或部分).如此，这个问题就最终转化为在圆上找一个到定直线距离最短的点.我们可以利用图3的模型1来作出直观解释.模型1 如图3，直线m 与⊙O 相离，过D 点O 作直线m 的垂线，垂足为点H ，交⊙O 与点P 、点Q ，则⊙O 上点P 到直线m 的距离最短，点Q 到直线m 的距离最长理由简述 在⊙O 上任意找一点P ′，过P ′作P H ′′⊥直线m ，垂足为点H ′.由三角形三边关系及直角三角形斜边大于直角边可得:OP P H OH OH ′′′′+>>，而OH OP PH =+,OP OP ′=，所以P H PH ′′>，所以点P 到直线m 的距离最短.类似的方法可以说明点P 到直线m 的距离最长.例2如图4，在边长为2的菱形ABCD 中，60,A M ∠=°对是AD 边的中点，N 是AB 边上一动点.将AMN ∆沿MN 所在的直线翻折得到A MN ′∆，连结A C ′，则A C ′长度的最小值是 .解 当点N 在AB 边上运动时，MA ′的长度固定不变，即1MA MA ′==，所以点A ′在以点M 为圆心，1为半径的圆上运动，如图5，连接CM ，与⊙M 交于点A ′，此时CA ′最短.过点C 作CG AD ⊥交AD 的延长线于点G .因为2,60CD CDG A =∠=∠=°，所以1,DG CG ==，在Rt CMG ∆中，由勾股定理，得CM == 点评 同例1，无论N 点在何处，沿MN 翻折后，线段MA ′的长度(1MA MA ′==)保持不变，而且点M 是定点，所以点A ′的运动轨迹是以M 为圆心，1为半径的圆(部分).要求A C ′的最小值，回归到模型1中，连结圆外定点C 与圆心M 与圆M 交于点A ′，此时A C ′的长度即为最小值.我们可以借助图6利用模型2来作出直观解释.模型2 如图6，点P 为⊙O 外一定点，连结PO 交⊙O 于点A ，延长线与⊙O 交于另一点B ，则PA 的长度为⊙O 外一点P 到⊙O 的最短距离，PB 的长度为⊙O 外一点P 到⊙O 的最长距离.理由简述 在⊙O 上再任意找一点A ′ ,连接PA ′，由三角形三边关系，可得OA PA OP ′′+>.又,OP OA AP OA OA ′=+=，所以PA PA ′>.类似的方法可以说明PB 的长度为⊙O 外一点P 到⊙O 的最长距离.例3 如图7，菱形ABCD 的边8,60AB B =∠=°,P 是AB 上一点，3,BP Q =是CD 边上一动点，将梯形APQD 沿直线PQ 折叠, A 的对应点为A ′.当 CA ′的长度最小时，CQ 的长为 .解 如图8，过C 作CE AB ⊥，连结AC .因为ABCD 是菱形，60B ∠=°，所以ABC ∆为等边三角形，所以84,3,12AE EB BP EP =====.要使CA ′的长度最小，则梯形APQD 沿直线PQ 折叠后A 的对应点A ′应落在CP 上，且对称轴PQ 应满足//PQ DE .由作图知，DEPQ 为平行四边形，所以1,817DQ EP CQ CD DQ ===−=−=.点评 点Q 在线段CD 上无论运动到何处，梯形APQD 沿直线PQ 折叠后PA ′的长度始终保持不变，因此A ′点的运动路径就是以点P 为圆心，PA 长为半径的圆.借助模型2，可知，当点A ′落在线段CP 与⊙P 的交点时，CA ′的长度最小.由PQ 平分,//APC CD AB ∠，可得CQ CP =.作CE AB ⊥，构造Rt CEP ∆，从而可以求出CP 的长.二、直角中的“隐形”圆例4 如图9，在正方形ABCD 中，动点,E F 分别从,D C 两点同时出发，以相同的速度在直线,DC CB 上移动.连结AE 和DF 交于点P ,由于点,E F 的移动，使得点P 也随之运动，请你画出点P 运动路径的草图.若2AD =,试求出线段CP 的最小值.解 由题意，可得DE CF =.又因为,90AD CD ADC DCB =∠=∠=°,所以ADE DCF ∆≅∆,所以DAE CDF ∠=∠.因为90ADP CDF ∠+∠=°，所以90DAE ADP ∠+∠=°.由于点P 在运动中保持90APD ∠=°.听以点P 的路径是一段以AD 为直径的弧.设AD 的中点为O ，连结OC 交弧于点P ，此时CP 的长度最小.在Rt ODC ∆中，OC ===，所以1CP OC OP =−=−. 点评 此题的本质是抓住动点,E F 在运动过程中，始终保持AE DF ⊥，即90APD ∠=°,这样点P 的运动路径就确定了，即点P 在以AD 为直径的圆弧上，再根据模型2求解即可.例5如图10, Rt ABC ∆中，,6,4,AB BC AB BC P ⊥==是ABC ∆内部的一个动点，且满足PAB PBC ∠=∠，则线段CP 长的最小值为 .解 因为90ABC ∠=°,所以90ABP PBC ∠+∠=°.又因为PAB PBC ∠=∠,所以90BAP ABP ∠+∠=°，即90APB ∠=°，所以点P 在以AB 为直径的⊙O 上.连结OC 交⊙O 于点P ，此时PC 最小，在Rt BCO ∆中，90,4,3OBC BC OB ∠=°==，可得5OC =,所以532PC OC OP =−=−=，即PC 最小值为2.点评 首先，根据题目的条件不难得出90APB ∠=°，从而可以证明点P 在以AB 直径的⊙O 上.利用模型2，连结OC ，与⊙O 交于点P ，此时PC 最小，利用勾股定理求出OC即可解决问题.以上例题说明，在求一类线段最值问题中，如果遇到动点的运动路径是圆时，只需利用上面提到的模型1或模型2就可以解决.然而难点在于如何知道动点的运动路径是圆，如何将这个隐身“圆”找出来?从以上例子中可以得出以下两种方法:①观察到定点的距离，即圆是到定点距离等于定长的点的集合;②“定弦对定张角”，如例5中线段AB是定值，当动点P在运动过程中，APB∠的大小不变等于90°(当然不一定为直角)，点P的运动路径也是圆(或弧).因此，教师在教学时，要让学生理解概念的本质，还要培养学生对常见模型的敏感性，从而在有限的考试时间内，能快速获得破解难题的策略.。

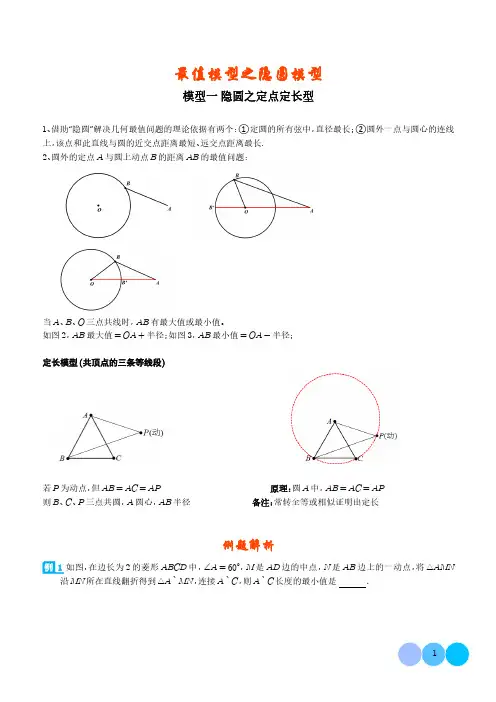
最值模型之隐圆模型模型一隐圆之定点定长型1、借助“隐圆”解决几何最值问题的理论依据有两个：①定圆的所有弦中，直径最长；②圆外一点与圆心的连线上，该点和此直线与圆的近交点距离最短、远交点距离最长.2、圆外的定点A与圆上动点B的距离AB的最值问题：当A、B、O三点共线时，AB有最大值或最小值。

如图2，AB最大值=OA+半径；如图3，AB最小值=OA-半径；定长模型(共顶点的三条等线段)若P为动点，但AB=AC=AP原理：圆A中，AB=AC=AP则B、C、P三点共圆，A圆心，AB半径备注：常转全等或相似证明出定长例题解析1如图，在边长为2的菱形ABCD中，∠A=60°，M是AD边的中点，N是AB边上的一动点，将△AMN 沿MN所在直线翻折得到△A`MN，连接A`C，则A`C长度的最小值是．2如图，在矩形ABCD中，AB=2,AD=7，动点P在矩形的边上沿B→C→D→A运动．当点P不与点A、B重合时，将△ABP沿AP对折，得到△AB P，连接CB ，则在点P的运动过程中，线段CB 的最小值为．变式训练1如图，在矩形ABCD中，AB=2，AD=3，点E，F分别为AD、DC边上的点，且EF=2，G 为EF的中点，P为BC边上一动点，则PA+PG的最小值为？2如图，在Rt△ABC中，∠C=90°，AC=6，BC=8，点F在边AC上，并且CF=2，点E为边BC上的动点，将△CEF沿直线EF翻折，点C落在点P处，则点P到边AB距离的最小值是．3如图，点A，B的坐标分别为A(6，0)，B(0，6)，C为坐标平面内一点，BC=22，M为线段AC的中点，连接OM，当OM取最大值时，点M的坐标为．△ABE沿BE翻折得到△FBE，连接GF．当GF最小时，AE的长是．EF，将四边形ABFE沿EF翻折，点A、B的对应点分别为A'、B'，连接A'D，则A'D的最小值为．模型二隐圆之定长定角型(1)直角圆周角模型固定线段AB所对动角∠C恒为90°原理：圆O中，圆周角为90°所对弦是直径则A、B、C三点共圆，AB为直径备注：常通过互余转换等证明出动角恒为直角解题技巧：若定角为90°，取定长AB的中点O为圆心，AB的一半为半径画辅助圆。