实验六傅里叶变换及其反变换

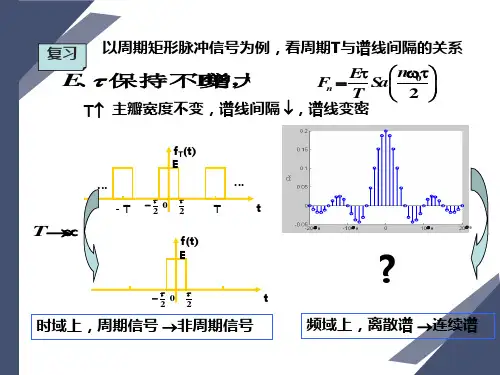
傅里叶变换原理
傅里叶变换是一种数学工具，用于将一个函数（通常是时域上的函数）转换为另一个函数（通常是频域上的函数）。

傅里叶变换的原理包括两个核心思想：信号可以表示为不同频率的正弦波的叠加，以及通过计算信号与不同频率正弦波之间的相关性来获得频谱信息。

一维连续时域信号在傅立叶域的变换公式可以表示为：
F(w) = ∫[从-∞到+∞] f(t) * e^(-j*w*t) dt
其中，F(w)表示频域信号，f(t)表示时域信号，e^(-j*w*t)表示
复指数函数，w表示角频率。

傅里叶变换的逆变换公式可以表示为：
f(t) = 1/2π ∫[从-∞到+∞] F(w) * e^(j*w*t) dw
其中，f(t)表示时域信号，F(w)表示频域信号，e^(j*w*t)表示
复指数函数，w表示角频率。

傅里叶变换在信号处理、图像处理、通信系统等领域广泛应用。

通过将信号从时域转换到频域，可以分析信号的频率成分、滤波、降噪等。

同时，傅里叶变换也可以通过逆变换将频域信号转换回时域，实现信号的还原和复原。

除了一维傅里叶变换，还存在二维和多维傅里叶变换，用于处理二维图像和多维信号。

二维傅里叶变换可以将二维图像转换到频域进行图像增强、滤波等处理，多维傅里叶变换可以对多
维信号进行频域分析。

总之，傅里叶变换是一种重要的数学工具，能够将时域信号转换到频域，通过分析频域信号可以获得信号的频率成分和特征，广泛应用于信号处理和图像处理领域。

课程大作业实验报告图像傅里叶变幻、反变换的实现课程名称：数字图像处理组长：王文雄学号：200730590323 年级专业班级：07通信3班成员一：庞柱坚学号：200730590318 年级专业班级：07通信3班成员二：王弥光学号：200730590322年级专业班级：07通信3班成员三：学号：年级专业班级：07通信3班指导教师邓继忠报告提交日期2010年6月1日项目答辩日期2010年6月1日目录1. 项目要求 (4)2. 项目开发环境 (4)3. 系统分析 (4)3.1. 系统的主要功能分析 (4)3.2. 系统的关键问题及解决方法（或思路） (7)4. 系统设计 (11)4.1. 程序流程图及说明 (11)4.2. 程序主要模块（或功能）介绍 (12)4.2.1. 一维FFT 和IFFT (12)4.2.2. 二维图像FFT 和IFFT： (14)5. 实验结果与分析 (15)5.1. 实验结果 (15)5.2. 项目的创新之处 (16)5.3. 存在问题及改进设想 (17)6. 心得体会 (17)6.1. 系统开发的体会 (17)6.2. 对本门课程的改进意见或建议 (18)7. 附件一 (19)1.项目要求1.基本要求：自修教材相关内容（P52-74）或其它参考资料，在CVI下编程对尺寸为2N(N 为正整数)的图像进行FFT(快速傅里叶变换)和(快速傅里叶反变换)。

（不能利用CVI下的函数）2.题目拓展：编程实现任意大小图像的二维傅立叶的变换与反变换。

2.项目开发环境项目开发环境主要分为软件环境和硬件环境软件：Lab Windows/CVI和IMAQ_Vision for LabWindows/CVI。

Lab Windows/CVI 是美国National Instrument(简称NI)公司开发的基于C语言的虚拟仪器开发平台，适用于自动测试、自动控制、测试仪器通信、测试硬件控制、信号分析及图像处理等软件的开发。

函数的傅里叶变换和反变换的性质傅里叶变换和反变换是函数分析中非常重要的概念，它们在信号处理和通信领域等多个应用中都有广泛的应用。

在本文中，我们将讨论傅里叶变换和反变换的性质，以期对函数分析、信号处理以及数学等领域更深入的了解。

一、傅里叶变换的性质傅里叶变换的定义是：任何函数可以表示成以时间为自变量的正弦和余弦函数的无穷级数的形式。

也就是说，将任何函数分解成一系列的正弦和余弦函数后，我们就可以用傅里叶变换来进行函数的处理和操作。

傅里叶变换可以分为离散和连续两种形式，而它们都具有一些很重要的性质。

下面将分别介绍这些性质：1. 线性性傅里叶变换具有线性性，也就是说如果对于两个函数 f(t) 和g(t)，它们的傅里叶变换分别是F(ω) 和G(ω)，那么对于函数 a ×f(t) + b × g(t)（其中 a 和 b 是任意实数），它的傅里叶变换就是 a × F(ω) + b × G(ω)。

2. 卷积定理卷积定理说明了傅里叶变换中频域的卷积运算可以通过时域中的乘积运算来实现。

如果函数 f(t) 和 g(t) 的傅里叶变换分别是F(ω) 和G(ω)，那么它们在时域的卷积 f(t) * g(t) 的傅里叶变换就是F(ω) × G(ω)。

3. 改变函数的时间和频率如果函数 f(t) 的傅里叶变换是F(ω)，而f(t − τ) 表示 f(t) 向右平移τ 个单位，那么f(t − τ) 的傅里叶变换就是F(ω) × e^{- iωτ}。

同样的道理，如果 f(t) 的傅里叶变换是F(ω)，而 f(at) 表示将 f(t) 的时间宽度缩小到原来的 a 倍，那么 f(at) 的傅里叶变换就是 (1/a) ×F(ω/a)。

二、傅里叶反变换的性质与傅里叶变换相对应的是傅里叶反变换，它可以将函数由频域转换到时域。

傅里叶反变换的定义是：如果一个函数的傅里叶变换为F(ω)，那么它的傅里叶反变换就是：f(t) = (1/2π) × ∫_{-∞}^{∞} F(ω) e^{iωt} dω同样的，傅里叶反变换也有一些很重要的性质：1. 线性性傅里叶反变换与傅里叶变换一样具有线性性，也就是说，如果一个函数的傅里叶变换为F(ω)，而另一个函数的傅里叶变换为G(ω)，那么对于函数a × F(ω) +b × G(ω)，它的傅里叶反变换就是a × f(t) + b × g(t)。

如何进行傅里叶逆变换傅里叶逆变换是信号处理中常用的一种数学工具，用于将频域信号转换为时域信号。

在本文中，我们将介绍如何进行傅里叶逆变换，并探讨其在实际应用中的重要性。

一、傅里叶逆变换的定义和基本原理傅里叶逆变换是傅里叶变换的逆运算，用于将频域信号转换为时域信号。

在数学上，傅里叶逆变换可以通过以下公式表示：f(t) = ∫F(ω)e^(jωt)dω其中，f(t)表示时域信号，F(ω)表示频域信号，e^(jωt)是欧拉公式中的复指数函数。

二、傅里叶逆变换的步骤进行傅里叶逆变换的步骤如下：1. 将频域信号F(ω)表示为复指数形式，即F(ω) = |F(ω)|e^(jφ)，其中|F(ω)|表示幅度，φ表示相位。

2. 将复指数形式的频域信号F(ω)代入傅里叶逆变换公式中，得到时域信号f(t)。

3. 对时域信号f(t)进行必要的处理，如幅度调整、相位校正等。

三、傅里叶逆变换的应用傅里叶逆变换在信号处理领域有着广泛的应用，以下是其中几个重要的应用领域：1. 通信系统：在数字通信系统中，傅里叶逆变换用于将频域信号转换为时域信号，以实现信号的解调和恢复。

2. 图像处理：在图像处理中，傅里叶逆变换用于将图像的频域表示转换为时域表示，以实现图像的恢复和增强。

3. 音频处理：在音频处理中，傅里叶逆变换用于将音频信号的频域表示转换为时域表示，以实现音频的解码和还原。

4. 控制系统：在控制系统中，傅里叶逆变换用于将频域信号转换为时域信号，以实现系统的状态估计和控制。

四、傅里叶逆变换的数值计算方法傅里叶逆变换的数值计算方法有多种，其中最常用的方法是快速傅里叶逆变换（IFFT）。

快速傅里叶逆变换是一种高效的算法，能够在计算复杂度较低的情况下实现傅里叶逆变换。

五、总结傅里叶逆变换是信号处理中重要的数学工具，用于将频域信号转换为时域信号。

通过傅里叶逆变换，我们可以实现信号的解调、图像的恢复、音频的解码等应用。

在实际应用中，我们可以利用快速傅里叶逆变换等数值计算方法来高效地进行傅里叶逆变换操作。

课程大作业实验报告图像傅里叶变幻、反变换的实现课程名称：数字图像处理组长：王文雄学号：200730590323 年级专业班级：07通信3班成员一：庞柱坚学号：200730590318 年级专业班级：07通信3班成员二：王弥光学号：200730590322年级专业班级：07通信3班成员三：学号：年级专业班级：07通信3班指导教师邓继忠报告提交日期2010年6月1日项目答辩日期2010年6月1日目录1. 项目要求 (3)2. 项目开发环境 (3)3. 系统分析 (3)3.1. 系统的主要功能分析 (3)3.2. 系统的关键问题及解决方法（或思路） (6)4. 系统设计 (8)4.1. 程序流程图及说明 (8)4.2. 程序主要模块（或功能）介绍 (10)4.2.1. 一维 FFT 和 IFFT (10)4.2.2. 二维图像 FFT 和 IFFT： (11)5. 实验结果与分析 (12)5.1. 实验结果 (12)5.2. 项目的创新之处 (13)5.3. 存在问题及改进设想 (13)6. 心得体会 (14)6.1. 系统开发的体会 (14)6.2. 对本门课程的改进意见或建议 (14)7. 附件一 (15)1.项目要求1.基本要求：自修教材相关内容（P52-74）或其它参考资料，在CVI下编程对尺寸为2N(N 为正整数)的图像进行FFT(快速傅里叶变换)和(快速傅里叶反变换)。

（不能利用CVI下的函数）2.题目拓展：编程实现任意大小图像的二维傅立叶的变换与反变换。

2.项目开发环境项目开发环境主要分为软件环境和硬件环境软件：Lab Windows/CVI和IMAQ_Vision for LabWindows/CVI。

Lab Windows/CVI是美国National Instrument(简称NI)公司开发的基于C语言的虚拟仪器开发平台，适用于自动测试、自动控制、测试仪器通信、测试硬件控制、信号分析及图像处理等软件的开发。

实验六、FFT与chirp-z变换实验六、FFT与chirp-z变换⼀、实验⽬的1、学会运⽤Matlab表⽰FFT和chirp-z变换的⽅法2、观察并熟悉这些信号的波形和特性⼆、实验原理基-2 FFT算法1、时间抽取基-2FFT算法2、频率抽取基-2FFT算法3、基-2IFFT算法三、实验内容1、已知信号由15ＨＺ幅值０.５的正弦信号和４０ＨＺ幅值２的正弦信号组成数据采样频率为１００HZ ，试分别绘制N=128点DFT 的幅频图和N=1024点ＤＦＴ幅频图。

解、由题意得：信号可写为)2sin(2)2sin(5.021∏∏+=t c t f x ，其中1f ＝１５HZ ，f2=40ＨＺMATLAB 程序设计如下：clffs=100; N=128; n=0:N-1; t=n/fs;x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t); y=fft(x,N);mag=abs(y);f=(0:length(y)-1)'*fs/length(y);subplot(221);plot(f,mag);xlabel('Frequence(HZ)');ylabel('Magnitude');title('N=128')gridsubplot(222);plot(f(1:N/2),mag(1:N/2));xlabel('Frequence(HZ)');ylabel('Magnitude');title('N=128')gridfs=100;N=1024;n=0:N-1;t=n/fs;x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t); y=fft(x,N); mag=abs(y);f=(0:length(y)-1)'*fs/length(y);subplot(223)plot(f,mag);xlabel('Frequence(HZ)');ylabel('Magnitude');title('N=1024')gridsubplot(224)plot(f(1:N/2),mag(1:N/2));xlabel('Frequence(HZ)');ylabel('Magnitude');title('N=1024')grid实验截图如下：50100050100150Frequence(HZ)M a g n i t u d eN=12820406050100150Frequence(HZ)M a g n i t u d eN=12850100020*******800Frequence(HZ)M a g n i t u d eN=1024204060020*******800Frequence(HZ)M a g n i t u d eN=1024２、已知带有测量噪声信号x(t)=sin(2πf 1t)+sin(2πf 2t)+2w(t),其中f 1=50Hz ，f 2=120Hz ，ω（t ）为均值为零的随机信号，采样频率为1000Hz ，数据点数N=1024。

傅里叶变换反比傅里叶变换是一种重要的数学工具，它在信号处理、图像处理、物理学、工程学等领域中被广泛应用。

它可以将一个时间域上的信号转换为频域上的信号，从而帮助我们更好地理解和分析信号的频谱特性。

傅里叶变换的基本思想是将一个周期性的信号分解成一系列不同频率的正弦和余弦函数的叠加。

我们知道，任何一个周期性的信号都可以表示为一系列不同频率的正弦和余弦函数的叠加，而傅里叶变换就是将这个叠加过程具体化。

傅里叶变换的核心是傅里叶级数展开，它将一个周期性信号分解成一系列不同频率的正弦和余弦函数的叠加。

这个过程可以理解为将一个信号在频域上进行了分解，得到了信号的频谱。

通过傅里叶级数展开，我们可以清晰地看到信号中各个频率分量的大小和相位信息。

傅里叶变换的数学表达式较为复杂，但我们可以通过实际应用来理解其作用。

以音频信号处理为例，我们知道音频信号是由不同频率的声波组成的，通过傅里叶变换，我们可以将音频信号转换为频谱图，从而直观地看到音频信号中各个频率分量的大小。

这对于音频信号的分析和处理非常有帮助，比如我们可以通过傅里叶变换来实现音频的降噪、均衡器调整等功能。

除了音频信号处理，傅里叶变换在图像处理中也有重要的应用。

图像可以看作是一个二维信号，通过傅里叶变换，我们可以将图像在频域上进行分解，得到图像的频谱。

这对于图像处理来说具有重要意义，比如我们可以通过傅里叶变换来实现图像的滤波、边缘检测等功能。

傅里叶变换的应用不仅局限于信号处理领域，它还在物理学、工程学等领域中得到了广泛应用。

比如在电力系统中，傅里叶变换可以用来分析电力信号的频谱，从而帮助我们更好地了解电力系统的运行情况。

在通信系统中，傅里叶变换可以用来分析信号的频谱特性，从而帮助我们设计更有效的通信系统。

傅里叶变换是一种强大的数学工具，它可以将一个时间域上的信号转换为频域上的信号，帮助我们更好地理解和分析信号的频谱特性。

通过傅里叶变换，我们可以清晰地看到信号中各个频率分量的大小和相位信息，从而实现对信号的精确分析和处理。