下载文档原格式
第1篇一、实验目的1. 了解噪声的基本概念和测量方法；2. 掌握噪声测量仪器的使用方法；3. 培养实验操作能力和数据分析能力。
二、实验原理噪声是指不规则、无规律的声音。
噪声的测量通常采用声级计，声级计是一种用于测量声音强度的仪器。
本实验采用声级计对实验室噪声进行测量，测量结果以分贝（dB）为单位。
三、实验仪器与设备1. 声级计：用于测量实验室噪声；2. 音频信号发生器：用于产生标准噪声信号；3. 电脑：用于数据采集和存储；4. 话筒：用于接收噪声信号；5. 实验室：实验场地。
四、实验步骤1. 准备工作：检查实验仪器是否完好，连接好声级计、音频信号发生器和电脑；2. 校准声级计：按照声级计说明书进行校准，确保测量结果的准确性；3. 测量实验室噪声：将声级计放置在实验室中央，距离地面1.2米处，开启声级计，调整测量频率为1kHz，开始测量实验室噪声；4. 数据采集：将测量结果记录在实验记录表上；5. 重复测量：为了提高测量结果的可靠性，对实验室噪声进行多次测量，取平均值；6. 测量标准噪声信号：开启音频信号发生器，产生标准噪声信号，调整声级计至标准噪声信号处，记录声级计读数；7. 数据分析：将实验室噪声测量结果与标准噪声信号进行对比，分析实验室噪声水平。
五、实验结果与分析1. 实验室噪声测量结果：经多次测量，实验室噪声平均值为60dB；2. 标准噪声信号测量结果：标准噪声信号声级为70dB；3. 实验室噪声分析：实验室噪声平均值为60dB，略低于标准噪声信号声级，说明实验室噪声水平相对较低。
六、实验结论通过本次实验，我们掌握了噪声的基本概念和测量方法，学会了使用声级计测量实验室噪声。
实验结果表明，实验室噪声水平相对较低，符合国家标准。
七、实验注意事项1. 实验过程中，注意保持实验室安静，避免外界噪声干扰；2. 声级计放置位置要稳定，避免晃动；3. 校准声级计时，要严格按照说明书进行操作；4. 实验结束后，将实验仪器归位，保持实验室整洁。
一、实验目的1. 掌握声级计的使用方法。
2. 熟悉噪声监测的基本原理和步骤。
3. 了解噪声对环境和人体健康的影响。
二、实验原理噪声的测定主要依据声学原理，通过测量声压级来评价噪声的大小。
声压级是指声压与参考声压的比值，以分贝（dB）为单位。
声压级与声能量的大小有关，声能量越大，声压级越高。
三、实验器材1. 声级计2. 传声器3. 测量支架4. 记录本5. 计时器四、实验步骤1. 准备工作a. 将声级计和传声器连接，检查设备是否正常工作。
b. 选择合适的测量位置，确保传声器距离地面1.2m，距离测量对象0.5m以上。
c. 记录实验日期、地点、天气状况等信息。
2. 噪声测量a. 将声级计置于测量位置，打开电源，预热设备。
b. 选择合适的测量档位，确保声级计能够覆盖待测噪声的范围。
c. 按下“测量”按钮，开始记录噪声数据。
d. 根据实验要求，进行多次测量，取平均值作为最终结果。
3. 数据处理a. 将测量得到的噪声数据记录在记录本上。
b. 计算等效声级（Leq）、最大声级（Lmax）等参数。
c. 分析噪声数据，评估噪声对环境和人体健康的影响。
五、实验结果与分析1. 实验数据a. 实验地点：XX小区b. 实验日期：2021年X月X日c. 天气状况：晴朗d. 噪声测量结果：- Leq：55dB- Lmax：70dB2. 分析a. XX小区的噪声水平在正常范围内，但最大声级较高，可能对居民生活产生一定影响。
b. 噪声来源主要包括交通噪声、建筑施工噪声等。
c. 噪声对环境和人体健康的影响：- 噪声污染可能导致听力损伤、心血管疾病、睡眠障碍等问题。
- 噪声干扰居民生活，降低生活质量。
六、实验总结1. 通过本次实验，掌握了声级计的使用方法和噪声监测的基本步骤。
2. 认识到噪声对环境和人体健康的危害，提高环保意识。
3. 建议加强噪声污染治理，改善居住环境。
七、实验报告实验名称：噪声的测定实验日期：2021年X月X日实验地点：XX小区实验目的：掌握声级计的使用方法，熟悉噪声监测的基本原理和步骤，了解噪声对环境和人体健康的影响。
4.3 理想白噪声、带限白噪声比较分析1、实验原理若一个具有零均值的平稳随机过程，其功率谱密度在某一个有限频率范围内均匀分布，而在此范围外为零，则称这个过程为带限白噪声。
带限白噪声分为低通型和带通型。
白噪声详细描述可参考马文平、李兵兵等编著.随机信号分析与应用.科学出版社，2006出版的书第2章节。
朱华、黄辉宁、李永庆、梅文博.随机信号分析.北京理工大学出版社,2000出版的书第4章节。
以及与随机信号分析相关的参考书籍。
2、实验任务与要求⑴通过实验掌握白噪声的特性以及带限白噪声的意义，重点在于系统测试与分析。
算法选用matlab或c/c++语言之一编写和仿真程序。
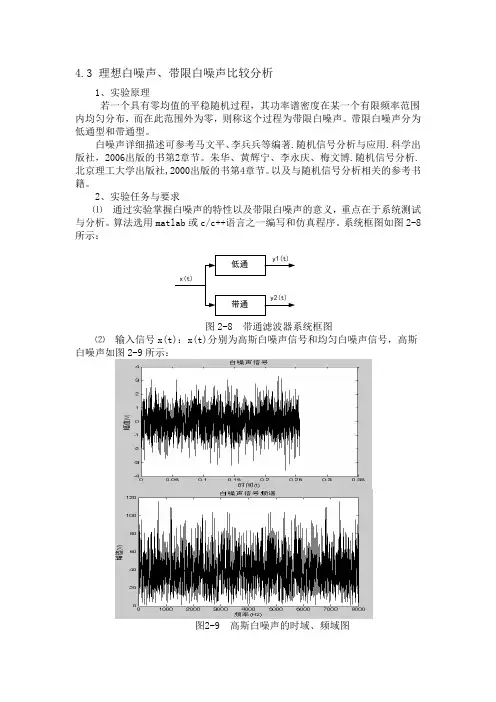
系统框图如图2-8所示：低通带通x(t)y1(t)y2(t)图2-8带通滤波器系统框图⑵输入信号x(t)：x(t)分别为高斯白噪声信号和均匀白噪声信号，高斯白噪声如图2-9所示：图2-9 高斯白噪声的时域、频域图要求测试白噪声的均值、均方值、方差，自相关函数、概率密度、频谱及功率谱密度并绘图。
分析实验结果，搞清楚均值、均方值、方差，自相关函数、频谱及功率谱密度的物理意义。
例：均值除了表示信号的平均值，它还表示信号中有了什么成分。
相关函数当τ=0时为什么会有一个冲击，表示什么，它又等于什么。
信号的时域波形有哪些特征，频域又有哪些特征。
频谱及功率谱密度有什么差异，什么噪声是白噪声，这个噪声符合白噪声的定义吗等等。
⑶设计一个低通滤波器和一个带通滤波器。
要求白噪声分别通过低通滤波器和带通滤波器后的信号能够表现出带限白噪声的特点。
测试低通滤波器和一个带通滤波器的时频特性和频域特性以验证其正确性。
⑷分别计算高斯白噪声、均匀白噪声经低通滤波、带通滤波器后的均值、均方值、方差、概率密度、自相关函数、频谱及功率谱密度，并加以分析。
⑸所有结果均用图示法来表示。
⑹白噪声在什么情况下为带限白噪声？⑺按要求写实验报告。
白噪声检验公式了解白噪声检验的计算公式白噪声检验是一种经典的统计检验方法，用于判断时间序列数据是否存在自相关性，即是否存在与时间相关的模式。
在金融领域、信号处理、经济学等领域中，白噪声检验被广泛应用。
本文将介绍白噪声检验的基本概念以及常用的计算公式。
一、白噪声检验的基本概念白噪声是指具有等间隔时间间隔和相同振幅的随机信号。
在时间序列分析中，我们常常需要判断某个数据序列是否符合白噪声的特征。
如果序列中存在自相关性，则表明序列中存在某种模式，不符合白噪声的特征。
二、白噪声检验的计算公式1. 自相关系数计算公式自相关系数是衡量序列内部各观测值之间相关性的一种指标。
其计算公式如下：其中，ρ(k)表示序列在时间间隔k下的自相关系数；x(i)表示序列中第i个观测值；x表示序列的平均值；n表示序列的观测值个数。
2. 白噪声检验统计量计算公式Ljung-Box Q检验是一种常用的白噪声检验方法，可以用来判断时间序列数据是否具有自相关性。
其计算公式如下：其中，Q(m)表示Ljung-Box Q统计量；ρ(k)表示序列在时间间隔k下的自相关系数；n表示序列的观测值个数；m表示滞后期数（通常取序列长度的1/4到1/2）。
3. 白噪声检验的拒绝域白噪声检验的拒绝域可以根据显著性水平确定。
常见的显著性水平有0.01和0.05。
一般情况下，当Q(m)大于拒绝域的临界值时，我们拒绝原假设，认为序列具有自相关性，不符合白噪声的特征。
三、实例分析以股票市场的每日收盘价为例，假设我们有100个观测值，想要判断该时间序列是否符合白噪声的特征。
我们可以按照以下步骤进行计算和判断：1. 计算自相关系数ρ(k)，其中k的取值范围可以根据需求进行设定。
2. 根据自相关系数计算Q(m)统计量，其中m的取值一般为观测值个数的1/4到1/2。
噪声测定实验报告噪声测定实验报告引言噪声是我们日常生活中无法避免的环境问题之一。
它不仅会对人们的身心健康产生负面影响，还可能干扰正常的工作和学习。
因此，准确测定噪声水平对于评估环境质量和采取相应措施具有重要意义。
本实验旨在通过噪声测定实验，了解噪声的特性、来源以及其对人体的影响，并探究不同环境下的噪声水平。
实验方法1. 实验仪器与设备本实验使用的仪器为声级计和噪声源。
声级计是一种专门用于测量声音强度的仪器，其测量结果以分贝（dB）为单位。
噪声源可以是机器设备、交通工具或其他产生噪声的物体。
2. 实验步骤（1）选择不同环境进行噪声测定，包括室内、室外、交通路口等。
（2）在每个环境中设置相同的测量距离，保持声级计与噪声源之间的距离不变。
（3）打开声级计，将其置于测量环境中。
（4）记录每个环境下的噪声水平，包括声音强度和频率分布。
实验结果与分析1. 室内环境下的噪声水平在室内环境中，我们选择了一个普通的办公室进行测定。
实验结果显示，办公室中的噪声水平较低，平均分贝数约为40dB。
这是因为办公室内通常没有大型机器设备运转，而且室内的隔音措施较好，能够减少外界噪声的干扰。
2. 室外环境下的噪声水平在室外环境中，我们选择了一个繁忙的市中心街道进行测定。
实验结果显示，街道上的噪声水平较高，平均分贝数约为70dB。
这是因为街道上存在大量交通工具行驶、行人交谈以及商贩叫卖等噪声源，同时缺乏隔音措施。
3. 交通路口的噪声水平在交通路口进行噪声测定，我们发现噪声水平较高，平均分贝数约为80dB。
这是由于交通路口是交通流量较大的地方，汽车、摩托车等交通工具的引擎声以及鸣笛声都是主要的噪声源。
此外，行人交谈声和交通信号灯的声音也会贡献一部分噪声。
结论与建议通过本次噪声测定实验，我们得出了以下结论：1. 室内环境下的噪声水平较低，对人体的影响较小。
2. 室外环境和交通路口的噪声水平较高，对人体的影响较大。
针对噪声问题，我们提出以下建议：1. 在室内环境中，可以采取隔音措施，如使用隔音玻璃、隔音门等，减少外界噪声的干扰。
白噪声检验的方法及原理咱得明白啥是白噪声。
白噪声啊，就像是一种杂乱无章但又有规律可循的声音信号。
在统计学和时间序列分析里，白噪声可是个重要的概念呢。
它具有一些特定的性质，比如说均值为零，方差是一个常数，不同时间点的取值相互独立。
简单来说，白噪声就是一种随机的、没有明显趋势和规律的信号。
那为啥要进行白噪声检验呢？这可重要啦！如果一个时间序列是白噪声，那就意味着它没有可预测的模式，是完全随机的。
在很多情况下，我们需要确定一个时间序列是不是白噪声，因为这关系到我们后续的分析和预测方法的选择。
如果一个时间序列不是白噪声，那就可能存在某种趋势、季节性或者周期性，我们就可以利用这些特征来进行预测和分析。
但如果它是白噪声，那我们就知道用传统的预测方法可能不太管用啦。
接下来，咱说说白噪声检验的方法。
常见的方法有好几种呢，比如说自相关函数检验、Ljung-Box 检验和单位根检验等。
自相关函数检验呢，就是看时间序列的自相关函数。
如果一个时间序列是白噪声，那么它的自相关函数在所有的滞后阶数上都应该接近于零。
啥意思呢？就是说不同时间点的取值之间没有明显的相关性。
我们可以通过计算时间序列的自相关函数，并观察它在不同滞后阶数上的值来判断是不是白噪声。
如果自相关函数的值都很小，接近零，那很可能就是白噪声；如果自相关函数在某些滞后阶数上有较大的值，那就不是白噪声啦。
Ljung-Box 检验也是个常用的方法。
这个检验主要是通过计算统计量来判断时间序列的自相关性。
它会比较实际的自相关系数和在白噪声假设下的预期自相关系数。
如果统计量的值很大，那就说明时间序列不是白噪声；如果统计量的值比较小，那就有可能是白噪声。
Ljung-Box 检验通常会给出一个p 值，我们可以根据p 值来判断是否拒绝白噪声假设。
如果p 值小于某个显著性水平，比如0.05，那就拒绝白噪声假设，说明时间序列不是白噪声；如果p 值大于显著性水平，那就不能拒绝白噪声假设，可能是白噪声。
实验室噪音测试方法咱就说，在实验室里，噪音测试可是个相当重要的事儿啊！这可不像咱平时在家里听听音乐那么简单。
你想想看，实验室里那么多仪器设备，要是噪音太大，那得多闹心啊！不仅会影响实验人员的心情，还可能干扰实验结果呢！那怎么进行噪音测试呢？首先，咱得准备好专门的噪音测试仪器，这就好比战士上战场得有趁手的兵器一样。
这仪器可得选好了，精度要高，不然测出来的数据不准确，那不就白忙活啦！然后呢，要选好测试的位置。
这位置可不能随便选，得找那些有代表性的地方，比如仪器旁边啊，实验人员经常工作的区域啊。
就好像你要了解一个城市的热闹程度，总不能去荒郊野外测吧，得去市中心那些人多的地方才行。
接着，在测试的时候，周围可不能有其他乱七八糟的声音干扰。
要是这边测着，那边有人在大声喧哗，那测出来的能准吗？这就跟你考试的时候旁边有人一直吵吵，你能安心答题吗？还有啊，测试的时间也得注意。
不能说就测那么一小会儿，得测足够长的时间，这样才能得到比较全面的数据。
就像你了解一个人的性格，不能只看他一天的表现，得长时间观察才行呢。
测完之后，可别以为就完事了。
还得好好分析分析数据，看看噪音的大小、频率啥的。
这就好比医生看检查报告，得从那些数据里看出门道来。
要是发现噪音超标了，那可得赶紧想办法解决啊！是给仪器加上隔音罩呢，还是调整实验布局呢？这可得好好琢磨琢磨。
总之啊，实验室噪音测试可不是一件小事，得认真对待。
只有把噪音控制好了，实验室才能有一个良好的工作环境，实验人员才能安心地搞研究。
不然整天在一个吵吵闹闹的环境里，能做出好的成果来吗？咱可不能让噪音成为实验的绊脚石啊！大家说是不是这个理儿？。
白噪声测试一、 实验目的⑴ 了解白噪声信号的特性，包括均值（数学期望）、均方值、方差、相关函数、概率密度、频谱及功率谱密度等。
⑵ 掌握白噪声信号的分析方法。
二、 实验原理所谓白噪声是指它的概率统计特性服从某种分布而它的功率谱密度又是均匀的。
确切的说，白噪声只是一种理想化的模型，因为实际的噪声功率谱密度不可能具有无限宽的带宽，否则它的平均功率将是无限大，是物理上不可实现的。
然而白噪声在数学处理上比较方便，所以它在通信及电子工程系统的分析中有十分重要的作用。
一般地说，只要噪声的功率谱密度的宽度远大于它所作用的系统的带宽，并且在系统的带内，它的功率谱密度基本上是常数，就可以作为白噪声处理了。
白噪声的功率谱密度为：2)(0N f S n =其中0N 为单边功率谱密度。
白噪声的自相关函数为：)(20τδτN R =）（ 白噪声的自相关函数是位于τ=0处、强度为20N 的冲击函数。
这表明白噪声在任何两个不同的瞬间的取值是不相关的。
同时也意味着白噪声能随时间无限快的变化，因为它的带宽是无限宽的。
下面我们给出几种分布的白噪声。
随机过程的几种分布前人已证明，要产生一个服从某种分布的随机数，可以先求出其分布函数的反函数的解析式，再将一个在[0，1]区间内的均匀分布的随机数的值代入其中，就可以计算出服从某种分布的随机数。
下面我们就求解这些随机数。
[0，1]区间均匀分布随机信号的产生：采用混合同余法产生[0，1]区间的均匀分布随机数。
混合同余法产生随机数的递推公式为：c ay y n n +=+1 n=0,1,2…… My x n n = n=1,2,3…… 由上式的出如下实用算法： ][1M c ax M c ax x n n n +-+=+ My x 00=其中：k M 2=，其中k 为计算几种数字尾部的字长14+=t a ，t 为任意选定的正整数0y ，为任意非负整数c ，为奇数 Matlab 语言中的rand （）函数是服从[0，1]均匀分布的，所以在以后的实验中如果用到均匀分布的随机数，我们统一使用rand()函数。
一、实验目的1. 了解噪声的基本概念和分类；2. 掌握噪声检测的基本原理和方法；3. 培养实验操作技能和数据分析能力。
二、实验原理噪声是指不希望存在的声音，它会对人们的身心健康产生负面影响。
噪声检测是通过对噪声的测量和分析，了解噪声的强度、频率、时间等特性，为噪声控制提供依据。
噪声检测的基本原理是根据声波在空气中的传播速度和声压级之间的关系，通过测量声压级来反映噪声的强度。
常用的噪声检测仪器有声级计、频谱分析仪等。
三、实验仪器与材料1. 声级计（数字式或模拟式）2. 频谱分析仪3. 噪声发生器4. 信号线5. 电脑6. 实验室噪声环境四、实验步骤1. 准备实验仪器和材料，确保声级计、频谱分析仪等设备正常工作。
2. 将声级计放置在实验环境中，调整距离和角度，使声级计能够准确测量噪声。
3. 打开噪声发生器，产生不同频率和强度的噪声信号。
4. 使用声级计测量噪声信号，记录数据。
5. 使用频谱分析仪分析噪声信号的频率特性，绘制频谱图。
6. 根据实验数据，分析噪声的强度、频率、时间等特性。
7. 将实验数据整理成表格和图表，撰写实验报告。
五、实验结果与分析1. 噪声强度通过声级计测量，实验环境中的噪声强度为70dB。
根据我国相关标准，该噪声强度属于中等水平。
2. 噪声频率特性通过频谱分析仪分析，实验环境中的噪声主要分布在100Hz至1000Hz之间，属于中高频噪声。
3. 噪声时间特性实验过程中，噪声信号的持续时间较长，表明噪声源持续产生噪声。
六、实验结论1. 实验验证了噪声检测的基本原理和方法，为噪声控制提供了依据。
2. 实验结果表明，实验环境中的噪声强度为70dB，属于中等水平；噪声频率主要分布在100Hz至1000Hz之间，属于中高频噪声。
3. 针对实验环境中的噪声问题，可采取以下措施进行控制：（1）加强噪声源的管理，降低噪声强度；（2）采取隔音、吸音等措施，减少噪声传播；（3）加强员工噪声防护意识，提高噪声防护措施。
一、实验背景白噪声是一种具有平坦频谱特性的噪声，其功率谱密度在所有频率范围内均相等。
白噪声在信号处理、通信、噪声控制等领域具有广泛的应用。
本实验旨在通过搭建实验装置，产生白噪声，并对其进行测量和分析。
二、实验目的1. 了解白噪声的产生原理；2. 掌握白噪声的产生方法；3. 学习白噪声的测量方法；4. 分析白噪声的特性。
三、实验原理白噪声的产生原理是通过随机信号源产生具有平坦频谱特性的噪声。
在实验中，我们可以通过以下方法产生白噪声：1. 采用随机噪声发生器，将随机信号经过滤波器处理后，得到具有平坦频谱特性的白噪声；2. 利用数字信号处理技术，通过随机信号生成算法产生白噪声。
四、实验仪器与设备1. 随机噪声发生器；2. 滤波器；3. 信号分析仪；4. 示波器；5. 数据采集卡；6. 计算机。
五、实验步骤1. 连接实验装置，将随机噪声发生器的输出信号输入滤波器；2. 调整滤波器参数，使滤波器输出信号具有平坦频谱特性；3. 将滤波器输出信号输入信号分析仪，进行频谱分析；4. 使用示波器观察白噪声的波形；5. 使用数据采集卡采集白噪声信号，进行进一步分析。
六、实验结果与分析1. 频谱分析通过信号分析仪对白噪声进行频谱分析，得到白噪声的功率谱密度。
从分析结果可以看出，白噪声的功率谱密度在所有频率范围内均相等，符合白噪声的特性。
2. 波形观察使用示波器观察白噪声的波形，可以看到白噪声的波形具有随机性，无明显规律。
3. 数据分析使用数据采集卡采集白噪声信号，进行进一步分析。
通过分析白噪声的时域特性、频域特性等，可以进一步了解白噪声的特性。
七、实验结论1. 成功搭建了白噪声产生实验装置，并产生了具有平坦频谱特性的白噪声；2. 掌握了白噪声的产生方法、测量方法和特性分析；3. 为后续白噪声在信号处理、通信、噪声控制等领域的应用奠定了基础。
八、实验总结本实验通过对白噪声的产生、测量和分析，使我们了解了白噪声的特性及其应用。
白噪声测试一、 实验目的⑴ 了解白噪声信号的特性，包括均值（数学期望）、均方值、方差、相关函数、概率密度、频谱及功率谱密度等。
⑵ 掌握白噪声信号的分析方法。
二、 实验原理所谓白噪声是指它的概率统计特性服从某种分布而它的功率谱密度又是均匀的。
确切的说，白噪声只是一种理想化的模型，因为实际的噪声功率谱密度不可能具有无限宽的带宽，否则它的平均功率将是无限大，是物理上不可实现的。
然而白噪声在数学处理上比较方便，所以它在通信及电子工程系统的分析中有十分重要的作用。
一般地说，只要噪声的功率谱密度的宽度远大于它所作用的系统的带宽，并且在系统的带内，它的功率谱密度基本上是常数，就可以作为白噪声处理了。
白噪声的功率谱密度为：2)(0N f S n =其中0N 为单边功率谱密度。
白噪声的自相关函数为：)(2τδτN R =）（ 白噪声的自相关函数是位于τ=0处、强度为2N 的冲击函数。
这表明白噪声在任何两个不同的瞬间的取值是不相关的。
同时也意味着白噪声能随时间无限快的变化，因为它的带宽是无限宽的。
下面我们给出几种分布的白噪声。
随机过程的几种分布 前人已证明，要产生一个服从某种分布的随机数，可以先求出其分布函数的反函数的解析式，再将一个在[0，1]区间内的均匀分布的随机数的值代入其中，就可以计算出服从某种分布的随机数。
下面我们就求解这些随机数。
[0，1]区间均匀分布随机信号的产生： 采用混合同余法产生[0，1]区间的均匀分布随机数。
混合同余法产生随机数的递推公式为：c ay y n n +=+1 n=0,1,2……My x nn =n=1,2,3…… 由上式的出如下实用算法：][1M cax M c ax x n n n +-+=+My x 00= 其中：k M 2=，其中k 为计算几种数字尾部的字长 14+=t a ，t 为任意选定的正整数 0y ，为任意非负整数c ，为奇数Matlab 语言中的rand （）函数是服从[0，1]均匀分布的，所以在以后的实验中如果用到均匀分布的随机数，我们统一使用rand()函数。
正态分布（高斯分布）随机信号的产生： 高斯分布的密度函数为：)2exp(21)(2x x f -=π采用变换法产生正态分布随机数，若1R 、2R 示[0，1]均匀分布随机数，则有正态分布随机数：212cos ln 2R R πξ-= 212sin ln 2R R πη-= 指数分布随机信号的产生：指数分布的密度函数为：x e x f αα-=*)( 当x>0时，当x ≤0时 f(x)=0，其中α>0它的反函数（指数分布随机数）为：)1ln(1)(1r r F x --==-α其中r 为[0，1]区间均匀分布的随机数。
三、 实验内容与结果1.产生五种概率分布的信号Matlab 程序：%生成各种分布的随机数x1=unifrnd(-1,1,1,1024);%生成长度为1024的均匀分布x2=normrnd(0,1,1,1024);%生成长度为1024的正态分布x3=exprnd(1,1,1024);%生成长度为1024的指数分布均值为零x4=raylrnd(1,1,1024);%生成长度为1024的瑞利分布x5=chi2rnd(1,1,1024);%生成长度为1024的卡方分布%时域特性曲线：figure;subplot(3,2,1),plot(1:1024,x1);grid on;title('均匀分布');xlabel('时间（t）');ylabel('幅度');axis([0 1024 -2 2 ]); subplot(3,2,2),plot(1:1024,x2);grid on;title('正态分布');xlabel('时间（t）');ylabel('幅度');axis([0 1024 -2 2 ]); subplot(3,2,3),plot(1:1024,x3);grid on;title('指数分布');xlabel('时间（t）');ylabel('幅度');axis([0 1024 -1 5 ]); subplot(3,2,4),plot(1:1024,x4);grid on;title('瑞利分布');xlabel('时间（t）');ylabel('幅度');axis([0 1024 -1 4 ]); subplot(3,2,5),plot(1:1024,x5);grid on;title('卡方分布');xlabel('时间（t）');ylabel('幅度');axis([0 1024 -1 5 ]);2.均值：均值E[x(t)]表示集合平均值或数学期望值。
基于随机过程的各态历经性，可用时间间隔t内的幅值平均值表示：均值表达了信号变化的中心趋势，或称之为直流分量。
在MATLAB中，可以用mean()函数来计算。
%求各种分布的均值figure;m1=mean(x1);m2=mean(x2);m3=mean(x3);m4=mean(x4);m5=mean(x5);subplot(3,2,1),plot(1:1024,m1);title('均匀分布均值');xlabel('时间（t）');ylabel('幅度');axis([0 1024 -2 2]); subplot(3,2,2),plot(1:1024,m2);title('高斯分布均值');xlabel('时间（t）');ylabel('幅度');axis([0 1024 -2 2]); subplot(3,2,3),plot(1:1024,m3);title('指数分布均值');xlabel('时间（t）');ylabel('幅度');axis([0 1024 -2 2]); subplot(3,2,4),plot(1:1024,m4);title('瑞利分布均值');xlabel('时间（t）');ylabel('幅度');axis([0 1024 -2 2]); subplot(3,2,5),plot(1:1024,m5);title('卡方分布均值');xlabel('时间（t）');ylabel('幅度');axis([0 1024 -2 2]);3.方差：随机过程的方差函数描述了随机过程所有样本函数在t时刻的函数值相对于其数学期望的偏离程度。
定义：其中σ(t)是随机过程的标准差。
当随即过程表征的是接收机输出端的噪声电压时，σ2(t)表示小号在单位电阻上的瞬时交流功率统计平均值，而σ(t)表示噪声电压相对于电压统计平均值的交流分量。
在MATLAB中，可以用std()函数计算出标准差σ(t)，再平方就可以得到方差。
%求各种分布的方差figure;v1=var(x1);v2=var(x2);v3=var(x3);v4=var(x4);v5=var(x5);subplot(3,2,1),plot(1:1024,v1);grid on;title('均匀分布方差');xlabel('时间（t）');ylabel('幅度'); subplot(3,2,2),plot(1:1024,v2);grid on;title('高斯分布方差');xlabel('时间（t）');ylabel('幅度'); subplot(3,2,3),plot(1:1024,v3);grid on;title('指数分布方差');xlabel('时间（t）');ylabel('幅度'); subplot(3,2,4),plot(1:1024,v4);grid on;title('瑞利分布方差');xlabel('时间（t）');ylabel('幅度'); subplot(3,2,5),plot(1:1024,v5);grid on;title('卡方分布方差');xlabel('时间（t）');ylabel('幅度');4.自相关：信号的相关性是指客观事物变化量之间的相依关系。
对于平稳随机过程x(t)和y(t)在两个不同时刻t和t+τ的起伏值的关联程度，可以用相关函数表示。
在离散情况下，信号x(n)和y(n)的相关函数定义为：随机信号的自相关函数表示波形自身不同时刻的相似程度。
与波形分析、频谱分析相比，它具有能够在强噪声干扰情况下准确地识别信号周期的特点。
%求各种分布的自相关函数figure;title('自相关函数图');[x_c1,lags]=xcorr(x1,200,'unbiased');[x_c2,lags]=xcorr(x2,200,'unbiased');[x_c3,lags]=xcorr(x3,200,'unbiased'); [x_c4,lags]=xcorr(x4,200,'unbiased');[x_c5,lags]=xcorr(x5,200,'unbiased');subplot(3,2,1),plot(lags,x_c1);grid on;title('均匀分布自相关');subplot(3,2,2),plot(lags,x_c2);grid on;title('正态分布自相关');subplot(3,2,3),plot(lags,x_c3);grid on;title('指数分布自相关');subplot(3,2,4),plot(lags,x_c4);grid on;title('瑞利分布自相关');subplot(3,2,5),plot(lags,x_c5);grid on;title('卡方分布自相关');5.概率密度函数：一维分布函数为：若F x (x 1;t 1)对x 1的一阶偏导存在，则一维概率密度为：在MATLAB 中，可以用ksdensity()函数来计算一维概率密度。
