系统建模与仿真 第四章

《建模与仿真》教学大纲课程名称：建模与仿真课程代码：INDE2038课程性质：专业选修课程学分/学时：2学分/36学时开课学期：第七学期适用专业：工业工程先修课程：概率统计、C语言程序设计后续课程：毕业设计开课单位：机电工程学院课程负责人：大纲执笔人：杨宏兵大纲审核人：一、课程性质和教学目标《建模与仿真》是面向工程实际的应用型课程，是工业工程系的专业课程之一。

学生通过本课程的学习能够初步运用仿真技术来发现生产系统中的关键问题，并通过改进措施的实现，提高生产能力和生产效率。

本课程的教学目标是培养学生的设计能力、创新能力和工程意识。

课程以制造型生产企业为核心，通过理论教学和实践环节相结合，阐述了离散事件系统建模与仿真技术在生产企业分析中的基本原理和方法。

其内容涉及计算机仿真技术在生产系统分析中的作用和原理、仿真软件的介绍，重点介绍排队系统、库存系统、加工系统以及输入、输出数据分析。

本课程的目的是要求学生通过学习、课堂教育和上机训练，能了解如何运用计算机仿真技术模拟生产系统的布置和调度管理；并熟悉和掌握计算机仿真软件的基本操作和能够实现的功能；使学生了解计算机仿真的基本步骤。

二、课程教学方法1、启发式课堂讨论针对关键知识点、典型题和难题，通过教师提问，鼓励学生回答问题或请到讲台前做题，并请其他学生评判或提出不同的答案或不同的解决方法。

目的是加强学生自主学习的能力和判断能力，培养主动思考的习惯，启发学生的探索精神。

2、重视在教学中加强知识演进的逻辑规律的讲解提高学生的逻辑思维能力，培养学生分析问题、解决问题的能力。

3、加强计算机辅助设计、分析将Flexsim仿真软件引入教学中。

应用计算机辅助设计、分析，能方便的改变系统结构参数，认识复杂系统的动态响应。

三、课程教学内容及学时分配第一章概论（2课时）教学目的：了解系统仿真技术的发展历史；掌握系统仿真技术的特点；理解系统仿真的应用；掌握系统仿真的优势与局限性；熟悉系统仿真的相关技术；了解系统仿真的研究热点和发展方向；教学重点：系统仿真的应用；系统仿真的优势与局限性；系统仿真的相关技术；教学难点：系统仿真的应用；第二章系统仿真基本知识（6课时）教学目的：了解生产系统的基本特征；理解掌握系统、系统模型、系统仿真等建模与仿真相关的基本概念；了解系统仿真的类型；理解离散系统与连续系统的区别；熟悉生产系统建模的方法与仿真研究的步骤；深入理解排队论的基本概念，熟悉排队系统的组成与排队模型的分类，掌握到达模式与服务机构刻画的参数，熟悉排队规则与队列的度量；熟悉几种常用的到达时间间隔和服务实践的理论分布（定长分布、泊松分布、埃尔朗分布、正态分布等）；掌握M/M/1排队系统与M/M/C排队系统的分析；掌握库存系统模型；熟悉库存系统；掌握库存系统模型；熟悉库存系统仿真及仿真结果分析；教学重点：系统、系统模型、系统仿真等建模与仿真相关的基本概念；离散系统与连续系统的区别；生产系统建模的方法与仿真研究的步骤；排队论的基本概念，排队系统的组成与排队模型的分类；几种常用的到达时间间隔和服务实践的理论分布（定长分布、泊松分布、埃尔朗分布、正态分布等）；M/M/1排队系统与M/M/C排队系统的分析；库存系统仿真方法；教学难点：系统、系统模型、系统仿真等建模与仿真相关的基本概念；离散系统与连续系统的区别；排队论的基本概念；M/M/1排队系统与M/M/C排队系统的分析；库存系统仿真；第三章随机数与随机变量（3课时）教学目的：理解掌握随机变量（离散、连续），以及连续随机变量的密度函数的概念；掌握随机变量的数字特征；理解掌握随机数的概念，熟悉产生连续均匀分布随机数的几种方法，掌握计算机产生随机数的方法；熟悉随机数的统计检验；掌握各种离散分布随机数的产生方法；熟悉非均匀连续分布随机数及其产生方法。

系统建模与仿真课程设计一、课程目标知识目标：1. 让学生理解系统建模与仿真的基本概念，掌握建模与仿真的基本原理；2. 使学生掌握运用数学模型描述实际问题的方法，提高解决实际问题的能力；3. 帮助学生了解不同类型的建模与仿真方法，并能够根据实际问题选择合适的建模与仿真方法。

技能目标：1. 培养学生运用计算机软件进行建模与仿真的操作能力；2. 提高学生分析问题、解决问题的能力，使学生能够独立完成简单的系统建模与仿真实验；3. 培养学生的团队协作能力，能够与他人合作完成复杂的系统建模与仿真项目。

情感态度价值观目标：1. 激发学生对系统建模与仿真的兴趣，培养学生主动探索、勇于创新的科学精神；2. 培养学生具备严谨、求实的学术态度，提高学生的学术素养；3. 引导学生关注建模与仿真在工程技术领域的应用，增强学生的社会责任感和使命感。

分析课程性质、学生特点和教学要求，本课程旨在通过理论教学与实践操作相结合，使学生在掌握基本知识的基础上，提高实际操作能力。

课程目标分解为具体的学习成果，以便后续的教学设计和评估。

通过本课程的学习，学生将能够运用所学知识解决实际问题，为未来的学术研究和职业发展打下坚实基础。

二、教学内容1. 系统建模与仿真基本概念：包括系统、模型、仿真的定义及其相互关系，介绍建模与仿真的发展历程；2. 建模与仿真原理：讲解建模与仿真的基本原理，如相似性原理、逼真度原理等；3. 数学模型构建：介绍常用的数学模型及其构建方法，如差分方程、微分方程等；4. 建模与仿真方法：分析不同类型的建模与仿真方法，如连续系统仿真、离散事件仿真等；5. 计算机软件应用：介绍常用的建模与仿真软件，如MATLAB、AnyLogic 等，并进行实际操作演示；6. 系统建模与仿真实践：结合实际案例，指导学生运用所学知识进行系统建模与仿真实验；7. 教学内容安排与进度：按照教材章节顺序，制定详细的教学大纲，明确各章节的教学内容和进度。

第四章离散事件系统仿真方法1d第4章离散事件系统仿真方法4.1离散事件系统仿真一般概念4.1.1 一般概念离散事件系统：系统中的状态只在离散时间点上发生变化，而且这些离散时间点一般是不确定的。

系统状态是离散变化的，而引发状态变化的事件是随机发生的，因此这类系统的模型很难用数学方程来描述。

随着系统科学和管理科学的不断发展及其在军事、航空航天、CIMS和国民经济各领域中应用的不断深入，逐步形成一些与连续系统不同的建模方法：流程图和网络图。

离散事件系统建模与仿真的基本概念：⑴ 实体：是描述系统的三（四）要素之一，是系统中可单独辨识和刻画的构成要素。

如：工厂中的机器，商店中的服务员，生产线上的工件，道路上的车辆等。

从仿真角度看，实际系统就是由相互间存在一定关系的实体集合组成的，实体间的相互联系和作用产生系统特定的行为。

实体可分为两大类：临时实体和永久实体临时实体――在系统中只存在一段时间的实体。

一般是按一定规律有系统外部到达系统，在系统中接受永久实体的作用，按照一定的流程通过系统，最后离开系统。

临时实体存在一段后即自行消失，消失有时是指实体从屋里意义上退出了系统的边界或自身不存在了；有时仅是逻辑意义上的取消，意味着不必再予以考虑。

如：进入商店的顾客、路口的车辆、生产线上的工件、进入防空火力网的飞机、停车场的汽车等。

永久实体――永久驻留在系统中的实体。

是系统产生功能的必要条件。

系统要对临时实体产生作用，就必须有永久实体的活动，也就d必须有永久实体。

可以说临时实体与永久实体共同完成了某项活动，永久实体作为活动的资源而被占用，如：理发店中的理发员、生产线上的加工装配机械、路口的信号灯等。

属性和行为相同或相近的实体可以用类来描述，这样可以简化系统的组成和关系。

如：理发店服务系统可以看成是由“服务员”和“顾客”两类实体组成的，两类实体之间存在服务与被服务的关系。

⑵ 属性是实体特征的描述，一般是系统所拥有的全部特征的一个子集，用特征参数或变量表示。

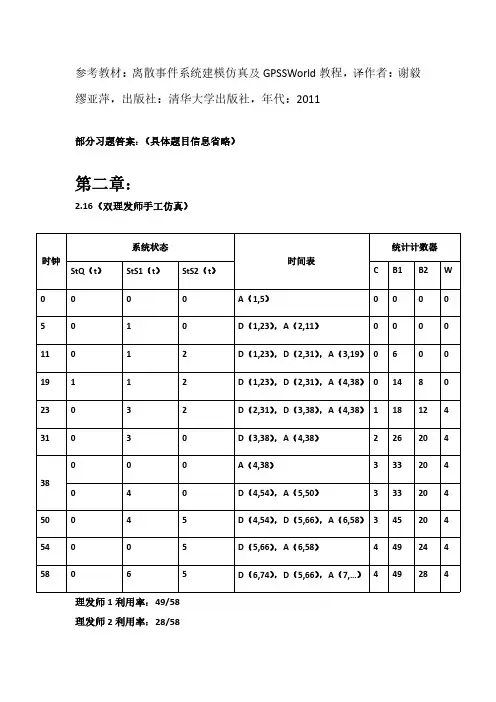
参考教材：离散事件系统建模仿真及GPSSWorld 教程，译作者：谢毅缪亚萍，出版社：清华大学出版社，年代：2011部分习题答案：（具体题目信息省略）第二章：2.16（双理发师手工仿真）理发师1利用率：49/58理发师2利用率：28/58时钟系统状态时间表统计计数器StQ （t ）StS1（t ）StS2（t ）C B1B2W 0000A （1,5）00005010D （1,23），A （2,11）00011012D （1,23），D （2,31），A （3,19）060019112D （1,23），D （2,31），A （4,38）0148023032D （2,31），D （3,38），A （4,38）11812431030D （3,38），A （4,38）2262043800A （4,38）333204040D （4,54），A （5,50）33320450045D （4,54），D （5,66），A （6,58）34520454005D （5,66），A （6,58）4492445865D （6,74），D （5,66），A （7,…）449284平均等待时间：4/6（min）第三章：3.3（货物出库）GENERATE10,5 TERMINATE10 GENERATE15 TERMINATE20 GENERATE30,10 TERMINATE50START20003.4（零件加工）GENERATE20,5ADD1QUEUE Q_ASEIZE ADEPART Q_AADVANCE16,5RELEASE AQUEUE Q_BSEIZE BDEPART Q_BADVANCE15,10RELEASE BQUEUE Q_CSEIZE CDEPART Q_CADVANCE10,2RELEASE C TRANSFER0.05,ADD2,ADD1ADD2TERMINATEGENERATE60TERMINATE1START40（仿真4个小时）若为生产200个合格零件，则ADD2改为：ADD2TERMINATE1START200（仿真4个小时）3.6（加工中心）S_A STORAGE2S_B STORAGE1S_C STORAGE3S_D STORAGE5GENERATE20,10QUEUE Q_AENTER S_ADEPART Q_AADVANCE30,15LEAVE S_ATRANSFER0.6,ADDC,ADDBADDC ENTER S_CADVANCE70,20LEAVE S_CTRANSFER,ADDDADDB ENTER S_BADVANCE20,10LEAVE S_BTRANSFER0.2,ADDD,ADDC ADDD ENTER S_DADVANCE90,30LEAVE S_DTERMINATEGENERATE60TERMINATE1START1003.7（汽车清洗店，顾客有偏好）注：可用BOTH或是ALL模式，但是相对比较复杂，可用SELECT，实现更简单。

了解MATLABSimulink进行系统建模与仿真MATLAB Simulink是一款功能强大的工具，专门用于系统建模和仿真。

它可以帮助工程师和科研人员设计复杂的系统、开展仿真分析，并支持快速原型设计和自动生成可执行代码。

本文将详细介绍MATLAB Simulink的基本概念、系统建模与仿真流程，以及其在各个领域中的应用。

第一章：MATLAB Simulink简介MATLAB Simulink是MathWorks公司开发的一款图形化建模和仿真环境。

它包含了一系列模块，可以通过简单地拖拽和连接来模拟和分析复杂的系统。

Simulink中的模块代表不同的系统组件，例如传感器、执行器、控制器等。

用户可以通过连接这些模块来构建整个系统，并通过仿真运行模型以评估系统的性能。

第二章：系统建模基础系统建模是使用Simulink进行系统设计的关键步骤。

在建模之前，需要明确系统的输入、输出和所涉及的物理量。

Simulink提供了广泛的模块库，包括数学运算、信号处理、控制等，这些模块可以方便地应用到系统中。

用户可以选择合适的模块，并通过线连接它们来形成系统结构。

此外，Simulink还支持用户自定义模块，以满足特定的需求。

第三章：MATLAB与Simulink的联合应用MATLAB和Simulink是密切相关的工具，它们可以互相配合使用。

MATLAB提供了强大的数学计算和数据分析功能，可以用于生成仿真所需的输入信号，以及分析仿真结果。

同时，Simulink也可以调用MATLAB代码，用户可以在模型中插入MATLAB函数块，以实现更复杂的计算和控制逻辑。

第四章：系统仿真与验证系统仿真是利用Simulink来验证系统设计的重要步骤。

通过设置仿真参数和初始条件，用户可以运行模型来模拟系统的行为。

仿真可以包括不同的输入场景和工况，以验证系统在不同条件下的性能和稳定性。

Simulink提供了丰富的仿真分析工具，例如波形显示器、频谱分析等，可以帮助用户分析仿真结果并进行必要的调整。

《系统建模与仿真》课程教学大纲一、课程基本信息课程编号：0904071课程中文名称：系统建模与仿真课程英文名称：System Modeling & Simulation课程性质：专业选修课程考核方式：考查开课专业：自动化、测控技术与仪器、电气工程及其自动化、探测制导与控制技术、生物医学工程开课学期：7总学时：24 （其中理论24学时，实验0学时）总学分：1.5二、课程目的《系统建摸与仿真》是测控技术与仪器等专业学生的一门选修课。

《系统建摸与仿真》课程以实验建摸方法为主要内容，包括经典实验建摸和以平稳随机过程理论为基础的现代实验建摸方法。

课程目的和任务：为本科高年级学生继续深造、开阔知识面，开设本课程；通过学习，使测控技术与仪器等的本科生掌握《系统建摸与仿真》基础理论、实验建摸基本方法，为今后从事系统建摸等工作、学习自适应控制等奠定扎实的基础。

三、教学基本要求（含素质教育与创新能力培养的要求）本课程要求学生有较好的“自动控制理论”基础和“线性代数”、“随机过程”等工程数学基础。

本课程将使学生掌握和了解以下主要基础理论和基本技能：干扰模型及随机过程；系统实验建摸基础；最小二乘法及其改进算法；模型阶次检验；闭环系统的参数辩识；神经网络建模；基于灰色系统理论的建模方法。

在教学中，注重培养学生的分析问题和解决问题的能力。

四、教学内容与学时分配第一章绪论（2学时）动态系统数学模型；建摸基本步骤与方法；连续时间系统的连续模型与离散模型。

第二章干扰模型及随机过程（4学时）干扰及干扰特性；随机过程基础；离散时间白噪声；工程中常用干扰随机模型；谱分解定理。

第三章系统建摸基础（2学时）过渡过程法；频率响应法与傅立叶分析；相关技术与频谱分析。

第四章最小二乘法（6学时）最小二乘算法；最小二乘估计的主要性质；最小二乘估计的递推算法；缓慢变化参数的估计方法；最小二乘法举例。

第五章最小二乘法改进算法（2学时）辅助变量法；广义最小二乘法；增广最小二乘法。

摘要ｆ利用ＥＤＡ软件平台对雷达系统的建模、仿真和设计方法进行研究，并建立一套相对完整的、具有统一框架的雷达系统软件库，可以为高效率地完成雷达系统的方案论证和性能评估。

以及新的算法研究提出新的思路，并提供了一条有效的途径，使雷达系统设计人员避免了重复劳动，可以将更大的精力投入到新课题的研究中去，从而实现系统设计的方便、高效和优化一本文基于工作站硬件平台和ＥＤＡ软件平台环境，在已有研究成果的基础上，对雷达系统软件库的进一步完善作了详细的探讨。

依照ＥＤＡ平台上ＳＰＷ建模的软件规范，本文在第三章讲述创建干扰信号库的相关工作，主要包括遮盖性干扰和欺骗性干扰的建模和仿真；第四章主要讲述建立数据处理库的工作，主要包括状态估计、机动目标跟踪和杂波环境下的目标跟踪方法的建模仿真，另外介绍使用ＳＰＷ的交互式仿真工具创建的一个对跟踪滤波进行动态演示的仿真界面。

本文的工作进一步完善了雷达系统软件库，为今后的雷达系统的建模、仿真和算法研究提供了方便并积累了、—一，—＿－’，一经验。

，关键词：ＥＤＡ雷达库建模与仿真数据处彰干扰ＡｂｓｔｒａｃｔＴｈｅｃｏｎｓｔｒｕｃｔｉｏｎｏｆａｎｉｎｔｅｇｒａｔｅｄｓｏｆｔｗａｒｅｌｉｂｒａｒｙｏｆｒａｄａｒｓｙｓｔｅｍｗｉｔｈｕｎｉｔｉｖｅｆｒａｍｅｐｒｏｖｉｄｅｓａｎｅｗｉｄｅａａｎｄａｎｅｆｆｅｃｔｉｖｅｗａｙｉｎｒｅａｌｉｚｉｎｇｔｈｅｒｅａｓｏｎｉｎｇｏｆｐｒｏｊｅｃｔａｎｄｔｈｅｐｅｒｆｏｒｍａｎｃｅｅｖａｌｕａｔｉｏｎ．Ｆｕｒｔｈｅｒｍｏｒｅ，ｔｈｅｒａｄａｒｓｙｓｔｅｍｄｅｓｉｇｎｅｒｓＣａｎｂｅｆｒｅｅｆｒｏｍｈａｒｄｍａｎｕａｌｐｒｏｇｒａｍｍｉｎｇａｎｄｒｅｐｅａｔｅｄｗｏｒｋＳＯｔｈａｔｍｏｒｅｍａｎｐｏｗｅｒｃａｌｌｂｅｄｅｖｏｔｅｄｔｏｎｅｗｒｅｓｅａｒｃｈ．Ｉｔｗｉｌｌａｃｈｉｅｖｅｓｕｃｈａｄｖａｎｔａｇｅｓａｓｔｈｅｃｏｎｖｅｎｉｅｎｃｅ，ｈｉｇｈ－ｅｆｆｉｃｉｅｎｃｙａｎｄｏｐｔｉｍｉｚａｔｉｏｎｉｎｔｈｅｄｅｓｉｇｎｏｆｒａｄａｒｓｙｓｔｅｍ．ＡｄｏｐｔｉｎｇｗｏｒｋｓｔａｔｉｏｎａｓｔｈｅｈａｒｄｗａｒｅｐｌａｔｆｏｒｍａｎｄＥＤＡｔｏｏｌａｓｔｈｅｓｏｆｔｗａｒｅｐｌａｔｆｏｒｍ，ａｎｄｂａｓｅｄｏｎｔｈｅａｃｈｉｅｖｅｍｅｎｔｔｈａｔｈａｖｅｂｅｅｎａｃｋｎｏｗｌｅｄｇｅｄ，ｔｈｉｓｐａｐｅｒｍａｉｎｌｙｆｏｃｕｓｅｓｏｎｔｈｅｆｎｒｔｈｅｒｐｅｒｆｅｃｔｉｏｎｏｆｔｈｅｓｏｆｔｗａｒｅｌｉｂｒａｒｙｏｆｒａｄａｒｓｙｓｔｅｍ．Ｃｈａｐｔｅｒ３ｉｓｍａｉｎｌｙｃｏｎｃｅｍｅｄｗｉｍｔｈｅｃｒｅａｔｉｏｎｏｆｔｈｅｍｏｄｅｌｓｆｏｒｐｒｏｄｕｃｉｎｇｊａｍｍｉｎｇｓｉｇｎａｌｓ．Ｃｈａｐｔｅｒ４ｉｎｔｒｏｄｕｃｅｓｔｈｅｃｒｅａｔｉｏｎａｎｄｓｉｍｕｌａｔｉｏｎｏｆｍｏｄｅｌｓｉｎｄａｔａｐｒｏｃｅｓｓｉｎｇｓｙｓｔｅｍ，ｉｎｃｌｕｄｉｎｇｔｈｅｍｅｔｈｏｄｏｆｅｓｔｉｍａｔｉｏｎ，ｔｒａｃｋｉｎｇｏｆｍａｎｅｕｖｅｒｉｎｇｔａｒｇｅｔａｎｄｔｒａｃｋｉｎｇｏｆｔａｒｇｅｔｓｉｎｃｏｍｐｌｅｘｅｎｖｉｒｏｎｍｅｎｔ，ａｎｄａｌｓｏｔｈｅＩＳＬｔｏｏｌｏｆＳＰＷｉＳｕｓｅｄｔｏｃｒｅａｔｅａｎｉｎｔｅｒｆａｃｅｏｆｄｙｎａｍｉｃｄｅｍｏｎｓｔｒａｔｉｏｎ．ＴｈｅＷＯｒｋｏｆｔｈｅｐａｐｅｒｅｘｔｅｎｄｅｄａｎｄｐｅｒｆｅｃｔｅｄｔｈｅｓｏｆｔｗａｒｅｌｉｂｒａｒｙｏｆｒａｄａｒｓｙｓｔｅｍ，ａｎｄｐｒｏｖｉｄｅｄａｎｄｃｏｎｖｅｎｉｅｎｃｅｔｏｆｕｒｔｈｅｒｓｔｕｄｉｅｓｉｎｔｈｅｍｏｄｅｌｌｉｎｇａｎｄｓｉｍｕｌａｔｉｏｎｏｆｔｈｅｅｘｐｅｒｉｅｎｃｅｒａｄａｒｓｙｓｔｅｍ．Ｋｅｙｗｏｒｄｓ：ＥＤＡｒａｄａｒｌｉｂｒａｒｙｍｏｄｅｌｌｉｎｇａｎｄｓｉｍｕｌａｔｉｏｎｄａｔａｐｒｏｃｅｓｓｉｎｇｊａｍｍｉｎｇ丑０５２６２＿堡创新性声明本人声明所呈交的论文是我个人在导师指导下进行的研究工作及取得的研究成果。

系统建模与仿真习题四及答案1. 假设函数，通过以下两种方法求该函数的laplace变换。

（1）F= int(f(t)*exp(-s*t),0,inf)计算（2）laplace(f)解：clc;clear;syms a t sf=(2*t^2+a*sin(t));F1=int(f*exp(-s*t),'t',0,inf)F2=laplace(2*t^2+a*sin(t))结果：F1 =limit(-(2*exp(-s*t)*s^4*t^2+2*exp(-s*t)*s^2*t^2+4*exp(-s*t)*s^3*t+4*s*t*exp(-s*t)+4*exp(-s*t)*s^2+4*exp(-s*t)+a*exp(-s*t)*s^3*cos(t)+a*exp(-s*t)*s^4*sin(t)-4-4*s^2-a*s^3)/s^3/(s^2+1),t = Inf) F2 =4/s^3+1/(s^2+1)*a2. 已知系统的传递函数为：求其输入为响应输出的解析解。

解：clc;clear;syms sG=(2*s^2+1)/((s+1)*(s+2));R=1/(s^2+1);y=ilaplace(G*R)结果y = -9/5*exp(-2*t)+3/10*cos(t)-1/10*sin(t)+3/2*exp(-t)3.考虑下面给出的多变量系统：（1）试求出系统的零点与极点；（2）绘制零极点图，判断系统的稳定性及系统是否为最小相位系统。

解：clc;clear;A=[-3 1 2 1;0 -4 -2 -1;1 2 -1 1;-1 -1 1 2]; B=[1 0;0 2;0 3;1 1];C=[1 2 2 -1;2 1 -1 2];D=[0 0;0 0];G=ss(A,B,C,D)[p,z] = pzmap(G)pzmap(G)结果：p =2.2361-2.2361-3.0000 + 0.0000i-3.0000 - 0.0000iz =-3.19830.6427系统不稳定，为非最小相位系统。