射频通信电路(01)

1.3 射频电路设计的特点1.3.1 分布参数集总参数元件：指一个独立的局域性元件，能够在一定的频率范围内提供特定的电路性能。

在低频电路设计中，可以把元件看作集总参数元件，认为元件的特性仅由二传手自身决定，元件的电磁场都集中在元件内部。

如电容、电阻、电感等；一个电容的容抗是由电容自身的特性决定，不会受周围元件的影响，如果把其他元件靠近这个电容器，其容抗不会随之产业化。

分布参数元件：指一个元件的特性延伸扩展到一定的空间范围内，不再局限于元件自身。

由于分布参数元件的电磁场分布在附近空间中，其特性要受周围环境的影响。

同一个元件，在低频电路设计中可以看作是集总参数元件，但是在射频电路设计中可能需要作为分布参数元件进行处理。

例如，一定长度的一段传输线，在低频电路中可以看作集总参数元件；在射频电路中，就必须看作分布参数元件。

分布电容（C D）：指在元件自身封装、元件之间、元件到接地平面和线路板布线间形成非期望电容。

分布电容与元件眯并联关系。

分布电感（L D）：指元件引脚、连线、线路板布线等形成的非期望电感。

分布电感通常与元件为串联关系。

**在低频电路设计中，通常忽略分布电容和分布电感对电路的影响。

随着电路工作频率的升高，在射频电路设计中必须同时考虑分布电容和分布电感的影响。

分布电容容抗计算公式：X D=1/ωC D=1/2πƒC D分布电感感抗计算公式：X D=ωL D=2πƒL D如：分布电容C D=1pF，其在ƒ=2kHz、2MHz和2GHz时的容抗：ƒ=2kHz时：X D=79.6MΩƒ=2MHz时：X D=79.6KΩƒ=2GHz时：X D=79.6Ω (接近与射频电路标准阻抗Z0=50Ω，并联影响明显)又如：分布电感L D=1nH，其在ƒ=2kHz、2MHz和2GHz时的感抗：ƒ=2kHz时：X D=12.6×10-6Ωƒ=2MHz时：X D=12.6×10-3Ωƒ=2GHz时：X D=12.6Ω (接近与射频电路标准阻抗Z0=50Ω，串联影响明显)1.3.2 λ/8设计准则随着工作波长变短，电路板上不同位置电压的相位差变大，因此必须考虑电压和电流空间分布的变化。

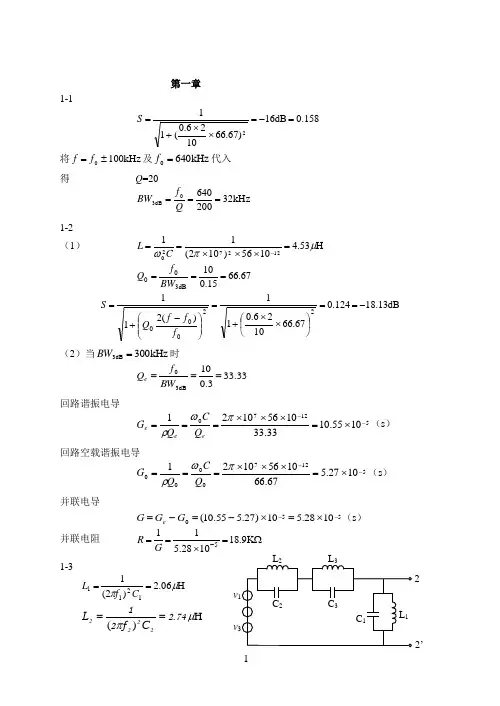
第一章 1-1158.0dB 16)67.661026.0(112=-=⨯⨯+=S将kHz 1000±=f f 及kHz 6400=f 代入 得 Q =20kHz322006400dB3===Qf BW1-2 （1） H 53.41056)102(11122720μπω=⨯⨯⨯==-CL67.6615.010dB300===BWf QdB 13.18124.067.661026.011)(21122000-==⎪⎭⎫⎝⎛⨯⨯+=⎪⎪⎭⎫⎝⎛-+=f f f Q S（2）当kHz 300dB 3=BW 时33.333.010dB30===BW f Q e回路谐振电导512701055.1033.3310561021--⨯=⨯⨯⨯===πωρee e Q C Q G （s ）回路空载谐振电导512700001027.567.6610561021--⨯=⨯⨯⨯===πωρQ C Q G （s ）并联电导5501028.510)27.555.10(--⨯=⨯-=-=G G G e （s ） 并联电阻 Ω=⨯==-K 9.181028.5115G R1-3H06.2)2(11211μπ==C f LH .)(μπ742212222==C f L2’2C 2 v 1v 3 L 2C 3L 3C 1L 1H 68.0)2(13233μπ==C f L1-4(a)LCf π210=(b)LCf π210=(c) )(21211L L C f +=π(d) 2121LCf π= 1221CL f π=2121221C C C C Lf +=π1-5由于回路为高Q ，所以回路谐振频率kHz 5.465103901030021216120=⨯⨯⨯=≈--ππLCf回路的损耗电阻Ω=⨯⨯⨯⨯==-4.1110010390105.4652630πωQ Lr回路的谐振阻抗Ω=+=K 114)1(20Q r R P考虑信号源内阻及负载后回路的总谐振阻抗为f 0x ff 0xff 2xff 1f 1 xff 2Ω==∑K 42||||L P S R R R R回路的有载Q 值为 372104203=⨯==∑Lf R Q e πρ通频带kHz56.12375.4650dB3===eQ f BW在kHz 10=∆f 处的选择性为：dB 47.5532.05.465203711211220-→=⎪⎭⎫ ⎝⎛⨯+=⎪⎪⎭⎫ ⎝⎛∆+=f f Q S e1-6回路特性阻抗 Ω=⨯⨯⨯==-159101001021211270ππρCf回路谐振阻抗 Ω=⨯==k 9.15100159Q R P ρ由SPLR P R R P 21221+=可求得336.02=P信号源内阻S R 折合到回路两端为：Ω===k 20)8.0(8.12221'P R R SS 负载电阻L R 折合到回路两端为：Ω===k 86.8)336.0(1222'P R R LL回路总谐振阻抗∑R 为ms226.0112.005.00629.086.812019.1511111''=++=++=++=∑LSPR R R R即Ω=∑k 43.4R回路有载Q 值为 8.271591043.43=⨯==∑ρR Q e回路的通频常 MHz 359.08.27101060dB 3=⨯==eQ f BW1-7由于eQ f BW 0dB 3= 所以回路有载5010201036dB30=⨯==BWf Q e回路谐振时的总电导为ms .020501015910211660=⨯⨯⨯⨯==-∑πωeLQG （即)Ω=∑K R 50回路的空载电导为ms .01010==LQ Gpω（即K R P 100=）信号源内阻折合到回路两端的电导值为ms .'010=-=∑p S G G G由于S S G P G 2'=，所以电容接入系数为：1.001.0101001.033'2=⇒=⨯==--P G G PSS回路总电容PF 15910159)1028.6(1162620=⨯⨯⨯==-LC ω∵接入系数2211C C CC P ==ωω所示PF15902==PC C11C C P =-，所以PF 1769.01591==C1-8PF 40'022=+=C C C因此回路的总电容为PF 3.18402040205''2121=+⨯+=+⋅+=∑C C C C C C i回路谐振频率rad/s 1026103.18108.01171260⨯=⨯⨯⨯==--∑LCω回路的空载谐振阻抗为Ω=⨯⨯⨯⨯===-k 9.20100108.0102667000LQ Q R P ωρ电阻0R 对回路的接入系数为31'211=+=C C C P考虑了i R 与0R 后的谐振阻抗∑R 为)ms(5.9k 17.05)31(1019.201111202Ω=++=++=∑R PR R R iP回路有载品质因数为281017.0130≈⨯⨯==-∑L R Q e ωρ回路通频常 1.48MHzrad/s .dB=⨯=⨯==77310930281026eQ BWω1-9设回路的空载∞=0Q ，设P 为电容接入系数211C C C P +=，由于有最大功率传输，∴ 333.02=→=P P R R L S∵ 100dB 3=→=e eQ Q f BW∵ L R Q e 0ω∑= →Ω==∑k 5.4||2P R R R L S可得： H 48.41010162105.4630μπω=⨯⨯⨯⨯==∑eQ R LPF221048.4)10162(11626202121=⨯⨯⨯⨯==+⋅=-πω∑LC C C C CPF 66333.0222===PC C ∑PF331=C1-10 4010251069dB300dB 3=⨯==→=BW f Q Q f BW e e,∵∑=C i e XR Q →25.14050==∑C X则必有25.12<C X ，由2R 与2C 组成的并联支路Q 大于4以上，则12>>Q ，此题可用高Q 计算。