下载文档原格式
课程设计报告书
其中载波信号C(t)用于搭载有用信号，其频率较高。
幅度调制信号g(t)含有有用信息，频率较低。
运用MATLAB 信号g(t)处理工具箱的有关函数可以对信号进行调制。
对于信号x(t),通信系统就可以有效而可靠的传输了。
在接收端，分析已调信号的频谱，进而对它进行解调，以恢复原调制信号。
解调器原理如图2所示。
对于调制解调的过程以及其中所包含的对于信号的频谱分析均可以通过MATLAB 的相关函数实现。
（2）频谱分析
当调制信号f(t)为确定信号时，已调信号的频谱为
()c c SDSB=1/2F -+1/2F(+)ωωωω. 双边带调幅频谱如图3所示。
图3 双边带调幅频谱
抑制载波的双边带调幅虽然节省了载波功率，但已调西那的频带宽度仍为调制信号的两倍，与常规双边带调幅时相同。
(3)功率谱密度分析 通信中，调制信号通常是平稳随机过程。
其功率谱密度与自相关函数之间是一对付氏变换关系。
这样就可以先找到信号的自相关函数，然后通过付氏变换来实现信号的功率谱密度。
MATLAB中的信号调制与解调技巧随着科技的不断发展，无线通信越来越成为人们生活中不可或缺的一部分。
在无线通信系统中，信号调制与解调技巧起到至关重要的作用。
而MATLAB作为一种强大的工具，能够帮助工程师们在信号调制与解调方面进行深入研究和实践。
一、信号调制的基本原理与方法信号调制是将原始信号（baseband signal）通过改变某些参数来转换为调制信号（modulated signal）。
常见的信号调制方法包括幅度调制（AM）、频率调制（FM）和相位调制（PM）。
1.1 幅度调制幅度调制是一种通过改变信号的振幅来调制信号的方法。
MATLAB提供了丰富的函数和工具箱，可以方便地进行幅度调制的模拟和分析。
例如，我们可以使用MATLAB中的ammod函数来模拟幅度调制过程。
首先，我们需要准备一个原始信号，可以是一个正弦波或任何其他波形。
然后，通过设置调制指数（modulation index）来改变振幅。
最后，使用ammod函数对原始信号进行调制，生成调制后的信号。
1.2 频率调制频率调制是一种通过改变信号的频率来实现调制的方法。
以调幅电台为例，电台信号的频率会随着音频信号的变化而改变。
在MATLAB中，我们可以利用fmmod函数来模拟频率调制过程。
类似于幅度调制，我们需要先准备一个原始信号。
然后，通过设置调制指数和载波频率来改变频率。
最后，使用fmmod函数对原始信号进行调制，生成调制后的信号。
1.3 相位调制相位调制是一种通过改变信号的相位来实现调制的方法。
在数字通信系统中，相位调制常用于传输和提取数字信息。
MATLAB中的pmmod函数可以方便地实现相位调制。
与前两种调制方法类似，我们需要先准备一个原始信号。
然后，设置调制指数和载波频率来改变相位。
最后，使用pmmod函数对原始信号进行调制，生成调制后的信号。
二、信号解调的基本原理与方法信号解调是将调制信号恢复为原始信号的过程。
解调方法通常与调制方法相对应，常见的解调方法包括幅度解调（AM）、频率解调（FM）和相位解调（PM）。
目录目录 (1)1．目标与内容 (2)2．设计方案 (2)2.1 调制方法 (2)2.2.1 滤波法 (2)2.2.2 相移法 (3)2.2 解调方法 (4)2.2.1 相干解调法 (4)2.2.2 载波插入法 (5)3.仿真与实验、分析 (5)参考文献 (9)单边带信号的调制与解调设计与仿真摘要： 单边带幅度调制由于占用更窄的频带和更高的频率利用率，在通信系统中得到更广泛的应用。
本文简单介绍了单边带调制解调的原理及设计方法，并以MATLAB 中的Simulink 为工具，对调制解调系统进行仿真，同时对其仿真结果进行分析。
关键字：单边带；调制；解调；Simulink ；仿真1．目标与内容随着通信业务的不断发展，频道拥挤的问题日益突出，占用较窄频带或能在同一频段内容纳更多用户的通信技术日渐受到了人们的重视。
语音信号的频率300 Hz ～3400Hz ，双边带信号的每一个边带都携带有语音信号的全部信息。
单边带幅度调制（Single Side Band Amplitude Modulation ）只传输频带幅度调制信号的一个边带，使用的带宽只有双边带调制信号的一半，具有更高的频率利用率，成为一种广泛使用的调制方式。
本文在介绍单边带调制与解调的方法后，利用MATLAB 的集成仿真环境Simulink 对单边带调制与解调系统进行了仿真。
2．设计方案2.1 调制方法2.2.1 滤波法单边带调制就是只传送双边带信号中的一个边带（上边带或下边带）。
产生单边带信号最直接、最常用的是滤波法，就是从双边带信号中滤出一个边带信号。
如图1所示，为滤波法模型的示意图。
()M t ()SSB s t 载波()c u t图1 滤波法调制模型基带信号与载波信号相乘得到双边带信号，双边带信号时域表达式如下双边带信号经过一个滤波器，可以得到单边带信号。
当取上边带时，单边带信号时域表达式为取下边带时，时域表达式为上下边带的选取决定于滤波器的选取。
实验二单边带幅度调制与解调实验目的：基于Matlab平台，通过对单边带和残留边带幅度调制过程的构建，理解信号频谱变化中的滤波处理，通过信道噪声的加入和解调实现，深刻理解一个基本通信过程中的信号变化情况。
实验内容：1.单边带调幅2.残留边带调幅3.幅度调制与解调的实现实验设备：笔记本电脑、Matlab7.1开发环境预备知识：1. Matlab基本操作2. 单边带调幅的数学运算过程3. 残留边带调幅的数学运算过程4. 噪声5. 信号频谱表示实验步骤：1. 单边带调幅1）。
打开Matlab，新建M文件；2）。
键入SSB程序，生成调制信号、载波信号，按照模拟调制的数学运算过程合成已调信号；3）。
编译程序，运行，获得各信号时域波形及其频谱；4）。
比较原理波形与实验结果，分析调制前后的信号幅值与频率变化；实验结果：（1）SSB调制信号；（2）该调制信号的功率谱密度；实验结论：SSB单边带抑制了一个边带，相对DSB减少了一半带宽，从而致使带宽效率翻番。
2. 残留边带调幅1）。
打开Matlab，新建M文件；2）。
完善残留边带调制VSB程序，生成调制信号、载波信号，按照模拟调制的数学运算过程合成已调信号；3）。
编译程序，运行，获得各信号时域波形及其频谱；4）。
比较原理波形与实验结果，分析调制前后的信号幅值与频率变化；5）。
比较实验步骤1 2的结果实验结果：（1）残留边带为0.2fm的VSB调制信号；（2）调制信号的功率谱密度实验结论：VSB残留边带只是显示出部分的宽带,功率谱与DSB没有太大的变化。
3. 幅度调制的解调1）。
打开Matlab，新建M文件；2）。
键入基本幅度调制AM、抑制载波幅度调制DSB以及单边带幅度调制SSB程序，生成调制信号、载波信号，在信道中引入各自经过带通滤波器后的窄带白噪声，进而完成解调程序；3）。
编译程序，运行，获得各信号时域波形及其频谱；4）。
比较原理波形与实验结果，分析调制前和被解调后的信号幅值与频率变化；实验结果：1）设A0=2，画出AM调制信号的相干解调后的信号波形；（2）设A0=1 ，画出DSB-SC调制信号的相干解调后的信号波形；（3）设A0=1 ，画出SSB调制信号的相干解调后的信号波形。
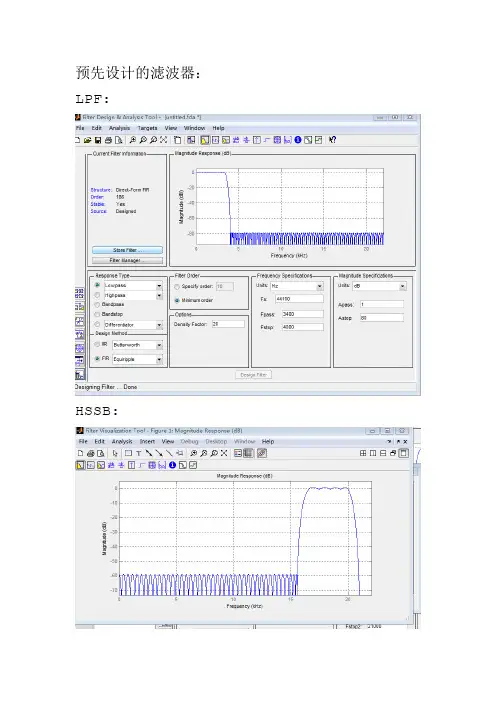
预先设计的滤波器：LPF:HSSB:1、调制程序function myfun()%采用滤波法产生SSB信号Fs=44100;%采样频率44100HZk1=input('k1=');%调制信号的参数k1fc=20000;%载波频率设定为20000HZ；Fc=2000;%调制信号的频率t=0:1/Fs:1;%采样时间m=k1*sin(2*pi*Fc*t);%产生调制信号subplot(2,1,1);plot(m);xlabel('时间t');ylabel('调制信号m（t）');%做出调制信号的图SDSB=m.*cos(2*pi*fc*t);%产生双边带调制信号SSB=conv(HSSB,SDSB);%让双边带信号通过预先设计好的HSSB带通滤波器);subplot(2,1,2);plot(SSB);xlabel('f');ylabel('已调信号SSB（t）');sound(SSB,44100);%通过声卡发送已调信号end2、在没有音频线传输信号时，模拟信道噪声程序SNR=40;%设定模拟信道信噪比SSB1=awgn(SSB,SNR);%加入模拟信道高斯白噪声3、解调程序function myfun()%采用相干解调解调SSB信号Fs=44100;%采样频率44100HZfc=20000;%载波频率设定为20000HZ；t=0:1/Fs:1;%采样时间SSB1=wavrecord(44101,44100);%通过声卡接收信号subplot(3,1,1);plot(SSB1);xlabel('t');ylabel('通过声卡的接收信号');%作图S=conv(SSB1,HSSB);%让接收到的信号通过带通滤波器subplot(3,1,2);plot(S);xlabel('t');ylabel('通过带通滤波器后的接收信号');%作图ii=1;S1=ones(1,44101);while ii<=44101S1(ii)=S(ii);ii=ii+1;end%通过循环截取前面的44101个数据点S2=conv(LPF,S1.*cos(2*pi*fc*t));%解调的核心程序subplot(3,1,3);plot(S2);xlabel('t');ylabel('解调后的信号');%作图end。
使用Matlab进行信号调制和解调技术信号调制和解调是通信系统中非常重要的环节，它们能够将原始信号转换为适合传输的调制信号，并在接收端将其恢复为原始信号。
Matlab是一种功能强大的工具，提供了丰富的信号处理函数和算法，可以方便地进行信号调制和解调的研究与实现。
本文将介绍如何使用Matlab进行信号调制和解调技术，并通过实例展示其在通信系统中的应用和效果。
一、调制技术概述调制技术是将需要传输的信息信号转换为载波信号的过程。
常见的调制技术包括幅度调制（AM）、频率调制（FM）和相位调制（PM）。
调制的目的是将低频信号转换为高频信号，使得信号能够在较长距离传输，并能够通过信道传输到接收端。
在Matlab中，可以使用内置函数如ammod、fmmod和pmmod来实现不同的调制技术。
以幅度调制为例，可以使用ammod函数来实现。
下面给出一个简单的幅度调制实例。
```matlabfs = 1000; % 采样频率t = 0:1/fs:1-1/fs; % 时间序列fc = 100; % 载波频率Ac = 1; % 载波幅度ym = sin(2*pi*10*t); % 原始信号ym_mod = ammod(ym, fc, fs, Ac); % 幅度调制```上述代码中，首先定义了采样频率fs、时间序列t、载波频率fc和载波幅度Ac。
然后，生成了一个原始信号ym，其中使用了sin函数生成了一个频率为10Hz的正弦波。
最后使用ammod函数对原始信号进行幅度调制，得到了调制后的信号ym_mod。
二、解调技术概述解调技术是将调制后的信号恢复为原始信号的过程。
解调技术主要包括幅度解调（AM）、频率解调（FM）和相位解调（PM）。
解调的目的是从调制信号中提取出原始信号，以实现信息的传输。
在Matlab中，可以使用内置函数如amdemod、fmdemod和pmdemod来实现不同的解调技术。
以幅度解调为例，可以使用amdemod函数来实现。
课程设计任务书学生姓名：吕义斌专业班级：电信1102班指导教师：桂林工作单位：武汉理工大学题目：信号分析处理课程设计－基于MATLAB的模拟信号单边带幅度调制（SSB）与解调分析初始条件：1.Matlab6.5以上版本软件；2.先修课程：通信原理等；要求完成的主要任务：（包括课程设计工作量及其技术要求，以及说明书撰写等具体要求）1、利用MATLAB中的simulink工具箱中的模块进行单边带幅度调制（SSB）与解调，观察波形变化；2、画出程序设计框图，编写程序代码，上机运行调试程序，记录实验结果（含计算结果和图表等），并对实验结果进行分析和总结；3、课程设计说明书按学校统一规范来撰写，具体包括：⑴目录；⑵理论分析；⑶程序设计；⑷程序运行结果及图表分析和总结；⑸课程设计的心得体会（至少800字，必须手写。
）；⑹参考文献（不少于5篇）。
时间安排：周一、周二查阅资料，了解设计内容；周三、周四程序设计，上机调试程序；周五、整理实验结果，撰写课程设计说明书。
指导教师签名：年月日系主任（或责任教师）签名：年月日目录1. 概述 (1)2. 设计方案 (1)2.1 SSB调制原理 (1)2.1.1 滤波法 (1)2.1.2 相移法 (2)2.2 解调原理 (4)2.2.1 相干解调 (4)2.2.2 2级单边带调制解调 (4)3. SSB调制与解调的MATLAB程序实现 (4)3.1 函数的使用 (4)3.2 MA TLAB程序实现 (5)3.3 模拟仿真结果分析 (9)4. SSB系统的Simulink仿真 (10)4.1 Simulink工作环境 (10)4.2 SSB信号调制 (11)4.2.1 调制模型构建与参数设置 (11)4.2.2 仿真结果及分析 (11)4.3 SSB相干解调 (14)4.3.1 相干解调模型构建与参数设置 (14)4.3.2 仿真结果及分析 (15)4.4 加入高斯噪声的SSB调制与解调 (17)4.4.1 模型构建 (17)4.4.2 仿真结果及分析 (18)5. 心得体会 (23)参考文献 (25)1. 概述本课程设计是实现SSB 的调制与相干解调，以及在不同噪声下对信道的影响。
基于matlab的ssb的调制与解调设计依据一、概述在通信领域中，调制与解调是一种重要的信号处理技术。
单边带调制（SSB）是一种常见的调制方式，它在频谱利用率和功率效率方面具有优势，因此被广泛应用于通信系统中。
为了实现SSB的调制与解调，需要设计相应的算法和实现方案。
而Matlab作为一种强大的工程软件，也被广泛用于数字信号处理领域。
本文将围绕基于Matlab的SSB调制与解调的设计依据展开阐述。
二、SSB调制的原理1. SSB调制的概念单边带调制（SSB），是将调制信号的频谱移到正频率轴或负频率轴上的其中一侧而不产生另一频谱的一种调制方式。
SSB调制有上下两种形式，分别称为上边带和下边带。
在实际应用中，常采用抑制载波的方式实现SSB调制。
2. SSB调制的数学表示对于一般的调制信号m(t)，经过SSB调制后得到的调制信号s(t)可表示为：s(t) = m(t)cos(2πfct) - jH[m(t)]sin(2πfct)其中，H[m(t)]为m(t)的希尔伯特变换。
三、SSB调制的设计依据1. 基带信号及滤波SSB调制的第一步是对基带信号进行处理，通常需要进行低通滤波以限制频谱范围。
Matlab提供了丰富的信号处理工具箱，可以方便地实现基带信号的生成和滤波处理。
2. 载波抑制和频谱转移在SSB调制中，需要实现对载波的抑制，从而得到单边带信号。
频谱转移可以通过Matlab中的频谱分析和变换函数来实现。
3. SSB调制系统的搭建基于Matlab，可以通过编写代码来搭建SSB调制系统，包括信号处理、频谱分析、滤波和调制等步骤。
四、SSB解调的原理1. SSB解调的概念SSB解调过程是对接收到的单边带信号进行处理，从而得到原始的基带信号。
解调过程中需要进行频谱转移和滤波，以还原原始信号。
2. SSB解调的数学表示对于接收到的SSB信号s(t)，经过解调后得到的解调信号m(t)可表示为：m(t) = s(t)cos(2πfct) - jH[s(t)]sin(2πfct)其中，H[s(t)]为s(t)的希尔伯特变换。
MATLAB中用M文件实现SSB解调一、课程设计目的本次课程设计是对通信原理课程理论教学和实验教学的综合和总结。
通过这次课程设计，使同学认识和理解通信系统，掌握信号是怎样经过发端处理、被送入信道、然后在接收端还原。
要求学生掌握通信原理的基本知识，运用所学的通信仿真的方法实现某种传输系统。
能够根据设计任务的具体要求，掌握软件设计、调试的具体方法、步骤和技巧。
对一个实际课题的软件设计有基本了解，拓展知识面，激发在此领域中继续学习和研究的兴趣，为学习后续课程做准备。
二、课程设计内容（1）熟悉MATLAB中M文件的使用方法，掌握SSB信号的解调原理，以此为基础用M文件编程实现SSB信号的解调。
（2）绘制出SSB信号解调前后在时域和频域中的波形，观察两者在解调前后的变化，通过对分析结果来加强对SSB信号解调原理的理解。
（3）对信号分别叠加大小不同的噪声后再进行解调，绘制出解调前后信号的时域和频域波形，比较未叠加噪声时和分别叠加大小噪声时解调信号的波形有何区别，借由所得结果来分析噪声对信号解调造成的影响。
（4）在老师的指导下，独立完成课程设计的全部内容，并按要求编写课程设计论文，文中能正确阐述和分析设计和实验结果。
三、设计原理1、 SSB解调原理在单边带信号的解调中，只需要对上、下边带的其中一个边带信号进行解调，就能够恢复原始信号。
这是因为双边带调制中上、下两个边带是完全对称的，它们所携带的信息相同，完全可以用一个边带来传输全部消息。
单边带解调通常采用相干解调的方式，它使用一个同步解调器，即由相乘器和低通滤波器组成。
在解调过程中，输入信号和噪声可以分别单独解调。
相干解调的原理框图如图a 所示：)(t S SSB )(1t S )(2t Sc(t)图a 相干解调原理框图此图表示单边带信号首先乘以一个同频同相的载波，再经过低通滤波器即可还原信号。
单边带信号的时域表达式为t t m t t m t S c c SSB ωωsin )(ˆ21cos )(21)( = )(t m 表示基带信号其中取“-”时为上边带，取“+”时为下边带。
乘上同频同相载波后得t t m t t m t m t t S t S c c c SSB ωωω2sin )(ˆ412cos )(41)(41cos )()(1 +== )(ˆt m表示)(t m 的希尔伯特变换 经低通滤波器可滤除2c ω的分量，所得解调输出为)(41)(2t m t S = 由此便可得到无失真的调制信号。
2、 SSB 解调的实现SSB 信号的产生在本次课程设计中，我选用频率为50Hz,初相位为0的余弦信号m 作为原始基带信号，在MATLAB 中表示为“m=cos(2*pi*50.*t);” ；设置载波信号c 为频率500Hz 的余弦信号，程序中表示为“fc=500; c=cos(2*pi*fc.*t);”。
在调制过程的实现中，通过语句“b=sin(2*pi*fc.*t); lssb=m.*c+imag(hilbert(m)).*b;”产生下边带信号。
接下来的解调过程主要就针对该下边带信号进行。
SSB 解调实现根据相干解调原理，在解调的实现中，我先用下边带调制信号乘以本地载波，再通过自己设计的低通滤波器滤除高频成分，如此便得到了解调后的信号。
相关的程序语句为：y=lssb.*c;[Y,y,dfl]=fft_seq(y,ts,df);Y=Y/fs;n_cutoff=floor(fl/dfl);H=zeros(size(f));H(1:n_cutoff)=2*ones(1,n_cutoff);H(length(f)-n_cutoff+1:length(f))=2*ones(1,n_cutoff);DEM=H.*Y;dem=real(ifft(DEM))*fs;在此段程序中，y 是下边带信号与本地载波相乘的结果，用数学表达式可以表示为t t m t t m t m t t lssb y c c c ωωω2sin )(ˆ412cos )(41)(41cos )( +== 根据此式可知，此低通滤波器的作用在于去除y 中包含的具有频率为c ω2的分量，滤波后就得到了基带信号。
Y 是对y 进行傅立叶变换求得的频谱函数。
通过“Y=Y/fs ”对结果进行缩放，用于满足显示要求和计算需要。
低通滤波器的设计是由“n_cutoff=floor(fl/dfl);”到“DEM=H.*Y;”之间的语句实现的，其中“fl ”表示低通滤波器的截止频率，混频信号y 中高于此频率的分量将被滤除，得到解调信号；而“DEM=H.*Y;”表示Y 与截止系数H 相乘后，其高频部分被滤去，所得结果DEM 即为过滤后的频谱函数，就是解调后信号的频谱。
最后再由“dem=real(ifft(DEM))*fs;”对DEM 进行傅立叶逆变换，取其实部，乘以采样频率后可得出滤波后的时域信号函数dem ，它就是解调后的信号。
另外要注意对采样频率fs 的选取。
由于MATLAB 仿真模拟信号是通过抽样来确定此信号的，所以能否通过抽样完全确定信号直接关系到仿真的成败。
我所设的载波频率为fc=500Hz ，根具抽样定理，要使得载波信号c 被所得到的抽样值完全确定，必须以T fc21≤秒的间隔对它进行等间隔抽样，即是fs ≥2fc 。
故fs 最小值应为2fc=1000Hz ，为了确保结果合理，我取fs=2500Hz。
其他一些参数设置为：信号保持时间t0=0.5s，滤波器截止频率fl=700Hz，频率分辨率df=0.1Hz。
在求频谱函数时，我调用了一个自己设定的函数“fft_seq”，它是对快速傅立叶变换函数fft的改进。
它通过提高频率分辨率，能更好地区分两个谱峰。
若设信号m的长度为T秒，则其频率分辨率为f∆＝1/T(Hz)。
因为输入计算机中的连续信号被转换成了离散的序列，而设其序列共有N个点，则两根谱线间的距离f∆＝fs/N，它也是频率分辨率的一种度量。
如果该式的f∆不够小，我们可以增加N来减小f∆。
而一种有效的方法是在离散序列后面补零，这不会破坏原来的信号。
函数“fft_seq”就是基于以上思想编成。
我在MATLAB中实现SSB解调的仿真就是基于以上的程序和参数设定，运行调用了plot函数的M文件，可以分别得出解调前后的频域与时域对比图，为了便于参照，将LSSB信号的时域与频域图也一同进行比较。
三者时域图比较结果如图b所示：图b 调制信号、LSSB信号、解调信号的时域对比图由图b可以看出，解调信号能够基本还原原始基带信号，只有少许失真，可见解调过程较为成功。
对于失真接问题接下来将会进行具体分析。
为了更好分析解调的结果，还必须将时域图与频域图进行比较，通过观察频域图能够更为直观的了解信号的频率分布，借此来讨论滤波器的作用特性。
三者的频域图比较如图c所示：图c调制信号、LSSB信号、解调信号的频域对比图由频域图可以明显地看出，下边带信号将基带信号的频谱向两侧进行了搬移，然后去除了其中上边带的那一半。
而解调后的频谱与基带信号在频率小于700Hz的范围内几乎没有区别，用肉眼很难观察出不同之处；解调信号在频率大于700Hz范围外的频谱已经被低通滤波器完全滤除，故没有波形，这就是解调信号与基带信号频谱差异最明显之处。
由于在理论上，解调过程可以完全恢复基带信号，但实际中仍然会产生少许失真，故失真的原因可以从参数的设置上入手找寻。
在解调过程中，相乘器是严格按照数学关系运算的，不会产生误差，失真的产生因该在低通滤波器环节。
为了探究低通滤波器的设置对解调的影响，我将滤波器的截止频率fl分别改为1000Hz和50Hz进行比较，根据结果来判断原因。
分量。
实际首先我选fl=1000Hz，它等于2fc，它应该无法滤除混频信号中的2c得出的时域和频域图结果如图d和图e：图d fl=1000Hz时的解调信号时域对比图图e fl=1000Hz时的解调信号频域对比图从时域比较图中可以明显看出解调信号严重失真，还保留着载波信号的频率变化；而频谱图中，解调信号频谱的两侧将近1000Hz处有两个高峰，可见解调信号频谱与基带信号频谱存在巨大差异。
原因很简单，低通滤波器的截止频率高于2fc，故无法滤除相乘器输出的混频信号 分量，完全没有起到低通滤波的作用，所以解调信号保留有高频分量，无y的高频2c法正确还原调制信号。
接下来将截止频率fl设为50Hz，观察在fl较低的情况下的解调输出结果。
此时，fl远远小于2fc，不存在无法滤除高频分量的问题，不会产生上一种情况的错误。
通过分析这种情况下的结果可以得出低截止频率对解调的影响。
在fl=50Hz时得出的时域和频域解调结果对比如图f和图g所示：图f fl=50Hz时解调信号时域对比图图g fl=50Hz时解调信号频域对比图由时域比较图中可以清晰地看出解调信号能够保持平滑的余弦波形，但幅度小了将近一倍，且两端的幅度明显小于中间。
由此可以估计出一种可能性：基带信号的一部分丢失了，解调信号只是原基带信号的一部分。
因此才会造成幅度下降的结果。
频谱对比图很好地验证了这种可能性。
观察发现解调信号的频谱被滤去频率大于50Hz的部分之后，虽然保持了原基带信号的主体部分，但两边的分量已经全部滤除。
这就是问题所在。
两边的分量也占据了一定的比重，滤除的越多，原基带信号损失的部分也越多，就如时域图中所示。
幅度减小的原因就在于此。
通过在fl=50Hz时对解调信号频域和时域的观察，可以得出结论：fl较低时，在滤ω分量的同时，也会连带去除基带信号中的一部分。
因此为了保全基带信号的去高频2c完整性，fl不宜过低。
ω分量无法滤除；而fl较低，又会使综上所述，截止频率fl过高时会导致高频2cω分量的情况得基带信号有部分被滤去。
经过调整分析，我认为fl应该在能够滤去2c下，尽可能高一点。
这样就能保证基带信号被滤去的部分减到最少。
所以开始所设的fl=700Hz是一个较为合适的值，解调结果也很接近基带信号。
实现解调还有一种方法，就是调用专用于SSB信号解调的函数ssbdemod(u,fc,fs)，此函数内部集成了解调过程，不需要自行再设置相乘器与滤波器。
为了与前一种方法对比，现简要用此函数来实现SSB的解调。
为了增强对比性，除了fl无需再设置外，其它的参数设置均与上一种方法相同：采样频率fs=2500Hz，信号保持时间t0=0.5s，频率分辨率df=0.1Hz，且调制信号不变。
在本程序中，实现调制过程使用语句“u=ssbmod(m,fc,fs);”，解调单边带信号则用“y=ssbdemod(u,fc,fs);”来实现。
运行本程序，所得基带信号、LSSB信号、解调信号的时域图对比情况如图h所示：图h 方法2中基带、LSSB、解调信号的时域对比图解调信号通过 MATLAB中函数ssbdemod()实现了解调并通过函数本身内设的低通滤波器，解调出了基带信号m(t)。
