当前位置：文档之家 › 1-4流体在圆管内流动阻力的计算

1-4流体在圆管内流动阻力的计算

  • 格式：ppt
  • 大小：935.00 KB
  • 文档页数：18

下载文档原格式

  / 18

合集下载

流体在管内的流动阻力

流体在管内的流动阻力

第四节流体在管内的流动阻力实际上理想流体是不存在的。

流体在流动过程中需要消耗能量来克服流动阻力，本节讨论流体流动阻力的产生、影响因素及其计算。

§1.4.1牛顿粘性定律与流体的粘度1、牛顿粘性定律设有间距很小的两平行板，两平板间充满液体(如图)。

下板固定，上板施加一平行于平板的切向力F，使上板作平行于下板的等速直线运动。

紧贴上板的液体层以与上板相同的速度流动，而紧贴固定板的液体层则静止不动。

两层平板之间液体的流速分布则是从上到下为由大到小的渐变。

此两板间的液体可看成为许多平行于平板的流体层，这种流动称为层流，而层与层之间存在着速度差，即各液层之间存在着相对运动。

运动较快的液层对与之相邻的运动较慢的液层作用着一个拖动其向运动方向前进的力；而与此同时，运动较慢的液层对其上运动较快的液层也作用着一个大小相等方向相反的力，从而阻碍较快的液层的运动。

这种运动着的流体内部相邻两流体层间的相互作用力称为流体的内摩擦力（粘滞力）。

流体流动时产生内摩擦力的这种特性称为粘性。

在上图中，若某层流体的速度为u，在其垂直距离为dy处的邻近流体层的速度为u+du，则du/dy表示速度沿法线方向上的变化率，称为速度梯度。

实验证明，内摩擦力F与两流体层间的接触面积S成正比，与速度梯度du/dy成正比。

即：F∝S·du/dy亦即：F=μS·du/dy剪应力τ：单位面积上的内摩擦力，即F/S, 单位N/㎡于是：τ=F/S=μ·du/dy——牛顿粘性定律μ为比例系数，称为粘性系数或动力粘度，简称粘度说明：①牛顿粘性定律可表达为剪应力与法向速度梯度成正比，与法向压力无关，流体的这一规律与固体表面的摩擦力的变化规律截然不同。

②牛顿粘性定律的使用条件：层流时的牛顿型流体。

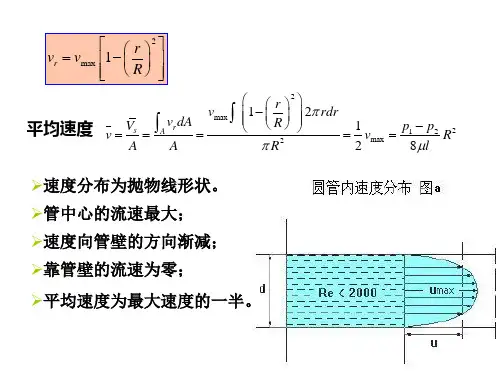
③根据此定律，粘性流体在管内的速度分布可以预示为：如图紧贴壁面的流体受壁面固体分子力的作用而处于静止状态，随着离壁距离的增加，流体的速度连续地增大，至管中心处速度达到最大。

流体阻力

流体阻力

1.4 流体流动现象
1.4.2 滞流与湍流的比较 ①流体质点运动的方式----基本特征
管内滞流时，流体质点沿管轴作有规则的平行运动，各质点 互不碰撞，互不干扰。 流体可以看作无数同心圆筒薄层一层套一层作同向平行运动。 管内湍流时，流体质点作不规则的杂乱运动，相互碰撞，产 生大大小小的漩涡。碰撞阻力＞＞黏性阻力 管内湍流时，流体质点在沿管轴流动的同时还伴着随机的 径向脉动，任一点处的速度大小和方向都随时变化。微观 上为不稳地流动，但宏观上可以当做稳定流动处理。
形体阻力：固体表面形状造成边界层分离而引起能量损耗
摩 擦 阻 力 流 体 绕 过 固 体 的 阻 力 （ 局 部 阻 力 ） 形 体 阻 力
流体在管径突然扩大或缩小，或流经直角、弯管、球体等情 况时，会发生倒流，引起流体与固体壁面发生分离现象，并 产生大量的旋涡，结果造成流体能量的损失。
1.4 流体流动现象
= d D
D
1.4 流体流动现象
2. 流动形态的判据---- Reynold’s number 雷诺数反映了流体流动的湍动程度，可以判断 流体的流动型态。 当Re≤2000，为滞流（层流）laminar flow Re≥4000，为湍流（紊流）turbulent flow Re≥10000时，为稳定的湍流。 2000＜Re＜4000，为过度流(transitional flow) 是一种不稳定的状态。
研究边界层的意义：
-速 度 梯 度 d u / d y 较 大 边 界 层 区 -速 主 流 区 度 梯 度 d u / d y ≈0
在边界层内，∵du/dy较大，∴内摩擦阻力也较大； 主流区内，du/dy≈0，内摩擦阻力也≈0，∴主流 区的流体可视为理想流体。 ∴粘性的影响限制在边界层内，并且传热和传质的阻力 也限制在边界层内，使实际流体的流动问题大大简化了

关于阻力计算的公式

关于阻力计算的公式

关于阻力计算的公式一、圆形直管内的流动阻力：1）计算水平圆管内阻力的一般公式—范宁（Fanning ）公式：22u d l f p ρ⋅⋅λ=∆①其中λ为摩擦系数，量纲为一；l 为管长；d 为管径；ρ为流体密度；u 为流速。

本式表明流体流动阻力Δp f 与流动管道长度呈正比；与管道直径呈反比，与流体动能ρu 2/2呈正比。

层流时摩擦系数有准确计算公式，是将式①和式②联立计算，完全靠理论推导方法得出。

公式如下：ρη=λu d 64由此式可见，圆形直管内流体层流流动时，摩擦系数与流体黏度呈正比，与管径、流速、流体密度呈反比。

湍流流动摩擦系数是根据实验得到的公式，最为常用是莫狄（Moody ）摩擦系数图。

2）层流时直圆管内的阻力计算公式—哈根-泊谡叶（Han gen-Poiseuille ）公式：2f lu 32p η=∆②由该式可见，层流时支管阻力Δp f 与管长l 、速度u 、黏度η的一次方成正比，与管径d 的平方呈反比。

二、局部阻力流体在管内流动时，还要受到管件、阀门等局部阻碍而增加的流动阻力，称为局部阻力。

它还包括由于流通截面的扩大或缩小而产生的阻力。

局部阻力可按式③计算：2u d l p 2e f ρλ=∆③或2u p 2f ρζ=∆④其中l e 为当量长度，即将局部阻力折合成相当长度的直管来计算；ζ成为局部阻力系数。

l e 和ζ都是由实验来确定的。

三、总阻力若将流体在管路中流动阻力归结为直管阻力和局部阻力之和，对于流体流动等直径管路，如果将局部阻力以当量长度表示，则阻力计算式为：g2u )d l l (g R h 2u )d l l (R p 2e f 2e f ∑+λ=∑=∑ρ∑+λ=∑ρ=∆或式中l —管路中直径为d 的直管长度，m;Σl e —管路上全部管件与阀门等的当量长度之和，m;u —流体流经管路的速度，m/s如果还有部分局部阻力必须用阻力系数表示，则阻力计算式为：g2u )d l l (g R h 2u )d l l (R p 2e f 2e f ζ∑+∑+λ=∑=∑ρζ∑+∑+λ=∑ρ=∆或式中Σζ—管路上部分管件和阀门等的阻力系数之和。

1.4 边界层和阻力公式

1.4 边界层和阻力公式
du dy 0, 0，
x 0
dp / dy 0, 认为是实际流体流动 , 产生流动阻力
u x u0，du dy 0， * 边界层外， y ， 看作是理想流体流动 , 无流动阻力
层流边界层 u∞ u∞ δ A x0 u∞
y 0、ux 0 * 壁面处，
湍流边界层
层流边界层 湍流边界层Biblioteka u 0.99uu∞
u∞
u∞
A
δ 层流内层 平板上的流动边界层
例：
x0
20C的空气以10m/s流过平板时，在距离平板前
缘100mm处，边界层厚度约为1.8mm
1、平板上流体的流动边界层 边界层意义：
流动阻力及速度梯度，主要集中在边界层内 边界层内， y ，u u
p：任意两点间的压力差
2、总阻力 直管阻力（粘滞力引起） 局部阻力（形体阻力） 总阻力=直管阻力+局部阻力
Pi2
FIC
Pi1
一、圆形直管内的阻力损失 1、范宁公式 公式推导： 稳态流动流体 作受力分析
F F F
P
G
Ff 0
压力差：FP ( p1 p2 ) A
重力：FG gpV cos gA( z1 z2 )
其中，n f ( Re )
Re： 1.1105 3.2 106时，n 1 7 u 0.82 （常用公式） umax
书P39 图1.4.12：给出算图，查取平均流速 坐标：
Re u Re,max umax
问题：求平均流速的方法
1、速度分布未知
2、速度分布已知
qV u S u 0.5umax （层流）
提出问题?
3、强化传递过程的流动条件及其代价。 湍流时传热、传质，传递阻力↓↓，强化过程。 代价： 流动阻力↑↑，动力消耗↑。

流体力学第九章流动阻力与管道计算

流体力学第九章流动阻力与管道计算

模拟实验 >
第2页
退出
返回
第九章 流动阻力与管道计算
第一节 流动状态与阻力分类
流速较低时，红色流线在玻璃管中呈一直线，与周围流体互不相混， 如图9.2（a）所示。流体质点仅作轴向运动而无横向运动，这种流动状 态称为层流。
当水流速度增大到某个值时，红线开始呈波纹状，如图9.2（b）所示。 这表明层流状态开始被破坏，流体质点除了沿主流（轴线）方向运动外， 还有垂直于主流方向的横向运动。继续增大流速，红线运动波动剧烈，最 后发生断裂，混杂在很多小旋涡中，红液很快充满全管，如图9.2（c）所 示。
一、紊流中物理量的表示方法
如前所述，紊流是一种不稳定流动。在管内作紊流运动的流体质点不
但速度有脉动，而且其压力也是脉动的。虽在流动瞬间流体仍服从粘性
流体的运动规律，但由于脉动的存在使得运动微分方程无法求解。研究
紊流运动规律的一个可行的方法就是统计时均法，即用时均值（某一时
间间隔内的平均值）代替瞬时值。
是可能的，因而在 t1 至 t2 时间段内脉动速度的平均值为
w tt21 t1
t2w d t1
t1
t2t1
t2 t1
w w t d tt21 t1
t1 t2w d tt21 t1t1 t2w td tw t w t 0（9.9）
即脉动速度w 的时均值为0。
同样，紊流中各点的瞬时压力也可以表示为时均压力和脉动压力之和，即
第9页
退出
返回
第九章 流动阻力与管道计算
第一节 流动状态与阻力分类
2. 局部阻力 流体在流动中遇到局部障碍而产生的阻力称局部阻力。所谓 局部障碍，包括流道发生弯曲，流通截面扩大或缩小，流体通道中设置 的各种各样的物件如阀门等等（图9.6）。至于局部阻力产生的原因，后 续章节中将作详细说明。

流体在管内流动阻力的计算

流体在管内流动阻力的计算

流体在管内流动阻⼒的计算第四节流体在管内流动阻⼒的计算⼀、压⼒降—流动阻⼒的表现流动阻⼒产⽣的根本原因——流体具有粘性，所以流动时产⽣内摩擦⼒。

如图1—11所⽰，在贮槽下部连接的⽔平管上开两个⼩孔（A、B），分别插⼊两个竖直敞⼝玻璃管，调节出⼝阀开度，观察现象：1) 当调节阀关闭时，即流体静⽌时，A、B管中液⾯⾼度与贮槽液⾯平齐（可⽤静⼒学⽅程解释）。

2) 当打开阀门，流体开始流动后，发现A管液⾯低于贮槽液⾯，⽽B管液⾯⼜低于A管液⾯。

3) 随着流速继续增⼤，A、B管液⾯⼜继续降低，但A仍⾼于B，分析如下：上述现象可⽤柏努利⽅程解释，分别取A、B点为截⾯，列柏努利⽅程： ++=Z2+++说明：（1）流体在⽆外功加⼊，直径不变的⽔平管内流动时，两截⾯间的压差与流动阻⼒⽽引起的压强降数值相等。

（2）若流体流动的管⼦是垂直或倾斜放置的，则两截⾯间的压差与流动阻⼒⽽引起的压强降数值不相等。

⼆、流体在圆型直管中阻⼒损失的计算通式流体在圆管内流动总阻⼒分为直管阻⼒（⼜称沿程阻⼒）和局部阻⼒两部分。

其中直管阻⼒是流体流经⼀定管径的直管时，由于流体的内摩擦⽽产⽣的阻⼒，这⾥讨论它的计算。

范宁（Fanning）公式是描述各种流型下直管阻⼒的计算通式。

（1—30）或（1—30a）式中λ——摩擦系数，⽆因次。

说明：（1）层流时，；（2）湍流时，。

利⽤范宁公式计算阻⼒时，主要问题是λ的确定。

（⼀）层流时λ的求取利⽤⽜顿粘性定律可推导出（1—31）则（1—32）（1—32a）式（1—32）及（1—32a）称为哈根—泊谡叶⽅程，是流体层流时直管阻⼒的计算式，它是有严格理论依据的理论公式。

（⼆）湍流时的确定由于湍流过程中质点运动情况复杂，所以尚⽆严格理论为依据，的求取⼀般采⽤经验式或⼯程图，这⾥介绍查取⽅便的图（摩擦因⼦图），如图1-12所⽰。

图 1—12 图该图中曲线分成四个区：层流区、过渡区、湍流区和完全湍流区。

1. 层流区即,在双数坐标中为⼀条直线，此时⽆关。

流体在管内的流动阻力

流体在管内的流动阻力

第四节流体在管内的流动阻力实际上理想流体是不存在的。

流体在流动过程中需要消耗能量来克服流动阻力，本节讨论流体流动阻力的产生、影响因素及其计算。

§1.4.1牛顿粘性定律与流体的粘度1、牛顿粘性定律设有间距很小的两平行板，两平板间充满液体(如图)。

下板固定，上板施加一平行于平板的切向力F，使上板作平行于下板的等速直线运动。

紧贴上板的液体层以与上板相同的速度流动，而紧贴固定板的液体层则静止不动。

两层平板之间液体的流速分布则是从上到下为由大到小的渐变。

此两板间的液体可看成为许多平行于平板的流体层，这种流动称为层流，而层与层之间存在着速度差，即各液层之间存在着相对运动。

运动较快的液层对与之相邻的运动较慢的液层作用着一个拖动其向运动方向前进的力；而与此同时，运动较慢的液层对其上运动较快的液层也作用着一个大小相等方向相反的力，从而阻碍较快的液层的运动。

这种运动着的流体内部相邻两流体层间的相互作用力称为流体的内摩擦力（粘滞力）。

流体流动时产生内摩擦力的这种特性称为粘性。

在上图中，若某层流体的速度为u，在其垂直距离为dy处的邻近流体层的速度为u+du，则du/dy表示速度沿法线方向上的变化率，称为速度梯度。

实验证明，内摩擦力F与两流体层间的接触面积S成正比，与速度梯度du/dy成正比。

即：F∝S·du/dy亦即：F=μS·du/dy剪应力τ：单位面积上的内摩擦力，即F/S, 单位N/㎡于是：τ=F/S=μ·du/dy——牛顿粘性定律μ为比例系数，称为粘性系数或动力粘度，简称粘度说明：①牛顿粘性定律可表达为剪应力与法向速度梯度成正比，与法向压力无关，流体的这一规律与固体表面的摩擦力的变化规律截然不同。

②牛顿粘性定律的使用条件：层流时的牛顿型流体。

③根据此定律，粘性流体在管内的速度分布可以预示为：如图紧贴壁面的流体受壁面固体分子力的作用而处于静止状态，随着离壁距离的增加，流体的速度连续地增大，至管中心处速度达到最大。

流体流动之摩擦阻力计算讲解

流体流动之摩擦阻力计算讲解

摩擦阻力
一、 牛顿粘性定律与流体的粘度
运动着的流体内部相邻两流体层间的相互作 用力称内摩擦力，这是产生流体阻力的根本原因。 这种表明流体流动时产生内摩擦力的特性称为粘 性，粘性是流动性的反面。
剪应力 F du
A dy
——比例系数，称为粘度（Viscosity) 。
摩擦阻力
Re du

0.0531 998.2 1.005 103
5.26104
4000
因此，可判断水在管中呈湍流。
注：无单位
摩擦阻力
二、流动类型与雷诺准数
重点强调
流体主体为湍流，但在管壁处会形成层流称之为“层流底层” u 0.5umax
且Re越大，层流底层越薄
章节小结
二、流动类型与雷诺准数
摩擦阻力
二、流动类型与雷诺准数 雷诺实验（1883年）
雷诺实验装置流动型态 Nhomakorabea层流 过渡流 湍流
摩擦阻力
二、流动类型与雷诺准数 层流（滞流）：流体质点仅沿着与管轴平行 的方向作直线运动，质点无径向脉动，质点 之间互不混合。
过渡流：介于层流和湍流之间，是一种不稳 定状态。
湍流（紊流）：流体质点除了沿管轴向前流 动外，还有径向脉动，各质点的速度在大小 和方向上都随时变化，质点互相碰撞和混合。
突然缩小 0.5
摩擦阻力
三、流体在圆管内流动时的阻力计算
局部阻力
h
/ f
当量长度法 把局部阻力折算成相应长度 le的直管阻力
hf


le d
u2 2
H f


le d
u2 2g
le 当量长度，见P31 表1-9

工程流体力学流体在圆管中的流动

工程流体力学流体在圆管中的流动

l
流速分布
l
dr
d
p2
u
z2 z1
p1 dG
1
速度分布：u
gh f 4l
(r0 2
r2)
p
4l
(r0 2
r2)
其中 r0是圆管半径。
此处p，并不仅仅是 ( p1 p2 )，当且仅当，z1 z2时，p p1 p2。
可见:
速度和半径之间呈二次抛物线关系，管轴处流速达到最大。
2、流量
层流化；
• 利用控制湍流拟序结构来控制湍流取得了显著的成就，例如，
湍流减阻和降低噪声。
➢ • 湍流实验是认识湍流的重要工具，湍流研究也促进了流 体力学实验技术的发展；
➢ • 流场显示技术（氢气泡技术，激光诱导荧光技术等）和 湍流场的精细定量测量技术（粒子图像测速法等）相结合， 可以获得既直观又可靠的湍流场信息
流速增大时，颜色水看是动荡，但仍保持 完整形状，管内液体仍为层流状态，当到 达到某一值 v时k ，颜色线开始抖动、分散。 这是一种由层流到湍流的过渡状态。
当流速达到一定值时，质点运动曾现一种 紊乱状态，质点流动杂乱无章，说明管中 质点流动不仅仅在轴向，在径向也有不规 则的脉动现象，各质点大量交换混杂，这 种流动状态称为湍流或紊流。
2、动量修正系数
v2dA
A
V 2A
4 3
动能修正系数和动量修正系数都是大于1的正数，且 速度分布越均匀，则修正系数越小。
4.2.4 层流的沿程损失 沿程能量损失可以用压强损失、水头损失或功率损失 三种形式表示：
1、压强损失
由：V qV p R2 pd 4
A 8l 32l
移相，得：p 32l V KV
流体的流动状态与管径有关。

流体在圆管内流动时的阻力计算(总)

流体在圆管内流动时的阻力计算(总)

解：
H
f1
l1 v12 6 4 l1 v12 3 2 µ l1 v1 = λ1 = = ρ g d 12 d1 2 g R e1 d 1 2 g
1 2 8 µ q v l1 3 2 µ l1 q v = = 2 ρ g d1 π d 2 π ρ g d 14 1 4
H
f 2
=
128µ q πρ g
v
解： d = 300 − 2 ×15 = 270mm = 0.27m, v =
0.27 × 1.635 × 890 = 2000 µ 0.197 λ = 64 / Re = 0.0305 Re = = dv ρ
300000 / 890 3600 ×
π
4
× 0.27 2
= 1.635m / s
l v2 160000 1.6352 Hf =λ = 0.0305 × × = 2465.1m d 2g 0.27 2 × 9.81 ∆p f = ρ gH f = 890 × 9.81× 2465.1 = 2.19 × 107 Pa ∆p f 60 ×10000 × 9.81 = 3.67 ≈ 4
r 2 vr = vmax 1 − R
平均速度 v = Vs = ∫A
A
vr dA A
vmax ∫ =
r 2 1 − 2π rdr p1 − p2 2 1 R = vmax = R 2 πR 2 8µ l
边界层分离→大量旋涡→消耗能量→ 边界层分离→大量旋涡→消耗能量→增大阻力
由于边界层分离造成的能量损失，称为形体阻力损失 由于边界层分离造成的能量损失，称为形体阻力损失 在流体输送中应设法避免或减轻边界层分离，措施：选择 在流体输送中应设法避免或减轻边界层分离，措施： 适宜的流速，改变固体的形体。 适宜的流速，改变固体的形体。 如汽车、飞机、 如汽车、飞机、桥墩都是流线型 在传热、传质混合中应加以利用。 在传热、传质混合中应加以利用。

1-4 流体在直管内的流动阻力

1-4 流体在直管内的流动阻力

知识点1-4 流体在直管内的流动阻力目的是解决流体在管截面上的速度分布及柏努利方程式中流动阻力Σh f的计算问题。

2．本知识点的重点（1）流体在管路中的流动阻力的计算问题。

管路阻力又包括包括直管阻力h f和局部阻力h f’本质不同的两大类。

前者主要是表面摩擦，后者以形体阻力为主。

同时，解决了管截面上的速度分布问题。

（2）流体在直管中的流动阻力因流型不同而采用不同的工程处理方法。

对于层流，通过过程本征方程（牛顿粘性定律）可用解析方法求解管截面上的速度分布及流动阻力；而对于湍流，需借助因次分析方法来规划试验，采用实验研究方法。

因次分析的基础是因次一致的原则和∏定理。

局部阻力也只能依靠实验方法测定有关参数（z或l e）。

（3）建立“当量”的概念（包括当量直径和当量长度）。

“当量”要具有和原物量在某方面的等效性，并依赖于经验。

3．本知识点的难点本知识点无难点，但对于因次分析方法的理解和应用尚需通过实践来加深。

4．应完成的习题1-12.在本题附图所示的实验装置中，于异径水平管段两截面间连一倒置U管压差计，以测量两截面之间的压强差。

当水的流量为10800kg/h时，U管压差计读数R为100mm。

粗、细管的直径分别为60×3.5mm与φ42×3mm。

计算：（1）1kg水流经两截面间的能量损失；（2）与该能量损失相当的压强降为若干Pa？[答：（1）4.41J/kg；（2）4.41×103Pa]1-13.密度为850kg/m3、粘度为8×10-3Pa·s的液体在内径为14mm的钢管内流动，溶液的流速为1m/s。

试计算：（1）雷诺准数，并指出属于何种流型；（2）局部速度等于平均速度处与管轴的距离；（3）该管路为水平管，若上游压强为147×103Pa，液体流经多长的管子其压强才下降到127.5×103Pa？[答：（1）1.49×103；（2）4.95mm；（3）14.93m]1-14.每小时将2×104kg的溶液用泵从反应器输送到高位槽（见本题附图）。

流体在管内的流动阻力

流体在管内的流动阻力
ε/d
l / d：管子的长径比；
du
Pf
： 雷诺数Re；反映流体的流动状态和湍动程度
u
2
： 欧拉准数，以Eu表示 。表示压力降与惯性力之比
数群（4）=变量（7）-基本因次（3）
3）数据处理
湍流流动，实验证明，l/d的指数b=1 。
Pf
l u 2 p f d 2 p f l u2 hf d 2
—— 圆形直管阻力所引起能量损失的通式（ 对于滞流或 湍流都适用），范宁公式。 λ为无因次的系数，称为摩擦因数 。
f (Re, / d )
2、 层流时的直管阻力损失
P 2 d umax 2u umax R R 4l 2 d 2 Pf P d 2 u 2u ( ) 32 l 4l 2
个无因次数群，减少变量数目。
π定理： i=n-m i----无因次数群个数 n----物理量个数 m----量纲个数
3）数据处理：建立过程的无因次数群之间的关系。 一般常采用幂函数形式π1=kπ2απ3β 线性化：1ogπ1=1ogk+α1ogπ2+β1ogπ3 线性回归参数：k、α、β
因次分析法 特点：通过因次分析法得到数目较少的无因次变量，按无因 次变量组织实验，从而大大减少了实验次数，使实验简 便易行。 依据：因次一致性原则 白金汉(Buckinghan)所提出的π定理。 凡是根据基本的物理规律导出的物理量方 因次一致原则 ： 程 f ( , ,... ) 0， 1 2 i 式中各项的因次必然相同，也就是说，物理 量方程式左边的因次应与右边的因次相同。
用幂函数表示为：p f 各物理量的因次：
k.d l u
a b c e f
p ML1t 2 3 ML1t 1 L ML

管路阻力计算公式

管路阻力计算公式

管路阻力计算公式管路阻力是指液体在管道内流动时所受到的阻碍，其大小取决于流体的性质、管道的几何尺寸和流动的条件。

在实际工程中，准确计算管路阻力对于流体输送和工艺设计至关重要。

下面将介绍管路阻力的计算公式。

1.法氏公式法氏公式是计算管道流动阻力最常用的公式之一、它适用于圆形截面的水平、直立管道以及部分较短的水平、上升弯头。

其计算公式如下：ΔP=λ(L/D)(ρV^2/2)其中，ΔP为管道中的压力损失，单位为帕斯卡(Pa)；λ为摩擦阻力系数，根据管道的材料及条件可以查表或参考标准值；L为管道的长度，单位为米(m)；D为管道的内径，单位为米(m)；ρ为流体的密度，单位为千克/立方米(kg/m^3)；V为流体的流速，单位为米/秒(m/s)。

2.公因数法公因数法是另一种计算管道阻力的常用方法，适用于两端是同一直径的水平、上升和下降的圆管。

其计算公式如下：ΔP=KρV^2/2其中，ΔP为压力损失，单位为帕斯卡(Pa)；K为公因数，其具体数值根据管道的条件可查表或参考标准值；ρ为流体的密度，单位为千克/立方米(kg/m^3)；V为流体的流速，单位为米/秒(m/s)。

3.长度加速度法长度加速度法适用于水平直管或上升/下降弯头的计算中。

其计算公式如下：ΔP=1/2ρv^2(fL+g)其中，ΔP为压力损失，单位为帕斯卡(Pa)；ρ为流体的密度，单位为千克/立方米(kg/m^3)；v为流体的流速，单位为米/秒(m/s)；f为管道长度与管径之比；L为管道长度，单位为米(m)；g为液体的头压。

4.简化法式对于实际工程中的一些简化计算，可以采用以下常见的简化公式：-窄圆管公式：ΔP=32μLV/D^2，其中μ为动力黏度；-多种流状态公式：ΔP=αρV^2/2，其中α为系数；-工程系数法式：ΔP=βρV^2/2，其中β为系数。

需要注意的是，以上列出的公式都是针对一些特定条件下的近似计算公式，实际计算中需要结合具体的工程情况和流体参数，选择合适的公式进行计算。

流体在管内的流动阻力 (2)

流体在管内的流动阻力 (2)

流体在管内的流动阻力默认分类2008-01-13 08:58:10 阅读194 评论0 字号：大中小订阅一、计算圆形直管阻力的通式流体在管内以一定逮度流动时，有两个方向相反的力相互作用着。

一个是促使流动的推动力，这个力的方向和流动方向一致，另一个是由内摩擦而引起的摩擦阻力，这个力起了阻上流体运动的作用，其方向与流体前流动方向相反。

只有在推动力与阻力达平衡的条件下，流动速度才能维持不变，即达到稳态流动。

图1-23 直管阻力通式的推导如图1-23所示，流体以速度。

在一段水平直管内作稳定流动，对于不可压缩流体可写出截面1-1′，与2-2′间的柏努利方程式为：因是直径相同的水平管，左翼Z1=Z2，u1=u2=u，上式可筒化为：（1-39）现分析流体在一段直径为d、长度为l的水平管内受力的情况：垂直作用于截面1-1′上的压力P1=p1A1-p1πd2/4垂直作用于截面2-2′上的压力P2=p2A2-p2πd2/4P1与P2的作用方向相反，所以有一个净压力(P1-P2)作用于整个流体柱上，推动它向前运动，这就是流动的推动力，它的作用方向与流动方向相同，其大小为：平行作用于流体柱表面上的摩擦力为：摩擦力阻止流体向前运动，这就是流动的阻力，它的作用方向与流动方向相反。

根据牛顿第二运动定律，要维持流体在管内作匀速运动，作用在流体柱上的推动力应与阻力的大小相等，方向相反，即：则以式1-39代入上式得：（1-40）上式就是流体在圆形直管内流动时能量损失与摩擦应力关系式，但还不能直接用来计算hf ，因为内摩擦应力所遵循的规律因流体流动类型而异，直接用τ计算hf 有困难，且在连续性方程式及柏努利方程式中均无此项，故式1-40直接应用于管路的计算很不方便。

下面将式1-40作进一步的变换，以消去式中的内摩擦应力τ。

由实验得知，流体只有在流动情况下才产生阻力。

在流体物理性质，管径与管长相同情况下，流速增大，能量损失也随之增加，可见流动阻力与流速有关。

3.4 管内流体流动的阻力

3.4 管内流体流动的阻力
(表压)，输送管路为φ108×4mm的钢管，直管长为(h+1.5)m。管
路中装有180º回弯头、90º标准弯头、截止阀各一个。若维持进料量 为50m3/h，问高位槽中的液面至少高出进料口多少米？ 料液的粘 度为1.510-3Pa.s，密度为900kg.m-3，
H1

u12 2g

p1
g

He
A
解：(1)C管单独全开时:
m0 mc
vc,0 （ dc ）2
vc
d0
7m
B 1m
地面
HA

u
2 A
2g

pA
g

He

HC

uC2 2g

pC
g

Hf AC
D C
7 1 l0uc2,0 lcuc2
d02g dc 2g

0.58vc2

1.22
v
2 c

1.8v
2 c
uc 1.83m3 s1
p u1.75~1.8
当Re 3 103 ~ 1108
(1.8 lg Re 1.5)2 柯纳柯夫（KypnaKOB）公式
粗糙管： 当Re 105, 接近一常数,其值主要取决于管壁的粗糙度。
(1.14 2 lg )2 尼库拉则(Nokuradse)公式
2
实际流体的Bernoulli方程:
? Z1

u12 2g

p1
g

He

Z2

u22 2g

p2
g

H
f
流体流动的阻力与流体的性质(如粘度等)、流体流动形态、导 管的长度、管径、壁面情况以及流动时的变动状态（如缩小、 扩张等）有关。

圆管流量公式

圆管流量公式

圆管流量公式圆管流量公式是描述液体或气体在圆管中流动时流量的数学表达式。

它是工程领域中广泛使用的重要公式之一，对于设计和分析管道系统的流动特性至关重要。

本文将介绍圆管流量公式的基本原理和应用，并探讨其在实际工程中的重要性。

一、圆管流量公式的基本原理圆管流量公式是基于质量守恒定律和动量守恒定律推导而来的。

根据质量守恒定律，流经管道截面的流体质量流量恒定，即入口质量流量等于出口质量流量。

根据动量守恒定律，流体在管道中的动量变化等于作用在管道上的力的总和。

通过对这两个定律的应用，可以得到描述圆管流量的公式。

二、圆管流量公式的应用圆管流量公式在工程中有广泛的应用，特别是在设计和分析管道系统的流动特性时。

它可以用来计算流体在管道中的流速、流量和压力等参数，为工程师提供重要的设计依据。

1. 圆管流速计算圆管流量公式可以用来计算流体在管道中的流速。

流速是指单位时间内流经管道截面的流体体积。

根据圆管流量公式，可以通过已知的流量和管道截面积来计算流速。

2. 圆管流量计算圆管流量公式还可以用来计算流体在管道中的流量。

流量是指单位时间内通过管道截面的流体体积。

根据圆管流量公式，可以通过已知的流速和管道截面积来计算流量。

3. 圆管压力计算圆管流量公式还可以用来计算流体在管道中的压力。

压力是指流体对单位面积的压力，是流体流动时产生的阻力。

根据圆管流量公式，可以通过已知的流量、管道截面积和流速来计算压力。

三、圆管流量公式在实际工程中的重要性圆管流量公式在实际工程中具有重要的应用价值。

它可以帮助工程师设计和分析管道系统的流动特性，确保系统运行安全和高效。

1. 管道系统设计在设计管道系统时，工程师需要考虑流体的流量、流速和压力等参数。

圆管流量公式可以提供这些参数的计算方法，帮助工程师确定合适的管道尺寸和流体流动条件，以满足系统的设计要求。

2. 管道系统分析在分析管道系统的性能时，工程师需要评估流体的流量、流速和压力等参数对系统性能的影响。

流体在圆管内流动时的阻力计算(总)

流体在圆管内流动时的阻力计算(总)

128 qv l1 32 l1 qv 2 g d1 d 2 g d14 1 4
Hf2 128 qv l2 4 g d 2
Hf2 H f1
l2 d14 2 1 1 4 4 l1 d2 1 2 8
例：某日化厂原料油在管中以层流流动，流量不变，问： （1）管长增加一倍，（2）管径增加一倍，（3）油 温升高使粘度为原来的1／2（设密度变化不大）。三 种情况下摩擦阻力变化情况。
完全湍流区 阻力平方区
0.02 0.015 0.01 0.008 0.006 0.004 0.002 0.001 0.0008 0.0006 0.0004 0.0002 0.0001 0.00005
e
d
层 过 流 渡 区 区
0.01 0.009 0.008 103
2
4
2
4
雷诺数 Re
dv
6 8 107
流体在管路中流动时的阻力有两种：
1、直管阻力——流体流径一定管径的直管时，因流 体内摩擦而产生的阻力。表皮阻力或摩擦阻力。 2、局部阻力——粘性流体绕过固体表面的阻力为摩 擦阻力与形体阻力之和。流体流径管路中的管件、阀门及 管截面的突然扩大或缩小等局部地方所产生的阻力。
一、滞流时的摩擦阻力
流体在半径为R 的水平管中作稳定流动。在流体中取一段长 为l，半径为r的流体圆柱体。在水平方向作用于此圆柱体的 力有两端的总压力(P1-P2)及圆柱体周围表面上的内摩擦力F。
湍流主体
缓冲层或过渡层
滞流内层或滞流底层
边界层的基本特征
（1） 与物体的特征长度相比，边界层的厚度很 小, .x （2） 边界层内沿厚度方向，存在很大的速度梯度。
（3） 边界层厚度沿流体流动方向是增加的。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

化 学 工. 程 基 础
17
（2）20℃水的物性：998.2kg/m3 1.00150 3Pas
R e d u0 .0 1 .0 7 90 1 .9 2 5 3 0 8 2 .21 .5 3 150
取钢管的绝对粗糙度ε为0.2mm，则
0.20.00286查得 0.27
d 70
所以能量损失 hf d lu 2 20.020 1 .0 707 2.2 229.3J3/kg
4
d22d12
4
d2d1π
d2d1
化 学 工. 程 基 础
11
二、阻力的计算：
7、局部阻力 h f ： 1）当量长度法：以当量长度 代替范宁公式中直管的长度进 行计算。 当量长度：管件、阀门产生 的阻力相当于同直径且阻力损 失相同的圆管的长度，以 le 表 示。
当量长度 共线图
化 学 工. 程 基 础
产生的阻力； 局部阻力：流体流经管件、阀门等局部地方由于流速
大小及方向的改变而引起的阻力。
总阻力=直管阻力+局部阻力
化 学 工. 程 基 础
3
一、概述：
3、阻力的表示法：
(1) hf:单位质量流体产生的阻力损失(J/kg).
(2) H f :单位重量流体产生的阻力损失(J/N=m).
(3) p f :单位体积流体产生的阻力损失(J/m3=Pa).
湍流时λ既与 Re有关，又与 有d 关，一般通过 因次分析法进行分析，得到一些经验公式，这里只 介绍比较常用的柏拉修斯式：
0.31R 60 4 e .25
适用范围：光滑管，Re在 313 0～110 5
化 学 工. 程 基 础
9
二、阻力的计算：
5、摩擦系数图（莫狄可（ 层按2d湍M0流一层0流o0区定与流过o完<区dR只R时R区渡全RyRh6eee4与fe，）也区<e湍<和与>24R可流图040ude000的按区越d）有000平都0湍：大关虚方有虚，，线成关线与以越正以R下小比e上无部关分
三种形式：
hf
l
u2 2g
pf
l
d
u2
2
化 学 工. 程 基 础
6
二、阻力的计算：
2、管壁粗糙度对λ的影响：
光滑:玻 管璃、管 黄铜、管 塑料管 粗糙:钢 管管 、铸铁管
1）粗糙度(绝对粗糙度)ε：壁面凸出部分的平均高度。
2）相对粗糙度 d ： 3）粗糙度对的影响：
层流时，无影响。
授课教师:邸凯
第四节 流体在圆管 内流动时的阻力
.
1
流体在圆管内流动时的阻力
本章的难点，包括阻力计算的 通式及层流和湍流的摩擦阻力
系数的计算。
化 学 工. 程 基 础
2
一、概述：
1、阻力产生的原因
（1）流体具有粘性，产生粘性阻力；
（2）形体阻力：流体流经不规则障碍物，边界层分 离，因涡流产生能量损失。 2、阻力分类： 直管阻力：流体流经一定直径的直管时由于内摩擦而
湍流时
无影响
有影响
化 学 工. 程 基 础
7
二、阻力的计算：
3、层流时的摩擦系数：
u p R2
8l
哈根-泊谡叶公 式
将R=d/2代入可得： pf p3d22lu
hf ?
与范宁公式比较可得：
64 du
64 Re
层流时摩擦系数λ是雷诺数Re的函数。
化 学 工. 程 基 础
8
二、阻力的计算：
4、湍流时的摩擦系数：
l le d
u2 )
2
化 学 工. 程 基 础
15
例：分别计算下列情况下，流体流过φ76×3mm、 长10m的水平钢管的能量损失、压头损失及压 力损失。 （1）密度为910kg/m3、粘度为72cP的油品， 流速为1.1m/s； （2）20℃的水，流速为2.2 m/s。
化 学 工. 程 基 础
16
hf
u2 2
H
f
u2 2g
p u2
2
说明：①变径时，以细管内流速计算局部阻力；
②突然扩大或突然缩小的阻力系数ζ：：局部阻
从管路进入容器： 1
力系数
从容器进入管路： 0.5
③管件、阀门的局部阻力系数：查手册
化 学 工. 程 基 础
14
二、阻力的计算
8、管路系统中的总能量损失
hf hf hf' (
解：（1）油品：
R edu0.07 7 2 911 0 310 .1972 3000R 64e967430.0658
所以能量损失 hf d lu 2 20.060 1 .5 00 8 1 7 .2 125.6J9/kg
压头损失
Hf
hf g
5.690.58m 9.81
压力损失 pf hf 91 5 .0 6 951 P7a8
hf与u的流一区次查方成正比。
化 学 工. 程 基 础
10
二、阻力的计算：
6、非圆形直管阻力损失的计算：
一般以当量直径代替直径进行计算。
当量直径de：与非圆形直管等长且阻力损失相
等的圆管的直径。
de
a
4流通截面积 润湿周边
非圆形管内 流动形态如
何确定？
b
de42aabba2 abb
d1 d2
de
阻力： FAd l
方向与流动方向相反 定态流动，受力平衡 (p1p2)d42 dl
pf pp1p24 dl
化 学 工. 程 基 础
du dy
du ? dy
5
二、阻力的计算：
4l l u2 8
pf
p d
d
2 u2
令
8 u 2
所以
pf
hf
l u2
d2
上式为流体在直管内流动阻力的通式，称为范宁 公式。式中λ为无因次系数，称为摩擦系数或摩擦因数， 与流体流动的Re及管壁状况有关。
注意：压力损失 p f 是流体流动能量损失的一种表示 形式，与两截面间的压力差 p(p1p2)意义不同， 只有当管路为水平、管径不变且无外功加入时，二 者才相等 。
化 学 工. 程 基 础
4
二、阻力的计算：
1、圆形直管内阻力计算公式：
如图所示，对1-1′和2-2′截面 间流体进行受力分析：
推动力： p1 p24 d2 方向与流动方向相同
12
局部阻力损失计算 100mm 的闸阀 1/2 关
le = 22m 100mm 的闸阀全开
le = 0.75m 100mm 的标准三通
le = 2.2m
化 学 工. 程 基 础
13
二、阻力的计算：
7、局部阻力 h f ：
2）局部阻力系数法： 因为阻力损失与 u 2 2 成正比，所以 可以将局部阻力损失表示为
压头损失
Hf
hf g
9.330.95m 9.81
压力损失 pf hf 9.9 2 9 8 .3 3 93 P1 a3
化 学 工. 程 基 础
18
如附图所示，料液由敞口高位槽流入精馏塔中。 塔内进料处的压力为30kPa(表压)，输送管路为