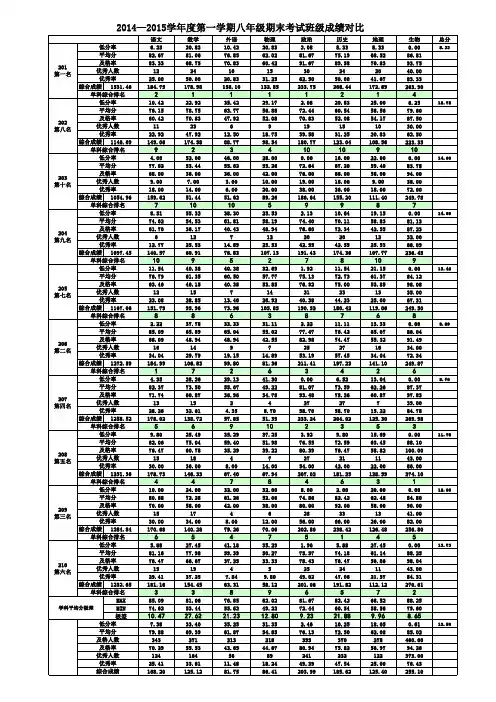
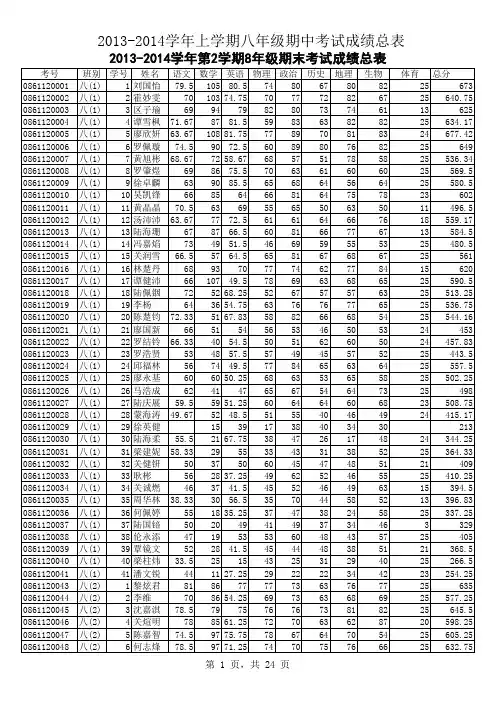
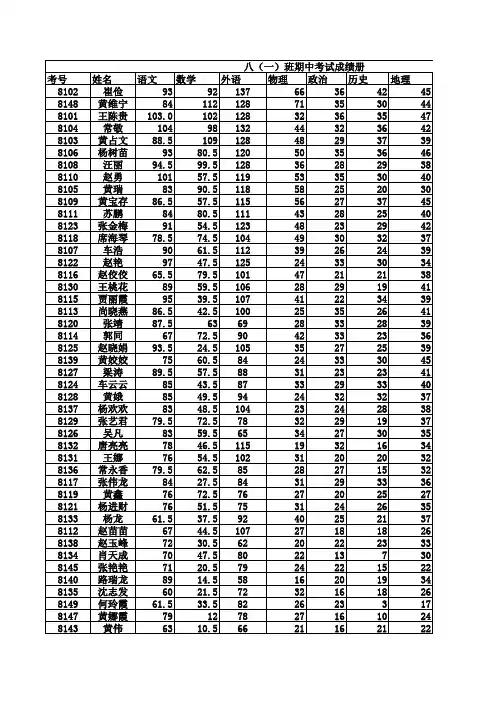
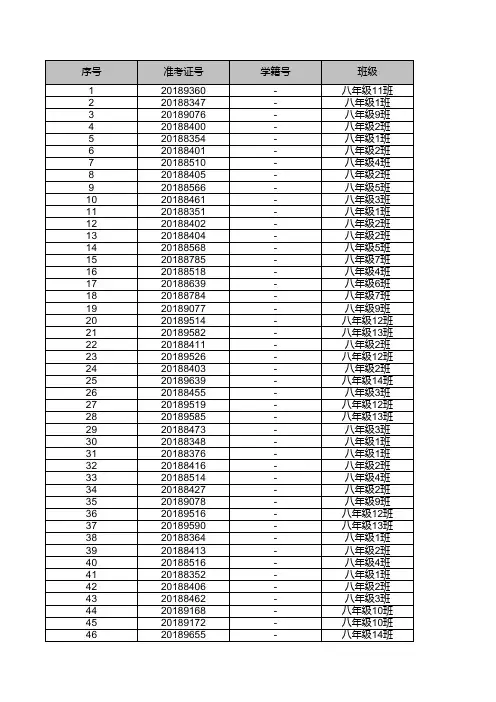
2015年八年级下学期期末考试考生成绩表(1)

格式：xls
大小：90.00 KB
文档页数：22

下载文档原格式

八年级期末考试成绩

5
27.45 77.98 66.67 19 37.25 154.45
4
41.18 59.39 37.25 4 7.84 63.31
7
35.29 50.27 33.33 5 9.80 58.12
5
1.96 75.57 78.43 25 49.02 201.06
1
5.88 74.18 76.47 24 47.06 191.82
2
88.25 79.60
10.47
7.38 79.88 343 70.29
27.62
33.40 69.39 271 55.53
21.23
35.25 61.87 213 43.65
12.80
31.35 54.85 218 44.67
9.23
2.46 76.13 395 80.94
21.88
10.25 72.50 370 75.82
3
31.11 55.02 42.55 7 14.89 81.36
8
2.22 77.47 82.98 25 53.19 211.41
7
11.11 76.42 74.47 27 57.45 197.23
6
13.33 65.07 55.32 16 34.04 141.10
8
0.00 86.04 91.49 34.00 72.34 249.87
总分
8.33
18.75
14.00
14.89
13.46
8.89
8.70
11.76
12.00
13.73
12.50
总分
2
20.83 60.54 52.08 15 31.25 123.04

2013-2014学年第2学期8年级期末考试成绩统计201407111344

2013-2014学年上学期八年级期中考试成绩总表
201 0861120001 0861120002 0861120003 0861120004 0861120005 0861120006 0861120007 0861120008 0861120009 0861120010 0861120011 0861120012 0861120013 0861120014 0861120015 0861120016 0861120017 0861120018 0861120019 0861120020 0861120021 0861120022 0861120023 0861120024 0861120025 0861120026 0861120027 0861120028 0861120029 0861120030 0861120031 0861120032 0861120033 0861120034 0861120035 0861120036 0861120037 0861120038 0861120039 0861120040 0861120041 0861120043 0861120044 0861120045 0861120046 0861120047 0861120048 班别学号姓名八(1) 1 刘国怡八(1) 2 霍妙雯八(1) 3 区子瑜八(1) 4 谭雪枫八(1) 5 廖欣妍八(1) 6 罗佩璇八(1) 7 黄旭彬八(1) 8 罗肇煜八(1) 9 徐卓麟八(1) 10 吴凯锋八(1) 11 黄晶晶八(1) 12 汤沛沛八(1) 13 陆海珊八(1) 14 冯嘉焰八(1) 15 关润雪八(1) 16 林楚丹八(1) 17 谭健沛八(1) 18 陆佩铟八(1) 19 李杨八(1) 20 陈楚钧八(1) 21 廖国新八(1) 22 罗结铃八(1) 23 罗浩贤八(1) 24 邱福林八(1) 25 廖永基八(1) 26 马浩成八(1) 27 陆庆展八(1) 28 蒙海涛八(1) 29 徐英健八(1) 30 陆海柔八(1) 31 梁建妮八(1) 32 关健钘八(1) 33 耿彬八(1) 34 关诚燃八(1) 35 周华林八(1) 36 何佩婷八(1) 37 陆国锫八(1) 38 伦永添八(1) 39 覃镜文八(1) 40 梁柱炜八(1) 41 潘文锐八(2) 1 黎炫君八(2) 2 李维八(2) 3 沈嘉淇八(2) 4 关煊明八(2) 5 陈嘉智八(2) 6 何志烽语文数学英语物理政治历史地理生物 79.5 105 80.5 74 80 67 80 82 70 103 74.75 70 77 72 82 67 69 94 79 82 80 73 74 61 71.67 87 81.5 59 83 63 82 82 63.67 108 81.75 77 89 70 81 83 74.5 90 72.5 60 89 80 76 82 68.67 72 58.67 68 57 51 78 58 69 86 75.5 70 63 61 60 60 63 90 85.5 65 68 64 56 64 66 85 64 66 81 64 75 78 70.5 63 69 55 65 50 63 50 63.67 77 72.5 61 61 64 66 76 67 87 66.5 60 81 66 77 67 73 49 51.5 46 69 59 55 53 66.5 57 64.5 65 81 67 68 67 68 93 70 77 74 62 77 84 66 107 49.5 78 69 63 68 65 72 52 68.25 52 67 57 57 63 64 36 54.75 63 76 76 77 65 72.33 51 67.83 58 82 66 68 54 66 51 54 56 53 46 50 53 66.33 40 54.5 50 51 62 60 50 53 48 57.5 57 49 45 57 52 56 74 49.5 77 84 65 63 64 60 60 50.25 68 63 53 65 58 62 41 47 65 67 54 64 73 59.5 59 51.25 60 64 64 60 68 49.67 52 48.5 51 55 40 46 49 15 39 17 38 40 34 30 55.5 21 67.75 38 47 26 17 48 58.33 29 55 33 43 31 38 52 50 37 50 60 45 47 48 51 56 28 37.25 49 62 52 46 55 46 37 41.5 45 52 46 49 63 38.33 30 56.5 35 70 44 58 52 55 18 35.25 37 47 38 24 58 50 20 49 41 49 37 34 46 47 19 53 53 60 48 43 57 52 28 41.5 45 44 48 38 51 33.5 25 15 43 25 31 29 40 44 11 27.25 29 22 22 34 42 81 86 77 77 73 63 76 77 70 86 54.25 69 73 63 68 69 78.5 79 75 76 76 73 81 82 78 85 61.25 72 70 63 62 87 74.5 97 75.75 78 67 64 70 54 78.5 97 71.25 74 70 75 76 66 体育 25 25 13 25 24 25 25 25 25 23 11 18 13 25 25 15 25 25 25 25 24 24 25 25 25 25 23 24 24 25 21 25 15 13 25 3 25 21 25 23 25 25 25 20 25 25 总分 673 640.75 625 634.17 677.42 649 536.34 569.5 580.5 602 496.5 559.17 584.5 480.5 561 620 590.5 513.25 536.75 544.16 453 457.83 443.5 557.5 502.25 498 508.75 415.17 213 344.25 364.33 409 410.25 394.5 396.83 337.25 329 405 368.5 266.5 254.25 635 577.25 645.5 598.25 605.25 632.75

八年级下第五次考试成绩单 (version 1)

94 94 99 85 88 92 100 96 94 97 97 94 91 95 86 100 98 97 91 95 95 86 97 97 94 97 91 85 93 84 99 94 95 92 95 92 91 97 93 88 100 94 96 95 95 98 97 92 91 92 94 91 95
1 孙寅鹏 2 唐天宇 3 谷云峰 1 王佳媛 3 刘宇航 1 刘雨双 6 丁旭 6 任石磊 2 高明宇 3 薛琦 6 张杨 1 梁嘉昊 1 苏劲多 2 朱文岩 3 王媛 4 常沛玉 7 刘琳 4 李泽宇 7 张艺馨 8 吕思奇 1 赵佳琦 6 孟纤婷 1 潘昱冰 6 姜磊 8 许立兵 7 孙鑫瑶 1 周洋 4 张楠 6 王紫薇 10 李健 3 李睿博 7 孙成月 11 王学智 1 陈玉婷 3 梁雪 7 刘志达 2 苏帅 6 户宇晗 1 吕金炽 10 华伟峰 5 刘议 1 李蔚 3 刘靖毓 1 朱南 10 潘鑫林 2 刘子琦 2 杨继伟 7 贺廿祎 2 张诗淇 3 李馨竹 8 黄启雪 11 王甜田 1 程华明
44 49 48 29 48 38 46 44 41 42 38 45 32 42 41 28 35 43 44 38 38 46 35 34 44 32 27 32 32 46 35 37 38 39 36 44 28 47 31 37 34 45 37 37 37 33 37 40 32 41 37 41 34
105 97 101 119 93 113 94 95 113 103 92 99 107 108 92 100 110 93 89 102 104 105 117 106 107 96 110 102 114 101 98 100 100 113 96 91 109 90 114 89 87 110 89 95 95 97 101 90 107 80 100 98 112

八年级(1)班期中考试成绩表

8142 黄挡挡 59 13.5 65 8141 张龙 71 44.5 24 8144 梁核蓉 72 13.5 69 8150 唐宁汇 59 12.5 74 8146 张转云 53.5 10.5 52 40分以下（人） 3 32 3 60分以上（人） 11 7 27 80分以上（人） 0 0 9 合格率 22.00% 14.00% 54.00% 后进率 6.00% 64.00% 6.00% 优秀率 0.00% 0.00% 18.00% 平均分 80.3 53.4 94.1 总分 4013.0 2671.5 4703.0
八（一）班期中考试成绩册姓名语文数学外语物理政治历史崔俭 93 92 137 66 36 黄维宁 84 112 128 71 35 王陈贵 103.0 102 128 32 36 常敬 104 98 132 44 32 黄占文 88.5 109 128 48 29 杨树苗 93 80.5 120 50 35 汪丽 94.5 99.5 128 36 28 赵勇 101 57.5 119 53 35 黄瑞 83 90.5 118 58 25 黄宝存 86.5 57.5 115 56 27 苏鹏 84 80.5 111 43 28 张金梅 91 54.5 123 48 23 席海琴 78.5 74.5 104 49 30 车浩 90 61.5 112 39 26 赵艳 97 47.5 125 24 33 赵佼佼 65.5 79.5 101 47 21 王桃花 89 59.5 106 28 29 贾丽霞 95 39.5 107 41 22 尚晓燕 86.5 42.5 100 25 35 张靖 87.5 63 69 28 33 郭同 67 72.5 90 42 33 赵晓娟 93.5 24.5 105 35 27 黄姣姣 75 60.5 84 24 33 梁涛 89.5 57.5 88 31 23 车云云 85 43.5 87 33 29 黄娥 85 49.5 94 24 32 杨欢欢 83 48.5 104 23 24 张艺君 79.5 72.5 78 32 29 吴凡 83 59.5 65 34 27 唐亮亮 78 46.5 115 19 32 王娜 76 54.5 102 31 20 常永香 79.5 62.5 85 28 27 张伟龙 84 27.5 84 31 29 黄鑫 76 72.5 76 27 20 杨进财 76 51.5 75 31 24 杨龙 61.5 37.5 92 40 25 赵苗苗 67 44.5 107 27 18 赵玉峰 72 30.5 62 20 22 肖天成 70 47.5 80 22 13 张艳艳 71 20.5 79 24 22 路瑞龙 89 14.5 58 16 20 沈志发 60 21.5 72 32 16 何玲霞 61.5 33.5 82 26 23 黄娜霞 79 12 78 27 16 63 黄伟 10.5 66 21 16

【山东省德州市齐河县齐河三中2015—2016学年第一学期八年级期末考试】全部考生成绩汇总

年级排名 123 1 1 73 32 32 32 32 73 123 32 73 1 73 32 73 169 20 20 123 73 256 123 73 20 1 1 32 256 73 73 32 73 73 1 123 20 20 73 169 32 32 298 169 73 169
得分 44 48 46 48 42 49 47 48 49 49 47 47 44 49 46 46 50 45 44 47 44 45 46 47 42 42 47 46 46 46 48 41 48 46 38 45 44 49 42 45 45 48 47 46 45 48
政治班级排名 2 24 7 8 6 24 25 28 3 8 37 20 13 33 1 3 6 4 1 12 1 13 10 3 8 4 7 46 13 1 6 5 1 3 7 4 3 12 13 1 16 1 11 19 2 28
年级排名 7 176 69 65 41 176 445 219 133 69 313 131 97 445 7 36 97 41 1 219 25 97 176 25 133 41 97 644 131 7 41 41 7 25 69 69 36 69 97 7 97 5 97 263 25 391
英语班级排名 3 1 1 3 2 12 1 10 5 1 2 17 6 1 6 4 2 1 4 1 4 1 3 4 3 13 16 7 2 4 10 6 18 25 5 2 2 25 17 22 15 29 4 1 7 9
年级排名 18 7 18 7 39 75 7 58 94 7 39 152 28 7 193 39 39 28 129 14 28 4 58 18 39 173 215 58 18 58 94 28 193 193 152 28 14 173 152 241 129 295 28 4 193 94

2015年8年级期末成绩

kh 830120002 830120009 830120013 830120015 830120014 830120027 830120078 830120060 830120008 830120037 830120074 830120095 830120036 830120101 830120080 830120061 830120083 830120124 830120145 830120055 830120129 830120150 830120160 830120138 830120162 830120131 830120159 830120164 830120158 830120201 830120178 830120197 830120211 830120193 830120239 830120306 830120227 830120280 830120232 830120295 830120262 830120293 830120332 830120315 830120318 830120301 830120322 830120328 830120345 830120341 830120346 830120355 830120385 830120374 830120401 830120386 830120402
kh 830120096 830120034 830120017 830120033 830120043 830120063 830120056 830120089 830120097 830120058 830120102 830120321 830120151 830120079 830120166 830120117 830120122 830120184 830120217 830120165 830120207 830120204 830120202 830120190 830120206 830120175 830120229 830120230 830120279 830120248 830120325 830120238 830120241 830120245 830120330 830120263 830120289 830120316 830120339 830120308 830120213 830120254 830120326 830120337 830120340 830120376 830120360 830120364 830120367 830120404 830120397 830120405

2013-2014学年度下学期期末考试八年级成绩表打印

注：
117 15.78 63.74 196.2 117 116 114 117 97 114 114 1 7 4 6.78 0 1 6.78 5.58 19.88 28.33 80.52 11 28 1.58 6 21 57.88 85.88 20 20 44.88
52.8 43.7 51.39 52.64 55.35 36.09 50.93 46.27 51 34.73 52.67 46.3 51.57 51.51 72.57 51.61 47.96 66.36 60.32 29.65 60.76 44.01 74.65 61.03 80.32 83.05 64.77
语文特优线 103
高分线 98
及格线 88
成绩评价表第2页总13页
表二.2
2013-2014学年度下学期八年级期末考试数学成绩分析表
单位最高分特优数高分数及格数平均分特优率高分率及格率得分率得分率折合平均值名次
城关实验里庄中学依汶中学马牧池中岸堤中学高湖中学岱庄中学孙祖中学双堠中学青驼中学张庄中学砖埠中学杨坡中学大庄中学辛集中学库沟中学蒲汪中学大王庄中湖头中学张哨中学苏村中学铜井中学沂南三中沂南四中卧龙东校卧龙北校全县
3.23 1.25 3.41 2.6 3.57 0 1.75 4.88 6.2 1.13 6 7.58 6.17 4.31 11.04 3.14 2.2 11.81 4.43 0 4.97 1.79 20.62 11.53 24.48 30.15 14.11
13.06 6.98 13.82 7.14 14.74 1.78 10.53 15.11 14.95 6.06 13.69 16.53 12.04 13.5 31.41 7.43 12.25 22.33 16.46 0.86 14.75 7.04 35.52 24.71 44.28 53.5 28

八年级测评成绩表2015.12 (2)

48 165 107 121 260 92 202 131 79 20 184 117 100 194 53 242 152 81 143 264 6 156 212 187 128 75 44 66 134 219 16 140 35 138 26 21 233 72 253 66 31 117 9 69 82 41 53 150 3 10 92 203 170 273
235 287 175 123 194 174 26 152 152 105 85 286 42 245 300 125 161 208 158 229 8 16 146 35 123 192 62 4 132 33 102 85 162 166 190 184 155 50 16 24 62 142 237 136 24 62 11 50 229 115 215 146 187 281 132
2001 2002 2003 2004 2005 2006 2007 2008 2009 2010 2011 2012 2013 2014 2015 2016 2017 2018 2019 2020 2021 2022 2023 2024 2025 2027 2029 2030 2031 2032 2033 2034 2035 2036 2037 2038 2039 2040 2041 2042 2043 2044 2045 2046 2047 2048 2049 2050 2052 2053 2054
八年级阶段测评成绩表
序号学号姓名
2015.12.10
语文数学英语物理
10月校序 10月总分 11月校序 11月总分
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55

八年级下学期中成绩表2014.7.4

语文 107 81 107 98 96 89 93 90 86 86 66 83 90 86 88 76 99 83 76 86 94 79 73 60 90 73 73 76 77 75 62 69 69 65 70 72 72 60 72 75 78 77 77 72 78 66 59 62 57 68 60 66 66
闫方昊张思宇王金辉付东杨郜嘉恒刘陆军
45 50 43 19 44 6
32 13 12 15 15 9
16 24 22 26 17 12
28 16 16 8 15 11
61 47 48 47 37 44
13.5 23.5 20.5 20.5 13.5 12
ቤተ መጻሕፍቲ ባይዱ
19.6 25.6 27.2 26.6 16.6 23.6
级下学期期末成绩单
姓名
2014.7.4
数学 92 114 94 105 98 102 96 97 87 67 93 85 74 89 84 84 82 70 88 72 72 87 69 69 43 49 64 78 73 78 76 41 45 67 62 65 61 81 60 47 53 26 26.5 36 29 40 22 23 23 7 10 6 7 英语 105 114 112 109 105 106 102 85 97 73 106 94 103 87 85 97 75 93 86 81 77 82 95 94 78 75 88 72 54 85 64 104 81 70 25 60 58 22 22 22 12 55 28 27 24 31 39 21 23 22 18 20 25
总分 584.2 581.4 580.6 576.4 568.3 568.2 552.5 540.8 515.6 514.8 511.6 510.5 508 507 506.6 490 486.8 481.7 475.8 464.4 464.1 461.6 454.5 447.7 442.8 439.4 439 437.7 433.6 433.4 431.1 430.1 413.5 413.4 402.9 392.9 372.8 363.3 337.3 326.8 323.5 306.9 305 278.6 270.9 267.9 263.7 247.9 242.3 234.2 232.4 226.1 218.1

新课标沪科版八年级物理下学期期末试卷及答案 (1)

新课标沪科版八年级物理下学期期末试卷（考试时间：80分钟满分：100分）一、选择题（将正确答案填入下面的方框中，否则不得分。

共30分）1．如图1所示，放在桌面上的茶壶处于静止状态，对于该静止的茶壶，下列说法中正确的是： ( )A ．茶壶受到重力和桌面对它的支持力，这是一对相互作用力B 茶壶受到重力和桌面对它的支持力，这是一对平衡力C ．茶壶静止是因为桌面对它的支持力小于茶壶受到的重力D ．茶壶静止是因为桌面对它的支持力大于茶壶受到的重力2．图5所示的用具中，属于省力杠杆的是（）3．随着生活水平的提高，小轿车已进入千家万户。

下列有关小轿车的说法正确的是（） A ．人用力推静止的车但未推动，是因为人对车的推力小于路面对车的摩擦力 B ．司机及前排乘员行驶时系安全带可以减小惯性C ．轿车行驶时车体上方空气对小车向下的压强大于车体下方空气向上的压强D ．行驶时以司机为参照物，轿车是静止的4．当轮船从东海驶向长江时，它受到的浮力将( )。

A ．不变 B ．变小 C ．变大 D ．无法判断 5、潜水艇从潜行变为上浮，在浮出水面之前，所受海水的压强和浮力变化情况正确的是（） A 、压强减小，浮力不变 B 、压强增大，浮力不变 C 、压强不变，浮力变大 D 、压强不变，浮力变小 6. 据美联社报道，“机遇号”火星探测器由于车轮陷入到细沙中而被困在火星表面的一个沙丘上，一直动弹不得，这与沙丘能够承受的压强较小有关．如果你是火星探测器的设计者，为了减小探测器对地面的压强，可行的改进方法是 ( ) A ．增大探测器的质量 B ．车轮使用履带式C ．减小车轮表面的粗糙程度D ．减少车轮与地面的接触面积 7．中国跳水队被人们称为“梦之队’，如图是跳水运动员跳水时的情景，运动员在离开跳板到落入水的过程中 ( )A 、运动员的动能一直增大，机械能不变B 、运动员的重力势能一直减小，机械能减小C 、运动员的动能先减小后增大，机械能不变D 、运动员的重力势能先减小后增大，机械能增大D 筷子 A 钳子 C 天平 B 镊子图18. 如图5所示，拉力F ＝125 N ，在10 s 内将重物匀速提升2m ，滑轮组的机械效率是80％则下列说法正确的是( )A ．拉力F 做的功是250 JB ．物体重是300 NC ．拉力F 的功率为25WD ．绳子自由端移动的速度为0.2m/s 10.如图7所示，桌面上是两个完全相同的圆柱形平底杯子，里面分别盛有质量相等的水和酒精，A B 、两点到杯子底部的距离相等。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

班别八（4）八（4）八（1）
姓名
八3
八（2）八（1）八（2）八（4）
八3
八（2）八（2）八（2）
八（4）
八（4）八（1）八（1）八（2）八（2）八（1）
八（1）八3
八（4）八（4）八（1）八（1）八（2）
八3
八（4）八（4）
八3
八（4）八（1）八（2）
八3
八（4）八（2）八（1）八（2）
物理
2015年八年级下学期考生期末成绩表
座号
126 117 137 27 103 29 142 38 55 33 121 67 86 54 87 25
班别八（4）八（2）八（2）八（1）
姓名
八3
八（1）八（2）
八3
八（2）
八3
八（1）八（1）八（4）
八（4）八3
八（4）
总分考试人数平均分及格人数及格率优秀人数优秀率
座号班别姓名
21 101 146 148 45 41 143 104 118 65 129 13 1 128 132 124 127 138 147 82 125 14 144 31 94 59 35 114 88 111 89 23 102 18 6 52 92 4 145 46 123 84 16 96
政治 74 84 81 69 80 76 79 90 72 75 72 80 58 88 73 90 78 81 68 74 58 66 79 72 75 80 84 84 78 70 72 80 81 72 80 72 70 60 69 78 76 62 72 67
历史 76 72 62 68 81 69 74 55 69 46 78 75 48 59 68 52 41 65 68 59 70 70 79 59 77 70 71 60 64 67 59 55 46 69 49 40 58 56 62 43 52 57 58 50
政治 72 76 70 48 82 73 64 76 48 65 73 51 72 72 78 72 67 62 56 60 70 74 60 68 58 58 51 42 53 64 45 52 72 40 56 62 58 62 64 36 54 50 56 50
历史 50 64 61 67 51 61 50 82 45 47 65 69 33 44 66 62 37 57 33 50 33 43 35 47 30 43 49 50 48 50 56 54 43 64 61 43 57 33 50 42 51 27 48 36
英语 70.83 65.83 84.17 66.67 39.17 64.17 71.67 80.00 77.50 78.33 63.33 58.33 75.83 66.67 65.83 68.33 75.83 63.33 66.67 52.50 68.33 50.00 52.50 44.17 52.50 42.50 53.33 58.33 63.33 53.33 57.50 60.00 66.67 63.33 67.50 75.00 52.92 61.67 48.33 56.67 51.67 73.33 55.00 64.17
班别八（1）八（2）八（1）八（2）八（2）八（2）
姓名
八3
八（2）八（1）八3
八（2）八3 八3 八3
八（1）八（4）八（2）八（4）
八（4）八（1）
八（2）八（2）八（1）
八3
八（4）八（4）八（2）八（1）八（2）八（1）
八3
八（2）
八（2）
八（1）八（1）八（4）
八3
八（4）八3 八（2）八（4）八（1）八（4）
八3
八（1）
八3 八3
八（4）
八3
八（1）八（2）八（2）
八3 八3 八（2）
八（1）八（4）八（4）八（4）八（1）八（4）八（4）
八3 八3
八（2）
八3
八（2）八（4）八（4）
语文 45 40 46 33 37 41 29 37 44 44 38 32 39 37 31 35 34 39 32 34 40 40 42 30 28 29 36 33 36 37 30 36 31 26 32 35 12 24 33 27 31 33 24 20
数学 12 6 24 34 16 30 49 12 29 25 12 12 17 15 23 12 26 13 47 24 15 15 8 29 42 43 12 15 21 12 28 9 12 21 9 13 37 14 15 12 18 12 15 37
语文 54 58 49 49 37 50 55 51 52 55 48 47 40 54 38 54 51 48 56 52 34 36 50 39 45 46 40 51 52 44 50 44 39 49 48 38 48 17 47 41 51 31 47 33
数学 26 20 23 43 57 31 10 13 18 34 27 27 64 16 38 18 36 24 22 43 48 56 17 60.5 25 36 26 21 16 34 28 27 33 12 15 33 29 63 31 35 21 23 12 29
英语 16.67 22.50 60.83 30.00 29.17 24.17 42.50 16.67 34.17 31.67 14.17 缺考缺考缺考缺考缺考
政治 64 52 22 52 42 56 30 44 18 20 28 28 缺考缺考缺考缺考
历史 36 41 42 27 33 24 39 24 27 27 24 27 缺考缺考缺考缺考
物理 85 78 74 90 86 91 86 68 76 62 82 68 63 71 73 82 69 65 59 61 69 63 57 57 60 64 51 49 50 41 46 61 39 47 51 44 63 45 52 36 32 31 31
2015年八年级下学期考生期末成绩表
期末成绩表
总分 522.67 494.50 487.50 475.83 474.67 461.75 456.17 454.33 450.50 435.67 430.83 429.75 429.08 427.67 423.67 418.50 416.50 416.00 414.00 413.50 411.50 408.83 405.67 401.33 398.50 391.67 390.83 388.17 385.83 380.17 378.50 376.00 372.83 372.17 370.83 368.67 366.50 363.83 361.00 359.50 353.00 351.83 340.33 302.33 平均分 87.11 82.42 81.25 79.31 79.11 76.96 76.03 75.72 75.08 72.61 71.81 71.63 71.51 71.28 70.61 69.75 69.42 69.33 69.00 68.92 68.58 68.14 67.61 66.89 66.42 65.28 65.14 64.69 64.31 63.36 63.08 62.67 62.14 62.03 61.81 61.44 61.08 60.64 60.17 59.92 58.83 58.64 56.72 年级排名 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 47
语文 66 63 64 60 59 64 66 72 58 68 46 60 60 60 66 61 46 61 67 53 50 48 58 45 67 56 59 49 53 53 64 55 58 49 54 65 48 45 52 46 50 58 52 37
数学 94 82 77 75 73 82 48 60 68 43 78 53 65 52 57 42 60 63 42 78 64 38 60 63 41 40 39 67 47 62 33 41 29 53 42 32 32 41 35 33 53 31 20 73
物理
4792.5 8192.0833 10073 8853 2628 144 143.00 144 144 43 33.3 57.29 70.0 61.5 61.1 22 76.00 111 79 25 0.1527778 0.53 0.7708333 0.5486111 0.5813953 3 18.00 45 30 7 0.0208333 0.13 0.3125 0.2083333 0.1627907
英语 62.50 52.50 36.67 54.17 50.00 30.83 40.83 25.00 60.83 45.00 37.50 60.00 60.83 52.92 21.67 36.67 53.33 41.67 44.17 43.33 51.67 37.50 63.33 32.50 48.33 33.33 56.67 62.50 43.33 36.67 40.00 42.08 35.00 40.00 31.67 36.25 18.33 48.33 18.33 62.50 20.00 48.33 24.17 23.33
八3
八（4）八3 八（1）八3 八（1）
沈路妹房买光妹唐光明唐龙房忠梅房金梅盘永辉房司平邓丽青房新仪沈金辉房瑞斌沈美英唐买胡妹唐二贵房三妹盘春艳沈香房桂峰邓婷房晴唐古民吊邓梅艳龙志勇李桥龙沈文金房智莲沈芳英房诗华房飞明唐观音唐丽英沈文军沈冬明唐国强房二妹房健荣邹桂珍李冬辉邓永光邓东坪房一妹盘辉唐结龙