初中数学竞赛专题复习第二篇平面几何第16章几何变换试题新人教版

第16章几何变换§16.1对称和平移16．1．1★设M 是边长为2的正三角形ABC 的边AB 的中点．P 是边BC 上的任意一点，求PA PM +的最小值．CA'M'PA M B解析 作正三角形ABC 关于BC 的对称图形A BC '△．M '是M 的对称点，故M 是A B '的中 点．PM PM '=，如图所示，则 PA PM PA PM AM ''+=+≥.连结CM '，易知90ACM '∠=︒，所以AM '=．所以，PA PM +16．1．2★★已知ABC △中，60A ∠<︒．试在ABC △的边AB 、AC 上分别找出一点P 、Q ，使BQ QP PC ++最小．解析 作B 关于直线AC 的对称点B '，C 关于直线AB 的对称点C '，连B C ''与AB 、AC 分别交于点P 、Q ，则P 、Q 即为所求，如图所示．CA'M'PA M B事实上，对于AB 、AC 上的任意点P '，Q '， BQ Q P P C B Q Q P P C ''''''''''++=++ B C B Q QP PC ''''=++≥ BQ QP PC =++．评注 因为60A ∠<︒，所以所作线段B C ''必与线段AB 、AC 相交．16．1．3★★求证：直角三角形的内接三角形的周长不小于斜边上高的两倍．解析 如图所示，设在直角三角形ABC 中，CD 是斜边上的高，PQR △是它的任一内接三角形．BDP ARC Q S VET G FU将Rt ABC △以BC 为对称轴反射为Rt BCE △，此时PQR △反射为SQV △，再将Rt BCE △以CE 为对称轴反射为Rt FCE △，此时SQV △反射为TUV △延长DC 交EF 于G ．易知FF AB ∥，所以CG CD =，即2GD CD =，且GD 是两平行线AB 与EF 之间的距离． 所以2PQ QR RP PQ QV VT GD CD ++=++=≥.16．1．4★★★在ABC △内取一点M 使10MAB ∠=︒，30MBA ∠=︒．设80ACB ∠=︒， AC BC =．求AMC ∠.CHBME解析 本题中ABC △为等腰三角形，这就提示我们利用对称性解题，先作一条对称轴，作ABC △的高CH 与直线BM 交于点E 由对称性知， 30EAB EBA ∠=∠=︒， 所以20EAM ∠=︒， 从而20CAE ∠=︒，因为40AME MAB MBA ∠=∠+∠=︒，又1402ACE ACB ∠=∠︒=，所以CAF △≌MAE △， 于是AC AM =，所以()118040702AMC ∠=︒-︒=︒． 16．1．5★★在ABC △中，AH 是高，H 在边BC 上，已知45BAC ∠=︒，2BH =，3CH =，求ABC △的面积．解析 作HAC △的关于AC 的对称图形MAC △，作H A B △的关于AB 的对称图形NAB △．分别延长MC 和NB ，它们相交于L ，如图所示．ANMBH CL易知90M N ∠=∠=︒，且 290NAM BAC ∠=∠=︒， AM AH AN ==．所以，四边形LMAN 是正方形． 设正方形LMAN 的边长为a ，则 3CL a =-，2BL a =-．在直角三角形BCL 中，由勾股定理知 222BL CL BC +=．()()222325a a -+-=．解方程，得6a =，即6AH =．所以1152ABC S BC AH =⋅=△． 16．1．6★★★如图，凸四边形PQRS 的四个顶点分别在边长为a 的正方形ABCD 的四条边上，求证：PQRS的周长不小于．解析 作正方形ABCD 关于BC 的轴对称图形，得到正方形11A BCD ，再作正方形11A BCD 关于1CD 的轴对称图形，得到正方形221A B CD ，再作正方形221A B CD 关于21A D 的轴对称图形，得到正方形2331A B C D ，而P 、Q 、R 、S 四点的对应点如图所示．A S DP B P 1A 1S 1D 1R 3C 3Q 3B 3P 3A 2P 2B 2Q 2R C R 1S 2Q显然，2AA =，23AP A P ∥，故32PP AA ∥，所以四边形PQRS 的周长 PQ QR RS SP +++ 11223PQ QR R S S P =+++32PP AA ==≥．即四边形PQRS的周长不小于．16．1．7★★★如图，ABC △和ADE △是两个不全等的等腰直角三角形， 90ABC ADE ∠=∠=︒，现固定ABC △而将ADE △绕点A 在平面上旋转，试证：不论ADE △旋转到什么位置，线段EC 上必存在点M 使BMD △力等腰直角三角形．BAD ECMA'解析 如图，设BMD △为等腰直角三角形，下面证明点M 在线段EC 上．作A 关于BD 的对称点A '，则ADB AD B '∠=∠． 因为902ADE BDM ∠=︒=∠，所以45EDM A DM A DB ''∠=∠=︒-∠ 45ADB =︒-∠， 又DA DA DE '==．所以A '又是E 关于DM 的对称点． 同理A '也是C 关于BM 的对称点，因此 EM D A M D '∠=∠，CMB A MD '∠=∠， 又因90BMD ∠=︒， 所以180CME ∠=︒．即M 在EC 上（且为EC 的中点）．16．1．8★★★如图，矩形ABCD 中，20AB =，10BC =，若在AC 、AB 上各取一点M 、N ，使BM MN +的值最小，试求出这个最小值．DEC GF ANP MBQ解析 作AB 关于直线AC 的对称线段AE ，即B 、E 关于AC 对称，作N 关于AC 的对称点F ，则F 在AE 上，且有BE AC ⊥于Q ，NF AC ⊥于P ．由对称变换可知，MN BM MF MB +=+.欲使M F BM +最小，必须BMF 共线，所以BM MN +最小值为点B 到AE 的距离BG .在Rt ABC △中，20AB =，10BC =，所以AB BCBQ AC⋅==2BE BQ == 在Rt ABQ △中，AQ =20AE AB ==，在ABE △中，1122ABE S BE AQ AE BG =⋅=⋅△，则16BE AQBG AE⋅==．从而BM MN +的最小值为16．16．1．9★★凸四边形ABCD 中，ABD CBD ∠>∠，ADB CDB ∠>∠．求证： AB AD BC CD +>+.D CEPA B解析将BCD △沿BD 翻折，点C 落在点P ．因为ABD CBD ∠>∠，ADB CDB ∠>∠，所以P 必定在ABD △内部．BP 延长线交AD 于点E ，则 AB AD BE FD BP PD BC CD +>+>+=+.16．1．10★★设S 表示凸四边形ABCD 的面积，证明1()2S AB CD BC AD ⋅+⋅≤．B ACD D'l解析如图，作点D 关于AC 的垂直平分线l 的对称点D '，显然ACD △与ACD '△关于l 成轴对称图形．所以 ABCD S S '= BAD BCD S S ''=+△△，11sin sin 22AB AD BAD BC CD BCD ''''=⋅⋅∠+⋅⋅∠ ()AB AD BC CD ''⋅+⋅≤ 1()2AB CD BC AD =⋅+⋅. 16．1．11★★在矩形ABCD 内取一点M ，使180BMC AMD ∠+∠=︒，试求BCM DAM ∠+∠的值．解析 如图将BMC △沿AB 平移至ADM '△，显然M M AD '⊥，BMC AM D '∠=∠．所以，由已知条件180AM D AMD '∠+∠=︒，即A 、M 、D 、M '四点共圆，从而 BCM DAM ADM DAM '∠+∠=∠+∠ 90AMM DAM '=∠+∠=︒．16．1．12★★设P 是平行四边形ABCD 内一点，使得PAB PCB ∠=∠， 证明：PBA PDA ∠=∠．A D PP'BC解析 如图，把AP 平移至DP '，则BAP CDP '∠=∠，及PBA P CD '∠=∠，PP BC '∥， 所以P PC BCP '∠=∠．又已知PAB PCB ∠=∠，故P PC CDP ''∠=∠，从而P 、D 、P '、C 四点共圆．于是 P PD P CD ''∠=∠，又PPDPD A '∠=∠， 所以PBA PDA ∠=∠．16．1．13★（1）如图（a ）所示，在梯形ABCD 中，AD BC ∥.已知：3AD BC +=，AC =，BD ABCD 的面积．（2）如图（b ），在梯形ABCD 中，AD BC ∥．M 是CD 的中点，MN AB ⊥于N ．设A B a =，MN h =，求梯形ABCD 的面积．解析（1）将BD 平移到CE ，连结DE，则CE BD ==DE BC =．所以B CAD E(a)A DENM CF B(b)3AE AD DE AD BC =+=+=．222AE AC CE =+．因此90ACE ∠=︒． 因为ABC CDE S S =△△，所以12ACE ABCD S S AC CE ==⋅=△梯形． （2）将AB 平移至EF ，如图（b ）所示，EF 过点M ．由于MDF △≌MCF △，所以 ABCD ABFE S S AB MN ah ==⋅=梯形梯形．评注 本题的两种添平行线法是解梯形问题的常用方法．16．1．14★★如图，在四边形ABCD 中，AD BC =，E 、F 分别是DC 及AB 中点，FE 的 延长线与AD 及BC 的延长线分别交于点H 、G ．求证：AHF BGF ∠=∠．G H DAB'F BCE (a)解析1如图（a ），将线段CB 平移至AB '．则四边形AB BC '为平行四边形．由于F 是AB 中 点，故C 、F 、B '共线．现在EF 是CDB '△的中位线，故EF D B '∥，所以 AHF ADB '∠=∠，BGF AB D '∠=∠．又显然AB BC AD '==．故ADB AB D ''∠=∠． 于是AHF BGF ∠=∠．G H E CD MAF B(b)解析2如图（b ），连结AC ，取AC 中点为M ，连结ME 、MF ，则ME 、MF 分别为CDA △、ABC △的中位线，所以12ME DA ∥，12MF BC ∥．故M EF AH F ∠=∠， AFE FGB ∠=∠，且M E M F =，故M EF M FE ∠=∠， 所以AHF FGB ∠=∠．16．1．15★★如图，A B ∠=∠，1AA 、1PP 、1BB 均垂直于11A B ，垂足为1A 、1P 、 1B ，117AA =，116PP =，120BB =，1112A B =．求AP BP +的值．A C D A 1P 1B 1E PB解析 将1PP 平移到1CA，C 在线段1AA 上，延长BP 交1AA 于D ，将1DA 平移到1EB ，E 在1BB 上．因为1AA 、1BB 、1PP 均垂直于11A B ，所以四边形11CAPP 和11DA B E 都是矩形． 由1116CA PP ==，117AA =，得1AC =．又11AA BB ∥，所以P D A B A ∠=∠=∠，90PCD PCA ∠=∠=︒，PC PC =．所以Rt PCD △≌Rt PCA △，PA PD =，1CD AC ==．于是AP BP BD +=， 11115DA AA AD EB =-==， 115BE BB EB =-=．在Rt BED △中，1112DE A B ==，13BD ==，也即 13AP BP +=．16．1．16★★在正三角形ABC 的三条边上，有三条相等的线段12A A 、12B B 、12C C ．证明：直线21B C 、21C A 、21A B 所成的三角形中，三条线段21B C 、21C A 、21A B 与包含它们的边 成比例．CABC 1C 23A 1A 2A 3B 1B 2B 3解析 如图，将12C C 平移到2B P ，连结1PA 、1PB 、2PC ．因为四边形12BC C P 为平行四边形，所以1260B B P A ∠=∠=︒，21212B P C C B B ==，故12B B P △为正三角形，112B P A A ∥．这样所得四边形121A A B P 为平行四边形，121A P A B ∥．因此，由21B C 、21C A 、21A B 这三条线段构成的三角形与12A PC △全等，而12A PC △≌333A B C △，从而命题得证．16．1．17★★如图所示，2AA BB CC '''===且共点于O ，60AOB BOC COA '''∠=∠=∠=︒，求证：AOB BOC COA S S S '''++△△△Q解析 将A OC '△沿A A '方向平移A A '长的距离，得AQR △，将BOC '△沿BB '方向平移BB '长的距离，得B PR ''△．由于 2OP OQ ==，60POQ ∠=︒， 所以2PQ =．又因'2QR R P OC OC CC ''+=+==，故R 与R '重合，且P 、R 、Q 三点共线．在正三角形POQ 中， AOB BOC COA S S S '''++△△△AOB B PR AQR S S S ''=++△△△22OPQ S <==△ 16．1．18★★★如图，由平行四边形的顶点B 引它的高BK 和BH ，已知KH a =，BD b =，求点B 到BKH △的垂心的距离． B PCHD KAaH 1解析 令1H 表示BKH △的垂心．考虑到1KH BH ⊥，D H BH ⊥，有1KH DH ∥．同理有1HH DK ∥，因而四边形1KDHH ，为平行四边形，平移1BKH △到PDH △位置，显然P 为BC 上一点，所求线段1BH 即PH ，已与KH 位于同一直角三角形中．由于四边形KDPB 为矩形，有PK BD =，于是1BH PH ==16．1．19★★★已知ABC △的面积为S ，D 、E 、F 分别为BC 、CA 、AB 上的点，且 1BD CE AF DC EA FB n===，试求以AD 、BE 、CF 为边的三角形的面积S '． GCEDF解析 如图，过点A 作AG 平行且等于FC ．连CG 、GD 、GE ，则四边形AFCG 为平行四边形，GCA CAB ∠=∠．又11CG AF AE AE AB AB AB CA n ====+， 所以CGE △≌ABC △，CEG ACB ∠=∠，因此GE CB ∥. 又因1=1GE BDBC n BC =+， 所以GE BD =．于是四边形GEBD 也为平行四边形，从而GD BE =，即ADG △为AD 、BE 、CF 所构成的三角形，它的面积为S '． 在梯形GABC 中， 1111GABC S GC AB GC S AB AB n +==+=++梯形， 所以111GABC S S n ⎛⎫=+ ⎪+⎝⎭梯形，而11ABD S BD S BC n ==+△， 所以111ABC CG CD nS BA BC n n ⋅==⋅⋅++△， 因此()2111111n S S n n n ⎡⎤⎛⎫'=+--⎢⎥ ⎪++⎝⎭+⎢⎥⎣⎦()2211n n S n ++=+．§16.2旋转16．2．1★★对于边长为1的正ABC △内任一点P PA PB PC ++．ACBPC'P'解析 把ABC △绕点B 旋转60︒到CBC '△．则PBP '△为正三角形，且 PC P C ''=，PB PP '=，因而PA PB PC PA PP P C AC ''''++=++≥16．2．2★★设P 是等边三角形ABC 内一点，3PC =，4PA =，5PB =．试求此等边三角形的边长．BACP 543解析 如图，把CBP △绕点C 逆时针旋转60︒，到达CAP '△的位置，显然， 60PCP '∠=︒，3P C PP ''==，5AP '=．在APP '△中，222222345AP P P AP ''+=+==，所以90APP '∠=︒．故 9060150APC APP P PC ''∠=∠+∠=︒+︒=︒. 在APC △中，由余弦定理，得 2222cos150AC AP PC AP PC =+-⋅⋅︒2234243=+⨯⨯+25=+所以，等边三角形ABC16．2．3★★设O 是正三角形ABC 内一点，已知115AOB ∠=︒，125BOC ∠=︒，求以线段OA 、OB 、OC 为边构成的三角形的各角．解析 以B 为旋转中心，将AOB △按逆时针方向旋转60︒，旋转至CDB △，如图所示． 连结OD ．由于OB OD =，60OBD ∠=︒，所以OBD △是正三角形，故OD OB =． 又CD OA =，故OCD △是以OA 、OB 、OC 为边构成的一个三角形． 因此COD BOC BOD ∠=∠-∠ 1256065=︒-︒=︒，ODC BDC BDO ∠=∠-∠ AOB BDO =∠-∠ 1156055=︒-︒=︒，从而180655560OCD ∠=︒-︒-︒=︒．所以，以线段OA 、OB 、OC 为边构成的三角形的各角分别为65︒、55︒和60︒． 16．2．4★★如图，两个正方形ABCD 与AKLM （顶点按顺时针方向排列），求证：这两个正方形的中心以及线段BM 、DK 的中点是某正方形的顶点．CDQ K LRM SAPB解析 设P 、R 分别是正方形ABCD 、AKLM 的中心，Q 、S 分别是线段DK 、BM 的中点，先证PSR △是以PR 为斜边的等腰直角三角形．连结BK 、DM ，将ADM △绕A 逆时针旋转90︒，则D 、M 分别到B 、K 位置，所以BK DM =，BK DM ⊥．因为P 、S 分别是BD 、BM 的中点，所以12PS DM ∥．同理12SR BK ∥．所以PS SR ⊥，且PS SR =．即PSR △是以PR 为斜边的等腰直角三角形．同理可证PQR △也是以PR 为斜边的等腰直角三角形．故P 、Q 、R 、S 是正方形的四个顶点．16．2．5★★正方形ABCD 内有一点P ，1PA =，3PB =．PD =ABCD 的面积．ADB CPP'解析 将PAB △绕A 点旋转90︒，得P AD '△．连结PP '．易知90PAP '∠=︒，1PA PA '==．于是PP '=在P PD '△中，222279P P PD P D ''+=+==．所以P PD '△是直角三角形，从而135APD ∠=︒．由余弦定理得222AD PA PD PD =+⋅8=16．2．6★★在正方形ABCD 的边AB 和AD 上分别取点M 和K ，使得AM AK =，在线段DM 上取点P ，使得PCD PKA ∠=∠．证明：APM ∠是直角．AM BL K PDC解析 如图所示，在边BC 上取点L ，使BL AK =，连结KL 、AP 、PL ．由于PCD PKA ∠=∠，所以P 、C 、D 、K 四点共圆，作四边形PCDK 的外接圆和矩形 KDCL 的外接圆，因为这两个外接圆均过K 、D 、C 三点，从而这两圆是相同的，所以 90LPD LKD ∠=∠=︒． 易知Rt MAD △≌Rt LBA △.故以正方形ABCD 的中心为旋转中心，将Rt LBA △以逆对针方向旋转90︒，则L B A △旋转至MAD △，从而AL D M ⊥．又LP D M ⊥，故A 、P 、L 三点共线，所以90APM ∠=︒． 16．2．7★★★已知凸六边形123456A A A A A A 中，1223A A A A =，3445A A A A =，5661A A A A =， 135246A A A A A A ∠+∠+∠=∠+∠+∠．求证：（1）24612345612A A A A A A A A A S S =△；（2）624212A A A A ∠=∠，246412A A A A ∠=∠，264612A A A A ∠=∠．A 1A 2A 3A 45A 6A'4解析 （1）将234A A A △绕点2A 旋转，使23A A 与21A A 重合，得到214A A A '△，如图所示．连结46A A '． 因为135246()()A A A A A A ∠+∠+∠+∠+∠+∠ 720=︒，所以135A A A ∠+∠+∠ 246360A A A =∠+∠+∠=︒． 因此4161412360A A A A A A A ''∠=︒-∠-∠ 135360A A A =︒-∠-∠=∠.从而146A A A '△≌546A A A △， 246A A A △≌246A A A '△， 所以24624641234561122A A A A A A A A A A A A A S S S '==△．（2）由（1）可知624624126324A A A A A A A A A A A A '∠=∠=∠+∠ 2624A A A A =∠-∠，所以624212A A A A ∠=∠．同理可证：246412A A A A ∠=∠，264612A A A A ∠=∠．评注 本题通过旋转，把234A A A △、456A A A △、612A A A △拼成一个与246A A A △全等的新三角形246A A A '.也可以采取向246A A A △内部旋转的方法，把234A A A △、456A A A △、612A A A △放在26A A A 4△的内部，使之恰好“拼成”246A A A △．16．2．8★★★如图所示，P 、Q 是边长为1的正方形ABCD 内两点，使得 45PAQ PCQ ∠=∠=︒，求PAB PCQ QAD S S S ++△△△的值．ADQ PBCADQPQ'BQ''C(a)(b)解析 将AQD △绕点A 顺时针旋转90︒至AQ B '△，CQD △绕点C 逆时针旋转90︒至CQ B ''△，连结PQ '、PQ ''，则APQ '△≌APQ △，CPQ ''△≌CPQ △．又90ABQ CBQ ADQ CDQ '''∠+∠=∠+∠=︒，所以Q '、B 、Q ''三点共线，且 BQ DQ BQ '''==， 故PBQ PBQ S S '''=△△， 所以PAB PCQ QAD S S S ++△△△PAQ PBC QCD S S S =++△△△1122ABCD S ==正方形． 16．2．9★★在ABC △中，120A ∠︒≥，点P 不与A 重合．求证PA PB PC AB AC ++>+. 解析 如图，将PAB △绕点A 旋转至P AB ''△的位置，使CA 与AB '共线．于是 AB AC AB AC PC PB ''+=+<+．B'ACPBP'又因为120P AB PAC BAP PAC BAC ''∠+∠=∠+∠=∠︒≥，所以 18060PAP BAC '∠=︒-∠︒≤． 故在等腰PAP '△中， PA P A PP ''=≥．因此PB PP P B PA P B PA PB ''''''++=+≤≤， 从而PA PB PC AB AC ++>+.评注 此题似乎依赖于图形，P 在BAC ∠内，事实上P 在其他位置照样成立，方法完全一样． 16．2．10★★★凸四边形ABCD 中，点M 、N 分别是BC 、CD 的中点，且AM AN a +=（a 是常数），求证：22ABCDa S <四边形．ED NC FMBA解析 如图所示，将ABM △绕点M 旋转180︒得FCM △，将ADN △绕点N 旋转180︒得ECN △，连EF ，于是360ECF ECN BCD FCM ∠=︒-∠-∠-∠ 360ADC BCD ABC =︒-∠-∠-∠ 180DAB =∠<︒，所以EF 与凸四边形ABCD 的边不相交．故 FCM ECN AEF ABCD AMCN S S S S S =++<△△△四边形四边形122AE AF AM AN ⋅=⋅≤ 22222AM AN a +⎛⎫⋅=⎪⎝⎭≤． 16．2．11★★★如图，设D 为锐角ABC △内一点，且AC BD AD BC ⋅=⋅， 90ADB ACB ∠=∠+︒，求AB CDAC BD⋅⋅的值．A DBC解析 将线段BD 绕点B 顺时针旋转90︒到BE ，连结DE 、CE ． 因为ADB CAD CBD ACB ∠=∠+∠+∠，90ADB ACB ∠=∠+︒，所以 90CAD CBD ∠+∠=︒，又90CBD CBE ∠+∠=︒， 则CAD CBE ∠=∠． 由AC BD AD BC ⋅=⋅，得AC AD ADBC BD BE==，于是ACD BCE △∽△，所以ACD BCE ∠=∠， AC AD CDBC BE EC ==．从而A C B A C D B C D E C B B C ∠=∠+∠=∠+∠=∠．所以，A B C D E△△∽，则AB ACDE DC=，即AB CD AC DE ⋅=⋅．在Rt BDE △中，BD BE =，DE =，故AB CDAC BD⋅⋅。

《竞赛数学解题研究》之平面几何专题一、平面几何中的一些重要定理：1、梅涅劳斯定理：设D 、E 、F 分别是ABC ∆三边（或其延长线）上的三点，则D 、E 、F 三点共线的充要条件是1=⋅⋅EACEFC BF DB AD 。

2、塞瓦定理：设D 、E 、F 分别是ABC ∆三边（或其延长线）上的三点，则AF 、BE 、CD 三点共线的充要条件是1=⋅⋅EACEFC BF DB AD 。

3、托勒密定理：四边形ABCD 内接于圆的充要条件是CD BC CD AB BD AC ⋅+⋅=⋅4、西摩松定理：设P 是ABC ∆外接圆上任一点，过P 向ABC ∆的三边分别作垂线，设垂足为D 、E 、F ，则D 、E 、F 三点共线。

5、斯德瓦特定理：设P 是ABC ∆的边BC 边上的任一点，则BC PC BP AP BC AB PC AC BP ⋅⋅+⋅=⋅+⋅2226、共角定理：设ABC ∆和C B A '''∆中有一个角相等或互补（不妨设A=A '）则 C A B A ACAB S S C B A ABC ''⋅''⋅='''∆∆7、共边定理：设ABC ∆和C B A '''∆中有一个边相等，则CA B A ACAB S S C B A ABC ''⋅''⋅='''∆∆举例说明：1、设M 、N 分别是正六边形ABCDEF 的对角线AC 、CE 上的点，且AM:AC=CN:CE=k,如果BMN 三点共线，试求k 。

（IMO23,1982）2、在四边形ABCD 中，ABD ∆、BCD ∆、ABC ∆的面积之比为3：4：1，点M 、N 分别 是AC 、CD 上的点，且AM:AC=CN:CD, 并且BMN 三点共线，求证：M 、N 分别是AC 、 CD 的中点。

中学平面几何竞赛练习题及答案1．两线平行与垂直的证明（1）利用两线平行与垂直的判定定理。

（2）利用平行四边形的性质可证明平行；利用等腰△的“三线合一”可证明垂直。

（3）利用比例关系可证明平行；利用勾股定理的逆定理可证明垂直等。

2．线段或角的和差倍分的证明（1）转化为相等问题。

如要证明a=b±c，可以先作出线段p=b±c，再去证明a=p，即所谓“截长补短”，角的问题仿此进行。

（2）直接用已知的定理。

例如：中位线定理，Rt△斜边上的中线等于斜边的一半；△的外角等于不相邻的内角之和；圆周角等于同弧所对圆心角的一半等等。

3．线段或角相等的证明（1）利用全等△或相似多边形；（2）利用等腰△；（3）利用平行四边形；（4）利用等量代换；（5）利用平行线的性质或利用比例关系（6）利用圆中的等量关系等。

【竞赛例题剖析】【例1】∠ABC的顶点B在⊙O外，BA、BC均与⊙O相交，过BA与圆的交点K引∠ABC 平分线的垂线，交⊙O于P，交BC于M。

求证：线段PM为圆心到∠ABC平分线距离的2倍。

【分析】若角平分线过O，则P、M重合，PM=0，结论显然成立。

若角平分线不过O，则延长DO至D‘，使OD’=OD，则只需证DD‘=PM。

连结D’P、DM，则只需证DMPD‘为平行四边形。

过O作m⊥PK，则DD’,K P，∴∠D‘PK=∠DKPBL平分∠ABC，MK⊥BL→BL为MK的中垂线→∠DKB=∠DMK∴∠D’PK=∠DMK，∴D‘P∥DM。

而D’ D∥PM，∴DMPD‘为平行四边形。

【例2】在△ABC中，AP为∠A的平分线，AM为BC边上的中线，过B作BH⊥AP于H，AM的延长线交BH于Q，求证：PQ∥AB。

【分析】方法1、结合中线和角平分线的性质，考虑用比例证明平行。

倍长中线：延长AM至M’，使AM=MA‘，连结BA’，如图6-1。

PQ∥AB←←←←∠A‘BQ=180°-(∠HBA+∠BAH+∠CAP)= 180°-90°-∠CAP=90°-∠BAP=∠ABQ方法2、结合角平分线和BH⊥AH联想对称知识。

初中数学竞赛第二轮专题复习（2）几何证明的基本方法（1)一、常用定理梅涅劳斯定理 设',','C B A 分别是ΔABC 的三边BC ，CA ，AB 或其延长线上的点，若',','C B A 三点共线，则.1''''''=⋅⋅BC AC A B CB C A BA 梅涅劳斯定理的逆定理 条件同上,若.1''''''=⋅⋅BC AC A B CB C A BA 则',','C B A 三点共线。

塞瓦定理 设',','C B A 分别是ΔABC 的三边BC ，CA ，AB 或其延长线上的点，若',','CC BB AA 三线平行或共点，则.1''''''=⋅⋅BC AC A B CB C A BA 塞瓦定理的逆定理 设',','C B A 分别是ΔABC 的三边BC ，CA ，AB 或其延长线上的点，若.1''''''=⋅⋅BC AC A B CB C A BA 则',','CC BB AA 三线共点或互相平行。

角元形式的塞瓦定理 ',','C B A 分别是ΔABC 的三边BC ，CA ，AB 所在直线上的点，则',','CC BB AA 平行或共点的充要条件是.1'sin 'sin 'sin 'sin 'sin 'sin =∠∠⋅∠∠⋅∠∠BAB CBB CBC ACC AC A BAA 广义托勒密定理 设ABCD 为任意凸四边形，则AB •CD+BC •AD ≥AC •BD,当且仅当A,B ，C ，D 四点共圆时取等号.斯特瓦特定理 设P 为ΔABC 的边BC 上任意一点，P 不同于B ，C ，则有AP 2=AB 2•BC PC +AC 2•BCBP -BP •PC 。

图形变换1、理解并掌握折叠，旋转，平移与几何图形的综合应用2、理解动点问题与几何图形的综合应用一、几何变换性质以及相关解题思路1、折叠3、平移2、旋转4、动点问题命题点1 轴对称图形和中心对称图形1.（2019年泰州中考第2题3分）如图图形中的轴对称图形是（）A．B．C．D．2.（2019年无锡中考第6题3分）下列图案中，是中心对称图形但不是轴对称图形的是（）3.（2019年盐城中考第2题3分）下列图形中，既是轴对称图形又是中心对称图形的是（）A．B．C．D．4.（2019年扬州中考第1题3分）下列图案中，是中心对称图形的是( )命题点2图形翻折1.（2019年连云港中考第8题3分）如图，在矩形ABCD 中，AD ＝AB ．将矩形ABCD 对折，得到折痕MN ；沿着CM 折叠，点D 的对应点为E ，ME 与BC 的交点为F ；再沿着MP 折叠，使得AM 与EM 重合，折痕为MP ，此时点B 的对应点为G ．下列结论：①△CMP 是直角三角形；②点C 、E 、G 不在同一条直线上；③PC ＝MP ；④BP ＝AB ；⑤点F 是△CMP 外接圆的圆心．其中正确的个数为（ ）A ．2个B ．3个C ．4个D ．5个2.（2019年淮安中考第16题3分）如图，在矩形ABCD 中，AB ＝3，BC ＝2，H 是AB 的中点，将△CBH 沿CH 折叠，点B 落在矩形内点P 处，连接AP ，则tan ∠HAP ＝__________．3.（2019年宿迁中考第18题3分）如图，正方形ABCD 的边长为4，E 为BC 上一点，且BE＝1，F为AB边上的一个动点，连接EF，以EF为边向右侧作等边△EFG，连接CG，则CG的最小值为．4.（2019年盐城中考第25题10分）如图①是一张矩形纸片，按以下步骤进行操作：（Ⅰ）将矩形纸片沿DF折叠，使点A落在CD边上点E处，如图②；（Ⅰ）在第一次折叠的基础上，过点C再次折叠，使得点B落在边CD上点B′处，如图③，两次折痕交于点O；（Ⅰ）展开纸片，分别连接OB、OE、OC、FD，如图④．【探究】（1）证明：△OBC≌△OED；（2）若AB＝8，设BC为x，OB2为y，求y关于x的关系式．5.（2019年连云港中考第27题14分）问题情境：如图1，在正方形ABCD中，E为边BC上一点（不与点B、C重合），垂直于AE的一条直线MN分别交AB、AE、CD于点M、P、N．判断线段DN、MB、EC之间的数量关系，并说明理由．问题探究：在“问题情境”的基础上，（1）如图2，若垂足P恰好为AE的中点，连接BD，交MN于点Q，连接EQ，并延长交边AD于点F．求∠AEF的度数；（2）如图3，当垂足P在正方形ABCD的对角线BD上时，连接AN，将△APN沿着AN翻折，点P落在点P'处．若正方形ABCD的边长为4 ，AD的中点为S，求P'S的最小值．问题拓展：如图4，在边长为4的正方形ABCD中，点M、N 分别为边AB、CD上的点，将正方形ABCD沿着MN翻折，使得BC的对应边B'C'恰好经过点A，C'N交AD于点F．分别过点A、F作AG⊥MN，FH⊥MN，垂足分别为G、H．若AG＝，请直接写出FH的长．命题点3图形旋转1.（2019年镇江中考第10题2分）将边长为1的正方形ABCD绕点C按顺时针方向旋转到FECG的位置（如图），使得点D落在对角线CF上，EF与AD相交于点H，则HD＝____________．（结果保留根号）2.（2019年淮安中考第27题12分）如图①，在△ABC中，AB＝AC＝3，∠BAC＝100°，D是BC的中点．小明对图①进行了如下探究：在线段AD上任取一点P，连接PB．将线段PB绕点P按逆时针方向旋转80°，点B的对应点是点E，连接BE，得到△BPE．小明发现，随着点P在线段AD上位置的变化，点E的位置也在变化，点E可能在直线AD的左侧，也可能在直线AD上，还可能在直线AD的右侧．请你帮助小明继续探究，并解答下列问题：（1）当点E在直线AD上时，如图②所示．①∠BEP＝°；②连接CE，直线CE与直线AB的位置关系是．（2）请在图③中画出△BPE，使点E在直线AD的右侧，连接CE．试判断直线CE与直线AB 的位置关系，并说明理由．（3）当点P在线段AD上运动时，求AE的最小值．3.（2019年宿迁第27题12分）如图①，在钝角△ABC中，∠ABC＝30°，AC＝4，点D为边AB中点，点E为边BC中点，将△BDE绕点B逆时针方向旋转α度（0≤α≤180）．（1）如图②，当0＜α＜180时，连接AD、CE．求证：△BDA∽△BEC；（2）如图③，直线CE、AD交于点G．在旋转过程中，∠AGC的大小是否发生变化？如变化，请说明理由；如不变，请求出这个角的度数；（3）将△BDE从图①位置绕点B逆时针方向旋转180°，求点G的运动路程．命题点4 动态几何探究1.（2019年镇江中考第17题3分）如图，菱形ABCD的顶点B、C在x轴上（B在C的左侧），顶点A、D在x轴上方，对角线BD的长是1032，点E（﹣2，0）为BC的中点，点P在菱形ABCD的边上运动．当点F（0，6）到EP所在直线的距离取得最大值时，点P恰好落在AB的中点处，则菱形ABCD的边长等于（）A ．310 B ． C ．316 D ．32.（2019年无锡中考第18题3分）如图，在△ABC 中，AB ＝AC ＝5，BC ＝，D 为边AB 上一动点（B 点除外），以CD 为一边作正方形CDEF ，连接BE ，则△BDE 面积的最大值为_____．3.（2019年苏州中考第27题10分）已知矩形ABCD 中，AB =5cm ，点P 为对角线AC 上的一点，且AP =2cm ．如图①，动点M 从点A 出发，在矩形边上沿着A→B→C 的方向匀速运动（不包含点C ）．设动点M 的运动时间为t （s ），△APM 的面积为S （cm 2），S 与t 的函数关系如图②所示．（1）直接写出动点M 的运动速度为cm/s ，BC 的长度为cm ；（2）如图③，动点M 重新从点A 出发，在矩形边上按原来的速度和方向匀速运动，同时，另一个动点N 从点D 出发，在矩形边上沿着D→C→B 的方向匀速运动，设动点N 的运动速度为v （cm/s ）．已知两动点M ，N 经过时间x （s ）在线段BC 上相遇（不包含点C ），动点M ，N 相遇后立即同时停止运动，记此时△APM 与△DPN 的面积分别为S 1（cm 2），S 2（cm 2） ①求动点N 运动速度v （cm/s ）的取值范围；②试探究S 1•S 2是否存在最大值，若存在，求出S 1•S 2的最大值并确定运动时间x 的值；若不存在，请说明理由.4.（2019年无锡中考第28题10分）如图1，在矩形ABCD 中，BC ＝3，动点P 从B 出发，以每秒1个单位的速度，沿射线BC 方向移动，作△PAB 关于直线PA 的对称△PAB′，设点P 的运动时间为t (s)．（1）若AB ＝．①如图2，当点B′落在AC 上时，显然△PAB′是直角三角形，求此时t 的值；②是否存在异于图2的时刻，使得△PCB′是直角三角形？若存在，请直接写出所有符合题意的t 的值？若不存在，请说明理由．（2）当P 点不与C 点重合时，若直线PB′与直线CD 相交于点M ，且当t ＜3时存在某一时刻有结论∠PAM ＝45°成立，试探究：对于t ＞3的任意时刻，结论∠PAM ＝45°是否总是成立？请说明理由．5.（2019年扬州中考第27题12分）问题呈现如图，四边形ABCD是矩形，AB=20，BC=10，以CD为一边向矩形外部作等腰直角△GDC，∠G=90°，点M在线段AB上，且AM=a，点P沿折线AD-DG运动，点Q沿折线BC-CG运动（与点G不重合），在运动过程中始终保持线段PQ∥AB.设PQ与AB之间的距离为x.（1）若a=12.①如图1，当点P在线段AD上时，若四边形AMQP的面积为48，则x的值为_________；②在运动过程中，求四边形AMQP的最大面积；（2）如图2，若点P在线段DG上时，要使四边形AMQP的面积始终不小于50，求a的取值范围.6.（2019年扬州中考第28题12分）如图，已知等边△ABC的边长为8，点P是A B边上的一个动点（与点A、B不重合），直线l是经过点P的一条直线，把△ABC沿直线l折叠，点B的对应点是点B’.（1）如图1，当PB=4时，若点B’恰好在AC边上，则AB’的长度为______；（2）如图2，当PB=5时，若直线l∥AC，则BB’的长度为；（3）如图3，点P在AB边上运动过程中，若直线l始终垂直于AC，△ACB’的面积是否变化？若变化，说明理由；若不变化，求出面积；（4）当PB=6时，在直线l变化过程中，求△ACB’面积的最大值。

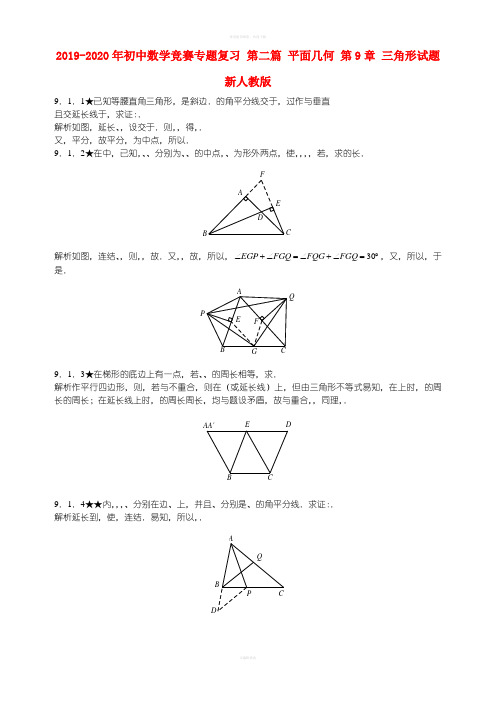
2019-2020年初中数学竞赛专题复习 第二篇 平面几何 第9章 三角形试题新人教版9．1．1★已知等腰直角三角形，是斜边．的角平分线交于，过作与垂直 且交延长线于，求证：． 解析如图，延长、，设交于．则，，得，． 又，平分，故平分，为中点，所以． 9．1．2★在中，已知，、、分别为、、的中点，、为形外两点，使，，，，若，求的长．F AE DBC解析如图，连结、，则，，故．又，，故，所以，30EGP FGQ FQG FGQ ∠+∠=∠+∠=︒，又，所以，于是．ACG QPEF9．1．3★在梯形的底边上有一点，若、、的周长相等，求．解析作平行四边形，则，若与不重合，则在（或延长线）上，但由三角形不等式易知，在上时，的周长的周长；在延长线上时，的周长周长，均与题设矛盾，故与重合，，同理，．B CEDAA'9．1．4★★内，，，、分别在边、上，并且、分别是、的角平分线．求证：． 解析延长到，使，连结．易知，所以，．ABCDQP因1402BDP BPD ABC ACB ∠=∠=∠=︒=∠，所以，AC AD AB BD AB BP ==+=+． 于是．9．1．5★★设等腰直角三角形中，是腰的中点，在斜边上，并且．求证： ．解析如图，作的平分线，在上．ABCEFD由于，，，故，故． 又，，于是，于是．9．1．6★★设、都是等腰直角三角形，、是各自的斜边，是的中点，求证：也是等腰直角三角形． 解析如图，作、、、分别垂直于直线，垂足为、、、．AE FGMBQ PCN由90EBM ABQ BAQ ∠=︒-∠=∠，，，故有，．同理，，所以， ．又得，且，故．又由，故 结论成立．9．1．7★★已知，，、在上（靠近），求证：的充要条件是．ABDEFC解析如图，作，且，则，又，故，，且． 若，则，因，得，则222222DE EF EC FC EC BD ==+=+． 反之，若，由得．又，故，又，于是．9．1．8★★两三角形全等且关于一直线对称，求证：可以将其中一个划分成3块，每一块通过平移、 旋转后拼成另一个三角形．解析如图，设与关于对称，分别找到各自的内心、，分别向三边作垂线、、 与、、，于是6个四边形……均为轴对称的筝形，且四边形四边形，所以两者可通过平移、旋转后重合；同理，另外两对筝形也可通过平移、旋转后重合．AECDF BA'B'C'D'F'E'l l'l9．1．9★★★已知：两个等底等高的锐角三角形，可以将每个三角形分别分成四个三角形，分别涂上红色、蓝色、黄色和绿色，使得同色三角形全等． 解析如图，设，至距离等于至距离，取各自的中位线、，则．由、均为锐角三角形，可在、上各取一点、，使图中标相同数字的角相等，于是，，，． 评注还有一种旋转而不是对称的构造法．A BC DEF A'B'D'C'E'F'123451465264152432519．1．10★已知与中，，，，与是否一定全等？AB CA'解析如图，让与重合，与重合，、在同侧，若与重合，则；否则由条件知四边形为梯形和圆内接四边形，于是它是一个等腰梯形，于是，，．综上，可知与全等．评注本题也可以运用三角形面积公式、余弦定理结合韦达定理来证明． 9．1．11★★如图所示，已知、均为正三角形，、、分别为、和的中点，求证：为正三角形．ABEDM TS CN L解析如图，设、中点分别为、，连结、、、．则四边形为平行四边形，设，则60180240NSM LTM θθ∠=︒+︒-=︒-=∠，360120240NCL θθ∠=︒-︒-=︒-，又，，故， ，于是为正三角形．评注注意有时在另一侧，此时120NSM LTM NCL θ∠=∠=∠=︒+，不影响最终结论． 9．1．12★★★中，，．，，是中点，、分别在、上（可落在端点），满足，求的最小值（用、、表示）．解析如图，延长至，使，连结、、、由于是、的中点，故，，，又垂直平分，故222222BP CQ BP BN PN PQ +=+==．取中点（图中未画出），则，于是的最小值为，取到等号仅当即四边形为矩形时．NMP CBQA9．1．13★★★已知为内一点，，由作、的垂线，垂足分别是、．C ABDEFMP L设为中点，求证：．解析如图所示，取中点，中点，连、、、．显然四边形是平行四边形，所以，．． 又由，所以，；同理，．由，所以D EM D EP PEM D FP PFL D FL ∠=∠+∠=∠+∠=∠，从而，所以． 9．1．14★★在中，已知，、分别是边、上的点，且，，，求的度数． 解析如图，延长到，使，连、．CEA DB F因为，所以，， ．CE ED DB DB BF DF =+=+=． 于是，，． 又因为，， 所以 ，，18020ECD CED EDC ∠=︒-∠-∠=︒． 在和中，，，，所以，故 ．于是，6020DCB CDE FCB ∠=︒-∠-∠=︒．9．1．15★★在中，、为锐角，、、分别为边、、上的点，满足，，且．求证：． 解析若，则在上取一点，使．连结并延长交于，连结．在与中，，，，故．于是有，，所以．又易知，因此．但另一方面，由，知，所以AFM NE BDC()12ACB ACB ACB >∠+∠=∠． 从而．矛盾，故假设不成立． 若，同法可证此假设不成立． 综上所述，于是由 知，从而．9．1．16★★如图，为边长是1的等边三角形，为顶角是的等腰三角形，以为顶点作一个角，角的两边分别交、于、，连结，形成一个． 求的周长． AM NBC DE解析延长到，使，连结．易知在与中有， ，，从而．所以，． 于是在与中有，，60MDN MDB CDN EDC CDN EDN ∠=︒=∠+∠=∠+∠=∠．从而，故．所以AM MN AN AM NE AN AM NC CE AN AM MB NC AN ++=++=+++=+++=．9．1．17★★★为等腰直角三角形，，点、分别为边和的中点，点在射线上，且，点在射线上，且，求证：．解析取中点，连．EADF MBNC在与中，，，，故．于是有，，． 同样易知，于是有． 在与中，，，由知，所以．于是有，90EFA ACN EFD ∠=∠=︒=∠． 从而在与中有，，故．于是有， ．总之，90EDF MDA EDF NAC EDF AEF EDF FED ∠+∠=∠+∠=∠+∠=∠+∠=︒，即 ．9．1．18★★★已知，延长至，使，连结与交于，为的外心，则、、、共圆．ADBC O PQ解析如图连好辅助线，由于DPA BAP PAD CQP ∠=∠=∠=∠，故，设 OCP OCQ OQC θ∠=∠=∠=，则，又，，故，于是，于是2BOD QOC QPC BCD ∠=∠=∠=∠，因此、、、共圆．9．1．19★★★已知和，，且，和分别是、的中点，，问两个三角形是否必定全等？解析如图，作出外心(及相应的、图中未画出)． 若在上，则，此时与未必全等． 若不与重合，则2sin 2sin BC B C AO A O A A ''''==='，cos cos OD BO A AO A==， ． 当、、共线，则，，所以，，从而 ． 当、、不共线，则，，于是（或），于是由三角形全等可得(或)，（或），故有（或）． 评注此题亦可用中线长公式证明． 9．1．20★★如果两个三角形满足“”，它们不一定全等，此时称它们是相近的，现在有一三角形，作与之“相近”，……一般有与相近，问是否存在一个，使与相做且不全等？解析这是不可能的．因为由正弦定理，与有等大的外接圆（它们有一对内角相等或互补），从而 推出与x 有等大的外接圆，它们不可能只相似不全等．9．1．21★★★是否存在两个全等的三角形与，可划分为两个三角形与，可划分成两个三角形与，使，与却不全等？解析这样的两个三角形是存在的，如图(a)、(b)，设不等边三角形，其中22''BC AB AC A B A C B C ''''=⋅=⋅=，不妨设是各自的最长边，则、为各自的最短边．在、上分别找、，使，，则由于，故，所以，又因为，，因此，而显然不与全等．（若，还可避免相似．）ABCDA'B'C'D'图(a)图(b)9．1．22★★★已知中，，是内心，的垂直平分线分别交、于、，、在上，，求证：． 解析如图，连结、、、．易诮与为全等之正三角形，， ．ANMTB E F CIS两端延长至与，使，则60SMB AMN BMI ∠=∠=∠=︒，于是，同理，因此180S T MIB NIC ∠+∠=∠+∠=︒，． 而、将三等分，、将三等分，于是由平行线分线段成比例，知()． 评注读者可以考虑：如果是否有． 9．1．23★★★已知锐角三角形，，，的垂心和外心分别为和，分别与、交于、，证明：的周长为，．解析如图，连结、、、．由可知在一侧，在一侧． 因，故，而，于是，．又90OAB C YAM ∠=︒-∠=∠，故，为正三角形． 又60XOB YOC YOC OCY ∠+∠=︒=∠+∠，故，，又，故，．于是．又，做()()112233OM XY YC AB AC AC AB AC AB AC ⎡⎤=-=+--+=-⎢⎥⎣⎦． §9．2特殊三角形9．2．1★在直角三角形中，是斜边，，是中点，是上一点，，求．BADEC解析如图，连结．设，因，，，则，．故AB == 9．2．2★已知中，，，，为在平分线上的射影，为中 点，求．解析延长交于．由．知，．又，故()()11128147222PM CQ AC AQ =-=⨯-=∥．ABCQ P M9．2．3★等腰三角形中，，为直线上一点，则 （在上）， （在外）．解析如图，设在上且较靠近．作于，则为中点，于是AB D E C()()BD CD BE DE CE DE ⋅=-⋅+．当在外时的结论同理可证．评注这是斯图沃特定理在等腰三角形的特殊情形，具有十分广泛的用途（例如题9．2．1），亦可用相 交弦定理证明．9．2．4★★已知锐角三角形中，、是高，为垂心，，是的中点，求证： ．AEBFDCH解析如图，连结，则．于是2222FH EF EH CH EF AH HD EF =-⋅=-⋅=-222AH HD HD HD EF HD AD ⋅-+=-⋅+22222HD EF HD BC HD EF HD =-⋅+=-⋅ ．由于，故12FH EF DH BC DH =-=-． 9．2．5★已知斜边为的直角三角形中，在上的投影为．若以、、为 三边可以构成一个直角三角形，求的所有可能值． BHAC解析显然由、、构成的直角三角形中，不是斜边，且． 若，则为斜边．设，，，则由的面积知，又，故．易知，则由前式知，得，故． 同理，若，可得． 所以的可能值为或．9．2．6★★已知中，为高，在上， 以下哪些条件能判定： (1)： (2)； (3)．AB D C解析设，，，则，． 先看条件(1)：．若，则；否则不妨设，则22x y -．得，于是，矛盾． 故．再看见条件（2）：．则，于是，故． 最后条件（3）：11y x =+．于是22x y xy -==．若，则()xy x y =+，仍有，矛盾，故．所以三个条件都能判定．9．2．7★已知是等腰直角三角形的斜边上任意一点，求． 解析如图，作于．ABD CP不妨设．在上，，则，，于是()()222221122BP CP a a a +=++-=+．又．故． 评注请读者考虑，若对上任一点，有为定值，是否可认为为等腰直角三角形． 9．2．8★★在中，，，，是内一点，过点向的 三边、、分别垂线、、，垂足分别为、、，且，求 的长．解析如图，由于2222220BD CD CE AE AF BF -+-+-=，于是AFEPBDC()()222222(17)18190BD BD CE CE AF AF --+--+--=，此即． 而，故．所以118BD BF BD AB AF AB +=+-=-=． 9．2．9★★已知中，，是的中垂线，，， 求．AFDB E C解析如图，不妨设，则，．作的平分线，由于3BDE BAE ABD BAE∠=∠=∠+∠，故．因此，，，从而，，所以．设，则，，因此()2221x x-=++，，，（舍）．于是，．9．2．10★★正三角形内有一点，关于、的对称点分别为、，作平行四边形，求证：．A SMRQB CP解析如图，设与交于，连结，则，垂直平分，，为正三角形，，于是四边形为等腰梯形，的中垂线即的中垂线．于是，．9．2．11★★与相切于点，与相交于、，若，，，求．BC D AKT解析如图，由题意可得，作于，则，又，故，．再作于，设，则，，．于是．9．2．12★已知大小相等的等边与等边有三组边分别平行，一个指向上方，一个指向下方，相交部分是一个六边形，则这个六边形的主对角线共点．A D KR QEHBFGCP解析如图，设两个三角形的边的交点依次为、、、、、．设、的高为，则正的高（与的距离）正的高，于是，、互相平分，同理、互相平分，于是、、的中点为同一点，结论成立． 9．2．13★★★★求证：过正三角形的中心任作一条直线，则、、三点至的距离平方和为常数．AlB'A'OC'B QC P解析如图，不妨设与、相交，且与延长线交于(平行容易计算)．由中位线及重心性质，知．故222222()B B C C A A B B C C B B C C '''''''++=++⋅．连结、，作，易知B BP QOP C CP ''△∽△∽△，故，． 对于等腰三角形，有．因此()()222222222223OQ OQ B B C C B B C C CP BP CP BP BC CP BP OP OP''''++⋅=++⋅=+⋅= ()222222333OQ BC OP OC OQ OP +-=(定值)，这里用到了． 于是、、三点至的距离平方和为，结论得证．§9．3三角形中的巧合点9．3．1★已知：是内一点，、、延长后分别交对边于、、，若 AH HD BH HE CH HF ⋅=⋅=⋅，则是的垂心， 解析如图，由条件知，故，同理，，故．A FEHBDC又，故，这样可得，故为之垂 心．9．3．2★★求证：到三角形三顶点的距离平方和最小的点是三角形的重心． 解析设中，、、是中线，是重心，是任一点．由斯图沃特定理，并考虑到 结论成立． ，得2222122339MG AM DM AD =+-．①又由中线长公式，有 ()22221124MD BM CM BC =+-， ()22221124GD BG CG BC =+-． 代入式①，得()()222222230MG MA MB MC GA GB GC =++-++≥．结论成立．9．3．3★★★已知，是锐角的垂心，是中点，过作的垂线，交、于、，求证：是中点．AQ NMHBD PC解析设两条高为、．又不妨设在上．由于，90AHM DHP HDC ∠=︒-∠=∠，故，于是，同理，又，故．9．3．4★★★的边、、上分别有点、、，且，求证：的重心与的重心是同一点．解析在上取一点，使，则，所以，四边形为平行四边形，设与交于，又设的中点为，连结、、，与交于，于是由，得，于是，于是，所以为与之重心．AFMG EBDPCN9．3．5★★★已知，，是重心，，求证：是正三角形． 解析设三条中线分别为、、．连为中位线．于是由条件知、、、共圆，故，于是．由于，，代入，得． 在外作等腰，使，，连结，．由圆心角与圆周角的关系，211333GP BP AD AD AD GD PD====+=+，故、、三点共线，故，于是，又，故为正三角形．AF EB DCPG9．3．6★★★已知是上一点，、、都是正三角形，、在同侧，在另一侧，求证：以这三个正三角形的中心为顶点的三角形是正三角形，且它的中心在上．又问此题如何推广？AB CEFRR'D Q'P'Q解析如图，设、、分别为、和的中心，则由题11．2．25知为正三角形．过、、分别作的垂线、、，则，又，故．又设中点为（图中未画出），于，则，且．设与交于，则，所以为的中点．评注此题不难推广，只需，，此时，、、为各自对应的重心，则必有之重心位于上．9．3．7★★★内有一点，连结、、并延长，分别与对边相交，把分成六个小三角形，若这六个小三角形中有三个面积相等，则点是否必为之重心？解析如图，设、、交于．由对称性，可分四种情况讨论．AFEPB D C（1）．于是，，由梅氏定理（或添平行线），得，为中心．（2）．此时，故、分别为、中点，为重心． （3）．此时有，由塞瓦定理，，于是，回到情形（1）． （4），见题15．1．58． 综上所知，答案是肯定的．9．3．8★★★设有一个三角形三角之比为，作两较大角的平分线，分别交对边于、．求证：这个三角形的重心在上．解析如图(a)，设为最小角，作中线，交于，于是只要证明．分别作，、在直线上，则，故问题变成，或1BC BC CM BN CF BEAB AC AM AN AG AG +=+=+=． 不妨设，，，，在上找一点，使，又作，在上，则各角大小如图(b)所示．于是，故 11BC AP CP BQ BCAC AC AC AB AB==-=1-=-． ABCD E FNMGA QP B C2θ3θ2θ3θ3θθθ图(a)图(b)9．3．9★★★不等边锐角中，、分别是其垂心和重心，求证：若， ．ABDECGH解析设的一条中线与高分别为、，则欲证结论等价于．熟知，．于是结论变为22cot cos 3AD BC AE A AB AC A =⋅⋅=⋅⋅． 设，，，则由中线长及余弦定理，知欲证式左端，右端，整理，得，于是剩下的任务是证明这个等价条件． ，同理有另两式，于是条件变为， 由正弦及余弦定理，知上式即，或()()22222222262()ac a c b b c a +-++-=+-，化简即得．9．3．10★★已知凸四边形中，，，是否一定为之外心？ABDC解析当固定．由题设、固定，于是、外接圆固定，它们的交点、固定，又若为外心时，确为的外接圆和的外接圆之异于的交点，因此，结论成立． 9．3．11★★★已知锐角的外接圆与内切圆的半径分别为、，是外心，至三边距离之和为，试用、表示． 解析易知()cos cos cos L R A B C =++．设三边分别为、、，由于等，则()()cos cos cos a b c A B C ++⋅++= cos cos cos a b c a A b B c C +++++，于是．①又等，可得()()11cos cos cos 22ABC R a A b B c C S r a b c ++==++△，故式①的右端．于是．9．3．12★★★★：已知，、分别在、上，、交于，，求证：、、、的外心四点共圆．AED BCOKO 1O 2解析如图，设、的外心分别为、，为的外心，于是垂直平分．垂直平分． 设，则由垂径定理知，，于是．易知过中点（由塞瓦定理或面积比），作，在上，则，又 12180KDF EFD O OO ∠=︒-∠=∠，故．又设，的外心分别为、（图中未画出），于是、分别在直线与上， 且，于是4312OO O KFD OO O ∠=∠=∠，于是、、、四点共圆．9．3．13★★★已知：中，，是中点，为重心，为外心，求证：． 解析1如图，延长交于，则，．连结并延长，分别交、于、，则为重心，，，易见2323BHDO BH DFAD AH AGAH ===． ADEF OGB H C又，90ODF ADE DAG ∠=︒-∠=∠，，对应边垂直，所以． 解析2为外心，故22222CO DO AO DO AD -=-=； 而由中线公式，CF =DF 于是22222CF DF AD CO DO -==-，于是．9．3．14★★★设和分别是的内心和外心，求证：的充分必要条件是．解析延长与外接圆交于点，连结、、，则 ．D由内心性质知，，结合托勒密定理得 AD BC AB CD AC BD ⋅=⋅+⋅ ， 所以，所以902AB ACAIO BC+∠︒⇔≤≤， 故的充要条件是．评注本题的关键是先把转换为，然后再用托勒密定理．托勒密定理是：圆内接四边形的对角线的乘积等于对边乘积的和．9．3．15★★★设是的外接圆，是三角形重心，延长、、，分别交于、、，则．AF ERQGBP DC 解析设、、的中点分别为、、，则由中线长公式及相交弦定理，有（此处三边分别设为、、） AG AG AGBP CP GD GP PD GP AP==⋅++22223133APAP BP CP AP BP CP AP AP ==⋅+⋅+ 2222222222222122211132244b c a b c a a b c b c a a +-+-==+++-+． 同理，有 ， ．三式相加，即得结论． 9．3．16★★在内，平分，，求证：是内心． 解析如图，作，在上，在上，则，，AEF BCI1902BEI IFC A BIC ∠=∠=︒+∠=∠．又1902EBI EIB A EIB FIC ∠+∠=︒-∠=∠+∠，故，于是，．而，故，，所以为内心．9．3．17★★已知：中，，是内心，与垂直于，求的值． 解析设三边长分别为、、，则． 易知若设，，则，． ，于是2133DE P a b c a a BE CE p a b c a -+-====⋅++． 9．3．18★★设中，最长，在其上分别找两点、，使，，又设为内心，求（用、、及其组合表示）．解析如图，连结、、、．CABM NI易知，，同理，为的外心，因此 MCN ACN BCM C ∠=∠+∠-∠11909022A B C =︒-∠+︒-∠-∠，2180MIN MCN C ∠=∠=︒-∠．9．3．19★★★★的边上有一点，与的内心与、四点共圆，求证： ．AMNE FBDCPI 1I 2解析如图，设与的内心分别为与．连结、、、、，两端延长，分别交、于、，则由条件知()1112AEF ABI EI B ABC ACB ∠=∠+∠=∠+∠，同理也是此值，于是．又设与交于，则由角平分线性质知，故由梅氏定理（直线截及直线截），得（此处、分别为、延长后与、之交点），又由角平分线性质，知，于是结论成立． 9．3．20★★★已知中，，、分别为其外心与内心，在上，，求证：． 解析如图，不妨设在内，且在“之上”(在形外、之下类似处理），连结、，则，故、、、共圆，于是ODC ICD OIK ICD ∠+∠=∠+∠．这里为、直线之交点．AD O KIBC由于，故9090OIK ICD BCI ICD ∠+∠=︒-∠+∠=︒，于是．9．3．21★★设为的重心，已知，且，求的面积．解析1由题意可画出图(a)，令为中点，，垂足为点，因为重心，可知．由勾股定理可知222222222GE GB EBGE GA EAGE GD DE⎧=-⎪=-⎨⎪=-⎩①②③，CA BD EG22322(a)令．由①与②可得(()(()2222c DE c DE-+=--，化简后可得，即，代入③得，再代入①式可得，解方程可得，，故的面积=的面积．解析2由题意可画出图(b)，令为中点，在的延长线上取点使得，因此之面积为之面积的一半．此时因与互相平分，可知四边形为平行四边形，也因此可知，即的三边长为2、、，故可知为直角三角形，故的面积为，所以的面积的面积．(b)22232GDBAC22E119．3．22★★★已知120AFB BFC CFA∠=∠=∠=︒，为异于的任一点，求证：PA PB PC FA FB FC++>++．解析如图，在外作正三角形，由于，，故四边形的内角均小于，是凸四边形．ADFF'PP'B C对于中任一异于的点，将、均以点为中心顺时针旋转，至希望能帮助您，欢迎下载可编辑修改 和，则与均为正三角形．由全等知AP BP CP PP DP CP CD DF F F FC AF BF CF ''''++=++>=++=++，这是因为是一条折线，而，，、、、四点共线且仅对于满足四点共线．评注当内角均小于时，满足条件的点称为的费马点（当有内角比如时，到、、距离之和最小的点正是点）． .。

图形的变换一、选择题1．下列几何图形中，一定是轴对称图形的有（）A．2个B．3个C．4个D．5个2．有一个四等分转盘，在它的上、右、下、左的位置分别挂着“众”、“志”、“成”、“城”四个字牌，如图1．若将位于上下位置的两个字牌对调，同时将位于左右位置的两个字牌对调，再将转盘顺时针旋转90°，则完成一次变换．图2，图3分别表示第1次变换和第2次变换．按上述规则完成第9次变换后，“众”字位于转盘的位置是（）A．上B．下C．左D．右3．下列图形中，既是轴对称图形，又是中心对称图形的是（）A．等腰梯形 B．平行四边形C．正三角形 D．矩形4．如图①～④是四种正多边形的瓷砖图案．其中，是轴对称图形但不是中心对称的图形为（）A．①③ B．①④ C．②③ D．②④5．如图，把矩形ABCD沿EF对折后使两部分重合，若∠1=50°，则∠AEF=（）A．110°B．115°C．120°D．130°6．下面四X扑克牌中，图案属于中心对称图形的是图中的（）A．B．C．D．7．下面的图形中，既是轴对称图形又是中心对称图形的是（）A．B．C．D．8．将如图所示的图案按顺时针方向旋转90°后可以得到的图案是（）A．B．C．D．9．若将图中的每个字母都看成独立的图案，则这七个图案中是中心对称图形的有（）A．1个B．2个C．3个D．4个10．下列图形中，是轴对称图形的是（）A．B．C．D．11．下面的图形中，是中心对称图形的是（）A．B． C．D．二、填空题12．如图，点G是△ABC的重心，CG的延长线交AB于D，GA=5cm，GC=4cm，GB=3cm，将△ADG绕点D旋转180°得到△BDE，则DE=cm，△ABC的面积=cm2．13．已知等腰三角形的一条腰长是5，底边长是6，则它底边上的高为．14．将线段AB平移1cm，得到线段A′B′，则点A到点A′的距离是cm．三、解答题15．如图，方格纸中的每个小正方形的边长均为1．（1）观察图1、2中所画的“L”型图形，然后各补画一个小正方形，使图1中所成的图形是轴对称图形，图2中所成的图形是中心对称图形；（2）补画后，图1、2中的图形是不是正方体的表面展开图？（填“是”或“不是”）16．如图，在平面直角坐标系中，△ABC和△A1B1C1关于点E成中心对称．（1）画出对称中心E，并写出点E、A、C的坐标；（2）P（a，b）是△ABC的边AC上一点，△ABC经平移后点P的对应点为P2（a+6，b+2），请画出上述平移后的△A2B2C2，并写出点A2、C2的坐标；（3）判断△A2B2C2和△A1B1C1的位置关系．（直接写出结果）17．在一平直河岸l同侧有A，B两个村庄，A，B到l的距离分别是3km和2km，AB=akm（a ＞1）．现计划在河岸l上建一抽水站P，用输水管向两个村庄供水．方案设计：某班数学兴趣小组设计了两种铺设管道方案：图1是方案一的示意图，设该方案中管道长度为d1，且d1=PB+BA（km）（其中BP⊥l于点p）；图2是方案二的示意图，设该方案中管道长度为d2，且d2=PA+PB（km）（其中点A'与点A关于I对称，A′B与l交于点P．观察计算：（1）在方案一中，d1=km（用含a的式子表示）；（2）在方案二中，组长小宇为了计算d2的长，作了如图3所示的辅助线，请你按小宇同学的思路计算，d2=km（用含a的式子表示）．探索归纳（1）①当a=4时，比较大小：d1（）d2（填“＞”、“=”或“＜”）；②当a=6时，比较大小：d1（）d2（填“＞”、“=”或“＜”）；（2）请你参考右边方框中的方法指导，就a（当a＞1时）的所有取值情况进行分析，要使铺设的管道长度较短，应选择方案一还是方案二？图形的变换参考答案与试题解析一、选择题1．下列几何图形中，一定是轴对称图形的有（）A．2个B．3个C．4个D．5个【考点】轴对称图形．【分析】关于某条直线对称的图形叫轴对称图形．【解答】解：所有图形沿某条直线折叠后直线两旁的部分能够完全重合，那么一定是轴对称图形的有5个，故选D．【点评】轴对称图形的判断方法：如果一个图形沿一条直线折叠后，直线两旁的部分能够互相重合，那么这个图形叫做轴对称图形．2．有一个四等分转盘，在它的上、右、下、左的位置分别挂着“众”、“志”、“成”、“城”四个字牌，如图1．若将位于上下位置的两个字牌对调，同时将位于左右位置的两个字牌对调，再将转盘顺时针旋转90°，则完成一次变换．图2，图3分别表示第1次变换和第2次变换．按上述规则完成第9次变换后，“众”字位于转盘的位置是（）A．上B．下C．左D．右【考点】旋转的性质．【专题】压轴题；操作型；规律型．【分析】根据题意可知每一次变换后相当于逆时针旋转了90°，经过4次变换后会回到原始位置，所以按上述规则完成第9次变换后，相当于第一次变化后的位置关系，分析比较可得答案．【解答】解：根据题意可知每一次变换后相当于逆时针旋转了90度，经过4次变换后会回到原始位置，所以按上述规则完成第9次变换后，“众”字位于转盘的位置是应该是第一次变换后的位置即在左边，比较可得C符合要求．故选C．【点评】本题考查旋转的性质：旋转变化前后，对应线段、对应角分别相等，图形的大小、形状都不改变．要注意旋转的三要素：①定点为旋转中心；②旋转方向；③旋转角度．关键是找到旋转的方向和角度．3．下列图形中，既是轴对称图形，又是中心对称图形的是（）A．等腰梯形 B．平行四边形C．正三角形 D．矩形【考点】中心对称图形；轴对称图形．【分析】根据轴对称图形与中心对称图形的概念和等腰梯形、平行四边形、正三角形、矩形的性质解答．【解答】解：A、是轴对称图形，不是中心对称图形，不符合题意；B、不是轴对称图形，是中心对称图形，不符合题意；C、是轴对称图形，不是中心对称图形，不符合题意；D、是轴对称图形，也是中心对称图形，符合题意．故选D．【点评】掌握中心对称图形与轴对称图形的概念．如果一个图形沿着一条直线对折后两部分完全重合，这样的图形叫做轴对称图形，这条直线叫做对称轴．如果一个图形绕某一点旋转180°后能够与自身重合，那么这个图形就叫做中心对称图形，这个点叫做对称中心．4．如图①～④是四种正多边形的瓷砖图案．其中，是轴对称图形但不是中心对称的图形为（）A．①③ B．①④ C．②③ D．②④【考点】中心对称图形；轴对称图形．【分析】根据轴对称图形与中心对称图形的概念和各图的特点求解．【解答】解：①、是轴对称图形，不是中心对称图形；②、是轴对称图形，也是中心对称图形；③、是轴对称图形，不是中心对称图形；④、是轴对称图形，也是中心对称图形．满足条件的是①③，故选A．【点评】掌握好中心对称图形与轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后两部分重合．5．如图，把矩形ABCD沿EF对折后使两部分重合，若∠1=50°，则∠AEF=（）A．110°B．115°C．120°D．130°【考点】翻折变换（折叠问题）．【专题】压轴题．【分析】根据折叠的性质，对折前后角相等．【解答】解：根据题意得：∠2=∠3，∵∠1+∠2+∠3=180°，∴∠2=（180°﹣50°）÷2=65°，∵四边形ABCD是矩形，∴AD∥BC，∴∠AEF+∠2=180°，∴∠AEF=180°﹣65°=115°．故选B．【点评】本题考查图形的翻折变换，解题过程中应注意折叠是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变，如本题中折叠前后角相等．6．下面四X扑克牌中，图案属于中心对称图形的是图中的（）A．B．C．D．【考点】中心对称图形；生活中的旋转现象．【分析】依据中心对称图形的定义即可求解．【解答】解：其中A选项、C选项及D选项旋转180度后新图形中间的桃心向下，原图形中间的桃心向上，所以不是中心对称图形．故选B．【点评】本题考查中心对称图形的定义：绕对称中心旋转180度后所得的图形与原图形完全重合．7．下面的图形中，既是轴对称图形又是中心对称图形的是（）A．B．C．D．【考点】中心对称图形；轴对称图形．【专题】常规题型．【分析】根据轴对称图形与中心对称图形的概念求解．【解答】解：A、不是轴对称图形，是中心对称图形，故A选项错误；B、不是轴对称图形，是中心对称图形，故B选项错误；C、既是轴对称图形，也是中心对称图形，故C选项正确；D、是轴对称图形，不是中心对称图形，故D选项错误．故选：C．【点评】本题考查了中心对称及轴对称的知识，解题时掌握好中心对称图形与轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后两部分重合．8．将如图所示的图案按顺时针方向旋转90°后可以得到的图案是（）A．B．C．D．【考点】生活中的旋转现象．【分析】根据旋转的意义，找出图中眼，眉毛，嘴5个关键处按顺时针方向旋转90°后的形状即可选择答案．【解答】解：根据旋转的意义，图片按顺时针方向旋转90°，即正立状态转为顺时针的横向状态，从而可确定为A图，故选A．【点评】本题考查了图形的旋转变化，学生主要要看清是顺时针还是逆时针旋转，旋转多少度，难度不大，但易错．9．若将图中的每个字母都看成独立的图案，则这七个图案中是中心对称图形的有（）A．1个B．2个C．3个D．4个【考点】中心对称图形．【分析】根据中心对称图形的概念求解．【解答】解：根据中心对称图形的概念可知，图案O、I是中心对称图形；而图案L、Y、M、P、C都不是中心对称图形．故选B．【点评】解答此题要掌握中心对称图形的概念：在同一平面内，如果把一个图形绕某一点旋转180度，旋转后的图形能和原图形完全重合，那么这个图形就叫做中心对称图形，这个旋转点，就叫做中心对称点．10．．下列图形中，是轴对称图形的是（）A．B．C．D．【考点】轴对称图形．【分析】根据轴对称图形的定义：如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴，这时，我们也可以说这个图形关于这条直线（成轴）对称，进而得出答案．【解答】解：A、不是轴对称图形，故A错误；B、是轴对称图形，故B正确；C、不是轴对称图形，故C错误；D、不是轴对称图形，故D错误．故选：B．【点评】本题考查了轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．11．下面的图形中，是中心对称图形的是（）A．B． C．D．【考点】中心对称图形．【分析】根据中心对称图形的概念求解．【解答】解：A、不是中心对称图形，故本选项错误；B、是中心对称图形，故本选项正确；C、不是中心对称图形，故本选项错误；D、不是中心对称图形，故本选项错误；故选B．【点评】本题考查了中心对称图形的知识，中心对称图形是要寻找对称中心，旋转180度后与原图重合．二、填空题12．如图，点G是△ABC的重心，CG的延长线交AB于D，GA=5cm，GC=4cm，GB=3cm，将△ADG绕点D旋转180°得到△BDE，则DE=2 cm，△ABC的面积=18 cm2．【考点】旋转的性质．【专题】压轴题．【分析】三角形的重心是三条中线的交点，根据中线的性质，S△ACD=S△BCD；再利用勾股定理逆定理证明BG⊥CE，从而得出△BCD的高，可求△BCD的面积．【解答】解：∵点G是△ABC的重心，∴DE=GD=GC=2，CD=3GD=6，∵GB=3，EG=GC=4，BE=GA=5，∴BG2+GE2=BE2，即BG⊥CE，∵CD为△ABC的中线，∴S△ACD=S△BCD，∴S△ABC=S△ACD+S△BCD=2S△BCD=2××BG×CD=18cm2．填：2，18．【点评】本题考查旋转的性质．旋转变化前后，对应点到旋转中心的距离相等以及每一对对应点与旋转中心连线所构成的旋转角相等．要注意旋转的三要素：①定点﹣旋转中心；②旋转方向；③旋转角度．13．已知等腰三角形的一条腰长是5，底边长是6，则它底边上的高为 4 ．【考点】等腰三角形的性质；勾股定理．【分析】根据等腰三角形三线合一的性质及勾股定理不难求得底边上的高．【解答】解：根据等腰三角形的三线合一，知：等腰三角形底边上的高也是底边上的中线．即底边的一半是3，再根据勾股定理得：底边上的高为4．故答案为：4【点评】考查等腰三角形的三线合一及勾股定理的运用．14．将线段AB平移1cm，得到线段A′B′，则点A到点A′的距离是1 cm．【考点】平移的性质．【专题】压轴题．【分析】根据题意，画出图形，由平移的性质直接求得结果．【解答】解：在平移的过程中各点的运动状态是一样的，现在将线段平移1cm，则每一点都平移1cm，即AA′=1cm，∴点A到点A′的距离是1cm．【点评】本题考查了平移的性质：由平移知识可得对应点间线段即为平移距离．学生在学习中应该借助图形，理解掌握平移的性质．三、解答题15．如图，方格纸中的每个小正方形的边长均为1．（1）观察图1、2中所画的“L”型图形，然后各补画一个小正方形，使图1中所成的图形是轴对称图形，图2中所成的图形是中心对称图形；（2）补画后，图1、2中的图形是不是正方体的表面展开图？（填“是”或“不是”）【考点】利用旋转设计图案；利用轴对称设计图案．【专题】网格型．【分析】（1）根据轴对称图形与中心对称的定义即可作出，首先确定对称轴，即可作出所要作的正方形；（2）利用折叠的方法进行验证即可．【解答】解：（1）如图（画对一个得3分）．（2）图1（不是）或图2（是），图3（是）．【点评】掌握轴对称的性质：沿着一直线折叠后重合．中心对称的性质：绕某一点旋转180°以后重合．16．如图，在平面直角坐标系中，△ABC和△A1B1C1关于点E成中心对称．（1）画出对称中心E，并写出点E、A、C的坐标；（2）P（a，b）是△ABC的边AC上一点，△ABC经平移后点P的对应点为P2（a+6，b+2），请画出上述平移后的△A2B2C2，并写出点A2、C2的坐标；（3）判断△A2B2C2和△A1B1C1的位置关系．（直接写出结果）【考点】作图﹣旋转变换；作图﹣平移变换．【专题】作图题；压轴题．【分析】（1）连接对应点，对应点的中点即为对称中心，在网格中可直接得出点E、A、C 的坐标；（2）根据“（a+6，b+2）”的规律求出对应点的坐标A2（3，4），C2（4，2），顺次连接即可；（3）由△A2B2C2和△A1B1C1的位置关系直接看出是关于原点O成中心对称．【解答】解：（1）如图，E（﹣3，﹣1），A（﹣3，2），C（﹣2，0）；（4分）（2）如图，A2（3，4），C2（4，2）；（8分）（3）△A2B2C2与△A1B1C1关于原点O成中心对称．（10分）【点评】本题考查的是平移变换与旋转变换作图．作平移图形时，找关键点的对应点也是关键的一步．平移作图的一般步骤为：①确定平移的方向和距离，先确定一组对应点；②确定图形中的关键点；③利用第一组对应点和平移的性质确定图中所有关键点的对应点；④按原图形顺序依次连接对应点，所得到的图形即为平移后的图形．作旋转后的图形的依据是旋转的性质，基本作法是①先确定图形的关键点；②利用旋转性质作出关键点的对应点；③按原图形中的方式顺次连接对应点．要注意旋转中心，旋转方向和角度．中心对称是旋转180度时的特殊情况．17．在一平直河岸l同侧有A，B两个村庄，A，B到l的距离分别是3km和2km，AB=akm（a ＞1）．现计划在河岸l上建一抽水站P，用输水管向两个村庄供水．方案设计：某班数学兴趣小组设计了两种铺设管道方案：图1是方案一的示意图，设该方案中管道长度为d1，且d1=PB+BA（km）（其中BP⊥l于点p）；图2是方案二的示意图，设该方案中管道长度为d2，且d2=PA+PB（km）（其中点A'与点A关于I对称，A′B与l交于点P．观察计算：（1）在方案一中，d1= a+2 km（用含a的式子表示）；（2）在方案二中，组长小宇为了计算d2的长，作了如图3所示的辅助线，请你按小宇同学的思路计算，d2=km（用含a的式子表示）．探索归纳（1）①当a=4时，比较大小：d1（）d2（填“＞”、“=”或“＜”）；②当a=6时，比较大小：d1（）d2（填“＞”、“=”或“＜”）；（2）请你参考右边方框中的方法指导，就a（当a＞1时）的所有取值情况进行分析，要使铺设的管道长度较短，应选择方案一还是方案二？【考点】作图—应用与设计作图．【专题】压轴题；阅读型；方案型．【分析】运用勾股定理和轴对称求出d2，根据方法指导，先求d12﹣d22，再根据差进行分类讨论选取合理方案．【解答】解：（1）∵A和A'关于直线l对称，∴PA=PA'，d1=PB+BA=PB+PA'=a+2；故答案为：a+2；（2）因为BK2=a2﹣1，A'B2=BK2+A'K2=a2﹣1+52=a2+24所以d2=．探索归纳：（1）①当a=4时，d1=6，d2=，d1＜d2；②当a=6时，d1=8，d2=，d1＞d2；（2）=4a﹣20．①当4a﹣20＞0，即a＞5时，d12﹣d22＞0，∴d1﹣d2＞0，∴d1＞d2；②当4a﹣20=0，即a=5时，d12﹣d22=0，∴d1﹣d2=0，∴d1=d2③当4a﹣20＜0，即a＜5时，d12﹣d22＜0，∴d1﹣d2＜0，∴d1＜d2综上可知：当a＞5时，选方案二；当a=5时，选方案一或方案二；当1＜a＜5（缺a＞1不扣分）时，选方案一．【点评】本题为方案设计题，综合考查了学生的作图能力，运用数学知识解决实际问题的能力，以及观察探究和分类讨论的数学思想方法．。

第13章 正弦定理与余弦定理已知点P 是ABC △内一点，使得PAB PBC PCA α∠=∠=∠=.求证：22221111sin sin sin sin A B Cα=++. 解析 如图，设ABC △的三边为a 、b 、c ，对应角分别为A ∠、B ∠、C ∠，180180BPC C C αα∠=︒--(∠-)=︒-∠，同理180CPA A ∠=︒-∠，180APB B ∠=︒-∠. 由正弦定理，sin sin BP AB B α=，故sin sin BP c B α=，同理sin CP a C α=，sin sin AP b Aα=，ABC ABP CBP S S S =++△△△ 221)sin sin Cα+. 于是22221111sin sin sin sin A B Cα=++. ABC △AC BC X Y ，使ABX YAC ∠=∠，AYB BXC ∠=∠，XC YB =，求ABC △的所有内角. 解析 如图，易知C AYB YAC BXC ABX BAC ∠=∠-∠=∠-∠=∠，故AB BC =. 又由正弦定理，sin sin sin sin BY XC BAY AYB BXC XBC AB BC∠=∠=∠=∠. 于是BAY XBC ∠=∠（易见180BAY XBC ∠+∠<︒），故BAC ABC ∠=∠，BC AC =. 于是ABC △为正三角形，各内角均为60︒.13.13 ★★★已知凸四边形ABCD ，AC BD ⊥，AB 、BC 、CD 、DA 上分别有点F 、G 、H 、E ，AB FD ⊥，BC DG ⊥，CD BH ⊥，AD BE ⊥，求证：FH 、GE 、AC 共点.解析 如图，设ABD △、BCD △垂心分别为M 、N ，FH 与AC 交于K ，EG 与AC 交于K '. 由正弦定理及四点共圆，有 sin sin sin sin sin sin MK HFD HBD DCAMF MKF MKF MKF ∠∠∠===∠∠∠， sin sin sin sin sin sin NK FHB FDB BACNH NKH MKF MKF∠∠∠===∠∠∠， 于是sin sin MK MF DCA AMNK NH BAC CN ∠=⋅=∠. 同理MK AM NK CN'='，得K 与K '重合，即FH 、GE 、AC 共点. 13.1.4 ★★★已知ABCD ，E 在BC 上，AE 、DC 延长后交于F ，O 是ECF △的外心（在ECF △内），若B 、O 、C 、D 共圆，则AD FD =.解析 如图，设CBO CDO θ∠=∠=，BCO α∠=，OFD β∠=.作OM BC ⊥，ON CF ⊥，M 、N 分别是CE 、CF 之中点.易知222221111111BM BE EM BE BE BC AD DF DC CD NDMC MC CM EC EC CE CF CF NF NF +==+=+=-=-=-=+=+=， 此即cos cos cos cos BO DO CO OF θθββ=，于是cos cos BO DOαβ=.又由正弦定理sin sin sin sin BO CO FO DOαθθβ===，于是tan tan αβ=，αβ=，BOC △≌DOF △，故AD BC DF ==.ABCD ，顶点均在一圆周上，且2AB =，3BC =，4CD =，5DA =，求ACBD的值.解析 由正弦定理知4ABC abcS R =△，其中a 、b 、c 为三边长，R 为外接圆半径.于是由ABC ACD ABD BCD S S S S +=+△△△△，并考虑4个三角形有共同的外接圆，故有AB BC CA CD DA CA ⋅⋅+⋅⋅=AB AD BD BC CD BD ⋅⋅+⋅⋅.代入数字，得6201012CA CA BD BD +=+，于是1113AC BD =. ABCD ，对角线交于P ，BP DP =，过P 的一条直线分别交AB 、CD 于G 、H ，过P 的另一条直线分别交AD 、BC 于E 、F ，GF 、EH 分别交BD 于M 、N ， 求证：PM PN =.解析 如图，设好1~6∠∠各角.由BP PD =知ABC ACD S S =△△，故sin(12)AB BC AD CD ⋅⋅∠+∠=⋅⋅ sin(34)∠+∠，由正弦不定理，知止式可改为sin 3sin 1sin 1sin 2sin(34)sin(12)∠∠∠∠=∠+∠∠+∠，于是sin 5sin 6sin(34)sin 3sin 4∠∠∠+∠=∠∠sin 5sin 6sin(12)sin 1sin 2∠∠⋅∠+∠∠∠，此即sin(34)sin(12)ED HD BG BF PE PH PG PF⋅∠+∠⋅∠+∠=⋅⋅，两边同时除去sin(56)∠+∠，即得BGF DEH PGF PEH S S S S =△△△△，此即BM DNPM PN=，故PM PN =. ABCD P ，又设APB θ∠=，则2222cos 2AD BC AB CD AC BDθ+--=⋅. 解析 如图，由余弦定理，2222cos AB AP BP AP BP θ=+-⋅， 2222cos CD CP DP CP DP θ=+-⋅，又222222cos(180)2cos BC BP CP BP CP BP CP BP CP θθ=+-⋅︒-=++⋅，2222cos AD AP DP AP DP θ=++⋅， 所以2cos AC BD θ=⋅⋅. 因此结论成立.ABCD ，AC BD ⊥，上底AD m =，下底BC n =，m n <，BA 、CD 延长后交于P ，P θ∠=，试用m 、n 、θ表示梯形的高.解析 如图，设AB a =，CD b =，则由AC BD ⊥，有2222a b m n +=+.又在BC 上找一点K ，使AK CD ∥.则由余弦定理，222()2cos m n a b ab θ-=+-， 于是cos ab mn θ=.设梯形的高为h ，则由ABK S △，有()sin tan n m k ab mn θθ-==，故tan mnh n mθ=-. ABC ，BD 为边AC 上的高，E 为AB 上一点，45AEC ∠=︒，2BD CE =，CE AC AD =+，求证：DE BC ∥.解析 如图，由11sin 4522ABC BD AC S AB CE ⋅⋅==⋅⋅⋅︒△及2BD CE =得AB =.因此224()AD AC AD =++，即 (25)(2)0AC AD AC AD -+=，故 52AC AD =.不妨设5AC =，则2AD =，3CD =，7CE =. 设AE x =，由45AEC ∠=︒，利用余弦定理得： 24927cos4525x x +-⋅⋅⋅︒=，解得 x =或当x =AE ABAD AC===，故 ED BC ∥.当x =AEC △中，cos 0A <.与ABC △为锐角三角形矛盾，故舍去. 试用身影定理推导余弦定理.解析 如图，对于ABC △，作AD BC ⊥，注意D 可在BC 外，则有（a 、b 、c 为ABC △的三对应边长）cos cos c B b C a +=，则理有cos cos a B b A c +=，cos cos a C c A b +=，三个方程联立，即解得222cos 2b c a A bc+-=等三个式子，这就是余弦定理.x 224(2)160x k x k +-+=，四边形ABCD 中，45CAD ∠=︒，60ADC ∠=︒，ABC S △1cos B k=（如图所示）.（1）当方程有两个相等实数根时，求B ∠及此方程的根； （2）若此实根等于AB 、BC 之和，求CD 之长. 解析 （1）因方程有两个相等实数根，故 224(2)640k k ∆=[-]-=，解得23k =或2k =-. 因|cos |1B ≤，故23k =不符合题意，应舍去，从而11cos 2B k ==-，所以120B ∠=︒. 此时原方程可化为：216640x x -+=，解得8x =.（21sin 2ABC S AB BC B AB BC ==⋅=⋅△，从而 10AB BC ⋅=.又 8AB BC +=， 故 54=.即 AC =因45CAD ∠=︒，60ADC ∠=︒，故由正弦定理得6CD =.P ，P 到顶点A 、B 、C 的距离分别是1、2、3，求正方形的面积.解析 如图所示，设AB x =，则在ABP △中，22413cos 44x x ABP x x+-+∠==；在PBC △中，22495cos 44x x PBC x x +--∠==.于是222235144x x x x ⎛⎫⎛⎫+-+= ⎪ ⎪⎝⎭⎝⎭，解得25x =±.注意到cos 0CBP ∠>，故25x =-应舍去.从而25x =+，即正方形面积为5+ABC △，AB AC >，AD 是高，E 是BC 中点，求证：222AB AC ED BC-=.并由此证明，若AB AC >，AS 是角平分线，T 在BS 上，BT CS =，则232()AT AS AB AC -=-.解析 如图，2222()()()AB AC BD CD BD CDBD CD BD CD BE ED CE ED BC BC BC--+==-=-=+--=2ED ，注意其中CD 可取负值. 又TS 中点也是E ，故22222AT AS AB AC ED ST BC --==， 而 ST BS BT BS CS =-=-AB BC AC BCAB AC⋅-⋅=+， 于是2222()AB AC BC AB AC AT AS AB AC BC---=⋅+ 评注 本题亦可先用余弦定理求出CD .ABC △，90ABC ∠=︒，延长AC 到点D ，连结BD ，若30CBD ∠=︒，且1AB CD ==，求AC 之长. 解析 如图，设AC x =，BD y =，则22BD y==. 又由余弦定理，2222cos120AD AB BD AB BD =+-⋅⋅︒，此即222(1)1x x x ⎛⎫+=++ ⎪⎝⎭.化简并整理，得 3(2)(2)0x x +-=，解得 12x =-（舍），2x =所以AC x =ABCD ，E 、F 分别在BC 、CD 上，AE 与AF 分别交BD 于G 、H ，若BE CF =，求证：以BG 、GH 、HD 为边的三角形有一内角是60︒.解析 设1AB =，BE x =，DF y =，则1x y +=，且1BG x BD x =+，1HD y BD y =+，11GH xBD x=--+ 112y xy y xy-=++. 于是由比例及余弦定理知只需证明2222212(1)(1)2xy x y xyxy x y xy ⎛⎫-=+- ⎪++++⎝⎭， 即22222(1)(1)(1)(2)xy x y y x xy xy -=+++-+.而右式222222()2(1)x y xy x y xy x y xy =+++-+=-=左式，证毕.ABC ，底边BC 上的高是h ，A θ∠=，P 是BC 上一动点，P 关于AB 、AC 的对称点分别是Q 、R ，四边形XQPR 是平行四边形，则X 至BC 的距离2(1cos )h h θ'=-.解析 如图，由于XP 、QR 互相平分，故h Q '=、R 至BC 距离之和sin sin PQ QPB PR RPC =∠+∠=222222cos 2(1cos )BC AB AC AB AC h h AB h AB θθ+-⋅==-. ABC △，点E 、F 分别是AC 、AB 的中点，点G 是重心，对BAC ∠的每一个值，有多少互不相似的ABC △，满足点A 、F 、G 、E 共圆？解析 如图，由A 、F 、G 、E 共圆，得CG CF CE CA ⋅=⋅.若设ABC △对应边为a 、b 、c ，对应中线为a m 、b m 、c m ，则上式变为222132c m b =.又由中线长公式知22221(32)4c m a b c =+-，消去c m ，得2222b c a +=.又由余弦定理，2222cos b c bc A a +-=，再将a 抵消，得 224cos 0b bc A c -+=.若设b c λ=，则24cos 10A λλ-+=，这个方程的24cos 1A ∆=4(-)，于是当1|cos |2A <时，方程无解；又当90A ∠>︒时，两边之比为负数，也不符合要求.除了以上两种情况，剩下来的便是60A ∠︒≤时，此时有互为倒数或相同的解，因此合乎要求的三角形恰有一个.ABC △，()2a b c p ++=，化简222()()()1cos 1cos 1cos a p a b p b c p c A B C ---+++++. 解析 由余弦定理，2222()()1cos ()22bc b c a b c a b c a a b cA p a bc bc bc ++-+++-+++===-，故22()1cos a p a a bcA a b c -=+++. 同理22()1cos b p b ab cB a b c -=+++， 22()1cos c p c abc C a b c -=+++， 三式相加，即得abc . ；22222()cos ()sin 22A Ab c b c a -++=. 解析 如图，不妨设AC AB ≥（即b c ≥），则在AC 上取一点D ，使AD AB =，又作AF BD ⊥于F ，CE BD ⊥于E ，则E 在BD 延长线上. 于是AF 平分BAC ∠，且22sin2A BD BF c ==，sin ()sin 2ADE CD ACE b c =∠=-，两式相加，得()sin 2ABE BD DE b c =+=+.又cos()cos 22A ACE CD b c ==-，由勾股定理，222BC BE CE =+，此即 22222()cos ()sin 22A Ab c b c a -++=. ABC △，A ∠的平分线、AC 上的中线、AB 上的高共点，且2A B ∠=∠，求A ∠. 解析 如图，由于中线BE 和角平分线AD 均在ABC △内，故A ∠与B ∠均为锐角. 设ABC △的三条对应边长为a 、b 、c .由塞瓦定理，有1AF BD FB DC ⋅=，即cos cos b A CD b a B BD c ==，故cos cos AB= ac，由余弦定理知 222222b c a a c b b c+-+-=.①由于2A B ∠=∠，有22a b bc =+，代入式①，化简有c b b cb c-+=，解得1)c b =，于是222cos 22b c a c b A bc b +--===45A ∠=︒. M BC ，则222AB CM AC BMBM CM AM BC⋅+⋅-⋅=. 解析 如图，由于180AMB AMC ∠+∠=︒，故cos cos 0AMB AMC ∠+∠=，分别在ABM △、AMC △用余弦定理代cos AMB ∠、cos AMC ∠，整理即得斯图沃特定理.评注 斯图沃特定理的一个著名的推论是中线长公式：若AM 为ABC △之中线，则AM =C ，将ABC △逆时针旋转为A B C ''△，设线段BA '、AC 、B C '的中点分别为M 、E 、F ，若AC BC ≠，且EM FM =，求EMF ∠.解析 首先，反复利用中线长公式得22222224ME A A BC A C AB A B AC '''=+++--，224MF A C '=+ 22222B B BC A B A B B C '''''++--，由ME MF =得2222A A AC B B B C '''-=-.由AA C '∽BB C '△知上式两端只能为零，否则相似比为1，有AC BC =，与题设矛盾.因此由BB B C ''=可知A AC '△与BB C '△均为正三角形.如图，设A C '中点为N ，连结MN 、NE 、EF .若设A CB θ'∠=（注意可负），则120ENM ECF θ∠=︒+=∠，又EC EN =，1122MN BC B C CF '===，故MNE △≌FCE △，于是ME EF =，因此MEF △为正三角形，60EMF ∠=︒. 评注 中线长公式正是余弦定理的推论.，在ABC △中，90C ∠=︒，D 是BC 上一点，45ADC ∠=︒，作DE AB ⊥于E ，且103AE BE =，若DE =求C ∠的平分线CF 之长.解析 设10AE k =，0k >，则3BE k =，AD BD =由于90C ∠=︒，45ADC ∠=︒，故AC CD ==由222AC BC AB +=，得222150169k k ++=，解得212k =或22225k =.因45ABC ADC ∠<∠=︒，而90DEB ∠=︒，故45EDB ∠>︒，从而BE DE >，所以22225k =应舍去，即k .于是AC =，BC AB =由角平分线定理知23AF AC FB BC ==.故255AF AB ==，3510FB AB ==.由斯图沃特定理知222311724682652525FB AF CF AC BC AF FB AB AB =⋅+⋅-⋅=⋅+⋅=.所以CF =评注 当C ∠为直角时，CF 还有简单的表达式CF =.。

2020年数学竞赛初二奥数之几何变换专题29 几何变换阅读与思考几何变换是指把一个几何图形1F 变换成另一个几何图形2F 的方法，若仅改变图形的位置，而不改变图形的形状和大小，这种变换称为合同变换，平移、对称、旋转是常见的合同变换.1.平移变换如图1，如果把图形1F 上的各点都按一定方向移动一定距离得到图形2F 后，则由1F 到2F 的变换叫平移变换.平移变换前后的对应线段相等且平行，对应角的两边分别平行且方向一致. 2.对称变换如图2，将平面图形1F 变换到与它成轴对称的图形2F ，这样的几何变换就叫做关于直线l （对称轴）的对称变换.对称变换前后的对应线段相等，对应角相等，其对称轴是连结各对应点线段的垂直平分线. 3.旋转变换如图3，将平面图形1F 绕这一平面内一定点M 旋转一个定角α，得到图形2F ，这样的变换叫旋转变换，M 叫旋转中心，α叫旋转角.旋转变换前后的图形是全等的，对应点到旋转中心的距离相等，对应线段的夹角等于旋转角.例题与求解【例l 】如图，∠AOB =045，角内有点P ，PO =10，在角的两边上有两点Q ，R （均不同于O ），则△PQR 的周长的最小值为_______________. （黄冈市竞赛试题）解题思路：作P 点关于OA ，OB 的对称点，确定Q ，R 的位置，化折线为直线，求△PQR 的最小值.l图3图2图1F 1F 2O【例2】如图，P 是等边△ABC 的内部一点，∠APB ，∠BPC ，∠CP A 的大小之比是5:6:7，则以P A ，PB ，PC 为边的三角形的三个角的大小之比（从小到大）是（ ）A. 2:3:4B. 3:4:5C. 4:5:6D.不能确定（全国通讯赛试题）解题思路：解本例的关键是如何构造以P A ，PB ，PC 为边的三角形，若把△P AB ，△PBC ，△PCA 中的任一个，绕一个顶点旋转060，就可以把P A ，PB ，PC 有效地集中在一起.【例3】如图，在△ABC 中，AD ⊥BC 于D ，∠B =2∠C ，求证：AB+BD=CD.（天津市竞赛试题）解题思路：用截长法或补短法证明，实质都利用AD 翻折造全等.【例4】如图，六边形ABCDEF 中，AB ∥DE ，BC ∥FE ，CD ∥AF ，对边之差BC -FE=ED -AB=AF -CD ＞0，求证：该六边形的各角都相等.（全俄数学奥林匹克竞赛试题）解题思路：设法能将复杂的条件BC -FE=ED -AB=AF -CD ＞0，用一个基本图形表示，题设条件有平行条件，考虑实施平移变换.BCC【例5】已知Rt △ABC 中，AC=BC ，∠ACB =090，∠MCN =045 （1） 如图1，当M 、N 在AB 上时，求证：222MN AM BN =+（2） 如图2，将∠MCN 绕C 点旋转，当M 在BA 的延长线时，上述结论是否成立？若成立，请证明；若不成立，请说明理由.（天津市中考试题）解题思路：222MN AM BN =+符合勾股定理的形式，需转化为直角三角形可将△ACM 沿直线CM 对折，得△DCM . 连DN ，只需证DN=BN ，∠MDN =090；或将△ACM (或△BCM )旋转.【例6】如图，∠DAC=012，∠DBC=024，∠CAB=036，∠ABD=048，求∠DCA 的度数.（日本算术奥林匹克试题）解题思路：已知角的度数都是12的倍数，0362460+=，这使我们想到构作正三角形.A图2图1MA B B能力训练1.在如图所示的单位正方形网格中，将△ABC 向右平移3个单位后得到△A B C '''，则BA A '∠的度数是_______.（泰安市中考试题）(第1题) （第2题） （第3题）2.如图，P 是等边△ABC 内一点，P A =6，PB =8，PC =10，则∠APB =_________.3.如图，直线143y x =与双曲线2(0)k y k x =>交于点A ，将直线143y x =向右平移92个单位后，与双曲线2k y x =交于点B ，与x 轴交于点C . 若2AOBC=，则k =______________. （武汉市中考试题） 4.如图，△ABC 中，∠BAC =045，AD ⊥BC ，DB =3，DC =2，则△ABC 的面积是___________. 5.如图，P 为正方形内一点，若::1:2:3PA PB PC =，则∠APB 的度数是（ ）. A. 0120 B. 0135 C. 0145 D. 01506.如图，边长为2的正方形ABCD 的对角线交于点O ，把边BA 、CD 分别绕点B 、C 同时逆时针旋转060，得四边形A BCD '',下列结论：①四边形A BCD ''为菱形；②12ABCD A BCD S S ''=正方形四边形；③线段OD '的长1. 其中正确的结论有（ ）.A. 0个B. 1个C. 2个D. 3个B（第6题）（第5题）（第4题）ACB ABDADA'7. 如图，A ，B 两个电话机离电话线l 的距离分别是3米，5米，CD =6米，若由L 上一点分别向A ，B 连电话线，最短为（ ）.A. 11米B. 10米C. 9米D. 8米8. 如图，在△ABC 中，∠BAC =0120，P 是△ABC 内一点，若记x PA PB PC =++，y AB AC =+，则（ ）.A. x y <B. x y =C. x y >D. x 与y 的大小关系不确定9. 如图，已知D 是△ABC 中BC 边的中点，过D 作DE ⊥DF ，分别交AB 于E ，交AC 于F ，求证：BE CF EF +>.（天津市竞赛试题）10.如图，△ABC ，△A B C '''其各边交成六边形DEFGHK ，且EF ∥KH ，GH ∥DE ，FG ∥KD ，0KH EF FG KD DE GH -=-=->. 求证：△ABC ，△A B C '''均为为正三角形.（“缙云杯”邀请赛试题）l第8题图第7题图CBBA B C A'11.如图，已知△ABC 中，AB=AC ，P ，Q 分别为AC ，AB 上的点，且AP=PQ=QB=BC ，求∠PCQ .（北京市竞赛试题）12.如图，已知在平面直角坐标系中，A ，B 两点的坐标分别为(2,3)A -，(4,1)B -. (1) 若(,0)P x 是x 轴上的一个动点，当△P AB 的周长最短时，求x 的值；（2）若(,0),(3,0)C a D a +是x 轴上的两个动点，当四边形ABCD 的周长最短时，求a 的值；（3）设M ，N 分别为x 轴，y 轴上的动点，问：是否存在这样的点(,0)M m 和(0,)N n ，使四边形ABMN 的周长最短？若存在，求出,m n 的值；若不存在，请说明理由.（浙江省湖州市中考试题）13.如图，梯形ABCD 中，AD ∥BC ，分别以两腰AB ，CD 为边向两边作正方形ABGE 和正方形DCHF ，设线段AD 的垂直平分线l 交线段EF 于点M ，EP ⊥l 于P ，FQ ⊥l 于Q ，求证：EP=FQ.（全国初中数学联赛试题）B14.如图所示，已知Rt △ABC 中，AB=BC ，在Rt △ADE 中，AD=DE ，连结EC ，取EC 中点M ，连结DM 和BM .（1）若点D 在边AC 上，点E 在边AB 上且与点B 不重合，如图1，求证：BM=DM ，且BM ⊥DM ； （2）如图2中的△ADE 绕点A 逆时针旋转小于045的角，那么（1）中的结论是否仍成立？如果不成立，请举出反例；如果成立，请给予证明.（广州市中考试题）15.如图，在△ABC 中，∠BAC =045，AD ⊥BC 于D ，若BD =3，CD =2，求△ABC 的面积.（山东省竞赛试题）图2图1ACBBCAB专题29 几何变换例1 210例2 A 提示：将ABP ∆绕B 点顺时针旋转︒60得CBD ∆，则ABP ∆≌CBD ∆，BPD ∆为等边三角形. 例3 提示:延长BD 至E ,使AB BE =,连接AE ,E ABC ∠=∠2.例4 提示:过E 作ER ∥,CD 过C 作CP ∥AB ,过A 作AQ ∥EF ,则PQR ∆为等边三角形.例5 (1)如图a ，由DCM ∆≌ACM ∆则AM DM AC DC ==,,,ACM DCM ∠=∠A CDM ∠=∠.又由CB CA =，得CB CD =.由DCM DCN ∠-︒=∠45,得BCN DCN ∠=∠,又CN CN =,则DCN ∆≌BCN ∆,有BN DN =,B CDN ∠=∠, ∴︒=∠+∠=∠+∠=∠90B A CDN CDM MDN ∴222DN MD MN +=即222BN AM MN +=(2)关系式: 222BN AM MN +=仍成立,方法同上,如图b 例6 如图,作ACD ∆关于AD 所在直线的轴对称图形,APD 则,12,60,APD ACD PAD CAD PAB AP AB AC ∠=∠∠=∠=∠===，连接PB ，则PAB 为正三角，得12PBD ∠=.123648,,,DAB DBA AD BD PAD PBD ∠=+==∠∴=∴≅故30.30APD BPD ACD APD ∠=∠=∴∠=∠=能力训练1. 452. 1503. 12 提示: 如图, 设4(,)3A a a 过A 作AD x ⊥轴, 交于点D , 过B 作BE x ⊥轴, 交于点E由,2AO AD OD AOD BCE BC BE CE ∴===, 则2912,,(,)23223a CE BE a B a a ==+ ,A B 都在双曲线上, 4291()3322a a a a ∴=+, 解得 123,0a a ==(舍去) 3412k ∴=⨯=4. 15 提示: 分别以,AB AC 为对称轴作D 点的对称点,E F , 连接,FC EB 相交于G , 证明四边形AFGE 为正方形5. B6. C7. B8. D9. 提示: 延长FD 至G , 使DG FD =, 连接EG10. 提示: 作//,//,//EQ FG PG KH KR DE ，交成等边三角形PQR11. 提示: 作//CD BQ , 连,PD CD ，∴四边形QBCD 为菱形, DQ QB = , 由,AP QB CD AQ PC === ,A PCD ∠=∠ 得,,DCP PAQ PD PQ QB QD ≅=== Q P D ∴为等边三角形, 又,CDP A PQA ∠=∠=∠2,QPC A ∠=∠360QPD A ∠=∠= 20,A ∴∠=80B ACB ∠=∠=又,QB BC = 50QCB ∴∠= 30PCQ ∠=12. 提示: (1) 作(4,1)B -关于x 轴对称点'(4,1)B ,连','AB AB 交x 轴于P ,PAB 周长最短, (3.5,0)P ∴ (2) 将点(4,1)B -向左平移3个单位得1(1,1)B -，再作1B 关于x 的对称点2(1,1)B ，连2AB 交x 轴于C ， 再将C 向右平移3个单位得点D ，(1.25,0), 1.25C a ∴=(3) 作点A 关于y 轴对称点'(2,3)A --,作点B 关于x 轴的对称点'(4,1)B ,连''A B 交x 轴于M , 交y 轴于N 5(2.5,0),(0,)3M N ∴-13. 提示: 过N 作'//NQ DF ,作'//,NP AE 作//,//.NS DC NR AB 由','PP N LNR RN AB AE P N ∠=∠=== 则''Rt PP N Rt LNR PP LN ≅∴= 同理可证: ''PP QQ =又 '//,'//EP AN FQ ND , 又''AN ND EP FP =∴= 从而'',''PE PP P E FQ FQ QQ =+=+则 PE FQ =14. 提示:(1)11,,BM EC DM EC BM DM ==∴= 由2BME BCM ∠=∠ 2,DME DCM ∠=∠2()90BMD BME DME BCM DCM ∴∠=∠+∠=∠+∠= B M D M ∴⊥(2) 延长DM 至点F ,使DM FM =,连,,BD BF FC . 可证:EMD CMF ≅,ED AD CF DEM FCN ∴==∠=∠ //ED CF延长AD ,交BC 于T ,交CF 延长线于S 90EDS CST ∠=∠= 又BTA CTS ∠=∠BAD BCF ∠=∠ ,,,AB CB ABD CBF BD BF ABD CBF =∴≅∴=∠=∠, 又90ABD DBC CBF DBC ∠+∠=∠+∠=, BDF ∴为等腰三角形, ,BM DM BM DM ∴=⊥15. 如图, 以AB 为对称轴作ADB 的对称AGB ,以AC 为对称轴作ADC 的对称AFC ,并延长,GB FC 交于点E ,则易知四边形AGEF 是正方形, 不妨设AD h =,则2,3,BE h CE h =-=-由2222222(2)(3)5560BC BE CE h h h h =+⇒-+-=⇒--=116561522ABC h SBC AD ⇒=⇒==⨯⨯=。

第16章几何变换§16.1对称和平移16．1．1★设M 是边长为2的正三角形ABC 的边AB 的中点．P 是边BC 上的任意一点，求PA PM +的最小值．CA'M'PA M B解析 作正三角形ABC 关于BC 的对称图形A BC '△．M '是M 的对称点，故M 是A B '的中 点．PM PM '=，如图所示，则 PA PM PA PM AM ''+=+≥.连结CM '，易知90ACM '∠=︒，所以AM '==．所以，PA PM +16．1．2★★已知ABC △中，60A ∠<︒．试在ABC △的边AB 、AC 上分别找出一点P 、Q ，使BQ QP PC ++最小．解析 作B 关于直线AC 的对称点B '，C 关于直线AB 的对称点C '，连B C ''与AB 、AC 分别交于点P 、Q ，则P 、Q 即为所求，如图所示．CA'M'PA M B事实上，对于AB 、AC 上的任意点P '，Q '， BQ Q P P C B Q Q P P C ''''''''''++=++ B C B Q QP PC ''''=++≥ BQ QP PC =++．评注 因为60A ∠<︒，所以所作线段B C ''必与线段AB 、AC 相交．16．1．3★★求证：直角三角形的内接三角形的周长不小于斜边上高的两倍．解析 如图所示，设在直角三角形ABC 中，CD 是斜边上的高，PQR △是它的任一内接三角形．BDP ARC Q S VET G FU将Rt ABC △以BC 为对称轴反射为Rt BCE △，此时PQR △反射为SQV △，再将Rt BCE △以CE 为对称轴反射为Rt FCE △，此时SQV △反射为TUV △延长DC 交EF 于G ．易知FF AB ∥，所以CG CD =，即2GD CD =，且GD 是两平行线AB 与EF 之间的距离． 所以2PQ QR RP PQ QV VT GD CD ++=++=≥.16．1．4★★★在ABC △内取一点M 使10MAB ∠=︒，30MBA ∠=︒．设80ACB ∠=︒， AC BC =．求AMC ∠.CHBME解析 本题中ABC △为等腰三角形，这就提示我们利用对称性解题，先作一条对称轴，作ABC △的高CH 与直线BM 交于点E 由对称性知， 30EAB EBA ∠=∠=︒， 所以20EAM ∠=︒， 从而20CAE ∠=︒，因为40AME MAB MBA ∠=∠+∠=︒，又1402ACE ACB ∠=∠︒=，所以CAF △≌MAE △， 于是AC AM =，所以()118040702AMC ∠=︒-︒=︒． 16．1．5★★在ABC △中，AH 是高，H 在边BC 上，已知45BAC ∠=︒，2BH =，3CH =，求ABC △的面积．解析 作HAC △的关于AC 的对称图形MAC △，作H A B △的关于AB 的对称图形NAB △．分别延长MC 和NB ，它们相交于L ，如图所示．ANMBH CL易知90M N ∠=∠=︒，且 290NAM BAC ∠=∠=︒， AM AH AN ==．所以，四边形LMAN 是正方形． 设正方形LMAN 的边长为a ，则 3CL a =-，2BL a =-．在直角三角形BCL 中，由勾股定理知 222BL CL BC +=．()()222325a a -+-=．解方程，得6a =，即6AH =．所以1152ABC S BC AH =⋅=△．16．1．6★★★如图，凸四边形PQRS 的四个顶点分别在边长为a 的正方形ABCD 的四条边上，求证：PQRS的周长不小于．解析 作正方形ABCD 关于BC 的轴对称图形，得到正方形11A BCD ，再作正方形11A BCD 关于1CD 的轴对称图形，得到正方形221A B CD ，再作正方形221A B CD 关于21A D 的轴对称图形，得到正方形2331A B C D ，而P 、Q 、R 、S 四点的对应点如图所示．A S DP B P 1A 1S 1D 1R 3C 3Q 3B 3P 3A 2P 2B 2Q 2R C R 1S 2Q显然，2AA =，23AP A P ∥，故 32PP AA ∥，所以四边形PQRS 的周长 PQ QR RS SP +++ 11223PQ QR R S S P =+++32PP AA ==≥．即四边形PQRS的周长不小于．16．1．7★★★如图，ABC △和ADE △是两个不全等的等腰直角三角形，90ABC ADE ∠=∠=︒，现固定ABC △而将ADE △绕点A 在平面上旋转，试证：不论ADE △旋转到什么位置，线段EC 上必存在点M 使BMD △力等腰直角三角形．BAD ECMA'解析 如图，设BMD △为等腰直角三角形，下面证明点M 在线段EC 上． 作A 关于BD 的对称点A '，则A DB ADB '∠=∠． 因为902ADE BDM ∠=︒=∠，所以45EDM A DM A DB ''∠=∠=︒-∠ 45ADB =︒-∠， 又DA DA DE '==．所以A '又是E 关于DM 的对称点． 同理A '也是C 关于BM 的对称点，因此 EMD A MD '∠=∠，CMB A MD '∠=∠， 又因90BMD ∠=︒， 所以180CME ∠=︒．即M 在EC 上（且为EC 的中点）．16．1．8★★★如图，矩形ABCD 中，20AB =，10BC =，若在AC 、AB 上各取一点M 、N ，使BM MN +的值最小，试求出这个最小值．DEC GF ANP MBQ解析 作AB 关于直线AC 的对称线段AE ，即B 、E 关于AC 对称，作N 关于AC 的对称点F ，则F 在AE 上，且有BE AC ⊥于Q ，NF AC ⊥于P ．由对称变换可知，MN BM MF MB +=+.欲使MF BM +最小，必须BMF 共线，所以BM MN +最小值为点B 到AE 的距离BG .在Rt ABC △中，20AB =，10BC =，所以AB BCBQ AC⋅==2BE BQ == 在Rt ABQ △中，AQ ===20AE AB ==，在ABE △中，1122ABE S BE AQ AE BG =⋅=⋅△，则16BE AQBG AE⋅==．从而BM MN +的最小值为16．16．1．9★★凸四边形ABCD 中，ABD CBD ∠>∠，ADB CDB ∠>∠．求证： AB AD BC CD +>+.D CEPA B解析将BCD △沿BD 翻折，点C 落在点P ．因为ABD CBD ∠>∠，ADB CDB ∠>∠，所以P 必定在ABD △内部．BP 延长线交AD 于点E ，则 AB AD BE FD BP PD BC CD +>+>+=+.16．1．10★★设S 表示凸四边形ABCD 的面积，证明1()2S AB CD BC AD ⋅+⋅≤．B ACD D'l解析如图，作点D 关于AC 的垂直平分线l 的对称点D '，显然ACD △与ACD '△关于l 成轴对称图形．所以 ABCD S S '= BAD BCD S S ''=+△△，11sin sin 22AB AD BAD BC CD BCD ''''=⋅⋅∠+⋅⋅∠ ()AB AD BC CD ''⋅+⋅≤ 1()2AB CD BC AD =⋅+⋅. 16．1．11★★在矩形ABCD 内取一点M ，使180BMC AMD ∠+∠=︒，试求BCM DAM ∠+∠的值．解析 如图将BMC △沿AB 平移至ADM '△，显然MM AD '⊥，BMC AM D '∠=∠．所以，由已知条件180AM D AMD '∠+∠=︒，即A 、M 、D 、M '四点共圆，从而 BCM DAM ADM DAM '∠+∠=∠+∠ 90AMM DAM '=∠+∠=︒．16．1．12★★设P 是平行四边形ABCD 内一点，使得PAB PCB ∠=∠， 证明：PBA PDA ∠=∠．A D PP'BC解析 如图，把AP 平移至DP '，则BAP CDP '∠=∠，及PBA P CD '∠=∠，PP BC '∥， 所以P PC BCP '∠=∠．又已知PAB PCB ∠=∠，故P PC CDP ''∠=∠，从而P 、D 、P '、C 四点共圆．于是 P PD P CD ''∠=∠， 又P PD PDA '∠=∠， 所以PBA PDA ∠=∠．16．1．13★（1）如图（a ）所示，在梯形ABCD 中，AD BC ∥.已知：3AD BC +=，AC ，BD =，求梯形ABCD 的面积．（2）如图（b ），在梯形ABCD 中，AD BC ∥．M 是CD 的中点，MN AB ⊥于N ．设A B a =，MN h =，求梯形ABCD 的面积．解析（1）将BD 平移到CE ，连结DE，则CE BD =，DE BC =．所以B CAD E(a)A DENM CF B(b)3AE AD DE AD BC =+=+=． 222AE AC CE =+．因此90ACE ∠=︒． 因为ABC CDE S S =△△，所以12ACE ABCD S S AC CE ==⋅△梯形 （2）将AB 平移至EF ，如图（b ）所示，EF 过点M ．由于MDF △≌MCF △，所以 ABCD ABFE S S AB MN ah ==⋅=梯形梯形．评注 本题的两种添平行线法是解梯形问题的常用方法．16．1．14★★如图，在四边形ABCD 中，AD BC =，E 、F 分别是DC 及AB 中点，FE 的 延长线与AD 及BC 的延长线分别交于点H 、G ．求证：AHF BGF ∠=∠．G H DAB'F BCE (a)解析1如图（a ），将线段CB 平移至AB '．则四边形AB BC '为平行四边形．由于F 是AB 中 点，故C 、F 、B '共线．现在EF 是CDB '△的中位线，故EF DB '∥，所以 AHF ADB '∠=∠，BGF AB D '∠=∠．又显然AB BC AD '==．故ADB AB D ''∠=∠． 于是AHF BGF ∠=∠．G H E CD MAF B(b)解析2如图（b ），连结AC ，取AC 中点为M ，连结ME 、MF ，则ME 、MF 分别为CDA △、ABC △的中位线，所以12ME DA ∥，12MF BC ∥．故MEF AHF ∠=∠， AFE FGB ∠=∠，且ME MF =，故MEF MFE ∠=∠， 所以AHF FGB ∠=∠．16．1．15★★如图，A B ∠=∠，1AA 、1PP 、1BB 均垂直于11A B ，垂足为1A 、1P 、 1B ，117AA =，116PP =，120BB =，1112A B =．求AP BP +的值．A C D A 1P 1B 1E PB解析 将1PP 平移到1CA ，C 在线段1AA 上，延长BP 交1AA 于D ，将1DA 平移到1EB ，E 在1BB 上．因为1AA 、1BB 、1PP 均垂直于11A B ，所以四边形11CAPP 和11DA B E 都是矩形． 由1116CA PP ==，117AA =，得1AC =．又11AA BB ∥，所以P D AB A ∠=∠=∠，90PCD PCA ∠=∠=︒，PC PC =．所以Rt PCD △≌Rt PCA △，PA PD =，1CD AC ==． 于是AP BP BD +=，11115DA AA AD EB =-==， 115BE BB EB =-=．在Rt BED △中，1112DE A B ==，13BD ==，也即13AP BP +=．16．1．16★★在正三角形ABC 的三条边上，有三条相等的线段12A A 、12B B 、12C C ．证明：直线21B C 、21C A 、21A B 所成的三角形中，三条线段21B C 、21C A 、21A B 与包含它们的边 成比例．CABC 1C 23A 1A 2A 3B 1B 2B 3解析 如图，将12C C 平移到2B P ，连结1PA 、1PB 、2PC ．因为四边形12BC C P 为平行四边形，所以1260B B P A ∠=∠=︒，21212B P C C B B ==，故12B B P △为正三角形，112B P A A ∥．这样所得四边形121A A B P 为平行四边形，121A P A B ∥．因此，由21B C 、21C A 、21A B 这三条线段构成的三角形与12A PC △全等，而12A PC △≌333A B C △，从而命题得证．16．1．17★★如图所示，2AA BB CC '''===且共点于O ，60AOB BOC COA '''∠=∠=∠=︒，求证：AOB BOC COA S S S '''++<△△△Q解析 将A OC '△沿A A '方向平移A A '长的距离，得AQR △，将B O C '△沿BB '方向平移BB '长的距离，得B PR ''△．由于 2OP OQ ==，60POQ ∠=︒， 所以2PQ =．又因'2QR R P OC OC CC ''+=+==，故R 与R '重合，且P 、R 、Q 三点共线．在正三角形POQ 中， AOB BOC COA S S S '''++△△△ AOB B PR AQR S S S ''=++△△△22OPQ S <△ 16．1．18★★★如图，由平行四边形的顶点B 引它的高BK 和BH ，已知KH a =，BD b =，求点B 到BKH △的垂心的距离． B PCHD KAaH 1解析 令1H 表示BKH △的垂心．考虑到1KH BH ⊥，DH BH ⊥，有1KH DH ∥．同理有1HH DK ∥，因而四边形1KDHH ，为平行四边形，平移1BKH △到PDH △位置，显然P 为BC 上一点，所求线段1BH 即PH ，已与KH 位于同一直角三角形中．由于四边形KDPB 为矩形，有PK BD =，于是1BH PH ===16．1．19★★★已知ABC △的面积为S ，D 、E 、F 分别为BC 、CA 、AB 上的点，且 1BD CE AF DC EA FB n===，试求以AD 、BE 、CF 为边的三角形的面积S '． GCEDBF A解析 如图，过点A 作AG 平行且等于FC ．连CG 、GD 、GE ，则四边形AFCG 为平行四边形，GCA CAB ∠=∠．又11CG AF AE AE AB AB AB CA n ====+， 所以CGE △≌ABC △，CEG ACB ∠=∠，因此GE CB ∥. 又因1=1GE BDBC n BC =+， 所以GE BD =．于是四边形GEBD 也为平行四边形，从而GD BE =，即AD G △为AD 、BE 、CF 所构成的三角形，它的面积为S '． 在梯形GABC 中， 1111GABC S GC AB GC S AB AB n +==+=++梯形， 所以111GABC S S n ⎛⎫=+ ⎪+⎝⎭梯形，而11ABD S BD S BC n ==+△， 所以111ABC CG CD nS BA BC n n ⋅==⋅⋅++△， 因此()2111111n S S n n n ⎡⎤⎛⎫'=+--⎢⎥ ⎪++⎝⎭+⎢⎥⎣⎦ ()2211n n S n ++=+．§16.2旋转16．2．1★★对于边长为1的正ABC △内任一点P PA PB PC ++．ACBPC'P'解析 把ABC △绕点B 旋转60︒到CBC '△．则PBP '△为正三角形，且 PC P C ''=，PB PP '=，因而PA PB PC PA PP P C AC ''''++=++≥．16．2．2★★设P 是等边三角形ABC 内一点，3PC =，4PA =，5PB =．试求此等边三角形的边长．BACP 543解析 如图，把CBP △绕点C 逆时针旋转60︒，到达CAP '△的位置，显然， 60PCP '∠=︒，3P C PP ''==，5AP '=．在APP '△中，222222345AP P P AP ''+=+==，所以90APP '∠=︒．故 9060150APC APP P PC ''∠=∠+∠=︒+︒=︒. 在APC △中，由余弦定理，得 2222cos150AC AP PC AP PC =+-⋅⋅︒2234243=+⨯⨯+25=+所以，等边三角形ABC16．2．3★★设O 是正三角形ABC 内一点，已知115AOB ∠=︒，125BOC ∠=︒，求以线段OA 、OB 、OC 为边构成的三角形的各角．解析 以B 为旋转中心，将AOB △按逆时针方向旋转60︒，旋转至CDB △，如图所示． 连结OD ．由于OB OD =，60OBD ∠=︒，所以OBD △是正三角形，故OD OB =． 又CD OA =，故OCD △是以OA 、OB 、OC 为边构成的一个三角形． 因此COD BOC BOD ∠=∠-∠ 1256065=︒-︒=︒，ODC BDC BDO ∠=∠-∠ AOB BDO =∠-∠1156055=︒-︒=︒，从而180655560OCD ∠=︒-︒-︒=︒．所以，以线段OA 、OB 、OC 为边构成的三角形的各角分别为65︒、55︒和60︒． 16．2．4★★如图，两个正方形ABCD 与AKLM （顶点按顺时针方向排列），求证：这两个正方形的中心以及线段BM 、DK 的中点是某正方形的顶点．CDQ K LRM SAPB解析 设P 、R 分别是正方形ABCD 、AKLM 的中心，Q 、S 分别是线段DK 、BM 的中点，先证PSR △是以PR 为斜边的等腰直角三角形．连结BK 、DM ，将ADM △绕A 逆时针旋转90︒，则D 、M 分别到B 、K 位置，所以BK DM =，BK DM ⊥．因为P 、S 分别是BD 、BM 的中点，所以12PS DM ∥．同理12SR BK ∥．所以PS SR ⊥，且PS SR =．即PSR △是以PR 为斜边的等腰直角三角形．同理可证PQR △也是以PR 为斜边的等腰直角三角形．故P 、Q 、R 、S 是正方形的四个顶点．16．2．5★★正方形ABCD 内有一点P ，1PA =，3PB =．PD =ABCD 的面积．ADB CPP'解析 将PAB △绕A 点旋转90︒，得P AD '△．连结PP '．易知90PAP '∠=︒，1PA P A '==．于是PP '=在P PD '△中，222279P P PD P D ''+=+==．所以P PD '△是直角三角形，从而135APD ∠=︒． 由余弦定理得222AD PA PD PD =+⋅8=16．2．6★★在正方形ABCD 的边AB 和AD 上分别取点M 和K ，使得AM AK =，在线段DM 上取点P ，使得PCD PKA ∠=∠．证明：APM ∠是直角．AM BL K PDC解析 如图所示，在边BC 上取点L ，使BL AK =，连结KL 、AP 、PL ．由于PCD PKA ∠=∠，所以P 、C 、D 、K 四点共圆，作四边形PCDK 的外接圆和矩形 KDCL 的外接圆，因为这两个外接圆均过K 、D 、C 三点，从而这两圆是相同的，所以 90LPD LKD ∠=∠=︒． 易知Rt MAD △≌Rt LBA △.故以正方形ABCD 的中心为旋转中心，将Rt LBA △以逆对针方向旋转90︒，则L B A △旋转至MAD △，从而AL DM ⊥．又LP DM ⊥，故A 、P 、L 三点共线，所以90APM ∠=︒． 16．2．7★★★已知凸六边形123456A A A A A A 中，1223A A A A =，3445A A A A =，5661A A A A =， 135246A A A A A A ∠+∠+∠=∠+∠+∠．求证：（1）24612345612A A A A A A A A A S S =△；（2）624212A A A A ∠=∠，246412A A A A ∠=∠，264612A A A A ∠=∠．A 1A 2A 3A 4A 5A 6A'4解析 （1）将234A A A △绕点2A 旋转，使23A A 与21A A 重合，得到214A A A '△，如图所示．连结46A A '． 因为135246()()A A A A A A ∠+∠+∠+∠+∠+∠720=︒，所以135A A A ∠+∠+∠ 246360A A A =∠+∠+∠=︒． 因此4161412360A A A A A A A ''∠=︒-∠-∠ 135360A A A =︒-∠-∠=∠.从而146A A A '△≌546A A A △， 246A A A △≌246A A A '△， 所以24624641234561122A A A A A A A A A A A A A S S S '==△．（2）由（1）可知624624126324A A A A A A A A A A A A '∠=∠=∠+∠2624A A A A =∠-∠，所以624212A A A A ∠=∠．同理可证：246412A A A A ∠=∠，264612A A A A ∠=∠．评注 本题通过旋转，把234A A A △、456A A A △、612A A A △拼成一个与246A A A △全等的新三角形246A A A '.也可以采取向246A A A △内部旋转的方法，把234A A A △、456A A A △、612A A A △放在26A A A 4△的内部，使之恰好“拼成”246A A A △．16．2．8★★★如图所示，P 、Q 是边长为1的正方形ABCD 内两点，使得 45PAQ PCQ ∠=∠=︒，求PAB PCQ QAD S S S ++△△△的值．ADQ PBCADQPQ'BQ''C(a)(b)解析 将AQD △绕点A 顺时针旋转90︒至AQ B '△，CQD △绕点C 逆时针旋转90︒至CQ B ''△，连结PQ '、PQ ''，则APQ '△≌APQ △，CPQ ''△≌CPQ △．又90ABQ CBQ ADQ CDQ '''∠+∠=∠+∠=︒，所以Q '、B 、Q ''三点共线，且 BQ DQ BQ '''==， 故PBQ PBQ S S '''=△△， 所以PAB PCQ QAD S S S ++△△△ PAQ PBC QCD S S S =++△△△1122ABCD S ==正方形． 16．2．9★★在ABC △中，120A ∠︒≥，点P 不与A 重合．求证PA PB PC AB AC ++>+. 解析 如图，将PAB △绕点A 旋转至P AB ''△的位置，使CA 与AB '共线．于是 AB AC AB AC PC PB ''+=+<+．B'ACPBP'又因为120P AB PAC BAP PAC BAC ''∠+∠=∠+∠=∠︒≥，所以 18060PAP BAC '∠=︒-∠︒≤． 故在等腰PAP '△中， PA P A PP ''=≥．因此PB PP P B PA P B PA PB ''''''++=+≤≤， 从而PA PB PC AB AC ++>+.评注 此题似乎依赖于图形，P 在BAC ∠内，事实上P 在其他位置照样成立，方法完全一样． 16．2．10★★★凸四边形ABCD 中，点M 、N 分别是BC 、CD 的中点，且AM AN a +=（a 是常数），求证：22ABCDa S <四边形．ED NC FMBA解析 如图所示，将ABM △绕点M 旋转180︒得FCM △，将ADN △绕点N 旋转180︒得ECN △，连EF ，于是360ECF ECN BCD FCM ∠=︒-∠-∠-∠ 360ADC BCD ABC =︒-∠-∠-∠180DAB =∠<︒，所以EF 与凸四边形ABCD 的边不相交．故FCM ECN AEF ABCD AMCN S S S S S =++<△△△四边形四边形122AE AF AM AN ⋅=⋅≤ 22222AM AN a +⎛⎫⋅=⎪⎝⎭≤． 16．2．11★★★如图，设D 为锐角ABC △内一点，且AC BD AD BC ⋅=⋅，90ADB ACB ∠=∠+︒，求AB CDAC BD⋅⋅的值．A DBC解析 将线段BD 绕点B 顺时针旋转90︒到BE ，连结DE 、CE ． 因为ADB CAD CBD ACB ∠=∠+∠+∠，90ADB ACB ∠=∠+︒，所以 90CAD CBD ∠+∠=︒，又90CBD CBE ∠+∠=︒， 则CAD CBE ∠=∠． 由AC BD AD BC ⋅=⋅，得AC AD ADBC BD BE==，于是ACD BCE △∽△，所以ACD BCE ∠=∠， AC AD CDBC BE EC==．从而A C B A C D B C D E C B B C ∠=∠+∠=∠+∠=∠．所以，A B C D E△△∽，则AB ACDE DC=，即AB CD AC DE ⋅=⋅．在Rt BDE △中，BD BE =，DE =，故AB CDAC BD⋅⋅。