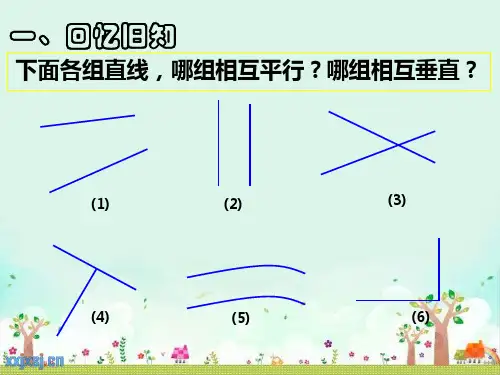
这样有意识地涉及两直线垂直、两直线的交点 等知识,既帮助学生整理、复习已学知识的结 构,也让学生在复习过程中自己“发现”尚未 解决的问题,使新授知识在原认知结构中找到 生长点,自然地引出新问题,符合学生的认知 规律,有利于学生形成合理、完善的认知结构。
教学程序
⑵课题解决:教学过程中,利用“从特殊到一般” 的方法(由特殊直线到一般直线;由特殊点到 一般的点),提出如下问题:
(3)求下列算两.条平行线的距离:2x+3y-8=0
2x+3y= -18
教学程序
⑷小结作业: 师生互动,共同总结公式的推导过程 以及公式的特征和应用,布置课后作 业。
教学设计几点说明
这样设计,使教学过程,逐步逼近目标,在这过程中 展示了数学知识产生的思维过程。
这样设计,学生能够自觉地、主动地参与进来,教师 的主导作用、学生的主体作用都得以充分体现,经常 这样做,学生的数学思维能力必将逐步得到提高。
这说明,当A=距0,离B≠A20时B2,以上公式仍然适用 同理,当B=0,A≠0时,公式也适用
教学程序
(3)例题练习:
(1)求原点到下列直线的距离:① 3x+2y-
26=0 ; ② x=y
(① ③2B)A(求推解(1-下,导和20固,列)出学3,公说 间 以)点3公 生,x式明 限 抽到+式 动y的: 制 学4直-之 手y1记练 , 生+线=后 练30忆习 时 在=的, 习0和时 间 黑;距通 ,②应要 允 板离过 进A用有 许 上(:例 一-。时可演2题步,3讲巩),2x+1=0;
点到直线的距离
主菜单
教材分析 教学目标
学生情况分析
教学方法 教学程序
教学设计几点说明