当前位置：文档之家 › 菲涅尔衍射.ppt

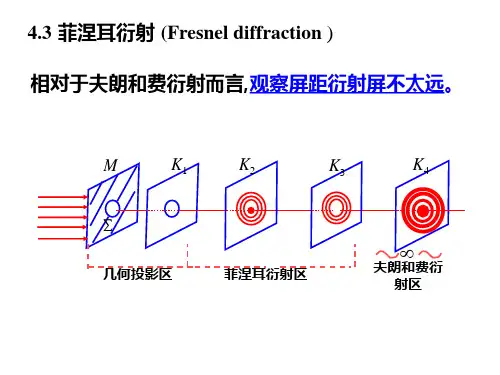
菲涅尔衍射.ppt

  • 格式：ppt
  • 大小：2.56 MB
  • 文档页数：28

下载文档原格式

  / 28

合集下载

工程光学下篇：第13.2节 菲涅耳衍射

工程光学下篇：第13.2节 菲涅耳衍射

泰伯效应（Talbot）
(x1, y1)
(x, y)
用菲涅耳衍射公式进行推导：
z
以振幅型正弦光栅为例
光栅的振幅透射系数为：t(x1,
y1)
1 2
1
cos
2
d
x1
采用单位振幅的平面波垂直照明
刚刚透过光栅的光场：E~1(x1, y1) t(x1, y1)（被调制 衍射）
在菲涅耳衍射区内距离为z处：
深圳大学光电工程学院
§13.2 菲涅耳衍射
泰伯效应（Talbot）
当用单色平面波垂直照明具有周期结构的衍射屏时，将 会在衍射屏后菲涅尔衍射区内的某个距离上出现该物体 的几何像
z
不用透镜即可对周期性物体成像的方法称为泰伯效应或 泰伯自成像（Self-imaging）
深圳大学光电工程学院
§13.2 菲涅耳衍射
2
e e d i z e e
i
2 d
(
x
)
i k 2 2z
i
2 d
x
iz
1 d
2
E~(x,
y)
eikz 2
1
e
iz
1 d
2
cos
2
d
x （常数相位深因圳子大学可光电省工略程学）院
§13.2 菲涅耳衍射
泰伯效应（Talbot）
用菲涅耳衍射公式进行推导：
(x1, y1)
(x, y)
第j个波带在P0的振幅：
|
E~j
|
C
Aj rj
1K(co) s
2
j rj ，cos
| E~1 || E~2 || E~3 |
振幅随j增大而减小

菲涅尔圆孔衍射和圆屏衍射修正版课件

菲涅尔圆孔衍射和圆屏衍射修正版课件

象的基本原理和特点。
02
重点与难点解析
课程重点讲解了衍射现象的数学模型和物理机制，以及如何通过实验手
段观察和验证衍射现象。同时，对于学习过程中的难点和疑点，课程提
供了详细的解析和解答。
03
课程特色与亮点
本课程采用理论与实践相结合的方式，既注重理论推导，又强调实验操
作。通过修正版课件，学习者可以更加直观地理解衍射现象，提高学习
圆屏衍射模型
圆屏衍射模型通常采用菲涅尔-基尔霍夫衍射积分 公式，该公式描述了光波通过圆孔或圆屏后在远 场产生的衍射强度分布。
圆屏衍射模型需要考虑光源、圆孔或圆屏、接收 屏幕等多个因素，通过积分公式计算出衍射光强 的分布情况。
衍射公式推 导
菲涅尔-基尔霍夫衍射积分公式是圆屏衍射模型的核心公式，其推导过程涉及到波动光学的基本 原理和数学运算。
更新与完善课程内容
随着科学技术的不断发展，菲涅尔圆孔衍射和圆屏衍射的相关研究也在不断深入。为了使 课程内容更加前沿和有深度，未来课程需要对内容进行定期更新和完善，以反映最新的研 究进展和成果。
清晰度
通过增加图解和实例分析，使知识 点更加清晰易懂。
实用性
修正后的课件更贴近实际，有助于 学生将理论知识与实验观察相结合。
课程实践与实验
实验设备与材料
光源
激光器或单色光源
菲涅尔圆孔
若干个不同直径的圆孔
圆屏
不同半径的圆屏
屏幕
用于接收衍射图像的白色 屏幕
测量工具
尺子、测角仪等
实验步骤与操作
1. 准备实验设备
效果。
对未来课程的展望
增加应用案例分析
在未来的课程中，可以增加更多关于菲涅尔圆孔衍射和圆屏衍射在实际应用中的案例分析， 使学习者更好地理解这两种衍射现象的应用价值。

惠更斯菲涅耳衍射课件

惠更斯菲涅耳衍射课件

生物医学成像
X射线成像
X射线在穿过人体组织时发生衍射 ，通过分析衍射产生的图像可以 诊断疾病。
超声成像
超声波在遇到人体组织时发生衍射 ，通过分析衍射产生的回波可以生 成人体内部结构的图像。
光学显微镜
光学显微镜利用光的衍射和干涉现 象来观察细胞和组织的结构。
04 实验演示
单缝衍射实验
总结词
通过单缝衍射实验，观察光通过单缝产生的衍射现象，了解衍射的基本原理。
的变化引起的，而物理衍射是由于波动性质引起的。
按光强分布分类
02
根据光强分布的不同，衍射可以分为会聚衍射、发散衍射和干
涉衍射等类型。
按波长与障碍物尺寸关系分类
03
根据波长与障碍物或孔缝尺寸的关系，衍射可以分为小孔衍射
、大孔衍射和多缝衍射等类型。
0动现象的基本方程，其形式为$frac{partial^2 Phi}{partial t^2} = c^2 nabla^2 Phi$，其中$Phi$是波动场，$c$是波速。
透镜制造
在制造透镜时，需要考虑 到材料的衍射特性，以消 除或减少像差。
干涉仪
干涉仪利用衍射原理来测 量波长和相干长度。
雷达 and sonar
目标识别
雷达和声纳通过分析衍射 产生的回波来识别目标。
距离测量
通过测量衍射回波的时间 差，可以计算出目标与探 测器之间的距离。
速度测量
通过分析衍射回波的多普 勒频移，可以测量目标的 速度。
实现更高效的衍射器件
利用衍射现象，可以设计出各种光学器件，如光束整形器 、光束分束器等。未来可以通过优化设计，提高这些器件 的效率和稳定性。
探索其他物理场的衍射现象
除了光学领域，其他物理场如电磁波、声波等也存在衍射 现象。未来可以进一步探索这些物理场的衍射现象及其应 用。

第九讲菲涅耳衍射

第九讲菲涅耳衍射

1, 0,
x0 y0 a 2 其它
2
2
提示 1. 用F.T.表达式, 并取x = y = 0,
2 2 2 2 x0 y0 x0 y0 exp( jkz ) U (0,0, z ) circ ( ) exp( jk )dx0 dy 0 j z a 2z
提示2. 用极坐标, 积分可求出.
exp( jkz) 2 U (0,0, z ) d 0 jz
r2 0 exp(jk 2 z )rdr
a
轴上强度分布:
2 I (0,0) z 4 sin a 2z
2
a2 a 2 2 j exp( jkz) exp( jk ) sin( ) 4z 2z
中央亮斑宽度: Dx =2z/a, Dy =2z/b ∴x, y方向的角展宽:
D x Dx , D y z a/2 b/2
-1 0 1
2
I/I(0)
1
与圆孔数量级相同. 孔尺寸越小,角展宽越大
ax/z
简单孔径的夫琅和费衍射：双缝
1 rect(x0/a) a/2 0 a/2
余弦型振幅光栅的复振幅透过率为
x t x a b cos d
式中，d 为光栅周期，a>b>0。观察平面与光栅相距z。用单色 平面波垂直照明光栅，当 z 分别取下列各数值时，确定在观察 平面上产生的强度分布。 （式中zT称作泰伯距离） （1）
zT d z
(x0+d/2)+ (x0-d/2)
x0
*
1
1
t (x0)
d/2
d/2
0 d/2
x0

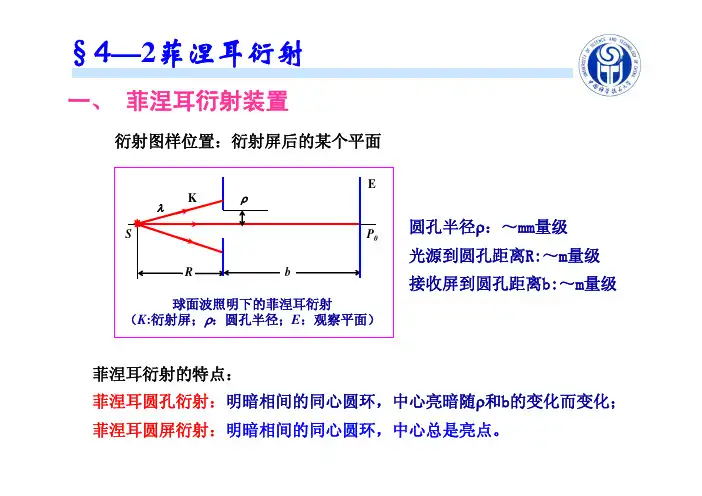
ch菲涅耳衍射

ch菲涅耳衍射

§4—2菲涅耳衍射一、菲涅耳衍射装置二、菲涅耳半波带法取波面Σ为以点源S为中心的球面，其顶点O到场点P的距离为b，以场点P为球心，分别以b+λ/2、b+λ、b+3λ/2、···为半径作球面，将透过小菲涅耳半波带，使得相邻两个波带的边缘波带的面积及半径计算：考察第k个波带，设其边沿点当dr=λ/2时，k d R r R bλΣπ=+菲涅耳半波带的特点：点引起的光振动相位相差π，故在PP点合振动振幅大小的计算：假设：同一波带上各点到P点的距离相等同一波带上各面元的法线与该面元中心到P点连线的夹角相等任一波带在P点产生的光振动的振幅仅仅与该波带到P点的距离及方向角有关，即随着波带级数的增大而单调地减小，可表示为：kEEEEEΔ>>Δ>Δ>Δ>Δ......4321相应的振动相位依次为：φ，φ+π，φ+2π，φ+3π，···φ+(k-1)π，φ+kπ。

由此可以得到：同一波带上各面元在P点产生的光振动具有相同的振幅和相位；由k 个波带在P 点引起的合振动的振幅为：()()k E E E E E P E Δ−++Δ−Δ+Δ−Δ=+11"A kA 3A 1E (P )轴上P点的菲涅耳衍射光强：点的合振动振幅约等于第一③给定b 、ρ、λ, P 点的衍射光强大小随波面的曲率半径大小R 变化，即沿轴向移动光源或衍射屏时，P 点的光强度出现亮暗交错变化。

④给定b 、R 、λ，P 点的衍射光强大小随孔的半径ρ变化：ρ=ρ1时：k=1，E (P )=ΔE 1=E max ρ=ρ2时：k=2，E (P )=ΔE 1-ΔE 2=E min ρ=ρ∞时：k=∞，E (P )=ΔE 1/2当波面不受限制时，即球面波在空间自由传播时，在P 点引起的合振动之振幅等于第一个波带对应的波面在P 点引起的光振动振幅的一半。

按惠更斯原理，波面不受限制时服从直线传播规律。

13-8 菲涅耳衍射 物理光学 教学课件

13-8 菲涅耳衍射 物理光学 教学课件

8
由以上两式可得：
讨论：
N
2 N
1 (
r0
1) R
▲ 对 P 点若S 恰好分成 N 个半波带时：
AP
1 2(a1
aN)
N为奇数 AP 12(a1 aN) N为偶数 AP 12(a1 aN)
最大 最小
▲ 对P 若S中还含有不完整的半波带时：
1 2(a 1aN)A P1 2(a 1aN)
光强介于最大 和最小之间
随r0增大，N减小，菲涅耳衍射效应显著；
当r0大到一定程度时，r0→∞，露出的波带数N不 变化，且为
N
Nmax
N2 R
称为菲涅耳数，它是一个描述圆孔 衍射效应的很重要的参量。
此后，随着r0的增大，P点光强不再出现明暗交替 的变化，逐渐进入夫朗和费衍射区。
而当r0很小时，N很大，衍射效应不明显。当r0小 到一定程度时，可视光为直线传播。- -几何区
所示，图中为了清楚起见，把偶数带画上了斜线。 – 这些波带在P点引起振动的振幅大小，不仅取决于波带的数目，还
取决于每个波带露出部分的大小。 – 精确计算P点的合成振动振幅是很复杂的，但可以预计，当Q点逐
渐偏离P0点时，有的地方衍射光会强些， 有些地方会弱些。
15
图1 轴外点波带的分法
图2 轴外点带的分布
19
菲涅耳波带片（透镜）与一般透镜特点的比较： （1）具有一般透镜的聚焦、成像作用 （2）除主焦距f外，对应f/3，f/5，f/7·······位置处 有一系列次焦点与实焦面对称还有一系列虚焦点存在 （3）菲涅耳波带片: f～1/λ；
一般透镜: f～λ 两者结合，有利于消除色差
20
【例题】波长为 0.45μm的单色平面波入射到不透明的屏

《菲涅耳衍射》PPT课件

《菲涅耳衍射》PPT课件

N
2 N
(1
R)
2 N
(78)
R r0 r0
AN
a1 2
aN 2
(76)
a1 a2 a3 aN
(4)轴外点的衍射
对于轴外任意点 P 的光强度，原则上也可以用同样 的方法进行讨论。
M
P
M0M2M
S
O1M 1
2
P
0
MN R N hN
rN=r0+N /
2
S
S O O
r0
P
0
(4)轴外点的衍射
通常在半定量处理菲涅耳衍射现象时，均采用比较 简单、物理概念很清晰的菲涅耳波带法或图解法。
4.3.1 菲涅耳圆孔衍射—菲涅耳波带法(Fresnel diffraction by a circular aperture — Fresnel's zone construction )
1. 菲涅耳波带法
N
1
2 2
(73)
(3)倾斜因子 由上图可见，倾斜因子为
K( ) 1 cos (74)
2
将(72)-(74)式代入(66)式，可以得到各个波带在 P0 点产生的光振动振幅
aN
πR
R r0
1
cos N
2
(75)
可见，各个波带产生的振幅 aN 的差别只取决于倾角
N。
aN
SN rN
K ( )
(66)
这说明，当孔小到只露出一个波带时，P0 点的光强 度由于衍射效应，增为无遮挡时 P0 点光强度的四倍。
I1 a12
只露出一个波带时的光强
A
a1 2
(80)
无遮挡时的光强

最新3.1 惠更斯— 菲涅耳原理菲涅耳衍射和夫琅禾费衍射幻灯片课件

最新3.1 惠更斯— 菲涅耳原理菲涅耳衍射和夫琅禾费衍射幻灯片课件
问题？
49
1.国外心理学发展简况
神灵主义时期 自然哲学时期 科学心理学时期
心理学开始成为一门独立的 现代科学的标志
1879年，冯特（Wundt W，1832-1920）在德国莱比 锡大学建立了世界上第一所心理物理实验室
19世纪末---20世纪初
医学心理学概念命名的著作出版， B.H.Lotze（德 国，1852年） –心理门诊建立，L.Witmer（美国，1896年） –心理测验，JM. Cattel（美国，1890年） –心理卫生协会成立，美国，1908年 –心身医学学会成立，美国，1930年
co n ,l)s ( 1co n ,r)s c (os则
K() 1c os
2
3.2菲涅耳衍射和夫琅禾费衍射
一、两类衍射现象的特点 1.衍射的分类
菲涅耳衍射
一、两类衍射现象的特点
1.菲涅耳衍射－近场衍射： 光源和接收屏到障碍物的距离都有限 或其中之一有限
2.夫琅禾费衍射－远场衍射： 光源和接收屏到障碍物的距离都无限（平行光束）
前言
一 、 光 的 衍 射 现 象
第3章 光的衍射与现代光学
一、光的衍射现象
第3章 光的衍射与现代光学
一、光的衍射现象
第3章 光的衍射与现代光学
一、光的衍射现象
第3章 光的衍射与现代光学
光在传播路径中遇到障碍物时，能绕过障碍物边缘而弯入 几何影区传播，并且产生强弱不均的光强分布，这种现象称为 光的衍射。
3.1惠更斯---菲涅耳原理
单色点光源S在波面上任一点Q产生的复振幅为
~
EQ
A exp(ikR)
R
假设：
*所有次波都有相同的初相位 *次波是球面波
* dEP ~ d

第九讲菲涅尔衍射夫琅和费衍射

第九讲菲涅尔衍射夫琅和费衍射
U ( x, y, z ) U ( x , y ,) exp( j

z

f x f y )



exp{j [ f x ( x x ) f y ( y y )]}df x df y dx dy
• 上式的四重积分是类似基尔霍夫公式的一个精确的表达式，尽 管它不含三角函数，但是使用起来仍很不方便。下面还是要按 照菲涅耳的办法进行化简，首先对不同传播距离衍射的情况做 个直观的说明




exp j x y jz z


exp( jkz) U ( x, y, z) U ( x , y , ) exp{ j [( x x ) ( y y ) ]}dx dy jz z
• 显然，这是一个根据边界条件求解波动方程的问题。 • 惠更斯—菲涅尔提出的子波干涉原理与基尔霍夫求解波动方程所 得的结果十分一致，都可以表示成类似的衍射公式
点光源照明平面屏幕的衍射
• 衍射公式
• 倾斜因子
e jkr U P C U P K ds r
cosn,r cos n,r ' K

• 在傍轴近似下，并利用二项式近似
K θ
r z x x y y



x x y y z z z
• 上述近似均代入得到菲涅尔衍射计算公式
1 k x x0 2 y y0 2 U x, y exp jkz U 0 x0 , y0 exp j jz 2z
夫琅和费衍射 : 在菲涅耳衍射公式中，对衍射孔采取更强的限制条 件，即取 则平方位相因子在整个孔径上近似为1，于是

菲涅耳原理光的衍射现象显示屏课件

菲涅耳原理光的衍射现象显示屏课件

B
C
1990年代
TFT-LCD技术出现，提高了LCD显示屏的显 示质量和对比度。
2000年代至今
OLED、QLED等新型显示技术不断涌现， 提高了显示效果和寿命。
D
显示屏技术的应用领域
消费电子
电视、显示器、手机、平板电脑等。
商业应用
广告牌、会议显示、展示台等。
工业应用
仪器仪表、自动化设备等。
医疗应用
菲涅耳原理在LED显示屏中的应用
LED显示屏（LED Panel）利用了发光二极管作为显示元件。每个LED像素由多个 不同颜色的LED小点组成，这些小点发出的光线通过菲涅耳原理中的衍射和干涉 效应，实现了对光线的控制和显示。
在LED显示屏中，每个像素由红、绿、蓝三色LED小点组成，通过调节各颜色 LED的亮度，可以混合出不同的颜色和亮度，最终实现全彩显示。LED发出的光 线经过像素结构中的透镜和小孔的衍射和干涉，形成了可见的光线。
医疗影像、手术室显示等。
菲涅耳原理在显示屏技术中的
05
应用
菲涅耳原理在液晶显示屏中的应用
液晶显示屏（LCD）利用了菲涅耳原理中的衍射和干涉效应 ，通过改变液晶分子的排列方式，实现了对光线的控制和显 示。
在LCD中，背光发出的光线经过由液晶分子构成的像素矩阵 ，由于液晶分子的排列方式不同，光线在通过像素时会发生 不同程度的衍射和干涉，从而呈现出不同的颜色和亮度。
详细描述
当光通过一个小的圆孔时，同样会发生衍射现象。根据菲涅耳原理，圆孔衍射 的强度和方向与圆孔的半径、光的波长等因素有关。通过该原理，可以解释和 预测圆孔衍射的观测结果，例如明暗交替的圆环现象。
菲涅耳原理在光栅衍射中的应用
总结词
菲涅耳原理在光栅衍射中解释了光通过周期性排列的狭缝时的衍射现象，广泛应用于光谱分析和光学 仪器设计等领域。

光学 菲涅耳衍射

光学 菲涅耳衍射

sin u u
B'
dx
θ
b
x
B
θ
P0
P F
三、光强分布特点
sin 2 u 由 I P = I 0 2 可知 : 不同的θ对应着不同的观察点 也对应着不同的光强值 , . u dI P d sin 2 u 2 sin u (u cos u sin u ) = 0 时, I P取得极值,即 : 2 = =0 当: 3 u du du u πb ① λ sin θ 0 = 0 u0 = 0 sin u = 0 uk = kπ πb sin θ = kπ ② 时取得极值. k λ tgu = u ③
决定，在居间位置，光强介于最大值和最小值之间。对线光源，整个花样 为平行于缝、并以中央条纹为中心、对称展开的明暗相间的直线状条纹。 2 2、各级亮条纹（最大值）光强不等。中央亮条纹强度最强；其余亮 条纹 （次最大）光强远小于中央条纹，并随级数的增大而很快减小。
λ
P0
3、条纹宽度—角宽度θ
亮条纹宽度—相邻暗条纹间的间隔。
L2
MD N
dx
θ
b
x
B
θ
P0
P
dE 0 =
A0 dx cos ω t b
F
由惠—菲原理可知： BB‘上所有窄带发出的次波在屏上叠加，就形成了衍射花样。 现取一束与原入射方向成θ角（称为衍射角）的光束，并作辅助平面BD垂直于衍 射方向，则BD面上任一点到P点的光程相等。
∴ M , B 两点沿 θ 方向到 P 点的光程差 δ = M N = x sin θ 又 : N 点的振动表达式为 A dx 复数式为 : dE = 0 e b dE = A0 dx 2π x sin θ ω t cos b λ ~ A0 dx i , 复振幅 d E = e b

菲涅尔衍射-菲涅尔衍射课件

菲涅尔衍射-菲涅尔衍射课件

实验结果分析
分析衍射条纹的形状和分布规律， 理解光的波动性和衍射原理。
比较不同障碍物（如狭缝、圆孔） 对衍射条纹的影响，探究衍射现
象与障碍物形状的关系。
通过实验数据，计算出光的波长 等参数，进一步验证光的波动性。
04
菲涅尔衍射的应用实例
光栅的制造
菲涅尔衍射在光栅制造中的应用
光栅是一种重要的光学元件，用于分光和光谱分析。 在光栅制造过程中，菲涅尔衍射原理被用来控制光束 的衍射方向和模式，从而实现精确的光束分离和光谱 分析。
行性和性能指标。
全息摄影技术
菲涅尔衍射在全息摄影技术中的应用
全息摄影技术是一种记录和重现三维图像的技术。在全息摄影过程中，菲涅尔衍射原理被用来控制光的衍射和干 涉，从而实现三维图像的记录和再现。
全息摄影技术的过程
全息摄影技术通常包括记录和再现两个步骤。在记录步骤中，利用菲涅尔衍射原理和干涉原理，将三维物体发出 的光波分散并记录在感光材料上。在再现步骤中，通过特定的衍射结构将记录的光波重新组合并投影到空气中或 特定的观察屏幕上，以重现三维图像。
THANKS
感谢观看
菲涅尔衍射公式
菲涅尔衍射公式描述了光波在遇到边缘或障碍物时，衍射光强度的分布情况。 该公式基于波动理论，能够准确预测衍射现象。
菲涅尔半波带法
菲涅尔半波带法是一种分析衍射现象 的方法，通过将衍射区域划分为一系 列半波带，分析各半波带的贡献来解 释衍射现象。
该方法有助于直观理解衍射现象，简 化分析过程。
菲涅尔衍射的应用
光学仪器设计
菲涅尔衍射在光学仪器设计中具有重 要应用，如透镜、反射镜、光栅等光 学元件的设计，都需要考虑菲涅尔衍 射的影响。
干涉测量
光信息处理

菲涅尔圆孔衍射和圆屏衍射PPT课件

菲涅尔圆孔衍射和圆屏衍射PPT课件
使被限制的波面细分为许多面积大小相等的细 波带。
14
(3）处理步骤
1) 将半波带分割成 m个更窄的小环带
2) 写出每个小环带在P0点的复振幅
U%1(P0 ) A(P0 )ei0 U% 2 (P0 ) A(P0 )ei(0 m) U%3 (P0 ) A(P0 )ei(0 2 /m)
A( P0 ) An1 An2 A

1 2
[
An1
(
1 )
A
]

1 2
An1
1 A(P0 ) 2 An1
I A2 (P0 )
9
（6）讨论：
1）圆孔衍射中心场点P0处的总振幅近似为：
A(P0 ) A1 A2 A3 (1)(n1) An
则：dr l / 2
k Rl 是一个常量
由菲涅耳原理可知：
Ak

k(k )
Rl
Rb
rk
Ak

R
k( k(k )
b
k
)
k rk
Ak仅随 k(k ) 变化，随k的增加缓慢减小，最后
趋近于零。即：
A1 A2 A3 Ak1 Ak2 A 0
邻露出波带间相差一个波长的光程差。 （3）波带片具有面积大、轻便、
可折叠等透镜不具备的………….
U% m (P0 ) A(P0 )ei(0 )
15
3)画出矢量图
注意： 矢量图是正多边形， 一个完整半波带首尾矢量的
位相差是
4)连接首尾矢量，得到合成矢
量，则半波带在P0点产生的光
强为：
I (P0 ) A2
m M Am
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

当波长、P点的位置r0、 圆孔位置R给定后，由
N


2 N
(1

1)
r0 R
N与圆孔的大小ρN有关，孔大，露出的的波带多， 衍射效应不显著，孔小，露出的的波带少，衍射效
应显著；
当孔趋于无限大- -即 没有光阑时，
播到任一点P时的振幅，只要把球面波相对于P分成半
波带，将第一个和最后一个（第N个）带所发出的次
波的振幅相加或相减即可。
12/28/2019
返回
(3) N与ρN间的关系
D
图示O为点光源，DD’ 为光阑，其上有一半径 为ρN的圆孔，S为通过
圆孔的波面－球冠(球 冠的高为h)，P为圆孔
对称由上任意一点。
半波带与观察点P的位置、圆孔的大小、波长等有关。
12/28/2019
返回
S BnN
(2) 合振幅的计算
Rh
rN
O R B0
r0
P
N个半波带的发次波在P点叠加
的合振幅AN
AN a1 a2 a3 a4 a5 ... (1) N 1 aN
aN：第N个半波带所发在P点的次波振幅 “－”：相邻两个半波带所发次波到达P点相位差为
(4)轴外点Q的衍射
12/28/2019
返回
(1)r0对衍射现象的影 响
当波长、圆孔位置R、大 小ρh给定后，由
N


2 N
(1

1)
r0 R
P点的振幅与P点的位置r0有关，即移动观察屏，P
点出现明暗交替变化；
随r0增大，N减小，菲涅耳衍射效应显著；
当r0大到一定程度时，r0→∞，露出的波带数N不 变化，且为
S N rN
R

, (5)
R r0
由此可见，SN/rN与N无关，则各个半波带对AN的 影响仅与倾斜因子K(N)有关；
K(N)随N的增大(增大)而缓慢减小，故aN将随N的 增大而缓慢减小。
结论：各个波带所发次波，传到P点时
振幅aN，随N的增大而缓慢减小； 相位逐个相差。
S 2R R(1 cos),(2)
接上页
cos R2 (R r0 )2 rk2 , (3分别微 分，并化简可得
dS 2RdrN , (4)
rN
R r0
由于rN远大于，故drN≈/2， dS看作是半波带的面积，则有
12/28/2019
P点的合振幅
所有次波在P点的合振幅为
AP

1 2
[a1
(1) N 1 aN ]
1 2
(a1
＋ ：N奇 数 aN ), － ：N隅 数
a1
a3
a5
a1
a3
a5
aN AP
结 论
a2
a4
aN AP
a2
a4
a6
N是偶数
N是奇数
应用惠更斯－菲涅耳原理来计算从点光源发出的光传
讨论aN的大小 按惠更斯－菲涅耳原理 aN为
aN

K ( N )S N
rN
, (1)
球冠的面积为 S 2R R(1 cos ),(2)
由余弦定理可得 cos R 2 (R r0 ) 2 rN2 , (3)
2R(R r0 )
12/28/2019
3.3 菲涅耳衍射
3.3.1 菲涅耳圆孔衍射- -菲涅耳波带法
1.菲涅耳波带法 2.菲涅耳圆孔衍射 3.菲涅耳圆屏衍射
3.3.2 菲涅耳直边衍射- -振幅矢量加法
1.振幅矢量加法 2.*菲涅耳直边衍射 3.*菲涅耳单缝衍射
12/28/2019 返回第3章
菲涅耳衍射
菲涅耳衍射是在菲涅耳近似条件成立的距离范围内所 观察到的衍射现象；
12/28/2019

2 N

Nr0 2r0h
又

2 N
R2
(R h)2

h


2 N
2R
由以上两式可得
N


2 N
(1

1)
讨论：
r0 R
▲ 对 P 点若S 恰好分成 N 个半波带时：
1 AP 2 (a1 aN )
N为奇数
AP

1 2 (a1
aN )
N为偶数
AP
(1)菲涅耳波带 - -菲涅耳半波带 (2)合振幅的计算 (3)波带数N与圆孔半径ρN间的关系
12/28/2019
返回
(1) 菲涅耳半波带
点光源O发出球面波，经DD’调制后为一球冠S，OP与 S交于B0点－－P对波面S的极点
将波面S分成许多以B0 为圆心的环形波带，并使：
S
r3=r2+λ/2
B3
r2=r1+λ/2 r1=r0+λ/2
B0P r0 B1P B0P B2 P B1P
B2
B1
B3P B2P …
O
R
B0 r0
●
P

BN P BN 1P 2
这样分成的环形波带
称为菲涅耳半波带。
任意相邻波带所发的次波到达P点时的光程差为/2;亦即它们同时到 达P点时的相位差为。

1 2 (a1
aN )
最大 最小
▲ 对P 若S中还含有不完整的半波带时：
1 2 (a1
aN )
AP

1 2 (a1
aN )
光强介于最大 和最小之间
12/28/2019
返回
2.菲涅耳圆孔衍射
圆孔衍射
S
*
HP
(1)r0对衍射现象的影响 (2)ρN对衍射现象的影响 (3)光源对衍射现象的影响
S
λ
A
· ρN
O R B B0
D’
N个完整菲涅 耳半波带数
rN r0
·P
BB0 h h r0
首先考虑通过圆孔N个完整菲涅耳半波带。图中
rN r0 N 2
由几何知识可得

2 N
rN2
(h r0 )2
(r0
N 2)2
(r0
h)2
Nr0 2r0h, (略去二阶小量h2 , N 22 )
N
N m ax

2 N
R
称为菲涅耳数，它是一个描述圆孔 衍射效应的很重要的参量。
此后，随着r0的增大，P点光强不再出现明暗交替 的变化，逐渐进入夫朗和费衍射区。
而当r0很小时，N很大，衍射效应不明显。当r0小 到一定程度时，可视光为直线传播。- -几何区
12/28/2019
返回
(2)ρN对衍射现象的影响
照射到衍射屏上的光波和离开衍射孔到达观察屏上的 波面都不能当作平面来处理。
直接运用菲涅耳-基尔霍夫公式定量分析菲涅耳衍射，
数学处理非常复杂；- -可用计算机进行数值运算
半定量法分析菲涅耳衍射 代数加法- -波带法(半波带法) 振幅矢量加法- -图解法
12/28/2019
1.菲涅耳波带法