单位根检验PPT课件
- 格式：ppt
- 大小：523.50 KB
- 文档页数：18
下载文档原格式
合集下载
平稳性和单位根检验71页PPT
不见自己的背脊。——非洲 2、最困难的事情就是认识自己。——希腊 3、有勇气承担命运这才是英雄好汉。——黑塞 4、与肝胆人共事，无字句处读书。——周恩来 5、阅读使人充实，会谈使人敏捷，写作使人精确。——培根
平稳性和单位根检验
6、法律的基础有两个，而且只有两个……公平和实用。——伯克 7、有两种和平的暴力，那就是法律和礼节。——歌德
8、法律就是秩序，有好的法律才有好的秩序。——亚里士多德 9、上帝把法律和公平凑合在一起，可是人类却把它拆开。——查·科尔顿 10、一切法律都是无用的，因为好人用不着它们，而坏人又不会因为它们而变得规矩起来。——德谟耶克斯
平稳性和单位根检验
6、法律的基础有两个，而且只有两个……公平和实用。——伯克 7、有两种和平的暴力，那就是法律和礼节。——歌德
8、法律就是秩序，有好的法律才有好的秩序。——亚里士多德 9、上帝把法律和公平凑合在一起，可是人类却把它拆开。——查·科尔顿 10、一切法律都是无用的，因为好人用不着它们，而坏人又不会因为它们而变得规矩起来。——德谟耶克斯
第4章单位根检验（讲稿）（★）
第4章单位根检验（讲稿）（★）第一篇：第4章单位根检验(讲稿)第4章单位根检验4.1 DF分布由于虚假回归问题的存在，在回归模型中应避免直接使用非平稳变量。
因此检验变量的平稳性是一个必须解决的问题。
在第二章中介绍用相关图判断时间序列的平稳性。
这一章则给出严格的统计检验方法，即单位根检验。
1）检验模型在介绍检验方法之前，先讨论所用统计量的分布。
给出三个简单的自回归数据生成过程（d.g.p.），yt = β yt-1 + ut ，(4.1) yt = μ + β yt-1 + ut ，(4.2)yt = μ + α t + β yt-1 + ut ,(4.3)y0 = 0, ut ~ IID(0, σ)其中μ称作位移项（漂移项），α t称为趋势项。
显然，对于以上三个模型：当|β| < 1时，yt 是平稳的，当|β| = 1时，yt 是非平稳的。
2）检验统计量分布以模型(4.1)为例，（1）若β= 0，统计量，2ˆ-0βˆ)t(β=t~(T-1)(4.4)ˆs(β)的极限分布为标准正态分布。
（2）若|β| < 1，统计量，ˆ-ββˆ)=t(βˆ)(4.5)s(β渐进服从标准正态分布。
根据中心极限定理，当T →∞时，ˆ-β)→ N(0, σ 2(1-β 2))(4.6)T(βTˆ)t(β（3）那么在|β| = 1条件下，统计量服从什么分布呢？当|β| = 1时，变量非平稳，上述极限分布发生退化（方差为零）。
①DF统计量检验单位根的一个统计量是DF统计量。
DF统计量的表达式与通常意义的t统计量完全相同。
ˆ-1ˆ-1ββˆ)=DF=t(β=Tˆs(β)s(y2)-1/2u∑t-1t=1 2=(∑yt-1)t=1T21/2∑uytt=1Tt=1Tt-12suT y∑t-1∑utyt-1= 当T →∞时，DF =ˆ-1βˆ)s(βsu(∑yt-12)1/2t=1t=1T(4.16)⇒(1/2)(W(1)2-1)(W(i)di)0⎰121/2(4.17)同理，对于模型(4.2)和(4.3)的DF统计量的极限分布也是Wiener过程的函数。
第13讲 单位根检验
第13讲 单位根检验由于虚假回归问题的存在，在回归模型中应避免直接使用不存在协积关系的非平稳变量。
因此检验变量的平稳性是一个必须解决的问题。
在第二章中介绍用相关图判断时间序列的平稳性。
这一章则给出序列平稳性的严格的统计检验方法，即单位根检验。
在介绍单位根检验之前，先认识四种典型的非平稳随机过程。
13.1 四种典型的非平稳随机过程（1）随机游走过程。
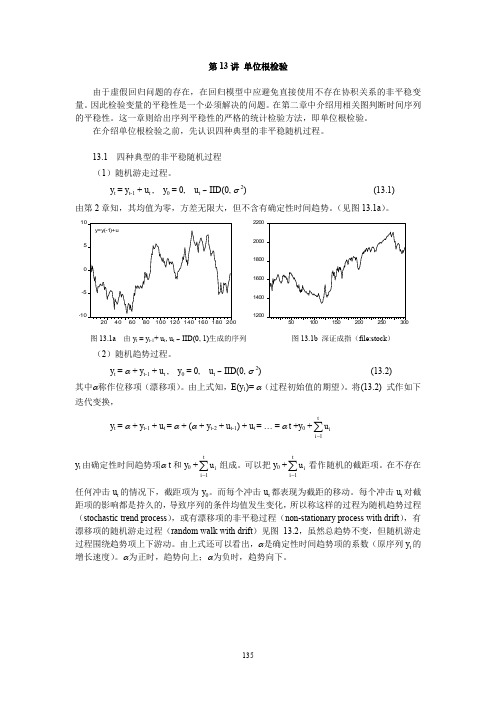
y t = y t -1 + u t , y 0 = 0, u t ~ IID(0, σ 2) (13.1) 由第2章知，其均值为零，方差无限大，但不含有确定性时间趋势。
（见图13.1a ）。
-10-551020406080100120140160180200y=y(-1)+u120014001600180020002200图13.1a 由y t = y t -1+ u t , u t ~ IID(0, 1)生成的序列 图13.1b 深证成指（file:stock ）（2）随机趋势过程。
y t = α + y t -1 + u t , y 0 = 0, u t ~ IID(0, σ 2) (13.2) 其中α称作位移项（漂移项）。
由上式知，E(y 1)= α（过程初始值的期望）。
将(13.2) 式作如下迭代变换，y t = α + y t -1 + u t = α + (α + y t -2 + u t -1) + u t = … = α t +y 0 +∑-ti i u 1y t 由确定性时间趋势项α t 和y 0 +∑-ti i u 1组成。
可以把y 0 +∑-ti i u 1看作随机的截距项。
在不存在任何冲击u t 的情况下，截距项为y 0。
而每个冲击u t 都表现为截距的移动。
每个冲击u t 对截距项的影响都是持久的，导致序列的条件均值发生变化，所以称这样的过程为随机趋势过程（stochastic trend process ），或有漂移项的非平稳过程（non-stationary process with drift ），有漂移项的随机游走过程（random walk with drift ）见图 13.2，虽然总趋势不变，但随机游走过程围绕趋势项上下游动。
平稳性和单位根检验 ppt课件
3.49
3.12
2.79
2.38
500
3.48 ppt课件3.11
2.78
2.38
38
>500
3.46
3.11
2.78
2.38
• 一个简单的检验过程：
– 同时估计出上述三个模型的适当形式，然后通过 ADF临界值表检验零假设H0：=0。
–例如：如果有两列时间序列数据表现出一致的变化趋势 （非平稳的），即使它们没有任何有意义的关系，但进 行回归也可表现出较高的可决系数。
ppt课件
5
2、平稳性的定义
• 假定某个时间序列是由某一随机过程（stochastic
process）生成的，即假定时间序列{Xt}（t=1, 2, …）
的每一个数值都是从一个概率分布中随机得到，如果
扩展实验
① x=0.5*x(-1)+u
② x=1+0.5*x(-1)+u
③ x=1.5*x(-1)+u
④ x=1+1.5*x(-1)+u
⑤ x=1+t+1.5*x(-1)+u
ppt课件
15
二、单整、趋势平稳与差分平稳
ppt课件
16
1、单整（integrated Serial）
• 如果一个时间序列经过一次差分变成平稳的， 就称原序列是一阶单整（integrated of 1）序列， 记为I(1)。
随机游走，非平稳
对该式回归，如果确实 发现ρ=1，则称随机变
量Xt有一个单位根。
X t ( 1) X t1 t X t1 t
等价于通过该式判断 是否存在δ=0。
• 通过上式判断Xt是否有单位根,就是时间序列 平稳性的单位根检验。
单位根检验详解
第2节 单位根检验由于虚假回归问题的存在，因此检验变量的平稳性是一个必须解决的问题。
在第十二章中介绍用相关图判断时间序列的平稳性。
这一章则给出序列平稳性的严格的统计检验方法，即单位根检验。
单位根检验有很多方法，这里主要介绍DF 和ADF 检验。
序列均值为0则无C ，序列无时间趋势则无trend在介绍单位根检验之前，先认识四种典型的非平稳随机过程。
1、四种典型的非平稳随机过程 （1）随机游走过程。
y t = y t -1 + u t , y 0 = 0, u t ~ IID(0, σ 2) 其均值为零，方差无限大（?），但不含有确定性时间趋势。
（见图1a ）。
-10-551020406080100120140160180200y=y(-1)+u12001400160018002000220050100150200250300图1a 由y t = y t -1+ u t 生成的序列 图1b 深证成指（2）随机趋势过程。
y t = α + y t -1 + u t , y 0 = 0, u t ~ IID(0, σ 2) 其中α称作位移项（漂移项）。
由上式知，E(y 1)= α（过程初始值的期望）。
将上式作如下迭代变换，y t = α + y t -1 + u t = α+ (α+ y t -2 + u t -1) + u t = … = αt +y 0 +∑-ti i u 1y t 由确定性时间趋势项αt 和y 0 +∑-t i i u 1组成。
可以把y 0 +∑-ti i u 1看作随机的截距项。
在不存在任何冲击u t 的情况下，截距项为y 0。
而每个冲击u t 都表现为截距的移动。
每个冲击u t 对截距项的影响都是持久的，导致序列的条件均值发生变化，所以称这样的过程为随机趋势过程（stochastic trend process ），或有漂移项的非平稳过程（non-stationary process with drift ），见图2，虽然总趋势不变，但随机游走过程围绕趋势项上下游动。
单位根检验操作PPT课件
方法2: 用自相关系数图判断
中国GDP时间序列的自相关系数不是很快地（如滞后期K=2，3
趋于零，即缓慢下降，再次表明序精选列是非平稳的.
7
方法3: 单位根检验
Quick Series Statistics
Unit Root Test
精选
8
输入变量名（本例：GDP）
精选
9
选择ADF检验 / Level（水平序列）/ Trend and Intercept （趋势项和漂移项）/ 滞后期数：2
(A)DF检验
PP检验
（2）检验对象
Level（水平序列）
1st difference（一阶差分序列）
2nd difference（二阶精差选分序列）
2
（3）检验式中应包括的附加项 Intercept（漂移项） Trend and Intercept（趋势项和漂移项） None（无附加项）
（4）检验式中因变量的滞后差分项的个数。
• 所以，对于一般的序列，采用画图的方法就可以了。
• 至于你检验出现的这种情况则是正常现象，因为检验序列显著性水平的T 统计量在原假设下的渐进分布依赖于单位根检验的不同形式。
精选
18
精选
3
例 根据《中国统计年鉴2004》，得到我国1978—2003年的
GDP序列，检验其是否为平稳序列。 中国1978—2003年度GDP序列
精选
4
精选
5
方法1: 用时序图判断
由GDP的时序图初步判断序列是不平稳的(可以看出该序列可能 存在趋势项，若需用ADF检验则选精选择第三种模型进行检验)。 6
• 滞后阶数的问题。最佳滞后阶数主要根 据AIC SC准则判定，当你选择好检验方 式，确定好常数项、趋势项选择后，在 lagged differences栏里可以从0开始尝试， 最大可以尝试到7。你一个个打开去观察， 看哪个滞后阶数使得结论最下方一栏中 的AIC 和SC值最小，那么该滞后阶数则 为最佳滞后阶数。
时间序列的平稳性和单位根检验.共65页PPT
谢谢！
•
29、在一切能够接受法律支配的人类 的状态 中，哪 里没有 法律， 那里就 没有自 由。— —洛克
•
30、风俗可以造就法律，也可以废除 法律。 ——塞·约翰逊
61、奢侈是舒适的，否则就不是奢侈 。——CocoCha nel 62、少而好学，如日出之阳；壮而好学 ，如日 中之光 ；志而 好学， 如炳烛 之光。 ——刘 向 63、三军可夺帅也，匹夫不可夺志也。 ——孔 丘 64、人生就是学校。在那里，与其说好 的教师 是幸福 ，不如 说好的 教师是 不幸。 ——海 贝尔 65、接受挑战，就可以享受胜利的喜悦 。——杰纳勒 尔·乔治·S·巴顿
时间序列的平稳性和单位根检验.
•
26、我们像鹰一样，生来就是自由的 ，但是 为了生 存，我 们不得 不为自 己编织 一个笼 子，然 后把自 己关在 里面。 ——博 莱索
•
27、法律如果不讲道理，即使延续时 间再长 ，也还 是没有 制约力 的。— —爱·科 克
•
28、好法律是由坏风俗创造出来的。 ——马 克罗维 乌斯
统计前沿--单位根检验
对非平稳时间序列进行平稳 化的常用方法是对其施行差分， 对于如上图中呈现出线性向上趋 势的非平稳时间序列，作一阶差 分即可平稳化，由于线性向上趋 势时间序列的趋势线为直线，直 线方程如下： Yt=a+bt 其一阶差分 △ Yt = Yt- Yt-1＝b （常数）
Yt
Y a bt
t
对于具有二次曲线变化趋势 的非平稳时间序列，作二阶差分 即可平稳化，（二次曲线的二阶 差分是常数）。时间序列Xt的一 、二阶差分的计算方法分别为：
四、单位根检验应用实例
例1 美国DPI的平稳性检 验及单整阶数的确定
我们现在研究美国1971 年第一季度至2004年第一季 度 的 个 人 可 支 配 收 入 DPI（ Disposable personal income ），下 面用单位根检验方法检验美 国DPI时间序列的平稳性。 1．DF检验 首先用DF检验方法来检验 DPI的平稳性。采用DF回归
说明滞后阶数p值的选择是合适 的。而ADF临界值为-1.94， 于是ADF统计量值<ADF临界值 ，即ADF检验结果为平稳的，也 即 DPI 的 一 阶 差 分 是 平 稳 的 ， DPI序列本身非平稳，但其一阶 差分是平稳的，于是美国的个人 可支配收入DPI的季度时间序列 数据是一阶单整。（同时这也是一
或
GENR DY＝Y-Y(-1) GENR DY2＝DY-DY(-1)
其中， Y(-1)表示Yt-1, DY(-1)表示DYt-1等，即滞 后一期变量。
二、单整（Integration） 设 Yt（t=1，2，…） 为 非 平稳的时间序列，若Yt 经过d 阶差分之后变为平稳序列 ， 而d-1阶差分之后仍为非平稳 序列，则称时间序列Yt 为d阶 单整，记为I(d)。称平稳时间 序列为0阶单整，记为I(0) 。 随机游动是一阶单整。
平稳性和单位根检验.72页PPT
平稳性和单位根检验.
46、法律有权打破平静。——马·格林 47、在一千磅法律里，没有一盎司仁 爱。— —英国
48、法律一多，公正就少。Fra bibliotek—托·富 勒 49、犯罪总是以惩罚相补偿；只有处 罚才能 使犯罪 得到偿 还。— —达雷 尔
50、弱者比强者更能得到法律的保护 。—— 威·厄尔
66、节制使快乐增加并使享受加强。 ——德 谟克利 特 67、今天应做的事没有做，明天再早也 是耽误 了。——裴斯 泰洛齐 68、决定一个人的一生，以及整个命运 的，只 是一瞬 之间。 ——歌 德 69、懒人无法享受休息之乐。——拉布 克 70、浪费时间是一桩大罪过。——卢梭
46、法律有权打破平静。——马·格林 47、在一千磅法律里，没有一盎司仁 爱。— —英国
48、法律一多，公正就少。Fra bibliotek—托·富 勒 49、犯罪总是以惩罚相补偿；只有处 罚才能 使犯罪 得到偿 还。— —达雷 尔
50、弱者比强者更能得到法律的保护 。—— 威·厄尔
66、节制使快乐增加并使享受加强。 ——德 谟克利 特 67、今天应做的事没有做，明天再早也 是耽误 了。——裴斯 泰洛齐 68、决定一个人的一生，以及整个命运 的，只 是一瞬 之间。 ——歌 德 69、懒人无法享受休息之乐。——拉布 克 70、浪费时间是一桩大罪过。——卢梭
平稳性和单位根检验.PPT文档72页
31、只有永远躺在泥坑里的人，才不会再掉进坑里。——黑格尔 32、希望的灯一旦熄灭，生活刹那间变成了一片黑暗。——普列姆昌德 33、希望是人生的乳母。——科策布 34、形成天才的决定因素应该是勤奋。——郭沫若 35、学到很多东西的诀窍，就是一下子不要学很多。——洛克
平稳性和单位根检验.
26、机遇对于有准备的头脑有特别的Hale Waihona Puke 亲和力 。 27、自信是人格的核心。
28、目标的坚定是性格中最必要的力 量泉源 之一， 也是成 功的利 器之一 。没有 它，天 才也会 在矛盾 无定的 迷径中 ，徒劳 无功。- -查士 德斐尔 爵士。 29、困难就是机遇。--温斯顿．丘吉 尔。 30、我奋斗，所以我快乐。--格林斯 潘。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
❖ 可以通过数学推导证明； ❖ 已知随机步游是非平稳的，当 | |1 时，
AR(1)过程 {yt}为一随机步游过程。
14
单位根检验：定义
❖ 看图识平稳 ：15源自单位根检验：定义❖ 看图识平稳 ：
16
单位根检验：定义
❖ 看图识平稳 ：
17
单位根检验：定义
❖ I(d)过程：有时原始序列是非平稳过程，但对 原始序列经过d次差分后可变为平稳过程，则 原序列记为I(d)过程；
12
单位根检验：定义
❖ AR(1)过程是平稳序列吗？
❖ 定理：若| |1，则AR(1)过程是平稳过程。因
为
（1）
Eyt
1
（2）cov(
yt
,
yt
h
)
2 |h| 1 2
var(
yt
)
1
2
2
（3） (t, h) |h|
❖ 证明过程略
13
单位根检验：定义
❖ 如果 | |1 ，AR(1)过程 {yt}还是平稳过程吗？ 为什么？
❖ 经济时间序列多为I(1)或I(2)过程； ❖ 显然，I(0)过程是平稳序列 。
18
单位根检验：定义
❖ 当回归模型中含有非平稳的I(d)序列时，常规 的统计推断都不再成立，因此必须检验被解 释变量和解释变量是不是平稳的。标准的检 验方法是“单位根检验”。
19
单位根检验：定义
❖ 一个随机过程的平稳性取决于其特征方程的 根的值。若所有的根都位于单位圆之外，则 该过程是平稳的。若某个(些)根的值位于单位 圆上或单位圆内，则该过程是非平稳的。若 特征方程的根取值为1，则称其为单位根。对 单位根的检验(即对随机过程单整阶数的检验) 也就是对随机过程平稳性的检验。
yt yt1 1 xt xt1 t
进行迭代估计，可以证明 ˆ 依概率收敛于零。
9
虚假回归（伪回归）：总结
❖ 总结： 1）伪回归现象：对于任何两个（或两个以 上）不相关的单位根过程，只要样本量足够 大，检验他们相关性的统计量一定呈显著性， 这就是伪回归现象。 2）回归分析将平稳过程当作非平稳过程来 处理是十分危险的。因此回归中必须分清平 稳过程和非平稳过程。 3）伪回归的本质问题是变量的非平稳性。
22
单位根检验：单位根过程
❖ 单位根过程是一种特别常见的非平稳过程。 其差分为平稳过程。
23
单位根检验：单位根过程
单位根过程的性质： ❖ 伪回归：如对于某些时间序列，可能它们本
身之间并不相关，但对资料进行计算可以得 到显著的相关系数和回归方程。这种现象称 为伪回归。这是因为回归估计中主要依靠的 是序列的趋势之间的关系，只要两个序列具 有一定的趋势关系，我们就可能会得到显著 的相关系数和回归系数。
计量经济学
❖ 虚假回归（伪回归） ❖ 单位根检验 ❖ 格兰杰因果检验 ❖ 协整与误差修正模型
1
虚假回归（伪回归）
❖ 定义 ❖ 伪回归产生的原因 ❖ 伪回归的检验和纠正方法 ❖ 总结
2
虚假回归（伪回归）：定义
❖ Banerjee 利用蒙特卡罗模拟得出结论：对于相
互独立的单整序列 yt xt，
u 1且, 1, x0 0, y0 0
5
虚假回归（伪回归）：检验和纠正
❖ 伪回归检验 可以利用残差的平稳性检验来判断是否存在 伪回归。如果残差非平稳，则是伪回归。
6
虚假回归（伪回归）：检验和纠正
❖ 伪回归的纠正方法： 1）在回归模型中包含自变量和因变量的一 阶滞后变量，即yt xt yt1 xt1 ut 通过这种方式可以消除伪回归。即当 y 和 x 不相关，则 ˆ 和 ˆ 依概率收敛于零。
20
单位根检验：定义
❖ 单位根过程是一种特别常见的非平稳过程。 其差分为平稳过程。
❖ 一般，如果一个非平稳过程的一阶差分是平 稳的，则称其为一阶单整的，记为I(1)；若非 平稳过程经过d次差分以后成为平稳的，则称 其为d阶单整的，记为I(d)。
21
单位根检验：定义
❖ 一阶单整序列一往往具有一个固定的增长趋 势，一般不会返回某个特定值。大多数宏观 经济流量指标和与人口规模相联系的存量指 标往往都是一阶单整的，如产出和就业人口； 二阶单整序列往往具有一个相对不变的增长 率，如物价指数；三阶及以上单整序列一般 不常见，但并非不存在，如恶性通货膨胀时 期的物价水平可能是三阶单整的。
❖ 虚假回归的后果：如果我们不能够判断出来哪些 变量之间是真正存在相关关系的，哪些不是真正 存在关系的，那么当我们用不存在关系的变量进 行相关分析和回归分析时，就会得出错误的结论
4
虚假回归（伪回归） ：产生原因
❖ 伪回归的产生原因：伪回归现象产生的根本 原因就是序列的非平稳性
❖ 当我们引入平稳和非平稳的概念，这些问题 就可以通过一定的方式解决。
7
虚假回归（伪回归）：检验和纠正
❖ 伪回归的纠正方法：
2）对 yt 和 xt 先做一阶差分，从而使得yt
和 xt
变成平稳过程，然后建立模
型
yt xt ut
yx
此时ˆ 能够消除伪回归。即当 和 不相关， 则 依概率收敛于零。
8
虚假回归（伪回归）：检验和纠正
❖ 伪回归的纠正方法： 3）Cochrane-Orcutt方法（自相关问题） 如果 yt xt ut 其中 ut ut1 t 则可根据广义差分法，建立模型
10
单位根检验
❖ 定义 ❖ 单位根过程 ❖ 单位根检验(DF和ADF检验) ❖ 单位根检验案例 ❖ 网上的问题 ❖ I(d)过程的检验
11
单位根检验：定义
平稳性定义：如随机过程{ Yt}满足以下条件，则它 是弱平稳的：
❖ （1）E( yt)与t无关 ❖ （2）Var( yt) 是与t无关的常数 ❖ （3）Cov( yt, ys) 是t-s的函数，但不是t或s的函数
，进行回归时，t
统计量显示比正常检验临界值水平还高。也就
是在相互独立的序列进行的实际回归中，经R2常 伴随着 高的 ，并且 系数显著。这种现象就
称为为伪回归（虚假回归）现象。
3
虚假回归（伪回归） ：定义
❖ 虚假回归：两个没有任何逻辑联系的序列进行回 归 ， 含 有很 高 的 R2， 因 为 两个 序 列 都与 时俱 进 （具有时间趋势，随时间推移而发生变化）。例 子，考研人数与手机数量。
24
单位根检验：单位根过程
单位根过程的性质： ❖ 长记忆时间序列和短记忆时间序列：一般地，平稳
AR(1)过程 {yt}为一随机步游过程。
14
单位根检验：定义
❖ 看图识平稳 ：15源自单位根检验：定义❖ 看图识平稳 ：
16
单位根检验：定义
❖ 看图识平稳 ：
17
单位根检验：定义
❖ I(d)过程：有时原始序列是非平稳过程，但对 原始序列经过d次差分后可变为平稳过程，则 原序列记为I(d)过程；
12
单位根检验：定义
❖ AR(1)过程是平稳序列吗？
❖ 定理：若| |1，则AR(1)过程是平稳过程。因
为
（1）
Eyt
1
（2）cov(
yt
,
yt
h
)
2 |h| 1 2
var(
yt
)
1
2
2
（3） (t, h) |h|
❖ 证明过程略
13
单位根检验：定义
❖ 如果 | |1 ，AR(1)过程 {yt}还是平稳过程吗？ 为什么？
❖ 经济时间序列多为I(1)或I(2)过程； ❖ 显然，I(0)过程是平稳序列 。
18
单位根检验：定义
❖ 当回归模型中含有非平稳的I(d)序列时，常规 的统计推断都不再成立，因此必须检验被解 释变量和解释变量是不是平稳的。标准的检 验方法是“单位根检验”。
19
单位根检验：定义
❖ 一个随机过程的平稳性取决于其特征方程的 根的值。若所有的根都位于单位圆之外，则 该过程是平稳的。若某个(些)根的值位于单位 圆上或单位圆内，则该过程是非平稳的。若 特征方程的根取值为1，则称其为单位根。对 单位根的检验(即对随机过程单整阶数的检验) 也就是对随机过程平稳性的检验。
yt yt1 1 xt xt1 t
进行迭代估计，可以证明 ˆ 依概率收敛于零。
9
虚假回归（伪回归）：总结
❖ 总结： 1）伪回归现象：对于任何两个（或两个以 上）不相关的单位根过程，只要样本量足够 大，检验他们相关性的统计量一定呈显著性， 这就是伪回归现象。 2）回归分析将平稳过程当作非平稳过程来 处理是十分危险的。因此回归中必须分清平 稳过程和非平稳过程。 3）伪回归的本质问题是变量的非平稳性。
22
单位根检验：单位根过程
❖ 单位根过程是一种特别常见的非平稳过程。 其差分为平稳过程。
23
单位根检验：单位根过程
单位根过程的性质： ❖ 伪回归：如对于某些时间序列，可能它们本
身之间并不相关，但对资料进行计算可以得 到显著的相关系数和回归方程。这种现象称 为伪回归。这是因为回归估计中主要依靠的 是序列的趋势之间的关系，只要两个序列具 有一定的趋势关系，我们就可能会得到显著 的相关系数和回归系数。
计量经济学
❖ 虚假回归（伪回归） ❖ 单位根检验 ❖ 格兰杰因果检验 ❖ 协整与误差修正模型
1
虚假回归（伪回归）
❖ 定义 ❖ 伪回归产生的原因 ❖ 伪回归的检验和纠正方法 ❖ 总结
2
虚假回归（伪回归）：定义
❖ Banerjee 利用蒙特卡罗模拟得出结论：对于相
互独立的单整序列 yt xt，
u 1且, 1, x0 0, y0 0
5
虚假回归（伪回归）：检验和纠正
❖ 伪回归检验 可以利用残差的平稳性检验来判断是否存在 伪回归。如果残差非平稳，则是伪回归。
6
虚假回归（伪回归）：检验和纠正
❖ 伪回归的纠正方法： 1）在回归模型中包含自变量和因变量的一 阶滞后变量，即yt xt yt1 xt1 ut 通过这种方式可以消除伪回归。即当 y 和 x 不相关，则 ˆ 和 ˆ 依概率收敛于零。
20
单位根检验：定义
❖ 单位根过程是一种特别常见的非平稳过程。 其差分为平稳过程。
❖ 一般，如果一个非平稳过程的一阶差分是平 稳的，则称其为一阶单整的，记为I(1)；若非 平稳过程经过d次差分以后成为平稳的，则称 其为d阶单整的，记为I(d)。
21
单位根检验：定义
❖ 一阶单整序列一往往具有一个固定的增长趋 势，一般不会返回某个特定值。大多数宏观 经济流量指标和与人口规模相联系的存量指 标往往都是一阶单整的，如产出和就业人口； 二阶单整序列往往具有一个相对不变的增长 率，如物价指数；三阶及以上单整序列一般 不常见，但并非不存在，如恶性通货膨胀时 期的物价水平可能是三阶单整的。
❖ 虚假回归的后果：如果我们不能够判断出来哪些 变量之间是真正存在相关关系的，哪些不是真正 存在关系的，那么当我们用不存在关系的变量进 行相关分析和回归分析时，就会得出错误的结论
4
虚假回归（伪回归） ：产生原因
❖ 伪回归的产生原因：伪回归现象产生的根本 原因就是序列的非平稳性
❖ 当我们引入平稳和非平稳的概念，这些问题 就可以通过一定的方式解决。
7
虚假回归（伪回归）：检验和纠正
❖ 伪回归的纠正方法：
2）对 yt 和 xt 先做一阶差分，从而使得yt
和 xt
变成平稳过程，然后建立模
型
yt xt ut
yx
此时ˆ 能够消除伪回归。即当 和 不相关， 则 依概率收敛于零。
8
虚假回归（伪回归）：检验和纠正
❖ 伪回归的纠正方法： 3）Cochrane-Orcutt方法（自相关问题） 如果 yt xt ut 其中 ut ut1 t 则可根据广义差分法，建立模型
10
单位根检验
❖ 定义 ❖ 单位根过程 ❖ 单位根检验(DF和ADF检验) ❖ 单位根检验案例 ❖ 网上的问题 ❖ I(d)过程的检验
11
单位根检验：定义
平稳性定义：如随机过程{ Yt}满足以下条件，则它 是弱平稳的：
❖ （1）E( yt)与t无关 ❖ （2）Var( yt) 是与t无关的常数 ❖ （3）Cov( yt, ys) 是t-s的函数，但不是t或s的函数
，进行回归时，t
统计量显示比正常检验临界值水平还高。也就
是在相互独立的序列进行的实际回归中，经R2常 伴随着 高的 ，并且 系数显著。这种现象就
称为为伪回归（虚假回归）现象。
3
虚假回归（伪回归） ：定义
❖ 虚假回归：两个没有任何逻辑联系的序列进行回 归 ， 含 有很 高 的 R2， 因 为 两个 序 列 都与 时俱 进 （具有时间趋势，随时间推移而发生变化）。例 子，考研人数与手机数量。
24
单位根检验：单位根过程
单位根过程的性质： ❖ 长记忆时间序列和短记忆时间序列：一般地，平稳