第二章 旋转机械振动分析基础汇总
- 格式:doc
- 大小:636.00 KB
- 文档页数:13

旋转机械常见振动故障及原因分析旋转机械是指主要依靠旋转动作完成特定功能的机械,典型的旋转机械有汽轮机、燃气轮机、离心式和轴流式压缩机、风机、泵、水轮机、发电机和航空发动机等,广泛应用于电力、石化、冶金和航空航天等部门。
大型旋转机械一般安装有振动监测保护和故障诊断系统,旋转机械主要的振动故障有不平衡、不对中、碰摩和松动等,但诱发因素多样。
本文就旋转设备中,常见的振动故障原因进行分析,与大家共同分享。
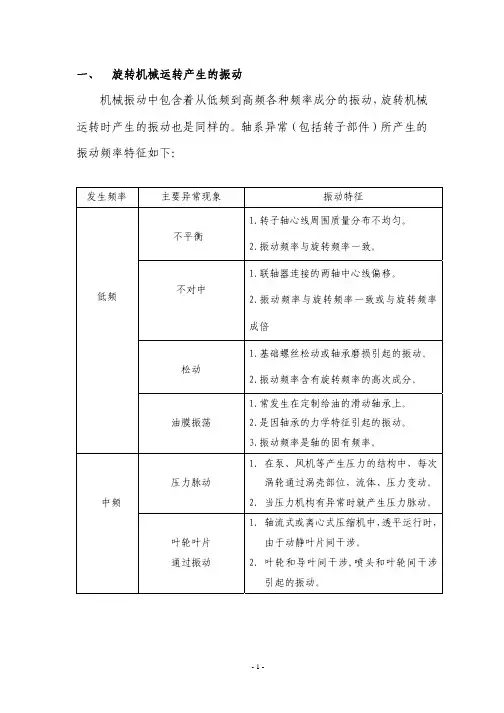
一、旋转机械运转产生的振动机械振动中包含着从低频到高频各种频率成分的振动,旋转机械运转时产生的振动也是同样的。
轴系异常(包括转子部件)所产生的振动频率特征如表1。
二、振动故障原因分析1、旋转失速旋转失速是压缩机中最常见的一种不稳定现象。
当压缩机流量减少时,由于冲角增大,叶栅背面将发生边界层分离,流道将部分或全部被堵塞。
这样失速区会以某速度向叶栅运动的反方向传播。
实验表明,失速区的相对速度低于叶栅转动的绝对速度,失速区沿转子的转动方向以低于工频的速度移动,这种相对叶栅的旋转运动即为旋转失速。
旋转失速使压缩机中的流动情况恶化,压比下降,流量及压力随时间波动。
在一定转速下,当入口流量减少到某一值时,机组会产生强烈的旋转失速。
强烈的旋转失速会进一步引起整个压缩机组系统产生危险性更大的不稳定气动现象,即喘振。
此外,旋转失速时压缩机叶片受到一种周期性的激振力,如旋转失速的频率与叶片的固有频率相吻合,将会引起强烈振动,使叶片疲劳损坏造成事故。
旋转失速故障的识别特征:1)振动发生在流量减小时,且随着流量的减小而增大;2)振动频率与工频之比为小于1X的常值;3)转子的轴向振动对转速和流量十分敏感;4)排气压力有波动现象;5)流量指示有波动现象;6)机组的压比有所下降,严重时压比可能会突降;7)分子量较大或压缩比较高的机组比较容易发生。
2、喘振旋转失速严重时可以导致喘振。
喘振除了与压缩机内部的气体流动情况有关,还同与之相连的管道网络系统的工作特性有密切的联系。


若用复数来表示,则有 机械振动学总结机 械 振 动 学 基 础第二节机械振动的运动学概念第三节机械振动是种特殊形式的运动。
在这运动过程中,机械振动系统将围绕其平衡位置作往复运动。
从 运动学的观点看,机械振动式研究机械系统的某些物理量在某一数值近旁随时间 t 变化的规律。
用函数关系式来描述其运动。
如果运动的函数值,对于相差常数 T 的不同时间有相同的数值,亦即可以用周期函数1来表示,则这一个运动时周期运动。
其中 T 的最小值叫做振动的周期,f 二1定义为振动的频率。
T简谐振动式最简单的振动,也是最简单的周期运动。
一、简谐振动.■, ... ■ ?. I .. ■;-.物体作简谐振动时,位移x 和时间t 的关系可用三角函数的表示为式中:A 为振幅,T 为周期,「和■■称为初相角。
如图所示的正弦波形表示了上式所描述的运动,角速度 •’称为简谐振动的角频率 简谐振动的速度和加速度就是位移表达式关于时间 t 的一阶和二阶导数,即可见,若位移为简谐函数,其速度和加速度也是简谐函数,且具有相同的频率。
因此在物体运动前 加速度是最早出现的量。
可以看出,简谐振动的加速度,其大小与位移成正比,而方向与位移相反,始终指向平衡位置。
这 是简谐振动的重要特征。
在振动分析中,有时我们用旋转矢量来表示简谐振动。
图 P6旋转矢量的模为振幅A ,角速度为角频率⑷z = Ae j(心z = Acos( t ) jAsin( t '-)用复指数形式描述简谐振动,给计算带来了很多方便。
因为复指数e j t 对时间求导一次相当于在其前乘以j ■,而每乘一次j ,相当于有初相角-2二•周期振动满足以下条件: 1)函数在一个周期内连续或只有有限个间断点,且间断点上函数左右极限存在;2)在一个周期内,只有有限个极大和极小值。
则都可展成Fourier 级数的形式,若周期为T 的周期振动函数,则有式中b n三、简谐振动的合成一、同方向振动的合成 1. 俩个同频率的简谐振动x 2 二 A 2sin( t 2) , x 2 二 A 2sin( 2t 2)它们的合成运动也是该频率的简谐振动2. 俩个不同频率振动的合成若「1—2,则合成运动为二、两垂直方向振动的合成1.同频率振动的合成如果沿x 方向的运动为沿y 方向的运动为2不同频率振动的合成对于俩个不等的简谐运动它们的合成运动也能在矩形中画出各种曲线第三节构成机械运动的基本元素构成机械振动的基本元素有惯性、 恢复性和阻尼。




旋转机械振动分析基础一、引言旋转机械振动是指旋转机械运行过程中产生的机械结构的振动现象。
由于旋转机械的工作原理决定了它们在运行过程中不可避免地产生振动,而过大的振动会导致机械的损坏和性能下降,因此旋转机械振动分析具有重要的工程应用价值。
本文将介绍旋转机械振动分析的基础概念和方法。
二、旋转机械振动的类型1.变速振动:由于旋转机械的传动系统存在齿轮啮合、轴承传动等机械系统,其传动系统的不平衡和不匀速会导致振动速度的变化,从而产生变速振动。
2.转子动平衡振动:旋转机械的转子由于质量轮廓不一致或者轴承刚度不平衡等原因,转子会产生不平衡力矩,从而使整个机械结构产生振动。
3.阻尼振动:阻尼振动是指由于旋转机械的结构材料存在内部摩擦、空气阻力等因素,使机械振动以一定的幅度逐渐减小并最终消失的振动。
4.外界激励振动:由于外界激励导致机械结构振动,比如由于机械运行过程中的悬挂系统、地震机械结构的振动,以及风吹草动、频率和振幅变化的源数据导致的振动。
三、旋转机械振动分析的方法和技术1.振动感知与测量:通过使用传感器,如加速度计、速度计和位移传感器等,来感知和测量旋转机械的振动状况。
这些传感器可以将振动信号转换为电信号,并通过数据采集和处理系统进行记录和分析。
2.振动特征分析:通过对振动信号进行频域分析和时域分析,可以获取机械振动的频率和幅值等特征。
其中频域分析方法常用的有傅里叶变换和功率谱分析,时域分析方法常用的有包络分析和相关分析等。
3.故障诊断与预测:通过对旋转机械振动的特征进行分析和比对,可以判断机械结构是否存在故障,并进行故障诊断。
同时,结合故障样本的统计学分析和机械振动特征的剩余寿命预测模型,可以对机械故障的发生时间进行预测。
4.振动控制与减振:通过采取振动控制的手段来减少旋转机械的振动。
常用的控制方法包括动平衡调整、减振剂和阻尼器的应用等。
四、旋转机械振动分析的应用领域1.机械设备的故障诊断与维修:通过振动分析技术,可以实时监测机械设备的振动状态,及时发现故障并进行维修,从而提高设备的可靠性和使用寿命。

旋转机械振动的基本特性概述绝大多数机械都有旋转件,所谓旋转机械是指主要功能由旋转运动来完成的机械,尤其是指主要部件作旋转运动的、转速较高的机械。
旋转机械种类繁多,有汽轮机、燃气轮机、离心式压缩机、发电机、水泵、水轮机、通风机以及电动机等。
这类设备的主要部件有转子、轴承系统、定子和机组壳体、联轴器等组成,转速从每分钟几十到几万、几十万转。
故障是指机器的功能失效,即其动态性能劣化,不符合技术要求。
例如,机器运行失稳,产生异常振动和噪声,工作转速、输出功率发生变化,以及介质的温度、压力、流量异常等。
机器发生故障的原因不同,所反映出的信息也不一样,根据这些特有的信息,可以对故障进行诊断。
但是,机器发生故障的原因往往不是单一的因素,一般都是多种因素共同作用的结果,所以对设备进行故障诊断时,必须进行全面的综合分析研究。
由于旋转机械的结构及零部件设计加工、安装调试、维护检修等方面的原因和运行操作方面的失误,使得机器在运行过程中会引起振动,其振动类型可分为径向振动、轴向振动和扭转振动三类,其中过大的径向振动往往是造成机器损坏的主要原因,也是状态监测的主要参数和进行故障诊断的主要依据。
从仿生学的角度来看,诊断设备的故障类似于确定人的病因:医生需要向患者询问病情、病史、切脉(听诊)以及量体温、验血相、测心电图等,根据获得的多种数据,进行综合分析才能得出诊断结果,提出治疗方案。
同样,对旋转机械的故障诊断,也应在获取机器的稳态数据、瞬态数据以及过程参数和运行状态等信息的基础上,通过信号分析和数据处理提取机器特有的故障症兆及故障敏感参数等,经过综合分析判断,才能确定故障原因,做出符合实际的诊断结论,提出治理措施。
根据故障原因和造成故障原因的不同阶段,可以将旋转机械的故障原因分为几个方面,见表1。
表1旋转机械故障原因分类故障分类主要原因①设计不当,动态特性不良,运行时发生强迫振动或自激振动②结构不合理,应力集中设计原因③设计工作转速接近或落人临界转速区④热膨胀量计算不准,导致热态对中不良制造原因①零部件加工制造不良,精度不够②零件材质不良,强度不够,制造缺陷③转子动平衡不符合技术要求安装、维修①机械安装不当,零部件错位,预负荷大②轴系对中不良③机器几何参数(如配合间隙、过盈量及相对位置)调整不当④管道应力大,机器在工作状态下改变了动态特性和安装精度⑤转子长期放置不当,改变了动平衡精度⑥未按规程检修,破坏了机器原有的配合性质和精度操作运行①工艺参数(如介质的温度、压力、流量、负荷等)偏离设计值,机器运行工况不正常②机器在超转速、超负荷下运行,改变了机器的工作特性③运行点接近或落入临界转速区④润滑或冷却不良⑤转子局部损坏或结垢⑥启停机或升降速过程操作不当,暖机不够,热膨胀不均匀或在临界区停留时间过久机器劣化①长期运行,转子挠度增大或动平衡劣化②转子局部损坏、脱落或产生裂纹③零部件磨损、点蚀或腐蚀等④配合面受力劣化,产生过盈不足或松动等,破坏了配合性质和精度⑤机器基础沉降不均匀,机器壳体变形旋转机械振动的基本特性(1)旋转机械的主要功能是由旋转部件来完成的,转子是其最主要的部件。


第二章 旋转机械振动分析基础振动在设备故障诊断中占了很大的比重,是影响设备安全、稳定运行的重要因素。
振动又是设备的“体温计”,直接反映了设备的健康情况,是设备安全评估的重要指标。
一台机组正常运行时,其振动值和振动变化值都应该比较小。
一旦机组振动值变大,或振动变的不稳定,都说明设备出现了一定程度的故障。
第一节 振动分析的基本概念振动是一个动态量。
图2.1所示是一种最简单的振动形式——简谐振动,即振动量按余弦或正弦函数规律周期性地变化,可以写为()ϕω+=t A y sin (3-1)f πω2=;Tf 1= 试中,y 振动位移;A 振动幅值,反映振动的大小;ϕ振动相位,反映信号在t=0时刻的初始状态;ω为圆频率;f 为振动频率,反映了振动量动态变化的快慢程度;T 为周期。
图2.1简谐振动波形图2.2给出了三组相似的振动波形:图2.2(a )为两信号幅值不等,图2.2(b )为两信号相位不等,图2.2(c )为两信号频率不等。
可见,为了完全描述一个振动信号,必须知道幅值、频率和相位这三个参数,人们称之为振动分析的三要素。
(a)幅值不等;(b)相位不等;(c)频率不等图2.2 三组相似的振动波型简谐振动时最简单的振动形式,实际发生的振动要比简谐振动复杂的多。
但是根据付立叶变换理论知道,不管振动信号多复杂,都可以将其分解为若干具有不同频率的简谐振动。
图2.3 付立叶变换图解旋转机械振动分析离不开转速,为了方便和直观起见,常以1x表示与转动频率相等的频率,又称为工(基)频,分别以0.5x、2x、3x等表示转动频率的0.5倍、2倍、3倍等相等的频率,又称为半频、二倍频、三倍频。
采用信号分析理论中的快速傅立叶变换可以很方便地求出复杂振动信号所含频率分量的幅值和相位。
目前频谱分析已成为振动故障诊断领域最基本的工具。
频谱分析所起的作用可以概括为以下两点:1)特定故障的频率特征具有必然性。
例如,转子不平衡的频率为工频,气流基振和油膜振荡等故障的频率为低频,电磁激振等故障为高频。
频率特征是故障判断的必要条件,因此根据频谱分析结果可以对故障性质作一个初步定性判断。
2)频率特征对故障判断不具备充分性,多种故障的频率特征具有很强的相似性。
例如,热变性、不平衡、共振、刚度不足、摩擦等故障的特征频率都是工频,仅根据频率特征无法将故障原因进一步定量细化。
为了能确诊故障原因,振动分析必须结合过程参数和相关试验数据进行,突出相似故障之间的微小差别。
第二节 振动位移、速度和加速度除了振动位移外,振动分析时还经常用到速度和加速度。
将位移信号对时间求一次和二次倒数,可以分别得到速度和加速度()()⎪⎪⎪⎭⎪⎪⎪⎬⎫++==⎪⎭⎫ ⎝⎛++==+=πϕωωπϕωωϕωt A dt y d v t A dt dy v t A y sin 2sin sin 222 (2-2) 反之,对振动加速度信号进行一次积分和二次积分可以分别得到速度和位移信号。
表2.1 振动位移、速度和加速度之间的关系从表2.1可以看出:1) 振动位移、速度和加速度信号的频率相同。
不管采用何种表示方式,故障性质不会变化,都可以用户振动监测。
三种方式在旋转机械振动分析中都有广泛应用。
2) 在相同位移幅值下,频率越高,振动所产生的交变应力越大,对设备的危害也越大。
因此故障率越高,位移幅值应该控制得越严格。
对于旋转机械而言,转速越高,振动标准越严。
3) 振动速度(或加速度)幅值是振动位移和频率(或频率平方)的乘积,幅值中同时反映了振动频率和位移幅值的影响,较单纯的振动位移幅值更全面。
4)振动加速度相位超前振动速度90度,振动速度相位又超前振动位移相位90度。
当采用不同的表达方式时,必须考虑相互之间的相位差。
5)应当指出的是,同一种故障在振动位移、速度和加速度谱中表现出来的故障特征不完全相同。
假设某故障振动位移信号频谱如图2.4(a)所示,频谱中10Hz、20Hz和50Hz分量都为10μm,由式(2-2)可以计算得到相应的速度和位移频谱,比较三个图可见,高频成分在速度、加速度得到了明显的放大,频率越高放大效果越明显,反之,相当于低频成分在位移频谱中得到放大。
因此,监测低频振动故障,应该监测振动位移,监测高频振动故障,应该监测振动加速度。
6)振动位移、速度和加速度之间可以相互转换。
虽然将位移信号对时间求导可以得到速度信号和加速度信号,但是由于求导过程中误差有可能放大,实际上很少进行这样的转换。
信号积分过程中的误差是收敛的,因此目前采用得比较多的是由加速度或速度信号积分求出位移信号。
一些采用加速度传感器的振动仪表可以通过积分,同时测量出振动加速度、速度和位移值。
图2.4 振动位移、速度和加速度频谱比较第三节:简单振动问题分析图2.5给出了一个由质量快、阻尼器和弹簧组成的简单振动模型。
设模型质量、阻尼系数和刚度系数分别为m 、c 、k ,现只考虑质量块在垂直方向上的运动。
质量块挂上后处于平衡位置0—0,弹簧有一静伸长k mg st /=δ。
在外界干扰力t F F ωsin 0=作用下,质量块将振动。
由牛顿第二定律可知,质量块的运动方程为()mg t F cy y k my st ++-+-=ωδsin 0''' (2-3) 简化后可得t m F y y y n n ωωζωsin 202'''=++(2-4) m k n =ω ()n m c ωζ2=式中n ω—系统角频率ξ—阻尼系数图2.5 简单振动模型一、无阻尼自由振动分析当不考虑阻尼力和外界干扰力作用时,式(2-4)变为02''=+y y n ω (2-5)其解为()ϕω+=t a y n sin ,系数a 和φ由t =0时刻质量的初始状态决定。
与这两个系数不同的是,自由振动频率n ω与外界因素无关,只取绝于系统本身的质量和刚度,因此成为系统的固有频率。
n ω正比于刚度,反比于质量,这是机械振动系统的通用规律,工程上经常据此调整系统固有频率,避开共振区。
我国早期生产的300MW 引进型汽轮发电机组励磁机振动不稳定。
该机原设计工作频率为60Hz ,固有频率极算值为40.8Hz ,两者不会出现共振。
但是该型励磁机实测固有频率高达45.8~46.7Hz ,而引进后的工作频率为50Hz ,两者之间避开裕度不够,导致工作转速下转子接近共振状态。
进一步分析表明,建模时没有考虑励磁机铁心与转轴过盈配合对转子刚度的增强作用,从而导致计算值偏低。
机组改型时,将励磁机转子发电机端轴段加长了300mm 。
转子加长后,刚度减小,质量增大,转子固有频率降低到2450~2500r/min ,在工作转速下避开了共振区。
(a )改型前; (b )改型后图2.6 300MW 引进型汽轮发电机组励磁机改型设计二、有阻尼系统自由振动分析有阻尼系统自由振动方程为022'''=++y y y n n ωζω (2—6)其解为12-=ξωωt t n n e ae y (2—7) 系数a 有t=0时刻质量块的初始状态决定。
有阻尼单自由度系统自由振动响应如图2.7所示,有阻尼系统自由振动解的性质取决于阻尼系数ξ。
1. 当1≥ξ时,系统阻尼较大,属于强阻尼状态,振动呈指数衰减。
2. 当1 ξ时,系统阻尼较小,属于弱阻尼状态,振动呈振荡衰减。
图2.7 有阻尼单自由度系统自由振动响应三、有阻尼系统强迫振动分析在阻尼力和激振力的共同作用下,系统方程为式(2-4),其特解为()ϕω-=t A y sin2222220411n n k F A ωωξωω+⎪⎪⎭⎫ ⎝⎛-=;2212ωωωξωϕ-=-n n tg (2-8) 如图2.8所示的偏心轮可以看作是一类最简单的旋转机械。
设半径r 处有偏心质量m ,偏心轮以角速度ω旋转。
当偏心轮旋转时,不平衡力在垂直方向上产生的激振力为 t mr F ωωsin 20= (2-9)将式(2-9)代入(2-8)得到22222111⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-=n n k mr A ωωξωω (2-10)图2.8 偏心轮激振模型偏心轮激振模型虽然简单,但是它包含了旋转机械振动分析中很多重要概念。
图2.9给出了不平衡力作用下振动幅值和相位随转速的变化情况,分别称为幅频图和相频图。
(a)幅频曲线;(b)相频曲线图2.9不同阻尼下的幅频、相频曲线从幅频曲线可以看出:1.振动幅值和偏心质量成正比,振动相位于偏心质量无关。
2.当偏心质量、系统阻尼等参数恒定时,振动响应幅值和相位随转速的变化而变化,因此旋转机械振动分析必须结合转速进行。
3.当转速频率接近系统固有频率时,振幅A迅速增大,系统处于共振状态。
旋转机械振动分析时,常把固有频率所对应的转速成为临界转速,临界转速之前,振动幅值随转速的增大而增大;临界转速之后,振动幅值随转速增大而减小,临界转速附近振动出现明显峰值。
4. 因为阻尼系数很小,在临界转速附近,幅值计算公式(2-10)中的分母很小。
该转速下的振动对激振力敏感,微小的激振力变化都可能引起很大的振动。
5. 在临界转速附近,阻尼力对振动幅值的抑制作用非常明显,阻尼力越大,共振幅值越小。
增大阻尼力,可以使机组平稳地通过临街转速,当工作远离临界转速时,阻尼力影响较小,继续增大阻尼力的效果并不明显。
从相频曲线可以看出1. 随着激振频率的变化,滞后角在00~0180范围内变化。
当n ωω 时,090 ϕ;当n ωω 时,090 ϕ;当n ωω=时,090=ϕ;2. 临界转速附近相位角变化明显。
在阻尼系数0=ζ的极限情况下,临界转速附近滞后角从00突变到0180。
随着阻尼系数的增加,临街转速附近滞后角的变化幅度减小。
工程上常根据振动幅值出现峰值和相位变化明显这两点来共同决定临界转速。
当幅频图上出现很多峰值或者共振峰不明显时,临界转速的确定必须结合相位变化来判断。
3. 滞后角与阻尼系数有关。
唯一例外的就是临界转速处的滞后角恒等于090,与阻尼系数无关。
该特点在旋转机械平衡工作中发挥了积极作用,大大提高了动平衡的准确度。
第四节:振动传感器传感器的基本功能是将振动信号转换成电信号,目前用的比较多的振动传感器有电涡流型、速度型、加速度型。
本节主要介绍这三种传感器的结构、工作原理和使用注意事项。
一、振动传感器基本原理电涡流传感器的外形如图3.5所示,它的外形与普通螺栓十分相似,其头部有扁平的感应线圈,将它固定在不锈钢螺栓一端,感应线圈的引线从螺栓另一端与高频电缆相连。
图3.5:电涡流传感器外形1—头部线圈;2—固定螺帽;3—高频电缆当头部感应线圈通上高频(1~2MHz)电流时,线圈周围就产生了高频电磁场,如其周围有金属导体,便会在金属表面产生感应电流,即电涡流,根据楞次定律,电涡流产生的电磁场与感应线圈的电磁场方向相反,这两个磁场相互叠加,改变了感应线圈的阻抗,感应线圈内阻抗变化可用下式表示。