2014年全国各地中考数学模拟试卷精选精练：数量和位置变化,平面直角坐标系(含答案)

平面直角坐标系(2014北京市在平面直角坐标系xOy中,对于点( P x y,,我们把点(11P y x'-++,叫做点P的伴随点,已知点1A的伴随点为2A,点2A的伴随点为3A,点3A的伴随点为4A,…,这样依次得到点1A,2A,3A,…,nA,….若点1A的坐标为(3,1,则点3A的坐标为,点2014A的坐标为;若点1A的坐标为(a,b,对于任意的正整数n,点nA均在x轴上方,则a,b应满足的条件为.(2014•赤峰如图所示,在象棋盘上建立平面直角坐标系,使“马”位于点(2,2,“炮”位于点(﹣1,2,写出“兵”所在位置的坐标(﹣2,3.考点:坐标确定位置分析:以“马”的位置向左2个单位,向下2个单位为坐标原点建立平面直角坐标系,然后写出兵的坐标即可.解答:解:建立平面直角坐标系如图,兵的坐标为(﹣2,3.故答案为:(﹣2,3.点评:本题考查了坐标确定位置,确定出原点的位置并建立平面直角坐标系是解题的关键. (2014•海南如图,△ABC与△DEF关于y轴对称,已知A(﹣4,6,B(﹣6,2,E(2, 1,则点D的坐标为((2014•呼和浩特已知线段CD是由线段AB平移得到的,点A(﹣1,4的对应点为C移线段AB,使点A落在A1(0,﹣1,点B落在点B1,则点B1的坐标为(1,1.考点:坐标与图形变化-平移.分析:根据网格结构找出点A1、B1的位置,然后根据平面直角坐标系写出点B1的坐标即可.解答:解:如图,点B1的坐标为(1,1.故答案为:(1,1.点评:本题考查了坐标与图形变化﹣平移,熟练掌握网格结构准确找出点的位置是解题的关键.(2014金华在棋盘中建立如图所示的直角坐标系,三颗棋子A,O,B的位置如图,它们的坐标分别是(-1,1,(0,0和(1,0。

(1如图2,添加棋子C,使A,O,B,C四颗棋子成为一个轴对称图形,请在图中画出该图形的对称轴;(2在其它格点位置添加一颗棋子P,使A,O,B,P成为一个轴对称图形,请直接写出棋子P的位置的坐标(写出2个即可。

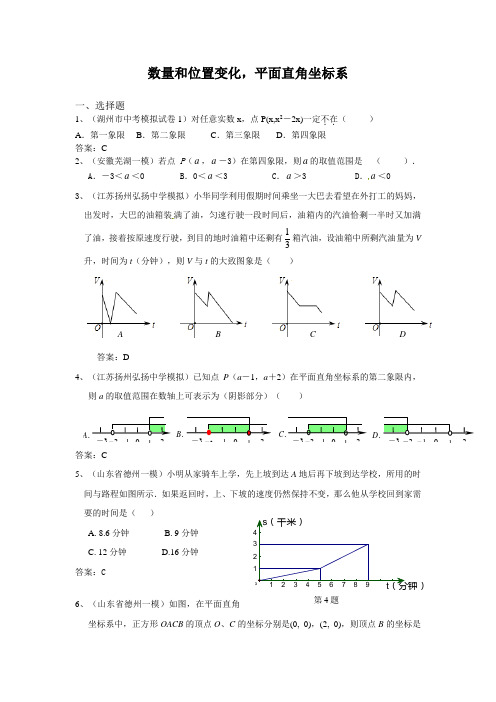
数量和位置变化，平面直角坐标系一、选择题1、（湖州市中考模拟试卷1）对任意实数x ，点P(x,x 2－2x)一定不在．．（ ） A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限 答案：C2、（安徽芜湖一模）若点 P （a ，a －3）在第四象限，则a 的取值范围是 （ ）． A ．－3＜a ＜0 B ．0＜a ＜3 C ．a ＞3D ．a ＜03、（江苏扬州弘扬中学模拟）小华同学利用假期时间乘坐一大巴去看望在外打工的妈妈，出发时，大巴的油箱装满了油，匀速行驶一段时间后，油箱内的汽油恰剩一半时又加满了油，接着按原速度行驶，到目的地时油箱中还剩有31箱汽油，设油箱中所剩汽油量为V 升，时间为t （分钟），则V 与t 的大致图象是（ ）答案：D4、（江苏扬州弘扬中学模拟）已知点P （a －1，a ＋2）在平面直角坐标系的第二象限内，则a 的取值范围在数轴上可表示为（阴影部分）（ ）答案：C5、（山东省德州一模）小明从家骑车上学，先上坡到达A 地后再下坡到达学校，所用的时间与路程如图所示．如果返回时，上、下坡的速度仍然保持不变，那么他从学校回到家需要的时间是（ ）A. 8.6分钟B. 9分钟C. 12分钟D.16分钟 答案：C6、（山东省德州一模）如图，在平面直角坐标系中，正方形OACB 的顶点O 、C 的坐标分别是(0, 0)，(2, 0)，则顶点B 的坐标是A B DCA 1 －2 －3 －1 0 2C 1 －－B 1 －2－D 1－2 －3 －1 02第4题第5题（ ）． A.（1，1） B.（－1，－1）C.（1，－1）D.（－1，1）答案：C7、 (河北省一摸)|如果点P(m ，1-2m)在第四象限，那么m 的取值范围是A ．102m <<B ．102m -<<C ．0m <D ．12m > 答案：D8、(河北省一摸)|如图5，三个大小相同的正方形拼成六边形ABCDEF ，一动点P 从点A 出发沿着A →B →C →D →E 方向匀速运动，最后到达点E ．运动过程中△PEF 的面积（S ）随时间（t ）变化的图象大致是答案：B 二、填空题1、(河北模拟)平面直角坐标系中，点A （2，3）关于x 轴的对称点坐标为． 答案：(2，-3)2、（温州一摸）在平面直角坐标系中，点（-3,2）到x 轴的距离是_____. 答案：23、（上海市）在平面直角坐标系中，如果点(1,3)A 与点(,3)B x 之间的距离是5，那么x 的值是 ▲ ． 答案：4-或6；4、（山东省德州一模）在直角坐标系中，点P （－3，2）关于X 轴对称的点Q 的坐标是 . 答案：（-3，-2）5、（山东省德州一模）如图， 在已建立直角坐标系的4×4正方形方格纸中，△ABC 是格点三角形（三角形的三个顶点都是小正方形的顶点）， 若以格点P 、A 、B 为顶点的三角形与△ABC 相似，则格点P 的坐标是 ．A ．． BDC图5 A BC DE.F.P.答案：（1，4），（3，4），（3，1）6、（温州市一模）在平面直角坐标系中，点P（-1，4）所在的象限是（）A．第一象限 B．第二象限 C．第三象限 D．第四象限答案：B7、(吉林中考模拟)在函数y=错误！未找到引用源。

济南市2014年初三年级学业水平考试数学全真模拟试卷(时间：120分钟 满分：120分)第Ⅰ卷（选择题 共45分）一、选择题（本大题共15个小题，每小题3分，共45分.在每小题所给的四个选项中，只有一项是符合题目要求的.） 1.-2的绝对值是( )11A. B.2 C. D.222- -2.我国第一艘航母“辽宁舰”最大排水量为67 500吨，用科学记数法表示这个数字是( )A.6.75×103 吨B.67.5×103吨C.6.75×104 吨D.6.75×105吨 3.16的平方根是( )A.4B.±4C.8 D ．±84.如图，直线l ∥m ，将含有45°角的三角板ABC 的直角顶点C 放在直线m 上，若∠1=25°，则∠2的度数为( )A.20°B.25°C.30°D.35° 5.下列等式成立的是( )A.a 2×a 5=a 10B.a b a b +=+C.(-a 3)6=a 18D.2a a =6.一个盒子里有完全相同的三个小球，球上分别标上数字-1、1、2.随机摸出一个小球（不放回）其数字记为p ，再随机摸出另一个小球其数字记为q ，则满足关于x 的方程x 2+px+q=0有实数根的概率是( )1125A. B. C. D.23367.分式方程12x 1x 1=-+的解是( ) A.1 B.-1 C.3 D.无解8.钟面上的分针的长为1，从9点到9点30分，分针在钟面上扫过的面积是( )111A. B. C. D.248π π π π9.如图，数轴上表示某不等式组的解集，则这个不等式组可能是( )x 10x 10A. B.2x 02x 0x 10x 10C. D.x 20x 20+≥+≤⎧⎧ ⎨⎨-≥-≥⎩⎩+≤+≥⎧⎧ ⎨⎨-≥-≥⎩⎩10.如图是一个正方体被截去一角后得到的几何体，它的俯视图是( )11.化简2(21)÷-的结果是( )A.221B.22C.12D. 22- - - +12.如图，在Rt △ABC 中，∠BAC=90°，D 、E 分别是AB 、BC 的中点，F 在CA 的延长线上，∠FDA=∠B ，AC=6，AB=8，则四边形AEDF 的周长为( )A.22B.20C.18D.1613.如图，过x 轴正半轴上的任意一点P ，作y 轴的平行线，分别与反比例函数64y y x x=-=和的图象交于A 、B 两点.若点C 是y 轴上任意一点，连接AC 、BC ，则△ABC的面积为( )A.3B.4C.5D.1014.如图，已知AB、CD是⊙O的两条直径，∠ABC=28°，那么∠BAD=( )A.28°B.42°C.56°D.84°15.如图，菱形ABCD的边长为2，∠B=30°.动点P从点B出发，沿B→C→D的路线向点D运动.设△ABP的面积为y（B、P两点重合时，△ABP的面积可以看做0），点P运动的路程为x，则y与x之间函数关系的图象大致为( )第Ⅱ卷（非选择题共75分）二、填空题（本大题共6个小题，每小题3分，共18分.把答案填在题中的横线上.）16.分解因式：（a+2）（a-2）+3a=________．17.已知点P（3，-1）关于y轴的对称点Q的坐标是（a+b，1-b），则ab的值为_________．18.如图，两建筑物的水平距离BC为18 m，从A点测得D点的俯角α为30°，测得C点的俯角β为60°．则建筑物CD的高度为________ m（结果不作近似计算）．19.三棱柱的三视图如图所示，△EFG中，EF=8 cm，EG=12 cm，∠EGF=30°，则AB的长为______cm．20.如图，边长为1的菱形ABCD中，∠DAB＝60°.连接对角线AC，以AC为边作第二个菱形ACC1D1，使∠D1AC＝60°，连接AC1，再以AC1为边作第三个菱形AC1C2D2，使∠D2AC1＝60°；…，按此规律所作的第n个菱形的边长为_______.21.如图，边长为1的小正方形网格中，⊙O的圆心在格点上，则∠AED的余弦值是________．三、解答题（本大题共7个小题，共57分.解答应写出文字说明、证明过程及演算步骤.）22.（本小题满分7分）（1）化简222x1x2x1. x1x x--+÷+-(2)解方程：15x2(x1)8x. 24++=+23.(本小题满分7分)(1)如图，AB=AE，∠1=∠2，∠C=∠D．求证：△ABC≌△AED．(2)如图所示，已知在平行四边形ABCD中，BE=DF.求证：AE=CF．24.（本小题满分8分）五一期间某校组织七、八年级的同学到某景点郊游，该景点的门票全票票价为15元/人，若为50～99人可以八折购票，100人以上则可六折购票.已知参加郊游的七年级同学少于50人、八年级同学少于100人.若七、八年级分别购票，两个年级共计应付门票费1 575元，若合在一起购买折扣票，总计应付门票费1 080元.（1）请你判断参加郊游的八年级同学是否也少于50人.（2）求参加郊游的七、八年级同学各为多少人？25.（本小题满分8分）某市某校对九年级学生进行“综合素质”评价，评价的结果为A（优）、B（良好）、C(合格)、D(不合格)四个等级，现从中抽取了若干名学生的“综合素质”等级作为样本进行数据处理，并作出如图所示的统计图，已知图中从左到右的四个长方形的高的比为：14∶9∶6∶1，评价结果为D等级的有2人，请你回答以下问题：(1)共抽取了多少人？(2)样本中B等级的频率是多少？C等级的频率是多少？(3)如果要绘制扇形统计图，A、D两个等级在扇形统计图中所占的圆心角分别是多少度？(4)该校九年级的毕业生共300人，假如“综合素质”等级为A或B的学生才能报考示范性高中，请你计算该校大约有多少名学生可以报考示范性高中？26.（本小题满分9分）如图，在△ABC中，以AB为直径的⊙O分别交AC、BC于点D、E，点F在AC的延长线上，且AC=CF，∠CBF=∠CFB.（1）求证：直线BF是⊙O的切线；（2）若点D，点E分别是弧AB的三等分点，当AD＝5时，求BF的长；（3）填空：在(2)的条件下，如果以点C为圆心，r为半径的圆上总存在不同的两点到点O 的距离为5，则r的取值范围为_________.27.（本小题满分9分）已知，如图二次函数y=ax2+bx+c(a≠0)的图象与y轴交于点C(0,4)与x轴交于点A、B，点B(4,0)，抛物线的对称轴为x=1.直线AD交抛物线于点D(2,m).（1）求二次函数的解析式并写出D点坐标；（2）点E是BD的中点，点Q是线段AB上一动点，当△QBE和△ABD相似时，求点Q的坐标；（3）抛物线与y轴交于点C，直线AD与y轴交于点F，点M为抛物线对称轴上的动点，点N在x轴上，当四边形CMNF周长取最小值时，求出满足条件的点M和点N的坐标.28.(本小题满分9分)如图，在⊙O中，直径AB⊥CD，垂足为E，点M在OC上，AM的延长线交⊙O于点G，交过C的直线于点F，∠1=∠2，连接CB与DG交于点N．（1）求证：CF 是⊙O 的切线； （2）求证：△ACM ∽△DCN ；（3）若点M 是CO 的中点，⊙O 的半径为4，cos ∠BOC=14，求BN 的长．参考答案1.D2.C3.B4.A5.C6.A7.C8.A9.A 10.A 11.D 12.D 13.C 14.A 15.C 16.（a-1）(a+4) 17.-10 18.123 19.6 20.n 13-（）21.25522.（1）解：原式=()()()2x 1x 1x x 1x.x 1x 1+--=+- （） (2)解：原方程可化为3x+2=8+x,合并同类项得：2x=6, 解得：x=3.23.(1)证明：∵∠1=∠2, ∴∠1+∠EAC=∠2+∠EAC, 即∠BAC=∠EAD.∵在△ABC 中和△AED 中，D C,BAC EAD,AB AE,∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ABC ≌△AED(AAS) (2)证明：∵BE=DF,∴BE-EF=DE-EF,∴DE=BF.∵四边形ABCD 是平行四边形， ∴AD=BC,AD ∥BC, ∴∠ADE=∠CBF,在△ADE 和△CBF 中，DE BF,ADE CBF,AD BC,=⎧⎪∠=∠⎨⎪=⎩∴△ADE ≌△CBF(SAS), ∴AE=CF. 24.解：（1）全票为15元，则八折票价为12元，六折票价为9元. ∵100×15=1 500<1 575,∴参加郊游的七、八年级同学的总人数必定超过100人,∴由此可判断参加郊游的八年同学不少于50人.（2）设七、八年级参加郊游的同学分别有x 人、y 人. 由（1）及已知可得，x<50,50<y<100,x+y>100. 依题意可得：()15x 12y 1 575,9x y 1 080,+=⎧⎨+=⎩ 解得:x 45,y 75.=⎧⎨=⎩答：参加郊游的七、八年级同学分别为45人和75人. 25.解：（1）D 等级所占比例为：111496130=+++，则共抽取的人数为：1260().30÷=人 （2）样本中B 等级的频率为：9100%30%;14961⨯=+++C 等级的频率为：6100%20%.14961⨯=+++ (3)样本中A 等级在扇形统计图中所占圆心角度数为：1430×360=168(度); D 等级在扇形统计图中所占圆心角度数为：130×360=12(度). （4）可报考示范性高中的总人数： 300×149()3030+=230(名). 26.(1)证明：∵∠CBF=∠CFB ， ∴BC=CF. ∵AC=CF ， ∴AC=BC ，∴∠ABC=∠BAC.在△ABF 中，∠ABC+∠CBF+∠BAF+∠F=180°, 即2(∠ABC+∠CBF)=180°, ∴∠ABC+∠CBF=90°， ∴BF 是⊙O 的切线;(2)解：连接BD.∵点D ，点E 是弧AB 的三等分点，AB 为直径， ∴∠ABD=30°，∠ADB=90°，∠A=60°. ∵AD=5，∴AB=10，()BFtan603ABBF 103;3535r 53 5.∴︒==∴=-<<+，27.解：（1）设二次函数的解析式为:y=ax 2+bx+c.221a c 4216a 4b c 0b 1b c 4,12a 1y x x 4.21D(2m)m 224 4.2⎧⎧=-⎪⎪=⎪⎪++==⎨⎨⎪⎪=⎪⎪-=⎩⎩=-++=-⨯++= ，，由题意有：，解得：，，所以，二次函数的解析式为：点，在抛物线上，即∴点D 的坐标为(2，4);（2）作DG 垂直于x 轴，垂足为G ，因为D （2，4），B （4，0）， 由勾股定理得:BD=25，∵E 是BD 的中点， ∴BE=5.BE BQ 1QBE ABD BD BA 2AB 2BQ Q 10BQ BE 5QBE DBA BD BA 6557BQ 25OQ 6337Q 0.3==∴=∴==∴=⨯==∴ 当≌时，，，点的坐标为（，）；当≌时，，，则，点的坐标（，） （3）如图，由A(-2,0),D(2,4)，可求得直线AD 的解析式为：y=x+2，则点F 的坐标为：F(0,2).过点F作关于x轴的对称点F′，即F′(0,-2)，连接CD，再连接DF′交对称轴于M′，交x轴于N′.由条件可知，点C，D关于对称轴x=1对称，∴DF′=210，F′N′=FN′，DM′=CM′，∴CF+FN′+M′N′+M′C=CF+DF′=2210+，∴四边形CFNM的周长=CF+FN+NM+MC≥CF+FN′+M′N′+M′C=2210+，即四边形CFNM的最短周长为：2210+，此时直线DF′的解析式为：y=3x-2，所以存在点N的坐标为2(,0)3，点M的坐标为(1，1)使四边形CMNF周长取最小值.28.（1）证明：∵△BCO中，BO=CO，∴∠B=∠BCO，在Rt△BCE中，∠2+∠B=90°，又∵∠1=∠2，∴∠1+∠BCO=90°，即∠FCO=90°，∴CF是⊙O的切线；（2）证明：∵AB是⊙O直径，∴∠ACB=∠FCO=90°，∴∠ACB-∠BCO=∠FCO-∠BCO，即∠ACO=∠1，∴∠ACO=∠2，∵∠CAM=∠D，∴△ACM∽△DCN；（3）解：∵⊙O的半径为4，即AO=CO=BO=4，在Rt△COE中，cos∠BOC=1 4，∴OE=CO ·cos ∠BOC=4×14=1， 由此可得：BE=3，AE=5，由勾股定理可得：222222222222CE CO OE 4115AC CE AE (15)5210,BC CE BE (15)326,=-=-==+=+==+=+= ∵AB 是⊙O 直径，AB ⊥CD ， ∴由垂径定理得：CD=2CE=215，∵△ACM ∽△DCN ，∴CM AC,CN CD= ∵点M 是CO 的中点，11CMOA 42,22==⨯= CM CD 2215CN 6,AC 210BN BC CN 266 6.⨯∴===∴=-=-=济南市2014年初三年级学业水平考试数学全真模拟试卷2第Ⅰ卷（选择题共45分）一、选择题（本大题共15个小题，每小题3分，共45分.在每小题所给的四个选项中，只有一项是符合题目要求的）.1.如果+30 m表示向东走30 m，那么向西走40 m表示为( )A.+40 mB.-40 mC.+30 mD.-30 m2.若实数a、b满足a+b=5，a2b+ab2=-10，则ab的值是( )A.-2B.2C.-50D.503.图中几何体的主视图是( )4.英国曼彻斯特大学的两位科学家因为成功地从石墨中分离出石墨烯，荣获了诺贝尔物理学奖．石墨烯目前是世上最薄却也是最坚硬的纳米材料，同时还是导电性最好的材料，其理论厚度仅0.000 000 000 34米，将这个数用科学记数法表示为( )A.0.34×10-9B.3.4×10-9C.3.4×10-10D.3.4×10-115.已知圆锥的底面半径为6 cm，高为8 cm，则这个圆锥的母线长为( )A.12 cmB.10 cmC.8 cmD.6 cm6.如图所示，在平行四边形纸片上作随机扎针实验，针头扎在阴影区域内的概率为( )1111A. B. C. D.34567.假期到了，17名女教师去外地培训，住宿时有2人间和3人间可供租住，每个房间都要住满，她们有几种租住方案( )A.5种B.4种C.3种D.2种8.某景点门票价格：成人票每张70元，儿童票每张35元.小明买20张门票共花了1 225元，设其中有x张成人票，y张儿童票.根据题意，下列方程组正确的是( )9.如图，△ABC中，AB=AC，∠A=36°，BD是AC边上的高，则∠DBC的度数是( )A.18°B.24°C.30°D.36°10.如图，已知等腰梯形ABCD的底角∠B=45°，高AE=1，上底AD=1，则其面积为( )A.4B. 22C.1D.211.如图，数轴上a,b两点表示的数分别为3和-1,点a关于点b的对称点为c，则点c所表示的数为( )A.23B.13C.23D.13-- -- -+ +12.如图，A、B、C是反比例函数kyx＝(x＜0)图象上三点，作直线l，使A、B、C到直线l的距离之比为3∶1∶1，则满足条件的直线l共有( )A.4条B.3条C.2条D.1条13.在一次“爱心互助”捐款活动中，某班第一小组8名同学捐款的金额（单位：元）如下表所示：这8名同学捐款的平均金额为( )A.3.5元B.6元C.6.5元D.7元14.已知关于x 的不等式组()4x 123x,6x ax 1,7⎧-+⎪⎨+-⎪⎩＞＜有且只有三个整数解，则a 的取值范围是( )A.-2≤a-1B.-2≤a ＜-1C.-2＜a ≤-1D.-2＜a ＜-1 15.如图，直线l :y=-x-2与坐标轴交于A 、C 两点，过A 、O 、C 三点作⊙O 1，点E 为劣弧 AO上一点，连接EC 、EA 、EO ，当点E 在劣弧上运动时（不与A 、O 两点重合），EC EA EO-的值是( )A.2 B.3 C.2 D.变化的第Ⅱ卷(非选择题 共75分)二、填空题（本大题共6个小题，每小题3分，共18分.把答案填在题中的横线上.）16.分解因式：a 3-ab 2=________. 17.计算124183-⨯=_________. 18.如图，在Rt △ABC 中，∠C=90°，∠B=60°，点D 是BC 边上的点，CD=1，将△ABC 沿直线AD 翻折，使点C 落在AB 边上的点E 处，若点P 是直线AD 上的动点，则△PEB 的周长的最小值是______．19.如图，在边长相同的小正方形组成的网格中，点A 、B 、C 、D 都在这些小正方形的顶点上，AB 、CD 相交于点P ，则tan ∠APD 的值是______.20.某校报名参加甲、乙、丙、丁四个兴趣小组的学生人数如图所示，那么报名参加甲组和丙组的人数之和占所有报名人数的百分比为_____________．21.若x 是不等于1的实数，我们把11x -称为x 的差倒数，如2的差倒数是112-=-1，-1的差倒数为()11112=--，现已知121x x 3=-，是x 1的差倒数，x 3是x 2的差倒数，x 4是x 3的差倒数，…，依次类推，则x 2 013=____________.三、解答题（本大题共7个小题，共57分.解答应写出文字说明、证明过程及演算步骤.） 22.（本小题满分7分）（1）解方程组2x 3y 3x 2y 2.-=⎧⎨+=-⎩，（2）化简：1a a ().22a 2a 1-÷++23.（本小题满分7分）(1)如图，在四边形ABCD 中，AB=BC ，∠ABC=∠CDA=90°，BE ⊥AD ，垂足为E. 求证：BE=DE.（2）如图，AB 是⊙O 的直径，DF ⊥AB 于点D ，交弦AC 于点E ，FC=FE. 求证：FC 是⊙O 的切线.24.(本小题满分8分)小明的妈妈在菜市场买回3斤萝卜、2斤排骨，准备做萝卜排骨汤.妈妈：“今天买这两样菜共花了45元，上月买同重量的这两样菜只要36元”；爸爸：“报纸上说了萝卜的单价上涨50%，排骨单价上涨20%”；小明：“爸爸、妈妈，我想知道今天买的萝卜和排骨的单价分别是多少？”请你通过列方程（组）求解这天萝卜、排骨的单价（单位：元/斤）.25.（本小题满分8分）某校为了开设武术、舞蹈、剪纸等三项活动课程以提升学生的体艺素养，随机抽取了部分学生对这三项活动的兴趣情况进行了调查（每人从中只能选一项），并将调查结果绘制成如图两幅统计图，请你结合图中信息解答问题.（1）将条形统计图补充完整；（2）本次抽样调查的样本容量是____________；（3）已知该校有1 200名学生，请你根据样本估计全校学生中喜欢剪纸的人数.26.（本小题满分9分）如图，O是菱形ABCD对角线AC与BD的交点，CD=5 cm，OD=3 cm；过点C作CE∥DB，过点B作BE∥AC，CE与BE相交于点E．（1）求OC的长；（2）求证：四边形OBEC为矩形；（3）求矩形OBEC的面积．27.(本小题满分9分)如图，直线1yx 4=与双曲线ky x =相交于A 、B 两点，BC ⊥x 轴于点C （-4，0）.（1）求A 、B 两点的坐标及双曲线的解析式；（2）若经过点A 的直线与x 轴的正半轴交于点D ，与y 轴的正半轴交于点E ，且△AOE 的面积为10，求CD 的长.28.（本小题满分9分） 如图，抛物线21y x 1=－交x 轴的正半轴于点A ，交y 轴于点B ，将此抛物线向右平移4个单位得抛物线y 2，两条抛物线相交于点 C.（1）请直接写出抛物线y 2的解析式；（2）若点 P 是x 轴上一动点，且满足∠CPA=∠OBA ，求出所有满足条件的P 点坐标; （3）在第四象限内抛物线y 2上，是否存在点Q ，使得△QOC 中OC 边上的高h 有最大值,若存在，请求出点Q 的坐标及h 的最大值；若不存在，请说明理由.参考答案1.B2.A3.D4.C5.B6.B7.C8.B9.A10.D 11.A 12.A 13.C 14.C 15.A19.2 20.40% 21.416.a(a+b)(a-b) 17.618.1323.(1)证明:作CF⊥BE,垂足为F.∵BE⊥AD,∴∠AEB=90°,∴∠FED=∠D=∠CFE=90°,∠CBE+∠ABE=90°,∠BAE+∠ABE=90°,∴∠BAE=∠CBF,∵四边形EFCD为矩形,∴DE=CF.在△BAE和△CBF中，有∠CBE=∠BAE,∠BFC=∠BEA=90°,AB=BC,∴△BAE≌△CBF,∴BE=CF=DE,即BE=DE.(2)证明:连接OC.∵FC=FE,∴∠FCE=∠FEC.又∵∠AED=∠FEC,∴∠FCE=∠AED.∵OC=OA,∴∠OCA=∠OAC,∴∠FCO=∠FCE+∠OCA=∠AED+∠OAC=180°-∠ADE.∵DF⊥AB,∴∠ADE=90°,∴∠FCO=90°,即OC⊥FC.又∵点C在⊙O上，∴FC是⊙O的切线;24.解法一：解：设上月萝卜的单价是x 元/斤，排骨的单价是y 元/斤，根据题意得：()()3x 2y 363150%x 2120%y 45x 2:y 15.+=⎧⎨+++=⎩=⎧⎨=⎩，，，解得这天萝卜的单价是(1+50%)x=(1+50%)×2=3（元/斤）, 这天排骨的单价是(1+20%)y=(1+20%)×15=18(元/斤). 答:这天萝卜的单价是3元/斤，排骨的单价是18/斤. 解法二:解：设这天萝卜的单价是x 元/斤，排骨的单价是y 元/斤，根据题意得：32x y 36150%120%3x 2y 45x 3:y 18.⎧+=⎪++⎨⎪+=⎩=⎧⎨=⎩，，，解得 答：这天萝卜的单价是3元/斤，排骨的单价18元/斤. 25.解：（1）∵根据扇形统计图可得出女生喜欢武术的占20%， 利用条形图中喜欢武术的女生有10人， ∴女生总人数为：10÷20%=50（人），∴女生中喜欢舞蹈的人数为：50-10-16=24（人）. 补充条形统计图，如图所示：（2）100（3）∵样本中喜欢剪纸的人数为30人，样本容量为100， ∴估计全校学生中喜欢剪纸的人数:1 200×30100=360人. 答：全校学生中喜欢剪纸的有360人. 26.解：（1）∵四边形ABCD 是菱形， ∴AC ⊥BD ，∴直角△OCD 中，2222OC CD OD 53 4 cm =-=-=；（2）∵CE ∥DB ，BE ∥AC ， ∴四边形OBEC 为平行四边形， 又∵AC ⊥BD ，即∠COB=90°， ∴平行四边形OBEC 为矩形； （3）∵OB=OD ，∴S 矩形OBEC =OB ·OC=4×3=12（cm 2）． 27.解：（1）∵BC ⊥x 轴，C （-4，0），∴B 的横坐标是-4，代入y=14x 得：y=-1，∴B 的坐标是（-4，-1）. ∵把B 的坐标代入ky k 4x==得：， ∴反比例函数的解析式是4y .x=∵解方程组12121y x x 4x 444y 1y 1y x⎧=⎪==-⎧⎧⎪⎨⎨⎨==-⎩⎩⎪=⎪⎩，，，得：，，，∴A 的坐标为（4，1），B 的坐标为（-4，-1）；（2）设OE=a ，OD=b ，则△AOE 面积S △AOE =S △EOD -S △AO D,AOE 1110ab b 1,221S a 410,2=- == 即：①并且，②由①，②可解得：a=5，b=5，即OD=5. ∵OC=|-4|=4，∴CD 的长为：4+5=9.28.解：（1）y=x 2-8x+15;（2）当 y 1= y 2，即x 2-1 =x 2-8x+15, ∴x=2,y=3, ∴C （2,3）.由题可知， A ( 1 , 0 ) , B ( 0 ，-1), ∴OA =OB= 1 ,∴∠OBA= 45°. 过点 C 作CD ⊥x 轴于点D, ∴D(2,0)，∴CD=3.当∠CPA=∠OBA=45°时，∴PD=CD=3 ,∴满足条件的点P有2个，分别为P1 (5,0)，P2（-1,0);（3）存在.过点C作CE⊥y轴于点E，过点Q作QF⊥y轴于点F，连接OC、QC、 OQ. 设Q （x0，y0） ,∵Q在y2上,∴y0=x02-8x0+15,∴CE=2,QF=x0，EF=3-y0，OE=3,OF=-y0.∵在△QOC中，OC边长为定值，∴当S△QOC取最大值时，OC边上的高h也取最大值.2014届中考数学模拟测试卷（本试卷满分150分，考试时间120分钟）一、选择题(本题有8小题，每小题3分，共24分) 1.12-的倒数为【 】 A ．12B ．2C ．2-D ．1-2．下列图形中，既是轴对称图形，又是中心对称图形的是【 】 A ．平行四边形 B ．等边三角形 C ．等腰梯形 D ．正方形3．已知地球距离月球表面约为383900千米，那么这个距离用科学记数法表示为（保留三个有效数字）【 】A ．3.84×104千米B ．3.84×105千米C ．3.84×106千米D ．38.4×104千米 4．已知⊙O 1与⊙O 2的半径分别为5cm 和3cm ，圆心距0102=7cm ，则两圆的位置关系为【 】 A ．外离 B ．外切 C ．相交 D ．内切5．如图是由七个相同的小正方体堆成的几何体，这个几何体的俯视图是【 】6．某校在开展“爱心捐助”的活动中，初三（一）班六名同学捐款的数额分别为：8，10，10，4，8，10(单位：元)，这组数据的众数是【 】A ．10B ．9C ．8D ．4 7．如图7，AB 是⊙O 的直径，点D 在AB 的延长线上， DC 切⊙O 于点C ，若∠A=25°，则∠D 等于【 】 A ．20°B ．30°C ．40° D.50°8．已知二次函数2(0)y ax bx c a =++≠的图象如右图8所示，下列结论①abc ＞0 ②b<a+c③2a-b=0 ④4a+2b+c ＞0 ⑤2c<3b⑥a+b ＞m(am+b)(m 为任意实数）， 其中正确的结论有【 】 A ． 1个 B ．2个 C ． 3个D ．4个二、填空题(本大题共10小题，每小题3分，共30分)9．扬州市某天的最高气温是6℃，最低气温是－3℃，那么当天的日温差是 ▲ ．10．函数12-+=x x y 中自变量x 的取值范围是 ▲ ． 11．如图11，四边形ABCD 中，AB//CD ，要使四边形ABCD 为平行四边形，则可添加的条件为 ▲ ．（填一个即可）.12．因式分解：m 3n －9mn= ▲ ．13．已知25-是一元二次方程240x x c -+=的一个根，则方程的另一个根是▲ ．14．在平面直角坐标系中，如果抛物线y=3x 2不动，而把x 轴、y 轴分别向上、向右平移3个单位，那么在新坐标系中此抛物线的解析式是 ▲ ． 15．已知关于x 的不等式组0521x a x -⎧⎨->⎩≥，只有四个整数解，则实数a 的取值范围是 ▲ ．16．已知一个圆锥的母线长为10cm ，将侧面展开后所得扇形的圆心角是144°，则这个圆锥的底面圆的半径是 ▲ cm ．17．如图，线段AB 的长为2，C 为AB 上一个动点，分别以AC 、BC 为斜边在AB 的同侧作两个等腰直角三角形△ACD 和△BCE ，那么DE 长的最小值是 ▲ ． 18．观察分析下列方程：①，②，③；请利用它们所蕴含的规律，求关于x 的方程（n 为正整数）的根，你的答案是： ▲ ．（用n 的代数式 ）三、解答题(本大题共有10小题，共96分) 19．（本题8分）(1) （4分）解方程组 ⎩⎨⎧=-=-;1383,32y x y x(2) （4分）821)14.3(45sin 2)31(02+-+︒--π 20．（本题8分）先化简：22a 1a 11a a +2a---÷，再选取一个合适的 a 值代入计算．21．（本题8分）如图，在△ABC 中，∠ACB=90°，AC=BC ，BE ⊥CE 于点E ，AD ⊥CE 于点D 。

2014中考数学模拟试题及答案1．本试卷共8页，共五道大题，25道小题，满分120分。

考试时间120分钟。

2．答题纸共8页，在规定位置准确填写学校名称、班级和姓名。

3．试题答案一律书写在答题纸上，在试卷上作答无效。

4．考试结束，请将答题纸交回，试卷和草稿纸可带走。

一、选择题（本题共32分，每小题4分）下面各题均有四个选项，其中只有一个是符合题意的．1．的绝对值是A. B. C. D.2. 2014年2月14日从北京航天飞行控制中心获悉，嫦娥二号卫星再次刷新我国深空探测最远距离记录，达到7 000万公里，这是我国航天器迄今为止飞行距离最远的一次“太空长征” ．将7 000万用科学记数法表示应为A. B. C. D.3．下列立体图形中，左视图是圆的是4. 小月的讲义夹里放了大小相同的试卷共12页，其中语文5页、数学4页、英语3页，她随机地从讲义夹中抽出1页，抽出的试卷恰好是数学试卷的概率是A. B. C. D.5. 如右图所示，AB∥CD，点E在CB的延长线上．若∠ABE＝70°，则∠ECD的度数为A.20°B.70°C .100° D.110°6. 下列正多边形中，内角和等于外角和的是A.正三边形B.正四边形C.正五边形D.正六边形7. 小贝家买了一辆小轿车,小贝记录了连续七天中每天行驶的路程:第1天第2天第3天第4天第5天第6天第7天路程(千米) 43 29 27 52 43 72 33则小贝家轿车这七天行驶路程的众数和中位数分别是A.33, 52B.43,52C.43,43D.52,438．如图，点在线段上，=8，=2，为线段上一动点，点绕点旋转后与点绕点旋转后重合于点 .设= ，的面积为 . 则下列图象中，能表示与的函数关系的图象大致是A. B. C. D.二、填空题（本题共16分，每小题4分）9．若二次根式有意义，则的取值范围是．10. 分解因式：．11．为了测量校园水平地面上一棵树的高度，数学兴趣小组利用一组标杆、皮尺，设计了如图所示的测量方案．已知测量同学眼睛、标杆顶端、树的顶端在同一直线上，此同学眼睛距地面1.6 ，标杆长为3.3 ，且，，则树高．12．如图，在平面直角坐标系中，已知点的坐标为(1，0)，将线段绕点按顺时针方向旋转，再将其长度伸长为的2倍，得到线段；又将线段绕点按顺时针方向旋转，再将其长度伸长为的2倍，得到线段，…，这样依次得到线段，，…，．则点的坐标为；当( 为自然数)时，点的坐标为．三、解答题（本题共30分，每小题5分）13．计算：．14．如图，, ，直线经过点，于点，于点．求证: ．15. 解分式方程：．16. 已知，求的值．17.在“母亲节”到来之际，某校九年级团支部组织全体团员到敬老院慰问.为筹集慰问金，团员们利用课余期间去卖鲜花．已知团员们从花店按每支1.5元的价格买进鲜花共支，并按每支5元的价格全部卖出，若从花店购买鲜花的同时，还用去50元购买包装材料．（1）求所筹集的慰问金（元）与（支）之间的函数表达式；（2）若要筹集不少于650元的慰问金，则至少要卖出鲜花多少支？18.如图，在平面直角坐标系中，点为坐标原点，直线分别交轴、轴于、两点，，且、的长分别是一元二次方程的两根．（1）求直线的函数表达式；（2）点是轴上的点，点是第一象限内的点.若以、、、为顶点的四边形是菱形，请直接写出点的坐标．四、解答题（本题共20分，每小题5分）19. 如图，在四边形中，，，，连接，的平分线交于点，且．（1）求的长；（2）若，求四边形的周长．20. 2014年春季，北京持续多天的雾霾天气让环保和健康问题成为人们关注的焦点．为了美丽的北京和师生的身心健康，某校开展以“倡导绿色出行，关爱师生健康”为主题的教育活动．为了了解本校师生的出行方式，在本校范围内随机抽查了部分师生，将收集的数据绘制成下列不完整的两种统计图．请根据统计图提供的信息，解答下列问题：（1）m = ；（2）已知随机抽查的教师人数为学生人数的一半，请根据上述信息补全条形统计图，并标明相应数据；（3）若全校师生共1800人，请你通过计算估计，全校师生乘私家车出行的有多少人？21. 如图，点是以为直径的圆上一点，直线与过点的切线相交于点，点是的中点，直线交直线于点 .（1）求证：是⊙O的切线；（2）若，，求⊙O的半径.22. 阅读下面材料：如果一个三角形和一个平行四边形满足条件：三角形的一边与平行四边形的一边重合，三角形这边所对的顶点在平行四边形这边的对边上，则称这样的平行四边形为三角形的“友好平行四边形”．如图1 所示，平行四边形即为的“友好平行四边形”．请解决下列问题:（1）仿照以上叙述,说明什么是一个三角形的“友好矩形”；（2）若是钝角三角形，则显然只有一个“友好矩形”，若是直角三角形，其“友好矩形”有个；（3）若是锐角三角形，且，如图2，请画出的所有“友好矩形”；指出其中周长最小的“友好矩形”并说明理由.五、解答题（本题共22分，第23题7分，第24题7分，第25题8分）23. 已知关于的一元二次方程有两个不相等的实数根．（1）求的取值范围；（2）当取最小的整数时，求抛物线的顶点坐标以及它与轴的交点坐标；（3）将(2)中求得的抛物线在轴下方的部分沿轴翻折到轴上方，图象的其余部分不变，得到一个新图象．请你画出这个新图象，并求出新图象与直线有三个不同公共点时的值．24.如图1，已知是等腰直角三角形，,点是的中点．作正方形，使点、分别在和上，连接，．（1）试猜想线段和的数量关系是；（2）将正方形绕点逆时针方向旋转，①判断（1）中的结论是否仍然成立？请利用图2证明你的结论；②若，当取最大值时，求的值．25. 定义：如果一个与的函数图象经过平移后能与某反比例函数的图象重合，那么称这个函数是与的“反比例平移函数”．例如: 的图象向左平移2个单位，再向下平移1个单位得到的图象，则是与的“反比例平移函数”．（1）若矩形的两边分别是2 、3 ，当这两边分别增加( )、( )后，得到的新矩形的面积为8 ，求与的函数表达式，并判断这个函数是否为“反比例平移函数”．（2）如图，在平面直角坐标系中，点为原点，矩形的顶点、的坐标分别为(9，0)、(0，3) ．点是的中点，连接、交于点，“反比例平移函数” 的图象经过、两点．则这个“反比例平移函数”的表达式为；这个“反比例平移函数”的图象经过适当的变换与某一个反比例函数的图象重合，请写出这个反比例函数的表达式．（3）在（2）的条件下，已知过线段中点的一条直线交这个“反比例平移函数”图象于、两点( 在的右侧)，若、、、为顶点组成的四边形面积为16，请求出点的坐标．数学试卷答案及评分参考2014年4月一、选择题（本题共32分，每小题4分）题号 1 2 3 4 5 6 7 8答案 A B D C D B C B二、填空题（本题共16分，每小题4分）题号 9 10 11 12答案 (0,-4),注：第12题第一空2分，第二空2分，写对一个给1分.(不写的取值范围不扣分)三、解答题（本题共30分，每小题5分）13．解：．．……………………4分……………………5分14．证明：∵，∴，……………………1分∴，∵，∴，∴．……………………2分在和中，∴≌．…………………4分∴．…………………5分15. 解：…………………2分…………………3分…………………4分经检验，是原分式方程的根. …………………5分16．解：原式= …………………2分== . …………………3分∵，∴ .∴原式= ，…………………4分= . …………………5分17.解：（1） . …………………2分（2）当时，即，…………………3分解得 . …………………4分答：若要筹集不少于650元的慰问金，至少要售出鲜花200支. …………………5分18.解：（1）∵，∴，∴， .∴点的坐标为(3,0)，点的坐标为(0,4) ．……………2分∵设直线的函数表达式为∴∴∴直线的函数表达式为 . ……………3分（2）点的坐标是(3，5)或(3, )．……………5分四、解答题（本题共20分，每小题5分）19.解：（1）延长交于点 .∵平分，∴ .∵，∴，∴，………1分∴ .∵，∴ . ……………2分∵，∴四边形是平行四边形，∴.………3分（2）过作的垂线，垂足为 .∵，，在中，，∴ . ………………4分∴四边形的周长………………5分20.解：（1）20%；………………1分（2）补全条形统计图如下图：………………3分（3）（人）（人）=480（人）………………5分答: 全校师生乘私家车出行的有480人．21.（1）证明：连接、，∵是直径，∴ . ………………1分∴ . m∵是的中点，∴，∴ . ………………2分∵是⊙的半径，（2）解:∵是的中点，、是⊙O的切线，∴， .∴，………………4分∴ .设⊙O的半径为 .∵∽，∴，∴ . ………………5分∴⊙O的半径为 .22. 解：（1）三角形的一边与矩形的一边重合，三角形这边所对的顶点在矩形这边的对边上. ………………1分（2）2；………………2分（3）画图:周长最小的“友好矩形”是矩形 . ………………4分理由:易知这三个矩形的面积都等于的面积的一半，所以这三个矩形的面积相等,令其为,设矩形，矩形，矩形的周长分别为、、，的边长，，，( )，则，，，∴，而，，∴，即 .同理可证 . ……………5分五、解答题（本题共22分，第23题7分，第24题7分，第25题8分）23.解：（1）由题意，得，∴．∴的取值范围为．…………2分（2）∵，且取最小的整数，∴．∴，则抛物线的顶点坐标为…………………3分∵的图象与轴相交，∴，∴，∴或，∴抛物线与轴相交于，．…………4分（3）翻折后所得新图象如图所示. …………5分平移直线知: 直线位于和时，它与新图象有三个不同的公共点．①当直线位于时，此时过点，∴，即．………………6分②当直线位于时，此时与函数的图象有一个公共点，∴方程，即有两个相等实根，∴，即．………………7分当时，满足，由①②知或．（2）①成立．以下给出证明：如图，连接，∵在Rt 中，为斜边中点，∴，，∴．…………………3分∵四边形为正方形，∴，且，∴，∴．……4分在和中，∴≌，∴．……………………5分②由①可得，当取得最大值时，取得最大值．当旋转角为时，，最大值为 . ………6分如图,此时．……………………7分25.解：（1），∴………………1分向右平移2个单位，再向上平移3个单位得到．∴是“反比例平移函数”．……2分（2）“反比例平移函数”的表达式为 . ……………3分变换后的反比例函数表达式为 . ……………4分（3）如图，当点在点左侧时，设线段的中点为，由反比例函数中心对称性，四边形为平行四边形.∵四边形的面积为16，∴=4，……………5分∵(9,3)，(6,2).是的“反比例平移函数”，∴= =4，(3,1)过作轴的垂线，与、轴分别交于、点..设，∴即………………6分∴∴(1，3) ，∴点的坐标为（7，5）. ………………7分当点在点右侧时，同理可得点的坐标为（15，）. ………8分(注：本卷中许多试题解法不唯一,请老师们根据评分标准酌情给分)。

2014年中考数学模拟试题（一）（本试卷分A卷（100分）、B卷（60分），满分160分，考试时间120分钟）A卷（共100分）一、选择题（本大题共12小题，每小题3分，共36分）1．下列四个实数中，绝对值最小的数是【】A．－5 B．2-C．1 D．42．一个几何体的三视图如图所示，那么这个几何体是【】A．B．C．D．3．某公司开发一个新的项目，总投入约11500000000元，11500000000元用科学记数法表示为【】A．1.15×1010B．0.115×1011C．1.15×1011D．1.15×1094．把不等式组x>1x23-⎧⎨+≤⎩的解集表示在数轴上，下列选项正确的是【】A．B．C．D．5．今年我市有近4万名考生参加中考，为了解这些考生的数学成绩，从中抽取1000名考生的数学成绩进行统计分析，以下说法正确的是【】A．这1000名考生是总体的一个样本B．近4万名考生是总体C．每位考生的数学成绩是个体D．1000名学生是样本容量6．把一块直尺与一块三角板如图放置，若∠1=40°，则∠2的度数为【】A ．125°B ．120°C ．140°D ．130°7．成渝路内江至成都段全长170千米，一辆小汽车和一辆客车同时从内江、成都两地相向开出，经过1小时10分钟相遇，小汽车比客车多行驶20千米．设小汽车和客车的平均速度为x 千米/小时和y 千米/小时，则下列方程组正确的是【 】A ．x y 2077x y 17066+=⎧⎪⎨+=⎪⎩B ．x y 2077x y 17066-=⎧⎪⎨+=⎪⎩C ．x y 2077x y 17066+=⎧⎪⎨-=⎪⎩ D ．77x y 1706677x y 2066⎧+=⎪⎪⎨⎪-=⎪⎩ 8．如图，在 ABCD 中，E 为CD 上一点，连接AE 、BD ，且AE 、BD 交于点F ，DEF ABF S S 425∆∆=：：，则DE ：EC=【 】A ．2：5B ．2：3C ．3：5D ．3：29．若抛物线2y x 2x c =-+与y 轴的交点为（0，﹣3），则下列说法不正确的是【 】 A ．抛物线开口向上 B ．抛物线的对称轴是x=1C ．当x=1时，y 的最大值为﹣4D ．抛物线与x 轴的交点为（－1，0），（3，0）10．同时抛掷A 、B 两个均匀的小立方体（每个面上分别标有数字1，2，3，4，5，6），设两立方体朝上的数字分别为x 、y ，并以此确定点P （x ，y ），那么点P 落在抛物线2y x 3x =-+上的概率为【 】A ．118 B ．112 C ．19 D ．1611．如图，反比例函数ky x=（x ＞0）的图象经过矩形OABC 对角线的交点M ，分别于AB 、BC 交于点D 、E ，若四边形ODBE 的面积为9，则k 的值为【 】A．1 B．2 C．3 D．412．如图，半圆O的直径AB=10cm，弦AC=6cm，AD平分∠BAC，则AD的长为【】A．45cm B．35cm C．55cm D．4cm二、填空题（每小题5分，共20分）13、分解因式：ab3﹣4ab=_________。

2014年中考数学模拟试题（本试卷分A 卷（100分）、B 卷（60分），满分160分，考试时间120分钟）A 卷（共100分）一、选择题（每小题3分，36分） 1、﹣6的相反数为（ ） A ：6 B ：61C ：－61D ：－62、下列计算正确的是（ ）A ：a 2+a 4=a 6B ： 2a+3b=5abC ：（a 2）3=a6D ：a 6÷a 3=a 23、已知反比例函数的图象经过点（1，﹣2），则k 的值为（ ）A ：2B ： －21 C ：1D ：－2 4、下列图形中，既是轴对称图形又是中心对称图形的有（ ）A ：4个B ：3个C ：2个D ：1个 5、如图，a ∥b ，∠1=65°，∠2=140°，则∠3=（ ）A ：100°B ：105°C ：110°D ：115°6、一组数据4，3，6，9，6，5的中位数和众数分别是（ ）A ：5和5.5B ：5.5和6C ：5和6D ：6和67、函数的图象在（ ）A ：第一象限B ：第一、三象限C ：第二象限D ：第二、四象限 8、如图，AB 是⊙O 的直径，弦CD ⊥AB ，∠CDB=30°，CD=，则阴影部分图形的面积为（ ）A ：4πB ：2πC ：πD ：32π 9、甲车行驶30千米与乙车行驶40千米所用时间相同，已知乙车每小时比甲车多行驶15千 米，设甲车的速度为x 千米/小时，依据题意列方程正确的是（ ） A ：x 30＝1540-x B ：x 40＝1530-x C ：x30＝1540+x D ：x 40＝1530+x 10、如图，在矩形ABCD 中，AB=10，BC=5，点E 、F 分别在AB 、CD 上，将矩形ABCD 沿EF 折叠，使点A 、D 分别落在矩形ABCD 外部的点A 1、D 1处，则阴影部分图形的周长为（ ）A ：15B ：20C ：25D ：3011、如图所示，△ABC 的顶点是正方形网格的格点，则sinA 的值为（ ） A ：21B ：55C ：1010D ：55212、如图，正△ABC 的边长为3cm ，动点P 从点A 出发，以每秒1cm 的速度，沿A →B →C的方向运动，到达点C 时停止，设运动时间为x （秒），y=PC 2，则y 关于x 的函数的图象大致为（ ）A ：B ：C ：D ：二、填空题（本大题共4小题，每小题5分，共20分） 13．若m 2－n 2=6，且m －n=2，则m ＋n= ▲ ． 14．函数2x 1y x 1+=-中自变量x 的取值范围是 ▲ ． 15．一组数据3，4，6，8，x 的中位数是x ，且x 是满足不等式组x 305x>0-≥⎧⎨-⎩的整数，则这组数据的平均数是 ▲ ．16．已知菱形ABCD 的两条对角线分别为6和8，M 、N 分别是边BC 、CD 的中点，P 是对角线BD 上一点，则PM+PN 的最小值= ▲ ．三、解答题（本大题共5小题，共44分） 17．计算：()()1201302sin 60534015131π-⎛⎫+---+-+ ⎪-⎝⎭．18．已知，如图，△ABC 和△ECD 都是等腰直角三角形，∠ACD=∠DCE=90°，D 为AB 边上一点．求证：BD=AE ．19．随着车辆的增加，交通违规的现象越来越严重，交警对某雷达测速区检测到的一组汽车的时速数据进行整理，得到其频数及频率如表（未完成）：数据段 频数 频率 30～40 10 0.05 40～50 36 50～60 0.39 60～70 70～80 20 0.10 总计2001注：30～40为时速大于等于30千米而小于40千米，其他类同 （1）请你把表中的数据填写完整； （2）补全频数分布直方图；（3）如果汽车时速不低于60千米即为违章，则违章车辆共有多少辆？20．如图，某校综合实践活动小组的同学欲测量公园内一棵树DE 的高度，他们在这棵树的正前方一座楼亭前的台阶上A 点处测得树顶端D 的仰角为30°，朝着这棵树的方向走到台阶下的点C 处，测得树顶端D 的仰角为60°．已知A 点的高度AB 为3米，台阶AC 的坡度为13：（即AB ：BC=13：），且B 、C 、E 三点在同一条直线上．请根据以上条件求出树DE 的高度（侧倾器的高度忽略不计）．21．某地区为了进一步缓解交通拥堵问题，决定修建一条长为6千米的公路．如果平均每天的修建费y（万元）与修建天数x（天）之间在30≤x≤120，具有一次函数的关系，如下表所示．x 50 60 90 120y 40 38 32 26（1）求y关于x的函数解析式；（2）后来在修建的过程中计划发生改变，政府决定多修2千米，因此在没有增减建设力量的情况下，修完这条路比计划晚了15天，求原计划每天的修建费．B卷（共60分）四、填空题（本大题共4小题，每小题6分，共24分）22．在△ABC中，已知∠C=90°，7sinA sinB5+=，则sinA sinB-=▲．23．如图，正六边形硬纸片ABCDEF在桌面上由图1的起始位置沿直线l不滑行地翻滚一周后到图2位置，若正六边形的边长为2cm，则正六边形的中心O运动的路程为▲cm．24．如图，已知直线l：y3x=，过点M（2，0）作x轴的垂线交直线l于点N，过点N 作直线l的垂线交x轴于点M1；过点M1作x轴的垂线交直线l于N1，过点N1作直线l的垂线交x轴于点M2，…；按此作法继续下去，则点M10的坐标为▲．25．在平面直角坐标系xOy 中，以原点O 为圆心的圆过点A （13，0），直线y kx 3k 4=-+与⊙O 交于B 、C 两点，则弦BC 的长的最小值为 ▲ ． 五、解答题（本大题共3小题，每小题12分，共36分）26．如图，AB 是半圆O 的直径，点P 在BA 的延长线上，PD 切⊙O 于点C ，BD ⊥PD ，垂足为D ，连接BC ．（1）求证：BC 平分∠PDB ； （2）求证：BC 2=AB•BD ；（3）若PA=6，PC=62，求BD 的长．27．如图，在等边△ABC 中，AB=3，D 、E 分别是AB 、AC 上的点，且DE ∥BC ，将△ADE 沿DE 翻折，与梯形BCED 重叠的部分记作图形L ． （1）求△ABC 的面积；（2）设AD=x ，图形L 的面积为y ，求y 关于x 的函数解析式；（3）已知图形L 的顶点均在⊙O 上，当图形L 的面积最大时，求⊙O 的面积．28．已知二次函数2y ax bx c =++（a ＞0）的图象与x 轴交于A （x 1，0）、B （x 2，0）（x 1＜x 2）两点，与y 轴交于点C ，x 1，x 2是方程2x 4x 50+-=的两根．（1）若抛物线的顶点为D，求S△ABC：S△ACD的值；（2）若∠ADC=90°，求二次函数的解析式．2014年中考数学模拟试题答案一、A CDCBB ADCDBC13. 314.1x2≥-且x≠115. 516. 517. 解：原式=3317 5311222-+-⨯-+=。

2014年中考数学模拟卷一、选择题(本大题共6小题，每小题5分，共30分)1.下列各数：pi;2，0，9，0.23bull;，cos60deg;，227，0.030 030 003，1-2中，无理数有( )A.2 个B.3 个C.4 个D.5 个2.在平面直角坐标系中，下面的点在第四象限的是( )A.(1,3)B.(0，-3)C.(-2，-3)D.(pi;，-1)3.下列图案中，既是轴对称图形又是中心对称图形的是( )4.形状相同、大小相等的两个小木块放置于桌面，其俯视图如图J2shy;1，则其正视图是( )5.如图J2shy;2，△ABC与△Aprime;Bprime;Cprime;是位似图形，点O是位似中心，若OA=2AAprime;，S△ABC=8，则S△Aprime;Bprime;Cprime;=()A.9B.16C.18D.24图J2shy;2 图J2shy;36.已知二次函数y=ax2+bx+c(ane;0)的图象如图J2shy;3，给出以下结论：①因为agt;0，所以函数y有最大值;②该函数图象关于直线x=-1对称;③当x=-2时，函数y的值大于0;④当x=-3或x=1时，函数y的值都等于0.其中正确结论的个数是( )A.1个B.2个C.3个D.4个二、填空题(本大题共4小题，每小题5分，共20分)7.如图J2shy;4，直线l与直线a，b相交.若a∥b，ang;1=70deg;，则ang;2的度数是________.图J2shy;4 图J2shy;58.已知某种型号的纸100张厚度约为1 cm，那么这种型号的纸13亿张厚度约为____________km.9.菱形OACB在平面直角坐标系中的位置如图J2shy;5，点C的坐标是(6,0)，点A的纵坐标是1，则点B 的坐标是________.10.函数y=1-kx的图象与直线y=x没有交点，那么k 的取值范围是____________.三、解答题(本大题共5小题，每小题10分，共50分)11.化简：x-1x÷x-2x-1x.12.如图J2shy;6，放置在水平桌面上的台灯的灯臂AB长为40 cm，灯罩BC长为30 cm，底座厚度为2 cm，灯臂与底座构成的ang;BAD=60deg;.使用发现，光线最佳时灯罩BC与水平线所成的角为30deg;，此时灯罩顶端C到桌面的高度CE是多少厘米?(结果精确到0.1 cm，参考数据：3asymp;1.732)13.已知：关于x的一元二次方程：x2-2mx+m2-4=0.(1)求证：这个方程有两个不相等的实数根;(2)当抛物线y=x2-2mx+m2-4与x轴的交点位于原点的两侧，且到原点的距离相等时，求此抛物线的解析式.14.某校为了解本校八年级学生的课外阅读喜好，随机抽取部分该校八年级学生进行问卷调查(每人只选一种书籍)，图J2shy;7是整理数据后画的两幅不完整的统计图，请你根据图中的信息，解答下列问题：(1)这次活动一共调查了________名学生;(2)在扇形统计图中，“其他”所在的扇形圆心角为________;(3)补全条形统计图;(4)若该校八年级有600人，请你估计喜欢“科普常识”的学生有________人.15.如图J2shy;8，在⊙O中，弦BC垂直于半径OA，垂足为E，点D是优弧上的一点，连接BD，AD，OC，ang;ADB=30deg;.。

2 014年学业水平数学试题模拟测试（一）一、单项选择题（每个选项中只有一个正确答案，请将正确答案的序号填入表格中。

每小题3分，共30分） 1、计算：32⋅a a 5a B . 6a C. 8aD. 9a 2、某种商品进价为800元，标价1200元，由于该商品积压，商店准备打折销售，但要保证利润率不低于20%，则至少可以打（ ）折。

A. 6折B. 7折C. 8折D. 9折3、 二次函数()213y x =--+图象的顶点坐标是Ａ．()13-， Ｂ．()13，Ｃ．()13--，Ｄ．()13-，4、若不等式组⎩⎨⎧>-<+m x x x 148的解集是x >3，则m 的取值范围是A ．m >3 B ．m ≥3 C ．m ≤3 D ．m <35、正方形ABCD 中，E 、F 分别为AB 、BC 的中点，AF 与DE 相交于点O ，则AODO= A ．13B ．23 D ．126、下列一组几何体的俯视图是7、下图是同一副扑克中的4张扑克牌的正面，将它们正面朝下洗匀后放在桌上，小明从 中抽出一张，则抽到偶数的概率是A ．13B ．12C ．34D ．238、某班派9名同学参加拔河比赛，他们的体重分别是（单位：千克）：67，59，61，59，63，57，70，59，65，这组数据的众数和中位数分别是A. 59，63 B. 59，61 C. 59，59D. 57，619、在同一直角坐标系中，函数y mx m =+和函数222y mx x =-++（m 是常数，且 0m ≠）的图象可能．．是CBOA图810、如图，正方形ABCD 的边长为2, 将长为2的线段QR 的两端放在正方形的相邻的两边上同时滑动。

若点Q 从点A 出发，沿图中所示按A →B →C →D →A 滑动到A 止，同时点R 从点B 出发，沿图中所示按B →C →D →A →B 滑动到B 止，在这个过程中，线段QR 的中点M 所经过的路线围成的图形的面积为A ．2 B ．4－π C ．π D ．1π- 二、填空题（每题4分，共20分）11、因式分解：2288x x -+ = .12、国家体育场“鸟巢”建筑面积25.8万平方米，将25.8万平方米用科学记数法（保留2个有效数字），可以表示为 平方米.13、 如图8，AB 是半圆O 的直径，∠BAC =30°，BC 为半圆的切线，且BC=O 到AC 的距离是．14、将一个正三角形纸片剪成四个全等的小正三角形，再将其中的一个按同样的方法剪成四个更小的正三角形，……如此继续下去，结果如下表：则a n ＝ （用含n 的代数式表示）． 15、如图是抛物线c bx ax y ++=2的一部分，其对称轴为直线x ＝1，若其与x 轴一交点为B （3，0），则由图象可知，不等式c bx ax ++2＞0的解集是三、解答题（共70分）16、（本题满分5分）计算：)2(2)(2006)2245---π+17、（本题满分5分）先化简，再求值：21(111a a a a --÷++，其中12a =．方法一 方法二18、（本题满分6分） 如图，阴影部分是由5个小正方形组成的一个直角图形，请用二种方法分别在下图方格内．．．添涂黑二个小正方形，使它们成为轴对称图形．19、（本题满分10分）甲、乙两人用如图所示的两个分格均匀的转盘做游戏：分别转动两个转盘，若转盘停止后，指针指向一个数字（若指针恰好停在分格线上，则重转一次），用所指的两个数字作乘积，如果积大于10，那么甲获胜；如果积不大于10，那么乙获胜．请你解决下列问题： （1）利用树状图（或列表）的方法表示游戏所有可能出现的结果； （2）求甲、乙两人获胜的概率．20、（本题满分10分）亮亮和颖颖住在同一幢住宅楼，两人准备用测量影子的方法测算其楼高，但恰逢阴天，于是两人商定改用下面方法：如图，亮亮蹲在地上，颖颖站在亮亮和楼之间，两人适当调整自己的位置，当楼的顶部M ，颖颖的头顶B 及亮亮的眼睛A 恰在一条直线上时，两人分别标定自己的位置C ，D ．然后测出两人之间的距离 1.25m CD =，颖颖与楼之间的距离30m DN =（C ，D ，N 在一条直线上），颖颖的身高 1.6m BD =，亮亮蹲地观测时眼睛到地面的距离0.8m AC =．你能根据以上测量数据帮助他们求出住宅楼的高度吗？MNB A CD 第20题图21、（本题满分10分）已知：如图，ABC △内接于⊙O ，点D 在OC 的延长线上，1sin 2B =，30CAD ∠=． （1）求证：AD 是⊙O 的切线；（2）若OD AB ⊥，5BC =，求AD 的长．22、（本题满分12分）如图所示，正方形网格中，ABC △为格点三角形（即三角形的顶点都在格点上）． （1）把ABC △沿BA 方向平移后，点A 移到点1A ，在网格中画出平移后得到的11A B C 1△； （2）把11A B C 1△绕点1A 按逆时针方向旋转90°，在网格中画出旋转后的22A B C 1△； （3）如果网格中小正方形的边长为1，求点B 经过（1）、（2）变换的路径总长．23、（本题满分12分） 阅读材料：如图26-①，过△ABC 的三个顶点分别作出与水平线垂直的三条直线，外侧两条直线之间的距离叫△ABC 的“水平宽”（a ），中间的这条直线在△ABC 内部的线段的长度叫△ABC 的“铅垂高”（h ）．我们可得出一种计算三角形面积的新方法：ah S ABC 21=∆，即三角形面积等于水平宽与铅垂高乘积的一半． 解答下列问题：如图26-②，抛物线顶点坐标为点C （1，4），交x 轴于点A （3，0），交y 轴于点B ．（1）求抛物线和直线AB 的解析式；（2）求CAB ∆的铅垂高CD 及CAB S ∆；（3）设点P 是抛物线（在第一象限内）上的一个动点，是否存在一点P，使Cy BD 1（图26-①）98PAB CAB S S ∆∆=，若存在，求出P 点的坐标；若不存在，请说明理由2010年学业水平数学模拟测试（一）一、选择题1.Ａ2.C3.B4.C5. D6.B7.C8. B9. D 10. B 二、填空题11. 22(2)x - 12. 5106.2⨯ 13.3 14.13+n ； 15.x ＜-1或x ＞3三、解答题16．解：原式41342=-+--21=-1= 17.原式=11a -， 122a =-将代入得 18(略)．19．解：（1）树状图法或列表法：（注：学生只用一种方法即可）（2）()()1233P P ==甲乙，．20.解：过A 作CN 的平行线交BD 于E ，交MN 于F ． 由已知可得0.8m FN ED AC ===，1.25m AE CD ==，30m EF DN ==，90AEB AFM ==∠∠．又BAE MAF =∠∠，ABE AMF ∴△∽△．BE AE MF AF ∴=． 即1.60.8 1.251.2530MF -=+． 解得()20m MF =．()200.820.8m M N M F F N ∴=+=+=．所以住宅楼高为20.8m ．21．解：（1）证明：如图，连结OA ． 因为1sin 2B =， 所以30B ∠=． 故60O ∠=． 又OA OC =，所以ACO △是等边三角形． 故60OAC ∠=．因为30CAD ∠=， 所以90OAD ∠=． 所以AD 是⊙O 的切线．（2）解：因为OD AB ⊥， 所以OC 垂直平分AB ．则5AC BC ==．所以5OA =． 在OAD △中，90OAD ∠=，由正切定义，有tan ADAOD OA∠=． 所以AD =⨯1 2 3 4 4 8 12 551015AB MFE C DN开始 4 5141424284312⨯=⨯=⨯=，，，3 1515252105315⨯=⨯=⨯=，，， 322．解：（1）画图正确． （2）画图正确． （3）1BB ==弧12B B的长901802==． 点B所走的路径总长2=． 23．解：（1）设抛物线的解析式为：4)1(21+-=x a y 把A （3，0）代入解析式求得1-=a 所以324)1(221++-=+--=x x x y 设直线AB 的解析式为：b kx y +=2 由3221++-=x x y 求得B 点的坐标为(03)，把(30)A ，，(03)B ，代入b kx y +=2中 解得：13k b =-=，所以32+-=x y（2）因为C 点坐标为（1，4）所以当x ＝１时，y 1＝4，y 2＝2 所以CD ＝4-2＝2 13232CAB S =⨯⨯=△（平方单位） （3）假设存在符合条件的点P ，设P 点的横坐标为x ()30<<x ，△PAB 的铅垂高为h ，则x x x x x y y h 3)3()32(2221+-=+--++-=-=由S △PAB =89S △CAB 得：389)3(3212⨯=+-⨯⨯x x 化简得：091242=+-x x 解得，23=x 将23=x 代入3221++-=x x y 中，解得P 点坐标为315()24，。

2014年初三数学中考模拟试题（考试时间90分钟，满分120分）A 卷（共100分）第Ⅰ卷（选择题，共30分）一、选择题（每小题3分，共30分）1、计算2a 2÷a 的结果是（ ）A ．2B ．2aC ．2a 3D ．2a 22．下列图形既是轴对称图形， 又是中心对称图形的是：（ ）3、资料显示，2010年“十 一”黄金周全国实现旅游收入约463亿元，用科学记数法表示463亿这个数是:（ ）A. 463×108×108×1010×10114、如图,是由相同小正方体组成的立体图形,它的主视图为（ ）A ．B ．C ．D 5、函数321-=x y 中，自变量x 的取值范围为（ ） A ．23>x B ．23≠x C ．23≠x 且0≠x D ．23<x6、如图,已知OB OA ,均为⊙O 上一点,若︒=∠80AOB ,则=∠ACB （ ） A ．80°B ．70°C ．60°D ．40°7、如图，四边形ABCD 为正方形，若E AB ,4=是AD 边上一点（点E 与点A 、D 不重合），BE 的中垂线交AB 于M ，交DC 于N ，设x AE =，则图中阴影部分的面积S 与x 的大致图像是（ ）8、一个均匀的立方体六个面上分别标有数字1，2，3，4，5，6，如图是这个立方体表面的展开A BCo (第6题图)A B C D (第4题图)图，抛掷这个立方体，则朝上一面的数字恰好等于朝下一面数字的21的概率是（ ） A ．61 B ．31 C ．21 D ．328题图 9题图9、如图，在△ABC 中，∠C =90°，AC ＞BC ，若以AC为底面圆的半径，BC 为高的圆锥的侧面积为S 1，若以BC 为底面圆的半径，AC为高的圆锥的侧面积为S 2 ， 则（ ） A ．S 1 =S 2 B ．S 1 ＞S 2 C ．S 1 ＜S 2 D ．S 1 ,S 2的大小大小不能确定10、在直角坐标系中，⊙O 的圆心在原点，半径为3，⊙A 的圆心A 的坐标为（－3，1），半径为1，那么⊙O 与⊙A 的位置关系为（ ）A 、外离B 、外切C 、内切D 、相交第Ⅱ卷（非选择题，共70分）二、填空题：（本大题共5题，每小题4分，共20分）11、为了估计湖里有多少条鱼，我们从湖里捕上100条做上标记，然后放回湖里，经过一段时间待带标记的鱼完全混合于鱼群中后，第二次捕得200查方式，我们可以估计湖里有鱼 ________条.12、不等式组⎩⎨⎧2x ＋1＞－1x ＋2＜≤3的整数解为 ．13、如图同心圆，大⊙O 的弦AB 切小⊙O 于P ，且AB=614、今年我省荔枝又喜获丰收. 目前市场价格稳定，荔枝种植户普遍获利枝总产量为50 000吨，销售收入为61 000万元. 已知“妃子笑”品种售价为万元/吨，其它品种平均售价为万元/吨，求“妃子笑”和其它品种的荔枝产量各多少吨. 如果设“妃子笑”荔枝产量为x 吨，其它品种荔枝产量为y15、如图，正比例函数y=kx 与反比例函数y =x1过B 作X 轴的垂线交X 轴于点C ，连接AC ，则△ABC三、解答题：（本大题共7个小题，共50分）16、（本题满分18分，每题6分）（1）计算： 131-⎪⎭⎫ ⎝⎛0232006⎪⎪⎭⎫ ⎝⎛--3-sin60°．（2）化简求值：12,122422-=++÷⎪⎪⎭⎫ ⎝⎛-+-x x x x x x 其中（3）解方程：3 x 2＋x ＝ 1x 2－x17、（本题满分7分）西部建设中，某工程队承包了一段72千米的铁轨的铺设任务，计划若干天完成，在铺设完一半后，增添工作设备，改进了工作方法，这样每天比原计划可多铺3千米，结果提前了2天完成任务。

DBCA 2014年中考调研测试（一）数 学 试 卷考生须知：1.本试卷满分为120分，考试时间为120分钟。

2.答题前，考生先将自己的“姓名”、“考号”、“考场”、“座位号”在答题卡上填写清楚，将“条形码”准确粘贴在条形码区域内。

3.请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试题纸上答题无效。

4.选择题使用2B 铅笔填涂；非选择题必须使用0.5毫米黑色字迹的签字笔书写，字体工整、笔记清楚。

5．保持卡面整洁，不要折叠、不要弄脏、弄皱，不准使用涂改液、刮纸刀。

第Ⅰ卷 选择题（共30分）（涂卡）一、选择题（每小题3分，共30分） 1.54的相反数是（ ） A. 45 B. 45- C. 54 D. 54-2.下列计算正确的是（ ）A ．34x x x +=B ．325()x x =C ．633x x x ÷=D ．2532x x x =⋅3.下列图形中既是轴对称图形又是中心对称图形的个数是（ ）A. 1个B. 2个C. 3个D. 4个 4．图1所示的几何体主视图是（ ）图1 A． B ．C ．D ．5.将抛物线2)2(3-=x y 向左平移3个单位得到的抛物线的解析式是（ ） A.2)5(3-=x y B.3)2(32+-=x y C.2)1(3+=x y D.3)2(32--=x y6.一个不透明的袋子里有5个红球和3个黄球，这些球除颜色外完全相同，从袋子中随机摸出一个球，它是黄球的概率是（ ）A.15 B. 31 C. 38 D. 587.已知反比例数3k y x+=的图象在每一象限内y 随x 的增大而增大，则k 的取值范围是（ ）A. k>3B. k<-3C. k>-3D. k<38.如图，Rt △ABC 中，∠ACB=90º，CD ⊥AB ，BC=3，AC=4， tan ∠BCD 等于（ ）A.34 B. 43 C. 35 D. 459.如图,矩形ABCD 中，两条对角线相交于点O ，折叠矩形，第8题图 EOA DE DACBAFEACBDx y （时）(千米）4207CO A B ED 使顶点D 与对角线交点O 重合，折痕为CE ，已知△CDE 的 周长是10cm,则矩形ABCD 的周长为（ ）A. 15cmB. 18cmC. 19cmD. 20cm10.快车与慢车分别从相距420千米的甲乙两地同时相向出发，匀速而行，快车到达乙地后停留1小时，然后按原路原速返回，快车比慢车晚1小时到达甲地.快慢两车距各自出发地的路程y （千米）与所用的时间x （时）的关系如图所示，下列说法正确的有 （ ）①快车返回的速度为140千米/时 ②慢车的速度为70千米/时 ③出发314小时时，快慢两车距各自出发地的路程相等④快慢两车出发错误！未找到引用源。