重庆市永川中学高中数学第18周练习一(立体几何1)

重庆市永川中学校2023-2024学年高一下学期6月月考数学试题一、单选题1．复数()i 3i z =+在复平面内对应的点所在的象限为（ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限2．已知向量()1,1a =-r ，()2,1b =r ，()2,c λ=r ．若()2c a b +∥r r r ，则λ=（ ） A ．12- B ．0 C ．12 D ．83．设a 、b 是不同的两条直线，α、β是不同的两个平面，下列说法正确的有（ ） A ．a α⊥，b β⊂，,⊥a b 则αβ⊥B ．α//β，a α⊥，b //β，则a b ⊥r rC ．,,a b αβ⊂⊂且//,//,a b βα则//αβD ．//,//,a b a β则b β//4．直三棱柱111ABC A B C -中，若90BAC ∠=︒，1AB AC AA ==，则异面直线1BA 与1AC 所成的角等于A ．30°B ．45°C ．60°D ．90°5．已知四边形ABCD 是矩形，||4AB =u u u r ，||3BC =u u u r ，则CA DB ⋅=u u u r u u u r （ ）A ．25B ．-7C ．7D ．-25 6．某居民小区户主人数和户主对住房户型结构的满意率分别如图1和图2所示，为了解该小区户主对户型结构的满意程度，用比例分配的分层随机抽样方法抽取25%的户主作为样本进行调查，则样本容量和抽取的户主对四居室满意的人数分别为（ ）A ．400，32B ．400，36C ．480，32D ．480，367．已知圆台上、下底面半径分别为1，2，侧面积为6π，则这个圆台的体积为（ ）A B ． C D 8．在ABC V 中，角A ，B ，C 的对边分别为a ，b ，c ．已知3B π=，8a =，cos cos 6b A a B +=，点O 是ABC V 的外心，若BO xBA yBC =+u u u r u u u r u u u r ，则x y +=（ ）A ．712B ．2336C ．2536D ．2936二、多选题9．已知平面向量()0,1a =r ，()b =r ，则下列说法正确的有（ ） A ．7a b +=r rB ．()()30a b a b +⋅-=-r r r rC ．向量a b +r r 在a r 上的投影向量为D ．向量a b +r r 与a r 的夹角为3π10．在ABC V 中，内角A ，B ，C 所对的边分别为a ，b ，c ，已知2b =，ABC S =V cos cos 2cos 0c B b C a A +-=，则有（ ）A ．a =B ．2C π= C ．3A π= D ．2c =11．如图，直四棱柱1111ABCD A B C D -的底面是梯形，AB CD ∥，AD DC ⊥，4BC CD ==，12DD AB ==，P 是棱1CC 的中点．Q 是棱11C D 上一动点（不包含端点），则（ ）A ． AC 与平面BPQ 有可能平行B ．11B D 与平面BPQ 有可能平行C ．三角形BPQD ．三棱锥A BPQ -的体积为定值三、填空题12．一组数据按从小到大的顺序排列为1，2，2，x ，5，10，其中5x ≠，已知该组数据的中位数是众数的32倍，则该组数据的标准差为． 13．已知ABC V 的内角,,A B C 所对的边分别,,a b c ，角π=3A ．若AM 是CAB ∠的平分线，交BC 于M ，且3AM =，则+2AB AC 的最小值为. 14．在三棱锥S ABC -中，底面ABC 为边长为3的正三角形，侧棱SA ⊥底面ABC ，若三棱锥的外接球的体积为36π，则该三棱锥的体积为.四、解答题15．在ABC V 中，角A ，B ，C 的对边分别为a ，b ，c ．已知222sin sin sin sin sin A C A C B +=+．(1)求角B 的大小；(2)若b =ABC V ABC V 的周长． 16．2022年4月16日，神舟13号载人飞船返回舱在东风着陆场成功着陆，这趟神奇之旅意义非凡，尤其是“天宫课堂”在广大学生心中引起强烈反响，激起了他们对太空知识的浓厚兴趣．某中学在进行太空知识讲座后，从全校学生中随机抽取了200名学生进行笔试（试卷满分100分），并记录下他们的成绩，将数据分成5组：[50,60),[60,70),[70,80),[80,90),[90,100]，并整理得到如下频率分布直方图．(1)求这部分学生成绩的中位数、平均数（同组数据用该组区间的中点值作代表）；(2)为了更好的了解学生对太空知识的掌握情况，学校决定在成绩高的第4、5组中用分层抽样的方法抽取6名学生，进行第二轮面试，最终从这6名学生中随机抽取2人参加市太空知识竞赛，求90分（包括90分）以上的同学恰有1人被抽到的概率．17．已知四棱锥P ABCD -满足：四边形ABCD 为正方形，△P AD 为等边三角形，且平面P AD ⊥平面ABCD ，2AD =，E 为P A 的中点．(1)证明：PC ∥平面BDE ；(2)求直线PC 和平面ABCD 所成角的正切值．18．如图，在四棱锥-P ABCD 中，PA ⊥平面ABCD ，四边形ABCD 为菱形，60ADC ∠=︒，4PA AD ==，E 为AD 的中点．(1)求证：平面PCE ⊥平面PAD ；(2)求二面角A PD C --的平面角的正弦值．19．由于某地连晴高温，森林防灭火形势严峻，某部门安排了甲、乙两名森林防火护林员对该区域开展巡查．现甲、乙两名森林防火护林员同时从A 地出发，乙沿着正西方向巡视走了3km 后到达D 点，甲向正南方向巡视若干公里后到达B 点，又沿着南偏西60°的方向巡视走到了C 点，经过测量发现60ACD ∠=︒．设ACB θ∠=，如图所示．(1)设甲护林员巡视走过的路程为S AB BC=+，请用θ表示S，并求S的最大值；△区域范围内储备应急物资，求(2)为了强化应急应战准备工作，有关部门决定在BCD△区域面积的最大值．BCD。

高2018级高一（下）第一次周考数学试卷班级： 姓名： 2016.2.28一、选择题：（本大题12个小题，每小题5分，共60分）在每小题给出的四个选项中，只有一项是符合题目要求的。

1、已知集合{}{}224,log 0x A x B x x =≤=>，则A B ⋂=（ ）A 、[]1,2B 、(]1,2C 、()0,1D 、(]0,1 2、已知扇形的中心角为3π，半径为2，则其面积为（ ） A ．6π B ．34π C ．3π D ．32π 3、 585sin 的值为（ ）A ．22-B ．22C ．23-D ．234、下列说法正确的是（ ）A.若向量a b 与同向，且a b > ，则a b >B.若,//,a b b c //则a c //C.单位向量都是共线向量D.单位向量的模都相等5、三个数2)3.0(=a ，3.0log 2=b ，3.02=c 之间的大小关系是（ ）A ．b c a <<B ．c b a <<C ．c a b <<D ．a c b <<6、已知函数()1254x f x x =+-，则()f x 的零点所在的区间为（ ） A 、()0,1 B 、()1,2C 、()2,3D 、()3,4 7、要得到函数x y cos =的图象，只需要将函数)32sin(π+=x y 图像上的所有点（ ） A.先向左平移6π个单位长度，再把横坐标伸长到原来的2倍（纵坐标不变）， B.先向左平移12π个单位长度，再把横坐标缩短到原来的21（纵坐标不变）， C.横坐标伸长到原来的2倍（纵坐标不变），再向左平移6π个单位长度D.横坐标伸长到原来的2倍（纵坐标不变），再向左平移3π个单位长度 8、已知函数)sin(2ϕω+=x y （2,0πϕω<>）的部分图象如图所示，则此函数的解析式为（ ）A.)62sin(2π-x B ．)44sin(2π+x C ．)62sin(2π+x D ．)64sin(2π+x9、已知定义在R 上的奇函数()f x 满足()()4f x f x +=恒成立，且()11f =，()()()201620172018f f f ++的值为（ ）A 、0B 、1C 、2D 、310、)120tan 3(10cos 70tan - 等于（ ）A ．1B ．2C ．﹣1D ．﹣2 11、已知关于x 的方程01242=-+⋅+m m x x 有实根，则实数m 的取值范围是（ ）A ．⎥⎦⎤⎢⎣⎡-332,332 B.⎪⎪⎭⎫⎢⎣⎡-1,332 C ．⎥⎦⎤⎢⎣⎡-1,332 D ．⎥⎦⎤⎢⎣⎡332,1 12、已知函数()()221,0log ,0x x f x x x ⎧+≤⎪=⎨>⎪⎩，若方程()f x a =有四个不同的解1x 、2x 、3x 、4x ，且1234x x x x <<<，则()3122341x x x x x ++的取值范围为（ ） A 、()1,-+∞ B 、(]1,1- C 、(),1-∞ D 、[)1,1-二、填空题：（本大题4个小题，每小题5分，共20分）13、函数3)4lg(--=x x y 的定义域是 14、化简：=++++AF BC FD CA DB15、当[)π2,0∈t 时，函数)cos 1)(sin 1()(t t t f ++=的最大值为16、已知函数)(x f y =对任意的R x ∈，都有0)1()5(=-++x f x f ，若方程0)(=x f 有且仅有7个不同的实数解，则这7个实数解之和为三、解答题：（本大题6个小题，共70分）（必须写出必要的文字说明、演算步骤或推理过程）．17、（1）求值：06.0lg 61lg )01.0()412(25325.02120++-⋅+⎪⎭⎫ ⎝⎛-- （2）已知⎪⎭⎫ ⎝⎛∈⎪⎭⎫ ⎝⎛∈=+=ππβπαβαα,2,2,0,31)sin(,322cos ，求βcos 的值．18、设集合{}{}222|40,|2(1)10A x x x B x x a x a =+==+++-=.（1）求集合A ；（2）若= A B A ，求a 的取值范围。

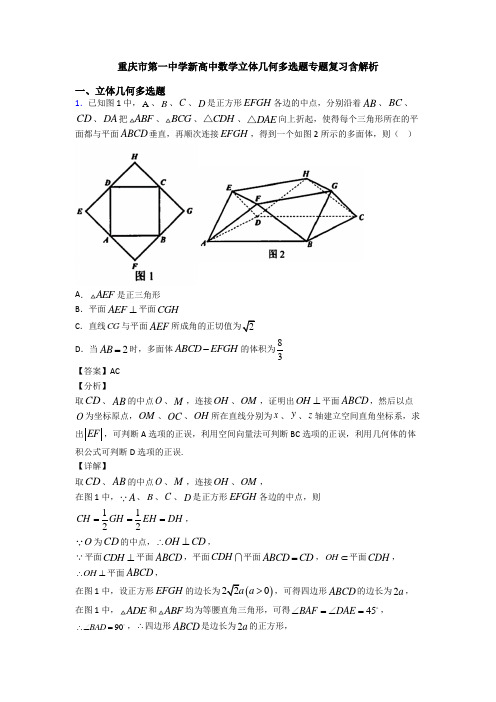
重庆市第一中学新高中数学立体几何多选题专题复习含解析一、立体几何多选题1．已知图1中，A 、B 、C 、D 是正方形EFGH 各边的中点，分别沿着AB 、BC 、CD 、DA 把ABF 、BCG 、CDH △、DAE △向上折起，使得每个三角形所在的平面都与平面ABCD 垂直，再顺次连接EFGH ，得到一个如图2所示的多面体，则（ ）A ．AEF 是正三角形B ．平面AEF ⊥平面CGHC ．直线CG 与平面AEF 2D ．当2AB =时，多面体ABCD EFGH -的体积为83 【答案】AC【分析】取CD 、AB 的中点O 、M ，连接OH 、OM ，证明出OH ⊥平面ABCD ，然后以点O 为坐标原点，OM 、OC 、OH 所在直线分别为x 、y 、z 轴建立空间直角坐标系，求出EF ，可判断A 选项的正误，利用空间向量法可判断BC 选项的正误，利用几何体的体积公式可判断D 选项的正误.【详解】取CD 、AB 的中点O 、M ，连接OH 、OM ，在图1中，A 、B 、C 、D 是正方形EFGH 各边的中点，则1122CH GH EH DH ===， O 为CD 的中点，OH CD ∴⊥，平面CDH ⊥平面ABCD ，平面CDH平面ABCD CD =，OH ⊂平面CDH ，OH ∴⊥平面ABCD ， 在图1中，设正方形EFGH 的边长为()220a a >，可得四边形ABCD 的边长为2a ， 在图1中，ADE 和ABF 均为等腰直角三角形，可得45BAF DAE ∠=∠=， 90BAD ∴∠=，∴四边形ABCD 是边长为2a 的正方形，O 、M 分别为CD 、AB 的中点，则//OC BM 且OC BM =，且90OCB ∠=， 所以，四边形OCBM 为矩形，所以，OM CD ⊥，以点O 为坐标原点，OM 、OC 、OH 所在直线分别为x 、y 、z 轴建立空间直角坐标系，则()2,,0A a a -、()2,,0B a a 、()0,,0C a 、()0,,0D a -、(),,E a a a -、()2,0,F a a 、(),,G a a a 、()0,0,H a .对于A 选项，由空间中两点间的距离公式可得2AE AF EF a ===， 所以，AEF 是正三角形，A 选项正确；对于B 选项，设平面AEF 的法向量为()111,,m x y z =，(),0,AE a a =-，()0,,AF a a =，由111100m AE ax az m AF ay az ⎧⋅=-+=⎪⎨⋅=+=⎪⎩，取11z =，则11x =，11y =-，则()1,1,1m =-， 设平面CGH 的法向量为()222,,n x y z =，(),0,CG a a =，()0,,CH a a =-， 由222200n CG ax az n CH ay az ⎧⋅=+=⎪⎨⋅=-+=⎪⎩，取21z =-，可得21x =，21y =-，则()1,1,1n =--， ()22111110m n ⋅=+--⨯=≠，所以，平面AEF 与平面CGH 不垂直，B 选项错误；对于C 选项，6cos ,23CG mCG m a CG m ⋅<>===⨯⋅， 设直线CG 与平面AEF 所成角为θ，则sin 6θ=，23cos 1sin θθ=-=， 所以，sin tan 2cos θθθ==，C 选项正确； 对于D 选项，以ABCD 为底面，以OH 为高将几何体ABCD EFGH -补成长方体1111ABCD A B C D -，则E 、F 、G 、H 分别为11A D 、11A B 、11B C 、11C D 的中点，因为2AB =，即1a =，则1OH =，长方体1111ABCD A B C D -的体积为2214V =⨯=，11211111113326A A EF A EF V S AA -=⋅=⨯⨯⨯=△， 因此，多面体ABCD EFGH -的体积为111044463ABCD EFGH A A EF V V V --=-=-⨯=， D 选项错误.故选：AC.【点睛】方法点睛：计算线面角，一般有如下几种方法：（1）利用面面垂直的性质定理，得到线面垂直，进而确定线面角的垂足，明确斜线在平面内的射影，即可确定线面角；（2）在构成线面角的直角三角形中，可利用等体积法求解垂线段的长度h ，从而不必作出线面角，则线面角θ满足sin h lθ=（l 为斜线段长），进而可求得线面角； （3）建立空间直角坐标系，利用向量法求解，设a 为直线l 的方向向量，n 为平面的法向量，则线面角θ的正弦值为sin cos ,a n θ=<>.2．如图所示，正三角形ABC 中，D ，E 分别为边AB ，AC 的中点，其中AB ＝8，把△ADE 沿着DE 翻折至A 'DE 位置，使得二面角A '-DE -B 为60°，则下列选项中正确的是（ ）A ．点A '到平面BCED 的距离为3B ．直线A 'D 与直线CE 所成的角的余弦值为58 C ．A 'D ⊥BDD ．四棱锥A '-BCED 237【答案】ABD【分析】作AM ⊥DE ，交DE 于M ,延长AM 交BC 于N ,连接A'M ,A'N .利用线面垂直的判定定理判定CD ⊥平面A'MN ,利用面面垂直的判定定理与性质定理得到'A 到平面面BCED 的高A'H ,并根据二面角的平面角，在直角三角形中计算求得A'H 的值，从而判定A;根据异面直线所成角的定义找到∠A'DN 就是直线A'D 与CE 所成的角，利用余弦定理计算即可判定B;利用勾股定理检验可以否定C;先证明底面的外接圆的圆心为N ,在利用外接球的球心的性质进行得到四棱锥A'-BCED 的外接球的球心为O ,则ON ⊥平面BCED ,且OA'=OC ,经过计算求解可得半径从而判定D.【详解】如图所示，作AM ⊥DE ，交DE 于M ,延长AM 交BC 于N ,连接A'M ,A'N .则A'M ⊥DE ,MN ⊥DE , ,∵'A M ∩MN =M ,∴CD ⊥平面A'MN ,又∵CD ⊂平面ABDC ,∴平面A'MN ⊥平面ABDC ,在平面A'MN 中作A'H ⊥MN ,则A'H ⊥平面BCED ,∵二面角A'-DE -B 为60°，∴∠A'EF =60°，∵正三角形ABC 中，AB =8,∴AN =∴A'M ,∴A'H =A'M sin60°=3，故A 正确； 连接DN ,易得DN ‖EC ,DN =EC =4,∠A'DN 就是直线A'D 与CE 所成的角，DN =DA'=4,A'N =A'M ,cos ∠A'DN =22441252448+-=⨯⨯,故B 正确；A'D =DB =4,==,∴222A D DB A B '≠'+,∴A'D 与BD 不垂直，故C 错误’易得NB =NC =ND =NG =4，∴N 为底面梯形BCED 的外接圆的圆心，设四棱锥A'-BCED 的外接球的球心为O ,则ON ⊥平面BCED ,且OA'=OC ,若O 在平面BCED 上方，入图①所示：设ON =x ,外接球的半径为R ,过O 作A'H 的垂线，垂足为P ,则HP =x ,易得()2222243x x R +=-+=,解得23x =-,舍去； 故O 在平面BCED 下方，如图②所示： 设ON =x ,外接球的半径为R ,过O 作A'H 的垂线，垂足为P ,则HP =x ,易得()2222243x x R +=++=, 解得23x =,∴244371699R ⨯=+=,R ∴=故D 正确. 故选:ABD .【点睛】本题考查立体几何中的折叠问题，涉及二面角问题，异面直线所成的角，用到线面、面面垂直的判定与性质及外接球的球心的性质和有关计算，余弦定理等，属综合性较强的题目，关键是利用线面垂直，面面垂直的判定和性质进行空间关系和结构的判定，注意球心在四棱锥的底面上方和下方的讨论与验证.3．在长方体1111ABCD A B C D -中，4AB BC ==，18AA =，点P 在线段11A C 上，M 为AB 的中点，则（ ）A ．BD ⊥平面PACB ．当P 为11AC 的中点时，四棱锥P ABCD -外接球半径为72C ．三棱锥A PCD -体积为定值D ．过点M 作长方体1111ABCD A B C D -的外接球截面，所得截面圆的面积的最小值为4π【答案】ACD【分析】利用线面垂直的判定定理可判断A 选项的正误；判断出四棱锥P ABCD -为正四棱锥，求出该四棱锥的外接球半径，可判断B 选项的正误；利用等体积法可判断C 选项的正误；计算出截面圆半径的最小值，求出截面圆面积的最小值，可判断D 选项的正误.【详解】对于A 选项，因为AB BC =，所以，矩形ABCD 为正方形，所以，BD AC ⊥， 在长方体1111ABCD A B C D -中，1AA ⊥底面ABCD ，BD ⊂平面ABCD ，1BD AA ∴⊥， 1AC AA A ⋂=，AC 、1AA ⊂平面PAC ，所以，BD ⊥平面PAC ，A 选项正确；对于B 选项，当点P 为11A C 的中点时，PA ===同理可得PB PC PD ===因为四边形ABCD 为正方形，所以，四棱锥P ABCD -为正四棱锥， 取AC 的中点N ，则PN平面ABCD ，且四棱锥P ABCD -的外接球球心在直线PN 上，设该四棱锥的外接球半径为R ，由几何关系可得222PN R AN R -+=，即2288R R -+=，解得92R =，B 选项错误； 对于C 选项，2114822ACD S AD CD =⋅=⨯=， 三棱锥P ACD -的高为18AA =，因此，116433A PCD P ACD ACD V V S AA --==⋅=△，C 选项正确； 对于D 选项，设长方体1111ABCD A B C D -的外接球球心为E ，则E 为1BD 的中点， 连接EN 、MN ，则1142EN DD ==，122MN AD ==， E 、N 分别为1BD 、BD 的中点，则1//EN DD ，1DD ⊥平面ABCD ，EN ∴⊥平面ABCD ，MN ⊂平面ABCD ，EN MN ∴⊥，EM ∴==过点M 作长方体1111ABCD A B C D -的外接球截面为平面α，点E 到平面α的距离为d ，直线EM 与平面α所成的角为θ，则sin d EM θθ==≤当且仅当2πθ=时，等号成立，长方体1111ABCD A B C D -的外接球半径为R '==，所以，截面圆的半径()()222226252r R d '=-≥-=，因此，截面圆面积的最小值为4π，D 选项正确.故选：ACD.【点睛】方法点睛：求空间多面体的外接球半径的常用方法：①补形法：侧面为直角三角形，或正四面体，或对棱二面角均相等的模型，可以还原到正方体或长方体中去求解；②利用球的性质：几何体中在不同面均对直角的棱必然是球大圆直径，也即球的直径； ③定义法：到各个顶点距离均相等的点为外接球的球心，借助有特殊性底面的外接圆圆心，找其垂线，则球心一定在垂线上，再根据带其他顶点距离也是半径，列关系求解即可.4．如图，正方体1111ABCD A B C D -的棱长为3，点E ，F 分别在1CC ，1BB 上，12C E EC →→=，12BF FB →→=.动点M 在侧面11ADD A 内(包含边界)运动，且满足直线//BM 平面1D EF ，则（ ）A ．过1D ，E ，F 的平面截正方体所得截面为等腰梯形B ．三棱锥1D EFM -的体积为定值C ．动点M 10D ．过B ，E ，M 的平面截正方体所得截面面积的最小值为10【答案】BCD【分析】由题做出过1D ，E ，F 的平面截正方体所得截面为梯形1D EFN ，进而计算即可排除A 选项；根据//BM 平面1D EF ，由等体积转化法得1111D EFM M D EF B D EF D BEF V V V V ----===即可得B 选项正确；取1AA 靠近1A 点的三等分点H ， 1DD 靠近D 点的三等分点I ，易知M 的轨迹为线段HI 10，故C 选项正确；过M 点做BE 的平行线交1AA 于P ，交1DD 于O ，连接,BP OE ，易知过B ，E ，M 的平面截正方体所得截面即为平行四边形BPOE ，进而得当H 位于点I 时，截面面积最小，为四边形ABEI 的面积，且面积为310S AB BE =⋅=【详解】解：对于A 选项，如图，取BF 中点G ，连接1A G ，由点E ，F 分别在1CC ，1BB 上，12C E EC →→=，12BF FB →→=，故四边形11A D EG 为平行四边形，故11//AG D E ，由于在11A B G △，F 为1B G 中点，当N 为11A B 中点时，有11////NF A G D E ，故过1D ，E ，F 的平面截正方体所得截面为梯形1D EFN ，此时221335322D N ⎛⎫=+= ⎪⎝⎭，223110EF =+=1D EFN 不是等腰梯形，故A 选项错误；对于B 选项，三棱锥1D EFM -的体积等于三棱锥1M D EF -的体积，由于//BM 平面1D EF ，故三棱锥1M D EF -的体积等于三棱锥1B D EF -的体积，三棱锥1B D EF -的体积等于三棱锥1D BEF -的体积，而三棱锥1D BEF -的体积为定值，故B 选项正确； 对于C 选项，取1AA 靠近1A 点的三等分点H ， 1DD 靠近D 点的三等分点I ，易知1////HB AG NF ，1//BI D F ，由于1,HI BI I NF D F F ==，故平面//BHI 平面1D EF ，故M 的轨迹为线段HI ，其长度为10，故C 选项正确；对于D 选项，过M 点做BE 的平行线交1AA 于P ，交1DD 于O ，连接,BP OE ，则过B ，E ，M 的平面截正方体所得截面即为平行四边形BPOE ，易知当H 位于点I 时，平行四边形BPOE 边BP 最小，且为AB ，此时截面平行四边形BPOE 的面积最小，为四边形ABEI 的面积，且面积为310S AB BE =⋅=，故D 选项正确；故选：BCD【点睛】 本题解题的关键在于根据题意，依次做出过1D ，E ，F 的平面截正方体所得截面为梯形1D EFN ，过B ，E ，M 的平面截正方体所得截面即为平行四边形BPOE ，进而讨论AD 选项，通过//BM 平面1D EF ，并结合等体积转化法得1111D EFM M D EF B D EF D BEF V V V V ----===知B 选项正确，通过构造面面平行得M 的轨迹为线段HI ，进而讨论C 选项，考查回归转化思想和空间思维能力，是中档题.5．在直角梯形ABCD 中，2ABC BCD π∠=∠=，1AB BC ==，2DC =，E 为DC 中点，现将ADE 沿AE 折起，得到一个四棱锥D ABCE -，则下列命题正确的有（ ） A ．在ADE 沿AE 折起的过程中，四棱锥D ABCE -体积的最大值为13 B ．在ADE 沿AE 折起的过程中，异面直线AD 与BC 所成的角恒为4π C ．在ADE 沿AE 折起的过程中，二面角A EC D --的大小为45︒D ．在四棱锥D ABCE -中，当D 在EC 上的射影恰好为EC 的中点F 时，DB 与平面ABCE所成的角的正切为155 【答案】ABD 【分析】 对于A ，四棱锥D ABCE -的底面面积是固定值，要使得体积最大，需要平面DAE ⊥平面ABCE ，此时DE CE ⊥，可求得1133D ABCE ABCE V S DE -=⋅=可判断A ；对于B ，在ADE 沿AE 折起的过程中，//AE BC ，所以异面直线AD 与AE 所成的角即为AD 与BC 所成角，由翻折前可知4DAE π∠=可判断B ；对于C ，利用线面垂直的判定定理，结合翻折前可知AE ⊥平面DEC ，又AE ⊂平面ABCE ，所以平面DEC ⊥平面ABCE ，即二面角A EC D --的在大小为2π判断C ；对于D ，利用线面垂直的判定定理可知DF ⊥平面ABCE ，所以DBF ∠为直线DB 与平面ABCE 所成的角，在直角DFB △中，15tan DF DBF BF ∠==，可判断D 正确；【详解】对于A ，ADE 沿AE 折起得到四棱锥D ABCE -，由四棱锥底面面积是固定值，要使得体积最大，需要四棱锥的高最大，即平面DAE ⊥平面ABCE ，此时DE CE ⊥，由已知得1DE =，则111111333D ABCE ABCE V S DE -=⋅=⨯⨯⨯=，故A 正确； 对于B ，在ADE 沿AE 折起的过程中，//AE BC ，所以异面直线AD 与AE 所成的角即为AD 与BC 所成角，又1AB BC ==，2DC =，E 为DC 中点，可知4DAE π∠=，即异面直线AD 与BC 所成的角恒为4π，故B 正确； 对于C ，由翻折前知，,AE EC AE ED ⊥⊥，且EC ED E =，则AE ⊥平面DEC ，又AE ⊂平面ABCE ，所以平面DEC ⊥平面ABCE ，即二面角A EC D --的大小为2π，故C 错误； 对于D ，如图连接,DF BF ，由C 选项知，AE ⊥平面DEC ，又DF ⊂平面DEC ，则AE DF ⊥，又由已知得EC DF ⊥，且EC AE E ⋂=，则DF ⊥平面ABCE ，所以DBF ∠为直线DB 与平面ABCE 所成的角，在直角DFB △中，222222113122152tan 5511122DE CE DFDBF BFBC CE ⎛⎫⎛⎫-- ⎪⎪⎝⎭⎝⎭∠=====⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭，所以DB 与平面ABCE 所成的角的正切为155，故D 正确； 故选：ABD 【点睛】关键点睛：本题考查立体几何综合问题，求体积，求线线角，线面角，面面角，解题的关键要熟悉几种角的定义，通过平移法找到线线角，通过证垂直找到线面角和面面角，再结合三角形求出角，考查了学生的逻辑推理能力，转化能力与运算求解能力，属于难题.6．如图，点E 为正方形ABCD 边CD 上异于点C ，D 的动点，将ADE 沿AE 翻折成SAE △，在翻折过程中，下列说法正确的是（ ）A ．存在点E 和某一翻折位置，使得SB SE ⊥ B ．存在点E 和某一翻折位置，使得//AE 平面SBCC ．存在点E 和某一翻折位置，使得直线SB 与平面ABC 所成的角为45°D ．存在点E 和某一翻折位置，使得二面角S AB C --的大小为60° 【答案】ACD 【分析】依次判断每个选项：当SE CE ⊥时，⊥SE SB ，A 正确，//AE 平面SBC ，则//AE CB ，这与已知矛盾，故B 错误，取二面角D AE B --的平面角为α，取4=AD ，计算得到2cos 3α=，C 正确，取二面角D AE B --的平面角为60︒，计算得到5tan 5θ=，故D 正确，得到答案. 【详解】当SE CE ⊥时，SE AB ⊥，SE SA ⊥，故SE ⊥平面SAB ，故⊥SE SB ，A 正确； 若//AE 平面SBC ，因AE ⊂平面ABC ，平面ABC 平面SBC BC =，则//AE CB ，这与已知矛盾，故B 错误；如图所示：DF AE ⊥交BC 于F ，交AE 于G ，S 在平面ABCE 的投影O 在GF 上， 连接BO ，故SBO ∠为直线SB 与平面ABC 所成的角，取二面角D AE B --的平面角为α，取4=AD ，3DE =，故5AE DF ==，1CE BF ==，125DG =，12cos 5OG α=，故只需满足12sin5SO OB α==， 在OFB △中，根据余弦定理：2221213121312sin 1cos 2cos cos 55555OFB ααα⎛⎫⎛⎫⎛⎫=+---∠ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，解得2cos 3α=，故C 正确； 过O 作OMAB ⊥交AB 于M ，则SMO ∠为二面角S AB C --的平面角，取二面角D AE B --的平面角为60︒，故只需满足22DG GO OM ==，设OAG OAM θ∠=∠=，84ππθ<<，则22DAG πθ∠=-，tan tan 22DG OGAG πθθ==⎛⎫- ⎪⎝⎭，化简得到2tan tan 21θθ=，解得5tan θ=，验证满足，故D 正确； 故选：ACD .【点睛】本题考查了线线垂直，线面平行，线面夹角，二面角，意在考查学生的计算能力，推断能力和空间想象能力.7．如图，点O 是正四面体P ABC -底面ABC 的中心，过点O 的直线交AC ，BC 于点M ，N ，S 是棱PC 上的点，平面SMN 与棱PA 的延长线相交于点Q ，与棱PB 的延长线相交于点R ，则（ ）A ．若//MN 平面PAB ，则//AB RQ B ．存在点S 与直线MN ，使PC ⊥平面SRQC ．存在点S 与直线MN ，使()0PS PQ PR ⋅+= D ．111PQPRPS++是常数【答案】ABD 【分析】对于选项A ，根据线面平行的性质定理，进行推理判断即可；对于选项B ，当直线MN 平行于直线AB ， 13SC PC =时，通过线面垂直的判定定理，证明此时PC ⊥平面SRQ ，即可证明，存在点S 与直线MN ，使PC ⊥平面SRQ ；对于选项C ，假设存在点S 与直线MN ，使()0PS PQ PR ⋅+=，利用线面垂直的判定定理可证得PC ⊥平面PAB ，此时通过反证法说明矛盾性，即可判断； 对于选项D ，利用S PQR O PSR O PSQ O PQR V V V V ----=++，即可求得111PQPRPS++是常数.【详解】 对于选项A ， 若//MN 平面PAB ，平面SMN 与棱PA 的延长线相交于点Q ，与棱PB 的延长线相交于点R ,∴平面SMN 平面PAB =RQ ，又MN ⊂平面SMN ，//MN 平面PAB ，∴//MN RQ ，点O 在面ABC 上，过点O 的直线交AC ，BC 于点M ，N ，∴MN ⊂平面ABC ，又//MN 平面PAB ，平面ABC平面PAB AB =，∴//MN AB ， ∴//AB RQ ，故A 正确； 对于选项B ，当直线MN 平行于直线AB ，S 为线段PC 上靠近C 的三等分点，即13SC PC =，此时PC ⊥平面SRQ ，以下给出证明： 在正四面体P ABC -中，设各棱长为a ，∴ABC ，PBC ，PAC △，PAB △均为正三角形，点O 为ABC 的中心，//MN AB ，∴由正三角形中的性质，易得23CN CM a ==， 在CNS 中，23CN a =，13SC a =，3SCN π∠=，∴由余弦定理得，3SN a ==， ∴222249SC SN a CN +==，则SN PC ⊥， 同理，SM PC ⊥，又SM SN S =，SM ⊂平面SRQ ，SN ⊂平面SRQ ，∴PC ⊥平面SRQ ，∴存在点S 与直线MN ，使PC ⊥平面SRQ ，故B 正确； 对于选项C ，假设存在点S 与直线MN ，使()0PS PQ PR ⋅+=， 设QR 中点为K ，则2PQ PR PK +=，∴PS PK ⊥，即PC PK ⊥，()cos cos 0PC AB PC PB PA PC PB CPB PC PA CPA ⋅=⋅-=⋅∠-⋅∠=，∴PC AB ⊥，又易知AB 与PK 为相交直线，AB 与PK 均在平面PQR 上，∴PC ⊥平面PQR ，即PC ⊥平面PAB ，与正四面体P ABC -相矛盾，所以假设不成立， 故C 错误； 对于选项D ，易知点O 到面PBC ，面PAC ，面PAB 的距离相等，记为d ， 记PC 与平面PAB 所处角的平面角为α，α为常数，则sin α也为常数， 则点S 到PQR 的距离为sin PS α， 又13sin 234PQRSPQ PR PQ PR π=⋅=⋅ ∴()()1133sin sin sin 33412S PQR PQRV PS S PS PQ PR PQ PR PS ααα-=⋅=⋅⋅=⋅⋅， 又13sin 234PSRSPS PR PS PR π=⋅=⋅， 13sin 234PSQS PS PQ PS PQ π=⋅=⋅， 13sin 234PQRSPQ PR PQ PR π=⋅=⋅， ()3S PQR O PSR O PSQ O PQR V V V V d PS PR PS PQ PQ PR ----=++=⋅+⋅+⋅， ∴()33sin 1212PQ PR PS d PS PR PS PQ PQ PR α⋅⋅=⋅+⋅+⋅， ∴111sin d PQPRPSα++=为常数，故D 正确. 故选：ABD. 【点睛】本题考查了线面平行的性质定理、线面垂直的判定定理，考查了三棱锥体积的计算，考查了向量的运算，考查了转化能力与探究能力，属于较难题.8．在正方体1111ABCD A B C D -中，如图，,M N 分别是正方形ABCD ，11BCC B 的中心.则下列结论正确的是（ ）A ．平面1D MN 与11BC 的交点是11B C 的中点 B ．平面1D MN 与BC 的交点是BC 的三点分点 C ．平面1D MN 与AD 的交点是AD 的三等分点 D ．平面1D MN 将正方体分成两部分的体积比为1∶1 【答案】BC 【分析】取BC 的中点E ，延长DE ，1D N ，并交于点F ，连FM 并延长分别交,BC AD 于,P Q ，连1,D Q PN 并延长交11B C 与H ，平面四边形1D HPQ 为所求的截面，进而求出,,P Q H 在各边的位置，利用割补法求出多面体11QPHD C CD 的体积，即可求出结论.【详解】如图，取BC 的中点E ，延长DE ，1D N ，并交于点F ， 连接FM 并延长，设FM BC P ⋂=，FM AD Q ⋂=， 连接PN 并延长交11B C 于点H .连接1D Q ，1D H ，则平面四边形1D HPQ 就是平面1D MN 与正方体的截面，如图所示.111111////,22NE CC DD NE CC DD ==，NE ∴为1DD F ∆的中位线，E ∴为DF 中点，连BF ， ,,90DCE FBE BF DC AB FBE DCE ∴∆≅∆==∠=∠=︒， ,,A B F ∴三点共线，取AB 中点S ，连MS ，则12//,,23BP FB MS BP MS BC MS FS =∴==， 22111,33236BP MS BC BC PE BC ∴==⨯=∴=， E 为DF 中点，11//,233PE DQ DQ PE BC AD ∴===N 分别是正方形11BCC B 的中心，11113C H BP C B ∴==所以点P 是线段BC 靠近点B 的三等分点， 点Q 是线段AD 靠近点D 的三等分点， 点H 是线段11B C 靠近点1C 的三等分点. 做出线段BC 的另一个三等分点P '， 做出线段11A D 靠近1D 的三等分点G ，连接QP '，HP '，QG ，GH ，1H QPP Q GHD V V '--=， 所以111113QPHD C CD QPHQ DCC D V V V -==多面体长方体正方体 从而平面1D MN 将正方体分成两部分体积比为2∶1. 故选:BC.【点睛】本题考查直线与平面的交点及多面体的体积，确定出平面与正方体的交线是解题的关键，考查直观想象、逻辑推理能力，属于较难题.9．如图，在正方体ABCD﹣A1B1C1D1中，点P在线段B1C上运动，则（）A．直线BD1⊥平面A1C1DB．三棱锥P﹣A1C1D的体积为定值C．异面直线AP与A1D所成角的取值范用是[45°，90°]D．直线C1P与平面A1C1D6【答案】ABD【分析】在A中，推导出A1C1⊥BD1，DC1⊥BD1，从而直线BD1⊥平面A1C1D；在B中，由B1C∥平面A1C1D，得到P到平面A1C1D的距离为定值，再由△A1C1D的面积是定值，从而三棱锥P ﹣A1C1D的体积为定值；在C中，异面直线AP与A1D所成角的取值范用是[60°，90°]；在D 中，以D为原点，DA为x轴，DC为y轴，DD1为z轴，建立空间直角坐标系，利用向量法能求出直线C1P与平面A1C1D 6．【详解】解：在A中，∵A1C1⊥B1D1，A1C1⊥BB1，B1D1∩BB1＝B1，∴A1C1⊥平面BB1D1，∴A1C1⊥BD1，同理，DC1⊥BD1，∵A1C1∩DC1＝C1，∴直线BD1⊥平面A1C1D，故A正确；在B中，∵A1D∥B1C，A1D⊂平面A1C1D，B1C⊄平面A1C1D，∴B1C∥平面A1C1D，∵点P 在线段B 1C 上运动，∴P 到平面A 1C 1D 的距离为定值，又△A 1C 1D 的面积是定值，∴三棱锥P ﹣A 1C 1D 的体积为定值，故B 正确； 在C 中，异面直线AP 与A 1D 所成角的取值范用是[60°，90°]，故C 错误；在D 中，以D 为原点，DA 为x 轴，DC 为y 轴，DD 1为z 轴，建立空间直角坐标系， 设正方体ABCD ﹣A 1B 1C 1D 1中棱长为1，P （a ，1，a ），则D （0，0，0），A 1（1，0，1），C 1（0，1，1），1DA ＝（1，0，1），1DC ＝（0，1，1），1C P ＝（a ，0，a ﹣1）， 设平面A 1C 1D 的法向量(),,n x y z =，则1100n DA x z n DC y z ⎧⋅=+=⎪⎨⋅=+=⎪⎩，取x ＝1，得1,1,1n，∴直线C 1P 与平面A 1C 1D 所成角的正弦值为：11||||||C P n C P n ⋅⋅＝22(1)3a a +-⋅＝21132()22a ⋅-+，∴当a ＝12时，直线C 1P 与平面A 1C 1D 所成角的正弦值的最大值为6，故D 正确． 故选：ABD ．【点睛】求直线与平面所成的角的一般步骤：（1）、①找直线与平面所成的角，即通过找直线在平面上的射影来完成；②计算，要把直线与平面所成的角转化到一个三角形中求解； （2）、用空间向量坐标公式求解.10．如图所示，在棱长为1的正方体1111ABCD A B C D -中，过对角线1BD 的一个平面交棱1AA 于点E ，交棱1CC 于点F ，得四边形1BFD E ，在以下结论中，正确的是（ ）A ．四边形1BFD E 有可能是梯形B ．四边形1BFD E 在底面ABCD 内的投影一定是正方形C ．四边形1BFDE 有可能垂直于平面11BB D D D ．四边形1BFD E 面积的最小值为62【答案】BCD 【分析】四边形1BFD E 有两组对边分别平行知是一个平行四边形四边形；1BFD E 在底面ABCD 内的投影是四边形ABCD ；当与两条棱上的交点是中点时，四边形1BFD E 垂直于面11BB D D ；当E ，F 分别是两条棱的中点时，四边形1BFD E 6【详解】过1BD 作平面与正方体1111ABCD A B C D -的截面为四边形1BFD E ， 如图所示，因为平面11//ABB A 平面11DCC D ，且平面1BFD E 平面11ABB A BE =.平面1BFD E平面1111,//DCC D D F BE D F =，因此，同理1//D E BF ，故四边形1BFD E 为平行四边形，因此A 错误；对于选项B ，四边形1BFD E 在底面ABCD 内的投影一定是正方形ABCD ，因此B 正确； 对于选项C ，当点E F 、分别为11,AA CC 的中点时，EF ⊥平面11BB D D ，又EF ⊂平面1BFD E ，则平面1BFD E ⊥平面11BB D D ，因此C 正确；对于选项D ，当F 点到线段1BD 的距离最小时，此时平行四边形1BFD E 的面积最小，此时点E F 、分别为11,AA CC 的中点，此时最小值为162322=，因此D 正确. 故选：BCD【点睛】关键点睛：解题的关键是理解想象出要画的平面是怎么样的平面，有哪些特殊的性质，考虑全面即可正确解题.。

2023-2024学年重庆市十八中高一数学上学期第一次月考卷全卷满分150分，考试时间120分钟.一、单项选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．已知集合{}N 13A x x =∈-<<，{}22B x x =-≤<，则A B = （）A ．{}12x x -<<B ．{}0,1C ．{}1,2D ．{}0,1,22．命题“20000,560x x x ∃>-+>”的否定是（）A ．20,560x x x ∀≤-+≤B ．20,560x x x ∀>-+≤C ．2000R,560x x x ∃≤-+≤D ．20000,560x x x ∃>-+≤3．一个等腰三角形的底边长是6，腰长是一元二次方程27120x x -+=的一根，则此三角形的周长是（）A ．12B ．13C ．14D ．12或144．二次函数2y ax bx c =++（a ，b ，c 为常数且0a ≠）的图象如图所示，则一次函数y ax b =+与反比例函数cy x =的图象可能是（）A．B ．C ．D．5．在一个不透明的袋子里装有四个小球，球上分别标有6，7，8，9四个数字，这些小球除数字外都相同.甲、乙两人玩“猜数字”游戏，甲先从袋中任意摸出一个小球，将小球上的数字记为m ，再由乙猜这个小球上的数字，记为n.如果m ，n 满足1m n -≤，那么就称甲、乙两人“心领神会”，则两人“心领神会”的概率是（）A ．14B ．38C ．12D ．586．若{|1,Z}6k A x x k ==+∈，1{|,Z}32k B x x k ==+∈，21{|,Z}32k C x x k ==+∈，则这三个集合间的关系是（）A ．ABC ⊆⊆B ．A C B ⊆⊆C ．C B A ⊆⊆D ．C A B⊆⊆7．如图，在Rt ABC △中，90ACB ∠=︒，将ABC 绕顶点C 逆时针旋转得到A B C ''' ，M 是BC 的中点，P 是A B ''的中点，连接PM .若2BC =，30BAC ∠=︒，则线段PM 的最大值是（）A ．4B ．3C ．2D ．18．记{}max ,a b 为a ，b 两数的最大值，当正数x ，()y x y >变化时，24max ,()t x y x y ⎧⎫=⎨⎬-⎩⎭的最小值为（）A ．4B ．5C ．6D ．7二、多项选择题：本题共4小题，每小题5分，共20分.在每小题给出的四个选项中，有多项符合题目要求.全部选对的得5分，有选错的得0分，部分选对的得2分.9．如图中阴影部分所表示的集合是（）A ．()U N M ⋂ðB ．()U M N ⋂ðC ．()()UM N N⋃⋂ðD ．()()UM N N⋂⋂ð10．如图，在直角坐标系中，直线122y x =-.与坐标轴交于A 、B 两点，与双曲线2(0)ky x x =>交于点C ，过点C 作CD x ⊥轴，垂足为D ，且OA AD =，则以下结论中正确结论的有（）A ．ADB ADCS S =△△B ．当03x <<时，12y y <C ．如图，当3x =时，83EF =D ．当0x >时，1y 随x 的增大而增大，2y 随x 的增大而减小11．已知正实数x ，y 满足1x y +=，则（）A ．40x y xy +-≥B ．221x y +≥C ．111112x y ⎛⎫⎛⎫++≥ ⎪ ⎪⎝⎭⎝⎭D ．14912x y +≥+12．对于集合{}22,,M a a x y x y ==-∈∈Z Z.给出如下结论，其中正确的结论是（）A ．如果1a M ∈，2a M ∈，那么12a a M ∈B ．如果1a M ∈，2a M∈，那么12a a M+∈C ．如果{}21,B b b n n ==+∈N .那么B M⊆D ．若{}2,C c c n n ==∈N .对于c C ∀∈，则有c M∈三、填空题：本题共4小题，每小题5分，共20分.13．设a ，b ∈R ，若集合{1,,}0,,b a b a b a ⎧⎫+=⎨⎬⎩⎭，则2a b -=.14．如图，直径8AB =的半圆，绕B 点顺时针旋转30︒，此时点A 到了点A '，则图中阴影部分的面积是.15．已知两个命题p ：0xy ≥，q ：x y x y+=+，则p 是q 的条件（充分不必要，必要不充分，充要，既不充分又不必要）.16．对于一个各数位数字均不为零的四位自然数m ，若千位与百位数字之和等于十位与个位数字之和，则称m 为“一致数”.设一个“一致数”m abcd =满足8a ≤且1d =.将m 的千位与十位数字对调，百位与个位数字对调得到新数m '.并记()101m m F m '+=；一个两位数102N a b =+，将N 的各个数位数字之和记为()G N ；当()()243F mG N a k --=+（k 为整数）时，则所有满足条件的“一致数”m 中，满足()G N 为偶数时，k 的值为，m 的值为.四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.17．已知集合{}123,0A x a x a a =-<+，{}24B x x =-<<.(1)当2a =时，求A B ⋃；(2)若A B ⋂=∅，求实数a 的取值范围.18．2023年以来，某区把垃圾分类纳入积分，建立文明账户，市民以行动换积分，以积分转习惯.区政府为了了解4月份甲、乙两个社区居民垃圾换积分的情况，分别从甲、乙两个社区各抽取10人，记录下他们的积分（单位：分），并进行整理和分析（积分用x 表示，共分为4组：:70A x <；:7080B x ≤<，:8090C x ≤<，:90100D x ≤≤），下面给出了部分信息：甲社区10人的积分：47，56，68，71，83，83，85，90，91，94；乙社区10人的积分在C 组中的积分分数为：81，83，84，84；两组数据的平均数，中位数，众数如下表所示：社区平均数中位数众数甲76.883b 乙76.8a84乙社区积分等级扇形图根据以上信息，解答下列问题：(1)填空：=a ______，b =______，m =______；(2)根据以上数据，你认为哪个社区在此次垃圾分类换积分活动中表现更好，请说明理由（一条即可）；(3)若4月份甲社区有700人参与活动，乙社区有800人参与活动，请估计4月份甲、乙两个社区积分在80分以上（包括80分）的一共有多少人？19．已知集合{}22A x x =-≤≤，集合50x B x x -⎧⎫=≤⎨⎬⎩⎭.(1)设a 为实数，若集合{}321C x a x a =≤≤+，且()C A B ⊆ ，求a 的取值范围；(2)设m 为实数，集合12D x m x m ⎧⎫=≤≤+⎨⎬⎩⎭，若“()x A B ∈U ”是“x D ∈”的必要不充分条件，判断满足条件的m 是否存在，若存在，求m的取值范围；若不存在，请说明理由.20．如图，一沙尘暴中心在A 地南偏西60︒的方向的B 处，正迅速向正东方向移动，经过一段时间，沙尘暴中心位于A 地西南方向的C 处，且120BC =千米.(1)求A ，C 之间的距离（保留准确值）；(2)距沙尘暴中心200千米的范围为受沙尘暴影响的区域，沙尘暴中心由点C 处开始将沿南偏东75︒的CP方向移动，请说明A 地是否会受到这次沙尘暴的影响？ 1.41≈ 1.73≈ 2.45≈）.21．（1）已知11a b -≤+≤，11a b -≤-≤，求23a b +的取值范围；（2）若实数a ，b ，c 满足2226a b c ++=.试判断221112a b +++与21123c -+的大小并说明理由.22．如图，在平面直角坐标系中，抛物线()250y ax bx a =++≠与x 轴交于点()1,0A -，()5,0B ，与y轴交于点C.点D 是抛物线对称轴上的一点，纵坐标为-5，P 是线段BC 上方抛物线上的一个动点，连接BP ，DP .(1)求抛物线的解析式；(2)当BDP △的面积取最大值时，求点P 的坐标和BDP △的面积的最大值；(3)将抛物线()250y ax bx a =++≠沿着射线BD 平移，使得新抛物线经过点D.新抛物线与x 轴交于E ，F 两点（点E 在点F 左侧），与y 轴交于点G ，点M 是新抛物线上的一动点，点N 是坐标平面上一点，当以点E ，G ，M ，N 为顶点的四边形是矩形时，写出所有符合条件的点M 的坐标，并写出求解点M 的坐标的其中一种情况的过程.1．B【分析】先求集合A ，再根据交集运算求解.【详解】由题意可得：{}0,1,2A =，所以{}0,1A B = .故选：B.2．B【分析】特称命题的否定：存在改任意并否定原结论，即可写出原命题的否定.【详解】由特称命题的否定为全称命题，则原命题的否定为20,560x x x ∀>-+≤.故选：B 3．C【分析】解方程并结合三角形的性质可得腰长为4，进而可得结果.【详解】因为27120x x -+=，解得3x =或4x =，且336+=，不合题意；4486+=>，符合题意，可知：腰长为4，所以此三角形的周长是44614++=.故选：C.4．A【分析】根据二次函数的开口方向、对称轴的位置、在纵轴的交点坐标的正负判断,,a b c 的正负性，再结合反比例函数、一次函数的图象特征逐一判断即可.【详解】由二次函数的图象可知：开口向上，因此0a >；对称轴为002bx b a =->⇒<，当0x =时，0y c =<；因为0c <，所以反比例函数cy x =的图象在二、四象限，排除BC ；因为0a >，0b <，所以一次函数y ax b =+的图象经过第一、三、四象限，故排除D ，故选：A 5．D【分析】根据古典概型的计算公式，结合绝对值不等式进行求解即可.【详解】根据题意，m ，n 的情况如下：()()()()()()()()6,6,6,7,6,8,6,9,7,6,7,7,7,8,7,9,()()()()()()()()8,6,8,7,8,8,8,9,9,6,9,7,9,8,9,9,共16种情况，其中m ，n 满足1m n -≤的情况如下：()()()()()()()()()()6,6,6,7,7,6,7,7,7,8,8,7,8,8,8,9,9,8,9,9,共10种情况，所以两人“心领神会”的概率是105168=，故选：D 6．C【分析】分析给定的三个集合的约束条件，探讨它们的关系即可判断作答.【详解】依题意，6(3)3{|,Z}{|,Z}66k k A x x k x x k +++==∈==∈，23{|,Z}6k B x x k +==∈，43223{|,Z}{|,Z}66k k C x x k x x k +⨯+==∈==∈，而{|3,Z}Z x x k k =+∈=，{偶数}{|2,Z}x x k k ==∈，因此集合C 中的任意元素都是集合B 中的元素，即有C B ⊆，集合B 中的每一个元素都是集合A 中的元素，即B A ⊆，所以C B A ⊆⊆.故选：C 7．B【分析】根据旋转变换的性质，结合三角形三边关系进行求解即可.【详解】在Rt ABC △中，90ACB ∠=︒，2BC =，30BAC ∠=︒，所以4AB =，因为M 是BC 的中点，所以112CM BC ==，因为ABC 绕顶点C 逆时针旋转得到A B C ''' ，所以4A B ''=，90A CB ''∠=︒，因为P 是A B ''的中点，所以122PC A B ''==，由三角形三边关系，得CP CM PM +>，当旋转到,,P C M 在一条直线上，且C 位于,P M 之间时，PM 有最大值，最大值为213+=，故选：B8．A【分析】根据题中定义，结合基本不等式进行求解即可.【详解】由24max ,()t x y x y ⎧⎫=⎨⎬-⎩⎭可得：2t x ≥，4()t y x y ≥-，所以有242()t x y x y ≥+-，因为x ，y 是正数，且x y >，所以224416()2y x y x y x y ≥=-+-⎛⎫ ⎪⎝⎭，当且仅当y x y =-时取等号，即当2x y =时取等号，于是有222416284()t x x t y x y x ≥+≥+≥=⇒≥-，当且仅当2216x x =时取等号，即当2,1x y ==时取等号，所以t 的最小值为4，故选：A【点睛】关键点睛：本题的关键是理解{}max ,a b 的含义，由24max ,()t x y x y ⎧⎫=⎨⎬-⎩⎭得到2t x ≥，4()t y x y ≥-.9．AD【分析】根据Venn 图，结合集合运算的概念即可得出答案.【详解】A 选项：U M =+①②ð，则U N M = ②ð，故A 正确；B 选项：U N =+④①ð，则U M N = ④ð，故B 错误；C 选项：()①= U M N ð，则()()UM N N ⋃⋂=∅ð，故C 错误；D 选项：()②+④①=+ U M N ð，()UM N N ⎡⎤⋂⋂=⎣⎦②ð，故D 正确.故选：AD.10．AC【分析】A 项，通过证明OBA CDA ≅ 即可得出结论；B 项，利用函数图象的交点即可得出结论；C 项，计算出3x =时12,y y的值，即可求出EF 的长；D 项，根据函数图象即可得出两函数增减性.【详解】由题意，A 选项，对于直线122y x =-,令0x =,得到2y =；令0y =,得到1x =，∴(1,0),(0,2)A B -,即1,2OA OB ==,在OBA △和CDA 中,90,,AOB ADC OAB DAC OA AD︒∠=∠=∠=∠=∴()OBA CDA AAS ≅ ∴()2,1,2,2CD OB OA AD C ====，∴ADB ADCS S =△△(同底等高三角形面积相等），A 正确；B 项，把点C 坐标代入反比例解析式得：4k =,即24y x =,由函数图象得:当02x <<时,12y y <，B 错误；C 项，当3x =时,1244,3y y ==,∴43348EF ==-，C 正确；D 项，当0x >时,1y随x 的增大而增大,2y 随x 的增大，D 错误；故选：AC.11．AD2x y +≤，即14≤xy ，所以选项A 正确；而222()122x y x y ++≥=可判断B 错误；将1111x y ⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭展开并结合14≤xy 可知C 错误；观察D 项分母可知12x y ++=，利用基本不等式“1”的妙用求最值，即可知D 正确.【详解】对于A2x y+≤，即14≤xy ，所以41xy x y ≤=+，即40x y xy +-≥；当且仅当12x y ==时，等号成立，故A 正确；对于B ，根据不等式222()122x y x y ++≥=，当且仅当12x y ==时，等号成立；所以B 错误；对于C ，1111112111119x y x y x y xy xy xy xy ⎛⎫+⎛⎫++=+++=++=+≥ ⎪ ⎪⎝⎭⎝⎭，当且仅当12x y ==时，等号成立；故C 错误；对于D ，根据1x y +=，观察分母可知12x y ++=为定值，则1411411419(1)145121212y x x y x y x y x y ⎛⎫⎛⎫⎛⎫++=+++=+++≥+= ⎪ ⎪ ⎪ ⎪+++⎝⎭⎝⎭⎝⎭，当且仅当21,33x y ==时，等号成立；故D 正确.故选：AD.12．AC【分析】对于A ：设2222111222,a x y a x y =-=-，则()()221212121221x x y y x y x a a y =+-+，进而分析判断；对于B ：先说明2M ∉，再取特值121a a ==，分析判断；对于C ：令1x n =+，,y n n =∈Z ，可知对任意b B ∈，均有b M ∈，所以B M ⊆，故C 正确；对于D ：取特值121a a ==，分析判断.【详解】对于选项A ：因为1a M ∈，2a M∈，设22221112221212,,,,,a x y a x y x x y y =-=-∈Z ，则()()()()()()222222221222222112212121221121212221x y x y x x y y x y x y x x y x y y a y x a =--=+-+=+-+，因为1212,,,x x y y ∈Z ，则12121221,x x y y x y x y +∈+∈Z Z，所以12a a M ∈，故A 正确；对于选项B ：因为2222a x y x y=-=-，不妨设,,x y x y ≥∈Z，若x y=，则22a x y =-=；若1x y =+，则()2222121a x y y y y =-=+-=+为奇数；若2x y ≥+，则()()22222414a x y y y y =-≥+-=+≥；综上可知：2M ∉.显然22101M -=∈，令121a a ==，则122a a M +=∉，故B 错误；对于选项C ：令1x n =+，,y n n =∈Z ，则()2222121b x y n n n M =-=+-=+∈，即对任意b B ∈，均有b M ∈，所以B M ⊆，故C 正确；对于选项D ：由选项B 可知：2,2C M ∈∉，故D 错误.故选：AC.13．0【分析】利用集合相等以及0a ≠，可得0a b +=，即1ba =-，代入原式可得,ab 的值，进而求出答案．【详解】由题意可知：0a ≠，因为{1,,}0,,b a b a b a ⎧⎫+=⎨⎬⎩⎭，则0a b +=，可得1b a =-，则{}{1,0,}0,1,a b =-，可得11a b =-⎧⎨=⎩，且满足0a b +=，所以()22110a b -=--=.故答案为：0.14．16π3【分析】由题意可知：阴影部分为以B 点为圆心，AB 为半径的扇形和以A B '为直径的半圆，减去以AB 为直径的半圆，进而结合扇形面积公式运算求解.【详解】由题意可知：阴影部分为以B 点为圆心，AB 为半径的扇形和以A B '为直径的半圆，减去以AB 为直径的半圆，且AB A B '=，即两个半圆的面积相等，则阴影部分的面积即为以B 点为圆心，AB 为半径的扇形得面积，为23016ππ83603︒⨯⨯=︒.故答案为：16π3.15．充要【分析】根据充分条件和必要条件的定义分析判断即可【详解】当0xy ≥时，若,x y 中至少有一个为零，则x y x y+=+成立，若0,0x y >>，则x y x y x y +=+=+，若0,0x y <<，则x y x y x y +=--=+，综上，当0xy ≥时，x y x y+=+成立，故充分性成立；当x y x y+=+时，()()22x y x y +=+，即222222x xy y x xy y ++=++，整理得xy xy=，所以0xy ≥成立，故必要性成立；所以p 是q 的充要条件.故答案为：充要16．6±2231【分析】设一个“一致数”m abcd =满足8a ≤且1d =，得出()()243F m G N a k --=+，然后分类讨论即可求解.【详解】解：设一个“一致数”m abcd =满足18a ≤≤且1,110d a b c a b =+=+⇒+≤，则1000100101m a b c =+++，100010010m c a b '=+++，所以10101011010101()10101101101m m a b c F m a b c '++++===+++，一个两位数102N a b =+，将N 的各个数位数字之和记为()G N ，则()()42529b G N a b b G N a b ≤=+≥=+-时，，时，，因为()()243F mG N a k --=+，即2210101224431591b a b c a b a k k a b +++---=≤=++-，时，，22101012+94315935a b c a b a k k a b b +++---=+=+-≥时，，，因为满足()G N 为偶数时，则5b ≥时a 奇为数，4b ≤时a 为偶数，逐项代入检验可得：当2,2a b ==时，则2366,3k k c ==±=，，当8,4;5,8a b a b ====时，则214410k a b =+>，，故舍去；所以2231m =.故答案为：6±；2231.【点睛】关键点睛：本题的关键是将m 表示成1000100101a b c +++，然后再分类讨论.17．(1){}27x x -<<(2)[5,)+∞【分析】（1）根据集合并集的定义进行求解即可；（2）根据集合交集运算的性质进行求解即可.【详解】（1）因为2a =，所以{}17A x x =<<，而{}24B x x =-<<，所以{}27A B x x ⋃=-<<；（2）因为A B ⋂=∅，所以14a -≥，或232a +≤-，由145a a -≥⇒≥，显然满足0a >；由52322a a +≤-⇒≤-，而0a >，所以不存在这种情况，综上所述：实数a 的取值范围[5,)+∞18．(1)83.5,83,30a b m ===(2)乙社区在此次垃圾分类换积分活动中表现更好，理由见解析(3)980【分析】（1）找出甲社区中出现次数最多的数据，即可求得b 的值，根据乙社区的扇形统计图，计算出,A B 两组的人数，再结合C 组的人数可求出a 的值，利用D 组的数除以10可求出m 的值，（2）从中位数和众数的解度进行分析即可，（3）分别利用总数乘以甲乙两个社区积分在80分以上所占的百分比，将积相加即可.【详解】（1）因为甲社区中出现次数最多的数据为83，所以83b =，由乙社区的扇形统计图可得乙社区A 组人数为1010%1⨯=，B 组人数为1020%2⨯=人，因为乙社区10人的积分在C 组中的积分分数为：81，83，84，84，所以乙社区的积分从小到大排列，第5个和第6个数据分别为83，84，所以1(8384)83.52a =⨯+=，因为乙社区D 组人数为101243---=人，所以D 组人数所占的百分比为3100%30%10⨯=，所以30m =，（2）乙社区在此次垃圾分类换积分活动中表现更好，理由如下：因为甲乙两个社区积分的平均数相同，但是乙社区的中位数和众数均比甲社区高，所以乙社区在此次垃圾分类换积分活动中表现更好，（3）因为甲社区积分在80分以上（包括80分）的人数所占的比例为60.610=，乙社区积分在80分以上（包括80分）的人数所占的比例为70.710=，所以4月份甲、乙两个社区积分在80分以上（包括80分）的一共有0.67000.7800980⨯+⨯=人.19．(1)10,(1,)2⎛⎤⋃+∞ ⎥⎝⎦(2)92,2⎡⎤-⎢⎥⎣⎦【分析】（1）化简集合，通过()C A B ⊆ 即可分类讨论求出a 的取值范围；（2）求出A B ⋃，利用“()x A B ∈U ”是“x D ∈”的必要不充分条件即可求出m 的取值范围.【详解】（1）由题意，化简集合，{}22A x x =-≤≤，{}05B x x =<≤，∴(0,2]A B ⋂=，在{}321C x a x a =≤≤+中，()C A B ⊆ ，当C =∅时,2131a a a +<⇒>,满足题意；当C ≠∅时,1a ≤，此时21210302a a a +≤⎧⇒<≤⎨>⎩综上，a 的取值范围为10,(1,)2⎛⎤⋃+∞ ⎥⎝⎦.（2）由题意及（1）得，{}22A x x =-≤≤，{}05B x x =<≤，∴[2,5]A B =-U ,在12D x m x m ⎧⎫=≤≤+⎨⎬⎩⎭中，“()x A B ∈U ”是“x D ∈”的必要不充分条件，∴2152m m ≥-⎧⎪⎨+≤⎪⎩(等号不同时成立)922m ⇒-≤≤∴满足条件的m 存在,取值范围是92,2⎡⎤-⎢⎥⎣⎦.20．(1)A ，C之间的距离60千米(2)A 地不会受到这次沙尘暴的影响【分析】（1）过A 作AD BD ⊥，垂足为D ，设AC m =千米，可得CD千米，BD 千米，再结合题意列式求解即可；（2）过A 作AE CP ⊥，垂足为E ，可得200.4AE ≈千米，对比分析即可.【详解】（1）过A 作AD BD ⊥，垂足为D ，设AC m =千米，在Rt ACD △中，可知：45CAD ∠=︒，可得2sin 2CD AD AC CAD m==∠=千米，在Rt △ABD 中，可知：60BAD ∠=︒，可得tan BD AD BAD =∠=千米，由题意可得：BD CD BC -=，即6212022m m -=，解得60m =，所以A ，C之间的距离60千米.（2）过A 作AE CP ⊥，垂足为E ，在Rt ACE 中，可知：60ACE ∠=︒，可得(sin 60303200.4AE AC ACE =∠=⨯≈千米，因为200.4200>，所以A 地不会受到这次沙尘暴的影响.21．（1）[]3,3-；（2）22211111223a b c +>-+++，理由见详解【分析】（1）根据题意可得()()512322a b a b a b +=+--，结合不等式性质运算求解；（2）令2221,2,3m a n b t c =+=+=+，可得112m n t++=，根据“1”的应用结合基本不等式运分析判断.【详解】（1）设()()()()23a b x a b y a b a x y b x y +=++-=++-，其中,x y ∈R ，则23x y x y +=⎧⎨-=⎩，解得5212x y ⎧=⎪⎪⎨⎪=-⎪⎩，即()()512322a b a b a b ⎛⎫+=++-- ⎪⎝⎭，因为11a b -≤+≤，11a b -≤-≤，则()555222a b -≤+≤，()111222a b -≤--≤，可得3233a b -≤+≤，所以23a b +的取值范围为[]3,3-；（2）令2221,2,3m a n b t c =+=+=+，则2221,2,3m a n b t c -=-=-=，可得()()()22212366a b c m n t m n t ++=-+-+-=++-=，即112m n t++=，则111111131212m n t n m t m n t m n t m n t m n m t t n ⎡⎤++⎛⎫⎛⎫⎛⎫⎛⎫++=++=++++++ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦133124⎛⎫≥+++= ⎪ ⎪⎝⎭，当且仅当n mm n t m m t t n n t ⎧=⎪⎪⎪=⎨⎪⎪=⎪⎩，即2224,3,2,1m n t a b c ======时，等号成立，可得2221111113112342m n t a b c ++=++≥>+++，即22211111223a b c +>-+++.22．(1)245y x x =-++(2)7299,636P ⎛⎫ ⎪⎝⎭，52924(3)()1,4-，()2,5-，⎫⎪⎪⎝⎭或⎫⎪⎪⎝⎭【分析】（1）将()1,0A -，()5,0B 代入抛物线即可得出解析式；（2）过点P 作//PQ BD ，得出PQ ，PB 的解析式，即可求出点P 的坐标和BDP △的面积的最大值；（3）求出平移二次函数的解析式，设出点M 坐标，构造矩形，即可求出点M 的坐标.【详解】（1）由题意，在()250y ax bx a =++≠中，()1,0A -，()5,0B 501,,255504a b a a b b ⎧-+==-⎧⎨⎨++==⎩⎩∴抛物线的函数表达式是：245y x x =-++.（2）由题意及（1）得，如下图1，抛物线的对称轴是直线1522x -+==，(2,5)D ∴-，(5,0)B ，∴直线BD 的解析式是:52533y x =-，过点P 作//PQ BD ，∴可设PQ 的解析式是:53y x b=+，由25453x x x b -++=+得27(5)03x x b -+-=，BPD 面积最大，∴方程由两个相等实数根，2706x ⎛⎫∴-= ⎪⎝⎭，7,6x ∴=当76x =时，277299456636y ⎛⎫=-+⨯+= ⎪⎝⎭，7299,636P ⎛⎫∴ ⎪⎝⎭，如图2，(5,0), B ∴直线PB 的解析式是:136566y x =-+，∴当2x =时，132y =，1323(5)22DE ∴=--=，1237529522624BDP S ⎛⎫∴=⨯⨯-=⎪⎝⎭ ，即BDP △的最大面积是52924.（3）由题意，（1）及（2）得，在245y x x =-++中，(5,0),(2,5)B D -平移后的关系式是2(1)4y x =-++，2(1)40,x ∴-++=解得：1x =或3-，∴(3,0),(0,3)E G -，如图3，当点M 落在抛物线2(1)4y x =-++的顶点(1,4)-时，90EGM ︒∠=，∵//,MN EG MN EG =，∴1(1,4)M -，NE ∴的解析式是3y x =--，∴2(1)43x x -++=--，解得：3x =-（舍）或2∴2(2,5)(5,2)M N '--,，当EG 是对角线时，设点()21,23M m m m --+，由22211M E M G EG +=得()()22222222(3)23233x x x x x x++--+++--=+，∴1234113,0,,22x x x x -+--=-===，∴点M 坐标为()1,4-，()2,5-，⎫⎪⎪⎝⎭或⎫⎪⎪⎝⎭.。

立体几何周练命题人---王利军一、选择题（每小题5分，共60分）1、线段AB 在平面α内，则直线AB 与平面α的位置关系是A 、AB α⊂ B 、AB α⊄C 、由线段AB 的长短而定D 、以上都不对2、下列说法正确的是A 、三点确定一个平面B 、四边形一定是平面图形C 、梯形一定是平面图形D 、平面α和平面β有不同在一条直线上的三个交点3、垂直于同一条直线的两条直线一定A 、平行B 、相交C 、异面D 、以上都有可能 4、在正方体1111ABCD A B C D -中，下列几种说法正确的是A 、11AC AD ⊥B 、11DC AB ⊥ C 、1AC 与DC 成45角D 、11AC 与1B C 成60角5、若直线l ∥平面α，直线a α⊂，则l 与a 的位置关系是A 、l ∥aB 、l 与a 异面C 、l 与a 相交D 、l 与a 没有公共点6、下列命题中：（1）、平行于同一直线的两个平面平行；（2）、平行于同一平面的两个平面平行； （3）、垂直于同一直线的两直线平行；（4）、垂直于同一平面的两直线平行.其中正确的个数有A 、1B 、2C 、3D 、47、在空间四边形ABCD 各边AB BC CD DA 、、、上分别取E F G H 、、、四点，如果与EF GH 、能相交于点P ，那么 A 、点必P 在直线AC 上 B 、点P 必在直线BD 上C 、点P 必在平面ABC 内D 、点P 必在平面ABC 外 8、a ，b ，c 表示直线，M 表示平面，给出下列四个命题：①若a ∥M ，b ∥M ，则a ∥b ；②若b ⊂M ，a ∥b ，则a ∥M ；③若a ⊥c ，b ⊥c ，则a ∥b ；④若a ⊥M ，b ⊥M ，则a ∥b .其中正确命题的个数有A 、0个B 、1个C 、2个D 、3个 9、一个棱柱是正四棱柱的条件是A 、底面是正方形，有两个侧面是矩形B 、底面是正方形，有两个侧面垂直于底面C 、底面是菱形，且有一个顶点处的三条棱两两垂直D 、每个侧面都是全等矩形的四棱柱10、在棱长为1的正方体上，分别用过共顶点的三条棱中点的平面截该正方体,则截去8个B 1C 1A 1D 1BACD三棱锥后,剩下的凸多面体的体积是 A 、23 B 、76 C 、45 D 、5611、已知二面角AB αβ--的平面角是锐角θ，α内一点C 到β的距离为3，点C 到棱AB的距离为4，那么tan θ的值等于A 、34B 、35C D12、如图:直三棱柱ABC —A 1B 1C 1的体积为V ，点P 、Q 分别在侧棱AA 1和CC 1上，AP=C 1Q ，则四棱锥B —APQC 的体积为A 、2VB 、3VC 、4VD 、5V13．设α、β、r 是互不重合的平面，m ，n 是互不重合的直线，给出四个命题： ①若m ⊥α，m ⊥β，则α∥β ②若α⊥r ，β⊥r ，则α∥β ③若m ⊥α，m ∥β，则α⊥β ④若m ∥α，n ⊥α，则m ⊥n 其中正确命题的个数是（ ）A ．1B ．2C ．3D ．414.△ABC 是边长为1的正三角形，那么△ABC 的斜二测平面直观图C B A '''∆的面积为（ ）A ．43 B ．83 C ．86 D ．166 15．设正方体的表面积为242cm ，一个球内切于该正方体，那么这个球的体积是 （ ） A ．π343cm B ．π63cm C ．π383cm D ．π3323cm16．四面体S ABC -中，各个侧面都是边长为a 的正三角形，,E F 分别是SC 和AB 的中点，则异面直线EF 与SA 所成的角等于（ ） A ．090 B ．060 C ．045 D ．030 17．三个平面把空间分成7部分时，它们的交线有（ ）Ａ．1条 Ｂ．2条 Ｃ．3条 Ｄ．1条或2条18．在长方体1111ABCD A B C D -，底面是边长为2的正方形，高为4，QPC'B'A'C BA则点1A 到截面11AB D 的距离为( )A ．83 B ． 38 C ．43 D ． 3419．直三棱柱111ABC A B C -中，各侧棱和底面的边长均为a ，点D 是1CC 上任意一点，连接11,,,A B BD A D AD ，则三棱锥1A A BD -的体积为（ ）A ．361a B ．3123a C ．363a D ．3121a 20．下列说法不正确的．．．．是（ ） A ．空间中，一组对边平行且相等的四边形是一定是平行四边形；B ．同一平面的两条垂线一定共面；C ．过直线上一点可以作无数条直线与这条直线垂直，且这些直线都在同一个平面内；D ．过一条直线有且只有一个平面与已知平面垂直. 二．解答题1．(本题满分12分) 在三棱锥V —ABC 中，VA=VB=AC=BC=2，AB=32，VC=1，求二面角V —AB —C 的大小．3主视图左视图俯视图ACDQ DBPCANM2．已知某几何体的三视图如下图所示，其中俯视图为正三角形,设D为AA1的中点。

高一年下学期期末考数学科试卷（2018.18）考试时间：120分钟 试卷总分：150分 本试卷分第I 卷和第II 卷两部分 第I 卷（选择题，共60分）一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求，每小题选出答案后，请把答案填写在答题卡相应位置上．．．．．．．．．．．．．．．。

1.某校高一共有10个班，编号1至10，某项调查要从中抽取三个班作为样本，现用抽签法抽取样本，每次抽取一个号码，共抽3次，设五班第一次被抽到的可能性为a ，第二次被抽到的可能性为b ，则（ ） A.103=a ，92=b B. 101=a ，91=b C. 103=a ，103=b D. 101=a ，101=b 2.下列事件为随机事件的是（ ）A.平时的百分制考试中，小强的考试成绩为118分B.边长为a ，b 的长方形面积为abC.100个零件中2个次品，98个正品，从中取出2个，2个都是次品D.抛一个硬币，落地后正面朝上或反面朝上3.某班级有50名学生，其中有30名男生和20名女生，随机询问了该班五名男生和五名女生在某次数学测验中的成绩，五名男生的成绩分别为86，94，88，92，90，五名女生的成绩分别为88，93，93，88，93．下列说法一定正确的是（ ）A.抽样方法是一种分层抽样B.该班级男生成绩的平均数必小于该班级女生成绩的平均数C.抽样方法是一种系统抽样D.这五名女生成绩的标准差必小于这五名男生成绩的标准差 4.我国古代数学名著《九章算术》有“米谷粒分”题：粮仓开仓收粮，有人送来米5319石，验得米内夹谷，抽样取米一把，数得252粒内夹谷28粒，则这批米内夹谷约为 （ ） A.490石B. 540石C.590石D. 640石5.如图，设A ，B 两点在河的两岸，一测量者在A 所在的同侧河岸边选定一点C ，测出AC 的距离为50 m ，∠ACB ＝45°，∠CAB ＝118°后，就可以计算出A ，B 两点的距离为( )． A. 50 3 mB. 50 2 mC. 25 2 mD. 2522m6.在样本的频率分布直方图中，共有8个小长方形，若最后一个小长方形的面积等于其它7个小长方形的面积和的41，且样本容量为200，则第8组的频数为（ ） A. 40B. 50C. 0.2D. 0.257.对某同学的6次数学测试成绩（满分100分）进行统计，作出如图所示茎叶图，给出关于该同学数学成绩的以下说法：①极差是12；②众数是85；③中位数是84；④平均数是85， 正确的是（ ） A. ③④B.②④C.①③D. ①②8.下列表格所示的五个散点，原本数据完整，且利用最小二乘法求得这五个散点的线性回归直线方程为 0.8155y x =-，后因某未知原因第5组数据的y 值模糊不清，此位置数据记为m （如下表所示），则利用回归方程可求得实数m 的值为（ ）A 、8B 、8.1C 、8.2D 、8.39.在Excel 中产生区间上均匀随机数的函数为“rand( )”，在用计算机模拟估计函数x y cos =的图象和x 轴在区间[]ππ,-上部分围成的图形面积时，随机点),(11b a 与该区域内的点),(b a 的坐标变换公式为( ) A.112),1(b b a a =-=πB. )1(2),1(211-=-=b b a a πC. 12,211+=-=b b a a ππD. 12,211-=+-=b b a a ππ10.阅读如图所示的语句：当输入的m=168，n=72时，输出的结果用5进制表示是（ ） A.)5(143 B.)5(44 C.)5(22D.)5(6第10题11.在以原点O 为圆心，1为半径的单位圆上有两点B A 、，︒=∠120AOB ，点C 是劣弧 AB（较短的弧）上一点，射线OC 与线段AB 交于点M ，则OM B ∆为钝角三角形的概率（ ）A.21B.32 C.43 D.65 12.设函数()f x 的定义域为R , ()()()(),2f x f x f x f x -==-, 当[]0,1x ∈时,()3f x x =, 则函数()()()cos g x x f x π=-在区间(]1,3-上的所有零点的和为（ ）.A ． 11B ．12C ． 7D ．8第II 卷（非选择题，共90分）二、填空题 ：本大题共4小题，每小题5分，共20分，请把答案填在答题卡的横线上．．．．．．．．．．．．．。

立体几何（1）1.设m,n 是不同的直线，,αβ是不同的平面，下列命题中正确的是（B ）A ．若m//,,,n m n αβαβ⊥⊥⊥则B ．若m//,,//,n m n αβαβ⊥⊥则C ．若m//,,,//n m n αβαβ⊥⊥则D ．若m//,,//,//n m n αβαβ⊥则2.直三棱柱111ABC A B C -中，090=∠BCA ，M N 、分别是1111A B A C 、的中点，1BC CA CC ==，则BM 与AN 所成的角的余弦值为（D ）A ．110B ．25C D 3.在三棱锥ABC S -中，底面是边长为1的等边三角形，侧棱长均为2，⊥SO 底面ABC ，O 为垂足，则侧棱SA 与底面ABC 所成角的余弦值为（D ）A ．23B ．21C ．33D ．634．如图，正方体1111ABCD A B C D -的棱长为1，点M 是面对角线1A B 上的动点，则1AM MD + 5．在正四面体A －BCD 中，棱长为4，M 是BC 的中点，点P 在线段AM 上运动(P 不与A ，M 重合)，过点P 作直线l ⊥平面ABC ，l 与平面BCD 交于点Q ，给出下列命题：①BC ⊥平面AMD ； ②Q 点一定在直线DM 上； ③V C －AMD ＝4 2.其中正确的是_①② ______6.如图是一个空间几何体的三视图，则该几何体的外接球的表面积为__.8π __7,已知两异面直线a ，b 所成的角为π3，直线l 分别与a ，b 所成的角都是θ，则θ的取值范围是________．[答案] [π6，π2]1． 若正四面体S —ABC 的面ABC 内有一动点P 分别到平面SAB 、平面SBC 、平面SAC 的距离成等差数列，则点P 的轨迹是（A ）A ．一条线段B ．一个点C ．一段圆弧D ．抛物线的一段8,如图，在平行四边形ABCD 中，CD ＝1，∠BCD ＝60°，且BD⊥CD，正方形ADEF 和平面ABCD 成直二面角，G ，H 分别是DF ，BE 的中点．(1)求证：BD⊥平面CDE ；(2)求证：GH∥平面CDE ； (3)求三棱锥D －CEF 的体积．答案：(1)证明：平面ADEF⊥平面ABCD ，交线为AD ， ∵ED ⊥AD ，∴ED ⊥平面ABCD.∴ED⊥BD. 又∵BD⊥CD，CD ∩ED ＝D ，∴BD ⊥平面CDE. (2)证明：连接EA ，则G 是AE 的中点， 在△EAB 中，GH ∥AB ，又∵AB∥CD，∴GH ∥CD.又∵GH 平面CDE ，∴GH ∥平面CDE. (3)解析：设Rt △BCD 中BC 边上的高为h ，依题意：12×2×h ＝12×1×3，∴h ＝32，即点C 到平面DEF 的距离为32. ∴V D －CEF ＝V C －DEF ＝13×12×2×2×32＝33.9,已知正三棱柱ABC －A 1B 1C 1的各棱长都是4，E 是BC 的中点，动点F 在侧棱CC 1上，且不与点C 重合．(1)当CF ＝1时，求证：EF ⊥A 1C ；(2)设二面角C －AF －E 的大小为θ，求tan θ的最小值．9,解法1：(1)建立如图3所示的空间直角坐标系，则由已知可得A (0,0,0)，B (23，2,0)，C (0,4,0)，A 1(0,0,4)，E (3，3,0)，F (0,4,1)，于是CA 1→＝(0，－4,4)，EF →＝(－3，1,1)，则CA 1→·EF →＝(0，－4,4)·(－3，1,1)＝0－4＋4＝0，故EF ⊥A 1C .(2)设CF ＝λ，(0<λ≤4)，平面AEF 的一个法向量为m ＝(x ，y ，z )，则由(1)得F (0,4，λ)，AE →＝(3，3,0)，AF →＝(0,4，λ)，于是由m ⊥AE →，m ⊥AF →可得⎩⎪⎨⎪⎧m ·AE →＝0，m ·AF →＝0，即⎩⎨⎧3x ＋3y ＝0，4y ＋λz ＝0.取m ＝(3λ，－λ，4)．又由直三棱柱的性质可取侧面AC 1的一个法向量为n ＝(1,0,0)， 于是由θ为锐角可得cos θ＝|m ·n ||m |·|n |＝3λ2λ2＋4，sin θ＝λ2＋162λ2＋4， 所以tan θ＝λ2＋163λ＝13＋163λ2. 由0<λ≤4，得1λ≥14，即tan θ≥13＋13＝63， 故当λ＝4，即点F 与点C 1重合时，tan θ取得最小值63. 10,如图，在ABC ∆中，090C ∠=，AC BC a ==，点P 在边AB 上，设(0)AP PB λλ=>，过点P 作//PE BC 交AC 于E ，作//PF AC 交BC 于F 。

重庆市第十八中学2023-2024学年高一下学期期中考试数学试题考试说明：1．考试时间120分钟 2．试题总分150分 3．试卷页数2页一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1. 的三个内角所对边的长分别为，若，，，则（ ）A. B.C. 4D.2. 复数的共轭复数等于（ ）A. B. C. D. 3. 若，是空间两条不同的直线，，是空间两个不同的平面，那么下列命题成立的是（ ）A 若，，则 B. 若，，则C. 若，，则 D. 若，，则4. 如图所示是水平放置的的直观图，其中，则原是一个（ ）A. 等边三角形B. 直角三角形C. 等腰三角形D. 等腰直角三角形5. 已知分别是三内角的对边，且满足，则的形状是（ ）A. 等腰三角形B. 直角三角形C. 等腰或直角三角形D. 等腰直角三角形6. 在边长为2的正方形中，是的中点，点在线段上运动，则的取值范围是（ ）A. B. C. D.7. 已知是平面内的一点，若，，且向量在向量上的投影向量.ABC V ,,A B C ,,a b c 3cos 5B =5c =3a =b =()32z i i =-z 23i--23i-+23i-23i+m n αβ//m α//n α//m n//αβm α⊂//m β//m α//αβ//m β//m αn ⊂α//m nABC V 1A O B O C O ''''''===ABC V ,,a b c ABC V ,,A B C sin cos a C a C b c +=+ABC V ABCD M BC E AB EM EC ⋅[]2,6[]28,[]0,2[]0,4M ABC AB AC ⊥ 2AM AB AC =+ BA BC为，则（ ）A. B. C. D. 8. 在中，的角平分线交于点，若，，则的面积的最小值为（ ）A.B. C.D.二、选择题：本题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求．全部选对的得6分，部分选对的得部分分，有选错的得0分．9. 已知平面向量，，且，则（ ）A. B. C. D. 10. 如图所示，在正方体中，，分别为棱，的中点，则下列四个结论正确的是（ ）A. 直线与是相交直线B. 直线与是平行直线C. 直线与是异面直线D. 直线与是异面直线11. 南宋数学家秦九韶在《数书九章》中提出“三斜求积术”，即以小斜幂，并大斜幂，减中斜幂，余半之，自乘于上：以小斜幂乘大斜幂，减上，余四约之，为实：一为从隅，开平方得积可用公式（其中为三角形的三边和面积）表示．在中，分别为角所对的边，若，则下列命题正确的是（）A B. C. 面积的最大值是 D..34BC u uu r MAC ∠=15306075ABC V ABC ∠BD AC D 2BD =π3ABC ∠=ABC V ()2,a m = ()1,1b =-22a b a b +=- 2m =π,3a b =a b⊥ a =1111ABCD A B C D -M N 11C D 1C C AM 1CC AM BN BN 1MB AM 1DD S =a b c S 、、、ABC V a b c 、、、、A B C 2a =()1tan A A C ==c a =ABC V ABC V三、填空题：本题共3小题，每小题5分，共15分．12. 已知复数，（为虚数单位）在复平面上对应的点分别为，则的面积为______．13. 已知在中，内角所对边分别为，点是的重心，且，则角的大小为______．14. 已知圆锥底面圆的直径为12，高为8，若球在圆锥内，则球的表面积的最大值为______，若在圆锥内放置一个棱长为的正四面体，且正四面体能任意转动，则的最大值为______．四、解答题：本题共5小题，共77分．解答应写出文字说明、证明过程或演算步骤．15.已知，，向量与的夹角．（1）若，求值；（2）求．16. 已知在中，内角所对的边分别为，分别以为直角边的等腰直角三角形的面积依次是，且（1）求；（2）若，求面积．17. 如图，是圆柱的底面直径，是圆柱的母线且，点是圆柱底面圆周上的点．（1）求圆柱的侧面积和体积；（2）若，是的中点，点在线段上，求的最小值．18. 如图，直四棱柱的底面为菱形，，，，分别为上一点且，．的的的12i z =+212i z =-+i 12,Z Z 12V OZ Z ABC V ,,A B C ,,a b c G ABC V 0357a b c GA GB GC ++=C SO 1O SO 1O SO a a 2= a 3b = a b 2π3θ=()a kb a +⊥k 32a b +ABC V ,,A B C ,,a b c ,,a b c 123,,S S S 123S S S +=C 3cos ,25A a ==ABC V AB AP 4AB AP ==C 2AC =D PB E AP CE DE +1111ABCD A B C D -120ADC ∠=︒16BB =3AB =,M N 1,BC AA 4AN =2BM =（1）证明：平面；（2）平面将该直四棱柱分成两部分，记这两部分中较大的体积为；较小的体积为，求的值．19. 如图1所示，在中，点在线段上，满足，是线段上的点，且满足，线段与线段交于点．（1）若，求实数的值；（2）若，求实数的值；（3）如图2，过点的直线与边分别交于点，设，；（ⅰ）求的最大值；（ⅱ）设的面积为，四边形的面积为，求的取值范围．//BN 1AMD 1AMD 1V 2V 12V V ABC V D BC 2CD DB =G AB 32AG GB =CG AD O AD xAB y AC =+,x y AO t AD =t O ,AB AC ,E F EB AE λ= ()0,0FC AF μλμ=>>λμAEF △1S BEFC 2S 21S S重庆市第十八中学2023-2024学年高一下学期期中考试数学试题简要答案一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．【1题答案】【答案】C【2题答案】【答案】C【3题答案】【答案】B【4题答案】【答案】C【5题答案】【答案】B【6题答案】【答案】A【7题答案】【答案】C【8题答案】【答案】D二、选择题：本题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求．全部选对的得6分，部分选对的得部分分，有选错的得0分．【9题答案】【答案】ACD【10题答案】【答案】CD【11题答案】【答案】AD三、填空题：本题共3小题，每小题5分，共15分．【12题答案】【答案】##【13题答案】【答案】【14题答案】【答案】①.②. 四、解答题：本题共5小题，共77分．解答应写出文字说明、证明过程或演算步骤．【15题答案】【答案】（1） （2）【16题答案】【答案】（1）； （2）.【17题答案】【答案】（1），； （2）【18题答案】【答案】（1）证明略 （2）【19题答案】【答案】（1）， （2）（3）（ⅰ）；（ⅱ）52 2.52π336π436π3C =ABC S =V 16π16π411313x =23y =2393223,4934⎛⎤ ⎥⎝⎦。

重庆重庆市第一中学校立体几何多选题试题含答案一、立体几何多选题1．在棱长为1的正方体1111ABCD A B C D -中，P 为底面ABCD 内（含边界）一点．（ ） A ．若13A P =，则满足条件的P 点有且只有一个 B ．若12A P =，则点P 的轨迹是一段圆弧 C ．若1//A P 平面11B DC ，则1A P 长的最小值为2D ．若12A P =且1//A P 平面11B DC ，则平面11A PC 截正方体外接球所得截面的面积为23π 【答案】ABD【分析】选项A ，B 可利用球的截面小圆的半径来判断；由平面1//A BD 平面11B D C ，知满足1//A P 平面11B D C 的点P 在BD 上，1A P 长的最大值为2；结合以上条件点P 与B 或D 重合，利用12sin 60A P r =︒，求出63r =，进而求出面积. 【详解】对A 选项，如下图：由13A P =，知点P 在以1A 为球心，半径为3的球上，又因为P 在底面ABCD 内（含边界），底面截球可得一个小圆，由1A A ⊥底面ABCD ，知点P 的轨迹是在底面上以A 为圆心的小圆圆弧，半径为22112r A P A A =-=，则只有唯一一点C满足，故A 正确；对B 选项，同理可得点P 在以A 为圆心，半径为22111r A P A A =-=的小圆圆弧上，在底面ABCD 内（含边界）中，可得点P 轨迹为四分之一圆弧BD .故B 正确；对C 选项，移动点P 可得两相交的动直线与平面11B D C 平行，则点P 必在过1A 且与平面11B D C 平行的平面内，由平面1//A BD 平面11B D C ，知满足1//A P 平面11B D C 的点P 在BD上，则1A P 长的最大值为12A B =，则C 不正确； 对选项D ，由以上推理可知，点P 既在以A 为圆心，半径为1的小圆圆弧上，又在线段BD 上，即与B 或D 重合，不妨取点B ，则平面11A PC 截正方体外接球所得截面为11A BC 的外接圆，利用2126622,,sin 60333A B r r S r ππ==∴=∴==︒.故D 正确.故选：ABD【点睛】（1）平面截球所得截面为圆面，且满足222=R r d +（其中R 为球半径，r 为小圆半径，d 为球心到小圆距离）；（2）过定点A 的动直线平行一平面α，则这些动直线都在过A 且与α平行的平面内.2．如图，正方体1111ABCD A B C D -的棱长为3，点E ，F 分别在1CC ，1BB 上，12C E EC →→=，12BF FB →→=.动点M 在侧面11ADD A 内(包含边界)运动，且满足直线//BM 平面1D EF ，则（ ）A ．过1D ，E ，F 的平面截正方体所得截面为等腰梯形B ．三棱锥1D EFM -的体积为定值C ．动点M 10D ．过B ，E ，M 的平面截正方体所得截面面积的最小值为10【答案】BCD【分析】由题做出过1D ，E ，F 的平面截正方体所得截面为梯形1D EFN ，进而计算即可排除A 选项；根据//BM 平面1D EF ，由等体积转化法得1111D EFM M D EF B D EF D BEF V V V V ----===即可得B 选项正确；取1AA 靠近1A 点的三等分点H ， 1DD 靠近D 点的三等分点I ，易知M 的轨迹为线段HI 10，故C 选项正确；过M 点做BE 的平行线交1AA 于P ，交1DD 于O ，连接,BP OE ，易知过B ，E ，M 的平面截正方体所得截面即为平行四边形BPOE ，进而得当H 位于点I 时，截面面积最小，为四边形ABEI 的面积，且面积为310S AB BE =⋅=【详解】解：对于A 选项，如图，取BF 中点G ，连接1A G ，由点E ，F 分别在1CC ，1BB 上，12C E EC →→=，12BF FB →→=，故四边形11A D EG 为平行四边形，故11//AG D E ，由于在11A B G △，F 为1B G 中点，当N 为11A B 中点时，有11////NF A G D E ，故过1D ，E ，F 的平面截正方体所得截面为梯形1D EFN ，此时221335322D N ⎛⎫=+= ⎪⎝⎭，223110EF =+=1D EFN 不是等腰梯形，故A 选项错误；对于B 选项，三棱锥1D EFM -的体积等于三棱锥1M D EF -的体积，由于//BM 平面1D EF ，故三棱锥1M D EF -的体积等于三棱锥1B D EF -的体积，三棱锥1B D EF -的体积等于三棱锥1D BEF -的体积，而三棱锥1D BEF -的体积为定值，故B 选项正确； 对于C 选项，取1AA 靠近1A 点的三等分点H ， 1DD 靠近D 点的三等分点I ，易知1////HB AG NF ，1//BI D F ，由于1,HI BI I NF D F F ==，故平面//BHI 平面1D EF ，故M 的轨迹为线段HI ，其长度为10，故C 选项正确；对于D 选项，过M 点做BE 的平行线交1AA 于P ，交1DD 于O ，连接,BP OE ，则过B ，E ，M 的平面截正方体所得截面即为平行四边形BPOE ，易知当H 位于点I 时，平行四边形BPOE 边BP 最小，且为AB ，此时截面平行四边形BPOE 的面积最小，为四边形ABEI 的面积，且面积为310S AB BE =⋅=，故D 选项正确；故选：BCD【点睛】本题解题的关键在于根据题意，依次做出过1D ，E ，F 的平面截正方体所得截面为梯形1D EFN ，过B ，E ，M 的平面截正方体所得截面即为平行四边形BPOE ，进而讨论AD 选项，通过//BM 平面1D EF ，并结合等体积转化法得1111D EFM M D EF B D EF D BEF V V V V ----===知B 选项正确，通过构造面面平行得M 的轨迹为线段HI ，进而讨论C 选项，考查回归转化思想和空间思维能力，是中档题.3．在三棱锥M ABC -中，下列命题正确的是（ ）A ．若1233AD AB AC =+，则3BC BD = B ．若G 为ABC 的重心，则111333MG MA MB MC =++ C ．若0MA BC ⋅=，0MC AB ⋅=，则0MB AC ⋅=D ．若三棱锥M ABC -的棱长都为2，P ，Q 分别为MA ，BC 中点，则2PQ =【答案】BC【分析】作出三棱锥M ABC -直观图，在每个三角形中利用向量的线性运算可得.【详解】对于A ，由已知12322233AD AB AC AD AC AB AD AC AB AD =+⇒=+⇒-=-，即2CD DB =，则32BD BD DC BC =+=，故A 错误； 对于B ，由G 为ABC 的重心，得0GA GB GC ++=，又MG MA AG =+，MG MB BG =+，MG MC CG =+，3MA MB MC MG ∴++=，即111333MG MA MB MC =++，故B 正确； 对于C ，若0MA BC ⋅=，0MC AB ⋅=，则0MC MA BC AB ⋅+⋅=，即()00MA BC AC CB MA BC AC C MC C M B M C ⋅++=⇒⋅++⋅⋅=⋅()00MA BC A MC MC MC MC C BC MA BC AC ⋅⋅⋅⇒⋅+-=⇒-+=⋅()000MC M CA BC AC AC CB AC CB AC C MC ⇒+=⇒+=⇒+=⋅⋅⋅⋅⋅，即0MB AC ⋅=，故C 正确；对于D ，111()()222PQ MQ MP MB MC MA MB MC MA ∴=-=+-=+- ()21122PQ MB MC MA MB MC MA ∴=+-=+-，又()2222222MB MC MA MB MC MA MB MC MB MA MC MA +-=+++⋅-⋅-⋅2221112222222222228222=+++⨯⨯⨯-⨯⨯⨯-⨯⨯⨯=，1822PQ ∴==，故D 错误.故选：BC【点睛】关键点睛：本题考查向量的运算，用已知向量表示某一向量的三个关键点：(1)用已知向量来表示某一向量，一定要结合图形，以图形为指导是解题的关键．(2)要正确理解向量加法、减法与数乘运算的几何意义，如首尾相接的若干向量之和，等于由起始向量的始点指向末尾向量的终点的向量．(3)在立体几何中三角形法则、平行四边形法则仍然成立．4．如图，已知四棱锥P ABCD -所有棱长均为4，点M 是侧棱PC 上的一个动点（不与点,P C 重合），若过点M 且垂直于PC 的截面将该四棱锥分成两部分，则下列结论正确的是（ ）A ．截面的形状可能为三角形、四边形、五边形B ．截面和底面ABCD 所成的锐二面角为4πC ．当1PM =时，截面的面积为52D ．当2PM =时，记被截面分成的两个几何体的体积分别为()1212,>V V V V ，则123=V V【答案】BCD【分析】点M 是侧棱PC 上的一个动点，根据其不同位置，对选项逐一进行判断即可.【详解】A 选项中，如图，连接BD ，当M 是PC 中点时，2MC =，由题意知三角形PDC 与三角形PBC 都是边长为4的正三角形，所以DM PC ⊥,BM BC ⊥，又DM ，BM 在面MBD 内，且相交，所以PC ⊥平面PBD ，三角形MBD 即为过点M 且垂直于PC 的截面，此时是三角形，点M 向下移动时，2MC <，如图，仍是三角形；若点M 由中点位置向上移动，2MC >，在平面PDC 内作EM PC ⊥，交PD 于E ，在平面PBC 内作FM PC ⊥交PB 于F ，平面MEF 交平面PAD 于EG ，交PAB 于FH ，即交平面ABCD 于GH ，则五边形MEGHF 即为过点M 且垂直于PC 的截面，此时是五边形； 故截面的形状可能为三角形、五边形，A 错误；B 选项中，因为截面总与PC 垂直，所以不同位置的截面均平行，截面与平面ABCD 所成的锐角为定值，不妨取M 是中点，连接AC ，BD ，MB ，MD ，设AC ，BD 交点是N ，连接PN ，由题意知，四边形ABCD 是边长为4的菱形，BD AC ⊥，因为MB =MD ，所以MN BD ⊥，故MNC ∠是截面与平面ABCD 所成的锐角，过点M 作MQ AC ⊥，垂足Q.在三角形PAC 中，MN =2，2，故在直角三角形MNQ 中，2cos 2NQ MNC MN ∠==，故4MNC π∠=，故B 正确；C 选项中，当PM =1时，M 是PC 中点，如图，五边形MEGHF 即为过点M 且垂直于PC 的截面，依题意，直角三角形PME 中，2cos PM PE EPM==∠，故E 为PD 的中点，同理，F 是PB 的中点，则EF 是三角形PBD 的中位线，1222EF BD ==G ，H 分别在,AD AB 的中点上，证明如下，当G ，H ，也是中点时，1//,2GH BD GH BD =，有//,22GH EF GH EF ==，四边形EFHG 是平行四边形.依题意，三角形PAC 中4,42PA PC AC ===，故PA PC ⊥，故PC GE ⊥，易见，正四棱锥中BD ⊥平面PAC ，故BD PC ⊥，GH PC ∴⊥，因为 ,GE GH 均在平面EFHG 内，且相交，所以PC ⊥平面EFHG ，故此时平面EFHG 和平面MEF 即同一平面.又BD ⊥平面PAC ，有GH ⊥面平面PAC ，GH GM ⊥，根据对称性有GH GE ⊥，四边形EFHG 是矩形. 即五边形MEGHF 即为过点M 且垂直于PC 的截面，平面图如下:依题意，22GH EF ==2EG FG ==，三角形高为()()22321h =-=， 面积是122122⨯=，四边形面积是22242=，故截面面积是52 故C 正确； D 选项中，若PM =2，看B 选项中的图可知，21124M BCD P BCD P ABCD V V V V ---===，故剩余部分134P ABCD V V -=，所以123=V V ，故D 正确. 故选：BCD.【点睛】 本题考查了棱锥的截面问题，考查了二面角、体积等计算问题，属于难题.5．（多选题）在四面体P ABC -中，以上说法正确的有（ ）A ．若1233AD AC AB =+，则可知3BC BD = B ．若Q 为△ABC 的重心，则111333PQ PA PB PC =++ C ．若0PA BC =，0PC AB =，则0PB AC =D ．若四面体P ABC -各棱长都为2，M N ，分别为,PA BC 的中点，则1MN =【答案】ABC【分析】作出四面体P ABC -直观图，在每个三角形中利用向量的线性运算可得.【详解】对于A ，1233AD AC AB =+，32AD AC AB ∴=+，22AD AB AC AD ∴-=- ， 2BD DC ∴=，3BD BD DC BC ∴=+=即3BD BC ∴=，故A 正确；对于B ，Q 为△ABC 的重心，则0QA QB QC ++=，33PQ QA QB QC PQ ∴+++=()()()3PQ QA PQ QB PQ QC PQ ∴+++++=,3PA PB PC PQ ∴++=即111333PQ PA PB PC ∴=++，故B 正确； 对于C ，若0PA BC =，0PC AB =，则0PA BC PC AB +=，()0PA BC PC AC CB ∴++=,0PA BC PC AC PC CB ∴++=0PA BC PC AC PC BC ∴+-=,()0PA PC BC PC AC ∴-+=0CA BC PC AC ∴+=,0AC CB PC AC ∴+= ()0AC PC CB ∴+=，0AC PB ∴=，故C 正确；对于D ，111()()222MN PN PM PB PC PA PB PC PA ∴=-=+-=+- 1122MN PB PC PA PA PB PC ∴=+-=--222222PA PB PC PA PB PC PA PB PA PC PC PB --=++--+ 22211122222222222222222=++-⨯⨯⨯-⨯⨯⨯+⨯⨯⨯= 2MN ∴=，故D 错误.故选：ABC【点睛】用已知向量表示某一向量的三个关键点(1)用已知向量来表示某一向量，一定要结合图形，以图形为指导是解题的关键．(2)要正确理解向量加法、减法与数乘运算的几何意义，如首尾相接的若干向量之和，等于由起始向量的始点指向末尾向量的终点的向量．(3)在立体几何中三角形法则、平行四边形法则仍然成立．6．M ，N 分别为菱形ABCD 的边BC ，CD 的中点，将菱形沿对角线AC 折起，使点D 不在平面ABC 内，则在翻折过程中，下列结论正确的有（ ）A ．MN ∥平面ABDB ．异面直线AC 与MN 所成的角为定值C ．在二面角D AC B --逐渐变小的过程中，三棱锥D ABC -外接球的半径先变小后变大D ．若存在某个位置，使得直线AD 与直线BC 垂直，则ABC ∠的取值范围是0,2π⎛⎫ ⎪⎝⎭ 【答案】ABD【分析】利用线面平行的判定即可判断选项A ；利用线面垂直的判定求出异面直线AC 与MN 所成的角即可判断选项B ；借助极限状态，当平面DAC 与平面ABC 重合时，三棱锥D ABC -外接球即是以ABC ∆外接圆圆心为球心，外接圆的半径为球的半径，当二面角D AC B --逐渐变大时，利用空间想象能力进行分析即可判断选项C;过A 作AH BC ⊥,垂足为H ,分ABC ∠为锐角、直角、钝角三种情况分别进行分析判断即可判断选项D.【详解】对于选项A:因为M ，N 分别为菱形ABCD 的边BC ，CD 的中点，所以MN 为BCD ∆的中位线，所以//MN BD ,因为MN ⊄平面ABD ,BD ⊂平面ABD ，所以MN ∥平面ABD ,故选项A 正确；对于选项B ：取AC 的中点O ，连接,DO BO ,作图如下：则,AC DO AC BO ⊥⊥,BO DO O =,由线面垂直的判定知，AC ⊥平面BOD ,所以AC BD ⊥,因为//MN BD ,所以AC MN ⊥,即异面直线AC 与MN 所成的角为定值90，故选项B 正确；对于选项C:借助极限状态，当平面DAC 与平面ABC 重合时，三棱锥D ABC -外接球即是以ABC ∆外接圆圆心为球心，外接圆的半径为球的半径，当二面角D AC B --逐渐变大时，球心离开平面ABC ，但是球心在底面的投影仍然是ABC ∆外接圆圆心，故二面角D AC B --逐渐变小的过程中，三棱锥D ABC -外接球的半径不可能先变小后变大， 故选项C 错误；对于选项D:过A 作AH BC ⊥,垂足为H ,若ABC ∠为锐角，H 在线段BC 上；若ABC ∠为直角，H 与B 重合；若ABC ∠为钝角，H 在线段BC 的延长线上；若存在某个位置，使得直线AD 与直线BC 垂直，因为AH BC ⊥，所以CB ⊥平面AHD ,由线面垂直的性质知,CB HD ⊥,若ABC ∠为直角，H 与B 重合，所以CB BD ⊥,在CBD ∆中，因为CB CD =, 所以CB BD ⊥不可能成立，即ABC ∠为直角不可能成立；若ABC ∠为钝角，H 在线段BC 的延长线上，则在原平面图菱形ABCD 中，DCB ∠为锐角，由于立体图中DB DO OB <+,所以立体图中DCB ∠一定比原平面图中更小，，所以DCB ∠为锐角，CB HD ⊥，故点H 在线段BC 与H 在线段BC 的延长线上矛盾，因此ABC ∠不可能为钝角；综上可知，ABC ∠的取值范围是0,2π⎛⎫ ⎪⎝⎭.故选项D 正确; 故选：ABD【点睛】本题考查异面垂直、线面平行与线面垂直的判定、多面体的外接球问题；考查空间想象能力和逻辑推理能力；借助极限状态和反证法思想的运用是求解本题的关键；属于综合型强、难度大型试题.7．如果一个棱锥的底面是正方形，且顶点在底面内的射影是底面的中心，那么这样的棱锥叫正四棱锥．若一正四棱锥的体积为18，则该正四棱锥的侧面积最小时，以下结论正确的是（ ）．A ．棱的高与底边长的比为22B ．侧棱与底面所成的角为4πC ．棱锥的高与底面边长的比为2D ．侧棱与底面所成的角为3π 【答案】AB【分析】 设四棱锥S ABCD -的高为h ，底面边长为a ，由21183V a h ==得254h a =，然后可得侧面积为242108a a+，运用导数可求出当32a =时侧面积取得最小值，此时3h =，然后求出棱锥的高与底面边长的比和SAO ∠即可选出答案.【详解】设四棱锥S ABCD -的高为h ，底面边长为a可得21183V a h ==，即254h a= 所以其侧面积为2222244215410842244a a a h a a a⋅⋅+=+=+令()242108f a a a =+，则()23321084f a a a ⨯'=- 令()233210840f a a a ⨯'=-=得32a = 当(0,32a ∈时()0f a '<，()f a 单调递减 当()32,a ∈+∞时()0f a '>，()f a 单调递增 所以当32a =时()f a 取得最小值，即四棱锥的侧面积最小此时3h = 所以棱锥的高与底面边长的比为22，故A 正确，C 错误 侧棱与底面所成的角为SAO ∠，由3h =，32a =可得3AO =所以4SAO π∠=，故B 正确，D 错误 故选：AB【点睛】本题考查的知识点有空间几何体的体积和表面积、线面角及利用导数求最值，属于综合题.8．如图所示，正方体ABCD A B C D ''''-的棱长为1，E ，F 分别是棱AA '，CC '的中点，过直线EF 的平面分别与棱BB '，DD '交于点M ，N ，以下四个命题中正确的是（ ）A ．0MN EF ⋅=B ．ME NE =C ．四边形MENF 的面积最小值与最大值之比为2:3D ．四棱锥A MENF -与多面体ABCD EMFN -体积之比为1:3【答案】ABD【分析】证明EF ⊥平面BDD B ''，进而得EF MN ⊥，即可得A 选项正确；证明四边形MENF 为菱形即可得B 选项正确；由菱形性质得四边形MENF 的面积12S MN EF =⋅，再分别讨论MN 的最大值与最小值即可；根据割补法求解体积即可.【详解】对于A 选项，如图，连接BD ，B D ''，MN ．由题易得EF BD ⊥，EF BB '⊥，BD BB B '⋂=，所以EF ⊥平面BDD B ''，又MN ⊂平面BDD B ''，所以EF MN ⊥，因此0MN EF ⋅=，故A 正确．对于B 选项，由正方体性质得：平面''//BCC B 平面''ADD A ，平面''BCC B 平面EMFN MF =，平面''ADD A 平面EMFN EN =， 所以//MF EN ，同理得//ME NF ，又EF MN ⊥，所以四边形MENF 为菱形， 因此ME NE =，故B 正确．对于C 选项，由B 易得四边形MENF 的面积12S MN EF =⋅， 所以当点M ，N 分别为BB '，DD '的中点时，四边形MENF 的面积S 最小，此时MN EF ==，即面积S 的最小值为1； 当点M ，N 分别与点B （或点B '），D （或D ）重合时，四边形MENF 的面积S 最大，此时MN =，即面积S 的最大值为2所以四边形MENF 的面积最小值与最大值之比为2C 不正确．对于D 选项，四棱锥A MENF -的体积1111336M AEF N AEF AEF V V V DB S --=+=⋅==△； 因为E ，F 分别是AA '，CC '的中点，所以BM D N '=，DN B M '=，于是被截面MENF 平分的两个多面体是完全相同的，则它们的体积也是相同的，因此多面体ABCD EMFN -的体积21122ABCD A B C D V V ''''-==正方体， 所以四棱锥A MENF -与多面体ABCD EMFN -体积之比为1:3，故D 正确． 故选：ABD ．【点睛】本题考查立体几何与向量的综合、截面面积的最值、几何体的体积，考查空间思维能力与运算求解能力，是中档题.本题解题的关键在于证明四边形MENF 为菱形，利用割补法将四棱锥A MENF -的体积转化为三棱锥M AEF - 和N AEF -的体积之和，将多面体ABCD EMFN -的体积转化为正方体的体积的一半求解.。

1、答题前填写好自己的姓名、班级、考号等信息2、请将答案正确填写在答题卡上2023-2024学年重庆市永川区高中数学人教B 版 必修四-立体几何初步-专项提升(1)姓名：____________ 班级：____________ 学号：____________考试时间：120分钟满分：150分题号一二三四五总分评分*注意事项：阅卷人得分一、选择题（共12题，共60分）内有无数条直线与平行， 平行于同一个平面， 平行于同一条直线， 垂直于同一个平面1. 设 ， 为两个不同的平面，则的一个充分条件是（ ）A.B.C.D. 平面在直线上存在一点E ，使得平面在直线上存在一点E ，使得平面2. 已知几何体是正方体，则（ ）A.B. C. D. 若直线a 在平面α外，则直线a 与平面内任何一点都只可以确定一个平面若a ，b 分别与两条异面直线都相交，则a ，b 是异面直线若直线a 平行于直线b ，则a 平行于过b 的任何一个平面若a ，b 是异面直线，则经过a 且与b 垂直的平面可能不存在3. 下列命题中正确的是（ ）A. B. C. D. 4. 如图，记正方形ABCD 四条边的中点为S ，M ，N ，T ，连接四个中点得小正方形SMNT ．将正方形ABCD ，正方形SMNT 绕对角线AC 旋转一周得到的两个旋转体的体积依次记为V 1 ， V 2 ， 则V 1：V 2=（ ）8：12：14：38：3A. B. C. D. 34π5. 在棱长为2的正方体ABCD ﹣A 1B 1C 1D 1中，P 为底面正方形ABCD 内一个动点，Q 为棱AA 1上的一个动点，若|PQ|=2，则PQ 的中点M 的轨迹所形成图形的面积是（ ）A.B.C. D. 6. 点，，在球表面上，，，，若球心到截面的距离为，则该球的体积为（ ）A.B.C. D.MN 与CC 1垂直MN 与AC 垂直MN 与BD 平行MN 与A 1B 1平行7. 如图，在正方体ABCD ﹣A 1B 1C 1D 1中，M ，N 分别是BC 1 ， CD 1的中点，则下列说法错误的是（）A. B. C. D.若，，， 则若 ，， 则若 ，， 则若 ， 且l 与所成的角和m 与所成的角相等，则8.设 ，是两个不同的平面，l ，m 是两条不同的直线，则下列命题中正确的是（ ）A. B. C. D. ①②②③①④③④9. 用表示三条不同的直线，表示平面，给出下列命题，其中说法正确命题的序号是（ ）①若，，则；②若，，则；③若，，则；④若，，则.A. B. C. D. 若直线l 平行于平面内的无数条直线,则若直线在平面外,则若直线 ,则10. 下列说法正确的是（ ）A. B. C.若直线 ，则直线 平行于 内的无数条直线D. 9π4π11. 在三棱锥中，，， 则三棱锥外接球的表面积是（ ）A. B.C. D.若 ，则若 且，则，，则若且，则12. 已知 为三条不同的直线， 为三个不同的平面，则下列说法正确的是（ ）A. B. C.D. 13. 所谓正三棱锥，指的是底面为正三角形，顶点在底面上的射影为底面三角形中心的三棱锥，在正三棱锥 中，AM 是PC 的中点，且 ，底面边长 ，则正三棱锥 的外接球的表面积为 ；AM 与底面AB C 所成角的正弦值为 ．14. 已知正方体的棱长为2，以A 为球心，为半径的球面与平面的交线长为 .15. 已知正四棱锥的体积为12，底面对角线长为 ，则侧面与底面所成的二面角等于 ．16. 已知某圆柱的轴截面是一个正方形，且该圆柱表面积（底面和侧面面积之和）为 ，其外接球的表面积为，则该圆柱的表面积与其外接球的表面积的比值.17. 如图， 是圆 的直径， 垂直圆 所在的平面， 是圆 上的点．(1) 求证： 平面 ；(2) 设 为的中点，为的重心，求证：平面．18. 如图，棱长为2的正四面体ABCD （所有棱长均相等的三棱锥）中，E ，F 为AB 和DC 的中点．(1) 证明：；(2) 求三棱锥的体积．19. 已知四棱锥的底面为直角梯形， , 底面且是的中点.(1) 求证：直线平面；(2) 若，求二面角的余弦值.20. 如图，四边形ABCD是矩形，AB＝2BC＝2，E为CD中点，以BE为折痕将△BEC折起，使C到C′的位置，且平面BEC′⊥平面ABED．(1) 求证：BC′⊥AE；(2) 求空间四边形ABC′E的体积．21. 如图，四棱锥P﹣ABCD的底面ABCD是平行四边形，PB⊥面ABCD，BA=BD= ，AD=2，E，F分别是棱AD，PC的中点．(1) 证明：EF∥平面PAB；(2) 若二面角P﹣AD﹣B为60°，求直线EF与平面PBC所成角的正弦值．答案及解析部分1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.(1)(2)(1)(2)19.(1)(2)20.(1)(2)21.(1)(2)。