当前位置：文档之家 › 第8章 非线性系统分析 参考答案汇总

第8章 非线性系统分析 参考答案汇总

  • 格式：doc
  • 大小：2.76 MB
  • 文档页数：14

下载文档原格式

  / 14

合集下载

自控例题解析

自控例题解析

·43·第8章 非线性控制系统的分析例题解析例8-1 设非线性系统具有典型结构，试用等效增益概念分析具有死区的三位置理想继电特性(见图8-1(a))对系统稳定性的影响。

图8-1 稳定性分析解：由等效增益定义x y K /=知，等效增益曲线如图8-1(b)所示，其中∆=/M K m 。

设系统不存在非线性时，临界稳定增益为K c ，于是① 若K c >K m ，如图8-1(b)所示，则因实际增益小于临界增益K c ，所以系统稳定 ② 若K c <K m ，如图8-1(c )所示，其中x 0=M./K c ，则当x<x 0时，因m K K >，系统不稳定，x 发散；当x 增加至使x >x 0时，此时m K K <，系统稳定，x 收敛；当x 减小至使x <x 0时，重复上述过程。

可见，在这种情况下，系统将出现以x 0为振幅的自激振荡。

③ 原系统加入具有死区的理想三位置继电特性后，改善了系统的稳定性。

不论原系统是否发散，现系统都不会发散，但可能产生一个以x 0为振幅的自激振荡。

例8-2 试求图8-2所示非线性环节的描述函数。

（a ） （b ）·44·图 8-2 非线性环节解：（1）对于图8-2（a ），因为t X x x y ωsin ,3==且单值奇对称，故A1＝03204320432043sin 4sin 1sin 11X t td X t d t X t td y B ====⎰⎰⎰πππωωπωωπωωπ21143)(X X A j X B X N =+=图 8-3（2）对于图8-2（b ），因为图示非线性可以分解为图8-3所示两个环节并联，所以 K XMX N X N X N +=+=π4)()()(21 例8-3 试将图8-4（a ），（b ）所示系统归化为一个非线性部分和一个线性部分串联的典型结构。

（a ） （b ）图 8-4解：（1）G 1与G 2是小回路的负反馈，则2111G G G G +=从而得典型结构，见图8-5。

精品文档-自动控制原理(王春侠)-第八章

精品文档-自动控制原理(王春侠)-第八章
19
8.2 描 述 函 数 法 8.2.1 描述函数的基本概念
设非线性环节的输入为 x(t)＝A sinωt
一般情况下，非线性环节的稳态输出y(t)是非正弦周期信号。 将y(t)用傅氏级数表示为
y t A0 An cos nt+Bn sin nt =A0 Yn sin nt+n
n =1
n =1
kx，
x ≤a
y Msignx， x ＞a
2
图8-1 饱和非线性特性
3
2． 死区特性
死区又称不灵敏区，如图8-2所示。其输入与输出之间关
系的表达式为
0，
x ≤Δ
y k x Δsignx， x ＞Δ
式中，Δ为死区范围； k为线性段的斜率。
当输入信号小于Δ时，对系统来说，虽然有输入但无输
出，只有当|x|＞Δ时才有输出，这时，输出与输入之间为
第八章 非线性控制系统分析
8.1 非线性系统的基本概念 8.2 描述函数法 8.3 相平面法 8.4 Matlab应用实例
1
8.1 非线性系统的基本概念 8.1.1 典型非线性特性
控制系统中含有本质非线性环节，如果这些本质非线性特 性能用简单的折线来描述，则称为典型非线性特性。
1. 饱和特性 饱和特性是一种常见的非线性特性，如图8-1所示。其数 学表达式为
最后指出，这种方法只适用于单个的非线性元件，如果有 两个以上的非线性元件，则必须把它们合并为一个模块，否则 第二个元件的输入就不会是正弦波。
22
8.2.2 典型非线性特性的描述函数 1． 死区特性 在具有死区的元件中，当输入在死区的幅值范围内时
就没有输出。图8-6所示为死区非线性特性及其输入、输出波 形。

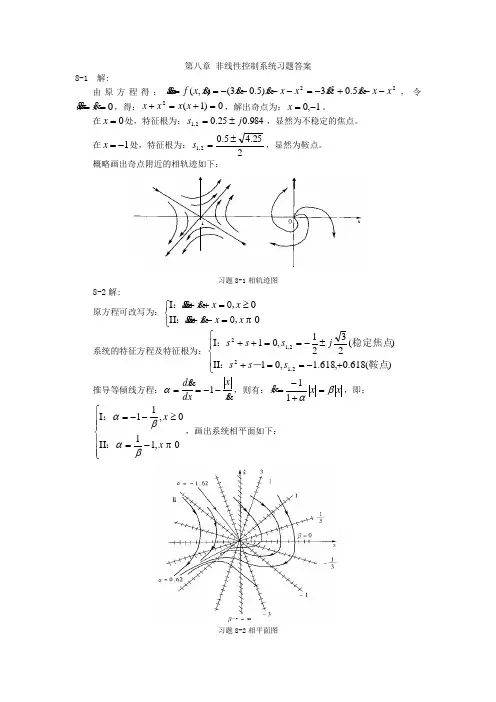
自动控制原理(孟华)第8章习题答案070520

自动控制原理(孟华)第8章习题答案070520

第八章 非线性控制系统习题答案8-1 解:由原方程得：2225.03)5.03(),(x x x x x x x x x x f x--+-=----== ，令0==x x，得：0)1(2=+=+x x x x ，解出奇点为：1,0-=x 。

在0=x 处，特征根为：984.025.02,1j s ±=，显然为不稳定的焦点。

在1-=x 处，特征根为：225.45.02,1±=s ，显然为鞍点。

概略画出奇点附近的相轨迹如下：-1习题8-1相轨迹图8-2解:原方程可改写为：⎩⎨⎧=-+≥=++0II 0Ix x x x x x x x 0,：0,：系统的特征方程及特征根为：⎪⎩⎪⎨⎧+-==+±-==++)(618.0,618.1,01II )(2321,01I 2,122,12鞍点－：稳定焦点：s s s js s s 推导等倾线方程：xx dx xd --==1α，则有：x x xβα=+-=11 ，即： ⎪⎪⎩⎪⎪⎨⎧-=≥--=0,11II 0,11I x x βαβα：：，画出系统相平面如下：习题8-2相平面图8-3 （1）解：相平面上任一点的相轨迹斜率为：x xxdxx dsin+-=，由=dxx d，得：),2,1,0(±±==kkxπ，因此在相平面的x轴上，),2,1,0(±±==kkxπ的点均为奇点。

在x轴上满足),2,1,0(2±±==kkxπ的所有奇点附近，由泰勒级数展开来验证这类奇点为稳定焦点。

在x轴上满足),2,1,0()12(±±=+=kkxπ的所有奇点附近，由泰勒级数展开来验证这类奇点为鞍点。

绘制相轨迹如下图所示：习题8-3（1）相轨迹图（2）解：原方程可改写为：⎩⎨⎧=-≥=+IIIxxxxxx0,：0,：系统的特征方程及特征根为：⎪⎩⎪⎨⎧±==±==+)(1,01II)(,01I2,122,12鞍点－：中心点：ssjss推导等倾线方程：⎪⎪⎩⎪⎪⎨⎧≥11xxxxxx,＝,－＝αα，画出系统相平面如下：习题8-3（2）相轨迹图（3）解：令0==xx，得0sin=x，得出系统的奇点：,2,,0ππ±±=x当,2,1,02±±==kx，κπ时，令2xx+=κπ，可以验证奇点,2,1,02±±==kx，κπ为中心点。

《自动控制原理》第八章 非线性控制系统分析

《自动控制原理》第八章 非线性控制系统分析

第八章 非线性控制系统分析8-1 非线性控制系统概述1. 研究非线性控制理论的意义以上各章详细地讨论了线性定常控制系统的分析和设计问题。

但实际上，理想的线性系统并不存在，因为组成控制系统的各元件的动态和静态特性都存在着不同程度的非线性。

以随动系统为例，放大元件由于受电源电压或输出功率的限制，在输入电压超过放大器的线性工作范围时，输出呈饱和现象，如图8-l(a)所示；执行元件电动机，由于轴上存在着摩擦力矩和负载力矩，只有在电枢电压达到一定数值后，电机才会转动，存在着死区，而当电枢电压超过一定数值时，电机的转速将不再增加，出现饱和现象，其特性如图8-1(b)所示；又如传动机构，受加工和装配精度的限制，换向时存在着间隙特性，如图8-1(c)所示。

在图8-2所示的柱形液位系统中，设H 为液位高度，Q i为液体流入量，Q o 为液体流出量，C 为贮槽的截面积。

根据水力学原理0Q k H = (8-1)其中比例系数k 是取决于液体的粘度和阀阻。

液位系统的动态方程为0i i dH CQ Q Q k H dt =-=-显然，液位H 和液体输入量Q i 的数学关系式为非线性微分方程。

由此可见，实际系统中普遍存在非线性因素。

当系统中含有一个或多个具有非线性特性的元件时，该系统称为非线性系统。

一般地，非线性系统的数学模型可以表示为：(,,...,,)(,,...,,)n m n m d y dy d r dr f t y g t r dt dt dt dt =(8-3)其中f(·)和g(·)为非线性函数。

当非线性程度不严重时，例如不灵敏区较小、输入信号幅值较小、传动机构间隙不大时，可以忽略非线性特性的影响，从而可将非线性环节视为线性环节；当系统方程解析且工作在某一数值附近的较小范围内时，可运用小偏差法将非线性模型线性化。

例如，设图8—2液位系统的液位H 在H 0附近变化，相应的液体输入量Q i 在Q i0，附近变化时，可取ΔH =H −H 0，ΔQ i =Q i −Q i0,对√H 作泰勒级数展开。

《自动控制原理》第八章非线性控制系统分析

《自动控制原理》第八章非线性控制系统分析

K G jw = ( ) S 0.1S+1)( 0.2S+1) ( K −0.3w− j(1−0.02w2 )] [ = 4 2 w 0.0004w + 0.05w +1) (
S= jw
令 ImG(jw) = 0 即 1 – 0.02w2 = 0 ，可得 G(jw) 曲线与负实轴交点的频率为：
1 wx = = 50 = 7.07rad / s 0.02
C(t)
∆2 ∆3 ∆ = ∆1 + + k k k2 1 1
K1 ，k2 ，k3 为传递函数各自的增益
处于系统前向通路最前边的元件，其死区所 造成的影响最大，而放大元件和执行元件的影响 可以通过提高这些元件前几项的传递函数来减小。 死区对系统的直接影响是造成稳态误差，降 低了定位精度。
≤ 时，输出量 y 与 x 是线 饱和：当输入量 x≤ a x> a > 时，输出量不再 性关系 y = kx ，当 随着输入量线性增长，而保持为某一常值。
两条曲线在交点处的幅值相等，即： −π
1 1 1 2 [arcsin + 4 1−( ) ] A A A = −1
得：A = 0.5 应用奈氏判据可以判断交点对应的周期运动 2.5sin7.07t 是稳定的，故当 k = 15 时，非线性系统 工作在自振状态，自振振幅 A = 2.5 ，频率 w = 7.07rad/s （2）欲使系统稳定地工作，不出现自振荡，由于 G(s) 的极点均在右半平面，故根据奈氏判据
相对负倒描述函数为：
A A2 ( ) 1 π π h h − =− =− NA ( ) 4 4 A2 h2 1−( ) ( ) −1 h A
采用相对描述函数后，系统的特征方程改写为：

第8章 非线性系统分析

第8章 非线性系统分析
dx/dt x
不稳定节点

x 2 n x n x 0
2

1 0
相轨迹振荡远离原点，为不 稳定焦点。
dx/dt x
不稳定焦点

x 2 n x n x 0
2

0
相轨迹为同心圆，该奇点为中心 点。
dx/dt x
中心点

x 2 n x n x 0
R(s) 例8-7 继电控制系统， + 阶跃信号作用下，试用 相平面法分析系统运动。
e
+M -M
m
C(s) K s(Ts 1)
解 （1）作相平面图 线性部分 T c c Km 误差方程 e(t ) r (t ) c(t ) ———— 阶跃信号 r (t ) 1(t ), r (t ) 0, r(t ) 0 误差方程 T e e Km

x x sin x 0


奇点为
f ( x, x) x sin x 0
x0 无穷多个。 x k

4、奇点邻域的运动性质
由于在奇点上，相轨迹的斜率不定， 所以可以引出无穷条相轨迹。

dx 0 dx 0
相轨迹在奇点邻域的运动可以分为
1.趋向于奇点 2.远离奇点 3.包围奇点
（4）滞环特性
滞环特性为正向行程与反向行程不重叠，输入输出曲 线出现闭合环路。又称换向不灵敏特性。通常是叠加 在其它传输关系上的附加特性。
f(e) k +M -e +e0 e -e0 0 +e -M f(e) +M -e 0 -M +e e 0 f(e) e
饱和滞环
继电滞环

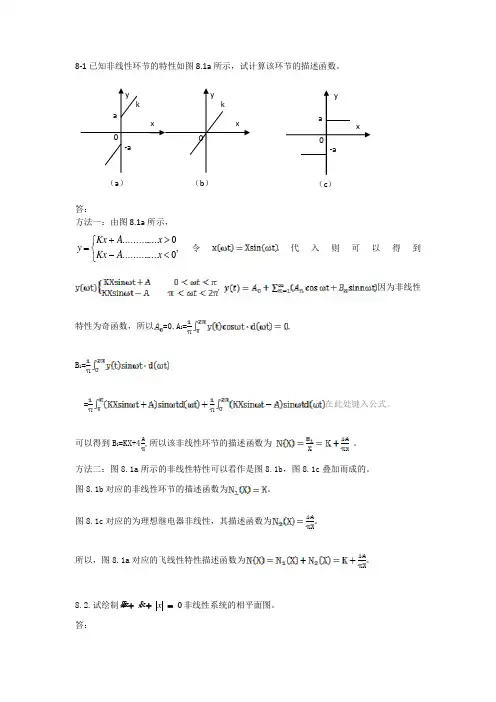
《自动控制原理》---丁红主编---第八章习题答案

《自动控制原理》---丁红主编---第八章习题答案

8-1已知非线性环节的特性如图8.1a 所示，试计算该环节的描述函数。

答：方法一：由图8.1a 所示，,0...............0...............⎩⎨⎧<->+=x A Kx x A Kx y 令代入则可以得到, 因为非线性特性为奇函数，所以=0,A 1=,B 1==在此处键入公式。

可以得到B 1=KX+4,所以该非线性环节的描述函数为 。

方法二：图8.1a 所示的非线性特性可以看作是图8.1b ，图8.1c 叠加而成的。

图8.1b 对应的非线性环节的描述函数为。

图8.1c 对应的为理想继电器非线性，其描述函数为。

所以，图8.1a 对应的飞线性特性描述函数为。

8.2.试绘制0=++x x x &&&非线性系统的相平面图。

答：y 0 -a a x k （a ） y 0 xk （b ） y（c ）0 -aa x由题意，此方程可以改写为：,开关线为x=0。

当x>0时，相轨迹方程对应的特征方程为+λ+1=0，，由可以得到.故奇点为稳定的焦点。

当x<0时，相轨迹方程对应的特征方程为+λ-1=0,,由可以得到此时的奇点为（0,0），奇点为鞍点，推导等倾线方程。

令=α，可以得到等倾线方程为,令等倾线的斜率为k ，即可以得到，得到,列写表格如下表所示。

K -3 -2 -10 1 2 3 +∞,8.3.系统方框图如图8-29所示，其中K>0，T>0。

当非线性元件N分别为理想继电特性;死区继电特性;滞环继电特性;带死区和滞环的继电特性，在cc&-相平面上绘制相平面图。

8-29系统方框图（1）具有死区的三位置继电特性线性部分的微分方程为当继电特性为具有死区的三位置继电特性时，上式可以写成分段微分方程为：C(t)r = 0- )1(+TssKN(e)e)开关线为,两条开关将相平面划分为三个线性区域，下面分区绘制相轨迹在区域，相轨迹方程为：类似于具有饱和特性的非线性控制系统时的讨论，像平面与该区域无奇点，相轨迹均渐进于的直线。

非线性控制系统分析(第八章)

非线性控制系统分析(第八章)

c(t ) c10 e c20 e 由初始条件决定。当取初始条件使 或 ， c10 , c 20 c10 0 则相轨迹为 或 ；而在其它情况下，由于特征 c20 0 根 远离虚轴，故第二项很快衰减，系统运动过程特别是过 c s2 c c s c 1 渡过程的后期主要取决于第一项。这一结果与相平面分析的 s2 结果一致。
s1
s2
a a 4b 2
0
a a2 4b 2
0
s1 , s 2 为两个符号相反的互异实根，系统相平面图见下张图。
13
Байду номын сангаас
三、相平面法（17）
由图可见，图中两条特殊的等倾线是相轨迹，也是其它相轨 迹的渐近线，此外作为相平 面的分隔线，还将相平面划 分为四个具有不同运动状态 的区域。当初始条件位于 c s2 c 对应的相轨迹，系 统的运动将趋于原点，但只 要受到极其微小的扰动，系 统的运动将偏离该相轨迹， 并最终沿着c s1 c对应的相 轨迹的方向发散 至无穷。 因此 b 0 时，线性二阶系统的运动是不稳定的。 14
15
dc
a
三、相平面法（19）
3）b 0 。取 a /(2 b ) ，并分以下几种情况加以分析： ① 0 1 。系统特征根为一对具有负实部的共轭复根。 系统的零输入响应为衰减振荡形式。取 ＝0.5, n 1， 运用等倾线法绘制系统的 相轨迹如右图所示。相 轨迹为向心螺旋线，最 终趋于原点。
f ( x, x ) a x

7
三、相平面法（11）
4）一般地，等倾线分布越密，则所作的相轨迹越准确。 但随所取等倾线的增加，绘图工作量增加，同时也使 作图产生的积累误差增大。为提高作图精度，可采用 平均斜率法，即取相邻两条等倾线所对应的斜率的平 均值为两条等倾线间直线的斜率。

自动控制原理 第8章习题解答(非线性系统分析)

自动控制原理 第8章习题解答(非线性系统分析)
(−∞ , −1) 段，方向向左，分别绘于上图 (a) (b) 上。 N
对于图
(a) 所示情形，G (
jω )
与
−
1 N
无交点，非线性系统不会产生自持振荡，
该非线性系统也是稳定的；
对于图 (b) 所示情形，G ( jω ) 与 − 1 有两个交点，其中交点 A 是稳定交点，
N
该非线性系统会产生自持振荡。
2 时， N(A)取极值。
2
−1
= − π ≈ −0.39
N ( A) A= 2
8
2
( ) （4）计算自振参数
− 1 =G N ( A)
jωg
A1 = 12.72 ，A2 = 0.503
即：系统将产生自振，振荡角频率为 ωg = 1 rad s ，振幅为 A = 12.72
12
【解】（1）将系统方框图化为标准结构
分析可得， ∆1 = 0.5
11
得系统等效方框图为：
（2）绘出线性部分的 G ( jω)曲线
与负实轴的交点处，ωg = 1
G( jω) =
10
=5
ω ⋅ ( 1+ ω 2 )2 ω =ωg
−0.39
（3）绘出非线性部分的
−
1 N
曲线
计算可得，当 A =
2e0 =
解得：
∆1
=
∆ k
+α
4
习题8.4 设有非线性控制系统，其中非线性特性为斜率 k = 1的饱
和特性。当不考虑饱和特性时，闭环系统稳定。试分析该非线性控制系统 是否有产生自持振荡的可能性。 【解】不考虑饱和因素时，稳定的线性系统的开环频率响应形式有多种，例如：
AB
考虑饱和因素，斜率为 k = 1的饱和特性的 − 1 曲线分布在负实轴上

应用回归分析,第8章课后习题参考答案讲解

应用回归分析,第8章课后习题参考答案讲解

第8章 非线性回归思考与练习参考答案8.1 在非线性回归线性化时，对因变量作变换应注意什么问题？答：在对非线性回归模型线性化时，对因变量作变换时不仅要注意回归函数的形式， 还要注意误差项的形式。

如：(1) 乘性误差项，模型形式为e y AK L αβε=， (2) 加性误差项，模型形式为y AK L αβε=+对乘法误差项模型（1）可通过两边取对数转化成线性模型，（2）不能线性化。

一般总是假定非线性模型误差项的形式就是能够使回归模型线性化的形式，为了方便通常省去误差项，仅考虑回归函数的形式。

8.2为了研究生产率与废料率之间的关系，记录了如表8.15所示的数据，请画出散点图，根据散点图的趋势拟合适当的回归模型。

表8.15生产率x （单位/周） 1000 2000 3000 3500 4000 4500 5000 废品率y （%）5.26.56.88.110.2 10.3 13.0解：先画出散点图如下图：5000.004000.003000.002000.001000.00x12.0010.008.006.00y从散点图大致可以判断出x 和y 之间呈抛物线或指数曲线，由此采用二次方程式和指数函数进行曲线回归。

（1）二次曲线 SPSS 输出结果如下：Model Summ ary.981.962.942.651R R SquareAdjusted R SquareStd. E rror of the EstimateThe independent variable is x.ANOVA42.571221.28650.160.0011.6974.42444.2696Regression Residual TotalSum of Squares dfMean SquareF Sig.The independent variable is x.Coe fficients-.001.001-.449-.891.4234.47E -007.0001.4172.812.0485.843 1.3244.414.012x x ** 2(Constant)B Std. E rror Unstandardized Coefficients BetaStandardizedCoefficientstSig.从上表可以得到回归方程为：72ˆ 5.8430.087 4.4710yx x -=-+⨯ 由x 的系数检验P 值大于0.05，得到x 的系数未通过显著性检验。

自动控制原理第八章习题答案

自动控制原理第八章习题答案

第八章 非线性控制系统分析练习题及答案8-2 设一阶非线性系统的微分方程为3x x x+-= 试确定系统有几个平衡状态，分析平衡状态的稳定性，并画出系统的相轨迹。

解 令 x=0 得 -+=-=-+=x x x x x x x 321110()()()系统平衡状态x e =-+011,,其中：0=e x ：稳定的平衡状态；1,1+-=e x ：不稳定平衡状态。

计算列表，画出相轨迹如图解8-1所示。

可见：当x ()01<时，系统最终收敛到稳定的平衡状态；当x ()01>时，系统发散；1)0(-<x 时，x t ()→-∞; 1)0(>x 时，x t ()→∞。

注：系统为一阶，故其相轨迹只有一条，不可能在整个 ~xx 平面上任意分布。

8-3 试确定下列方程的奇点及其类型，并用等倾斜线法绘制相平面图。

(1) x xx ++=0 (5) ⎩⎨⎧+=+=2122112x x xx x x解 （1） 系统方程为x -2 -1 -13 0 131 2x-6 0 0.385 0 -0.385 0 6 x 11 2 01 0211图解8-1 系统相轨迹⎩⎨⎧<=-+I I >=++I )0(0:)0(0:x x x x x x x x令0x x ==，得平衡点：0e x =。

系统特征方程及特征根：21,221,21:10,()2:10, 1.618,0.618()s s s s s s I II ⎧++==-±⎪⎨⎪+-==-+⎩稳定的焦点鞍点(, ) , , x f x x x x dxdxxx x dx dx x x x x x==--=--==--=-+=ααβ111⎪⎪⎩⎪⎪⎨⎧<-=>--=)0(11:II )0(11:I x x βαβα计算列表用等倾斜线法绘制系统相平面图如图解8-2（a ）所示。

图解8-2（a ）系统相平面图（5） xx x 112=+ ① 2122x x x+= ② 由式①： x xx 211=- ③ 式③代入②： ( )( )x xx x x 111112-=+- 即 x x x 11120--= ④ 令 x x110== 得平衡点： x e =0 由式④得特征方程及特征根为 ⎩⎨⎧-==--414.0414.20122,12λs s （鞍点） 画相轨迹，由④式x xdxdx x x x 1111112===+α xx 112=-α 计算列表用等倾斜线法绘制系统相平面图如图解8-2（b ）所示。

自动控制原理原理第8章

自动控制原理原理第8章
y (t )
KX sint Ka
0 ≤t≤1 1≤ t≤
2
第8章 非线性系统分析
y
y
Ka
a
K
0
a
x
x
0 1 1 2
t
0 1
（a）
（c）
1
1
t （b）
饱和特性及输入、输出波形
第8章 非线性系统分析
（2）由于饱和特性为单值斜对称，所以， A0 0 A1 0 1 0
X a
这是一个与输入正弦函数的振幅有关的复函数，说明输出的 基波分量对输入是有相位差的，输出滞后于输入。
第8章 非线性系统分析
4．继电器特性的描述函数 继电器特性的输入、输出特性及在正弦函数输入时的输出波形 y y 如图。 E
0 ma
a x
0 1 2
3 4
2
t
1 2
3
0
x
死区特性描述函数为
N ( X ) B1 2 K a a a arcsin 1 ( ) 2 X 2 X X X
( X a)
3．间隙特性的描述函数
间隙特性的输入、输出特性及在正弦函数输入时的输出波形
如图。 其输出表达式为
第8章 非线性系统分析
y
K
y
2
A1 B1
A1
1


2
0
y (t ) costdt
B1

1
2
0
y (t ) sin tdt
第8章 非线性系统分析
2．描述函数定义 非线性元件在正弦输入时，输出的基波分量与输入正弦量的 复数比，称为该非线性元件的描述函数。 描述函数用符号 N 表示，即

第8章非线性系统分析

第8章非线性系统分析

其中 f (x, x) 是单值连续的函数
x 2 x f (x, x) 2 x
(x, x)
f (x, x) 2 x 2
x 2x 2 (x, x)
δ值取决于变量 x 和x,若 x 和x的变化很小, δ可以看作是一个常量，例
如在相平面的点P1(x1, x1)附近，δ的值就可以取为：
d arctg x0 n x0
d x0
对x(t)求导，消去时间t，整理后得：
x
n x2
d 2 x2

c exp
2n d
arctg
x
n x d x

c

A2d
2
exp
2n d

它是一条通过初始点(x0 , x0 ), 绕 在相平面坐标原点上的对数螺 旋线。
若原方程可以分解为： g(x)dx h(x)dx
则通过积分，也可直接得到 x和x的关系，并绘制相轨迹。
例8-1 设描述系统运动的微分方程为：x x 0
初始条件为x(0)=x0， x(0) 0, 试绘制系统运动的相轨迹。
解： 先用第一种解析法求解。根据初始条件可以求得系统运动微分方程 的解为：
0
x
注意事项：
第一，横轴(x轴)与纵轴(dx/dt轴)所选用的比例尺应当一致，这样α值 才与相轨迹切线的几何斜率相同。
第二，在相平面的上半平面，相轨迹总是沿着x增加的方向运动(向右 运动)；而在下半平面,相轨迹总是沿着x减小的方向运动(向左运动)。
第三，除平衡点(即x的各阶导数为零的点)外，通过x轴时相轨迹的斜率
1
f (x1, x1) 2 x1 2
x P1(x1 ,x)

自动控制原理第八章非线性控制系统分析

自动控制原理第八章非线性控制系统分析

第八章非线性控制系统分析l、基本内容和要求（l）非线性系统的基本概念非线性系统的定义。

本质非线性和非本质非线性。

典型非线性特性。

非线性系统的特点。

两种分析非线性系统的方法——描述函数法和相平面法。

（2）谐波线性化与描述函数描述函数法是在一定条件下用频率特性分析非线性系统的一种近似方法。

谐波线性化的概念。

描述函数定义和求取方法。

描述函数法的适用条件。

（3）典型非线性特性的描述函数（4）用描述函数分析非线性系统非线性系统的一般结构。

借用奈氏判据的概念建立在奈氏图上判别非线性反馈系统稳定性的方法，非线性稳定的概念，稳定判据。

（5）相平面法的基本概念非线性系统的数学模型。

相平面法的概念和内容。

相轨迹的定义。

（6）绘制相轨迹的方法解析法求取相轨迹；作图法求取相轨迹。

（7）从相轨迹求取系统暂态响应相轨迹与暂态响应的关系，相轨迹上各点相应的时间求取方法。

（8）非线性系统的相平面分析以二阶系统为例说明相轨迹与系统性能间的关系，奇点和极限环的定义，它们与系统稳定性及响应的关系。

用相平面法分析非线性系统，非线性系统相轨迹的组成。

改变非线性特性的参量及线性部分的参量对系统稳定性的影响。

2、重点（l）非线性系统的特点（2）用描述函数和相轨迹分析非线性的性能，特别注重于非线性特性或线性部分对系统性能的影响。

8-1非线性控制系统分析1研究非线性控制理论的意义实际系统都具有程度不同的非线性特性，绝大多数系统在工作点附近，小范围工作时，都能作线性化处理。

应用线性系统控制理论，能够方便地分析和设计线性控制系统。

如果工作范围较大，或在工作点处不能线性化，系统为非线性系统。

线性系统控制理论不能很好地分析非线性系统。

因非线性特性千差万别，无统一普遍使用的处理方法。

非线性元件(环节)：元件的输入输出不满足(比例+叠加)线性关系，而且在工作范围内不能作线性化处理(本质非线性)。

非线性系统：含有非线性环节的系统。

非线性系统的组成：本章讨论的非线性系统是，在控制回路中能够分为线性部分和非线性部分两部分串联的系统。

自控第8章 非线性系统

自控第8章 非线性系统

6. 非线性系统中，当输入量是正弦信号时，输出稳态分 量包含大量的谐波成分，频率响应复杂，输出波形会 很容易畸变。
11
三、非线性系统的分析方法
1、相平面法
时域分析法中的一种图解分析法。不适用于高阶系统。 2、描述函数法 结合频域分析法和非线性的谐波线性化的一综合图解分
析法。分析非线性系统稳定性和自激振荡比较有效。
二、继电特性
1、特性曲线
M y
来源：继电器是继电
特性的典型元件。
0
-M
x
继电特性 具有图示性质的继电特性称理想继电器。
15
2、数学表达式
y
M y M
x0

M
x 0
0
-M
x
造成的影响:
继电特性
（1）改善系统性能，简化系统结构。
（2）可能会产生自激振荡，使系统不稳定。
16
旋线，这种奇点称为稳定
焦点。 系统欠阻尼运动时的相轨迹
51
4、稳定节点
1
x(t ) A1e
q1t
这时方程的解为
A2e
q2t
其中
A1
x0 x0 2
1 2
A2
x0 x0 1
1 2
(t ) A1q1e q1t A2q2e q2t x
相轨迹: 描绘相平面上的点随时间变化的曲线叫相轨迹。
相轨迹方程：x2和 x1的关系方程。
35
例1 弹簧—质量块运动系统如图。
m 是物体质量；
k 是弹性系数； x 是偏离平衡点的位移。
为方便计算令 m=k=1 ；
已知初始条件
x(0) x0 x(0) x0

第8章非线性控制系统汇总

第8章非线性控制系统汇总

自动控制原理
16
8.3.1相平面的基本概念
考虑二阶线性系统 (8-2) 式中 与 n 是阻尼比和无阻尼自然振荡频率。 设系统仅由初始条件激励。这一系统的状态可以用两 个变量， x 和 x 来描述。若令，则方程(8-2)可化为 x1 x, x2 x (8-3) 2 (8-4) x2 n x1 2n x2 (0) ，由这两 x2 (0)或 x(0)、x 只要给定初始条件 x1 (0) 、 个一阶联立微分方程便可唯一地确定系统的状态。如 此定义的变量和称为相变量(或状态变量)。图8.9(a) 绘出了初始条件为 x(0) x0 , x(0) 0，在不同阻尼下的 时间响应曲线。
自动控制原理
3
8.1.1典型非线性特性
y
1. 饱和特性 2. 死区特性 3.间隙特性
y
M 近似饱和特性 -b 0 -M b
实际饱和特性 x
图8.1 饱和非线性特性
y
K
- 0 K
-b
x

0
b
x
图8.2 死区非线性特性
图8.3 间隙非线性特性
自动控制原理
4
4. 继电器特性
y M 0 -M (a) y M - y M y M
自动控制原理
13
1.相平面法: 一种图解分析方法，适用于具有严重非线性 特性的一阶、二阶系统，该方法通过在相平面绘 制相轨迹曲线，确定非线性微分方程在不同初始 条件下解的运动形式。 2.描述函数法: 一种等效线性化的图解分析方法，该方法对 于满足结构要求的非线性系统，通过谐波线性化， 将非线性特性近似为复变增益环节，然后推广应 用频率法，分析非线性系统的稳定性或自激振荡。
自动控制原理
6

第8章非线性系统分析参考答案汇总

第8章非线性系统分析参考答案汇总

10参考答案一、 填空题1.非本质；本质2.自持振荡3.初始条件；输入信号大小4.饱和非线性；死区非线性； 间隙非线性；继电器非线性5.不稳定6.稳定；不稳定；半稳定7.自左向右；自右向左 二、 分析与计算题 1.求y(t) =ax 3(t)的描述函数。

解：由于y(t)=ax 3(t)是单值奇函数，所以其傅里叶级数展开式中 将x(t) =Asin o t 代入B 1的计算公式，可得 1 2兀 Bl =— 0' y(t)sin ©td ©t A 0=O 、 A i =0、如=0, 所以兀0=1「aA 'si n 3o ；i tsi n /d E J T =— 血A 3 si n 43td o5t兀、兀 1—cos2eo t 2刁,0 (—2—)如2.兀1 -2cos2cc t +cos 卸, •0---------- : --------- 如 2aA 3兀 2aA 3兀2aA 3兀2aA 3兀 2aA 3兀 3aA 3-44 ^2cos ^^^COs ^t广 ---------- :—2—如-^cosZ 灼t +1cos 知)d 期'b 8 2- 3 1(一兀— si n2<3t 8 48 + —sin 滋t32 兀 0)3M / A \ Bl 3aAN(A)=—= ------- A 4A =3aA 242 .设具有滞环继电器非线性特性的非线性系统结构如题图试判断系统是否存在自持振荡，若存在，则求出自持振荡的幅值和频率。

8.1所示，已知b=1, a=0.3,r=0+题图8.1解：具有滞环的继电器非线性特性的描述函数为4b a 9 4abN(A) — j 1-(—)2-j —2 兀A Y A 兀A(A>a)其描述函数负倒数特性为 可见，描述函数负倒数特性的虚部为常数 2 .Jia"a ，即 14bN(A) 4bJiA (A>a)N(A)曲线为一条虚部为:a 的直线。

第八章 习题答案

第八章 习题答案

第八章 习题解答8-1考虑并回答下面的问题：（a ）在确定非线性元件的描述函数时，要求非线性元件不是时间的函数，并要求有斜对称性，这是为什么？（b ）什么样的非线性元件是无记忆的？什么样的非线性元件是有记忆的？它们的描述函数各有什么特点？（c ）线性元件的传递函数与非线性元件的描述函数，有什么是相同的？有什么是不同的？线性元件可以有描述函数吗？非线性元件可以有传递函数吗？（d ）非线性系统线性部分的频率特性曲线与非线性元件的负倒描述函数曲线相交时，系统一定能产生稳定的自激振荡吗？ 解：（a ）描述函数法只能用来研究非线性定常系统的特性，这要求非线性元件的特性不随时间发生变化。

在用描述函数法研究非线性系统的自振特性时，要求在正弦输入下非线性特性的输出没有直流分量，这要求非线性元件的特性是斜对称的。

（b ）一般情况下用代数方程描述的非线性特性是无记忆的，根据非线性环节当前的输入就可以决定非线性环节的输出。

用微分方程描述的非线性特性是有记忆的，不能简单地根据非线性环节当前的输入决定非线性环节的输出。

无记忆非线性特性的描述函数一般为实数，有记忆非线性特性的描述函数一般为复数。

（c ）线性元件的传递函数与非线性元件的描述函数都是元件的外部描述。

线性元件的传递函数表述的是元件输出拉氏变换与输入拉氏变换之比，而非线性元件的描述函数表示的是元件在正弦输入下输出基波特性。

由传递函数可以得到系统的频率特性，而描述函数一般不是频率的函数，线性元件可以有描述函数，但传递函数只适用于线性系统，非线性系统没有传递函数。

（d ）只有稳定的交点才对应稳定的自激振荡。

8-2设非线性元件的输入、输出特性为35135()()()()y t b x t b x t b x t =++证明该非线性元件的描述函数为2413535()48N A b b A b A =++式中A 为非线性元件输入正弦信号的幅值。

解：由于非线性特性是单值斜对称的，所以10A =，10φ=。

第8章 非线性系统分析

第8章 非线性系统分析
线性二阶系统只在阻尼比=0时给予阶跃作用， 将产生周期性响应过程,这时系统处于临界稳定 状态。
实际上,一旦该系统参数发生微小变化,该周 期性状态就无法维持,要么发散至无穷大,要么 衰减至零。
而非线性系统中，除了稳定和不稳定运动形 式外，还有一个重要特征，就是系统可能发生 自持振荡----在没有周期
很小时 作为线性特性处理
较大时 将使系统静态误差增加， 系统低速不平滑性
理想死区特性的的数学描述为：
k(x a) y 0
k(x a)
x a | x | a xa
死区特性可能给控制系统带来不利影响，它会使 控制的灵敏度下降，稳态误差加大；死区特性也 可能给控制系统带来有利的影响，有些系统人为 引入死区以提高抗干扰能力。
一定条件下，可进行线性化处理，作为线性系 统来分析。这类系统统称为非本质非线性系统。
但当系统的非线性特征明显且不能进行线性化 处理时，就必须采用非线性系统理论来分析。 这类非线性称为本质非线性。
本章主要介绍分析非线性系统的两种常用方法： 相平面法和描述函数法。
如果一个控制系统包含一个或一个以上具有非线 性特性的元件或环节,则此系统即为非线性系统。
x(t) Ae ntsin(d t ) d 1 2n
式中,A、为由初始条件确定的常数。时域 响应过程是衰减振荡的。
可求出系统有一个位于相平面原点的平衡点（奇 点），不同初始条件出发的相轨迹呈对数螺旋线 收敛于该平衡点，这样的奇点称为稳定焦点。
欠阻尼二阶线性系统的响应和相轨迹
3、过阻尼运动（＞1）
1.相平面的基本概念
考察二阶非线性时不变微分方程:
..
.
x f (x, x)
•
描述该系统特性必须有两个变量 x 和 x ，

第8章非线性系统分析参考答案汇总

第8章非线性系统分析参考答案汇总

参照答案一、填空题1. 非实质；实质2. 自持振荡3. 初始条件；输入信号大小4. 饱和非线性；死区非线性；空隙非线性；继电器非线性5.不稳固 6. 稳固；不稳固；半稳固 7. 自左向右；自右向左 二、剖析与计算题1. 求 y(t )ax 3 (t ) 的描绘函数。

解：因为 y(t ) 3A 0 =0、 A 1=0、φ1=0 ，ax (t ) 是单值奇函数，所以其傅里叶级数睁开式中 将 x( t) Asin t 代入 B 1 的计算公式，可得1 B 112y(t )sin td t 02 3 sin 3 t sin td taA 02aA 3 sin 4 td t2 aA3( 1 cos2t) 2 d t22 aA 31 2cos2 t cos 2 2 td t42 aA 31 2cos2 t 1 cos4 t2d t42 aA3(3 1cos2 t 1cos4 t )d t2 aA 30 8 2 83 1 sin 2 t1 t )( 4 0 sin 4832 0 3aA 34所以N(A)B 13aA 3 3 aA 2A4 A 42．设拥有滞环继电器非线性特征的非线性系统构造如题图 8.1 所示，已知 b=1，a=0.3， 试判断系统能否存在自持振荡，若存在，则求出自持振荡的幅值和频次。

ybr=0xy10c+-a 0 a x--b(2 s 1)(0.4s 1)题图 8.1解：拥有滞环的继电器非线性特征的描绘函数为4b a 2 j 4abN(A) 1 ( )2 ( A a) A A A其描绘函数负倒数特征为1A 1 ( a )2ja( A a)N ( A)4bA4b可见，描绘函数负倒数特征的虚部为常数1曲线为一条虚部为a的直线。

a，即4bN(A)4b因为 G(s)10，所以(2 s1)(0.4s 1)G(j )101)(0.4j 1)(2j 10(1 2j )(1 0.4j )(1 4 2 )(1 0.16 2)10(1 2.4j 0.8 2)(14 2 )(1 0.16 2)1082j24(1 4 2 )(1 0.16 (1 4 2 )(1 0.16 2 )2) 由以上可知，1 ) 必有交点，并且交点为稳固的，所以会产生自持振荡。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

参考答案一、填空题1. 非本质；本质2. 自持振荡3. 初始条件；输入信号大小4. 饱和非线性；死区非线性；间隙非线性；继电器非线性5. 不稳定6. 稳定；不稳定；半稳定7. 自左向右；自右向左 二、分析与计算题1. 求3()()y t ax t =的描述函数。

解：由于3()()y t ax t =是单值奇函数，所以其傅里叶级数展开式中A 0=0、A 1=0、φ1=0，将()sin x t A t ω=代入B 1的计算公式，可得2102330340320320303031()sin 1sin sin 2sin 21cos 2()2212cos 2cos 241cos 412cos 22242311(cos 2cos 4)828231(sin 284B y t td taA t td t aA td t aA t d t aA t t d t tt aA d t aA t t d t aA πππππππωωπωωωπωωπωωπωωωπωωωπωωωπππ===-=-+=+-+==-+=-⎰⎰⎰⎰⎰⎰⎰31sin 4)003234t t aA ππωω+=所以32133()44B aA N A aA A A ===2．设具有滞环继电器非线性特性的非线性系统结构如题图8.1所示，已知b =1，a =0.3，试判断系统是否存在自持振荡，若存在，则求出自持振荡的幅值和频率。

题图8.1解：具有滞环的继电器非线性特性的描述函数为24()j()abN A A a A π=≥其描述函数负倒数特性为1j ()()4a A a N A bπ-=≥ 可见，描述函数负倒数特性的虚部为常数4a b π-，即1()N A -曲线为一条虚部为4abπ-的直线。

由于10()(21)(0.41)G s s s =++，所以222222222210(j )(2j 1)(0.4j 1)10(12j )(10.4j )(14)(10.16)10(1 2.4j 0.8)(14)(10.16)10824j (14)(10.16)(14)(10.16)G ωωωωωωωωωωωωωωωωω=++--=++--=++-=-++++由以上可知，1()N A -曲线与(j )G ω必有交点，而且交点为稳定的，因此会产生自持振荡。

令1(j )()G N A ω-=，此时有22222108(14)(10.16)244(14)(10.16)a b ωωωπωωω⎧-=⎪++⎪⎨-⎪-=⎪++⎩将b =1，a =0.3代入可得ω=5.02rad/s ，A =0.57。

所以，该系统存在自持振荡，振荡的幅值为0.57，角频率为ω=5.02rad/s 。

3.设具有死区继电器非线性特性的非线性系统结构如题图8.2所示，已知b =3，a =1。

试分析系统的稳定性，并求系统不产生自持振荡时a 与b 应满足什么关系。

题图8.2解：具有死区继电器非线性特性的描述函数为()N A A a =≥其描述函数的负倒数特性为1()()A a N A -=≥对上式求导，并令导数等于0，可知当A 时，1()N A -有极大值2abπ-。

将b =3，a =1代入，可得当A =时，1()N A -有极大值6π-，即1()N A -在负实轴上的最大值为6π-。

由于4()(0.51)(1)G s s s s =++，所以22222224(j )j (0.5j 1)(j 1)4j(10.5j )(1j )(10.25)(1)642j (10.25)(1)(10.25)(1)G ωωωωωωωωωωωωωωω=++---=++--=-++++令G (j ω)的虚部为0，即Im[G (j ω)] = 22242(10.25)(1)ωωωω-++0，可得ω=。

将ω=入到G (j ω)的实部，可得2264Re[(j )](10.25)(1)3G ωωωω--=++。

所以G (j ω)曲线与负实轴的交点是(43-，j0)。

由于43-小于6π-，所以G (j ω)曲线与1()N A -曲线必有交点，如题3解图所示。

令1(j )()G N A ω-=，可得43=-，解之得A 1=4.9896，A 2=1.0207。

由于A 2=1.0207小于A =A 2=1.0207处不稳定，而A 1=4.9896大于A =A 1=4.9896处稳定，产生自持振荡。

即系统会产生自持振荡，振幅为4.9896，频率为1.414 rad/s 。

题3解图要想使系统不产生自持振荡，只需G (j ω)曲线与1()N A -曲线没有交点即可，即满足 423ab π-<- 可得83a b π>当83a b π>时，系统不会产生自持振荡。

4. 具有理想继电器非线性特性的非线性系统如题图8.3所示，已知b =1。

(1) 当 τ=0时，系统受到扰动后会出现什么样的运动形式？(2) 当τ≠0时，如果系统输出产生一个振幅为4、角频率为1rad/s 的自持振荡，求系统参数K 和τ的值。

题图8.3解：(1)理想继电器非线性特性的描述函数为4()b N A Aπ= 其负倒数特性为1()4A N A bπ-=- 将b =1代入可得1()4A N A π-=-，即1()N A -曲线为负实轴。

当 τ=0时，线性部分的开环幅相频特性为2222222(j )j (j 1)(j 2)j(1j )(2j )(1)(4)32j (1)(4)(1)(4)KG K K K K ωωωωωωωωωωωωωωω=++---=++--=-++++令G (j ω)的虚部为0，即Im[G (j ω)] = 2222(1)(4)K K ωωωω-++=0，可得ω=。

将ω=入到G (j ω)的实部，可得223Re[(j )](1)(4)6K KG ωωωω--=++。

所以G (j ω)曲线与负实轴的交点是(6K-，j0)，如题4解图所示。

题4解图所以G (j ω)曲线与1()N A -曲线必有交点，并且交点坐标与A 和K 值有关，并且，当A 增大时，1()N A -曲线将从不稳定区进入稳定区域，所以交点为稳定点，会产生自持振荡。

因此，系统受到扰动后会产生稳定的自持振荡。

(2) 当τ≠0时，线性部分的开环幅相频特性为j (j )j (j 1)(j 2)Ke G τωωωωω-=++由于系统要产生振幅为4、角频率为1rad/s 的自持振荡，即ω=1rad/s 。

14()441A N A b πππ-=-=-=-⨯ j (j1)j 1(j 11)(j 12)Ke G τ-===++π=，K =9.935。

又因为o (j 1)57.390arctan1arctan0.5180G τ∠=----=-所以τ=0.32。

5. 判断如题图8.4所示的系统是否稳定，是否存在自持振荡。

G(a) (b) (c) (d)题图8.4解：(a) G (j ω)曲线与1()N A -曲线有交点B ，但当A 增大时，1()N A -由G (j ω)左侧进入右侧，即从稳定区进入不稳定区，所以交点B 不是稳定工作点，不会产生自持振荡。

(b) G (j ω)曲线与1()N A -曲线有交点B 、C 。

对于B 点，当A 增大时，1()N A -由G (j ω)左侧稳定区进入右侧不稳定区，所以交点B 不是稳定工作点，不会产生自持振荡。

对于交点C ，当A 增大时，1()N A -由G (j ω)右侧不稳定区进入左侧稳定区，所以交点C 是稳定工作点，会产生自持振荡。

(c) G (j ω)曲线与1()N A -曲线有交点B 、C 。

对于B 点，当A 增大时，1()N A -由G (j ω)右侧稳定区进入左侧不稳定区，所以交点B 不是稳定工作点，不会产生自持振荡。

对于交点C ，当A 增大时，1()N A -由G (j ω)右侧不稳定区进入左侧稳定区，所以交点C 是稳定工作点，会产生自持振荡。

(d) G (j ω)曲线与1()N A -曲线有交点B ，但当A 增大时，1()N A -由G (j ω)的不稳定区进入稳定区，所以交点B 是稳定工作点，会产生自持振荡。

6. 将题图8.5所示的非线性系统化为串联形式，并求出等效的开环传递函数。

题图8.5解：系统结构图的简化如题6解图所示。

题6解图所以2()KsG s Ts K=+。

7. 设具有死区继电器非线性特性的非线性系统结构如题图8.6所示，已知a =1，b =3。

试用描述函数法分析K 值与系统产生自持振荡的关系，并求K =3时自持振荡的振幅和振荡频率。

题图8.6解：具有死区继电器非线性特性的描述函数为()N A A a =≥其描述函数的负倒数特性为1()()A a N A -=≥对上式求导，并令导数等于0，可知当A 时，1()N A -有极大值2abπ-。

将b =3，a =1代入，可得当A =时，1()N A -有极大值6π-，即1()N A -在负实轴上的最大值为6π-。

由于()(0.51)(1)KG s s s s =++，所以2222222(j )j (0.5j 1)(j 1)j(10.5j )(1j )(10.25)(1)1.5(10.5)j (10.25)(1)(10.25)(1)KG K K K ωωωωωωωωωωωωωωω=++---=++--=-++++令G (j ω)的虚部为0，即Im[G (j ω)] = 222(10.5)0(10.25)(1)K ωωωω-=++，可得ω=。

将ω=代入到G (j ω)的实部，可得221.5Re[(j )](10.25)(1)3K KG ωωωω--=++。

所以G (j ω)曲线与负实轴的交点是(3K-，j0)，如题7解图所示。

题7解图当G (j ω)曲线与1()N A -曲线有交点时，即1(j )()G N A ω-=时系统产生自持振荡，从而可得36K π-<-时产生自持振荡，解之得2K π>，所以当2K π>时系统会产生自持振荡。

当K =3时，221.53Re[(j )]1(10.25)(1)G ωωωω-⨯=-++，所以11()N A -===-解之得A 1=3.6756，A 2=1.0392。

由于A 2=1.0392小于A =A 2=1.0392处不稳定，而A 1=3.6756大于A =，所以系统在A 1=3.6756处稳定，产生自持振荡。

即系统会产生自持振荡，振幅为3.6756，频率为1.414 rad/s 。

所以，当K =3时系统的振荡振幅A =3.6756，振荡频率ω=。

8. 设非线性系统结构如题8.7所示，已知a 1=a 2=a 3=1，k 1=k 2= k 3=1，b =1。

分析当T =0.5时系统是否存在自持振荡，如果存在，求出振荡时的振幅和频率，并讨论参数T 的变化对系统自振的影响。