对勾函数的性质课件

对勾函数一、定义对勾函数是由两个幂函数相加得到的，对勾函数是一种类似于反比例函数的一般双曲函数，其标准形式为f(x)=ax+（其中ab>0）。

由于函数图像形似两个中心对称的对勾，因此得名“对勾函数”，又被称为“双勾函数”、“勾函数”、“对号函数”、“双飞燕函数”等。

在许多情况下，为了简化分析，常取a=b=1，即函数形式为f(x)=x+。

研究初等函数的一般路径，背景—概念—图象—性质—应用二、图象及性质图像特征：1、对勾函数的图像是分别以y 轴和直线y=ax 为渐近线的两支曲线。

2、图像上任意一点到两条渐近线的距离之积恰为渐近线夹角（0-180°）的正弦值与|b|的乘积。

3、函数图像整体呈两个“对勾”的形状，且关于原点呈中心对称。

定义域：，即除了x=0外，所有实数都是其定义域内的元素。

值域：。

单调性：函数在(−∞,−1)∪(1,+∞)上单调递增，在(1,0)∪(0,1)上单调递减。

奇偶性：对勾函数是奇函数，即满足f(−x)=−f(x)。

x 122严禁复制三、题型1、基础计算题给定对勾函数表达式，求函数在特定点的值或特定区间的最值。

2.、图像结合题根据对勾函数的图像，判断函数在哪些区间内满足特定条件（如大于某值、小于某值）。

利用图像分析函数与直线、其他曲线的交点情况。

3.、综合应用题求最值问题：利用对勾函数的性质，可以快速求解形如ax+（ab>0）的函数的最值问题。

不等式证明：在不等式证明中，对勾函数的性质也常被用来进行放缩或构造反例。

实际问题建模：在某些经济学问题中，如成本分析、收益最大化等，也可能涉及到对勾函数的应用。

4、参数变化分析：探讨参数a 和b 变化时，对勾函数图像和性质的变化规律。

5、复杂函数组合将对勾函数与其他函数（如二次函数、指数函数等）组合，分析新函数的性质和应用。

四、解题步骤1、对勾函数求最值问题的解题步骤（1）理解函数形式确认函数f(x)=ax+的形式，注意a 和b 都是正数且不相等。

对勾函数的图象及其性质对勾函数，是一种类似于反比例函数的一般函数。

所谓的对勾函数，是形如())0(>+=a xa x x f 的函数，是一种教材上没有但考试老喜欢考的函数，所以更加要注意和学习。

一般的函数图像形似两个中心对称的对勾，故名对勾函数，又被称为“双勾函数”、"勾函数"等。

也被形象称为“耐克函数”问题1：已知函数()x x x f 1+=，（1） 求该函数的定义域；（2） 判断该函数的单调性和奇偶性；（3） 求该函数的值域；（4） 画出该函数的图像。

问题2：由函数()x x x f 1+=的图像性质类比出函数())0(>+=a xa x x f 的性质。

1、定义域：{}0≠x x 2、值域： (][)+∞-∞-,22,a a ， 在正数部分仅当x=a 取最小值2a ，在负数部分仅当x=a -取最大值-2a3、奇偶性：奇函数，关于原点对称4、单调区间： (]a -∞-,单调递增 [a -,0)] 单调递减 (0,a ] 单调递减 [a ，+∞) 单调递增问题3：如果函数()xx x f b2+=在(]4,0上单调递减，在[)+∞,4上单调递增，求实数b 的值。

问题4：当()xa x x f +=中的条件变为0<a 时，单调性怎样？ 例1、求函数()x x x f 3+=在下列条件下的值域。

（1）()()+∞∞-,00, ； （2）()2,0； （3）(]2,3--； （4）(]2,1；例2 、函数())0(>+=a xa x x f 在区间[])0(,>m n m 取得最大值6，取得最小值2，那么此函数在区间[]m n --,上是否存在最值？请说明理由。

例3、求下列函数的值域。

（1）1)(2+=x x x f （2）x x x x f 23)(2++= （3）15)(-+=x x x f 练习：1、已知函数1)(+=x x x f ，求该函数的定义域、值域，判断单调性和奇偶性，并画出图像； 2、求函数33)(22+-=x x x f 的值域； 3、 求函数13)(+=x x f 在]5,2[上的最大值和最小值。

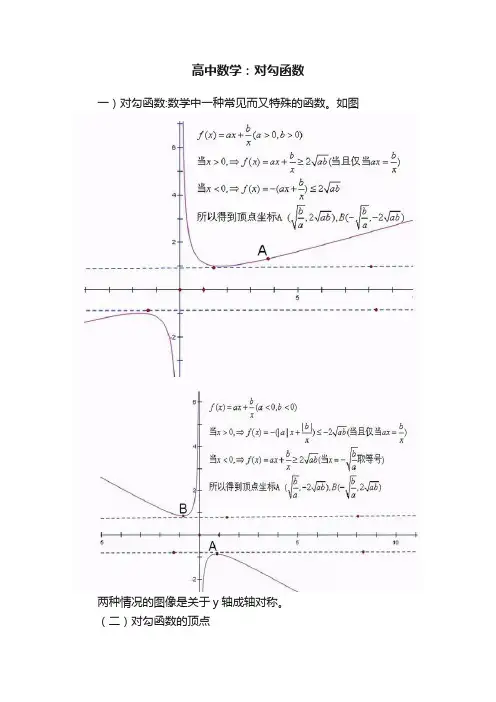
高中数学：对勾函数
一）对勾函数:数学中一种常见而又特殊的函数。

如图
两种情况的图像是关于y轴成轴对称。

（二）对勾函数的顶点
对勾函数性质的研究离不开均值不等式。

利用均值不等式可以得到：
当x>0时，
当x＜0时，
即对勾函数的定点坐标：
(三) 对勾函数的定义域、值域
由（二）得到了对勾函数的顶点坐标，从而我们也就确定了对勾函数的定义域、值域等性质。

定义域：x≠0
值域：
（四）对勾函数的单调性：参考函数图像
(五) 对勾函数的渐进线
(六) 对勾函数的奇偶性：对勾函数在定义域内是奇函数练习：。

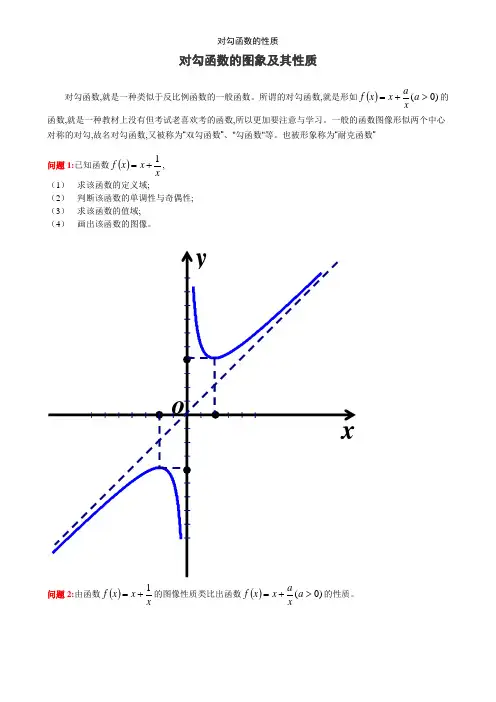
对勾函数的图象及其性质对勾函数,就是一种类似于反比例函数的一般函数。

所谓的对勾函数,就是形如())0(>+=a xa x x f 的函数,就是一种教材上没有但考试老喜欢考的函数,所以更加要注意与学习。

一般的函数图像形似两个中心对称的对勾,故名对勾函数,又被称为“双勾函数”、"勾函数"等。

也被形象称为“耐克函数”问题1:已知函数()x x x f 1+=, （1）求该函数的定义域; （2）判断该函数的单调性与奇偶性; （3）求该函数的值域; （4） 画出该函数的图像。

问题2:由函数()x x x f 1+=的图像性质类比出函数())0(>+=a xa x x f 的性质。

1、定义域:{}0≠x x 2、值域: (][)+∞-∞-,22,a a Y , 在正数部分仅当x=a 取最小值2a ,在负数部分仅当x=a -取最大值-2a3、奇偶性:奇函数,关于原点对称4、单调区间: (]a -∞-,单调递增 [a -,0)] 单调递减 (0, a ] 单调递减 [a ,+∞) 单调递增问题3:如果函数()xx x f b2+=在(]4,0上单调递减,在[)+∞,4上单调递增,求实数b 的值。

问题4:当()xa x x f +=中的条件变为0<a 时,单调性怎样？ 例1、求函数()x x x f 3+=在下列条件下的值域。

(1)()()+∞∞-,00,Y ; (2)()2,0; (3)(]2,3--; (4)(]2,1;例 2 、函数())0(>+=a xa x x f 在区间[])0(,>m n m 取得最大值6,取得最小值2,那么此函数在区间[]m n --,上就是否存在最值？请说明理由。

例3、求下列函数的值域。

(1)1)(2+=x x x f (2)x x x x f 23)(2++= (3)15)(-+=x x x f 练习:1、已知函数1)(+=x x x f ,求该函数的定义域、值域,判断单调性与奇偶性,并画出图像; 2、求函数33)(22+-=x x x f 的值域; 3、 求函数13)(+=x x f 在]5,2[上的最大值与最小值。

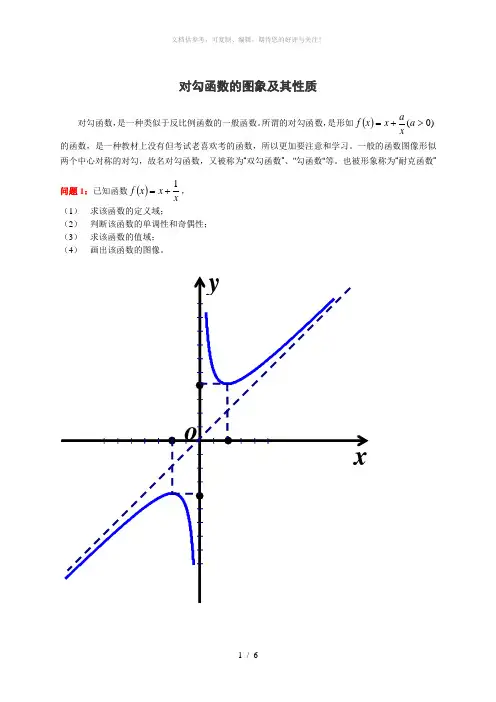
对勾函数的图象及其性质对勾函数，是一种类似于反比例函数的一般函数。

所谓的对勾函数，是形如())0(>+=a xa x x f 的函数，是一种教材上没有但考试老喜欢考的函数，所以更加要注意和学习。

一般的函数图像形似两个中心对称的对勾，故名对勾函数，又被称为“双勾函数”、"勾函数"等。

也被形象称为“耐克函数” 问题1：已知函数()x x x f 1+=， （1）求该函数的定义域； （2）判断该函数的单调性和奇偶性； （3）求该函数的值域； （4） 画出该函数的图像。

问题2：由函数()x x x f 1+=的图像性质类比出函数())0(>+=a xa x x f 的性质。

1、定义域：{}0≠x x 2、值域： (][)+∞-∞-,22,a a ， 在正数部分仅当x=a 取最小值2a ，在负数部分仅当x=a -取最大值-2a3、奇偶性：奇函数，关于原点对称4、单调区间： (]a -∞-,单调递增 [a -,0)] 单调递减 (0, a ] 单调递减 [a ，+∞) 单调递增问题3：如果函数()xx x f b2+=在(]4,0上单调递减，在[)+∞,4上单调递增，求实数b 的值。

问题4：当()xa x x f +=中的条件变为0<a 时，单调性怎样？ 例1、求函数()x x x f 3+=在下列条件下的值域。

（1）()()+∞∞-,00, ； （2）()2,0； （3）(]2,3--； （4）(]2,1；例2 、函数())0(>+=a xa x x f 在区间[])0(,>m n m 取得最大值6，取得最小值2，那么此函数在区间[]m n --,上是否存在最值？请说明理由。

例3、求下列函数的值域。

（1）1)(2+=x x x f （2）xx x x f 23)(2++= （3）15)(-+=x x x f 练习：1、已知函数1)(+=x x x f ，求该函数的定义域、值域，判断单调性和奇偶性，并画出图像； 2、求函数33)(22+-=x x x f 的值域；3、 求函数13)(+=x x f 在]5,2[上的最大值和最小值。