4多元线性回归实验的报告材料

计量经济学实验报告多元线性回归、多重共线性、异方差实验报告、研究目的和要求:随着经济的发展，人们生活水平的提高，旅游业已经成为中国社会新的经济增长点。

旅游产业是一个关联性很强的综合产业，一次完整的旅游活动包括吃、住、行、游、购、娱六大要素，旅游产业的发展可以直接或者间接推动第三产业、第二产业和第一产业的发展。

尤其是假日旅游，有力刺激了居民消费而拉动内需。

2012年，我国全年国内旅游人数达到30.0亿人次，同比增长13.6%，国内旅游收入2.3万亿元，同比增长19.1%。

旅游业的发展不仅对增加就业和扩大内需起到重要的推动作用，优化产业结构，而且可以增加国家外汇收入，促进国际收支平衡，加强国家、地区间的文化交流。

为了研究影响旅游景区收入增长的主要原因，分析旅游收入增长规律，需要建立计量经济模型。

影响旅游业发展的因素很多，但据分析主要因素可能有国内和国际两个方面，因此在进行旅游景区收入分析模型设定时，引入城镇居民可支配收入和旅游外汇收入为解释变量。

旅游业很大程度上受其产业本身的发展水平和从业人数影响，固定资产和从业人数体现了旅游产业发展规模的内在影响因素，因此引入旅游景区固定资产和旅游业从业人数作为解释变量。

因此选取我国31个省市地区的旅游业相关数据进行定量分析我国旅游业发展的影响因素。

二、模型设定根据以上的分析，建立以下模型57丫=仇+ B1X 1+ 伍X 2+ B 3X 3+ 34 X 4 +Ut参数说明：旅游景区营业收入/万元X 1 旅游业从业人员/人 X 2 旅游景区固定资产/万元 X 3 旅游外汇收入/万美元 X 4城镇居民可支配收入/元收集到的数据如下（见表 2.1）:表2.1 2011年全国旅游景区营业收入及相关数据（按地区分） 地区 北 京 天 津 河 北 山 西内蒙 古辽 丿jA吉营业收入145249.0148712.3182226.8729465.0 70313.0 25665.3 20389.3 从业人 数1454 66 247879645771 3626 64812906 固定资产694252.393529.67 420342.7121809.7206819.146573.27 87827.16外汇收入可支配 收入5416017555 447655671967097 2713138528 32903. 0326920. 8618292. 2318123. 8720407.20466. 8417796.林0 6 57 黑龙38367.8 3034 137426.215696.91762江 1 1 7 18 上194762. 9110 563007.4 57511 36230. 海 3 6 4 8 48 江316051. 1401 1195000. 56529 26340. 苏65 54 60 7 73 浙385976. 1324 1110975. 45417 30970. 江92 59 20 3 68 安79562.7 5584 139769.0 11791 18606. 徽 5 0 2 8 13 福155378. 8030 151897.6 36344 24907. 建95 3 9 4 40 江54961.6 4179 17494.85528.05 41500西 6 1 87 山116995. 1430 327733.2 25507 22791. 东67 26 9 6 84 河222108. 7016 482005.3 18194.54903南33 4 2 80 湖104565. 6276 243794.618373.94018北58 7 2 87 湖118180. 806110143 18844.257226.7南87 5 4 05 广476345. 2265 1160675. 13906 26897. 东50 39 4 19 48 广66195.5 4987 143982.0 10518 18854. 西 5 6 3 8 06 海29081.6 3075 18368.70386.55 37615南0 9 95 重86713.6 5016 230124.0 96806 20249.庆7 0 0 70 四218624. 7075 464763.5 17899.59383川03 6 2 12 贵42214.1 2768 16495.62415.21 13507州 4 3 01 云135897. 6267 348426.0 16086 18575. 南97 9 4 1 62 西30406.7 462971.0 16195.6023 12963藏 3 3 56 陕48692.1 5707 154529.1 12950 18245. 西7 7 9 5 23 —30949.0 3128 14988.56684.68 1740肃0 0 68 青15603.1 -J 638.43 8741 9851.28 2659海31 /宁49509.8 1219 17578.23149.90 620夏 6 6 92 新28993.1 4045 15513.52280.36 46519疆 1 1 62 数据来源：1.中国统计年鉴2012，2.中国旅游年鉴2012。

第1篇一、实验目的本次实验旨在通过多元线性回归模型，分析多个自变量与因变量之间的关系，掌握多元线性回归模型的基本原理、建模方法、参数估计以及模型检验等技能，提高运用计量经济学方法解决实际问题的能力。

二、实验背景随着经济的发展和社会的进步，影响一个变量的因素越来越多。

在经济学、管理学等领域，多元线性回归模型被广泛应用于分析多个变量之间的关系。

本实验以某地区居民消费支出为例，探讨影响居民消费支出的因素。

三、实验数据本实验数据来源于某地区统计局，包括以下变量：1. 消费支出（Y）：表示居民年消费支出，单位为元；2. 家庭收入（X1）：表示居民家庭年收入，单位为元；3. 房产价值（X2）：表示居民家庭房产价值，单位为万元；4. 教育水平（X3）：表示居民受教育程度，分为小学、初中、高中、大专及以上四个等级；5. 通货膨胀率（X4）：表示居民消费价格指数，单位为百分比。

四、实验步骤1. 数据预处理：对数据进行清洗、缺失值处理和异常值处理，确保数据质量。

2. 模型设定：根据理论知识和实际情况，建立多元线性回归模型：Y = β0 + β1X1 + β2X2 + β3X3 + β4X4 + ε其中，Y为因变量，X1、X2、X3、X4为自变量，β0为截距项，β1、β2、β3、β4为回归系数，ε为误差项。

3. 模型估计：利用统计软件（如SPSS、R等）对模型进行参数估计，得到回归系数的估计值。

4. 模型检验：对估计得到的模型进行检验，包括以下内容：（1）拟合优度检验：通过计算R²、F统计量等指标，判断模型的整体拟合效果；（2）t检验：对回归系数进行显著性检验，判断各变量对因变量的影响是否显著；（3）方差膨胀因子（VIF）检验：检验模型是否存在多重共线性问题。

5. 结果分析：根据模型检验结果，分析各变量对因变量的影响程度和显著性，得出结论。

五、实验结果与分析1. 拟合优度检验：根据计算结果，R²为0.812，F统计量为30.456，P值为0.000，说明模型整体拟合效果较好。

实验报告课程名称计量经济学实验项目名称多元线性回归自相关异方差多重共线性班级与班级代码 08国际商务1班实验室名称（或课室）实验楼910 专业国际商务任课教师刘照德学号： 0825******* 姓名：张柳文实验日期： 2011 年 06 月 23日广东商学院教务处制姓名张柳文实验报告成绩评语：指导教师（签名）年月日说明：指导教师评分后，实验报告交院（系）办公室保存。

计量经济学实验报告实验项目：多元线性回归、自相关、异方差、多重共线性实验目的：掌握多元线性回归模型、自相关模型、异方差模型、多重共线性模型的估计和检验方法和处理方法实验要求：选择方程进行多元线性回归；熟悉图形法检验和掌握D-W 检验，理解广义差分法变换和掌握迭代法；掌握Park或Glejser检验，理解同方差性变换；实验原理：普通最小二乘法图形检验法 D-W检验广义差分变换加权最小二乘法 Park检验等实验步骤：首先：选择数据为了研究影响中国税收收入增长的主要原因，选择国内生产总值（GDP）、财政支出（ED）、商品零售价格指数（RPI）做为解释变量，对税收收入（Y）做多元线性回归。

从《中国统计年鉴》2011中收集1978—2009年各项影响因素的数据。

如下表所示：实验一：多元线性回归1、将数据导入eviews5.0后，分别对三个解释变量与被解释变量做散点图，选择两个变量作为group打开，在数据表“group”中点击view/graph/scatter/simple scatter，出现数据的散点图，分别如下图所示：从散点图看，变量间不一定呈现线性关系，可以试着作线性回归。

2、进行因果关系检验在“workfile”中按住“ctrl”键，点击所要选择的变量，作为组打开后，在“View”下拉列表中选择“Grange Causality”，滞后期为2，得出如下结果：Pairwise Granger Causality TestsDate: 06/23/11 Time: 16:14Sample: 1978 2009Lags: 2Null Hypothesis: Obs F-Statistic ProbabilityED does not Granger Cause Y 30 8.90261 0.00120Y does not Granger Cause ED 18.8091 1.0E-05Pairwise Granger Causality TestsDate: 06/23/11 Time: 16:15Sample: 1978 2009Lags: 2Null Hypothesis: Obs F-Statistic ProbabilityGDP does not Granger Cause Y 30 1.01199 0.37790Y does not Granger Cause GDP 0.91874 0.41208Pairwise Granger Causality TestsDate: 06/23/11 Time: 16:19Sample: 1978 2009Lags: 2Null Hypothesis: Obs F-Statistic ProbabilityRPI does not Granger Cause Y 30 0.66167 0.52479Y does not Granger Cause RPI 1.60624 0.22067 从因果关系检验看，ED明显影响财政收入Y，其他两个因素影响不显著。

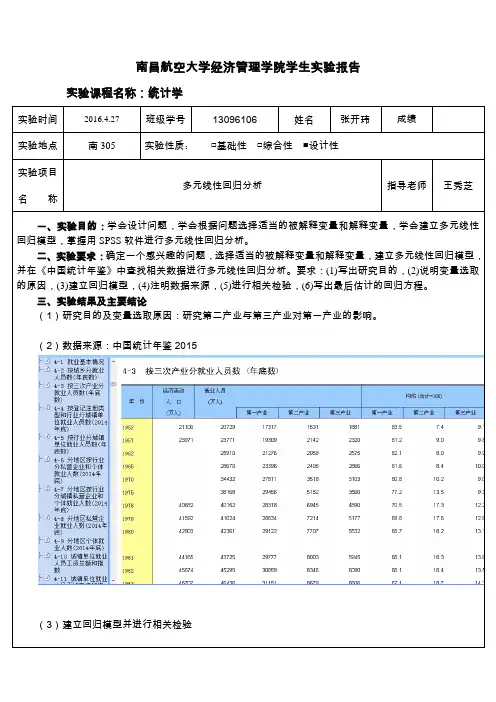
南昌航空大学经济管理学院学生实验报告
实验课程名称：统计学
一、实验目的：学会设计问题，学会根据问题选择适当的被解释变量和解释变量，学会建立多元线性回归模型，掌握用SPSS软件进行多元线性回归分析。

二、实验要求：确定一个感兴趣的问题，选择适当的被解释变量和解释变量，建立多元线性回归模型，并在《中国统计年鉴》中查找相关数据进行多元线性回归分析。

要求：(1)写出研究目的，(2)说明变量选取的原因，(3)建立回归模型，(4)注明数据来源，(5)进行相关检验，(6)写出最后估计的回归方程。

三、实验结果及主要结论
（1）研究目的及变量选取原因：研究第二产业与第三产业对第一产业的影响。

（2）数据来源：中国统计年鉴2015
（3）建立回归模型并进行相关检验
由表可以看出，当增加一个解释变量时，回归方程调整的R2由0.962增加为1.000。

方程的拟合优度较高。

两个回归方程F统计量的显著性水平都接近与0，表明两个方程都是显著的。

由表可知，第一个方程只有一个解释变量，回归系数显著；第二个方程有两个解释变量，其中第三产。

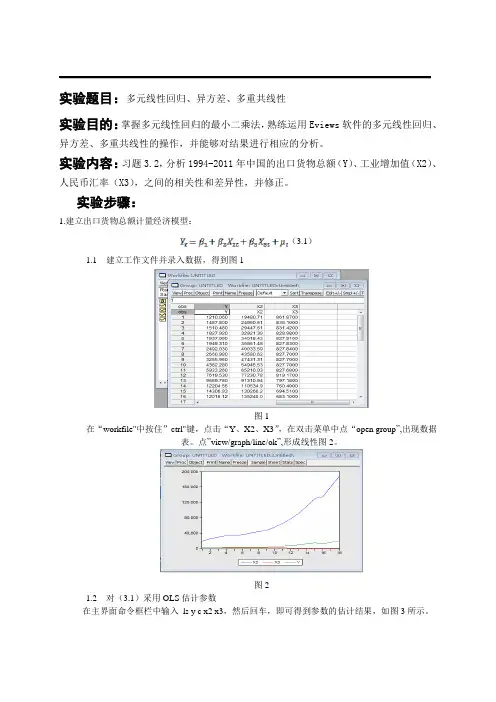
实验题目：多元线性回归、异方差、多重共线性实验目的：掌握多元线性回归的最小二乘法，熟练运用Eviews软件的多元线性回归、异方差、多重共线性的操作，并能够对结果进行相应的分析。

实验内容：习题3.2，分析1994-2011年中国的出口货物总额（Y）、工业增加值（X2）、人民币汇率（X3），之间的相关性和差异性，并修正。

实验步骤：1.建立出口货物总额计量经济模型：（3.1）1.1建立工作文件并录入数据，得到图1图1在“workfile"中按住”ctrl"键，点击“Y、X2、X3”，在双击菜单中点“open group”,出现数据表。

点”view/graph/line/ok”,形成线性图2。

图21.2对（3.1）采用OLS估计参数在主界面命令框栏中输入ls y c x2 x3，然后回车，即可得到参数的估计结果，如图3所示。

图 3根据图3中的数据，得到模型（3.1）的估计结果为（8638.216）（0.012799）（9.776181）t=(-2.110573) (10.58454) (1.928512)F=522.0976从上回归结果可以看出，拟合优度很高，整体效果的F检验通过。

但当=0.05时，= 2.131.有重要变量X3的t检验不显著，可能存在严重的多重共线性。

2．多重共线性模型的识别2.1计算解释变量x2、x3的简单相关系数矩阵。

点击Eviews主画面的顶部的Quick/Group Statistics/Correlatios弹出对话框在对话框中输入解释变量x2、x3，点击OK，即可得出相关系数矩阵（同图4）。

相关系数矩阵图4由图4相关系数矩阵可以看出，各解释变量相互之间的相关系数较高，证实解释变量之间存在多重共线性。

2.2多重共线性模型的修正将各变量进行对数变换，在对以下模型进行估计。

利用eviews软件，对、X2、X3分别取对数，分别生成lnY、lnX2、lnX3的数据，采用OLS方法估计模型参数，得到回归结果，如图：图5图6模型估计结果为：ln=-20.52+1.5642lnX2+1.7607lnX3(5.4325) (0.0890) (0.6821)t =-3.778 17.578 2.581F=539.736该模型可决系数很高，F检验值，明显显著。

计量经济学实验报告多元线性回归自相关 Document number【980KGB-6898YT-769T8CB-246UT-18GG08】实验报告课程名称计量经济学实验项目名称多元线性回归自相关异方差多重共线性班级与班级代码 08国际商务1班实验室名称（或课室）实验楼910 专业国际商务任课教师刘照德学号： 043姓名：张柳文实验日期： 2011 年 06 月 23日广东商学院教务处制姓名张柳文实验报告成绩评语：指导教师（签名）年月日说明：指导教师评分后，实验报告交院（系）办公室保存。

计量经济学实验报告实验项目：多元线性回归、自相关、异方差、多重共线性实验目的：掌握多元线性回归模型、自相关模型、异方差模型、多重共线性模型的估计和检验方法和处理方法实验要求：选择方程进行多元线性回归；熟悉图形法检验和掌握D-W 检验，理解广义差分法变换和掌握迭代法；掌握Park或Glejser检验，理解同方差性变换；实验原理：普通最小二乘法图形检验法 D-W检验广义差分变换加权最小二乘法 Park检验等实验步骤：首先：选择数据为了研究影响中国税收收入增长的主要原因，选择国内生产总值（GDP）、财政支出（ED）、商品零售价格指数（RPI）做为解释变量，对税收收入（Y）做多元线性回归。

从《中国统计年鉴》2011中收集1978—2009年各项影响因素的数据。

如下表所示：199219931994199519961997199819992000200120022003200420052006200720082009实验一：多元线性回归1、将数据导入后，分别对三个解释变量与被解释变量做散点图，选择两个变量作为group打开，在数据表“group”中点击view/graph/scatter/simple scatter，出现数据的散点图，分别如下图所示：从散点图看，变量间不一定呈现线性关系，可以试着作线性回归。

2、进行因果关系检验在“workfile”中按住“ctrl”键，点击所要选择的变量，作为组打开后，在“View”下拉列表中选择“Grange Causality”，滞后期为2，得出如下结果：Pairwise Granger Causality TestsDate: 06/23/11 Time: 16:14Sample: 1978 2009Lags: 2Null Hypothesis:Obs F-Statistic ProbabilityED does not Granger Cause Y30Y does not Granger Cause EDPairwise Granger Causality TestsDate: 06/23/11 Time: 16:15Sample: 1978 2009Lags: 2Null Hypothesis:Obs F-Statistic ProbabilityGDP does not Granger Cause Y30Y does not Granger Cause GDPPairwise Granger Causality TestsDate: 06/23/11 Time: 16:19Sample: 1978 2009Lags: 2Null Hypothesis:Obs F-Statistic ProbabilityRPI does not Granger Cause Y30Y does not Granger Cause RPI从因果关系检验看，ED明显影响财政收入Y，其他两个因素影响不显着。

南昌大学实验报告学生姓名：李丹学号： 5400112052 专业班级：经济学121 座位号： 43实验类型：□验证□综合□设计□创新实验日期： 4.15.2014 实验成绩：（以下主要内容由学生完成）一、实验项目名称：线形回归计算机习题C3.4.二、实验目的：能在Eview 环境下实现多元线形回归，并理解和掌握相关概念。

三、实验基本原理：最小二乘法四、主要仪器设备及耗材：EView软件电脑五、实验数据（按题目填写相应数据文件的名称）：ATTEND.RAW六、实验步骤及处理结果（1）open workfile ATTEND.RAW,打开atndrte,点击view，选择descripitive statistic,选择stats tableATNDRTEMean 81.70956Median 87.50000Maximum 100.0000Minimum 6.250000同样方法打开priGPA和ACTACTMean 22.51029Median 22.00000Maximum 32.00000Minimum 13.00000TERMGPAMean 2.601000Median 2.670000Maximum 4.000000（2）打开workfile HPRICE1.RAW,选定atndrte，priGPA和ACT ，右击选择asequations ,在点击新出的表格中的view,点击representationsEstimation Command:=========================LS ATNDRTE ACT PRIGPA CEstimation Equation:=========================ATNDRTE = C(1)*ACT + C(2)*PRIGPA + C(3)Substituted Coefficients:=========================ATNDRTE = -1.71655295804*ACT + 17.2605911661*PRIGPA + 75.7004050638方程为ATNDRTE = -1.71655295804*ACT + 17.2605911661*PRIGPA + 75.7004050638解释截距：当PRIGPA和ACT保持不变时，估计ATNDRTE为77.7701914749 （3）PRIGPA的斜率系数表示当一个学生ACT保持不变时，PRIGPA增加一个单位的变化，会导致ATNDRTE发生增加17%的变化。

多元线性回归模型实验报告计量经济学多元线性回归模型是一种比较常见的经济学建模方法，其可用于对多个自变量和一个因变量之间的关系进行分析和预测。

在本次实验中，我们将使用一个包含多个自变量的数据集，对其进行多元线性回归分析，并对分析结果进行解释。

数据集介绍本次实验使用的数据集来自于UCI Machine Learning Repository，数据集包含有关汽车试验的多个自变量和一个连续因变量。

数据集中包含了204条记录，其中每条记录包含了一辆汽车的14个属性，分别是：MPG（燃油效率），气缸数（Cylinders）、排量（Displacement）、马力（Horsepower）、重量（Weight）、加速度（Acceleration）、模型年（Model Year）、产地（Origin）等。

模型建立在进行多元线性回归分析之前，我们首先需要对数据进行预处理。

为了确保数据的可用性，我们需要先检查数据是否存在缺失值和异常值。

如果有，需要进行相应的处理，以确保因变量和自变量之间的关系受到了正确地分析。

在对数据进行预处理之后，我们可以使用Python中的statsmodels包来对数据进行多元线性回归分析。

具体建模过程如下：```import statsmodels.api as sm# 准备自变量和因变量数据X = data[['Cylinders', 'Displacement', 'Horsepower', 'Weight', 'Acceleration', 'Model Year', 'Origin']]y = data['MPG']# 添加常数项X = sm.add_constant(X)# 拟合线性回归模型model = sm.OLS(y, X).fit()# 输出模型摘要print(model.summary())```在上述代码中，我们首先通过data[['Cylinders', 'Displacement', 'Horsepower', 'Weight', 'Acceleration', 'Model Year', 'Origin']]选择了所有自变量列，用于进行多元线性回归分析；然后，我们又通过`sm.add_constant(X)`，向自变量数据中添加了一列全为1的常数项，用于对截距进行建模；最后，我们使用`sm.OLS(y, X).fit()`来拟合线性回归模型，并使用`model.summary()`输出模型摘要。

回归分析实验报告实验报告实验课程：[信息分析]专业：[信息管理与信息系统]班级：[ ]学⽣姓名：[ ]指导教师：[请输⼊姓名]完成时间：2013年6⽉28⽇⼀．实验⽬的多元线性回归简单地说是涉及多个⾃变量的回归分析，主要功能是处理两个变量之间的线性关系，建⽴线性数学模型并进⾏评价预测。

本实验要求掌握附带残差分析的多元线性回归理论与⽅法。

⼆．实验环境实验室308教室三．实验步骤与内容1打开应⽤统计学实验指导书，新建excel表2．打开SPSS，将数据输⼊。

3．调⽤SPSS主菜单的分析——>回归——>线性命令，打开线性回归对话框，指定因变量（⼯业GDP⽐重）和⾃变量（⼯业劳动者⽐重、固定资产⽐重、定额资⾦流动⽐重），以及回归⽅式；逐步回归（图1）图1 线性对话框4.在统计栏中，选择估计以输出回归系数B的估计值、t统计量等，选择Duribin-watson以进⾏DW检验；选择模型拟合度输出拟合优度统计量值，如R^2、F统计量值等（图2）。

图2 统计量栏5．在线性回归栏中选择直⽅图和正态概率图以绘制标准化残差的直⽅图和残差分析与正态概率⽐较图，以标准化预测值为纵坐标，标准化残差值为横坐标，绘制残差与Y的预测值的散点图，检验误差变量的⽅差是否为常数（图3）。

图3 绘制栏6.提交分析，并在输出窗⼝中查看结果，以及对结果进⾏分析。

系统在进⾏逐步分析的过程中产⽣了两个回归模型，模型1先将与因变量（销售收⼊）线性关系的⾃变量地区⼈⼝引⼊模型，建⽴他们之间的⼀元线性关系。

⽽后逐步引⼊其他变量，表1中模型2表明将⾃变量⼈均收⼊引⼊，建⽴⼆元线性回归模型，可见地区⼈⼝和⼈均收⼊对销售收⼊的影响同等重要。

从表2中给出了两个模型各⾃的R^2和调整后的R^2,第⼀个模型中的销售收⼊中有99%的变动可以⽤地区⼈⼝的变动解释，第⼆个模型中地区⼈⼝和⼈均收⼊的变动可以解释销售收⼊中99.9%的变动，显然第⼆个模型的拟合数据效果⽐较好⼀点。

线性回归法实验报告线性回归是一种基本的统计学方法，用来建立一个自变量和一个或多个因变量之间的线性关系模型。

其基本原理是寻找最佳的直线来拟合数据，以预测或解释因变量的数值。

本篇实验报告将介绍线性回归的基本原理和实验过程，并通过一个具体的案例进行分析和实现。

二、实验目的1. 理解线性回归的基本原理和模型；2. 掌握如何使用Python进行线性回归分析；3. 使用线性回归模型分析实际数据，并对结果进行解释和评估。

三、实验步骤1. 数据准备：选择一个合适的数据集，包括自变量和因变量。

2. 数据预处理：对数据进行清洗和归一化处理，使其符合线性回归的要求。

3. 数据分割：将数据集分为训练集和测试集，用于训练和评估模型。

4. 模型训练：使用训练集数据拟合线性回归模型。

5. 模型评估：使用测试集数据对模型进行评估，包括计算预测误差和确定模型的可靠性。

6. 结果解释和可视化：根据模型结果和评估指标，对结果进行解释和可视化展示。

四、实验案例本次实验选择一个汽车销售数据集进行分析，其中自变量为汽车的年龄和公里数，因变量为汽车的价格。

我们的目标是建立一个线性模型，以预测汽车的价格。

1. 数据准备首先，我们需要收集关于汽车价格、年龄和公里数的数据。

可以通过互联网查找相关的数据集，或者自己收集数据。

收集到数据后，可以将其保存为CSV或Excel 文件。

2. 数据预处理在进行线性回归分析之前，我们需要对数据进行预处理。

首先，对数据进行清洗，处理缺失值和异常值。

然后，对数据进行归一化处理，使其在相同的量级上。

3. 数据分割将数据集分为训练集和测试集的过程称为数据分割。

一般情况下，我们将70%的数据用于训练模型，将30%的数据用于测试模型。

4. 模型训练使用训练集数据来训练线性回归模型。

可以使用Python中的机器学习库，如scikit-learn来实现线性回归模型的训练。

5. 模型评估使用测试集数据对训练好的模型进行评估。

可以计算预测误差，如均方根误差(RMSE)和平均绝对误差(MAE)，来评估模型的预测能力。