当前位置：文档之家 › 时间序列分析--第五章非平稳序列的随机分析精选文档PPT课件

时间序列分析--第五章非平稳序列的随机分析精选文档PPT课件

  • 格式：ppt
  • 大小：522.00 KB
  • 文档页数：40

下载文档原格式

  / 40

合集下载

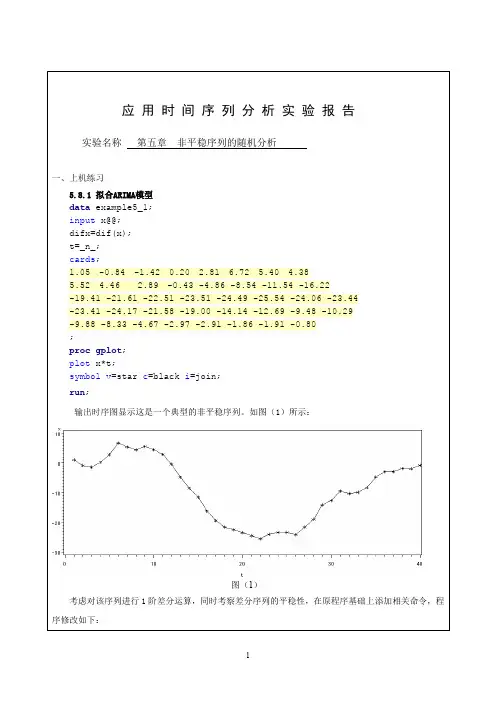
时间序列分析第五章非平稳序列的随机分析

时间序列分析第五章非平稳序列的随机分析
xt xt xt1
考察差分运算对该序列线性趋势信息的提 取作用
2020/3/12
时间序列分析
差分前后时序图
原序列时序图
差分后序列时序图
2020/3/12
时间序列分析
例5.2
尝试提取1950年——1999年北京市民用 车辆拥有量序列的确定性信息
2020/3/12
时间序列分析
Green函数递推公式
1 1 1 2 1 1 2 2

j 1 j1 pd j pd j
t


2
,
E(
t
s
)

0,
s

t
Exs t 0,s t
2020/3/12
时间序列分析
ARIMA 模型族
d=0 ARIMA(p,d,q)=ARMA(p,q)
P=0 ARIMA(P,d,q)=IMA(d,q)
q=0 ARIMA(P,d,q)=ARI(p,d)
d=1,P=q=0 ARIMA(P,d,q)=random walk model
差分后序列时序图
一阶差分
二阶差分
2020/3/12
时间序列分析
例5.3
差分运算提取1962年1月——1975年12月平均 每头奶牛的月产奶量序列中的确定性信息
2020/3/12
时间序列分析
差分后差分
2020/3/12
时间序列分析
过差分
足够多次的差分运算可以充分地提取原 序列中的非平稳确定性信息
2020/3/12
时间序列分析
随机游走模型( random walk)
模型结构

时间序列分析 第五章-非平稳序列的随机分析

时间序列分析 第五章-非平稳序列的随机分析

图（1）考虑对该序列进行1阶差分运算，同时考察差分序列的平稳性，在原程序基础上添加相关命令，程序修改如下：图（2）时序图显示差分后序列difx没有明显的非平稳特征。

（2）“identify var=x(1);”，使用该命令可以识别差分后序列的平稳性。

纯随机性和适当的拟合图（6）普通最小二乘估计结果图（8）最终拟合模型输出结果图（9）拟合效果图图（12）带有延迟因变量的回归模型拟合效果图5.8.3拟合GARCH模型SAS系统中AUTOREG过程功能非常强大，不仅可以提供上述的分析功能，还可以提供异方差性检验乃至条件异方差模型建模。

以临时数据集example5_3数据为例，介绍GARCH模型的拟合，相关命令如下：data example5_3;input x@@;t=_n_;cards;10.77 13.30 16.64 19.54 18.97 20.52 24.3623.51 27.16 30.80 31.84 31.63 32.68 34.9033.85 33.09 35.46 35.32 39.94 37.47 35.2433.03 32.67 35.20 32.36 32.34 38.45 38.1732.14 39.70 49.42 47.86 48.34 62.50 63.5667.61 64.59 66.17 67.50 76.12 79.31 78.8581.34 87.06 86.41 93.20 82.95 72.96 61.1061.27 71.58 88.34 98.70 97.31 97.17 91.1780.20 85.12 81.40 70.87 57.75 52.35 67.5087.95 85.46 84.55 98.16 102.42 113.02 119.95122.37 126.96 122.79 127.96 139.20 141.05 140.87137.08 145.53 145.59 134.36 122.54 106.92 97.23110.39 132.40 152.30 154.91 152.69 162.67 160.31142.57 146.54 153.83 141.81 157.83 161.79 142.07139.43 140.92 154.61 172.33 191.78 199.27 197.57189.29 181.49 166.84 154.28 150.12 165.17 170.32;proc gplot data=example5_3;plot x*t=1;symbol1c=black i=join v=start;proc autoreg data=example5_3;model x=t/nlag=5dwprob archtest;model x=t/nlag=2noint garch=(p=1,q=1);output out=out p=p residual=residual lcl=lcl ucl=ucl cev=cev;data out;set out;l95=-1.96*sqrt(51.42515);u95=1.96*sqrt(51.42515);Lcl_GARCH=-1.96*sqrt(cev);Ucl_GARCH=1.96*sqrt(cev);Lcl_p=p-1.96*sqrt(cev);Ucl_p=p+1.96*sqrt(cev);proc gplot data=out;plot residual*t=2 l95*t=3 Lcl_GARCH*t=4 u95*t=3 Ucl_GARCH*t=4/overlay; plot x*t=5 lcl*t=3 LCL_p*t=4 ucl*t=3 UCL_p*t=4/overlay;symbol2c=green i=needle v=none;symbol3v=black i=join c=none w=2l=2;symbol4c=red i=join v=none;symbol5c=green i=join v=none;run;该序列输出时序图如图（13）所示。

【2019年整理】时间序列分析--第五章非平稳序列的随机分析

【2019年整理】时间序列分析--第五章非平稳序列的随机分析

尝试提取1950年——1999年北京市民用 车辆拥有量序列的确定性信息
4/8/2019
时间序列分析
差分后序列时序图

一阶差分

二阶差分
4/8/2019
时间序列分析
例5.3

差分运算提取1962年1月——1975年12月平均 每头奶牛的月产奶量序列中的确定性信息
4/8/2019
时间序列分析
差分后序列时序图
4/8/2019
时间序列分析
差分方式的选择



序列蕴含着显著的线性趋势，一阶差分 就可以实现趋势平稳 序列蕴含着曲线趋势，通常低阶（二阶 或三阶）差分就可以提取出曲线趋势的 影响 对于蕴含着固定周期的序列进行步长为 周期长度的差分运算，通常可以较好地 提取周期信息
时间序列分析
4/8/2019
例5.1
时间序列分析
ARIMA模型建模步骤
获 得 观 察 值 序 列 平稳性 检验 N 差分 运算 Y 白噪声 检验 N 拟合 ARMA 模型
时间序列分析
Y
分 析 结 束
4/8/2019
例5.6

对1952年——1988年中国农业实际国民 收入指数序列建模
4/8/2019
时间序列分析
一阶差分序列时序图
第五章
非平稳序列的随机分析
4/8/2019
时间序列分析
本章结构


差分运算 ARIMA模型 Auto-Regressive模型 异方差的性质 方差齐性变化 条件异方差模型
4/8/2019
时间序列分析
5.1 差分运算

差分运算的实质 差分方式的选择 过差分

非平稳时间序列

非平稳时间序列
l
t l
1 t l 2
风险管理—识别风险、度量风险和控制风险
金融资产收益率特点
不相关，或者相关程度很弱；只有相关 滞后长度很小有相关性，相关度不大 资产收益率的平方存在很强的相关性
假设Yt是收益率，关于X1t, …, Xpt的一般回 归模型可以表示为 Yt f ( X 1t , , X pt ) t
因此，无条件均值、无条件方差不受误差过程（2）的影响。 3） t 的条件均值是
E ( t t 1 , t 2 ,) Et 1vt Et 1 ( 0 1 t21 )1/ 2 0
4） t 的条件方差是
E ( t2 t 1 , t 2 ,) 0 1 t21
异方差性破坏了古典模型的基本假定，如 果我们直接应用最小二乘法估计回归模型 ，将得不到准确、有效的结果。
异方差性
异方差性另一例子：
波动率聚类性。 资本市场的波动性通常用收益率的标准差 来度量,也称为波动率.大量研究表明股票 收益率表现为在某个时间段波动大,而在 另一个时间段收益率波动又比较小的现 象, 这种现象被称为波动率聚类性。
直观考察美国1963年4月——1971年7月 短期国库券的月度收益率序列的方差齐性。
一阶差分后残差图
一阶差分后残差平方图
异方差处理方法
假如已知异方差函数具体形式，进行方差 齐性变化 假如不知异方差函数的具体形式，拟合条 件异方差模型
方差齐性变换
使用场合
序列显示出显著的异方差性，且方差与均值之间具有 某种函数关系 2
例子—纽约证券交易所综合指数每日的变化
0.4 0.3 0.2 0.1 0.0 -0.1 -0.2 500 1000 1500 SHZSRX 2000 2500

《统计学第五章》PPT课件

《统计学第五章》PPT课件
累计增长量：a1 a0, a2 a0, a3 a0, , an a0 累计增长量等于相应各期逐期增长量之和， 相邻两累计增长量之差等于相应的逐期增长量。
2.平均增长量
平均增长量是时间序列中逐期增长量 的序时平均数，它表明现象在一定时段内平均每 期增加（减少）的数量，其计算公式为：
(yi yi1) / n
计算公式c为：a b
例:某企业2005年计划产值和产值计划完成程度的资 料如下表所示。求平均计划完成程度。
1季 2季 3季 4季
计划产值（万元）b 860 887 875 898 计划完成（%） c 130 135 138 125
10
计划完成程度
实际产值 计划产值
ca b
bc b
bc n bn
定基发展速度是报告期水平与某一固定时期水平（通常是最 初水平）的比值，用 ai 表示，则有
ai
yi y0
2．环比发展速度
环比发展速度是报告期水平与前一期水平的比值，用 bi 表示，
则有
bi
yi yi1
定基发展速度与环比发展速度的数量依存关系：
第一，定基发展速度等于相应时期内各环比 发展速度的连乘积。
（二）时间序列的模型 1．加法模型 加法模型是指时间序列的各个观察值是 上述四种因素之和 :
Y T SCI
2．乘法模型 假设四种因素是相互交错影响的关系，时
间序列（Y）即为 :
Y T SCI
式中 Y ， T ，均为绝对指标；S ，C ，
I 则是比率，或称为指数，是在100% 上下波
动，对原数列指标增加或减少的百分比。
2．高次方程法 高次方程法也称累计法。采用这一方法的原
理是：各期发展水平等于序列初始水平与各期环比发 展速度的连乘积，即

非平稳时间序列解析

非平稳时间序列解析
2 预测方差为{1+(1 12 ) (1 12 s-1 )} 2
动态乘子的比较
趋势平稳过程 动态乘子:
xt t+( B) t
xt s t

2 趋势平稳过程满足 j 0 j , 所以
xt s lims 0. t
单整序列
差分一次变为平稳过程，记为I(1) 平稳过程记为I(0) 如果差分n-1次不平稳，差分n次平稳，称 为n阶单整的，记为I(n)
趋势平稳过程和单位根过程比较
预测比较
H 0 : xt xt 1 t H1 : xt t ( xt 1 t ) t ,| | 1
包含一个确定性趋势和一个随机趋势
单位根过程
满足下面表达式的过程成为单位根过程
(1 B) xt t 1 t 1
其中

(B) t
(1) 0, j 0 2 j , (u ) 0根在单位圆外.
单位根过程对时间序列的增量进行刻画，增 量平稳，但水平变量不平稳。
2.方差有界并且不随时间变化,是常数. 称为方差齐性
平稳ARMA模型, 可表示为
xt t 1 t 1
,

i 0
| i |
t WN (0, )
2
此类模型的特点 3. 长期预测趋于无条件均值 4. 预测误差的方差有界
序列分解
xt l t l 1 t l 1 et (l )
预测误差
l 1 t 1 l t l 1 t 1 ˆt (l ) x
预测值

ˆ (l ) E ( xt l xt , xt 1 , ) x Var ( xt l xt , xt 1 , ) Var[et (l )]

时间序列分析-第五章非平稳序列的随机分析

【例1.1】1964年——1999年中国纱年产 量序列蕴含着一个近似线性的递增趋势。 对该序列进行一阶差分运算
xt xt xt1
考察差分运算对该序列线性趋势信息的提 取作用
2020/1/4
时间序列分析
差分前后时序图
原序列时序图
差分后序列时序图
2020/1/4
时间序列分析
例5.2
第五章
非平稳序列的随机分析
2020/1/4
时间序列分析
本章结构
差分运算 ARIMA模型 Auto-Regressive模型 异方差的性质 方差齐性变化 条件异方差模型
2020/1/4
时间序列分析
5.1 差分运算
差分运算的实质 差分方式的选择 过差分
2020/1/4
时间序列分析
差分运算的实质
差分方法是一种非常简便、有效的确定 性信息提取方法
Cramer分解定理在理论上保证了适当阶 数的差分一定可以充分提取确定性信息
差分运算的实质是使用自回归的方式提 取确定性信息
d
d xt (1 B)d xt (1)i Cdi xti i0
尝试提取1950年——1999年北京市民用 车辆拥有量序列的确定性信息
2020/1/4
时间序列分析
差分后序列时序图
一阶差分
二阶差分
2020/1/4
时间序列分析
例5.3
差分运算提取1962年1月——1975年12月平均 每头奶牛的月产奶量序列中的确定性信息
2020/1/4
时间序列分析
2020/1/4
时间序列分析
ARIMA模型的平稳性
ARIMA(p,d,q) 模 型 例5.5

第五章 非平稳序列的随机分析041019123931

第五章 非平稳序列的随机分析非平稳序列的确定性因素分解方法（第四章）的优点为原理简单、操作简便、易于解释等，因此在宏观经济管理与预测领域有着广泛的应用。

缺点主要有：(1)确定性因素分解方法只能提取强劲的确定性信息，对随机性信息浪费严重。

(2)确定性因素分解方法把所有序列的变化都归结为四大因素的综合影响，却始终无法提供明确、有效的方法判断各大因素之间确切的作用关系。

这些问题导致确定性因素分解方法不能允分提取观察值序列中的有效信息，导致模型拟合精度通常不够理想。

随机时序分析方法发展的必要性：弥补确定性因素分解方法的不足，为人们提供更加丰富、更加精确的时序分析工具。

5.1 差分运算5.1.1 差分运算的实质拿到观察值序列之后，无论是采用确定性时序分析方法还是随机时序分析方法，分析的第一步都是要通过有效的手段提取序列中所蕴含的确定性信息。

确定性信息的提取方法非常多，前面我们介绍过的构造季节指数、拟合长期趋势模型、移动平均、指数平滑等诸多方法都是确定性信息提取方法。

但是它们对确定性信息的提取都不够充分。

Cox 和Jenkins 在Time Series Analysis Forecasting and Control 一书中特别强调差分方法的使用，他们使用大量的案例分析证明差分方法是一种非常简便、有效的确定性信息提取方法。

而Cramer 分解定理则在理论上保证了适当阶数的差分一定可以充分提取确定性信息。

根据Cramer 分解定理，方差齐性非平稳序列都可以分解为如下形式：式中，为零均值白噪声序列。

{}t a 离散序列的d 阶差分就相当于连续变量的d 阶求导，显然，在Cramer 分解定理的保证下，d 阶差分就可以将中蕴含的d 次（关于时间的）确定性信息充分提取。

（如何证明？）{}t a展开1阶差分，有等价于这意味着1阶差分实质上就是一个自回归过程，它是用延迟一期的历史数据作为自变{}1-t x量来解释当期序列值的变动状况，差分序列度量的是l 阶自回归过程中产生{}t x {}t x ∇{}t x 的随机误差的大小。

时间序列分析--第五章非平稳序列的随机分析

第五章
非平稳序列的随机分析
2020/6/14
课件
1
本章结构
差分运算 ARIMA模型 Auto-Regressive模型 异方差的性质 方差齐性变化 条件异方差模型
2020/6/14
课件
2
5.1 差分运算
差分运算的实质 差分方式的选择 过差分
2020/6/14
课件
3
差分运算的实质
方差大
Var(xt ) Var(at at1)
2 2
Var(2xt ) Var(at 2at1 at2 )
6 2
2020/6/14
课件ቤተ መጻሕፍቲ ባይዱ
14
5.2 ARIMA模型
ARIMA模型结构 ARIMA模型性质 ARIMA模型建模 ARIMA模型预测 疏系数模型 季节模型
2020/6/14
1 1 1 2 1 1 2 2
j 1 j1 pd j pd j
2020/6/14
课件
28
预测值
xtl ( tl 1 tl1 l1 t1) ( l t l1 t1 )
et (l)
xˆt (l)
E[et (l)] 0
Var[et (l)]
(1
2 1
2 l 1
)
2
2020/6/14
课件
29
例5.7
已知ARIMA(1,1,1)模型为
(1 0.8B)(1 B)xt (1 0.6B) t
且 xt1 4.5
xt 5.3
t 0.8
2
1
求 xt3 的95％的置信区间
2020/6/14
课件
30
预测值
等价形式
(11.8B 0.8B2 )xt (1 0.6B)t xt 1.8xt1 0.8xt2 t 0.6t1

非平稳时间序列的随机分析


4、ARIMA模型预测
PPT文档演模板
非平稳时间序列的随机分析
4、ARIMA模型预测
PPT文档演模板
非平稳时间序列的随机分析
预测值：线性最小方差预测原则
•>arima(x = chafen, order = c(0, 0, 1), method =
"ML")
•Coefficients:
•
ma1 intercept
• 0.6710 4.9947
•s.e. 0.1648 2.0139
•sigma^2 estimated as 53.42: log likelihood = -
PPT文档演模板
•平稳性 •检验
•N
•差分 •运算
•Y •白噪声 •检验
•N
•拟合 •ARMA •模型
•Y •分 •析 •结 •束
非平稳时间序列的随机分析
例4.6
n 对1952年——1988年中国农业实际国民 收入指数序列建模
>d=read.csv("shouru.csv",head=F)
>shouru=ts(d,start=1952,end=1988,freq =1)
非平稳时间序列的随机 分析
PPT文档演模板
2021/1/4
非平稳时间序列的随机分析
•4.1 时间序列的分解 •4.1.1 Wold分解定理 •4.1.2 Cramer分解定理
•引 例
PPT文档演模板
非平稳时间序列的随机分析
4.1.1、Wold分解定理（1938）
n 对于任何一个离散平稳过程 它都可以分解为两个 不相关的平稳序列之和，其中一个为确定性的，另 一个为随机性的，不妨记作
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2020/8/1
课件
31
预测值
等价形式
(11.8B 0.8B 2)xt(10.6B )t xt1.8xt 10.8xt 2t0.6t 1
2 统计量 15.33 18.33 24.66
P值 0.0178 0.1060 0.1344
2020/8/1
课件
26
拟合ARMA模型
偏自相关图
2020/8/1
课件
27
建模
定阶
ARIMA(0,1,1)
参数估计
(1 B )xt4 .99 ( 6 1 0 6 .710B )7 t 66
Va(rt)56.48763
2020/8/1
课件
5
差分方式的选择
序列蕴含着显著的线性趋势，一阶差分 就可以实现趋势平稳
序列蕴含着曲线趋势，通常低阶（二来自 或三阶）差分就可以提取出曲线趋势的 影响
对于蕴含着固定周期的序列进行步长为 周期长度的差分运算，通常可以较好地 提取周期信息
2020/8/1
课件
6
例5.1
【例1.1】1964年——2019年中国纱年产 量序列蕴含着一个近似线性的递增趋势。 对该序列进行一阶差分运算
22
Va(r2xt)Va(atr2at1at2)
62
2020/8/1
课件
15
5.2 ARIMA模型
ARIMA模型结构 ARIMA模型性质 ARIMA模型建模 ARIMA模型预测 疏系数模型 季节模型
2020/8/1
课件
16
ARIMA模型结构
使用场合
差分平稳序列拟合
模型结构
E((Bt))d0x， t Va((B r)t)t2,E(ts)0,st Esxt 0,st
课件
18
随机游走模型( random walk)
模型结构
xt xt1t E(t)0， Va(rt)2,E(ts)0,st Esxt 0,st
模型产生典故
Karl Pearson(1905)在《自然》杂志上提问：假如有个 醉汉醉得非常严重，完全丧失方向感，把他放在荒郊 野外，一段时间之后再去找他，在什么地方找到他的 概率最大呢？
模型检验
模型显著 参数显著
2020/8/1
课件
28
ARIMA模型预测
原则
最小均方误差预测原理
Green函数递推公式
1 1 1 2 11 2 2
j 1j1 pdjpd j
2020/8/1
课件
29
预测值
x t l (t l 1 t l 1 l 1 t 1 ) (lt l 1 t 1 )
课件
3
5.1 差分运算
差分运算的实质 差分方式的选择 过差分
2020/8/1
课件
4
差分运算的实质
差分方法是一种非常简便、有效的确定 性信息提取方法
Cramer分解定理在理论上保证了适当阶 数的差分一定可以充分提取确定性信息
差分运算的实质是使用自回归的方式提 取确定性信息
d
dxt (1B)dxt (1)iC d ixti i0
et (l)
xˆt (l)
E[et(l)]0
Va[etr(l)](112 l21)2
2020/8/1
课件
30
例5.7
已知ARIMA(1,1,1)模型为
( 1 0 .8 B )1 (B )x t ( 1 0 .6 B )t
且 xt1 4.5
xt 5.3
t 0.8
2
1
求 x t 3 的95％的置信区间
xt xt xt1
考察差分运算对该序列线性趋势信息的提 取作用
2020/8/1
课件
7
差分前后时序图
原序列时序图
差分后序列时序图
2020/8/1
课件
8
例5.2
尝试提取1950年——2019年北京市民用 车辆拥有量序列的确定性信息
2020/8/1
课件
9
差分后序列时序图
一阶差分
二阶差分
2020/8/1
d 0时，原序列方差非齐性
AR(I0,1 M ,0)模 A 型
Va (xt)rVa (x0rtt1 1)t2
d阶差分后，差分后序列方差齐性
ARIM(0,A1,0)模型
Va(rxt)Va(rt)2
2020/8/1
课件
21
ARIMA模型建模步骤
获 得 观 察 值 序 列
2020/8/1
平稳性 检验
课件
10
例5.3
差分运算提取1962年1月——1975年12月平均 每头奶牛的月产奶量序列中的确定性信息
2020/8/1
课件
11
差分后序列时序图
一阶差分
1阶－12步差分
2020/8/1
课件
12
过差分
足够多次的差分运算可以充分地提取原 序列中的非平稳确定性信息
但过度的差分会造成有用信息的浪费
2020/8/1
课件
17
ARIMA 模型族
d=0 ARIMA(p,d,q)=ARMA(p,q)
P=0 ARIMA(P,d,q)=IMA(d,q)
q=0 ARIMA(P,d,q)=ARI(p,d)
d=1,P=q=0 ARIMA(P,d,q)=random walk model
2020/8/1
2020/8/1
课件
19
ARIMA模型的平稳性
ARIMA(p,d,q) 模 型 例5.5
共 有 p+d 个 特 征 根 ， 其中p个在单位圆
ARIMA(0,1,0)时序图
内，d个在单位圆
上。所以当 d 0时
ARIMA(p,d,q) 模 型
非平稳。
2020/8/1
课件
20
ARIMA模型的方差齐性
第五章
非平稳序列的随机分析
2020/8/1
课件
1
整体概况
概况一
点击此处输入 相关文本内容
01
概况二
点击此处输入 相关文本内容
02
概况三
点击此处输入 相关文本内容
03
本章结构
差分运算 ARIMA模型 Auto-Regressive模型 异方差的性质 方差齐性变化 条件异方差模型
2020/8/1
N
差分 运算
Y 白噪声 检验
N
拟合 ARMA 模型
Y分 析 结 束
课件
22
例5.6
对1952年——1988年中国农业实际国民 收入指数序列建模
2020/8/1
课件
23
一阶差分序列时序图
2020/8/1
课件
24
一阶差分序列自相关图
2020/8/1
课件
25
一阶差分后序列白噪声检验
延迟阶数 6 12 18
2020/8/1
课件
13
例5.4
假设序列如下
xt 01tat
考察一阶差分后序列和二阶差分序列 的平稳性与方差
2020/8/1
课件
14
比较
一阶差分
平稳
xt xt xt1
1 at at1 方差小
二阶差分（过差分）
平稳
2xt xt xt1 at 2at1at2
方差大
Va( rxt)Va(art at1)