下载文档原格式
高中数学选修2-2知识点总结第一章、导数1．函数的平均变化率为=∆∆=∆∆xfx y x x f x x f x x x f x f ∆-∆+=--)()()()(111212 注1：其中x ∆是自变量的改变量，平均变化率 可正，可负，可零。
注2：函数的平均变化率可以看作是物体运动的平均速度。
2、导函数的概念:函数)(x f y =在0x x =处的瞬时变化率是xx f x x f x yx x ∆-∆+=∆∆→∆→∆)()(lim lim 0000，则称函数)(x f y =在点0x 处可导，并把这个极限叫做)(x f y =在0x 处的导数，记作)(0'x f 或|'x x y =，即)(0'x f =xx f x x f x yx x ∆-∆+=∆∆→∆→∆)()(lim lim 0000.3.函数的平均变化率的几何意义是割线的斜率； 函数的导数的几何意义是切线的斜率。
4导数的背景（1）切线的斜率；（2）瞬时速度；5、常见的函数导数 函数 导函数 (1)y c ='y =0 (2)n y x =()*n N ∈ 1'n y nx -= (3)x y a =()0,1a a >≠ 'ln x y a a =(4)x y e ='x y e =(5)log a y x =()0,1,0a a x >≠> 1'ln y x a =(6)ln y x = 1'y x=(7)sin y x = 'cos y x =(8)cos y x = 'sin y x =-6、常见的导数和定积分运算公式:若()f x ，()g x 均可导（可积），则有： 和差的导数运算[]'''()()()()f x g x f x g x ±=± 积的导数运算[]'''()()()()()()f x g x f x g x f x g x ⋅=±特别地：()()''Cf x Cf x =⎡⎤⎣⎦商的导数运算[]'''2()()()()()(()0)()()f x f x g x f x g x g x g x g x ⎡⎤-=≠⎢⎥⎣⎦ 特别地：()()21'()'g x g x g x ⎡⎤-=⎢⎥⎣⎦复合函数的导数x u x y y u '''=⋅微积分基本定理()baf x dx =⎰F(a)--F(b)（其中()()'F x f x =）和差的积分运算1212[()()]()()b bbaaaf x f x dx f x dx f x dx±=±⎰⎰⎰ 特别地：()()()bb aakf x dx k f x dx k =⎰⎰为常数积分的区间可加性()()()()bcbaacf x dx f x dx f x dx a c b =+<<⎰⎰⎰其中.用导数求函数单调区间的步骤: ①求函数f (x )的导数'()f x②令'()f x >0,解不等式，得x 的范围就是递增区间. ③令'()f x <0,解不等式，得x 的范围，就是递减区间； [注]：求单调区间之前一定要先看原函数的定义域。
高中数学选修2-2,2-3知识点、考点、典型例题高中数学选修2-2,2-3知识点、考点、典型例题一、2-2数列的概念、数列的通项公式及递推公式1. 数列的概念数列是按照一定规律排列的一系列数，一般用字母 an 表示第n 个数。
2. 数列的通项公式数列的通项公式是指通过数列的位置 n，直接求出该位置上的数 an 的公式。
通项公式可以是一个数学式子，也可以是一个算法。
3. 数列的递推公式数列的递推公式是指通过数列前一项或前几项的值，推导出数列下一项的公式。
递推公式是数列中相邻两项之间的关系式。
4. 常见数列的通项公式和递推公式- 等差数列：an = a1 + (n-1)d （通项公式），an = an-1 + d （递推公式）- 等比数列：an = a1 * q^(n-1) （通项公式），an = an-1 * q （递推公式）- 斐波那契数列：an = an-1 + an-2 （递推公式）二、2-3数列的求和、数列的性质及应用1. 数列的求和- 等差数列的前 n 项和：Sn = (a1 + an) * n / 2- 等比数列的前 n 项和（q ≠ 1）：Sn = a1 * (1 - q^n) / (1 - q) - 斐波那契数列的前 n 项和：Sn = Fn+2 - 12. 数列的性质- 常数列：数列中的每一项都是一个常数。
- 奇数列：数列中的每一项都是奇数。
- 偶数列：数列中的每一项都是偶数。
- 单调递增数列：数列中的每一项都比前一项大。
- 单调递减数列：数列中的每一项都比前一项小。
- 正项数列：数列中的每一项都是正数。
- 负项数列：数列中的每一项都是负数。
3. 数列的应用- 利用数列的递推关系，求解实际问题中的特定数值。
- 利用数列的性质，进行数学推理和证明。
- 利用数列的规律，设计算法解决问题。
典型例题：1. 已知等差数列的前三项分别为 1，5，9，求数列的通项公式和第 n 项的值。
解：设数列的首项为 a，公差为 d，则有以下等差数列的递推公式：a2 = a1 + d = 1 + da3 = a2 + d = (1 + d) + d = 1 + 2d将 a1，a2，a3 分别代入等差数列的通项公式，可得：a1 = a = 1a2 = a + d = 1 + d = 5 --> d = 4a3 = a1 + 2d = 1 + 2(4) = 9所以该等差数列的通项公式为 an = a + (n-1)d = 1 + 4(n-1) = 4n - 3第 n 项的值为：an = 4n - 32. 求等差数列 3，6，9，...，101 的前 n 项和。
选修2-2 知识点及习题答案解析导数及其应用一.导数概念的引入1.导数的物理意义：瞬时速率。
一般的，函数()y f x =在0x x =处的瞬时变化率是000()()limx f x x f x x∆→+∆-∆，我们称它为函数()y f x =在0x x =处的导数，记作0()f x '或0|x x y ='，即0()f x '=000()()limx f x x f x x∆→+∆-∆2.导数的几何意义：曲线的切线.通过图像,我们可以看出当点n P 趋近于P 时，直线PT 及曲线相切。
容易知道，割线n PP 的斜率是，当点n P 趋近于P 时，函数()y f x =在0x x =处的导数就是切线PT 的斜率k ，即000()()lim ()n x n f x f x k f x x x ∆→-'==-3.导函数：当x 变化时，()f x '便是x 的一个函数，我们称它为()f x 的导函数. ()y f x =的导函数有时也记作y ',即()()()limx f x x f x f x x∆→+∆-'=∆二.导数的计算基本初等函数的导数公式: 1若()f x c =(c为常数)，则()0f x '=； 2 若()f x x α=,则1()f x x αα-'=;3 若()sin f x x =,则()cos f x x '=4 若()cos f x x =,则()sin f x x '=-;5 若()x f x a =,则()ln x f x a a '=6 若()xf x e=,则()x f x e '=7 若()log xa f x =,则 8 若()ln f x x =,则导数的运算法则1. [()()]()()f x g x f x g x '''±=±2.[()()]()()()()f x g x f x g x f x g x '''•=•+• 3. 2()()()()()[]()[()]f x f xg x f x g x g x g x ''•-•'=复合函数求导()y f u =和()u g x =,称则y 可以表示成为x 的函数,即(())y f g x =为一个复合函数(())()y f g x g x '''=•三.导数在研究函数中的应用 1.函数的单调性及导数:一般的,函数的单调性及其导数的正负有如下关系： 在某个区间(,)a b 内(1)如果()0f x '>，那么函数()y f x =在这个区间单调递增；(2)如果()0f x '<，那么函数()y f x =在这个区间单调递减.2.函数的极值及导数极值反映的是函数在某一点附近的大小情况. 求函数()y f x =的极值的方法是:（1）如果在0x 附近的左侧()0f x '>,右侧()0f x '<,那么0()f x 是极大值（2）如果在0x 附近的左侧()0f x '<,右侧()0f x '>,那么0()f x 是极小值;4.函数的最大(小)值及导数 求函数()y f x =在[,]a b 上的最大值及最小值的步骤：（1）求函数()y f x =在(,)a b 内的极值；（2）将函数()y f x =的各极值及端点处的函数值()f a ，()f b 比较，其中最大的是一个最大值，最小的是最小值.推理及证明考点一合情推理及类比推理根据一类事物的部分对象具有某种性质,退出这类事物的所有对象都具有这种性质的推理,叫做归纳推理,归纳是从特殊到一般的过程,它属于合情推理根据两类不同事物之间具有某些类似(或一致)性,推测其中一类事物具有及另外一类事物类似的性质的推理,叫做类比推理.类比推理的一般步骤:(1)找出两类事物的相似性或一致性;(2)用一类事物的性质去推测另一类事物的性质,得出一个明确的命题(猜想);(3)一般的,事物之间的各个性质并不是孤立存在的,而是相互制约的.如果两个事物在某些性质上相同或相似,那么他们在另一写性质上也可能相同或类似,类比的结论可能是真的.(4)一般情况下,如果类比的相似性越多,相似的性质及推测的性质之间越相关,那么类比得出的命题越可靠.考点二演绎推理(俗称三段论)由一般性的命题推出特殊命题的过程,这种推理称为演绎推理.考点三数学归纳法1.它是一个递推的数学论证方法.2.步骤:A.命题在n=1（或0n）时成立，这是递推的基础；B.假设在n=k时命题成立； C.证明n=k+1时命题也成立,完成这两步,就可以断定对任何自然数(或n>=0n ,且n N ∈)结论都成立。
新课程标准数学选修2—2第二章课后习题解答第二章 推理与证明2．1合情推理与演绎推理 练习（P77）1、由12341a a a a ====，猜想1n a =.2、相邻两行数之间的关系是：每一行首尾的数都是1，其他的数都等于上一行中与之相邻的两个数的和.3、设111O PQ R V -和222O P Q R V -分别是四面体111O PQ R -和222O P Q R -的体积， 则111222111222O PQR O P Q R V OP OQ OR V OP OQ OR --=⋅⋅. 练习（P81） 1、略.2、因为通项公式为n a 的数列{}n a ，若1n na p a +=，其中p 是非零常数，则{}n a 是等比数列； ……………………大前提又因为0cq ≠，则0q ≠，则11n n nn a cq q a cq++==； ……………………………小前提所以，通项公式为(0)n n a cq cq =≠的数列{}n a 是等比数列. ……………………结论3、由AD BD >，得到ACD BCD ∠>∠的推理是错误的. 因为这个推理的大前提是“在同一个三角形中，大边对大角”，小前提是“AD BD >”，而AD 与BD 不在同一个三角形中.习题2.1 A 组（P83）1、21n a n =+()n N *∈. 2、2F V E +=+. 3、当6n ≤时，122(1)n n -<+；当7n =时，122(1)n n -=+；当8n =时，122(1)n n ->+()n N *∈.4、212111(2)n n A A A n π++≥-（2n >，且n N *∈）. 5、121217n n b b b b b b -=（17n <，且n N *∈）.6、如图，作DE ∥AB 交BC 于E .因为两组对边分别平行的四边形是平行四边形， 又因为AD ∥BE ，AB ∥DE . 所以四边形ABED 是平行四边形. 因为平行四边形的对边相等.又因为四边形ABED 是平行四边形. 所以AB DE =.因为与同一条线段等长的两条线段的长度相等，又因为AB DE =，AB DC =, 所以DE DC = 因为等腰三角形的两底角是相等的.又因为△DEC 是等腰三角形, 所以DEC C ∠=∠ 因为平行线的同位角相等又因为DEC ∠与B ∠是平行线AB 和DE 的同位角, 所以DEC B ∠=∠ 因为等于同角的两个角是相等的，又因为DEC C ∠=∠，DEC B ∠=∠, 所以B C ∠=∠ 习题2.1 B 组（P84）1、由123S =-，234S =-，345S =-，456S =-，567S =-，猜想12n n S n +=-+.2、略.3、略. 2．2直接证明与间接证明 练习（P89）1、因为442222cos sin (cos sin )(cos sin )cos 2θθθθθθθ-=+-=，所以，命题得证.2>，只需证22>，即证1313+>+>，只需要22>，即证4240>，这是显然成立的. 所以，命题得证. 3、因为 222222222()()()(2sin )(2tan )16sin tan a b a b a b αααα-=-+==， 又因为sin (1cos )sin (1cos )1616(tan sin )(tan sin )16cos cos ab αααααααααα+-=+-=⋅22222222sin (1cos )sin sin 161616sin tan cos cos αααααααα-===， 从而222()16a b ab -=，所以，命题成立.说明：进一步熟悉运用综合法、分析法证明数学命题的思考过程与特点.练习（P91）1、假设B ∠不是锐角，则90B ∠≥︒. 因此9090180C B ∠+∠≥︒+︒=︒. 这与三角形的内角和等于180°矛盾.所以，假设不成立. 从而，B ∠一定是锐角.2=所以22=，化简得5=225=，即2540=， 这是不可能的. 所以，假设不成立..说明：进一步熟悉运用反证法证明数学命题的思考过程与特点. 习题2.2 A 组（P91）1、由于0a ≠，因此方程至少有一个跟bx a=.假设方程不止一个根，则至少有两个根，不妨设12,x x 是它的两个不同的根，则 1ax b = ①2ax b = ②①－②得12()0a x x -=因为12x x ≠，所以120x x -≠，从而0a =，这与已知条件矛盾，故假设不成立.2、因为 (1tan )(1tan )2A B ++=展开得 1tan tan tan tan 2A B A B +++=，即tan tan 1tan tan A B A B +=-. ①假设1tan tan 0A B -=，则cos cos sin sin 0cos cos A B A B A B -=，即cos()0cos cos A B A B+=所以cos()0A B +=.因为A ，B 都是锐角，所以0A B π<+<，从而2A B π+=，与已知矛盾.因此1tan tan 0A B -≠.①式变形得tan tan 11tan tan A BA B +=-， 即tan()1A B +=. 又因为0A B π<+<，所以4A B π+=.说明：本题也可以把综合法和分析法综合使用完成证明.3、因为1tan 12tan αα-=+，所以12tan 0α+=，从而2sin cos 0αα+=. 另一方面，要证 3sin 24cos2αα=-，只要证226sin cos 4(cos sin )αααα=--即证 222sin 3sin cos 2cos 0αααα--=， 即证 (2sin cos )(sin 2cos )0αααα+-=由2sin cos 0αα+=可得，(2sin cos )(sin 2cos )0αααα+-=，于是命题得证.说明：本题可以单独使用综合法或分析法进行证明，但把综合法和分析法结合使用进行证明的思路更清晰.4、因为,,a b c 的倒数成等差数列，所以211b ac =+.假设2B π<不成立，即2B π≥，则B 是ABC ∆的最大内角，所以,b a b c >>（在三角形中，大角对大边）， 从而11112a c b b b +>+=. 这与211b a c=+矛盾. 所以，假设不成立，因此，2B π<.习题2.2 B 组（P91）1、要证2s a <，由于22s ab <，所以只需要2s s b<，即证b s <.因为1()2s a b c =++，所以只需要2b a b c <++，即证b a c <+. 由于,,a b c 为一个三角形的三条边，所以上式成立. 于是原命题成立. 2、由已知条件得 2b ac = ① 2x a b =+，2y b c =+ ② 要证2a cx y+=，只要证2ay cx xy +=，只要证224ay cx xy += 由①②，得 22()()2ay cx a b c c a b ab ac bc +=+++=++， 24()()2xy a b b c ab b ac bc ab ac bc =++=+++=++， 所以，224ay cx xy +=，于是命题得证. 3、由 tan()2tan αβα+= 得sin()2sin cos()cos αβααβα+=+，即sin()cos 2cos()sin αβααβα+=+. ……①要证 3sin sin(2)βαβ=+即证 3sin[()]sin[()]αβααβα+-=++ 即证3[sin()cos cos()sin ]sin()cos cos()sin αβααβααβααβα+-+=+++ 化简得sin()cos 2cos()sin αβααβα+=+，这就是①式.所以，命题成立.说明：用综合法和分析法证明命题时，经常需要把两者结合起来使用. 2．3数学归纳法 练习（P95）1、先证明：首项是1a ，公差是d 的等差数列的通项公式是1(1)n a a n d =+-. （1）当1n =时，左边＝1a ，右边＝11(11)a d a +-=，因此，左边＝右边. 所以，当1n =时命题成立. （2）假设当n k =时，命题成立，即1(1)k a a k d =+-. 那么，11(1)[(1)1]k k k a a d a k d d a k d +=+=+-+=++-. 所以，当1n k =+时，命题也成立.根据（1）和（2），可知命题对任何n N *∈都成立.再证明：该数列的前n 项和的公式是1(1)2n n n S na d -=+. （1）当1n =时，左边＝11S a =，右边＝111(11)12a d a ⨯-⨯+=，因此，左边＝右边. 所以，当1n =时命题成立.（2）假设当n k =时，命题成立，即1(1)2k k k S ka d -=+.那么，1111(1)[(1)1]2k k k k k S S a ka d a k d ++-=+=++++-1(1)(1)[1]2k k a k d -=+++1(1)(1)2k kk a d +=++所以，当1n k =+时，命题也成立.根据（1）和（2），可知命题对任何n N *∈都成立. 2、略.习题2.3 A 组（P96） 1、（1）略.（2）证明：①当1n =时，左边＝1，右边＝211=，因此，左边＝右边. 所以，当1n =时，等式成立.②假设当n k =时等式成立，即2135(21)k k ++++-=.那么，22135(21)(21)(21)(1)k k k k k ++++-++=++=+.所以，当1n k =+时，等式也成立. 根据①和②，可知等式对任何n N *∈都成立.（3）略.2、1111122S ==-⨯，2111111(1)()112232233S =+=-+-=-⨯⨯，3111111111(1)()()1122334223344S =++=-+-+-=-⨯⨯⨯.由此猜想：111n S n =-+.下面我们用数学归纳法证明这个猜想.（1）当1n =时，左边＝111111222S ==-=⨯，右边＝11111122n -=-=+，因此，左边＝右边. 所以，当1n =时，猜想成立. （2）假设当n k =时，猜想成立，即111111122334(1)1k k k ++++=-⨯⨯⨯++.那么，11111111122334(1)(1)(2)1(1)(2)k k k k k k k +++++=-+⨯⨯⨯++++++.111(1)12k k =--++ 121111122k k k k +-=-⋅=-+++所以，当1n k =+时，猜想也成立.根据（1）和（2），可知猜想对任何n N *∈都成立. 习题2.3 B 组（P96）1、略2、证明：（1）当1n =时，左边＝111⨯=，右边＝11(11)(12)16⨯⨯+⨯+=，因此，左边＝右边. 所以，当1n =时，等式成立. （2）假设当n k =时，等式成立，即112(1)3(2)1(1)(2)6k k k k k k k ⨯+⨯-+⨯-++⨯=++.那么，1(1)2[(1)1]3[(1)2](1)1k k k k ⨯++⨯+-+⨯+-+++⨯.[12(1)3(2)1][123(1)]k k k k k =⨯+⨯-+⨯-++⨯++++++11(1)(2)(1)(2)62k k k k k =+++++ 1(1)(2)(3)6k k k =+++ 所以，当1n k =+时，等式也成立.根据（1）和（2），可知等式对任何n N *∈都成立.第二章 复习参考题A 组（P98）1、图略，共有(1)1n n -+（n N *∈）个圆圈.2、333n 个（n N *∈）.3、因为2(2)(1)4f f ==，所以(1)2f =，(3)(2)(1)8f f f ==，(4)(3)(1)16f f f ==…… 猜想()2n f n =.4、运算的结果总等于1.5、如图，设O 是四面体A BCD -内任意一点，连结AO ，BO ，CO ，DO 并延长交对面于A '，B '，C '，D '，则1OA OB OC OD AA BB CC DD''''+++=''''用“体积法”证明： OA OB OC OD AA BB CC DD ''''+++'''' O BCD O CDA O DAB O ABCA BCDB CDAC DABD ABCV V V V V V V V --------=+++1A BCD A BCDVV --==6、要证 (1tan )(1tan )2A B ++=只需证 1tan tan tan tan 2A B A B +++=（第5题）即证 tan tan 1tan tan A B A B +=-由54A B π+=，得tan()1A B +=. ①又因为2A B k ππ+≠+，所以tan tan 11tan tan A BA B+=-，变形即得①式. 所以，命题得证.7、证明：（1）当1n =时，左边＝1-，右边＝1(1)11-⨯=-，因此，左边＝右边. 所以，当1n =时，等式成立.（2）假设当n k =时，等式成立，即135(1)(21)(1)k k k k -+-++--=-.那么，1135(1)(21)(1)[2(1)1]k k k k +-+-++--+-+-.1(1)(1)[2(1)1]k k k k +=-+-+- 1(1)[2(1)1]k k k +=--++- 1(1)(1)k k +=-+所以，当1n k =+时，等式也成立.根据（1）和（2），可知等式对任何n N *∈都成立.第二章 复习参考题B 组（P47）1、（1）25条线段，16部分； （2）2n 条线段；（3）最多将圆分割成1(1)12n n ++部分.下面用数学归纳法证明这个结论. ①当1n =时，结论成立.②假设当n k =时，结论成立，即：k 条线段，两两相交，最多将圆分割成1(1)12k k ++部分当1n k =+时，其中的k 条线段12,,,k l l l 两两相交，最多将圆分割成1(1)12k k ++ 部分，第1k +条线段1k a +与线段12,,,k l l l 都相交，最多增加1k +个部分，因此，1k +条线段，两两相交，最多将圆分割成11(1)1(1)(1)(2)122k k k k k ++++=+++ 部分所以，当1n k =+时，结论也成立.根据①和②，可知结论对任何n N *∈都成立.2、要证 cos 44cos 43βα-=因为 cos 44cos 4cos(22)4cos(22)βαβα-=⨯-⨯ 2212sin 24(12sin 2)βα=--⨯-222218sin cos 4(18sin cos )ββαα=--⨯- 222218sin (1sin )4[18sin (1sin )]ββαα=---⨯-- 只需证 222218sin (1sin )4[18sin (1sin )]3ββαα---⨯--= 由已知条件，得 sin cos sin 2θθα+=，2sin sin cos βθθ=， 代入上式的左端，得 222218sin (1sin )4[18sin (1sin )]ββαα---⨯-- 2238sin cos (1sin cos )32sin (1sin )θθθθαα=---+-2238sin cos 8sin cos 2(12sin cos )(32sin cos )θθθθθθθθ=--+++-222238sin cos 8sin cos 68sin cos 8sin cos θθθθθθθθ=--++-+ 3= 因此，cos 44cos 43βα-=。
高中数学选修2-2(人教A版)知识点总结含同步练习题及答案第二章 推理与证明 2. 3数学归纳法一、学习任务1. 了解数学归纳法原理．2. 能用数学归纳法证明一些简单的数学命题．3. 掌握数学归纳法的特点和步骤．二、课后作业 （查看更多本章节同步练习题，请到快乐学）答案：1. 用数学归纳法证明 第一步应验证 A ．B ．C ．D ．C ⩾(n ⩾3,n ∈N )3n n 3()n =1n =2n =3n =4答案：2. 用数学归纳法证明，"当 为正奇数时， 能被 整除"时，第二步归纳假设应写成A ．假设 时正确，再推证 正确B ．假设 时正确，再推证 正确C ．假设 时正确，再推证 正确D ．假设 时正确，再推证 正确Bn +x n y n x +y ()n =2k +1(k ∈)N ∗n =2k +3n =2k −1(k ∈)N ∗n =2k +1n =k (k ⩾1,k ∈)N ∗n =k +2n ⩽k (k ⩾1,k ∈)N ∗n =k +2答案：解析：3. 用数学归纳法证明等式 的过程中，第二步假设 时等式成立，则当 时应得到 A ．B ．C ．D ．B时，等式左边 ．1+3+5+⋯+(2n −1)=(n ∈)n 2N ∗n =k n =k +1()1+3+5+⋯+(2k +1)=k 21+3+5+⋯+(2k +1)=(k +1)21+3+5+⋯+(2k +1)=(k +2)21+3+5+⋯+(2k +1)=(k +3)2∵n =k +1=1+3+5+…+(2k −1)+(2k +1)=+(2k +1)=k 2(k +1)24. 设平面内有 条直线，其中任何两条不平行，任何三条不共点，设 条直线的交点个数为 ，则 与 的关系是 A ．B ．C ．D ．k k f (k )f (k +1)f (k )()f (k +1)=f (k )+k −1f (k +1)=f (k )+k +1f (k +1)=f (k )+k +2f (k +1)=f (k )+k高考不提分，赔付1万元，关注快乐学了解详情。
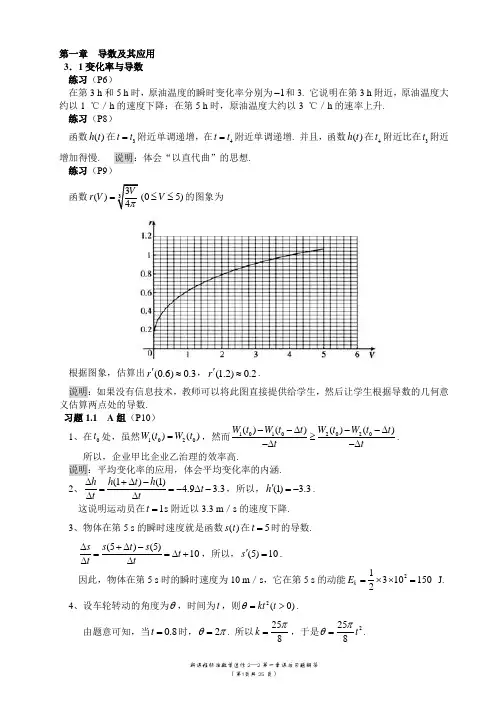
第一章 导数及其应用 3．1变化率与导数 练习（P6）在第3 h 和5 h 时，原油温度的瞬时变化率分别为1-和3. 它说明在第3 h 附近，原油温度大约以1 ℃／h 的速度下降；在第5 h 时，原油温度大约以3 ℃／h 的速率上升. 练习（P8）函数()h t 在3t t =附近单调递增，在4t t =附近单调递增. 并且，函数()h t 在4t 附近比在3t 附近增加得慢. 说明：体会“以直代曲”的思想. 练习（P9） 函数33()4Vr V π=(05)V ≤≤的图象为根据图象，估算出(0.6)0.3r '≈，(1.2)0.2r '≈.说明：如果没有信息技术，教师可以将此图直接提供给学生，然后让学生根据导数的几何意义估算两点处的导数. 习题1.1 A 组（P10）1、在0t 处，虽然1020()()W t W t =，然而10102020()()()()W t W t t W t W t t t t--∆--∆≥-∆-∆. 所以，企业甲比企业乙治理的效率高.说明：平均变化率的应用，体会平均变化率的内涵.2、(1)(1) 4.9 3.3h h t h t t t∆+∆-==-∆-∆∆，所以，(1) 3.3h '=-.这说明运动员在1t =s 附近以3.3 m ／s 的速度下降. 3、物体在第5 s 的瞬时速度就是函数()s t 在5t =时的导数.(5)(5)10s s t s t t t∆+∆-==∆+∆∆，所以，(5)10s '=. 因此，物体在第5 s 时的瞬时速度为10 m ／s ，它在第5 s 的动能213101502k E =⨯⨯= J. 4、设车轮转动的角度为θ，时间为t ，则2(0)kt t θ=>. 由题意可知，当0.8t =时，2θπ=. 所以258k π=，于是2258t πθ=.车轮转动开始后第3.2 s 时的瞬时角速度就是函数()t θ在 3.2t =时的导数.(3.2)(3.2)25208t t t t θθθππ∆+∆-==∆+∆∆，所以(3.2)20θπ'=. 因此，车轮在开始转动后第3.2 s 时的瞬时角速度为20π1s -. 说明：第2,3,4题是对了解导数定义及熟悉其符号表示的巩固.5、由图可知，函数()f x 在5x =-处切线的斜率大于零，所以函数在5x =-附近单调递增. 同理可得，函数()f x 在4x =-，2-，0，2附近分别单调递增，几乎没有变化，单调递减，单调递减. 说明：“以直代曲”思想的应用.6、第一个函数的图象是一条直线，其斜率是一个小于零的常数，因此，其导数()f x '的图象如图（1）所示；第二个函数的导数()f x '恒大于零，并且随着x 的增加，()f x '的值也在增加；对于第三个函数，当x 小于零时，()f x '小于零，当x 大于零时，()f x '大于零，并且随着x 的增加，()f x '的值也在增加. 以下给出了满足上述条件的导函数图象中的一种.说明：本题意在让学生将导数与曲线的切线斜率相联系. 习题3.1 B 组（P11）1、高度关于时间的导数刻画的是运动变化的快慢，即速度；速度关于时间的导数刻画的是速度变化的快慢，根据物理知识，这个量就是加速度.2、说明：由给出的()v t 的信息获得()s t 的相关信息，并据此画出()s t 的图象的大致形状. 这个过程基于对导数内涵的了解，以及数与形之间的相互转换.3、由（1）的题意可知，函数()f x 的图象在点(1,5)-处的切线斜率为1-，所以此点附近曲线呈下降趋势. 首先画出切线的图象，然后再画出此点附近函数的图象. 同理可得（2）（3）某点处函数图象的大致形状. 下面是一种参考答案.说明：这是一个综合性问题，包含了对导数内涵、导数几何意义的了解，以及对以直代曲思想的领悟. 本题的答案不唯一. 1．2导数的计算 练习（P18）1、()27f x x '=-，所以，(2)3f '=-，(6)5f '=.2、（1）1ln 2y x '=； （2）2x y e '=； （3）4106y x x '=-； （4）3sin 4cos y x x '=--；（5）1sin 33xy '=-； （6）21y x '=-.习题1.2 A 组（P18）1、()()2S S r r S r r r r r π∆+∆-==+∆∆∆，所以，0()lim(2)2r S r r r r ππ∆→'=+∆=.2、()9.8 6.5h t t '=-+.3、3213()34r V Vπ'=. 4、（1）213ln 2y x x '=+； （2）1n x n x y nx e x e -'=+； （3）2323sin cos cos sin x x x x x y x-+'=； （4）9899(1)y x '=+； （5）2x y e -'=-； （6）2sin(25)4cos(25)y x x x '=+++. 5、()822f x x '=-+. 由0()4f x '=有 04822x =-+，解得032x =. 6、（1）ln 1y x '=+； （2）1y x =-. 7、1xy π=-+.8、（1）氨气的散发速度()500ln 0.8340.834t A t '=⨯⨯.（2）(7)25.5A '=-，它表示氨气在第7天左右时，以25.5克／天的速率减少.习题1.2 B 组（P19） 1、（1）（2）当h 越来越小时，sin()sin x h xy h+-=就越来越逼近函数cos y x =.（3）sin y x =的导数为cos y x =.2、当0y =时，0x =. 所以函数图象与x 轴交于点(0,0)P . x y e '=-，所以01x y ='=-.所以，曲线在点P 处的切线的方程为y x =-.2、()4sin d t t '=-. 所以，上午6:00时潮水的速度为0.42-m ／h ；上午9:00时潮水的速度为0.63-m ／h ；中午12:00时潮水的速度为0.83-m ／h ；下午6:00时潮水的速度为 1.24-m ／h.1．3导数在研究函数中的应用 练习（P26）1、（1）因为2()24f x x x =-+，所以()22f x x '=-.当()0f x '>，即1x >时，函数2()24f x x x =-+单调递增； 当()0f x '<，即1x <时，函数2()24f x x x =-+单调递减. （2）因为()x f x e x =-，所以()1x f x e '=-.当()0f x '>，即0x >时，函数()x f x e x =-单调递增； 当()0f x '<，即0x <时，函数()x f x e x =-单调递减. （3）因为3()3f x x x =-，所以2()33f x x '=-.当()0f x '>，即11x -<<时，函数3()3f x x x =-单调递增； 当()0f x '<，即1x <-或1x >时，函数3()3f x x x =-单调递减. （4）因为32()f x x x x =--，所以2()321f x x x '=--.当()0f x '>，即13x <-或1x >时，函数32()f x x x x =--单调递增；当()0f x '<，即113x -<<时，函数32()f x x x x =--单调递减.2、3、因为2()(0)f x ax bx c a =++≠，所以()2f x ax b '=+. （1）当0a >时，()0f x '>，即2bx a >-时，函数2()(0)f x ax bx c a =++≠单调递增； ()0f x '<，即2bx a<-时，函数2()(0)f x ax bx c a =++≠单调递减.（2）当0a <时，()0f x '>，即2bx a <-时，函数2()(0)f x ax bx c a =++≠单调递增；()0f x '<，即2bx a>-时，函数2()(0)f x ax bx c a =++≠单调递减. 4、证明：因为32()267f x x x =-+，所以2()612f x x x '=-. 当(0,2)x ∈时，2()6120f x x x '=-<，因此函数32()267f x x x =-+在(0,2)内是减函数. 练习（P29）1、24,x x 是函数()y f x =的极值点，其中2x x =是函数()y f x =的极大值点，4x x =是函数()y f x =的极小值点. 2、（1）因为2()62f x x x =--，所以()121f x x '=-. 令()1210f x x '=-=，得112x =. 当112x >时，()0f x '>，()f x 单调递增；当112x <时，()0f x '<，()f x 单调递减. 所以，当112x =时，()f x 有极小值，并且极小值为211149()6()212121224f =⨯--=-.（2）因为3()27f x x x =-，所以2()327f x x '=-. 令2()3270f x x '=-=，得3x =±. 下面分两种情况讨论：①当()0f x '>，即3x <-或3x >时；②当()0f x '<，即33x -<<时. 当x 变化时，()f x '，()f x 变化情况如下表：注：图象形状不唯一.因此，当3x =-时，()f x 有极大值，并且极大值为54；当3x =时，()f x 有极小值，并且极小值为54-.（3）因为3()612f x x x =+-，所以2()123f x x '=-. 令2()1230f x x '=-=，得2x =±. 下面分两种情况讨论：①当()0f x '>，即22x -<<时；②当()0f x '<，即2x <-或2x >时. 当x 变化时，()f x '，()f x 变化情况如下表：因此，当2x =-时，()f x 有极小值，并且极小值为10-；当2x =时，()f x 有极大值，并且极大值为22（4）因为3()3f x x x =-，所以2()33f x x '=-. 令2()330f x x '=-=，得1x =±. 下面分两种情况讨论：①当()0f x '>，即11x -<<时；②当()0f x '<，即1x <-或1x >时. 当x 变化时，()f x '，()f x 变化情况如下表：因此，当1x =-时，()f x 有极小值，并且极小值为2-；当1x =时，()f x 有极大值，并且极大值为2练习（P31）（1）在[0,2]上，当112x =时，2()62f x x x =--有极小值，并且极小值为149()1224f =-. 又由于(0)2f =-，(2)20f =.因此，函数2()62f x x x =--在[0,2]上的最大值是20、最小值是4924-. （2）在[4,4]-上，当3x =-时，3()27f x x x =-有极大值，并且极大值为(3)54f -=；当3x =时，3()27f x x x =-有极小值，并且极小值为(3)54f =-；又由于(4)44f -=，(4)44f =-.因此，函数3()27f x x x =-在[4,4]-上的最大值是54、最小值是54-.（3）在1[,3]3-上，当2x =时，3()612f x x x =+-有极大值，并且极大值为(2)22f =.又由于155()327f -=，(3)15f =.因此，函数3()612f x x x =+-在1[,3]3-上的最大值是22、最小值是5527.（4）在[2,3]上，函数3()3f x x x =-无极值. 因为(2)2f =-，(3)18f =-.因此，函数3()3f x x x =-在[2,3]上的最大值是2-、最小值是18-. 习题1.3 A 组（P31）1、（1）因为()21f x x =-+，所以()20f x '=-<. 因此，函数()21f x x =-+是单调递减函数.（2）因为()cos f x x x =+，(0,)2x π∈，所以()1sin 0f x x '=->，(0,)2x π∈. 因此，函数()cos f x x x =+在(0,)2π上是单调递增函数. （3）因为()24f x x =--，所以()20f x '=-<. 因此，函数()24f x x =-是单调递减函数. （4）因为3()24f x x x =+，所以2()640f x x '=+>. 因此，函数3()24f x x x =+是单调递增函数.2、（1）因为2()24f x x x =+-，所以()22f x x '=+.当()0f x '>，即1x >-时，函数2()24f x x x =+-单调递增. 当()0f x '<，即1x <-时，函数2()24f x x x =+-单调递减. （2）因为2()233f x x x =-+，所以()43f x x '=-.当()0f x '>，即34x >时，函数2()233f x x x =-+单调递增. 当()0f x '<，即34x <时，函数2()233f x x x =-+单调递减.（3）因为3()3f x x x =+，所以2()330f x x '=+>. 因此，函数3()3f x x x =+是单调递增函数. （4）因为32()f x x x x =+-，所以2()321f x x x '=+-. 当()0f x '>，即1x <-或13x >时，函数32()f x x x x =+-单调递增. 当()0f x '<，即113x -<<时，函数32()f x x x x =+-单调递减.3、（1）图略. （2）加速度等于0.4、（1）在2x x =处，导函数()y f x '=有极大值； （2）在1x x =和4x x =处，导函数()y f x '=有极小值； （3）在3x x =处，函数()y f x =有极大值； （4）在5x x =处，函数()y f x =有极小值.5、（1）因为2()62f x x x =++，所以()121f x x '=+. 令()1210f x x '=+=，得112x =-. 当112x >-时，()0f x '>，()f x 单调递增； 当112x <-时，()0f x '<，()f x 单调递减.所以，112x =-时，()f x 有极小值，并且极小值为211149()6()212121224f -=⨯---=-.（2）因为3()12f x x x =-，所以2()312f x x '=-. 令2()3120f x x '=-=，得2x =±. 下面分两种情况讨论：①当()0f x '>，即2x <-或2x >时；②当()0f x '<，即22x -<<时. 当x 变化时，()f x '，()f x 变化情况如下表：因此，当2x =-时，()f x 有极大值，并且极大值为16；当2x =时，()f x 有极小值，并且极小值为16-.（3）因为3()612f x x x =-+，所以2()123f x x '=-+. 令2()1230f x x '=-+=，得2x =±. 下面分两种情况讨论：①当()0f x '>，即2x <-或2x >时；②当()0f x '<，即22x -<<时. 当x 变化时，()f x '，()f x 变化情况如下表：因此，当2x =-时，()f x 有极大值，并且极大值为22；当2x =时，()f x 有极小值，并且极小值为10-.（4）因为3()48f x x x =-，所以2()483f x x '=-. 令2()4830f x x '=-=，得4x =±. 下面分两种情况讨论：①当()0f x '>，即2x <-或2x >时；②当()0f x '<，即22x -<<时. 当x 变化时，()f x '，()f x 变化情况如下表：因此，当4x =-时，()f x 有极小值，并且极小值为128-；当4x =时，()f x 有极大值，并且极大值为128.6、（1）在[1,1]-上，当112x =-时，函数2()62f x x x =++有极小值，并且极小值为4724. 由于(1)7f -=，(1)9f =，所以，函数2()62f x x x =++在[1,1]-上的最大值和最小值分别为9，4724. （2）在[3,3]-上，当2x =-时，函数3()12f x x x =-有极大值，并且极大值为16； 当2x =时，函数3()12f x x x =-有极小值，并且极小值为16-. 由于(3)9f -=，(3)9f =-，所以，函数3()12f x x x =-在[3,3]-上的最大值和最小值分别为16，16-.（3）在1[,1]3-上，函数3()612f x x x =-+在1[,1]3-上无极值.由于1269()327f -=，(1)5f =-，所以，函数3()612f x x x =-+在1[,1]3-上的最大值和最小值分别为26927，5-.（4）当4x =时，()f x 有极大值，并且极大值为128.. 由于(3)117f -=-，(5)115f =，所以，函数3()48f x x x =-在[3,5]-上的最大值和最小值分别为128，117-. 习题3.3 B 组（P32）1、（1）证明：设()sin f x x x =-，(0,)x π∈. 因为()cos 10f x x '=-<，(0,)x π∈ 所以()sin f x x x =-在(0,)π内单调递减因此()sin (0)0f x x x f =-<=，(0,)x π∈，即sin x x <，(0,)x π∈. 图略 （2）证明：设2()f x x x =-，(0,1)x ∈. 因为()12f x x '=-，(0,1)x ∈所以，当1(0,)2x ∈时，()120f x x '=->，()f x 单调递增，2()(0)0f x x x f =->=；当1(,1)2x ∈时，()120f x x '=-<，()f x 单调递减，2()(1)0f x x x f =->=；又11()024f =>. 因此，20x x ->，(0,1)x ∈. 图略（3）证明：设()1x f x e x =--，0x ≠. 因为()1x f x e '=-，0x ≠所以，当0x >时，()10x f x e '=->，()f x 单调递增，()1(0)0x f x e x f =-->=；当0x <时，()10x f x e '=-<，()f x 单调递减，()1(0)0x f x e x f =-->=；综上，1x e x ->，0x ≠. 图略 （4）证明：设()ln f x x x =-，0x >. 因为1()1f x x'=-，0x ≠ 所以，当01x <<时，1()10f x x'=->，()f x 单调递增， ()ln (1)10f x x x f =-<=-<；当1x >时，1()10f x x'=-<，()f x 单调递减， ()ln (1)10f x x x f =-<=-<；当1x =时，显然ln11<. 因此，ln x x <. 由（3）可知，1x e x x >+>，0x >.. 综上，ln x x x e <<，0x > 图略2、（1）函数32()f x ax bx cx d =+++的图象大致是个“双峰”图象，类似“”或“”的形状. 若有极值，则在整个定义域上有且仅有一个极大值和一个极小值，从图象上能大致估计它的单调区间.（2）因为32()f x ax bx cx d =+++，所以2()32f x ax bx c '=++.下面分类讨论：当0a ≠时，分0a >和0a <两种情形： ①当0a >，且230b ac ->时，设方程2()320f x ax bx c '=++=的两根分别为12,x x ，且12x x <，当2()320f x ax bx c '=++>，即1x x <或2x x >时，函数32()f x ax bx cx d =+++单调递增； 当2()320f x ax bx c '=++<，即12x x x <<时，函数32()f x ax bx cx d =+++单调递减. 当0a >，且230b ac -≤时，此时2()320f x ax bx c '=++≥，函数32()f x ax bx cx d =+++单调递增. ②当0a <，且230b ac ->时，设方程2()320f x ax bx c '=++=的两根分别为12,x x ，且12x x <，当2()320f x ax bx c '=++>，即12x x x <<时，函数32()f x ax bx cx d =+++单调递增； 当2()320f x ax bx c '=++<，即1x x <或2x x >时，函数32()f x ax bx cx d =+++单调递减. 当0a <，且230b ac -≤时，此时2()320f x ax bx c '=++≤，函数32()f x ax bx cx d =+++单调递减 1．4生活中的优化问题举例 习题1.4 A 组（P37）1、设两段铁丝的长度分别为x ，l x -，则这两个正方形的边长分别为4x ，4l x -，两个正方形的面积和为 22221()()()(22)4416x l x S f x x lx l -==+=-+，0x l <<.令()0f x '=，即420x l -=，2lx =.当(0,)2l x ∈时，()0f x '<；当(,)2lx l ∈时，()0f x '>.因此，2lx =是函数()f x 的极小值点，也是最小值点.所以，当两段铁丝的长度分别是2l时，两个正方形的面积和最小.2、如图所示，由于在边长为a 的正方形铁片的四角截去 四个边长为x 的小正方形，做成一个无盖方盒，所以无 盖方盒的底面为正方形，且边长为2a x -，高为x .（1）无盖方盒的容积2()(2)V x a x x =-，02ax <<.（2）因为322()44V x x ax a x =-+，所以22()128V x x ax a '=-+.令()0V x '=，得2a x =（舍去），或6a x =. 当(0,)6a x ∈时，()0V x '>；当(,)62a ax ∈时，()0V x '<.因此，6ax =是函数()V x 的极大值点，也是最大值点.所以，当6ax =时，无盖方盒的容积最大.3、如图，设圆柱的高为h ，底半径为R ， 则表面积222S Rh R ππ=+由2V R h π=，得2V h R π=. 因此，2222()222V V S R R R R R R ππππ=+=+，0R >. 令2()40VS R R Rπ'=-+=，解得R =.当R ∈时，()0S R '<；当)R ∈+∞时，()0S R '>.因此，R =是函数()S R 的极小值点，也是最小值点.此时，22V h R R π===. 所以，当罐高与底面直径相等时，所用材料最省.4、证明：由于211()()n i i f x x a n ==-∑，所以12()()n i i f x x a n ='=-∑.令()0f x '=，得11ni i x a n ==∑，可以得到，11ni i x a n ==∑是函数()f x 的极小值点，也是最小值点.这个结果说明，用n 个数据的平均值11ni i a n =∑表示这个物体的长度是合理的，这就是最小二乘法的基本原理.5、设矩形的底宽为x m ，则半圆的半径为2xm ，半圆的面积为28x π2m ，（第3题）矩形的面积为28x a π-2m ，矩形的另一边长为()8a xx π-m因此铁丝的长为22()(1)244xa x al x x x x xπππ=++-=++，0x <<令22()104al x xπ'=+-=，得x =.当x ∈时，()0l x '<；当x ∈时，()0l x '>.因此，x =()l x 的极小值点，也是最小值点.时，所用材料最省. 6、利润L 等于收入R 减去成本C ，而收入R 等于产量乘单价. 由此可得出利润L 与产量q 的函数关系式，再用导数求最大利润.收入211(25)2588R q p q q q q =⋅=-=-，利润2211(25)(1004)2110088L R C q q q q q =-=--+=-+-，0200q <<.求导得1214L q '=-+令0L '=，即12104q -+=，84q =.当(0,84)q ∈时，0L '>；当(84,200)q ∈时，0L '<；因此，84q =是函数L 的极大值点，也是最大值点.所以，产量为84时，利润L 最大,习题1.4 B 组（P37）1、设每个房间每天的定价为x 元，那么宾馆利润21801()(50)(20)7013601010x L x x x x -=--=-+-，180680x <<. 令1()7005L x x '=-+=，解得350x =.当(180,350)x ∈时，()0L x '>；当(350,680)x ∈时，()0L x '>. 因此，350x =是函数()L x 的极大值点，也是最大值点. 所以，当每个房间每天的定价为350元时，宾馆利润最大. 2、设销售价为x 元／件时，利润4()()(4)()(5)b x L x x a c cc x a x b b -=-+⨯=--，54ba x <<. 令845()0c ac bc L x xb b +'=-+=，解得458a bx +=. 当45(,)8a b x a +∈时，()0L x '>；当455(,)84a b bx +∈时，()0L x '<.当458a bx +=是函数()L x 的极大值点，也是最大值点.所以，销售价为458a b+元／件时，可获得最大利润.1．5定积分的概念 练习（P42） 83. 说明：进一步熟悉求曲边梯形面积的方法和步骤，体会“以直代曲”和“逼近”的思想. 练习（P45）1、22112()[()2]()i i i i i s s v t n n n n n n'∆≈∆=∆=-+⋅=-⋅+⋅，1,2,,i n =.于是 111()n n ni i i i i is s s v t n ==='=∆≈∆=∆∑∑∑2112[()]ni i n n n ==-⋅+⋅∑22211111()()()2n n n n n n n n -=-⋅--⋅-⋅+2231[12]2n n=-++++31(1)(21)26n n n n ++=-⋅+111(1)(1)232n n=-+++取极值，得1111115lim [()]lim [(1)(1)2]323nnn n i i i s v n n n n →∞→∞====-+++=∑∑说明：进一步体会“以不变代变”和“逼近”的思想.2、223km.说明：进一步体会“以不变代变”和“逼近”的思想，熟悉求变速直线运动物体路程的方法和步骤.练习（P48）2304x dx =⎰. 说明：进一步熟悉定积分的定义和几何意义.从几何上看，表示由曲线3y x =与直线0x =，2x =，0y =所围成的曲边梯形的面积4S =.习题1.5 A 组（P50） 1、（1）10021111(1)[(1)1]0.495100100i i x dx =--≈+-⨯=∑⎰； （2）50021111(1)[(1)1]0.499500500i i x dx =--≈+-⨯=∑⎰； （3）100021111(1)[(1)1]0.499510001000i i x dx =--≈+-⨯=∑⎰. 说明：体会通过分割、近似替换、求和得到定积分的近似值的方法.2、距离的不足近似值为：18112171310140⨯+⨯+⨯+⨯+⨯=（m ）； 距离的过剩近似值为：271181121713167⨯+⨯+⨯+⨯+⨯=（m ）.3、证明：令()1f x =. 用分点 011i i n a x x x x x b -=<<<<<<=将区间[,]a b 等分成n 个小区间，在每个小区间1[,]i i x x -上任取一点(1,2,,)i i n ξ=作和式11()nni i i b af x b a nξ==-∆==-∑∑， 从而11lim nban i b adx b a n→∞=-==-∑⎰， 说明：进一步熟悉定积分的概念. 4、根据定积分的几何意义，0⎰表示由直线0x =，1x =，0y =以及曲线y =所围成的曲边梯形的面积，即四分之一单位圆的面积，因此04π=⎰.5、（1）03114x dx -=-⎰.由于在区间[1,0]-上30x ≤，所以定积分031x dx -⎰表示由直线0x =，1x =-，0y =和曲线3y x =所围成的曲边梯形的面积的相反数.（2）根据定积分的性质，得1133311011044x dx x dx x dx --=+=-+=⎰⎰⎰.由于在区间[1,0]-上30x ≤，在区间[0,1]上30x ≥，所以定积分131x dx -⎰等于位于x 轴上方的曲边梯形面积减去位于x 轴下方的曲边梯形面积.（3）根据定积分的性质，得202333110115444x dx x dx x dx --=+=-+=⎰⎰⎰由于在区间[1,0]-上30x ≤，在区间[0,2]上30x ≥，所以定积分231x dx -⎰等于位于x 轴上方的曲边梯形面积减去位于x 轴下方的曲边梯形面积.说明：在（3）中，由于3x 在区间[1,0]-上是非正的，在区间[0,2]上是非负的，如果直接利用定义把区间[1,2]-分成n 等份来求这个定积分，那么和式中既有正项又有负项，而且无法抵挡一些项，求和会非常麻烦. 利用性质3可以将定积分231x dx -⎰化为02331x dx x dx -+⎰⎰，这样，3x 在区间[1,0]-和区间[0,2]上的符号都是不变的，再利用定积分的定义，容易求出031x dx -⎰，230x dx ⎰，进而得到定积分231x dx -⎰的值. 由此可见，利用定积分的性质可以化简运算.在（2）（3）中，被积函数在积分区间上的函数值有正有负，通过练习进一步体会定积分的几何意义.习题1.5 B 组（P50）1、该物体在0t =到6t =（单位：s ）之间走过的路程大约为145 m.说明：根据定积分的几何意义，通过估算曲边梯形内包含单位正方形的个数来估计物体走过的路程. 2、（1）9.81v t =.（2）过剩近似值：8111899.819.8188.292242i i =⨯⨯⨯=⨯⨯=∑（m ）；不足近似值：81111879.819.8168.672242i i =-⨯⨯⨯=⨯⨯=∑（m ） （3）49.81tdt ⎰；49.81d 78.48t t =⎰（m ）.3、（1）分割在区间[0,]l 上等间隔地插入1n -个分点，将它分成n 个小区间：[0,]l n ，2[,]l l n n ，……，(2)[,]n l l n -， 记第i 个区间为(1)[,]i l iln n-（1,2,i n =），其长度为 (1)il i l l x n n n-∆=-=.把细棒在小段[0,]l n ，2[,]l l n n ，……，(2)[,]n ll n-上质量分别记作：12,,,n m m m ∆∆∆，则细棒的质量1ni i m m ==∆∑.（2）近似代替当n 很大，即x ∆很小时，在小区间(1)[,]i l iln n-上，可以认为线密度2()x x ρ=的值变化很小，近似地等于一个常数，不妨认为它近似地等于任意一点(1)[,]i i l iln nξ-∈处的函数值2()i i ρξξ=. 于是，细棒在小段(1)[,]i l il n n -上质量 2()i i i lm x nρξξ∆≈∆=（1,2,i n =）.（3）求和得细棒的质量 2111()nnni i i i i i l m m x nρξξ====∆≈∆=∑∑∑. （4）取极限细棒的质量 21lim ni n i lm n ξ→∞==∑，所以20l m x dx =⎰..。
选修2-2 知识点及习题答案解析导数及其应用一.导数概念的引入1. 导数的物理意义：瞬时速率。
一般的，函数()y f x =在0x x =处的瞬时变化率是000()()lim x f x x f x x∆→+∆-∆，我们称它为函数()y f x =在x x =处的导数，记作0()f x '或|x x y ='，即0()f x '=000()()limx f x x f x x∆→+∆-∆2.导数的几何意义：曲线的切线.通过图像,我们可以看出当点n P 趋近于P 时，直线PT 与曲线相切。
容易知道，割线n PP 的斜率是00()()n nn f x f x k x x -=-，当点n P 趋近于P 时，函数()y f x =在0x x =处的导数就是切线PT 的斜率k ，即00()()lim ()n x n f x f x k f x x x ∆→-'==-3. 导函数：当x 变化时，()f x '便是x 的一个函数，我们称它为()f x 的导函数.()y f x =的导函数有时也记作y ',即()()()limx f x x f x f x x∆→+∆-'=∆二.导数的计算基本初等函数的导数公式:1若()f x c =(c 为常数)，则()0f x '=； 2 若()f x x α=,则1()f x x αα-'=;3 若()sin f x x =,则()cos f x x '=4 若()cos f x x =,则()sin f x x '=-;5 若()x f x a =,则()ln x f x a a '=6 若()x f x e =,则()x f x e '=7 若()log xaf x =,则1()ln f x x a '= 8 若()ln f x x =,则1()f x x'=导数的运算法则1. [()()]()()f x g x f x g x '''±=±2.[()()]()()()()f x g x f x g x f x g x '''•=•+•3. 2()()()()()[]()[()]f x f xg x f x g x g x g x ''•-•'= 复合函数求导 ()y f u =和()u g x =,称则y 可以表示成为x 的函数,即(())y f g x =为一个复合函数(())()y f g x g x '''=• 三.导数在研究函数中的应用1.函数的单调性与导数:一般的,函数的单调性与其导数的正负有如下关系： 在某个区间(,)a b 内(1)如果()0f x '>，那么函数()y f x =在这个区间单调递增；(2)如果()0f x '<，那么函数()y f x =在这个区间单调递减. 2.函数的极值与导数极值反映的是函数在某一点附近的大小情况.求函数()y f x =的极值的方法是:（1）如果在0x 附近的左侧()0f x '>,右侧()0f x '<,那么0()f x 是极大值（2）如果在0x 附近的左侧()0f x '<,右侧()0f x '>,那么0()f x 是极小值; 4.函数的最大(小)值与导数求函数()y f x =在[,]a b 上的最大值与最小值的步骤： （1）求函数()y f x =在(,)a b 内的极值； （2） 将函数()y f x =的各极值与端点处的函数值()f a ，()f b 比较，其中最大的是一个最大值，最小的是最小值.推理与证明考点一 合情推理与类比推理根据一类事物的部分对象具有某种性质,退出这类事物的所有对象都具有这种性质的推理,叫做归纳推理,归纳是从特殊到一般的过程,它属于合情推理根据两类不同事物之间具有某些类似(或一致)性,推测其中一类事物具有与另外一类事物类似的性质的推理,叫做类比推理.类比推理的一般步骤:(1) 找出两类事物的相似性或一致性;(2) 用一类事物的性质去推测另一类事物的性质,得出一个明确的命题(猜想);(3) 一般的,事物之间的各个性质并不是孤立存在的,而是相互制约的.如果两个事物在某些性质上相同或相似,那么他们在另一写性质上也可能相同或类似,类比的结论可能是真的.(4) 一般情况下,如果类比的相似性越多,相似的性质与推测的性质之间越相关,那么类比得出的命题越可靠.考点二 演绎推理(俗称三段论)由一般性的命题推出特殊命题的过程,这种推理称为演绎推理. 考点三 数学归纳法1. 它是一个递推的数学论证方法.2. 步骤:A.命题在n=1（或0n ）时成立，这是递推的基础；B.假设在n=k 时命题成立； C.证明n=k+1时命题也成立,完成这两步,就可以断定对任何自然数(或n>=0n ,且n N ∈)结论都成立。
考点三 证明1. 反证法: 2、分析法: 3、综合法:数系的扩充和复数的概念 复数的概念(1) 复数:形如(,)a bi a R b R +∈∈的数叫做复数，a 和b 分别叫它的实部和虚部. (2) 分类:复数(,)a bi a R b R +∈∈中,当0b =,就是实数;0b ≠,叫做虚数;当0,0a b =≠时,叫做纯虚数.(3) 复数相等:如果两个复数实部相等且虚部相等就说这两个复数相等.(4) 共轭复数:当两个复数实部相等,虚部互为相反数时,这两个复数互为共轭复数.(5) 复平面:建立直角坐标系来表示复数的平面叫做复平面,x 轴叫做实轴，y 轴除去原点的部分叫做虚轴。
(6) 两个实数可以比较大小，但两个复数如果不全是实数就不能比较大小。
复数的运算1.复数的加，减，乘，除按以下法则进行 设12,(,,,)z a bi z c di a b c d R =+=+∈则 （1）12()()z z a c b d i ±=±+± （2）12()()z z ac bd ad bc i •=-++ （3）12222()()(0)z ac bd ad bc i z z c d-++=≠+ 2,几个重要的结论(1) 2222121212||||2(||||)z z z z z z ++-=+ (2) 22||||z z z z •== (3)若z 为虚数,则22||z z ≠ 3.运算律 (1)m n m n z z z +•=;(2) ()m n mn z z =;(3)1212()(,)n n n z z z z m n R •=•∈4.关于虚数单位i 的一些固定结论：（1）21i=- （2）3i i =- （3）41i = （2）2340n n n n i i i i ++++++=练习一组一、选择题1．在平均变化率的定义中，自变量x 在x 0处的增量Δx ( ) A ．大于零 B ．小于零 C ．等于零D ．不等于零[答案] D[解析] Δx 可正，可负，但不为0，故应选D.2．设函数y ＝f (x )，当自变量x 由x 0变化到x 0＋Δx 时，函数的改变量Δy 为( ) A ．f (x 0＋Δx ) B ．f (x 0)＋Δx C ．f (x 0)·ΔxD ．f (x 0＋Δx )－f (x 0)[答案] D[解析] 由定义，函数值的改变量Δy ＝f (x 0＋Δx )－f (x 0)，故应选D. 3．已知函数f (x )＝－x 2＋x ，则f (x )从－1到－0.9的平均变化率为( ) A ．3B ．0.29C ．2.09D ．2.9[答案] D[解析] f (－1)＝－(－1)2＋(－1)＝－2.f (－0.9)＝－(－0.9)2＋(－0.9)＝－1.71.∴平均变化率为f (－0.9)－f (－1)－0.9－(－1)＝－1.71－(－2)0.1＝2.9，故应选D.4．已知函数f (x )＝x 2＋4上两点A ，B ，x A ＝1，x B ＝1.3，则直线AB 的斜率为( ) A ．2B ．2.3C ．2.09D ．2.1[答案] B[解析] f (1)＝5，f (1.3)＝5.69. ∴k AB ＝f (1.3)－f (1)1.3－1＝5.69－50.3＝2.3，故应选B.5．已知函数f (x )＝－x 2＋2x ，函数f (x )从2到2＋Δx 的平均变化率为( ) A ．2－Δx B ．－2－Δx C ．2＋ΔxD ．(Δx )2－2·Δx[答案] B[解析] ∵f (2)＝－22＋2×2＝0， ∴f (2＋Δx )＝－(2＋Δx )2＋2(2＋Δx ) ＝－2Δx －(Δx )2，∴f (2＋Δx )－f (2)2＋Δx －2＝－2－Δx ，故应选B.6．已知函数y ＝x 2＋1的图象上一点(1,2)及邻近一点(1＋Δx,2＋Δy )，则ΔyΔx 等于( )A ．2B ．2xC ．2＋ΔxD ．2＋(Δx )2[答案] C[解析] Δy Δx ＝f (1＋Δx )－f (1)Δx＝[(1＋Δx )2＋1]－2Δx＝2＋Δx .故应选C.7．质点运动规律S (t )＝t 2＋3，则从3到3.3内，质点运动的平均速度为( ) A ．6.3 B ．36.3 C ．3.3D ．9.3[答案] A[解析] S (3)＝12，S (3.3)＝13.89， ∴平均速度v ＝S (3.3)－S (3)3.3－3＝1.890.3＝6.3，故应选A.8．在x ＝1附近，取Δx ＝0.3，在四个函数①y ＝x 、②y ＝x 2、③y ＝x 3、④y ＝1x中，平均变化率最大的是( )A ．④B ．③C ．②D ．①[答案] B[解析] Δx ＝0.3时，①y ＝x 在x ＝1附近的平均变化率k 1＝1；②y ＝x 2在x ＝1附近的平均变化率k 2＝2＋Δx ＝2.3；③y ＝x 3在x ＝1附近的平均变化率k 3＝3＋3Δx ＋(Δx )2＝3.99；④y ＝1x 在x ＝1附近的平均变化率k 4＝－11＋Δx ＝－1013.∴k 3＞k 2＞k 1＞k 4，故应选B.9．物体做直线运动所经过的路程s 可以表示为时间t 的函数s ＝s (t )，则物体在时间间隔[t 0，t 0＋Δt ]内的平均速度是( )A ．v 0B.Δts (t 0＋Δt )－s (t 0)C.s (t 0＋Δt )－s (t 0)ΔtD.s (t )t[答案] C[解析] 由平均变化率的概念知C 正确，故应选C.10．已知曲线y ＝14x 2和这条曲线上的一点P ⎝ ⎛⎭⎪⎫1，14，Q 是曲线上点P 附近的一点，则点Q 的坐标为( )A.⎝⎛⎭⎪⎫1＋Δx ，14(Δx )2B.⎝⎛⎭⎪⎫Δx ，14(Δx )2 C.⎝⎛⎭⎪⎫1＋Δx ，14(Δx ＋1)2 D.⎝⎛⎭⎪⎫Δx ，14(1＋Δx )2 [答案] C[解析] 点Q 的横坐标应为1＋Δx ，所以其纵坐标为f (1＋Δx )＝14(Δx ＋1)2，故应选C.二、填空题11．已知函数y ＝x 3－2，当x ＝2时，ΔyΔx＝________.[答案] (Δx )2＋6Δx ＋12[解析] Δy Δx ＝(2＋Δx )3－2－(23－2)Δx＝(Δx )3＋6(Δx )2＋12ΔxΔx＝(Δx )2＋6Δx ＋12.12．在x ＝2附近，Δx ＝14时，函数y ＝1x 的平均变化率为________．[答案] －29[解析] Δy Δx ＝12＋Δx －12Δx ＝－14＋2Δx ＝－29.13．函数y ＝x 在x ＝1附近，当Δx ＝12时的平均变化率为________．[答案] 6－2[解析]Δy Δx ＝1＋Δx －1Δx ＝11＋Δx ＋1＝6－2. 14．已知曲线y ＝x 2－1上两点A (2,3)，B (2＋Δx,3＋Δy )，当Δx ＝1时，割线AB 的斜率是________；当Δx ＝0.1时，割线AB 的斜率是________．[答案] 5 4.1[解析] 当Δx ＝1时，割线AB 的斜率k 1＝Δy Δx ＝(2＋Δx )2－1－22＋1Δx ＝(2＋1)2－221＝5.当Δx ＝0.1时，割线AB 的斜率 k 2＝Δy Δx ＝(2＋0.1)2－1－22＋10.1＝4.1.三、解答题15．已知函数f (x )＝2x ＋1，g (x )＝－2x ，分别计算在区间[－3，－1]，[0,5]上函数f (x )及g (x )的平均变化率．[解析] 函数f (x )在[－3，－1]上的平均变化率为f (－1)－f (－3)－1－(－3)＝[2×(－1)＋1]－[2×(－3)＋1]2＝2.函数f (x )在[0,5]上的平均变化率为f (5)－f (0)5－0＝2.函数g (x )在[－3，－1]上的平均变化率为g (－1)－g (－3)－1－(－3)＝－2.函数g (x )在[0,5]上的平均变化率为g (5)－g (0)5－0＝－2.16．过曲线f (x )＝2x2的图象上两点A (1,2)，B (1＋Δx,2＋Δy )作曲线的割线AB ，求出当Δx ＝14时割线的斜率．[解析] 割线AB 的斜率k ＝(2＋Δy )－2(1＋Δx )－1＝ΔyΔx＝2(1＋Δx )2－2Δx ＝－2(Δx ＋2)(1＋Δx )2＝－7225.17．求函数y ＝x 2在x ＝1、2、3附近的平均变化率，判断哪一点附近平均变化率最大？ [解析] 在x ＝2附近的平均变化率为k 1＝f (1＋Δx )－f (1)Δx ＝(1＋Δx )2－1Δx＝2＋Δx ；在x ＝2附近的平均变化率为k 2＝f (2＋Δx )－f (2)Δx ＝(2＋Δx )2－22Δx＝4＋Δx ；在x ＝3附近的平均变化率为k 3＝f (3＋Δx )－f (3)Δx ＝(3＋Δx )2－32Δx＝6＋Δx .对任意Δx 有，k 1＜k 2＜k 3， ∴在x ＝3附近的平均变化率最大．18．路灯距地面8m ，一个身高为1.6m 的人以84m/min 的速度在地面上从路灯在地面上的射影点C 处沿直线离开路灯．(1)求身影的长度y 与人距路灯的距离x 之间的关系式； (2)求人离开路灯的第一个10s 内身影的平均变化率．[解析] (1)如图所示，设人从C 点运动到B 处的路程为x m ，AB 为身影长度，AB 的长度为y m ，由于CD ∥BE ，则AB AC ＝BE CD， 即yy ＋x ＝1.68，所以y ＝f (x )＝14x . (2)84m/min ＝1.4m/s ，在[0,10]内自变量的增量为x 2－x 1＝1.4×10－1.4×0＝14，f (x 2)－f (x 1)＝14×14－14×0＝72.所以f (x 2)－f (x 1)x 2－x 1＝7214＝14.即人离开路灯的第一个10s 内身影的平均变化率为14.练习二组一、选择题1．函数在某一点的导数是( )A ．在该点的函数值的增量与自变量的增量的比B ．一个函数C ．一个常数，不是变数D ．函数在这一点到它附近一点之间的平均变化率 [答案] C[解析] 由定义，f ′(x 0)是当Δx 无限趋近于0时，ΔyΔx 无限趋近的常数，故应选C.2．如果质点A 按照规律s ＝3t 2运动，则在t 0＝3时的瞬时速度为( ) A ．6B ．18C ．54D ．81[答案] B[解析] ∵s (t )＝3t 2，t 0＝3，∴Δs ＝s (t 0＋Δt )－s (t 0)＝3(3＋Δt )2－3·32 ＝18Δt ＋3(Δt )2∴ΔsΔt＝18＋3Δt . 当Δt →0时，ΔsΔt →18，故应选B.3．y ＝x 2在x ＝1处的导数为( ) A ．2x B ．2 C ．2＋ΔxD ．1[答案] B[解析] ∵f (x )＝x 2，x ＝1，∴Δy ＝f (1＋Δx )2－f (1)＝(1＋Δx )2－1＝2·Δx ＋(Δx )2 ∴ΔyΔx＝2＋Δx 当Δx →0时，ΔyΔx →2∴f ′(1)＝2，故应选B.4．一质点做直线运动，若它所经过的路程与时间的关系为s (t )＝4t 2－3(s (t )的单位：m ，t 的单位：s)，则t ＝5时的瞬时速度为( )A ．37B ．38C ．39D ．40[答案] D[解析] ∵Δs Δt ＝4(5＋Δt )2－3－4×52＋3Δt ＝40＋4Δt ，∴s ′(5)＝li m Δt →0 ΔsΔt ＝li m Δt →0 (40＋4Δt )＝40.故应选D.5．已知函数y ＝f (x )，那么下列说法错误的是( ) A ．Δy ＝f (x 0＋Δx )－f (x 0)叫做函数值的增量B.Δy Δx ＝f (x 0＋Δx )－f (x 0)Δx 叫做函数在x 0到x 0＋Δx 之间的平均变化率 C ．f (x )在x 0处的导数记为y ′ D ．f (x )在x 0处的导数记为f ′(x 0) [答案] C[解析] 由导数的定义可知C 错误．故应选C.6．函数f (x )在x ＝x 0处的导数可表示为y ′|x ＝x 0，即( ) A ．f ′(x 0)＝f (x 0＋Δx )－f (x 0) B ．f ′(x 0)＝li m Δx →0[f (x 0＋Δx )－f (x 0)]C ．f ′(x 0)＝f (x 0＋Δx )－f (x 0)ΔxD ．f ′(x 0)＝li m Δx →0 f (x 0＋Δx )－f (x 0)Δx[答案] D[解析] 由导数的定义知D 正确．故应选D.7．函数y ＝ax 2＋bx ＋c (a ≠0，a ，b ，c 为常数)在x ＝2时的瞬时变化率等于( ) A ．4a B ．2a ＋b C ．bD ．4a ＋b[答案] D[解析] ∵Δy Δx ＝a (2＋Δx )2＋b (2＋Δx )＋c －4a －2b －cΔx＝4a ＋b ＋a Δx ，∴y ′|x ＝2＝li m Δx →0 ΔyΔx ＝li m Δx →0 (4a ＋b ＋a ·Δx )＝4a ＋b .故应选D.8．如果一个函数的瞬时变化率处处为0，则这个函数的图象是( )A ．圆B ．抛物线C ．椭圆D ．直线[答案] D[解析] 当f (x )＝b 时，f ′(x )＝0，所以f (x )的图象为一条直线，故应选D.9．一物体作直线运动，其位移s 与时间t 的关系是s ＝3t －t 2，则物体的初速度为() A ．0 B ．3C ．－2D ．3－2t[答案] B[解析] ∵ΔsΔt ＝3(0＋Δt )－(0＋Δt )2Δt ＝3－Δt ，∴s ′(0)＝li m Δt →0 ΔsΔt ＝3.故应选B.10．设f (x )＝1x ，则li m x →a f (x )－f (a )x －a 等于( )A ．－1a B.2aC ．－1a 2 D.1a 2[答案] C[解析] li m x →a f (x )－f (a )x －a ＝li m x →a 1x －1ax －a＝li m x →a a －x (x －a )·xa ＝－li m x →a 1ax ＝－1a 2.二、填空题11．已知函数y ＝f (x )在x ＝x 0处的导数为11，则li m Δx →0f (x 0－Δx )－f (x 0)Δx＝________； li m x →x 0f (x )－f (x 0)2(x 0－x )＝________. [答案] －11，－112[解析] li m Δx →0 f (x 0－Δx )－f (x 0)Δx＝－li m Δx →0 f (x 0－Δx )－f (x 0)－Δx＝－f ′(x 0)＝－11； li m x →x 0 f (x )－f (x 0)2(x 0－x )＝－12li m Δx →0 f (x 0＋Δx )－f (x 0)Δx＝－12f ′(x 0)＝－112. 12．函数y ＝x ＋1x在x ＝1处的导数是________． [答案] 0[解析] ∵Δy ＝⎝ ⎛⎭⎪⎫1＋Δx ＋11＋Δx －⎝ ⎛⎭⎪⎫1＋11 ＝Δx －1＋1Δx ＋1＝(Δx )2Δx ＋1， ∴Δy Δx ＝Δx Δx ＋1.∴y ′|x ＝1＝li m Δx →0 Δx Δx ＋1＝0. 13．已知函数f (x )＝ax ＋4，若f ′(2)＝2，则a 等于______．[答案] 2[解析] ∵Δy Δx ＝a (2＋Δx )＋4－2a －4Δx＝a ， ∴f ′(1)＝li m Δx →0 Δy Δx＝a .∴a ＝2. 14．已知f ′(x 0)＝li m x →x 0 f (x )－f (x 0)x －x 0，f (3)＝2，f ′(3)＝－2，则li m x →3 2x －3f (x )x －3的值是________．[答案] 8[解析] li m x →3 2x －3f (x )x －3＝li m x →3 2x －3f (x )＋3f (3)－3f (3)x －3＝lim x →3 2x －3f (3)x －3＋li m x →3 3(f (3)－f (x ))x －3. 由于f (3)＝2，上式可化为li m x →3 2(x －3)x －3－3li m x →3 f (x )－f (3)x －3＝2－3×(－2)＝8. 三、解答题15．设f (x )＝x 2，求f ′(x 0)，f ′(－1)，f ′(2)．[解析] 由导数定义有f ′(x 0)＝li m Δx →0 f (x 0＋Δx )－f (x 0)Δx＝li m Δx →0 (x 0＋Δx )2－x 20Δx ＝li m Δx →0 Δx (2x 0＋Δx )Δx＝2x 0，16．枪弹在枪筒中运动可以看做匀加速运动，如果它的加速度是5.0×105m/s 2，枪弹从枪口射出时所用时间为1.6×10－3s ，求枪弹射出枪口时的瞬时速度．[解析] 位移公式为s ＝12at 2 ∵Δs ＝12a (t 0＋Δt )2－12at 20＝at 0Δt ＋12a (Δt )2 ∴Δs Δt ＝at 0＋12a Δt ， ∴li m Δt →0Δs Δt ＝li m Δt →0 ⎝ ⎛⎭⎪⎫at 0＋12a Δt ＝at 0， 已知a ＝5.0×105m/s 2，t 0＝1.6×10－3s ，∴at 0＝800m/s.所以枪弹射出枪口时的瞬时速度为800m/s.17．在曲线y ＝f (x )＝x 2＋3的图象上取一点P (1,4)及附近一点(1＋Δx,4＋Δy )， 求(1)Δy Δx(2)f ′(1)．[解析] (1)Δy Δx ＝f (1＋Δx )－f (1)Δx＝(1＋Δx )2＋3－12－3Δx＝2＋Δx . (2)f ′(1)＝lim Δx →0 f (1＋Δx )－f (1)Δx＝lim Δx →0(2＋Δx )＝2. 18．函数f (x )＝|x |(1＋x )在点x 0＝0处是否有导数？若有，求出来，若没有，说明理由．[解析] f (x )＝⎩⎨⎧x ＋x 2 (x ≥0)－x －x 2 (x <0)Δy ＝f (0＋Δx )－f (0)＝f (Δx ) ＝⎩⎨⎧ Δx ＋(Δx )2 (Δx >0)－Δx －(Δx )2 (Δx <0) ∴lim x →0＋ Δy Δx ＝lim Δx →0＋(1＋Δx )＝1， lim Δx →0－ Δy Δx ＝lim Δx →0－(－1－Δx )＝－1， ∵lim Δx →0－Δy Δx ≠lim Δx →0＋ Δy Δx ，∴Δx →0时，Δy Δx 无极限． ∴函数f (x )＝|x |(1＋x )在点x 0＝0处没有导数，即不可导．(x →0＋表示x 从大于0的一边无限趋近于0，即x ＞0且x 趋近于0)练习三组1．如果曲线y ＝f (x )在点(x 0，f (x 0))处的切线方程为x ＋2y －3＝0，那么( )A ．f ′(x 0)＞0B ．f ′(x 0)＜0C ．f ′(x 0)＝0D ．f ′(x 0)不存在 [答案] B[解析] 切线x ＋2y －3＝0的斜率k ＝－12，即f ′(x 0)＝－12＜0.故应选B. 2．曲线y ＝12x 2－2在点⎝⎛⎭⎪⎫1，－32处切线的倾斜角为( ) A ．1B.π4C.54πD ．－π4 [答案] B[解析] ∵y ′＝li m Δx →0 [12(x ＋Δx )2－2]－(12x 2－2)Δx＝li m Δx →0 (x ＋12Δx )＝x ∴切线的斜率k ＝y ′|x ＝1＝1.∴切线的倾斜角为π4，故应选B. 3．在曲线y ＝x 2上切线的倾斜角为π4的点是( ) A ．(0,0)B ．(2,4) C.⎝ ⎛⎭⎪⎫14，116 D.⎝ ⎛⎭⎪⎫12，14 [答案] D [解析] 易求y ′＝2x ，设在点P (x 0，x 20)处切线的倾斜角为π4，则2x 0＝1，∴x 0＝12，∴P ⎝ ⎛⎭⎪⎫12，14. 4．曲线y ＝x 3－3x 2＋1在点(1，－1)处的切线方程为( )A．y＝3x－4 B．y＝－3x＋2 C．y＝－4x＋3 D．y＝4x－5 [答案] B[解析] y′＝3x2－6x，∴y′|x＝1＝－3.由点斜式有y＋1＝－3(x－1)．即y＝－3x＋2.5．设f(x)为可导函数，且满足limx→0f(1)－f(1－2x)2x＝－1，则过曲线y＝f(x)上点(1，f(1))处的切线斜率为( )A．2 B．－1C．1 D．－2[答案] B[解析] limx→0f(1)－f(1－2x)2x＝limx→0f(1－2x)－f(1)－2x＝－1，即y′|x＝1＝－1，则y＝f(x)在点(1，f(1))处的切线斜率为－1，故选B.6．设f′(x0)＝0，则曲线y＝f(x)在点(x0，f(x0))处的切线( )A．不存在B．与x轴平行或重合C．与x轴垂直D．与x轴斜交[答案] B[解析] 由导数的几何意义知B正确，故应选B.7．已知曲线y＝f(x)在x＝5处的切线方程是y＝－x＋8，则f(5)及f′(5)分别为( ) A．3,3 B．3，－1C．－1,3 D．－1，－1[答案] B[解析] 由题意易得：f(5)＝－5＋8＝3，f′(5)＝－1，故应选B.8．曲线f(x)＝x3＋x－2在P点处的切线平行于直线y＝4x－1，则P点的坐标为( ) A．(1,0)或(－1，－4) B．(0,1)C．(－1,0) D．(1,4)[答案] A[解析] ∵f(x)＝x3＋x－2，设x P＝x0，∴Δy ＝3x 20·Δx ＋3x 0·(Δx )2＋(Δx )3＋Δx ，∴Δy Δx＝3x 20＋1＋3x 0(Δx )＋(Δx )2， ∴f ′(x 0)＝3x 20＋1，又k ＝4，∴3x 20＋1＝4，x 20＝1.∴x 0＝±1，故P (1,0)或(－1，－4)，故应选A.9．设点P 是曲线y ＝x 3－3x ＋23上的任意一点，P 点处的切线倾斜角为α，则α的取值范围为( )A.⎣⎢⎡⎭⎪⎫0，π2∪⎣⎢⎡⎭⎪⎫23π，π B.⎣⎢⎡⎭⎪⎫0，π2∪⎣⎢⎡⎭⎪⎫56π，π C.⎣⎢⎡⎭⎪⎫23π，πD.⎝ ⎛⎦⎥⎤π2，56π [答案] A[解析] 设P (x 0，y 0)， ∵f ′(x )＝li m Δx →0 (x ＋Δx )3－3(x ＋Δx )＋23－x 3＋3x －23Δx＝3x 2－3，∴切线的斜率k ＝3x 20－3，∴tan α＝3x 20－3≥－ 3.∴α∈⎣⎢⎡⎭⎪⎫0，π2∪⎣⎢⎡⎭⎪⎫23π，π.故应选A. 10．设P 为曲线C ：y ＝x 2＋2x ＋3上的点，且曲线C 在点P 处切线倾斜角的取值范围为[0，π4]，则点P 横坐标的取值范围为( ) A ．[－1，－12] B ．[－1,0] C ．[0,1]D ．[12，1] [答案] A[解析] 考查导数的几何意义．∵y ′＝2x ＋2，且切线倾斜角θ∈[0，π4]，∴切线的斜率k 满足0≤k ≤1，即0≤2x ＋2≤1，∴－1≤x ≤－12. 11．已知函数f (x )＝x 2＋3，则f (x )在(2，f (2))处的切线方程为________．[答案] 4x －y －1＝0[解析] ∵f (x )＝x 2＋3，x 0＝2∴f (2)＝7，Δy ＝f (2＋Δx )－f (2)＝4·Δx ＋(Δx )2∴Δy Δx＝4＋Δx .∴li m Δx →0 Δy Δx ＝4.即f ′(2)＝4. 又切线过(2,7)点，所以f (x )在(2，f (2))处的切线方程为y －7＝4(x －2) 即4x －y －1＝0.12．若函数f (x )＝x －1x，则它与x 轴交点处的切线的方程为________． [答案] y ＝2(x －1)或y ＝2(x ＋1)[解析] 由f (x )＝x －1x＝0得x ＝±1，即与x 轴交点坐标为(1,0)或(－1,0)． ∵f ′(x )＝li m Δx →0 (x ＋Δx )－1x ＋Δx －x ＋1x Δx＝li m Δx →0 ⎣⎢⎡⎦⎥⎤1＋1x (x ＋Δx )＝1＋1x 2. ∴切线的斜率k ＝1＋11＝2. ∴切线的方程为y ＝2(x －1)或y ＝2(x ＋1)．13．曲线C 在点P (x 0，y 0)处有切线l ，则直线l 与曲线C 的公共点有________个．[答案] 至少一[解析] 由切线的定义，直线l 与曲线在P (x 0，y 0)处相切，但也可能与曲线其他部分有公共点，故虽然相切，但直线与曲线公共点至少一个．14．曲线y ＝x 3＋3x 2＋6x －10的切线中，斜率最小的切线方程为________．[答案] 3x －y －11＝0[解析] 设切点P (x 0，y 0)，则过P (x 0，y 0)的切线斜率为，它是x 0的函数，求出其最小值．设切点为P (x 0，y 0)，过点P 的切线斜率k ＝＝3x 20＋6x 0＋6＝3(x 0＋1)2＋3.当x 0＝－1时k 有最小值3，此时P 的坐标为(－1，－14)，其切线方程为3x －y －11＝0.三、解答题15．求曲线y ＝1x －x 上一点P ⎝⎛⎭⎪⎫4，－74处的切线方程． [解析] ∴y ′＝lim Δx →0 ⎝ ⎛⎭⎪⎫1x ＋Δx －1x －(x ＋Δx －x )Δx＝lim Δx →0 －Δx x (x ＋Δx )－Δx x ＋Δx ＋x Δx＝lim Δx →0 ⎝ ⎛⎭⎪⎫－1x (x ＋Δx )－1x ＋Δx ＋x ＝－1x 2－12x . ∴y ′|x ＝4＝－116－14＝－516， ∴曲线在点P ⎝⎛⎭⎪⎫4，－74处的切线方程为： y ＋74＝－516(x －4)． 即5x ＋16y ＋8＝0.16．已知函数f (x )＝x 3－3x 及y ＝f (x )上一点P (1，－2)，过点P 作直线l .(1)求使直线l 和y ＝f (x )相切且以P 为切点的直线方程；(2)求使直线l 和y ＝f (x )相切且切点异于点P 的直线方程y ＝g (x )．[解析] (1)y ′＝li m Δx →0 (x ＋Δx )3－3(x ＋Δx )－3x 3＋3x Δx＝3x 2－3. 则过点P 且以P (1，－2)为切点的直线的斜率k 1＝f ′(1)＝0，∴所求直线方程为y ＝－2.(2)设切点坐标为(x 0，x 30－3x 0)，则直线l 的斜率k 2＝f ′(x 0)＝3x 20－3，∴直线l 的方程为y －(x 30－3x 0)＝(3x 20－3)(x －x 0)又直线l 过点P (1，－2)，∴－2－(x 30－3x 0)＝(3x 20－3)(1－x 0)，∴x 30－3x 0＋2＝(3x 20－3)(x 0－1)，解得x 0＝1(舍去)或x 0＝－12. 故所求直线斜率k ＝3x 20－3＝－94， 于是：y －(－2)＝－94(x －1)，即y ＝－94x ＋14. 17．求证：函数y ＝x ＋1x图象上的各点处的切线斜率小于1. [解析] y ′＝li m Δx →0 f (x ＋Δx )－f (x )Δx＝li m Δx →0 ⎝ ⎛⎭⎪⎫x ＋Δx ＋1x ＋Δx －⎝ ⎛⎭⎪⎫x ＋1x Δx＝li m Δx →0 x ·Δx (x ＋Δx )－Δx (x ＋Δx )·x ·Δx＝li m Δx →0(x ＋Δx )x －1(x ＋Δx )x ＝x 2－1x 2＝1－1x 2＜1， ∴y ＝x ＋1x图象上的各点处的切线斜率小于1. 18．已知直线l 1为曲线y ＝x 2＋x －2在点(1,0)处的切线，l 2为该曲线的另一条切线，且l 1⊥l 2.(1)求直线l 2的方程；(2)求由直线l 1、l 2和x 轴所围成的三角形的面积．[解析] (1)y ′|x ＝1＝li m Δx →0 (1＋Δx )2＋(1＋Δx )－2－(12＋1－2)Δx＝3， 所以l 1的方程为：y ＝3(x －1)，即y ＝3x －3.设l 2过曲线y ＝x 2＋x －2上的点B (b ，b 2＋b －2)，y ′|x ＝b ＝li m Δx →0 (b ＋Δx )2＋(b ＋Δx )－2－(b 2＋b －2)Δx＝2b ＋1，所以l 2的方程为：y －(b 2＋b －2)＝(2b ＋1)·(x －b )，即y ＝(2b ＋1)x －b 2－2.因为l 1⊥l 2，所以3×(2b ＋1)＝－1，所以b ＝－23，所以l 2的方程为：y ＝－13x －229. (2)由⎩⎨⎧ y ＝3x －3，y ＝－13x －229，得⎩⎪⎨⎪⎧x ＝16，y ＝－52， 即l 1与l 2的交点坐标为⎝ ⎛⎭⎪⎫16，－52. 又l 1，l 2与x 轴交点坐标分别为(1,0)，⎝ ⎛⎭⎪⎫－223，0. 所以所求三角形面积S ＝12×⎪⎪⎪⎪⎪⎪－52×⎪⎪⎪⎪⎪⎪1＋223＝12512.练习三组1．下列结论不正确的是( )A ．若y ＝0，则y ′＝0B ．若y ＝5x ，则y ′＝5C ．若y ＝x －1，则y ′＝－x －2[答案] D2.曲线y ＝13x 3－2在点⎝ ⎛⎭⎪⎫－1，－73处切线的倾斜角为( )A ．30°B ．45°C ．135°D ．60°[答案] B[解析] y ′|x ＝－1＝1，∴倾斜角为45°.3.函数y ＝(x ＋1)2(x －1)在x ＝1处的导数等于( )A ．1B ．2C ．3D ．4[答案] D[解析] y ′＝[(x ＋1)2]′(x －1)＋(x ＋1)2(x －1)′＝2(x ＋1)·(x －1)＋(x ＋1)2＝3x 2＋2x －1，∴y ′|x ＝1＝4.4.设f (x )＝ax 3＋bx 2＋cx ＋d (a >0)，则f (x )为R 上增函数的充要条件是() A ．b 2－4ac >0 B ．b >0，c >0C ．b ＝0，c >0D ．b 2－3ac <0[答案] D[解析] ∵a >0，f (x )为增函数，∴f′(x)＝3ax2＋2bx＋c>0恒成立，∴Δ＝(2b)2－4×3a×c＝4b2－12ac<0，∴b2－3ac<0.5．已知函数f (x )在点x 0处连续，下列命题中，正确的是( )A ．导数为零的点一定是极值点B ．如果在点x 0附近的左侧f ′(x )>0，右侧f ′(x )<0，那么f (x 0)是极小值C ．如果在点x 0附近的左侧f ′(x )>0，右侧f ′(x )<0，那么f (x 0)是极大值D ．如果在点x 0附近的左侧f ′(x )<0，右侧f ′(x )>0，那么f (x 0)是极大值[答案] C[解析] 导数为0的点不一定是极值点，例如f (x )＝x 3，f ′(x )＝3x 2，f ′(0)＝0，但x ＝0不是f (x )的极值点，故A 错；由极值的定义可知C 正确，故应选C.6.函数y ＝f (x )在区间[a ，b ]上的最大值是M ，最小值是m ，若M ＝m ，则f ′(x )( )A ．等于0B ．大于0C ．小于0D ．以上都有可能[答案] A[解析] ∵M ＝m ，∴y ＝f (x )是常数函数∴f ′(x )＝0，故应选A.7.内接于半径为R 的球且体积最大的圆锥的高为( )A ．RB ．2R C.43R D.34R [答案] C[解析] 设圆锥高为h ，底面半径为r ，则R 2＝(R －h )2＋r 2，∴r 2＝2Rh －h 2∴V ＝13πr 2h ＝π3h (2Rh －h 2)＝23πRh 2－π3h 3 V ′＝43πRh －πh 2.令V ′＝0得h ＝43R . 当0<h <43R 时，V ′>0；当4R 3<h <2R 时，V ′<0. 因此当h ＝43R 时，圆锥体积最大．故应选C.8.．和式∑i ＝15(y i ＋1)可表示为( )A ．(y 1＋1)＋(y 5＋1)B ．y 1＋y 2＋y 3＋y 4＋y 5＋1C ．y 1＋y 2＋y 3＋y 4＋y 5＋5D ．(y 1＋1)(y 2＋1)…(y 5＋1)[答案] C[解析] ∑i ＝15(y i ＋1)＝(y 1＋1)＋(y 2＋1)＋(y 3＋1)＋(y 4＋1)＋(y 5＋1)＝y 1＋y 2＋y 3＋y 4＋y 5＋5，故选C.9．设f (x )是[a ，b ]上的连续函数，则f (x )d x －f (t )d t 的值( )A ．小于零B ．等于零C ．大于零D ．不能确定[答案] B[解析] f (x )d x 和f (t )d t 都表示曲线y ＝f (x )与x ＝a ，x ＝b 及y ＝0围成的曲边梯形面积，不因曲线中变量字母不同而改变曲线的形状和位置．所以其值为0. 10.．设f (x )＝⎩⎨⎧x 2 (0≤x <1)2－x (1≤x ≤2)，则f (x )d x 等于( ) A.34 B.45 C.56D ．不存在[答案] C [解析] f (x )d x ＝x 2d x ＋(2－x )d x取F 1(x )＝13x 3，F 2(x )＝2x －12x 2， 则F ′1(x )＝x 2，F ′2(x )＝2－x∴f (x )d x ＝F 1(1)－F 1(0)＋F 2(2)－F 2(1)＝13－0＋2×2－12×22－⎝ ⎛⎭⎪⎫2×1－12×12＝56.故应选C.11.．如图所示，阴影部分的面积为( )A.f (x )d xB.g (x )d xC.[f (x )－g (x )]d xD.[g (x )－f (x )]d x [答案] C[解析] 由题图易知，当x ∈[a ，b ]时，f (x )>g (x )，所以阴影部分的面积为[f (x )－g (x )]d x .12已知f (x )＝x 3的切线的斜率等于1，则其切线方程有( )A ．1个B ．2个C ．多于两个D ．不能确定[答案] B[解析] ∵f (x )＝x 3，∴f ′(x )＝3x 2，令3x 2＝1，得x ＝±33， 即切点坐标为⎝ ⎛⎭⎪⎫33，39或⎝ ⎛⎭⎪⎫－33，－39. 由点斜式可得切线方程为y －39＝x －33或y ＋39＝x ＋33，即y ＝x －239或y ＝x ＋239.故应选B. 13.若曲线y ＝x 2＋ax ＋b 在点(0，b )处的切线方程是x －y ＋1＝0，则( )A ．a ＝1，b ＝1B ．a ＝－1，b ＝1C ．a ＝1，b ＝－1D ．a ＝－1，b ＝－1[答案] A[解析] y′＝2x＋a，∴y′|x＝0＝(2x＋a)|x＝0＝a＝1，将(0，b)代入切线方程得b＝1.14.关于归纳推理，下列说法正确的是( )A．归纳推理是一般到一般的推理B．归纳推理是一般到个别的推理C．归纳推理的结论一定是正确的D．归纳推理的结论是或然性的[答案] D[解析] 归纳推理是由特殊到一般的推理，其结论的正确性不一定．故应选D.15.下列说法正确的是( )A．由合情推理得出的结论一定是正确的B．合情推理必须有前提有结论C．合情推理不能猜想D．合情推理得出的结论无法判定正误[答案] B[解析] 由合情推理得出的结论不一定正确，A不正确；B正确；合情推理的结论本身就是一个猜想，C不正确；合情推理结论可以通过证明来判定正误，D也不正确，故应选B.16.“∵四边形ABCD是矩形，∴四边形ABCD的对角线相等”，补充以上推理的大前提是( )A．正方形都是对角线相等的四边形B．矩形都是对角线相等的四边形C．等腰梯形都是对角线相等的四边形D．矩形都是对边平行且相等的四边形[答案] B[解析] 由大前提、小前提、结论三者的关系，知大前提是：矩形是对角线相等的四边形．故应选B.17.证明命题“f(x)＝e x＋1e x在(0，＋∞)上是增函数”，一个同学给出的证法如下：∵f (x )＝e x ＋1e x ，∴f ′(x )＝e x －1e x . ∵x >0，∴e x >1,0<1e x <1 ∴e x －1e x >0，即f ′(x )>0， ∴f (x )在(0，＋∞)上是增函数，他使用的证明方法是( )A ．综合法B ．分析法C ．反证法D ．以上都不是[答案] A[解析] 该证明方法符合综合法的定义，应为综合法．故应选A.18.否定结论“至多有两个解”的说法中，正确的是( )A ．有一个解B ．有两个解C ．至少有三个解D ．至少有两个解[答案] C[解析] 在逻辑中“至多有n 个”的否定是“至少有n ＋1个”，所以“至多有两个解”的否定为“至少有三个解”，故应选C.19.用数学归纳法证明1＋12＋13＋…＋12n －1<n (n ∈N *，n >1)时，第一步应验证不等式( )A ．1＋12<2 B ．1＋12＋13＜2 C ．1＋12＋13＜3 D ．1＋12＋13＋14＜3 [答案] B[解析] ∵n ∈N *，n ＞1，∴n 取第一个自然数为2，左端分母最大的项为122－1＝13，故选B.20.命题“对于任意角θ，cos 4θ－sin 4θ＝cos2θ”的证明：“cos 4θ－sin 4θ＝(cos 2θ－sin 2θ)(cos 2θ＋sin 2θ)＝cos 2θ－sin 2θ＝cos2θ”的过程应用了( )A ．分析法B ．综合法C ．综合法、分析法综合使用D ．以上都不是[答案] B[解析] 所用方法符合综合法的定义，故应选B.21.．锐角三角形的面积等于底乘高的一半；直角三角形的面积等于底乘高的一半；钝角三角形的面积等于底乘高的一半；所以，凡是三角形的面积都等于底乘高的一半．以上推理运用的推理规则是( )A ．三段论推理B ．假言推理C ．关系推理D ．完全归纳推理[答案] D[解析] 所有三角形按角分，只有锐角三角形、Rt 三角形和钝角三角形三种情形，上述推理穷尽了所有的可能情形，故为完全归纳推理．22.i 是虚数单位，计算i ＋i 2＋i 3＝( )A ．－1B ．1C ．－iD ．i[答案] A[解析] i ＋i 2＋i 3＝i －1－i ＝－1.23.．如果复数a ＋b i(a ，b ∈R )在复平面内的对应点在第二象限，则( )A ．a >0，b <0B ．a >0，b >0C ．a <0，b <0D ．a <0，b >0[答案] D[解析] 复数z ＝a ＋b i 在复平面内的对应点坐标为(a ，b )，该点在第二象限，需a <0且b >0，故应选D.24.i 是虚数单位，i3＋3i ＝( ) A.14－312i B.14＋312i C.12＋36i D.12－36i [答案] B[解析] i3＋3i ＝i(3－3i)(3＋3i)(3－3i) ＝3＋3i 12＝14＋312i ，故选B. 25.复数z 是实数的充分而不必要条件为( )A ．|z |＝zB ．z ＝zC ．z 2是实数D ．z ＋z 是实数[答案] A[解析] 由|z |＝z 可知z 必为实数，但由z 为实数不一定得出|z |＝z ，如z ＝－2，此时|z |≠z ，故|z |＝z 是z 为实数的充分不必要条件，故选A.26.．复数i 3(1＋i)2＝( )A ．2B ．－2C ．2iD ．－2i[答案] A[解析] 考查复数代数形式的运算．i 3(1＋i)2＝－i·(2i)＝2.27.复数⎝ ⎛⎭⎪⎫3－i 1＋i 2＝( ) A ．－3－4i B ．－3＋4iC ．3－4iD ．3＋4i[答案] A[解析] ⎝ ⎛⎭⎪⎫3－i 1＋i 2＝8－6i 2i ＝－3－4i.。
