机械原理机构力分析
- 格式:ppt
- 大小:2.98 MB
- 文档页数:46

第4章平面机构的力分析4.1 复习笔记一、机构力分析的任务、目的和方法1.作用在机械上的力根据力对机械运动影响的不同,可分为两大类。
(1)驱动力①定义驱动机械运动的力称为驱动力。
②特点驱动力与其作用点的速度方向相同或成锐角,其所作的功为正功,称为驱动功或输入功。
(2)阻抗力①定义阻止机械运动的力称为阻抗力。
②特点阻抗力与其作用点的速度方向相反或成钝角,其所作的功为负功,称为阻抗功。
③分类a.有效阻抗力机械在生产过程中为了改变工作物的外形、位置或状态而受到的阻力,即工作阻力。
克服这类阻力所完成的功称为有效功或输出功。
b.有害阻抗力机械在运转过程中所受到的非生产阻力。
克服这类阻力所作的功称为损失功。
2.机构力分析的任务和目的(1)确定运动副中的反力运动副反力是指运动副两元素接触处彼此作用的正压力和摩擦力的合力。
(2)确定机械上的平衡力或平衡力偶平衡力是指机械在已知外力的作用下,为了使该机构能按给定的运动规律运动,必须加于机械上的未知外力。
3.机构力分析的方法对于不同的研究对象,适用的方法不同。
(1)低速机械惯性力可以忽略不计,只需要对机械作静力分析。
(2)高速及重型机械①惯性力不可以忽略,需对机械作动态静力分析。
②设计新机械时,由于各构件尺寸、材料、质量及转动惯量未知,因此其动态静力分析方法如下:a.对机构作静力分析及静强度计算,初步确定各构件尺寸;b.对机构进行动态静力分析及强度计算,并据此对各构件尺寸作必要修正;c.重复上述分析及计算过程,直到获得可以接受的设计为止。
二、构件惯性力的确定构件惯性力的确定有一般力学法和质量代换法。
1.一般力学方法如图4-1-1(a)所示为曲柄滑块机构,借此说明不同运动形式构件所产生的惯性力。
(1)作平面复合运动的构件惯性力系有两种简化方式。
①简化为一个加在质心S i上的惯性力F I2和一个惯性力偶矩M I2,即F I2=-m2a S2,M I2=-J S2α2②简化为一个大小等于F I2,而作用线偏离质心S2一定距离l h2的总惯性力F I2′,而l h2=M I2/F I2F′I2对质心S2之矩的方向应与α2的方向相反。


机械原理机构力分析机械原理是机械学的基础,它主要研究机械系统中各个构件之间的相互作用和力的传递方式。
而机构是机械系统中起传递、变换和控制运动的作用的装置。
机构力分析是指通过力学原理来解析机械机构中的力以及力的传递和平衡关系。
机械原理机构力分析的目的是为了了解机械机构的运动规律和力学特性,从而为机械设计和性能优化提供理论依据。
在机械系统中,机构是由多个构件组成的,这些构件之间通过连接件连接在一起,形成一个整体。
当机构运动时,各构件之间会受到相互作用力,这些力是通过连接件传递的。
机构力分析的关键是要确定连接件的受力情况,包括连接件上的作用力大小、方向和点位等。
在机构力分析中,首先需要建立机构的运动模型,确定各个构件之间的相对位置和运动方式。
然后,通过应用牛顿第二定律等力学原理,可以得出每个构件所受到的作用力。
在实际应用中,机构力分析可以通过数值计算、有限元分析等方法来进行。
对于复杂的机构,力分析可能会更加困难。
这时可以使用力图和力闭合法来进行分析。
力图是一种通过标注和连接力的方法,直观地表示出受力情况的图形。
力闭合法是一种通过闭合力系统来分析受力情况的方法,通过构造闭合力系统和使用受力平衡条件,可以解析机构中的力学问题。
机构力分析在机械设计和优化中起着重要的作用。
通过对机构力学特性的研究,可以确定机构的运动规律、力学效率和强度等参数。
这些参数对于机械系统的结构设计和性能优化都至关重要。
例如,在设计机械传动系统时,需要对传动链条、齿轮、轴承等部件进行力学分析,以确定它们的合理尺寸和强度;在设计机械臂、摆线机构等复杂机构时,也需要进行力学分析,以确定它们的运动规律和受力情况。
在实际工程中,机械原理机构力分析常常与CAD技术相结合。
通过CAD软件的建模功能和力学分析插件,可以方便地进行机构的三维建模和力学分析。
这不仅提高了设计效率,还减少了设计中的错误和风险。
总之,机械原理机构力分析是机械学中重要的一部分。
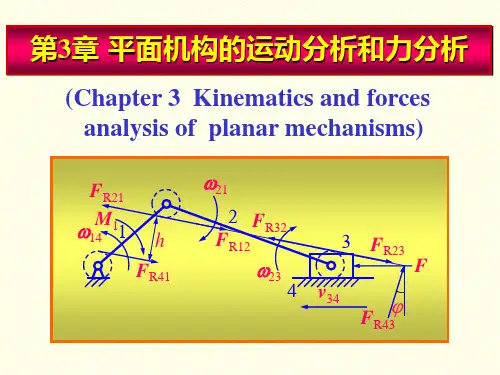





机械原理-平面机构的力分析、效率和自锁第三讲平面机构的力分析、效率和自锁平面机构的力分析知识点:一、作用在机械上的力1.驱动力:定义:驱使机械运动的力特征:该力与其作用点速度的方向相同或成锐角,其所作的功为正功,称为驱动功或输入功。
来源:原动机加在机械上的力2.阻抗力:定义:阻止机械产生运动的力称为阻抗力特征:该力与其作用点速度的方向相反或成钝角,其所作的功为负功,称为阻抗功。
分类:生产阻力(有效阻力):有效功(输出功)有害阻力:非生产阻力:损失功二、构件惯性力的确定(考的较少)1、一般力学方法(1) 作平面复合运动的构件对于作平面复合运动且具有平行于运动平面的对称面的构件(如连杆2),其惯性力系可简化为一个加在质心S2 上的惯性力F I2和一个惯性力偶矩M I2, 即F I2 = -m2a S2 , M I2 = -J S2α2也可将其再简化为一个大小等于F I2,而作用线偏离质心S2一距离l h2的总惯性力F′I2,l h2 = M I2/ F I2F′I2对质心S2之矩的方向应与α2的方向相反。
(2) 作平面移动的构件如滑块3,当其作变速移动时,仅有一个加在质心S3上的惯性力F13=-m3a S3。
(3) 绕定轴转动的构件如曲柄1,若其轴线不通过质心,当构件为变速转动时,其上作用有惯性力F I1=-m1a S1及惯性力偶矩M I1=-J S1α1,或简化为一个总惯性力F′I1;如果回转轴线通过构件质心,则只有惯性力偶矩M I1=-JS1α1。
2、质量代换法(记住定义和条件)1.基本定义:(1)质量代换法:按一定条件将构件质量假想地用集中于若干个选定点上的集中质量来代替的方法叫质量代换法。
(2)代换点:选定的点称为代换点。
(3)代换质量:假想集中于代换点上的集中质量叫代换质量。
2.应满足条件(1)代换前后构件的质量不变。
(2)代换前后构件的质心位置不变。
(3)代换前后构件对质心的转动惯量不变。

