经典数学函数图像大全
- 格式：doc
- 大小：3.78 MB
- 文档页数：19
下载文档原格式
合集下载
经典数学函数图像大全-数学函数图像-函数图像全之欧阳语创编
函数图形基本初等函数幂函数（1)幂函数（2)幂函数（3)指数函数（1）指数函数（2）指数函数（3）对数函数（1）对数函数（2）三角函数（1）三角函数（2）三角函数（3）三角函数（4）三角函数（5）反三角函数（1）反三角函数（2）反三角函数（3）反三角函数（4）反三角函数（5）反三角函数（6）反三角函数（7）反三角函数（8）双曲函数（1）双曲函数（2）双曲函数（3）双曲函数（4）双曲函数（5）双曲函数（6）双曲函数（7）反双曲函数（1）反双曲函数（2）反双曲函数（3）反双曲函数（4）反双曲函数（5）反双曲函数（6）y=sin(1/x) (1)y=sin(1/x) (2)y=sin(1/x) (3)y=sin(1/x) (4)y = [1/x](1)y = [1/x](2)y=21/xy=21/x (2)y=xsin(1/x)y=arctan(1/x)y=e1/xy=sinx (x>∞)绝对值函数y = |x|符号函数y = sgnx取整函数y= [x]极限的几何解释(1)极限的几何解释(2)极限的几何解释(3)极限的性质(1) (局部保号性)极限的性质(2) (局部保号性)极限的性质(3) (不等式性质)极限的性质(4) (局部有界性)极限的性质(5) (局部有界性)两个重要极限y=sinx/x (1)y=sinx/x (2)limsinx/x的一般形式y=(1+1/x)^x (1)y=(1+1/x)^x (2)lim(1+1/x)^x 的一般形式(1)lim(1+1/x)^x 的一般形式(2)lim(1+1/x)^x 的一般形式(3)e的值(1)e的值(2)等价无穷小(x>0)sinx等价于xarcsinx等价于xtanx等价于xarctanx等价于x1cosx等价于x^2/2sinx等价于x数列的极限的几何解释海涅定理渐近线水平渐近线铅直渐近线y=(x+1)/(x1)y=sinx/x (x>∞)夹逼定理(1)夹逼定理(2)数列的夹逼性(1)数列的夹逼性(2)。
经典数学函数图像大全
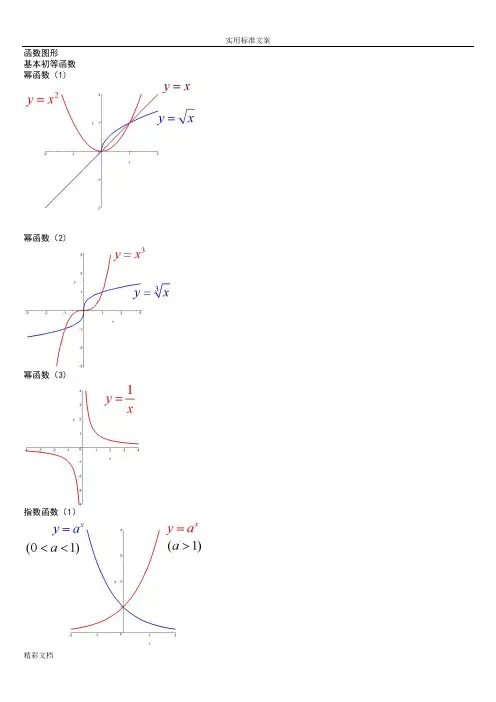
函数图形 基本初等函数 幂函数（1)幂函数（2)幂函数（3)指数函数（1）指数函数（2）指数函数（3）对数函数（1）对数函数（2）三角函数（1）三角函数（2）三角函数（3）三角函数（4）三角函数（5）反三角函数（1）反三角函数（2）反三角函数（3）反三角函数（4）反三角函数（5）反三角函数（6）反三角函数（7）反三角函数（8）双曲函数（1）双曲函数（2）双曲函数（3）双曲函数（4）双曲函数（5）双曲函数（6）双曲函数（7）反双曲函数（1）反双曲函数（2）反双曲函数（3）反双曲函数（4）反双曲函数（5）反双曲函数（6）y=sin(1/x) (1)y=sin(1/x) (2)y=sin(1/x) (3)y=sin(1/x) (4)y = [1/x](1)y = [1/x](2)y=21/xy=21/x (2)y=xsin(1/x)y=arctan(1/x)y=e1/xy=sinx (x->∞)绝对值函数 y = |x|符号函数 y = sgnx取整函数 y= [x]极限的几何解释(1)极限的几何解释(2)极限的几何解释(3)极限的性质 (1) (局部保号性)极限的性质 (2) (局部保号性)极限的性质 (3) (不等式性质) 极限的性质 (4) (局部有界性) 极限的性质 (5) (局部有界性)两个重要极限y=sinx/x (1)y=sinx/x (2)limsinx/x 的一般形式y=(1+1/x)^x (1)y=(1+1/x)^x (2)lim(1+1/x)^x 的一般形式(1)lim(1+1/x)^x 的一般形式(2)lim(1+1/x)^x 的一般形式(3)e 的值(1)e 的值(2)等价无穷小(x->0)sinx 等价于xarcsinx等价于xtanx等价于xarctanx 等价于x 1-cosx 等价于x^2/2sinx 等价于x数列的极限的几何解释海涅定理渐近线水平渐近线铅直渐近线实用标准文案精彩文档y=(x+1)/(x-1)y=sinx/x (x->∞)夹逼定理(1) 夹逼定理(2) 数列的夹逼性 (1) 数列的夹逼性 (2)。
经典数学函数图像大全
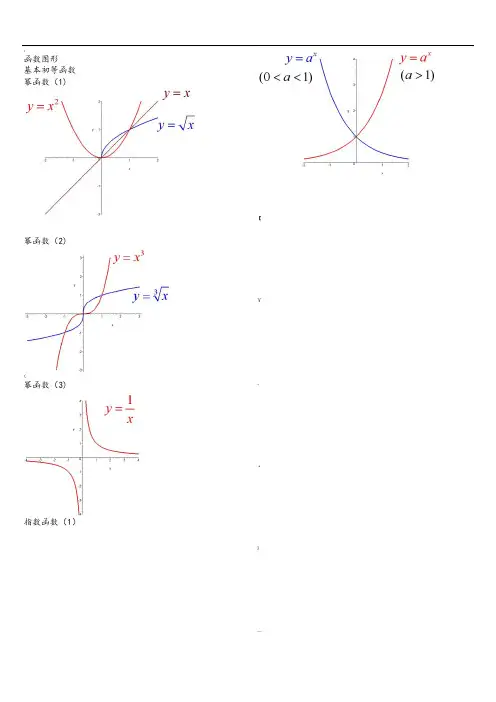
：函数图形基本初等函数幂函数（1)幂函数（2)<幂函数（3)指数函数（1）【￥、·》—【：指数函数（2）指数函数（3）对数函数（1）对数函数（2）-￥、~ ）—, }·三角函数（1）三角函数（2）三角函数（3）~ ！@ …! ：^~>三角函数（5）反三角函数（1）反三角函数（2）;反三角函数（3）>—;￥% 、>\.反三角函数（4）反三角函数（5）反三角函数（6）反三角函数（7）【！…·?…|[￥反三角函数（8）双曲函数（1）~双曲函数（2）双曲函数（3）】, } - \ ] - " 双曲函数（4）%双曲函数（5）双曲函数（6）双曲函数（7）&￥，￥> ￥% ' ，反双曲函数（1）反双曲函数（2）反双曲函数（3）反双曲函数（4）' . 。
" 、/ ] ~反双曲函数（5）反双曲函数（6） y=sin(1/x) (1)`y=sin(1/x) (2)) < \ , ( 、/?y=sin(1/x) (3) y=sin(1/x) (4) y = [1/x](1)~《`y = [1/x](2) } | —…&y=21/x<y=21/x (2)y=xsin(1/x)y=arctan(1/x)y=e1/x。
y=sinx (x->∞)绝对值函数 y = |x|符号函数 y = sgnx 取整函数 y= [x]<) ].,}*^极限的几何解释 (1)、极限的几何解释 (2)极限的几何解释 (3)极限的性质 (1) (局部保号性)~极限的性质 (2) (局部保号性)@ ; | ￥} 。
#极限的性质 (3) (不等式性质)极限的性质 (4) (局部有界性) \极限的性质 (5) (局部有界性)` . 、# ）—，-两个重要极限y=sinx/x (1)y=sinx/x (2)；limsinx/x的一般形式y=(1+1/x)^x (1): 》？。
经典数学函数图像大全
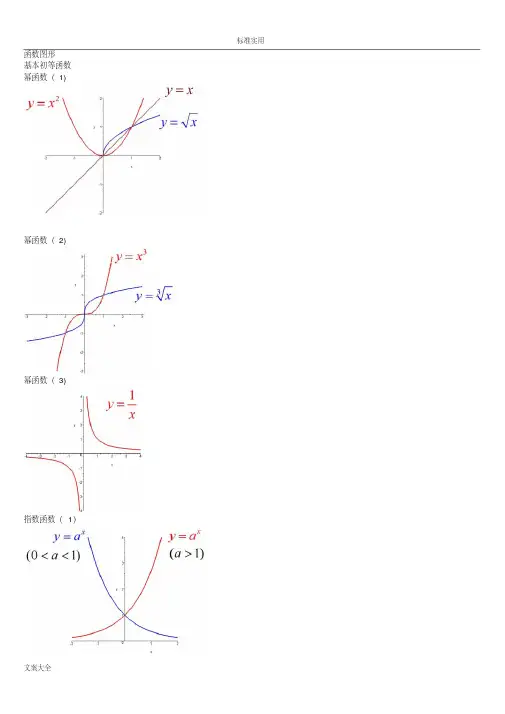
函数图形基本初等函数幂函数（1)幂函数（2)幂函数（3)指数函数（1）指数函数（2）指数函数（3）对数函数（1）对数函数（2）三角函数（1）三角函数（2）三角函数（3）三角函数（4）三角函数（5）反三角函数（1）反三角函数（2）反三角函数（3）反三角函数（4）反三角函数（5）反三角函数（6）反三角函数（7）反三角函数（8）双曲函数（1）双曲函数（2）双曲函数（3）双曲函数（4）双曲函数（5）双曲函数（6）双曲函数（7）反双曲函数（4）反双曲函数（1）反双曲函数（2）反双曲函数（3）反双曲函数（5）反双曲函数（6）y=sin(1/x) (1) y=sin(1/x) (2)y=sin(1/x) (3) y=sin(1/x) (4) y = [1/x](1) y = [1/x](2)y=21/xy=21/x (2)y=xsin(1/x)y=arctan(1/x)y=e1/xy=sinx (x->∞)绝对值函数y = |x| 符号函数y = sgnx 取整函数y= [x]极限的几何解释(1)极限的几何解释(2)极限的几何解释(3)极限的性质(1) (局部保号性)极限的性质(2) (局部保号性)极限的性质(3) (不等式性质)极限的性质(4) (局部有界性)极限的性质(5) (局部有界性)两个重要极限y=sinx/x (1)y=sinx/x (2)limsinx/x的一般形式y=(1+1/x)^x (1)y=(1+1/x)^x (2)lim(1+1/x)^x 的一般形式(1) lim(1+1/x)^x 的一般形式(2) lim(1+1/x)^x 的一般形式(3)e的值(1)e的值(2)等价无穷小(x->0)sinx等价于xarcsinx等价于xtanx等价于xarctanx等价于x1-cosx等价于x^2/2sinx等价于x数列的极限的几何解释海涅定理渐近线水平渐近线铅直渐近线y=(x+1)/(x-1)y=sinx/x (x->∞) 夹逼定理(1)夹逼定理(2) 数列的夹逼性(1) 数列的夹逼性(2)。
考研数学函数图像大全
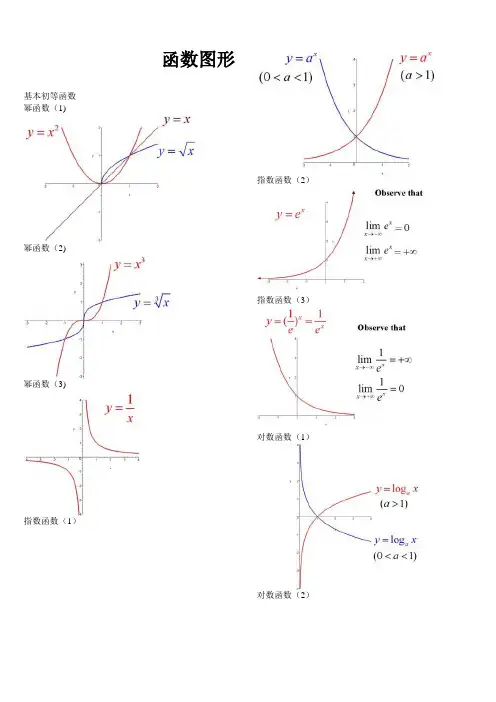
函数图形基本初等函数 幂函数（1)幂函数（2)幂函数（3)指数函数（1）指数函数（2）指数函数（3）对数函数（1）对数函数（2）三角函数（1）三角函数（2）三角函数（3）三角函数（4）三角函数（5）反三角函数（1）反三角函数（2）反三角函数（3）反三角函数（4）反三角函数（5）反三角函数（6）反三角函数（7）反三角函数（8）双曲函数（1）双曲函数（2）双曲函数（3）双曲函数（4）双曲函数（5）双曲函数（6）双曲函数（7）反双曲函数（1）反双曲函数（2）反双曲函数（3）反双曲函数（4）反双曲函数（5）反双曲函数（6）y=sin(1/x) (1)y=sin(1/x) (2)y=sin(1/x) (3)y=sin(1/x) (4)y = [1/x](1)y = [1/x](2)y=21/xy=21/x (2)y=xsin(1/x)y=arctan(1/x)y=e1/xy=sinx (x->∞)绝对值函数 y = |x|符号函数 y = sgnx取整函数 y= [x]极限的几何解释(1)极限的几何解释(2)极限的几何解释(3)极限的性质 (1) (局部保号性)极限的性质 (2) (局部保号性)极限的性质 (3) (不等式性质)极限的性质 (4) (局部有界性)极限的性质 (5) (局部有界性)两个重要极限y=sinx/x (1)y=sinx/x (2)limsinx/x 的一般形式y=(1+1/x)^x (1)y=(1+1/x)^x (2)lim(1+1/x)^x 的一般形式(1)lim(1+1/x)^x 的一般形式(2)lim(1+1/x)^x 的一般形式(3)等价无穷小(x->0)sinx 等价于xarcsinx 等价于xtanx 等价于xarctanx 等价于x 1-cosx 等价于x^2/2sinx等价于x数列的极限的几何解释海涅定理渐近线水平渐近线铅直渐近线y=(x+1)/(x-1)y=sinx/x (x->∞) 夹逼定理(1)夹逼定理(2)数列的夹逼性(1)数列的夹逼性(2)。
经典数学函数图像大全-数学函数图像-函数图像全之欧阳音创编
函数图形基本初等函数幂函数（1)幂函数（2)幂函数（3)指数函数（1）指数函数（2）指数函数（3）对数函数（1）对数函数（2）三角函数（1）三角函数（2）三角函数（3）三角函数（4）三角函数（5）反三角函数（1）反三角函数（2）反三角函数（3）反三角函数（4）反三角函数（5）反三角函数（6）反三角函数（7）反三角函数（8）双曲函数（1）双曲函数（2）双曲函数（3）双曲函数（4）双曲函数（5）双曲函数（6）双曲函数（7）反双曲函数（1）反双曲函数（2）反双曲函数（3）反双曲函数（4）反双曲函数（5）反双曲函数（6）y=sin(1/x) (1)y=sin(1/x) (2)y=sin(1/x) (3)y=sin(1/x) (4)y = [1/x](1)y = [1/x](2)y=21/xy=21/x (2)y=xsin(1/x)y=arctan(1/x)y=e1/xy=sinx (x>∞)绝对值函数 y = |x|符号函数 y = sgnx取整函数 y= [x]极限的几何解释 (1)极限的几何解释 (2)极限的几何解释 (3)极限的性质 (1) (局部保号性)极限的性质 (2) (局部保号性)极限的性质 (3) (不等式性质)极限的性质 (4) (局部有界性)极限的性质 (5) (局部有界性)两个重要极限y=sinx/x (1)y=sinx/x (2)limsinx/x的一般形式y=(1+1/x)^x (1)y=(1+1/x)^x (2)lim(1+1/x)^x 的一般形式(1)lim(1+1/x)^x 的一般形式(2)lim(1+1/x)^x 的一般形式(3)e的值(1)e的值(2)等价无穷小(x>0)sinx等价于xarcsinx等价于xtanx等价于xarctanx等价于x1cosx等价于x^2/2 sinx等价于x数列的极限的几何解释海涅定理渐近线水平渐近线铅直渐近线y=(x+1)/(x1)y=sinx/x (x>∞)夹逼定理(1)夹逼定理(2)数列的夹逼性 (1)数列的夹逼性 (2)。
数学函数图像大全
7.万能公式 $sin(a)= (2tan(a/2))/(1+tan^2(a/2))$ $cos(a)= (1-tan^2(a/2))/(1+tan^2(a/2))$ $tan(a)= (2tan(a/2))/(1-tan^2(a/2))$
8.其它公式(推导出来的 )
$a*sin(a)+b*cos(a)=sqrt(a^2+b^2)sin(a+c)$ 其中 $tan(c)=b/a$ $a*sin(a)-b*cos(a)=sqrt(a^2+b^2)cos(a-c)$ 其中 $tan(c)=a/b$ $1+sin(a)=(sin(a/2)+cos(a/2))^2$ $1-sin(a)=(sin(a/2)-cos(a/2))^2$
$sin(a)+sin(b)=2sin((a+b)/2)cos((a-b)/2)$ $sin(a)−sin(b)=2cos((a+b)/2)sin((a-b)/2)$ $cos(a)+cos(b)=2cos((a+b)/2)cos((a-b)/2)$ $cos(a)-cos(b)=-2sin((a+b)/2)sin((a-b)/2)$ 4.积化和差公式 (上面公式反过来就得到了) $sin(a)sin(b)=-1/2*[cos(a+b)-cos(a-b)]$ $cos(a)cos(b)=1/2*[cos(a+b)+cos(a-b)]$ $sin(a)cos(b)=1/2*[sin(a+b)+sin(a-b)]$
y=sin(1/x) (4) y = [1/x](1)
y = [1/x](2)
y=21/x y=21/x (2) y=xsin(1/x)
8.其它公式(推导出来的 )
$a*sin(a)+b*cos(a)=sqrt(a^2+b^2)sin(a+c)$ 其中 $tan(c)=b/a$ $a*sin(a)-b*cos(a)=sqrt(a^2+b^2)cos(a-c)$ 其中 $tan(c)=a/b$ $1+sin(a)=(sin(a/2)+cos(a/2))^2$ $1-sin(a)=(sin(a/2)-cos(a/2))^2$
$sin(a)+sin(b)=2sin((a+b)/2)cos((a-b)/2)$ $sin(a)−sin(b)=2cos((a+b)/2)sin((a-b)/2)$ $cos(a)+cos(b)=2cos((a+b)/2)cos((a-b)/2)$ $cos(a)-cos(b)=-2sin((a+b)/2)sin((a-b)/2)$ 4.积化和差公式 (上面公式反过来就得到了) $sin(a)sin(b)=-1/2*[cos(a+b)-cos(a-b)]$ $cos(a)cos(b)=1/2*[cos(a+b)+cos(a-b)]$ $sin(a)cos(b)=1/2*[sin(a+b)+sin(a-b)]$
y=sin(1/x) (4) y = [1/x](1)
y = [1/x](2)
y=21/x y=21/x (2) y=xsin(1/x)
数学函数图像大全
函数图形基本初等函数幂函数1幂函数2请浏览后下载资料供参考期待您的好评与关注
函数2)
幂函数（3)
指数函数（1）
指数函数（2）
指数函数（3）
对数函数（1）
对数函数（2）
三角函数（1）
三角函数（2）
三角函数（3）
三角函数（4）
三角函数（5）
反三角函数（1）
反三角函数（2）
y=sin(1/x) (2)
y=sin(1/x) (3)
y=sin(1/x) (4)
y = [1/x](1)
y = [1/x](2)
反三角函数（3）
反三角函数（4）
反三角函数（5）
反三角函数（6）
反三角函数（7）
反三角函数（8）
双曲函数（1）
双曲函数（2）
双曲函数（3）
双曲函数（4）
双曲函数（5）
双曲函数（6）
双曲函数（7）
反双曲函数（1）
反双曲函数（2）
反双曲函数（3）
反双曲函数（4）
反双曲函数（5）
反双曲函数（6）
y=sin(1/x) (1)
函数2)
幂函数（3)
指数函数（1）
指数函数（2）
指数函数（3）
对数函数（1）
对数函数（2）
三角函数（1）
三角函数（2）
三角函数（3）
三角函数（4）
三角函数（5）
反三角函数（1）
反三角函数（2）
y=sin(1/x) (2)
y=sin(1/x) (3)
y=sin(1/x) (4)
y = [1/x](1)
y = [1/x](2)
反三角函数（3）
反三角函数（4）
反三角函数（5）
反三角函数（6）
反三角函数（7）
反三角函数（8）
双曲函数（1）
双曲函数（2）
双曲函数（3）
双曲函数（4）
双曲函数（5）
双曲函数（6）
双曲函数（7）
反双曲函数（1）
反双曲函数（2）
反双曲函数（3）
反双曲函数（4）
反双曲函数（5）
反双曲函数（6）
y=sin(1/x) (1)
经典数学函数图像(大全)
经典数学函数图像(大全)1. 一次函数图像一次函数图像是一条直线，其一般形式为 y = mx + b，其中 m是斜率，b 是 y 轴截距。
当 m > 0 时，直线向上倾斜；当 m < 0 时，直线向下倾斜。
2. 二次函数图像二次函数图像是一个抛物线，其一般形式为 y = ax^2 + bx + c，其中 a、b、c 是常数。
当 a > 0 时，抛物线开口向上；当 a < 0 时，抛物线开口向下。
3. 三角函数图像三角函数图像包括正弦函数、余弦函数和正切函数。
正弦函数图像是一条波动曲线，余弦函数图像与正弦函数图像相似，但相位差为π/2。
正切函数图像是一条周期性振荡的曲线。
4. 指数函数图像指数函数图像是一条上升或下降的曲线，其一般形式为 y = a^x，其中 a 是底数，x 是指数。
当 a > 1 时，曲线上升；当 0 < a < 1 时，曲线下降。
5. 对数函数图像对数函数图像是一条上升或下降的曲线，其一般形式为 y =log_a(x)，其中 a 是底数，x 是真数。
当 a > 1 时，曲线上升；当0 < a < 1 时，曲线下降。
6. 双曲函数图像双曲函数图像包括双曲正弦函数、双曲余弦函数和双曲正切函数。
双曲正弦函数和双曲余弦函数图像都是上升或下降的曲线，而双曲正切函数图像是一条周期性振荡的曲线。
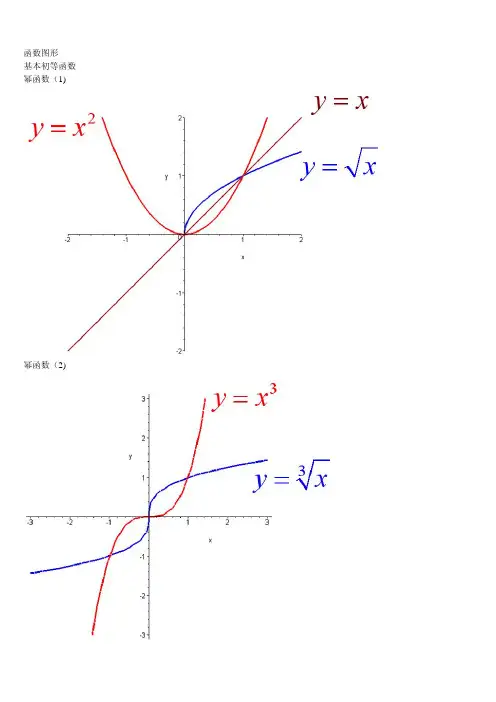
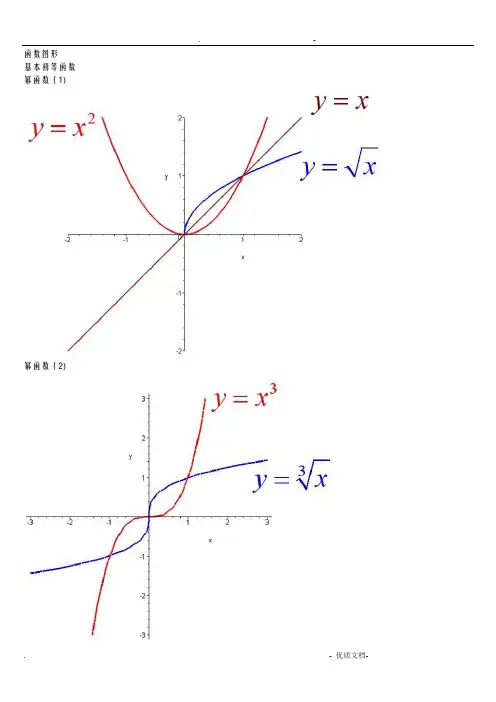
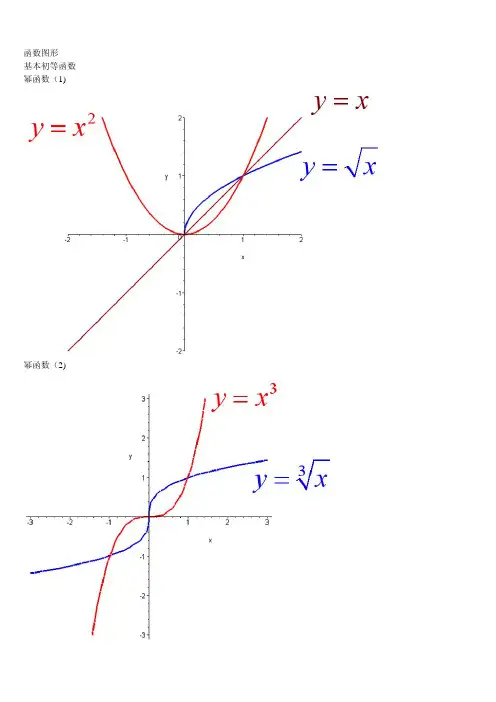
7. 幂函数图像幂函数图像是一条上升或下降的曲线，其一般形式为 y = x^n，其中 n 是指数。
当 n > 0 时，曲线上升；当 n < 0 时，曲线下降。
8. 反比例函数图像反比例函数图像是一条双曲线，其一般形式为 y = k/x，其中 k是常数。
当 k > 0 时，曲线位于第一和第三象限；当 k < 0 时，曲线位于第二和第四象限。
经典数学函数图像(大全)3. 反三角函数图像反三角函数是三角函数的反函数，包括反正弦函数、反余弦函数和反正切函数。
经典数学函数图像大全-数学函数图像-函数图像 全
函数图形基本初等函数幂函数（1)幂函数（2)幂函数（3)指数函数（1）指数函数（2）指数函数（3）对数函数（1）对数函数（2）三角函数（1）三角函数（2）三角函数（3）三角函数（4）三角函数（5）反三角函数（1）反三角函数（2）反三角函数（3）反三角函数（4）反三角函数（5）反三角函数（6）反三角函数（7）反三角函数（8）双曲函数（1）双曲函数（2）双曲函数（3）双曲函数（4）双曲函数（5）双曲函数（6）双曲函数（7）反双曲函数（1）反双曲函数（2）反双曲函数（3）反双曲函数（4）反双曲函数（5）反双曲函数（6）y=sin(1/x) (1) y=sin(1/x) (2)y=sin(1/x) (3)y=sin(1/x) (4)y = [1/x](1)y = [1/x](2)y=21/xy=21/x (2) y=xsin(1/x) y=arctan(1/x)y=e1/xy=sinx (x->∞)绝对值函数y = |x| 符号函数y = sgnx 取整函数y= [x]极限的几何解释(1) 极限的几何解释(2)极限的几何解释(3)极限的性质(1) (局部保号性) 极限的性质(2) (局部保号性)极限的性质(3) (不等式性质) 极限的性质(4) (局部有界性) 极限的性质(5) (局部有界性)两个重要极限y=sinx/x (1)y=sinx/x (2)limsinx/x的一般形式y=(1+1/x)^x (1)y=(1+1/x)^x (2)lim(1+1/x)^x 的一般形式(1) lim(1+1/x)^x 的一般形式(2) lim(1+1/x)^x 的一般形式(3) e的值(1)e的值(2)等价无穷小(x->0)sinx等价于x arcsinx等价于xarctanx等价于x1-cosx等价于x^2/2sinx等价于x数列的极限的几何解释海涅定理渐近线水平渐近线铅直渐近线y=(x+1)/(x-1)y=sinx/x (x->∞) 夹逼定理(1)夹逼定理(2) 数列的夹逼性(1) 数列的夹逼性(2)。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
函数图形
基本初等函数幂函数（1)
幂函数（2)
幂函数（3)
指数函数（1）
指数函数（2）
指数函数（3）
对数函数（1）
对数函数（2）
三角函数（1）
三角函数（2）
三角函数（3）
三角函数（4）
反三角函数（1）
反三角函数（2）
反三角函数（3）
反三角函数（5）
反三角函数（6）
反三角函数（7）
双曲函数（1）
双曲函数（2）
双曲函数（3）
双曲函数（5）
双曲函数（6）
双曲函数（7）
反双曲函数（2）
反双曲函数（3）
反双曲函数（4）
反双曲函数（6）
y=sin(1/x) (1)
y=sin(1/x) (2)
y = [1/x](2) y=sin(1/x) (3)
y=sin(1/x) (4)
y = [1/x](1)
y=21/x
y=21/x (2)
y=xsin(1/x)
y=arctan(1/x)
y=e1/x
y=sinx (x->∞)
绝对值函数 y = |x|符号函数 y = sgnx
极限的性质 (2) (局部保号性)极限的几何解释 (1)
极限的几何解释 (2)
极限的几何解释 (3)
极限的性质 (1) (局部保号性)
极限的性质 (3) (不等式性质)
极限的性质 (4) (局部有界性)
极限的性质 (5) (局部有界性)
两个重要极限
y=sinx/x (1)
y=sinx/x (2)
limsinx/x的一般形式
y=(1+1/x)^x (1)
y=(1+1/x)^x (2)
lim(1+1/x)^x 的一般形式(1)
lim(1+1/x)^x 的一般形式(2)
lim(1+1/x)^x 的一般形式(3)
e的值(1)
e的值(2)
等价无穷小
(x->0)
sinx等价于x
arcsinx等价于x
tanx等价于x
arctanx等价于x
1-cosx等价于x^2/2
sinx等价于x
数列的极限的几何解释
海涅定理
渐近线
水平渐近线
铅直渐近线
y=(x+1)/(x-1)
y=sinx/x (x->∞)夹逼定理(1)
夹逼定理(2)数列的夹逼性 (1)数列的夹逼性 (2)
.。