正态分布表资料
- 格式：doc
- 大小：362.50 KB
- 文档页数：11
下载文档原格式
合集下载
正态分布及其应用医本
二、正态分布的应用
表9-1 某地140名正常成年男性血清尿素氮浓度(mmol/L)
6.00
5.28
3.90
5.30
4.20
3.90
5.60
5.66
4.10
4.00
4.50
3.77
4.34
4.30
4.22
5.30
5.13
3.79
4.80
5.20
4.70
2.94
5.90
4.50
2.10
5.60
5.90
5.90
2.85
4.90
4.22
5.63
3.21
4.66
3.00
5.96
3.45
3.50
4.23
3.90
3.88
4.24
4.53
4.88
2.48
3.40
3.26
3.21
3.60
2.73
4.15
4.60
4.35
4.96
5.61
5.87
5.01
4.33
5.74
4.87
3.96
3.00
3.93
3.15
5.00
3、标准正态分布
正态分布的图形由 和 所决定，即N（ ， 2） 对上式进行 u 代换，即： 可使一般的正态分布转换为标准正态分布（u 分布），此时 N（0，1）。 x = 0 = 1
问题：为什么一般的正态分布要转换成标准正态分布？
01
表中曲线下面积为 - ~ u 的面积；即 P ( u) P299
第九章 数值变量资料的统计分析 第二节 正态分布及其应用
单击此处添加副标题
温医环境公卫学院黄陈平
表9-1 某地140名正常成年男性血清尿素氮浓度(mmol/L)
6.00
5.28
3.90
5.30
4.20
3.90
5.60
5.66
4.10
4.00
4.50
3.77
4.34
4.30
4.22
5.30
5.13
3.79
4.80
5.20
4.70
2.94
5.90
4.50
2.10
5.60
5.90
5.90
2.85
4.90
4.22
5.63
3.21
4.66
3.00
5.96
3.45
3.50
4.23
3.90
3.88
4.24
4.53
4.88
2.48
3.40
3.26
3.21
3.60
2.73
4.15
4.60
4.35
4.96
5.61
5.87
5.01
4.33
5.74
4.87
3.96
3.00
3.93
3.15
5.00
3、标准正态分布
正态分布的图形由 和 所决定，即N（ ， 2） 对上式进行 u 代换，即： 可使一般的正态分布转换为标准正态分布（u 分布），此时 N（0，1）。 x = 0 = 1
问题：为什么一般的正态分布要转换成标准正态分布？
01
表中曲线下面积为 - ~ u 的面积；即 P ( u) P299
第九章 数值变量资料的统计分析 第二节 正态分布及其应用
单击此处添加副标题
温医环境公卫学院黄陈平
正态分布和其应用
限和上限，即双侧界值；有些指标如
肺活量一般只以过低为异常，血铅以
过高为异常，只需要拟定下限或上限， 即单侧界值。
根据资料旳分布类型有下列两种计 算医学参照值范围旳常用措施。
➢正态近似法 合用于服从正态分布或近 似正态分布旳资料
➢双侧1 参照值范围
x u 2s➢单侧 1 源自照值范围x u s 或 x u s
或称 变换u 。
u x
• 实际应用中，经u 变换后，就可把 求解任意一种正态分布曲线下面积旳问 题，转化成原则正态分布曲线下相应旳 面积问题。附表1给出了原则正态分布 曲线下从 到 u旳面积，根据正态分布 旳对称性，我们能够求出任何一种区间 内原则正态分布曲线下旳面积，也就是
u 落在任何一种区间内旳概率。
1
2
exp(
(X )2 2 2
)
其中参数为均值， 为原则差，由此
决定旳正态分布记作 N (, 2 ) 。
正态分布概率密度曲线示意图
➢ 三．特征
➢ 正态分布是单峰曲线，形状呈钟型，中间高，两
端低，以 X 为对称轴，左右完全对称。
➢ 在 X 处，f ( X ) 取得最大值。
➢ 有两个参数：位置参数 和变异度参数 。 一定， 越大，数据越分散，曲线越平坦； 一
➢百分位数法 合用于偏态分布资料、分 布型未知旳资料以及分布末端有不拟定 值旳资料。
➢双侧95%参照值范围
P2.5 ~ P97.5
➢单侧95%参照值范围
P5 或 P95
• 根据正态 分布旳对称性知，外侧尾部面 积 u 2.21 与外侧尾部面积 u 2.21 相同，查附表1，得相应旳概率为0.0136， 体重在50kg以上旳12岁小朋友占1.36%。
第三节 医学参照值范围旳制定
肺活量一般只以过低为异常，血铅以
过高为异常，只需要拟定下限或上限， 即单侧界值。
根据资料旳分布类型有下列两种计 算医学参照值范围旳常用措施。
➢正态近似法 合用于服从正态分布或近 似正态分布旳资料
➢双侧1 参照值范围
x u 2s➢单侧 1 源自照值范围x u s 或 x u s
或称 变换u 。
u x
• 实际应用中，经u 变换后，就可把 求解任意一种正态分布曲线下面积旳问 题，转化成原则正态分布曲线下相应旳 面积问题。附表1给出了原则正态分布 曲线下从 到 u旳面积，根据正态分布 旳对称性，我们能够求出任何一种区间 内原则正态分布曲线下旳面积，也就是
u 落在任何一种区间内旳概率。
1
2
exp(
(X )2 2 2
)
其中参数为均值， 为原则差，由此
决定旳正态分布记作 N (, 2 ) 。
正态分布概率密度曲线示意图
➢ 三．特征
➢ 正态分布是单峰曲线，形状呈钟型，中间高，两
端低，以 X 为对称轴，左右完全对称。
➢ 在 X 处，f ( X ) 取得最大值。
➢ 有两个参数：位置参数 和变异度参数 。 一定， 越大，数据越分散，曲线越平坦； 一
➢百分位数法 合用于偏态分布资料、分 布型未知旳资料以及分布末端有不拟定 值旳资料。
➢双侧95%参照值范围
P2.5 ~ P97.5
➢单侧95%参照值范围
P5 或 P95
• 根据正态 分布旳对称性知，外侧尾部面 积 u 2.21 与外侧尾部面积 u 2.21 相同，查附表1，得相应旳概率为0.0136， 体重在50kg以上旳12岁小朋友占1.36%。
第三节 医学参照值范围旳制定
直方图、正态分布、柏拉图
2.5 6
直方图、正态分布、柏拉图
2.6 正态分布应用
确定医学参考值范围 质量控制图
直方图、正态分布、柏拉图
2.6.1确定医学参考值范围
概念：医学参考值范围，又称参考值范围或正常值范围，是指特定 健康人群的解剖、生理、生化等各种数据的波动范围。习惯上是确 定包括95%的人的界值。
单双侧： 根据指标的实际用途， 有的指标有上下界值（双侧）； 某些指标只需确定上限（单）； 某些指标只需确定下限（单）。
直方图(Histogram)又称质量分布图。是一种统计报告图，由一系列高 度不等的纵向条纹或线段表示数据分布的情况。 一般用横轴表示数据类 型，纵轴表示分布情况。
1.2 直方图绘制
收集数据（n≥50）
确定数据极差R 确定组数 确定组距
数据N 组数K
50-100 6-10
组距=极差R/组数
100-250 7-12
的概率 • 对称区域面积相等。
2.4 3原则
区间 (-, +] (-2, +2] (-3, +3]
取值概率 68.3% 95.4% 99.7%
我们从上图看到，正态总体在 2,2以外取值的概率
只有4.6％，在 3,3以外取值的概率只有0.3 ％。
当 a 3 时正态总体的 X 取值几乎总取值于区间 ( 3 , 3 ) 之内,其他区间取值几乎不可能.在实 际运用中就只考虑这个区间,称为 3 原则.
直方图、正态分布、柏拉图
3.3 柏拉图作用
1、作为降低不良依据。
1、80%的问题由20%的原因引起；
2、决定改善的攻击目标。
2、80%的索赔发生在20%的生产线上；
3、确认改善效果。
3、80%的销售额由20%的产品带来；
标准正态分布示意图
lgG = lg(12571032040)=lg(571032040)1/12=1/1 2(7lg5+3lg10+lg20+lg40)=0.89966
为简化计算, 可两边取对数
G = lg-1(lgG)= lg-10.89966 = 7.94
加权法: G=lg-1( lgx/ ), 当变量值个数 较多或变量值为频数表资料时
(3） （4）=（2）（3） （5）=（2）（4）
1 127
16129
• 129 131
4 524
68644
• 133 135
9 1215
164025
• 137 139
28 3829
540988
• 141 143
35 5005
715715
• 145 147
27 3969
583443
• 149 151
11 1661
250811
• 153 155
4 620
96100
• 157161 159 • 合计 •
1 159
120 17172
（ƒ）（ ƒx）
25181
2461136
（ ƒx2）
•
2461136 - （17172）2/120
• s=
•
120 - 1
•
• 三、变异系数: 又称离散系数。代号为CV。
甲的变异程度>乙组
一、极差和四分位间距
• （一）全距: R(range), 亦称极差。即一组变量 值中最大值与最小值之差。
• R甲=4.0 - 2.8 = 1.2 • R乙=3.8 - 3.0 = 0.8 • 优点: 简单明了 • 缺点: 仅考虑了资料的最大值与最小值, 不能反
正态分布的概念及表和查表方法
正态分布概念及图表正态分布（Normal distribution），也称“常态分布”，又名高斯分布（Gaussian distribution），最早由A·棣莫弗在求二项分布的渐近公式中得到。
C.F.高斯在研究测量误差时从另一个角度导出了它。
P·S·拉普拉斯和高斯研究了它的性质。
是一个在数学、物理及工程等领域都非常重要的概率分布，在统计学的许多方面有着重大的影响力。
正态曲线呈钟型，两头低，中间高，左右对称因其曲线呈钟形，因此人们又经常称之为钟形曲线。
若随机变量X服从一个数学期望为μ、方差为σ^2的正态分布，记为N(μ，σ^2)。
其概率密度函数为正态分布的期望值μ决定了其位置，其标准差σ决定了分布的幅度。
当μ = 0,σ = 1时的正态分布是标准正态分布。
目录1历史发展2定理3定义▪一维正态分布▪标准正态分布4性质5分布曲线▪图形特征▪参数含义6研究过程7曲线应用▪综述▪频数分布▪综合素质研究▪医学参考值历史发展正态分布概念是由德国的数学家和天文学家Moivre于1733年首次提出的，但由于德国数学家Gauss率先将其应用于天文学家研究，故正态分布又叫高斯分布，高斯这项工作对后世的影响极大，他使正态分布同时有了“高斯分布”的名称，后世之所以多将最小二乘法的发明权归之于他，也是出于这一工作。
但现今德国10马克的印有高斯头像的钞票，其上还印有正态分布的密度曲线。
这传达了一种想法：在高斯的一切科学贡献中，其对人类文明影响最大者，就是这一项。
在高斯刚作出这个发现之初，也许人们还只能从其理论的简化上来评价其优越性，其全部影响还不能充分看出来。
这要到20世纪正态小样本理论充分发展起来以后。
拉普拉斯很快得知高斯的工作，并马上将其与他发现的中心极限定理联系起来，为此，他在即将发表的一篇文章（发表于1810年）上加上了一点补充，指出如若误差可看成许多量的叠加，根据他的中心极限定理，误差理应有高斯分布。
讲稿21正态分布
正态分布及其应用刘关键四川大学华西临床医学院 循证医学与临床流行病学教研室正态分布(normal distribution) 又称高斯分布(Gaussian distribution) 是一种很重要的连续型分布，是统 计理论基础中最重要的分布之一， 应用甚广。
学习正态分布的数学特征，目的是 了解统计学中有关“分布”的概念。
正态分布的密度函数在统计上，某个分布的密度函数，即指 该分布的曲线方程。
正态分布的曲线方 程（密度函数）可由下式表达：f(X ) = 1 -(X -μ ) 2σ 2 e2σ2πf(X)μ－ ∞ ＜ X＜ ∞X正态分布曲线图正态分布的参数按此方程可绘出其图形。
式中μ为均数，σ为标准差；π为圆周率， 即3.14159；ｅ为自然对数的底，即2.7183。
以上均为常量，仅X为变量。
当X确定后， 就可由此式求得其密度函数f(X)，也就是相 应的纵坐标高度。
所以已知μ和σ ，就能按公式绘出正态曲线 的图形。
两个参数(parameter)，即均数μ、标准差σ。
当标准差σ不变，均数μ越大，则曲线沿横轴 向右移动；反之，均数μ越小，则曲线沿横轴 向左移动，故均数μ是反映正态分布在横轴上 位置的参数。
当均数μ不变，标准差σ越大，表示数据越分 散，曲线越“胖”；标准差σ越小，表示数据越 集中，曲线越“瘦”，故标准差σ是反映正态分 布变异大小的参数。
可见有了μ和σ，就把正态分布确定下来了， 为了叙述方便，一般用N(μ，σ2)表示均数为 μ，方差为σ2的正态分布。
1正态分布曲线的特征正态分布是一簇单峰分布，当X =μ时，也 就是均数处，其曲线峰值，即函数f(X)的值 最大。
正态分布以均数μ为中心，左右对称。
因 为，式中(X – μ)的值无论正负，只要绝对 值相等，则函数的值(纵高)相等。
正态分布是以μ，σ2为参数的多个分布的总 称，即正态分布是多条曲线的总称。
正态分布的分布函数统计上，某个分布的分布函数，就是指该曲线 方程下的面积，它可由曲线方程的定积分所 得，故正态分布的分布函数可由下式表达：X F(X) = 1σ2π⌠ ⎮ ⎮ ⌡-(X-μ) 2 2 e 2σdX-∞正态分布曲线下的面积规律式中F(X)为正态变量X的累计分布 函数，反映正态曲线下，横轴尺度 自-∞到X的面积，即下侧累计面积 (概率)。
医学统计学(第2章)正态分布
dx
（2-18） ）
F（X）
p(a〈x〈b)
0 12.00 14.50 17.00 19.50 22.00 24.50 27.00 29.50 32.00
正态分布曲线下面积的含义
1.表示变量值（x）在a-b区间变量值所占 1.表示变量值 表示变量值（ 全部（总体）变量值的比例或概率 比例或概率(p)。 全部（总体）变量值的比例或概率(p)。 2变量值在整个曲线下的面积为100%,或 变量值在整个曲线下的面积为100%,或 出现的概率为1 出现的概率为1。
第五节 医学参考值范围的制定
一、概念 医学参考值是指包括绝大多数“ 医学参考值是指包括绝大多数“正 常人” 的各种生理及生化指标常数， 常人 ” 的各种生理及生化指标常数 ， 也 称正常值。 称正常值。 正常值是指在一定范围内波动的值， 正常值是指在一定范围内波动的值， 医学上常用95% 医学上常用95%的范围作为判定正常或 异常的参考标准。 异常的参考标准。
二、 标准正态分布
1.标准正态分布及标准化变量值（u） 标准正态分布及标准化变量值（ ） 标准正态分布及标准化变量值 任何正态分布的X值通过 值转换后,称为标 任何正态分布的 值通过u值转换后 称为标 准化的正态分布， 准化的正态分布，即u ~N（ µ=0 ， σ2=1） （ ） 概率密度函数为： 。概率密度函数为： 2
Φ(−u) 表示从－∞到- u值对应曲线范围 表示从－ 值分布比例。 内X值分布比例。
例1： ：
Φ(u = −1) = 0.1587 Φ(µ =1) =1− Φ(u = −1)
=1− 0.1587 = 0.8413
例2：标准正态变量值u=（-1，1）和u= 标准正态变量值u=（ 1.96，1.96）区间内面积各为多少？ （ -1.96，1.96）区间内面积各为多少？
3 医学统计学正态分布与参考值
…… 0.06 0.07 0.08 0.09 …… 0.0011 0.0011 0.0010 0.0010 …… 0.0015 0.0015 0.0014 0.0014 …… …… …… …… …… …… 0.0052 0.0051 0.0049 0.0048 …… …… …… …… …… …… 0.0250 0.0244 0.0239 0.0233 …… …… …… …… …… …… 0.4364 0.4325 0.4286 0.4247 …… 0.4761 0.4721 0.4681 0.4641
2. 计算法:常用偏度与峰度进行评定，其度 量指标分别为偏度系数和峰度系数。
Expected Normal Value Expected CumProb
Normal Q-Q Plot of BLOOD
90
80
70
60
60
70
80
90
Observed Value
图6-8 108个原始数据的Q-Q图
Normal P-P Plot of BLOOD
表6-2 108名正常成年女子血清总蛋白(g/L)频数分布
组段 ⑴
64.0～ 66.0～ 68.0～ 70.0～ 72.0～ 74.0～ 76.0～ 78.0～ 80.0～ 82.0～84.0 合计
频数,f ⑵
2 6 8 15 25 23 14 7 6 2 108
组中值,X ⑶
65.0 67.0 69.0 71.0 73.0 75.0 77.0 79.0 81.0 83.0 －
x越远离μ，f (x)值越小。
3. 位置参数μ,
f (x)
f (μ)
形态参数σ
4. μ±ϭ为拐点的横坐标
第四章 正 态 分 布 体育统计学
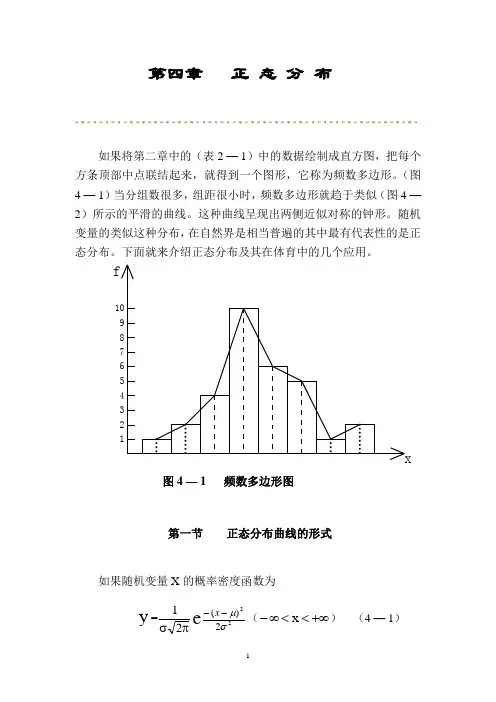
第四章 正 态 分 布如果将第二章中的（表2 — 1）中的数据绘制成直方图，把每个方条顶部中点联结起来，就得到一个图形，它称为频数多边形。
（图4 — 1）当分组数很多，组距很小时，频数多边形就趋于类似（图4 —2）所示的平滑的曲线。
这种曲线呈现出两侧近似对称的钟形。
随机变量的类似这种分布，在自然界是相当普遍的其中最有代表性的是正态分布。
下面就来介绍正态分布及其在体育中的几个应用。
12345678910x图4 — 1 频数多边形图第一节 正态分布曲线的形式如果随机变量X 的概率密度函数为y =πσ21e 222)(σμ--x （+∞<<∞-x ） （4 — 1）则称随机变量X 是服从正态分布的由上式绘出的图形叫做正态曲线。
（图4 — 2）X 的变动范围在 ∞- 至 +∞ 间。
YX0μ图4 — 2 正态分布曲线正态分布曲线中有两个参数：均值 μ 及方差 2σ。
为了应用方便，对式（4 — 1）中的随机变量经过一个称为标准化的变换，即令u 来代替原式中的 σμ-x ， 寻这时的随机变量u 的概率密度函数成为：y = π21e 22u - （4 — 2） 按照（4 — 2）式绘出的图形，称作标准正态曲线。
（图4 — 3）Y00.40.30.20.1-1-2-3123μ图4 — 3 标准正态分布曲线第二节正态分布曲线的特征正态分布曲线有许多特点，它们对实际工作有很大的帮助。
它的主要特点有以下几个方面：一，正态分布的形式是对称的（但对称的分布不一定是正态分布）。
在正态分布中均值与中位数相重合。
二，从中央最高点逐渐向两侧降低，降低的速度是先慢后快，以后又再次减慢，最后接近横轴，但终究不能与横轴相交。
三，从中央向两侧逐渐下降，它的方向是先向内弯，达到离均值左右各一个标准差时又改向外弯，是以σμ1±的点为曲线从内弯转向外弯的转折点，即正态曲线中标准差与曲线有固定的关系。
四，因为正态曲线是对称的，在曲线下不仅平均数的两侧面积相等，各相当距离间的面积相等，而且各相当距离间的曲线高度也相等，正态曲线下（与横轴间）的总面积为1. 00。
正态分布
正态分布normal distribution一种概率分布。
正态分布是具有两个参数μ和σ2的连续型随机变量的分布，第一参数μ是服从正态分布的随机变量的均值，第二个参数σ2是此随机变量的方差，所以正态分布记作N(μ，σ2 )。
服从正态分布的随机变量的概率规律为取与μ邻近的值的概率大，而取离μ越远的值的概率越小；σ越小，分布越集中在μ附近，σ越大，分布越分散。
正态分布的密度函数的特点是：关于μ对称，在μ处达到最大值，在正（负）无穷远处取值为0，在μ±σ处有拐点。
它的形状是中间高两边低，图像是一条位于x轴上方的钟形曲线。
当μ＝0，σ2 ＝1时，称为标准正态分布，记为N（0，1）。
μ维随机向量具有类似的概率规律时，称此随机向量遵从多维正态分布。
多元正态分布有很好的性质，例如，多元正态分布的边缘分布仍为正态分布，它经任何线性变换得到的随机向量仍为多维正态分布，特别它的线性组合为一元正态分布。
正态分布最早由A.棣莫弗在求二项分布的渐近公式中得到。
C.F.高斯在研究测量误差时从另一个角度导出了它。
P.S.拉普拉斯和高斯研究了它的性质。
生产与科学实验中很多随机变量的概率分布都可以近似地用正态分布来描述。
例如，在生产条件不变的情况下，产品的强力、抗压强度、口径、长度等指标；同一种生物体的身长、体重等指标；同一种种子的重量；测量同一物体的误差；弹着点沿某一方向的偏差；某个地区的年降水量；以及理想气体分子的速度分量，等等。
一般来说，如果一个量是由许多微小的独立随机因素影响的结果，那么就可以认为这个量具有正态分布（见中心极限定理）。
从理论上看，正态分布具有很多良好的性质，许多概率分布可以用它来近似；还有一些常用的概率分布是由它直接导出的，例如对数正态分布、t分布、F分布等。
正态分布应用最广泛的连续概率分布，其特征是“钟”形曲线。
from (一)正态分布1.正态分布若的密度函数（频率曲线）为正态函数（曲线）(3-1)则称服从正态分布，记号～。
正态分布[2-2]
![正态分布[2-2]](https://img.taocdn.com/s1/m/bb3e54a60029bd64783e2cf5.png)
(X − X) u=
S
3.曲线下对称于 的区间，面积相等。 曲线下对称于0的区间，面积相等。 曲线下对称于 的区间 4.曲线下横轴上的面积为 曲线下横轴上的面积为100%或1。 曲线下横轴上的面积为 或 。
正态分布是一种对称分布，其对称轴为直线 正态分布是一种对称分布，其对称轴为直线X=µ， ， 即均数位置，理论上： 即均数位置，理论上： µ±1σ范围内曲线下的面积占总面积的 ± 范围内曲线下的面积占总面积的 范围内曲线下的面积占总面积的68.27% µ±1.96σ范围内曲线下的面积占总面积的 ± 范围内曲线下的面积占总面积的95% 范围内曲线下的面积占总面积的 µ±2.58σ范围内曲线下的面积占总面积的 ± 范围内曲线下的面积占总面积的99% 范围内曲线下的面积占总面积的 实际应用中： 实际应用中： 范围内曲线下的面积占总面积的68.27% ±1 S范围内曲线下的面积占总面积的 范围内曲线下的面积占总面积的 范围内曲线下的面积占总面积的95% ±1.96 S范围内曲线下的面积占总面积的 范围内曲线下的面积占总面积的 范围内曲线下的面积占总面积的99% ±2.58 S范围内曲线下的面积占总面积的 范围内曲线下的面积占总面积的
u=
X −µ
σ
二、正态分布的特征
1. 关于 心，左右对称。 左右对称。 2. 在 在 处取得概率密度函数的最大值， 处取得概率密度函数的最大值， 处有拐点，表现为钟形曲线。 处有拐点，表现为钟形曲线。即正 拐点 对称。 对称。即正态分布以均数为中
态曲线在横轴上方均数处最高。 态曲线在横轴上方均数处最高。
双侧---过高、 双侧 过高、过低均异常 过高
异常
正常
正常
异常
异常
正常
异常
第三章正态分布.
第三章 正态分布一、教学大纲要求(一) 掌握内容1．正态分布的概念和特征 （1）正态分布的概念和两个参数； （2）正态曲线下面积分布规律。
2．标准正态分布标准正态分布的概念和标准化变换。
3．正态分布的应用 （1）估计频数分布； （2）制定参考值范围。
(二) 熟悉内容 标准正态分布表。
(三) 了解内容1．利用正态分布进行质量控制 2．正态分布是许多统计方法的基础二、教学内容精要(一)正态分布 1.正态分布若X 的密度函数（频率曲线）为正态函数（曲线）2．正态分布的特征服从正态分布的变量的频数分布由μ、σ完全决定。
(1)μ是正态分布的位置参数，描述正态分布的集中趋势位置。
正态分布以x μ=为对称轴，左右完全对称。
正态分布的均数、中位数、众数相同，均等于μ。
(2)σ描述正态分布资料数据分布的离散程度，σ越大，数据分布越分散，σ越小，数据分布越集中。
σ也称为是正态分布的形状参数，σ越大，曲线越扁平，反之，σ越小，曲线越瘦高。
(二)标准正态分布1．标准正态分布是一种特殊的正态分布，标准正态分布的0=μ，12=σ ，通常用u（或Z ）表示服从标准正态分布的变量，记为u ～N （0，21）。
2．标准化变换：σμ-=X u ，此变换有特性：若X 服从正态分布),(2σμN ，则u 就服从标准正态分布，故该变换被称为标准化变换。
3. 标准正态分布表标准正态分布表中列出了标准正态曲线下从-∞到u 范围内的面积比例()u Φ。
（三）正态曲线下面积分布1．实际工作中，正态曲线下横轴上一定区间的面积反映该区间的例数占总例数的百分比，或变量值落在该区间的概率（概率分布）。
不同),(21X X 范围内正态曲线下的面积可用公式3-2计算。
)()(2112)22(2)(21u u dx eD X X X Φ-Φ==--⎰σμπσ （3-2）1212X X u u μμσσ--==其中， ， 。
2.几个重要的面积比例X 轴与正态曲线之间的面积恒等于1。
正态分布3
2011-11-13
医学统计学
10
标准正态分布( 标准正态分布(standard normal distribution) ) 均数为0 标准差为1的正态分布（ 均数为0，标准差为1的正态分布（图3-5）。
f (X) =
1
− ( X − µ )2
σ 2π
e
2σ 2
(−∞ < X < +∞)
⇒ ψ (u) =
医学统计学
15
标准正态分布
− 1 . 96 −1 − 2 . 58
0
+ 1 . 96 +1 + 2 . 58
常用的u值 常用的 值 曲线下面积（%） 曲线下面积（ ） 99 95 90 80 68.27 双侧u值（±） 双侧 值 2.58 1.96 1.645 1.282 1 单侧u值（±） 单侧 值 2.33 1.645 1.282 0.842
正 态 分 布
(normal distribution)
2011-11-13
医学统计学
1
120名12岁健康男孩身高(cm)的频数分布 120名12岁健康男孩身高(cm)的频数分布 岁健康男孩身高 组 段(1) 125~ 125 129~ 129 133~ 133 137~ 137 141~ 141 145~ 145 149~ 149 153~ 153 157~161 157 161 合 计
2011-11-13
医学统计学
14
标准正态分布曲线下左侧任一区间的面积： 标准正态分布曲线下左侧任一区间的面积：
φ (u ) =
1 2π
∫
u
−∞
e
u2 − 2
du
附表1 标准正态分布曲线下左侧尾部面积(u分布界值表) (u分布界值表 附表1 标准正态分布曲线下左侧尾部面积(u分布界值表)
正态分布的概念及表和查表方法
正态分布的概念及表和查表方法本页仅作为文档封面，使用时可以删除This document is for reference only-rar21year.March正态分布概念及图表正态分布（Normal distribution），也称“常态分布”，又名高斯分布（Gaussian distribution），最早由A·棣莫弗在求二项分布的渐近公式中得到。
.高斯在研究测量误差时从另一个角度导出了它。
P·S·拉普拉斯和高斯研究了它的性质。
是一个在数学、物理及工程等领域都非常重要的概率分布，在统计学的许多方面有着重大的影响力。
正态曲线呈钟型，两头低，中间高，左右对称因其曲线呈钟形，因此人们又经常称之为钟形曲线。
若随机变量X服从一个数学期望为μ、方差为σ^2的正态分布，记为N(μ，σ^2)。
其概率密度函数为正态分布的期望值μ决定了其位置，其标准差σ决定了分布的幅度。
当μ = 0,σ = 1时的正态分布是标准正态分布。
目录1历史发展2定理3定义▪一维正态分布▪标准正态分布4性质5分布曲线▪图形特征▪参数含义6研究过程7曲线应用▪综述▪频数分布▪综合素质研究▪医学参考值历史发展正态分布概念是由德国的数学家和天文学家Moivre于1733年首次提出的，但由于德国数学家Gauss率先将其应用于天文学家研究，故正态分布又叫高斯分布，高斯这项工作对后世的影响极大，他使正态分布同时有了“高斯分布”的名称，后世之所以多将最小二乘法的发明权归之于他，也是出于这一工作。
但现今德国10马克的印有高斯头像的钞票，其上还印有正态分布的密度曲线。
这传达了一种想法：在高斯的一切科学贡献中，其对人类文明影响最大者，就是这一项。
在高斯刚作出这个发现之初，也许人们还只能从其理论的简化上来评价其优越性，其全部影响还不能充分看出来。
这要到20世纪正态小样本理论充分发展起来以后。
拉普拉斯很快得知高斯的工作，并马上将其与他发现的中心极限定理联系起来，为此，他在即将发表的一篇文章（发表于1810年）上加上了一点补充，指出如若误差可看成许多量的叠加，根据他的中心极限定理，误差理应有高斯分布。
3.正态分布
u u2
e 2du
2
φ(u)表示从－∞到u值范围内X分布面积
附表1（P245）就是根据此公式和图形制定的
2021/8/8
陈学芬 制作
20
概率密度函数与累积分布函数
1
f(X) F(X) 0.8
0.6 0.4 0.2
0 -4 -3 -2 -1 0 1 2 3 4
X
3.正态曲线下面积的分布规律
曲线下面积分布规律
▪ 总体标准差σ是变异度参数：描述正态分布离散趋势， 越小，分布越集中，曲线形状越“瘦高”；反之越“矮 胖”。
正态曲线由，两个参数共同决定
2021/8/8
陈学芬 制作
7
1.正态分布的概念和特征
三种不同均值的正态分布 σ恒定
-∞
μ1
μ2
μ3
+∞
μ 1<μ 2<μ 3
μ越大，曲线沿横轴越向右移动
2021/8/8
68.27%
95.00%
99.00%
-2.58 -1.96 -1
0
1 1.96 2.58
标准正态分布
面积或概率
-1～1
68.27%
-1.96～1.96
95.00%
-2.58～2.58
99.00%
标准正态曲线 横轴为u值
3.正态曲线下面积的分布规律
将变量值（x）转换为u值后，统计学家按φ(u)公式编制成了附 表1，即标准正态分布表 查表注意事项：
2021/8/8
陈学芬 制作
23
3.正态曲线下面积的分布规律
例 1.求区间（2.58，+∞）的面积。
因为区间（2.58，+∞）和区间（-∞ ，-2.58）对称 所以只需求出（-∞ ，-2.58）的面积即可，
2定性数据统计描述正态分布及其应用
0
95.00%
99.00%
1 1.96 2.58 μ-2.58σ μ-1.96σ μ-σ
μ
μ+σ μ+1.96σ μ+2.58σ
标准正态分布 正态分布
-1～1
μ±σ
-1.96～1.96 μ±1.96σ
-2.58～2.58 μ±2.58σ
面积或概率 68.27% 95.00% 99.00%
以上讨论的是标准正态分布，对一般的正态分布，某指标X~N(μ,σ2),则 u=(x-μ)/σ~N(0,1) 即-1.96<u<1.96的面积为0.95 μ-1.96σ<x<μ+1.96σ的面积为0.95
2.百分位数法
应用条件 : 任何分布，特别是偏态分布资料 计算公式：
双侧界值：P2.5 ~ P97.5 单侧 上界：P95 单侧 下界：P5 630名正常女性血清甘油三酯含量的资料
注意
95%参考范围（reference range）或正常范围（normal range）仅仅告知健康者中 95%的人测定值在此范围之内，并非告知凡在此范围之内皆健康，也非告知凡在此范围之外 皆不健康，所以不可将之作为诊断标准。
同期暴露人口数
可能发生该病的人群
不可能发病
1、 发病率（incidence rate）
IR= 某期某人群中某病的新病例数 × K
同期暴露人口数
该时期的平均人口数 （1）年中人口数（2）平均值
分子 观察期内新发生的病人； 同一个体多次患病，应多次计数； 发病时间较难确定的以初次诊断作为发病时间。 分母 应为易感人口，实际大样本调查多用平均人口。
小结 1.描述一组观察值，除需要表示其平均水平外，还要说明它的离散或变异的情况。 2.衡量变异程度大小的指标有多种: 极差、四分位数间距、方差、标准差和变异系数。其中应用最多 的是标准差和变异系数。 3.标准差与均数结合能够完整地描述一个正态分布。对任何参数的正态分布，都可以通过一个简单的 变量变换化成标准正态分布。正态分布可以很容易地确定其数值出现在任意指定范围内的概率。
95.00%
99.00%
1 1.96 2.58 μ-2.58σ μ-1.96σ μ-σ
μ
μ+σ μ+1.96σ μ+2.58σ
标准正态分布 正态分布
-1～1
μ±σ
-1.96～1.96 μ±1.96σ
-2.58～2.58 μ±2.58σ
面积或概率 68.27% 95.00% 99.00%
以上讨论的是标准正态分布，对一般的正态分布，某指标X~N(μ,σ2),则 u=(x-μ)/σ~N(0,1) 即-1.96<u<1.96的面积为0.95 μ-1.96σ<x<μ+1.96σ的面积为0.95
2.百分位数法
应用条件 : 任何分布，特别是偏态分布资料 计算公式：
双侧界值：P2.5 ~ P97.5 单侧 上界：P95 单侧 下界：P5 630名正常女性血清甘油三酯含量的资料
注意
95%参考范围（reference range）或正常范围（normal range）仅仅告知健康者中 95%的人测定值在此范围之内，并非告知凡在此范围之内皆健康，也非告知凡在此范围之外 皆不健康，所以不可将之作为诊断标准。
同期暴露人口数
可能发生该病的人群
不可能发病
1、 发病率（incidence rate）
IR= 某期某人群中某病的新病例数 × K
同期暴露人口数
该时期的平均人口数 （1）年中人口数（2）平均值
分子 观察期内新发生的病人； 同一个体多次患病，应多次计数； 发病时间较难确定的以初次诊断作为发病时间。 分母 应为易感人口，实际大样本调查多用平均人口。
小结 1.描述一组观察值，除需要表示其平均水平外，还要说明它的离散或变异的情况。 2.衡量变异程度大小的指标有多种: 极差、四分位数间距、方差、标准差和变异系数。其中应用最多 的是标准差和变异系数。 3.标准差与均数结合能够完整地描述一个正态分布。对任何参数的正态分布，都可以通过一个简单的 变量变换化成标准正态分布。正态分布可以很容易地确定其数值出现在任意指定范围内的概率。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
正态分布的应用1、用Z 的公式将原始分数转换成标准分数条件是原始分数的分布是正态的。
例如：已知某班期末考试中语文的平均分为76，标准差为10，数学的平均分为83，标准差为15。
某学生在这次期末考试的语文成绩为79，数学成绩为87，问该生这两科成绩哪一个更好一些？答：该考生的语文成绩更好一些。
2、确定录用分数线在选拔兴或竞赛性的考试中，录取或授奖的人数（或比赛）往往是事先确定的。
这就是用标准分数的作用发挥。
假定为正态分布，可将录取或授奖的人数比率作为正态分布中分线右侧，即上端的面积，由此找出相应标准分数Z 值，然后根据Z 公式计算出原始分数X.例如：在某年的高考中某省的平均分为420，标准差为100，分数呈正态分布，某考生得了456分。
设当年的该省的录取率为40%，问该生的成绩是否上线？解：根据Z 分数的计算公式，得当P=0.40时，0.5-0.40=0.10然后查附表，找到对应的Z=0.25 因为0.36>0.25,所以该考生上线了。
又如：某年某市参加数学竞赛的学生有850人，考试的平均分为68，标准差为9。
而这次计划只给最优秀的5%颁奖，问授奖分数线为多少？某个考生在这次考试中得了76分，问这位考生是否获奖？解：根据0.05的P 值计算差表，得Z=1.65 因为82.85>76, 所以该考生不可能获奖。
例.某区拟对参加数学竞赛的2000人中的前500人予以奖励，考试的平均分数为75分，标准差为9分，问授奖的分数线是多少？（授奖分数线为81.03分。
）例：某考试2500人参加，成绩服从正态分布，μ＝80 σ2＝25，求分数在88分以上的人数。
解:n ＝N·P ＝2500×0.0548＝137（人）例：某招生考试，选拔２０％，考生成绩服从正态分布，μ＝70 σ＝10，录取标准应划在哪里？ 解Z ＝0.84 X ＝10×0.84+70＝78.4 分数线为78.4例：某地13岁女孩118人的身高(cm)资料，估计该地13岁正常女孩身高在135厘米以下及155厘米以上者各占正常女孩总人数的百分比。
身高（X ）～N (μ，σ2)，但μ和σ未知，只知来自该总体的样本的身高均数x =144.29(cm)和标准差s =5.41(cm)，由于样本含量n=118很大，所以可以用x 和s 估计μ和σ来计算u 值。
身高（X ）小于135(cm)的概率为:()()11135u U P x X P <==<88801.65Z -==00()0.20(0)0.3p Z Z p Z Z >=⇒<<=72.141.529.14413511-=-=-=s x x u ()()()()04272.072.172.1135111=-Φ=-=<=<==<u U P u U P x X P身高（X ）大于155(cm)的概率为：()()22155u U P x X P >==>98.141.529.14415522=-=-=s x x u ()()()()02385.097615.0198.1198.1155222=-=Φ-==>=>==>u U P u U P x X P 该地13岁正常女孩身高在135厘米以下者占正常女孩总人数的4.272%，身高在155厘米以上者占正常女孩总人数的2.385%。
3、确定等级评定的人数因为人的许多属性为正态分布，因此在教育生活中，许多情况下，用正态分布来计算各等级的人数。
例如：假定某年级有250人，我们要对这些人某种能力作一等级评定，假定这种能力为正态分布，且准备划分为五个等级：甲乙丙丁戊，问各个等级各有多少人？解：首先要把正态分布基线平均分一下。
因为这里要分为5个等级，因此各等级所包含区间为6除以5，等于1.2个标准差。
然后确定每一等级的取值范围。
通常我们从最高开始，最高等级为甲，应该从Z=3开始往下，则3减去1.2等于1.8，甲等就分布在这个区间1.8~3；往下顺延，得乙所在区间为0.6~1.8；丙再往下顺延1.2个标准差，得到丙的所在区间为-0.6~0.6；根据对称性，得丁的区间为-1.8~-0.6，戊的区间为-3~-1.8。
再次，要查正态表。
计算各个区间的面积，即人数比率。
要查两个定点之间的面积为多少。
（1）查Z=0到Z=1.8的面积，为0.46407，用0.5减去0.46407得到0.03593，即为甲的区间面积。
（2）查Z=0到Z=0.6的面积，为0.22575，这时用0.46407减去0.22575得0.22832，即为乙的区间面积。
（3）0.22575乘以2得0.45150，即为丙的区间面积。
（4）根据对称性得到丁的区间面积为0.22832，戊的区间面积为0.03593。
最后，将各个等级的比率乘以总人数，即得到各个等级的人数。
计算得甲等为9人，乙等为60人，丙等为112人，丁等为60人，戊等为9人。
答：甲乙丙丁戊五个等级依次有9、60、112、60、9人。
4、品质评定数量化一般在教育中可以综合各个老师对某一个学生的评定。
5、独立样本平均数差异的显著性检验 综合应用例1：某省在高考后，为了分析男、女考生对语文学习上的差异，随机抽取了各20名男、女考生的语文成绩，并且计算得到男生平均成绩=54.6，标准差=16.9，女生的平均成绩=59.7，标准差=10.4，试分析男、女考生语文高考成绩是否有显著差异？解：先进行方差齐性检验：1．提出假设2．计算检验的统计量3．统计决断查附表3，得F(19,19)0.05=2.16 F=2.64>F(19,19)0.05=2.16，p<0.05，即方差不齐性。
然后，进行平均数差异的显著性检验：1．提出假设2．计算检验的统计量3．确定检验形式 双侧检验4．统计决断 1.12<2.093，P>0.05所以，要保留零假设，即男、女考生语文高考成绩无显著差异。
例2：为了对某门课的教学方法进行改革，某大学对各方面情况相似的两个班进行教改实验，甲班32人，采用教师面授的教学方法，乙班25人，采用教师讲授要点，学生讨论的方法。
一学期后，用统一试卷对两个班学生进行测验，得到以下结果：甲班平均成绩=80.3，标准差=11.9，乙班平均成绩=86.7，标准差=10.2，试问两种教学方法的效果是否有显著性差异？解：先进行方差齐性检验：1．提出假设2．计算检验的统计量3．统计决断查附表3，得F(31,24)0.05=1.94 F=1.35<F(31,24)0.05=1.94，p>0.05，即方差齐性。
然后，进行平均数差异的显著性检验：1．提出假设2．计算检验的统计量3．确定检验形式 双侧检验 4．统计决断 当df=55时，t=2.105>2.009，P<0.05所以，要在0.05的显著性水平上零假设，即两种教学方法的效果有显著性差异。
例3为了研究一种新语文教学方法是否能提高学生语文学习成绩，采用了实验方法进行研究，选择了学习情况基本相同的两个班分别作为实验班与对照班，实验结果如下： 班别 人数 平均分 标准差 教学方法 实验班 42 80 10 新教学方法 对照班 44 75 11 传统教学方法试分析新语文教学方法是否比传统教学方法在提高学生学习成绩更有效？（双总体Z 体验） 原假设H0:μ1≤μ2，备择假设：μ1>μ2. n1=42,x1ˉ=80,ο1=10, n2=44,x2ˉ=75,ο2=11, 取显著性水平为0.05，得拒绝域为z≥z0.05=1.645, Z=(80-75)/√(10^2/42+11^2/44)=2.207>1.645, 拒绝原假设H0,即可以认为新方法显著有效。
例9.某市全体7岁男童体重平均数为21.61kg ，标准差为2.21kg ，某小学70个7岁男童体重的平均数为22.9kg 。
问该校7岁男童体重与全市是否一样？（ |Z|=4.88**＞2.58=Z0.01P ＜0.01，在0.01显著性水平上拒绝H0，接受H1，即该校7岁男童体重与全市有极其显著的差异。
一．总体平均数的显著性检验例１：某小学历届毕业生汉语拼音测验平均分数为66分，标准差为11.7。
现以同样的试题测验应届毕业生（假定应届与历届毕业生条件基本相同），并从中随机抽18份试卷，算得平均分为69分，问该校应届与历届毕业生汉语拼音测验成绩是否一样？♦ ⑴. 提出假设H0：μ＝μ0， H1：μ≠μ0 或 H0：μ＝66， H1：μ≠66♦ ⑵.选择检验统计量并计算统计量的值♦ 学生汉语拼音成绩可以假定是从正态总体中抽出的随机样本。
总体标准差已知，样本统计量的抽样分布服从正态，以Z 为检验统计量计算♦ ⑶.确定显著性水平和检验形式 显著性水平为α=0.05，双侧检验♦ ⑷.做出统计结论♦ 查表得Z α=1.96，而计算得到的Z=1.09 ♦ |Z|＜Ｚα，则概率P ＞0.05♦ 差异不显著,应在0.05显著性水平接受零假设♦ 结论:该校应届毕业生与历届毕业生汉语拼音测验成绩一致，没有显著差异。
n X Z σμ0-=187.116669-=09.1=例.某次数学竞赛，甲校6名男同学的成绩为69，73，84，91，86和76；13个女同学的得分为90，62，58，74，69，85，87，92，60，76，81，84，77。
问男女同学数学竞赛成绩是否有显著性差异？ （查表知:F(12,5)0.05=4.68＞1.297=F ∴保留H0,拒绝H1,方差齐性.）例.某区某年高考化学平均分数为72.4，标准差为12.6，该区某校28名学生此次考试的平均分数为74.7。
问该校此次考试成绩是否高于全区平均水平？(Z|=0.97＜1.65=Z0.05，P ＞0.05，保留H0，拒绝H1，即该校成绩并不高于全区平均水平。
例2：某市高中入学考试数学平均分数为68分，标准差为8.6。
其中某所中学参加此次考试的46名学生的平均分数为63。
过去的资料表明，该校数学成绩低于全市平均水平，问此次考试该校数学平均分数是否仍显著低于全市的平均分数？Ｚ＝-3.94例３：某区初三英语统一测验平均分数为65，该区某校20份试卷的平均分数为69.8，标准差为9.234。
问该校初三年级英语平均分数与全区是否一样？ t ＝2.266例４：某校上一届初一学生自学能力平均分数为38，这一届初一24个学生自学能力平均分数为42，标准差为 5.7，假定这一届初一学生的学习条件与上一届相同，试问这一届初一学生的自学能力是否高于上一届？t ＝3.365例5：某年高考某市数学平均分数为60，现从参加此次考试的文科学生中，随机抽取94份试卷，算得平均分数为58，标准差为9.2，问文科学生的数学成绩与全市考生是否相同？Ｚ＝-2.11例5.6 单侧检验（右）某一小麦品种的平均产量为5200㎏/公顷。