周转轮系与复合轮系的传动比
- 格式:pdf
- 大小:277.55 KB
- 文档页数:5



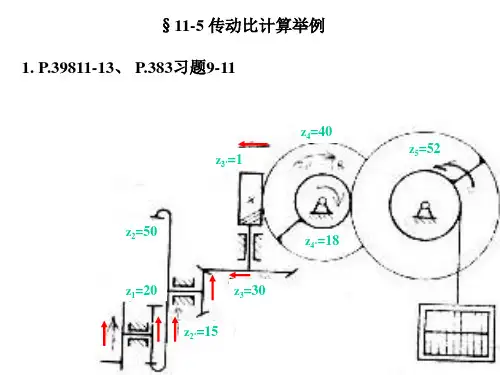

行星齿轮传动比分析与计算一、行星轮系传动比的计算 (一)行星轮系的分类若轮系中,至少有一个齿轮的几何轴线不固定,而绕其它齿轮的固定几何轴线回转,则称为行星轮系。
行星轮系的组成:行星轮、行星架(系杆)、太阳轮 (二)行星轮系传动比的计算以差动轮系为例(反转法) 转化机构(定轴轮系) T 的机构1234差动轮系:2个运动行星轮系:,对于行量轮系:H H W W W -=111W H H W W W -=222W H H W W W -=333W 0=-=H H H H W W W H W 13313113)1(Z Z W W W W W W i H HH H H⋅'-=--==03=W 1310Z Z W W W H H-=--11311+==Z Z W W i H H )(z f W W W W W W iH B H A H BH A HAB=--==0=B W∴∴例12.2:图示为一大传动比的减速器,Z 1=100,Z 2=101,Z 2'=100,Z 3=99。
求:输入件H 对输出件1的传动比i H1解:1,3中心轮;2,2'行星轮;H 行星架 给整个机构(-W H )绕OO 轴转动∵W 3=0∴∴若Z 1=99行星轮系传动比是计算出来的,而不是判断出来的。
AHHA H H A H AB i W WW W W i -=-=--=110HAB AH i i -=1213223113)1('⋅⋅⋅-=--=Z Z Z Z W W W W i H HHH H Hi Z Z Z Z W W W 13213210'=--H H i Z Z Z Z W W 13213211'=+-HH i i 131100100991011⨯⨯-=100001001009910111111=⨯⨯-==HH i i 1001-=H i(三)复合轮系传动比的计算复合轮系:轮系中既含有定轴轮系又含有行星轮系,或是包含由几个基本行星轮系的复合轮系。

机械设计基础公式汇总机械设计基础公式大家了解吗?以下是XX为大家整理好的机械设计基础公式汇总,一起来学习吧.零件:独立的制造单元构件:独立的运动单元体机构:用来传递运动和力的、有一个构件为机架的、用构件间能够相对运动的连接方式组成的构件系统机器:是执行机械运动的装置,用来变换或传递能量、物料、信息机械:机器和机构的总称机构运动简图:用简单的线条和符号来代表构件和运动副,并按一定比例确定各运动副的相对位置,这种表示机构中各构件间相对运动关系的简单图形称为机构运动简图运动副:由两个构件直接接触而组成的可动的连接运动副元素:把两构件上能够参加接触而构成的运动副表面运动副的自由度和约束数的关系f=6-s运动链:构件通过运动副的连接而构成的可相对运动系统高副:两构件通过点线接触而构成的运动副低副:两构件通过面接触而构成的运动副平面运动副的最大约束数为2,最小约束数为1;引入一个约束的运动副为高副,引入两个约束的运动副为平面低副平面自由度计算公式:F=3n-2PL-PH机构可动的条件:机构的自由度大于零机构具有确定运动的条件:机构的原动件的数目应等于机构的自由度数目虚约束:对机构不起限制作用的约束局部自由度:与输出机构运动无关的自由度复合铰链:两个以上构件同时在一处用转动副相连接速度瞬心:互作平面相对运动的两构件上瞬时速度相等的重合点。
若绝对速度为零,则该瞬心称为绝对瞬心相对速度瞬心与绝对速度瞬心的相同点:互作平面相对运动的两构件上瞬时相对速度为零的点;不同点:后者绝对速度为零,前者不是三心定理:三个彼此作平面运动的构件的三个瞬心必位于同一直线上机构的瞬心数:N=K(K-1)/2机械自锁:有些机械中,有些机械按其结构情况分析是可以运动的,但由于摩擦的存在却会出现无论如何增大驱动力也无法使其运动曲柄:作整周定轴回转的构件;连杆:作平面运动的构件;摇杆:作定轴摆动的构件;连架杆:与机架相联的构件;周转副:能作360?相对回转的运动副摆转副:只能作有限角度摆动的运动副。

《机械原理》第九章齿轮系及其设计——周转轮系传动比的计算2H 2H 1313反转原理:给整个周转轮系加上“-ωH ”,不改变轮系中各构件之间的相对运动,但原周转轮系将转化成为一定轴轮系,可按定轴轮系的公式计算转化后轮系的传动比。
转化后所得轮系称为原周转轮系的2K-H 型“转化轮系”-ωH1 ω1将轮系按-ωH 反转后,各构件的角速度的变化如下:2 ω23 ω3H ωH转化后: 系杆=>机架,周转轮系=>定轴轮系构件原角速度转化后的角速度2H 13ω1H =ω1-ωHω2H =ω2-ωH ω3H =ω3-ωHωH H =ωH -ωH =02H 13上式“-”说明在转化轮系中ω1H 与ω3H 方向相反。
H H H i3113ωω=2132z z z z -=13z z -=H Hωωωω--=312H 132H 131133i ωω=周转轮系中1、3之间的传动比2132z z z z -=H Hωωωω--=31H H H i3113ωω=13z z -=通用表达式:Hn Hm ωωωω--=m n m n =±转化轮系中由至各从动轮齿数的乘积转化轮系中由至各主动轮齿数的乘积H nH m H mniωω=1. 齿轮m 、n 和H 的轴线必须平行。
2.公式中的“±” 不能去掉,它不仅表明转化轮系中两个太阳轮m 、n 之间的转向关系,而且影响到ωm 、ωn 、ωH 的计算结果。
特别注意:通用表达式:Hn H m ωωωω--=m n m n =±转化轮系中由至各从动轮齿数的乘积转化轮系中由至各主动轮齿数的乘积H nH m H mniωω=特别注意:3. ωm 、ωn 、ωH 的已知值代入上式时必须带正负号,当假定其中某一已知值的转向为正时,则转向与之相同的取正,与之相反的取负。
4.i mn H ≠i mn ,i mn H 为转化轮系中m 、n 两轮的角速度之比,其大小和方向按定轴轮系传动比的计算来确定;i mn 为周转轮系中m 、n 两轮的绝对速度之比,其大小和方向按其转化轮系的公式推导出来。


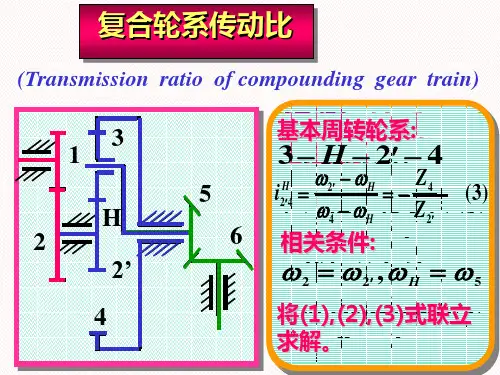

复合轮系传动比的计算方法
由前述可知,复合轮系是由基本周转轮系与定轴轮系组成,或者由儿个周转轮系组成。
对于这样的复杂轮系传动比的计算,既不能直接套用定轴轮系的公式,也不能直接套用周转轮系的公式。
例如对如图5-3(a)所示的复合轮系,如果给整个轮系一
个公共角速度(一。
),使其绕0-0轴线反转后,原来的周转轮系部分虽然转化成了定轴轮系,可原来的定轴轮系却因机架反转而变成了周转轮系,这样,整个轮系还是复合轮系。
所以解决复合轮系传动比可遵循以下步骤:地磅
(1)正确划分各革本轮系;
(2)分别列出各基本轮系传动比的方程式;
(3)找出各基本轮系之间的联系;
(4)将各基本轮系传动比方程式联立求解,即可求得复合轮系的传动比。
这里最为关键的一步是正确划分各基本轮系。
基本轮系是指单一的定轴轮系或单一的周转轮系。
在划分基本轮系时应先找出单一的周转轮系,根据周转轮系具有行星轮的特点,首先找出轴线位置不固定的行星轮,支持行星轮作公转的构件就是系杆H(值得注意的是,有时系杆不一定是杆状),而几何轴线与系杆H的回转轴线相
重合、且直接与行星轮相啮合的定轴齿轮就是中心轮。
这样的行星轮、系杆H和中心轮便组成一个基本周转轮系。
划分一个墓本的周转轮系后,还要判断是否还有其他行星轮被另一个系杆支承,每一个系杆对应一个基本周转轮系。
在逐一找出所有的周转轮系后,剩下的就是由定轴齿轮所组成的定轴轮系了。
本文来源于地磅转载请请注明。
内 容图8-8如图8-8b 所示的转化轮系中,齿轮1对齿轮3的传动比为H 11H 23H 13H 3H 123n n n z z i n n z z n -⨯===--⨯ 推广为周转轮系传动比一般式:H GK i = H G n= n G -n H=± 从G 到K 所有各对啮合齿轮中从动轮齿数的连乘积(8-2)H K n n K -n H 从G 到K 所有各对啮合齿轮中主动轮齿数的连乘积 (二)周转轮系传动比计算时的注意事项1.式(8-2)中,由于G 、H 、K 的转速直接相减,故该式只能用于G 、K 、H 的轴线互相平行的场合;2.式(8-2)齿数比前面一定有“+”号或“-”号。
至于应该取“+”号还是“-”号,与G 、K 两轮的真实转向无关,而取决于转化轮系中G 、K 两轮的转向关系,当转向相同时为“+”号,转向相反时为“-”号;3.若已知G n 、H n 、K n 中任意两个转速,则可求得第三个转速。
需注意的是,这里的各转速均为代数值,在计算时要带有相应的正、负号;4.由于行星轮系中有一个中心轮固定,如中心轮K 固定,则K n =0,代入式(8-2)得:H GK i =G H GH H10n n i n -=--,此时H GH GK 1i i =-,这就是行星轮系的传动比计算公式; 5.G H H GK K H n n i n n -=-GK i ≠,GK i =G Kn n ; 6.周转轮系中,轮的真实转向只能根据计算结果来确定,而不能画箭头来确定。
【例8-2】在如图8-9所示轮系中,已知1z =100,2z =101,2z '=100,3z =99,求传动比H1i 。
解 这是一个2、2'为行星轮,H 为行星架,1、3为中心轮的行星轮系。
1H 1H 23H 133H H 12101990100100n n n n z z i n n n z z --⨯===+='--⨯H 1H 131019911110010010000i i ⨯∴=-=-=⨯ 则H1i =10000,结果表明,若中心轮1转1圈,则行星架H 同方向转10000圈。