匀速圆周运动(含动画)

高一物理匀速圆周运动、向心力、向心加速度【本讲主要内容】匀速圆周运动、向心力、向心加速度本节主要学习匀速圆周运动的概念和描述圆周运动的各物理量及各量之间的关系。

【知识掌握】【知识点精析】质点沿圆周运动，如果在相等的时间里通过的圆弧长度相等，这种运动就叫做匀速圆周运动。

地球绕太阳的公转、地球上物体随地球自转的运动、电风扇正常运转时叶片上任一点的运动等均可以作为匀速圆周运动处理。

对匀速圆周运动的运动描述，主要通过引入周期T 、频率f （或转速n ）、线速度V 、角速度ω、向心加速度a 、向心力F 向 来进行。

①周期T ：做圆周运动的物体运动一周的时间。

如：地球公转周期T ＝365天，自转周期T ＝24h ，手表上的秒针周期为1min ，分针周期为1h ，时针周期为12h 等等。

②频率f ：单位时间内质点完成周期性运动的次数。

单位为“Hz ”。

T1f = ③线速度V ：定义：走过的弧长S 与相应时间t 的比值 公式：tSV =，单位：m/s 线速度是矢量，其方向沿圆周该点的切线方向， 如图中所示的V A 、V B④角速度ω：定义：半径转过的角度（以弧度作单位）与相应时间的比值，即有：tθ=ω，单位：rad/s 。

角速度也是一个矢量，但它的方向在中学里不讨论，质点做匀速圆周运动时，其角速度是恒定不变的。

⑤向心力F 向：物体做匀速圆周运动时，必定受到与速度方向不在同一条直线上的合力的作用，这个力总是沿着半径指向圆心，所以叫向心力。

向心力的方向总与物体的运动方向垂直，向心力的大小：F ＝22mR RV m ω= 向心力是效果力不是物体实际受到的力，而是由某个力充当或由物体所受的合力来充当，所以我们在研究问题时要找到向心力的来源。

⑥向心加速度a ：匀速圆周运动是一种曲线运动，线速度V 方向不断在变化，故，它是一种变速运动，每时每刻都具有加速度，但由于线速度大小不变，故这一加速度每时每刻都与速度垂直，指向圆心，如图中a A 、a B 所示，计算公式：22R RV a ω==，单位：“m/s 2”。

【知识梳理】一、匀速圆周运动：质点沿圆周运动，如果在相等的时间里通过的圆弧长度相等，这种运动就叫做匀速圆周运动。

（举例：电风扇转动时，其上各点所做的运动；地球和各个行星绕太阳的运动，都认为是匀速圆周运动。

）注意：匀速圆周运动是变速曲线运动，匀速圆周运动的轨迹是圆，是曲线运动，运动的速度方向时刻在变化，因而匀速圆周运动不是匀速运动，而是变速曲线。

“匀速”二字仅指在相等的时间里通过相等的弧长。

二、线速度：物体做匀速圆周运动时，通过的弧长S 与时间t 的比值就是线速度的大小。

用符号v 表示： tS v =1、线速度是物体做匀速圆周运动的瞬时速度。

2、线速度是矢量，它既有大小，也有方向．线速度的方向-----在圆周各点的切线方向上．3、匀速圆周运动的线速度不是恒定的，方向是时刻变化的三、角速度：圆周半径转过的角度ϕ与所用时间t 的比值。

用ω表示：公式：tϕω=单位：s rad /匀速圆周运动的快慢也可以用角速度来描述。

物体在圆周上运动得越快，连接运动物体和圆心的半径在同样的时间内转过的角度就越大。

对某一确定的匀速圆周运动而言，角速度ω是恒定。

注意：同一条链子或绳子上的线速度相同，同一个轮子上的角速度相同。

两交合轮边缘上的线速度大小相等四、周期和频率匀速圆周运动是一种周期性的运动．周期（T ）：做匀速圆周运动的物体运动一周所用的时间，单位是s 。

周期也是描述匀速圆周运动快慢的物理量，周期长运动慢，周期短运动快。

频率（f ）：物体ls 由完成匀速圆周运动的圈数，单位是赫兹，记作“Hz ”．周期和频率互为倒数．频率也是描述匀速圆周运动快慢的物理量，频率低运动慢，频率高运动快。

Tf 1=转速n ：做匀速圆周运动的物体单位时间内转过的圈数叫转速。

单位是r/s 、r/min 。

五、线速度、角速度、周期间的关系 1、定性关系三个物理量都是描述匀速圆周运动的快慢，匀速圆周运动得越快，线速度越大、角速度越大、周期越小． 2、定量关系设想物体沿半径为r 的圆周做匀速圆周运动，则在一个周期内转过的弧长为π2r ，转过的角度为π2，因此有T r v π2=，Tπω2= 比较可知：v ＝ωr ＝2πnr ＝2πfr 结论：由v ＝r ω知，当v 一定时，ω与r 成反比；当ω一定时，v 与r 成正比；当r 一定时，v 与ω成正比。

匀速圆周运动的数学模型
匀速圆周运动是物理学中的一种基本运动形式，其数学模型是描述一个点绕圆心做速度大小不变的圆周运动。

该模型在数学上通常使用极坐标系来描述，其中半径r和角度θ是两个重要的参数。

在这个模型中，点在圆周上运动，其速度v的大小恒定，方向始终垂直于半径。

因此，速度v可以表示为：v = w×r，其中w是角速度，表示单位时间内转过的角度。

同时，向心加速度a n表示点向圆心运动的趋势，其大小为a n = v²/r。

另外，向心力F表示点受到的使它做圆周运动的力，其大小为F = m ×v²/r，其中m是点的质量。

而离心力则表示点离开圆心运动的趋势，其大小为F = m×w²×r。

这些公式构成了匀速圆周运动的数学模型，可以用来描述和分析圆周运动的各种性质和规律。

例如，通过向心加速度和向心力公式可以推导出角速度和半径之间的关系，也可以用来计算物体在圆周运动中的轨迹和运动规律。

总之，匀速圆周运动的数学模型是一个重要的工具，可以用来描述和分析圆周运动的各种性质和规律，在物理学、工程学等领域有着广泛的应用。

高中物理教案：匀速圆周运动高一物理教案：匀速圆周运动一、教学任务分析匀速圆周运动是继直线运动后学习的第一个曲线运动，是对如何描述和研究比直线运动复杂的运动的拓展，是力与运动关系知识的进一步延伸，也是以后学习其他更复杂曲线运动（平抛运动、单摆的简谐振动等）的基础。

学习匀速圆周运动需要以匀速直线运动、牛顿运动定律等知识为基础。

从观察生活与实验中的现象入手，使学生知道物体做曲线运动的条件，归纳认识到匀速圆周运动是最基本、最简单的圆周运动，体会建立理想模型的科学研究方法。

通过设置情境，使学生感受圆周运动快慢不同的情况，认识到需要引入描述圆周运动快慢的物理量，再通过与匀速直线运动的类比和多媒体动画的辅助，学习线速度与角速度的概念。

通过小组讨论、实验探究、相互交流等方式，创设平台，让学生根据本节课所学的知识，对几个实际问题进行讨论分析，调动学生学习的情感，学会合作与交流，养成严谨务实的科学品质。

通过生活实例，认识圆周运动在生活中是普遍存在的，学习和研究圆周运动是非常必要和十分重要的，激发学习热情和兴趣。

二、教学目标1、知识与技能（1）知道物体做曲线运动的条件。

（2）知道圆周运动；理解匀速圆周运动。

（3）理解线速度和角速度。

（4）会在实际问题中计算线速度和角速度的大小并判断线速度的方向。

2、过程与方法（1）通过对匀速圆周运动概念的形成过程，认识建立理想模型的物理方法。

（2）通过学习匀速圆周运动的定义和线速度、角速度的定义，认识类比方法的运用。

3、态度、情感与价值观（1）从生活实例认识圆周运动的普遍性和研究圆周运动的必要性，激发学习兴趣和求知欲。

（2）通过共同探讨、相互交流的学习过程，懂得合作、交流对于学习的重要作用，在活动中乐于与人合作，尊重同学的见解，善于与人交流。

三、教学重点难点重点：（1）匀速圆周运动概念。

（2）用线速度、角速度描述圆周运动的快慢。

难点：理解线速度方向是圆弧上各点的切线方向。

四、教学资源1、器材：壁挂式钟，回力玩具小车，边缘带孔的旋转圆盘，玻璃板，建筑用黄沙，乒乓球，斜面，刻度尺，带有细绳连接的小球。

匀速圆周运动是物理学中经常遇到的一个问题，其中追及相遇问题更是一个经典之题。

在本文中，我们将深入探讨匀速圆周运动追及相遇问题，并求解其轨迹方程。

让我们简单了解一下匀速圆周运动的概念。

匀速圆周运动是指运动物体围绕一个固定圆周轨迹做匀速运动的情况。

这种运动的速度大小和方向在整个运动过程中保持不变，但速度方向始终朝向圆心。

在匀速圆周运动中，可以用一系列公式来描述物体的位置、速度和加速度。

接下来，我们将着重讨论匀速圆周运动追及相遇问题。

在这个问题中，通常会给出两个物体分别以匀速圆周运动的形式运动，并要求求解它们相遇时的位置和轨迹。

这是一个典型的相遇问题，常常需要使用参数方程进行求解。

假设有两个物体，分别以匀速圆周运动的形式沿着各自的圆周轨迹运动，我们需要求解它们相遇时的轨迹方程。

我们可以考虑建立一个参数方程来描述它们的位置。

设第一个物体的圆周运动轨迹方程为x1=f(t)，y1=g(t)，第二个物体的圆周运动轨迹方程为x2=h(t)，y2=k(t)。

我们可以通过参数方程来表示它们的位置：x1=f(t1)，y1=g(t1)x2=h(t2)，y2=k(t2)其中t1和t2分别表示两个物体运动的时间。

接下来，我们需要考虑它们相遇时的条件。

在匀速圆周运动中，两个物体相遇意味着它们在同一个位置、同时出现在同一个坐标点上。

我们可以将两个参数方程联立，得到它们相遇时的位置：f(t1)=h(t2)g(t1)=k(t2)通过联立这两个方程，我们可以求解出物体相遇时的时间t1和t2，然后将其代入参数方程，就可以求解出它们相遇时的位置。

进一步地，通过整理参数方程，我们可以得到相遇时的轨迹方程。

在实际求解过程中，常常需要通过数学工具来辅助完成。

比如利用数值方法、微积分方法等来求解参数方程。

还需要考虑到特殊情况和限制条件，比如两个物体的初始位置、运动方向、速度大小等。

这些都将对最终的结果产生影响。

匀速圆周运动追及相遇问题求解轨迹方程是一个需要深入思考和分析的问题。

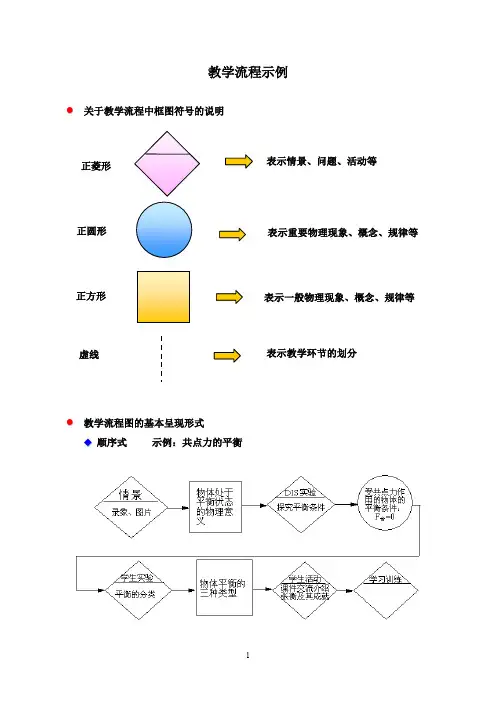
教学流程示例
● 关于教学流程中框图符号的说明
● 教学流程图的基本呈现形式
◆ 顺序式 示例：共点力的平衡
表示情景、问题、活动等
表示重要物理现象、概念、规律等
表示一般物理现象、概念、规律等
表示教学环节的划分
正菱形
正圆形 正方形
虚线
◆并列式 1 示例：匀速圆周运动（4个主要教学环节）
◆并列式 2 示例：匀速圆周运动（设计方案2，分3个主要教学环节）
●设计思路示例：牛顿第二定律——设计方案之一（3个主要教学环节）
示例：牛顿第二定律——设计方案之二（初稿）
示例：牛顿第二定律——设计方案之二（初稿）
注意：红色线条的箭头表达不正确（其中左上第一个双箭头应删去）。