体育成绩频数分布直方表
- 格式:docx
- 大小:37.02 KB
- 文档页数:2

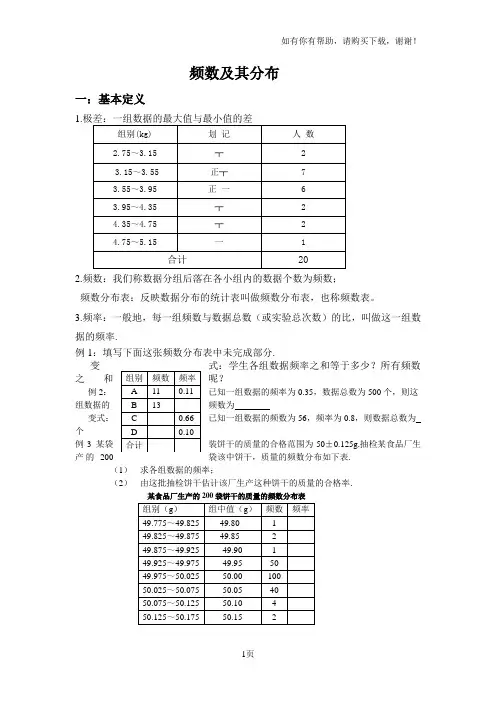
频数及其分布一:基本定义1.2.频数:我们称数据分组后落在各小组内的数据个数为频数;频数分布表:反映数据分布的统计表叫做频数分布表,也称频数表。
3.频率:一般地,每一组频数与数据总数(或实验总次数)的比,叫做这一组数据的频率.例1:填写下面这张频数分布表中未完成部分.变式:学生各组数据频率之和等于多少?所有频数Array之和呢?例2:已知一组数据的频率为0.35,数据总数为500个,则这组数据的频数为变式:已知一组数据的频数为56,频率为0.8,则数据总数为个例3 某袋装饼干的质量的合格范围为50±0.125g.抽检某食品厂生产的200袋该中饼干,质量的频数分布如下表.(1)求各组数据的频率;(2)由这批抽检饼干估计该厂生产这种饼干的质量的合格率.某食品厂生产的200袋饼干的质量的频数分布表二:频数分布直方图一:用来表示频数分布的基本统计图叫做频数分布直方图,简称直方图(Mstogram).在统计数据时,按照频数分布表,在平面直角坐标系中,横轴标出每个组的端点,纵轴表示频数,每个矩形的高代表对应的频数,我们称这样的统计图为频数分布直方图,如图12-5所示,直方图中各矩形之间没有空隙.【说明】在画频数分布直方图时,首先要列出频数分布表.在分组时要注意:(1)组数适当;(2)组距相等.同时,分组要遵循三个原则:(1)不空,即该组必须有数据;(2)不重,即一个数据只能在一个组中;(3)不漏,即不能漏掉某一个数据.思考:频数分布直方图与条形统计图的区别?(1)条形统计图中,横轴上的数据是孤立的,是一个具体的数据。
而直方图中,横轴上的数据是连续的,是一个范围。
(2)条形统计图中,各个数据之间是相对独立的,各个条形之间是有空隙的。
而在直方图中,各长方形对应的是一个范围,由于每两个相邻范围之间不重叠、不遗漏,因此在直方图中,长方形之间没有空隙。
例.请观察图,并回答下面的问题:(1)被检测的矿泉水总数有多少种?(2)被检测矿泉水的最低pH为多少?(3)组界为6.9~7.3这一组的频数、频率分别是多少(每一组包括前一个边界值,不包括后一个边界值)?(4)根据我国2001年公布的生活饮用水卫生规范,饮用水的pH应在6.5—8.5的范围内.被检测的矿泉水不符合这一标准的有多少种?占总数的百分之几?思考:图中的频数分布直方图的每一组的边界值为多少?A.10.5 B.14.5 C.12.5 D.8.5三:拆线统计图及其特点折线统计图是用一个单位长度表示一定的数量,根据数量的多少描出各点,然后用线段顺次把各点连接起来.它既可以表示出项目的具体数量,又能清楚地反映事物变化的情况.折线统计图的特点:易于显示数据的变化趋势,如图12-4所示.例.超速行驶是交通事故频发的主要原因之一.交警部门统计某日7:00~9:00经过高速公路某测速点的汽车的速度,得到如下频数分布折线图(1)这一天7:00~9:00经过该观察点的车辆总数是多少(2)数据分组的组距是多少(3)若该路段汽车限速为110km/h,请问超速行驶的汽车有多少辆?占总数的百分之几(4)简单描述折线的波动情况,并说明它所表示的实际意义四:扇形统计图用圆代表总体,圆中的各个扇形分别代表总体中的不同部分,扇形的大小反映部分占总体的百分比的大小,这样的统计图叫做扇形统计图.扇形统计图主要是反映具体问题中的部分与整体的数量关系.扇形统计图的各部分占总体的百分比之和为100%或1,如图12-2所示.例1 如图12-6所示的是扇形统计图,求扇形B占总体的百分比.例每人捐书的册数/册 5 10 15 20相应的捐书人数/人17 22 4 2(1)该班的学生共多少名?(2)全班一共捐了多少册书?(3)若该班所捐图书按图12-7所示的比例分,则送给山区学校的书比送给本市兄弟学校的书多多少册?总结:条形统计图显示每组中的具体数据;扇形图显示部分在总体中占的百分比;频数直方图显示数据的分布情况;折线图显示数据的变化趋势综合练习:1 为了了解小学生的体能情况,抽取了某小学同年级学生进行跳绳测试,将所得数据整理后,画出如图12-11所示的频率分布直方图,已知图中从左到右前三个小组的频率分别是0.1,0.3,0.4,第一小组的频数为5,则第四小组的频率是,参加这次测试的学生有人.2某班同学参加环保知识竞赛,将学生的成绩(得分取整数)进行整理后分成五组,绘制成频率分布直方图,如图12-12所示,图中从左到右各小组的长方形的高的比是1∶3∶6∶4∶2,最右边一组的频数是6,结合直方图提供的信息,解答下列问题.。


2021 级男生体测立定跳远成绩区间统计表在学校体育锻炼活动中,体测始终是学生们关注的焦点之一。
其中,立定跳远作为体能的一项重要指标,不仅考察了学生的爆发力和肌肉协调能力,更是对学生整体身体素质的一次检验。
针对2021级男生的立定跳远成绩,我们进行了统计和分析,希望通过这份统计表,帮助大家更全面地了解和掌握同龄人的体能水平。
我们针对2021级男生的立定跳远成绩进行了大范围的调查和数据收集,分析了成绩的分布情况。
根据我们的统计数据,我们将立定跳远成绩分为以下几个区间:1. 0-1米:在这个区间的同学们需要更加努力去提高自己的爆发力和跳跃能力。
可以通过针对性的训练来提升自己的立定跳远成绩,比如增加腿部力量训练和灵活性训练。
2. 1-1.5米:这个区间的同学们已经有了一定的基础,但仍然需要更多的练习和技巧的提高。
可以通过学习正确的起跳姿势和着陆姿势,来提高自己的成绩。
3. 1.5-2米:属于中上水平的同学们,他们的爆发力和技巧已经比较过硬,但仍有提升空间。
可以通过增加跳远训练的次数和强度,以及加强核心肌裙的锻炼来继续提高成绩。
4. 2米以上:这个区间的同学们已经达到了较高水平,需要更精细的技术和力量训练来提高自己的成绩,同时也可以通过观摩和学习优秀的跳远选手,来提高自己的比赛心态和技巧。
通过对这些区间的统计和分析,我们可以看到2021级男生的整体立定跳远水平还有待进一步提高。
作为一项重要的体能指标,立定跳远不仅仅是身体素质的体现,更是对同学们意志品质和毅力的考验。
在今后的学习和训练中,我们希望同学们可以更加重视体育锻炼,提高自己的身体素质,从而更好地应对学习和生活中的各种挑战。
通过对2021级男生立定跳远成绩的统计和分析,我们可以清晰地看到不同成绩区间的同学们的体能表现,也为我们提供了分析班级体能水平的参考数据。
希望同学们能够在未来的体测中,通过努力训练和提高,提升自己的立定跳远成绩,更好地锻炼自己的身体素质。

体育分数换算表一、足球比赛1. 全场比分:- 主队胜:主队X - 客队X- 客队胜:主队X - 客队X- 平局:主队X - 客队X2. 半场比分:- 主队领先:主队X - 客队X- 客队领先:主队X - 客队X- 平局:主队X - 客队X3. 进球数换算:- 一球:1-0、0-1- 两球:2-0、0-2、1-1- 三球:3-0、0-3、2-1、1-2- 四球:4-0、0-4、3-1、1-3、2-2- 五球:5-0、0-5、4-1、1-4、3-2、2-3- 六球:6-0、0-6、5-1、1-5、4-2、2-4、3-3- 七球:7-0、0-7、6-1、1-6、5-2、2-5、4-3、3-4- 八球:8-0、0-8、7-1、1-7、6-2、2-6、5-3、3-5、4-4二、篮球比赛1. 全场比分:- 主队胜:主队X - 客队X- 客队胜:主队X - 客队X2. 四节比分:- 第一节:主队X - 客队X- 第二节:主队X - 客队X- 第三节:主队X - 客队X- 第四节:主队X - 客队X3. 得分换算:- 一分:1-0、0-1- 两分:2-0、0-2、1-1- 三分:3-0、0-3、2-1、1-2- 四分:4-0、0-4、3-1、1-3、2-2- 五分:5-0、0-5、4-1、1-4、3-2、2-3- 六分:6-0、0-6、5-1、1-5、4-2、2-4、3-3- 七分:7-0、0-7、6-1、1-6、5-2、2-5、4-3、3-4- 八分:8-0、0-8、7-1、1-7、6-2、2-6、5-3、3-5、4-4三、网球比赛1. 比分:- 完胜:X-0- 胜:X-X- 平局:X-X2. 相差球数:- 一分:1-0、0-1- 两分:2-0、0-2、1-1- 三分:3-0、0-3、2-1、1-2- 四分:4-0、0-4、3-1、1-3、2-2- 五分:5-0、0-5、4-1、1-4、3-2、2-3- 六分:6-0、0-6、5-1、1-5、4-2、2-4、3-3- 七分:7-0、0-7、6-1、1-6、5-2、2-5、4-3、3-4- 八分:8-0、0-8、7-1、1-7、6-2、2-6、5-3、3-5、4-4四、乒乓球比赛1. 比分:- 完胜:X-0- 胜:X-X- 平局:X-X2. 相差球数:- 一分:1-0、0-1- 两分:2-0、0-2、1-1- 三分:3-0、0-3、2-1、1-2- 四分:4-0、0-4、3-1、1-3、2-2- 五分:5-0、0-5、4-1、1-4、3-2、2-3- 六分:6-0、0-6、5-1、1-5、4-2、2-4、3-3- 七分:7-0、0-7、6-1、1-6、5-2、2-5、4-3、3-4- 八分:8-0、0-8、7-1、1-7、6-2、2-6、5-3、3-5、4-4五、游泳比赛1. 成绩:- 第一名:X秒- 第二名:X秒- 第三名:X秒- 其他名次:X秒2. 相差时间:- 一秒:X秒- 两秒:X秒- 三秒:X秒- 四秒:X秒- 五秒:X秒- 六秒:X秒- 七秒:X秒- 八秒:X秒六、田径比赛1. 成绩:- 第一名:X秒/米- 第二名:X秒/米- 第三名:X秒/米- 其他名次:X秒/米2. 相差时间/距离:- 一秒/米:X秒/米- 两秒/米:X秒/米- 三秒/米:X秒/米- 四秒/米:X秒/米- 五秒/米:X秒/米- 六秒/米:X秒/米- 七秒/米:X秒/米- 八秒/米:X秒/米以上是一些常见体育比赛的分数换算表,希望对大家有所帮助。

体考篮球足球排球评分表及评分办法为保障考生健康,经论证,决定取消所有考试项目中有身体直接接触的对抗性考试内容(涉及足球、篮球、排球专项技术项目考试内容中的“比赛”部分),保留的考试内容得分按比例扩大,保持专项总分满分40分不变。
其余考试项目和内容不变请考生参照下列考试项目评分标准(考试场内最高得分28分,剩余分值按比例计算后计入总得分)篮球专项考试办法及评分标准表1一、考试项目及分值1、往返运球投篮(14分)2、一分钟投篮(14分)2二、考试办法及评分细则(一)往返运球投篮1、考试办法由球场右侧边线中点开始,面向球篮用右手运球上篮,同时开始计时;球投中篮后,仍用右手运至左侧边线中点;然后折转换左手运球上篮;投中篮后,还用左手运球回到原起点,同样重复上述运球投篮一次,再回到原起点时停表。
每人做两次,计其中一次最好成绩。
要求:连续运球,不得远推运球上篮;必须投中篮后,才能继续运球,投不中要继续再投,直到投中,投篮的手(左手或右手投)不加限制。
2、评分标准按其计时成绩评分,满分为14分,详见评分表。
(二)一分钟投篮1、考试办法以篮圈垂直投影中心为圆心,以该点至罚球线的距离为半径,划一圆弧。
开始时,考生在弧线处作跳投,开始计时:投篮后自己抢篮板球,再运至弧线外再跳投,连续做一分钟(女生投篮可作原地投篮,也可以跳投)。
每人做一次,按成绩查所得分。
要求:男生必须双脚离地起跳投篮,否则不算投篮;投篮时不得踏线或过线,不得带球跑,违者投中无效。
2、评分标准按其1分钟内投中次数计分,满分为14分,详见评分表。
足球专项考试办法及评分标准表 1一、考试项目及分值 1、定位球传准(14分) 2、20米运球过杆射门(14分)2二、考试办法及评分细则(一)定位球传准1、场地设置(1)以O为圆心,以2.5米和3.5米为半径,画两个同心圆。
圆心处放置一标志盘,作为传准的目标。
(2)男子场地:距圆心25米外划一条5米长传球限制线(见图1)。

学生体育成绩统计表.齐村镇郭村小学 2009学年度第二学期期末学生体育成绩统计2008- 1班一年级成姓成姓张兴王董晓董文孟顾国王业高禇博胡董文董文卓忆林子张张瑶杨董高宋均黄振董文杜新悦宋姿若分以上为优秀,三-六年注:以年级为单位统计,一二年级90 分以上为优秀。
80级.齐村镇郭村小学 2008学年度第二学期期末学生体育成绩统计2007- 1班一年级成姓成姓潘禇孔李杜俊王董董文董文宋子禇衍彭显禇衍徐顾顾林梦顾丽孙经张林淑婷分以上为优秀,三-六年90注:以年级为单位统计,一二年级分以上为优秀。
80级.齐村镇郭村小学 2008学年度第二学期期末学生体育成绩统计2007- 2班一年级成成姓姓孔任董玉王董徐董思张馨王张董云李兴蔡顾张文孔马熙董犇蔡刘春张淇王甜林李萍分以上为优秀,三-六年90注:以年级为单位统计,一二年级分以上为优秀。
80级.齐村镇郭村小学学年度第二学期期末学生体育成绩统计-20082007班二年级1成姓姓成杨家王广陈忠房雅董文房华杨桦王诗杜雨黄浩薛兆何文杜昆侯前杜以禇庆孔祥孔祥房潇杨桦林兴王越郑董冬冬义注:以年级为单位统计,一二年级90分以上为优秀,三-六优分以上为优秀。
80年级.齐村镇郭村小学学年度第二学期期末学生体育成绩统计2007-2008班二年级1成姓姓成董师刘董文秀,三-六90注:以年级为单位统计,一二年级分以上为优优分以上为优秀。
80年级.齐村镇郭村小学 2008学年度第二学期期末学生体育成绩统计2007- 1班三年级成成姓姓卓文薛董文王培宋媛张张泽杨董文杨董文刘董秀邵颜士张宋任亚董王绥房增刘晋张育董薛李董富黄董王启超禇庆豪薛强分以上为优秀,三-六年注:以年级为单位统计,一二年级90 分以上为优秀。
80级.齐村镇郭村小学 2008学年度第二学期期末学生体育成绩统计2007-班三年级1成姓姓成邵珠张董宋宏李智董董建侯雨冯兆董董文王分以上为优秀,三-六年注:以年级为单位统计,一二年级90 分以上为优秀。

频数分布直方图典例剖析例1.某校为了了解九年级学生体育测试成绩情况,抽查了一部分学生的体育测试成绩,甲、乙、丙三位同学将抽查出的学生的测试成绩按A 、B 、C 、D 四个等级进行统计,并将统计结果绘制成如下统计图(如图1),其中测试成绩在90~100分为A 级,75~89分为B 级, 60~74分为C 级,60分以下为D 级.甲同学计算出成绩为C 的频率是0.2,乙同学计算出成绩为A 、B 、C 的频率之和为0.96,丙同学计算出成绩为A 的频数与成绩为B 的频数之比为7:12.结合统计图回答下列问题: (1)这次抽查了多少人?(2)所抽查学生体育测试成绩的中位数在哪个等级内?(3)若该校九年级学生共有500人,请你估计这次体育测试成绩为A 级和B 级的学生共有多少人?分析:(1)由于甲同学计算出成绩为C 的频率是0.2,再结合条形统计图提供的信息C 等级的人为10,然后利用公式=频数总数频率,即可算出总人数; (2)算出A ,B ,C ,D 四个等级的人数后,再确定频数是第25,26个在第几小组即可; (3)先算出A 级和B 级的频率和,然后再乘以500即可.解:(1)由题意知:C 级人数为10人,所以10500.2=(人), 所以这次抽查了50人.(2)D 级的频率是1-0.96=0.04,各等级的人数分别是:D 级人数是0.04×50=2,B级图1人数是12(50102)24712⨯--=+,A 级人数是50-2-10-24=14,因此,所抽查学生体育测试成绩的中位数在B 等级内. (3)142450038050+⨯=(人),所以次体育测试成绩为A 级和B 级的学生共有380人. 点评:本题考查同学们对频数、频率以及频数分布直方图的理解和掌握,同时也考查根据数据处理问题的能力.如何求一组数据的频数、频率的方法以及动手操作能力.例2.某校数学兴趣小组成员小华对本班上期期末考试数学成绩(成绩取整数,满分为100分)作了统计分析,绘制成如下频数、频率分布表和频数分布直方图(图2). 请你根据图表提供的信息,解答下列问题:(1)频数、频率分布表中a = ,b = ; (2)补全频数分布直方图;(3)数学老师准备从不低于90分的学生中选1人介绍学习经验, 那么取得了93分的小华被选上的概率是多少?分析: 能从统计图表中获取正确的信息并熟记频数和频率的计算方法、正确理解横轴、综轴的意义是解决本题的关键.解:(1)由题意易得:a =8,b =0.08. (2)如图3分组 49.5~59.5 59.5~69.569.5~79.5 79.5~89.5 89.5~100.5 合计 频数 2 a 20 16 4 50频率0.04 0.160.400.32b 1) 图21(3)小华被选上的概率是:4点评:题考查有关频数分布直方图的有关知识.频数分布直方图可以直观地看出各种量的大小,通常以补全频数分布直方图、找出图中相关信息并能进行简单计算为考查重点考查频数频率及其运用,考查阅读统计图表的能力.试一试吧!1.为了增强环境保护意识,6月5日“世界环境日”当天,在环保局工作人员指导下,若干名“环保小卫士”组成的“控制噪声污染”课题学习研究小组,抽样调查了全市40个噪声测量点在某时刻的噪声声级(单位:dB),将调查的数据进行处理(设所测数据是正整数),得频数分布表如下:根据表中提供的信息解答下列问题:(1)频数分布表中的a =________,b=________,c =_________;(2)补充完整频数分布直方图;(3)如果全市共有200个测量点,那么在这一时刻噪声声级小于75dB的测量点约有多少个?2.某县七年级有15000名学生参加安全应急预案知识竞赛活动,为了了解本次知识竞赛的成绩分布情况,从中抽取了400名学生的得分(得分取正整数,满分100分)进行统计:频 率 分 布 表请你根据不完整的频率分布表. 解答下列问题: (1)补全频率分布表; (2)补全频数分布直方图;(3)若将得分转化为等级,规定得分低于59.5 分评为“D ”,59.5~69.5分评为“C ”,69.5~89.5 分评为“B ”,89.5~100.5分评为“A ”,这次15000 名学生中约有多少人评为“D ”?如果随机抽取一名 参赛学生的成绩等级,则这名学生的成绩评为“A ”、 “B ”、“C ”、“D ”哪一个等级的可能性大?请说明理由.图4成绩(分)图5参考答案1.分析:(1)补全频数分布表;(2)补全频数分布直方图;(3)根据样本中噪声声级小于75dB的测量点的频率是0.3;现有200个测量点,则0.3×200=60得出在这一时噪声声级小于75dB的测量点约有60个.解:(1)a=8,b=12,c=0.3.(2)略;(3)算出样本中噪声声级小于75dB的测量点的频率是0.3,0.3×200=60,∴在这一时噪声声级小于75dB的测量点约有60个.2.解:(1)已知49.5—59.5分数段的学生人数及学生总数,可求出这一分数段学生的频率为0.05,再根据频率之和为1,各范围频数之和等于总数可求出69.5—79.5分数段的人数为:80人,求出79.5—89.5分数段的频率为0.31.(2)略(3)用样本的频率估计总体频率,所以15000名学生中评为“D”的约有:15000×0.05=750人.算出A,B,C,D,各等级的频率,用频率近似估计概率,判断可能性大小即可.。

体育综合分一分一段表摘要:一、前言二、体育综合分的定义和意义三、体育综合分一分一段表的制定背景四、体育综合分一分一段表的具体内容1.分数分配2.评分标准3.考试科目及权重五、体育综合分一分一段表的实际应用六、对我国体育教育的影响七、结论正文:一、前言随着我国体育事业的蓬勃发展,体育教育逐渐受到重视。
为了更好地衡量学生的体育水平,体育综合分一分一段表应运而生。
本文将对这一评分体系进行详细解读。
二、体育综合分的定义和意义体育综合分是指学生在体育课程中的各项表现和成绩的综合评价。
它旨在全面反映学生的体育素质,激发学生参与体育活动的积极性,培养学生的终身体育意识。
三、体育综合分一分一段表的制定背景体育综合分一分一段表是在我国教育部门指导下,由体育教育专家和教师共同制定的。
它的出现,有助于统一体育评分标准,减轻教师评分负担,提高评分公正性。
四、体育综合分一分一段表的具体内容1.分数分配:体育综合分一分一段表将学生的体育成绩分为四个等级,分别为优秀、良好、及格和不及格,分别对应100 分、80 分、60 分和0 分。
2.评分标准:评分标准包括课堂表现、体育竞赛成绩、体育锻炼情况等多个方面。
学生需在各项指标中达到一定要求,方可获得相应分数。
3.考试科目及权重:体育综合分一分一段表涵盖了田径、球类、武术等多个体育项目。
各项体育项目的权重不同,以体现项目的重要性和特点。
五、体育综合分一分一段表的实际应用体育综合分一分一段表已在我国各地广泛应用于初中、高中的体育教育评价中。
通过这一体系,学校可以更好地了解学生的体育状况,为提高体育教育质量提供依据。
六、对我国体育教育的影响体育综合分一分一段表的实施,有助于提高我国体育教育的科学性和规范性,推动体育教育的发展。
同时,它还能激发学生的体育兴趣,培养学生全面发展。
七、结论体育综合分一分一段表是一种全面、科学、合理的体育评价体系,有助于提高我国体育教育的质量。
体育成绩频数分布直方表
体育成绩频数分布直方表是一种统计图表,用于显示不同成绩区间的频数分布。
它由一个X轴和一个Y轴组成,X轴表示
成绩区间,Y轴表示该区间内的频数。
下面是一个示例的体育成绩频数分布直方表:
成绩区间频数
60-69 3
70-79 6
80-89 7
90-100 4
这个直方表显示了某个班级学生在体育考试中的成绩分布情况。
例如,在60-69分数段内有3个学生,70-79分数段内有6个
学生,以此类推。
通过直方表,我们可以更直观地了解成绩分布情况,比如哪个分数段的学生人数最多或最少,平均成绩是多少等。
2021 级男生体测立定跳远成绩区间统计表标题:探索2021级男生体测立定跳远成绩区间统计表一、引言在学校里,体育课是学生们锻炼身体、增强体魄的重要途径。
而学校的体测项目也是学生们在体育课上展现自己身体素质的重要机会之一。
其中,立定跳远作为一项基本的体能测试项目,能够全面考察学生的爆发力和协调性。
本文将根据2021级男生体测立定跳远成绩区间统计表,对该项测试的结果进行深入分析,并就成绩的分布、相关因素等方面展开讨论。
二、成绩区间统计让我们来看一下2021级男生体测立定跳远成绩的整体分布情况。
根据提供的数据,我们将成绩分为不同区间进行统计。
在该统计表中,成绩区间分为90分以上、80-89分、70-79分、60-69分、60分以下五个区间。
通过对数据的分析,我们发现90分以上和60分以下两个区间的学生人数相对较少,而80-89分和70-79分的学生人数较为均衡,60-69分的学生人数较多。
这一分布情况引发了我们对成绩背后的原因进行思考。
三、成绩分布背后的因素在分析成绩区间统计表时,我们不得不思考背后的因素。
立定跳远成绩受到个体身体素质、训练程度、技巧等多方面的影响。
身体素质较好的学生在进行立定跳远测试时往往能够取得较好的成绩。
另外,定期的体能训练和专业指导也能够有效提高学生的成绩。
还有一些学生可能在测试时遇到了心理压力或技术不足的问题,从而影响了成绩的表现。
我们建议学校应该加强对学生的体能训练,提供更多的关于立定跳远技巧和方法的指导,并且对于那些成绩不理想的学生进行心理辅导和个性化训练,以帮助他们提高成绩。
四、对立定跳远成绩的个人观点和理解就我个人而言,我对立定跳远成绩有着自己独特的认识。
我认为立定跳远不仅是一项体能测试项目,更是一种身体协调和爆发力的体现。
每个人都有不同的身体素质和潜力,因此在进行立定跳远测试时,并不要求每个学生都能达到完美的成绩。
重要的是,学生们在练习和测试过程中能够全身心地投入,不断提高自己的技巧和爆发力,从而在整个过程中获得快乐和成就感。
频数及其分布一:基本定义1.极差:一组数据的最大值与最小值的差组别(kg) 2.75~3.15 3.15~3.55 3.55~3.95 3.95~4.35 4.35~4.75 4.75~5.15 划 记 ┬ 正┬ 正 一 ┬ ┬ 一 人 数 2 7 6 2 2 1合计202.频数:我们称数据分组后落在各小组内的数据个数为频数; 频数分布表:反映数据分布的统计表叫做频数分布表,也称频数表。
3.频率:一般地,每一组频数与数据总数(或实验总次数)的比,叫做这一组数 据的频率.例 1:填写下面这张频数分布表中未完成部分.组别 A B C D 合计频数 11 13频率 0.11 0.66 0.10变式:学生各组数据频率之和等于多少?所有频数之和呢?例 2:已知一组数据的频率为 0.35,数据总数为 500 个,则这组数据的频数为 变式:已知一组数据的频数为 56,频率为 0.8,则数据总数为 个例 3 某袋装饼干的质量的合格范围为 50±0.125g.抽检某食品厂生产的 200 袋该中饼干,质 量的频数分布如下表. (1) 求各组数据的频率; (2) 由这批抽检饼干估计该厂生产这种饼干的质量的合格率.某食品厂生产的 200 袋饼干的质量的频数分布表组别(g) 49.775~49.825 49.825~49.875 49.875~49.925 49.925~49.975 49.975~50.025 50.025~50.075 50.075~50.125 50.125~50.175组中值(g) 49.80 49.85 49.90 49.95 50.00 50.05 50.10 50.15频数 1 2 1 50 100 40 4 2频率二:频数分布直方图一:用来表示频数分布的基本统计图叫做频数分布直方图,简称直方图(Mstogram). 在统计数据时,按照频数分布表,在平面直角坐标系中,横轴标出每个组的端点,纵轴 表示频数,每个矩形的高代表对应的频数,我们称这样的统计图为频数分布直方图,如图 12-5 所示,直方图中各矩形之间没有空隙.【说明】 在画频数分布直方图时,首先要列出频数分布表.在分组时要注意: (1)组 数适当; (2)组距相等. 同时,分组要遵循三个原则: (1)不空,即该组必须有数据; (2)不重,即一个数据只 能在一个组中; (3)不漏,即不能漏掉某一个数据.思考:频数分布直方图与条形统计图的区别?(1)条形统计图中,横轴上的数据是孤立的,是一个具体的数据。
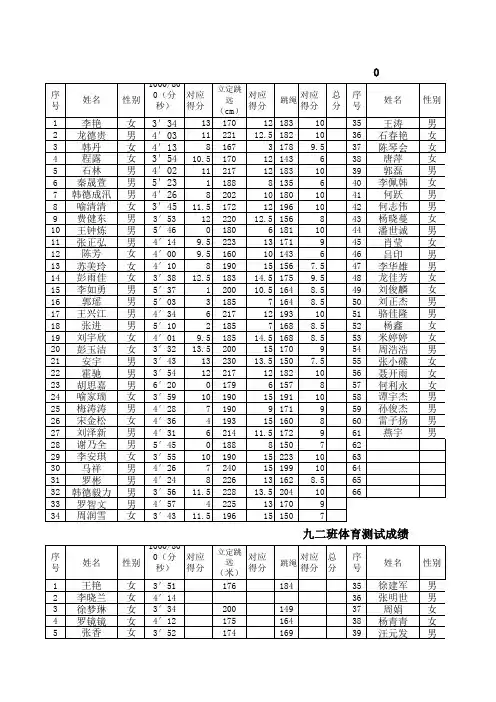
小学六年级体育成绩情况统计表.
(1)根据上表绘制统计图.
(2)90分以上(含90分)是优秀,哪个班的优秀学生多?多多少?
(3)你还能提出什么教学问题?
(4)对于不及格的学生(60分以下)你有什么好的建议给他们?
【分析】(1)根据统计表中的学生的体育成绩的统计表,画出统计图即可;
(2)六年级一班90分以上(含90分)的学生有24+7人,六年级二班90分以上(含90分)的学生有10+30人,由此得出哪个班的优秀学生多,多的人数;
(3)两个班100分的人数中,哪个班的多;
(4)和成绩优秀的学生结对子,做到互帮互学;加强基础知识的训练.
(1)如图,
(2)四年级一班90分以上(含90分)的学生有:24+7=31(人),
四年级二班90分以上(含90分)的学生有:10+30=40(人),
因为40>31,
所以四年级二班的优秀学生多,
多的人数:40-31=9(人);
(3)两个班100分的人数中,哪个班的多;
六年级一班100分的人有:7人,
六年级二班100分的人有10,
所以六年级二班100分的人数多;
(4)和成绩优秀的学生结对子,做到互帮互学;加强基础知识的训练.。
体育成绩频数分布直方表
体育是一项重要的活动,对于学生的身心健康发展起着重要的作用。
而体育成绩的评估和分析对于学生的学习和发展也具有重要意义。
为
了更好地了解学生的体育成绩分布情况,我们可以使用频数分布直方
表进行分析。
频数分布直方表是一种统计图表,用于展示一组数据的频数分布情况。
它将数据按照一定的区间进行分组,并统计每个区间内的数据个数,然后以直方图的形式展示出来。
通过观察直方图,我们可以直观
地了解数据的分布情况,进而进行更深入的分析。
假设我们要分析一所学校的学生体育成绩情况,我们可以将成绩分
为若干个区间,比如60-69分、70-79分、80-89分、90-100分等。
然后,我们统计每个区间内的学生人数,并将结果绘制成频数分布直方图。
下面是一个示例的频数分布直方表:
区间频数
60-69分 10
70-79分 20
80-89分 30
90-100分 15
根据上述直方表,我们可以得出以下结论:
1. 大部分学生的体育成绩集中在80-89分区间,共有30名学生,占总人数的最大比例。
2. 70-79分区间的学生人数次之,共有20名学生。
3. 60-69分区间的学生人数最少,只有10名学生。
4. 90-100分区间的学生人数为15名,属于较高水平。
通过频数分布直方表,我们可以直观地了解到学生体育成绩的整体分布情况。
同时,我们还可以进一步分析不同区间的学生人数比例,以及不同区间的学生所占比例。
这些数据可以帮助学校和教师更好地了解学生的体育水平,制定相应的教学和训练计划,以提高学生的体育成绩。
除了了解整体分布情况,频数分布直方表还可以帮助我们发现一些特殊情况。
比如,如果某个区间的学生人数明显偏多或偏少,我们可以进一步分析原因,并采取相应的措施。
另外,我们还可以比较不同年级、不同性别、不同班级的体育成绩分布情况,以了解不同群体的体育水平差异。
总之,频数分布直方表是一种简单而有效的统计工具,可以帮助我们了解学生的体育成绩分布情况。
通过分析直方表,我们可以得出一些结论,并采取相应的措施来提高学生的体育水平。
希望学校和教师能够充分利用这一工具,为学生的体育发展提供更好的支持和指导。