河北省衡水市高三数学第三次联考试题 理

2019-2020学年河北省衡水市第三中学高三数学理联考试题含解析一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有是一个符合题目要求的1. 设等比数列的前项和为，若，，则公比A．1 B.2 C．4 D．8参考答案：C2. 设a，b是两条不同直线，α，β是两个不同平面，下列四个命题中正确的是（）A．若a，b与α所成的角相等，则a∥bB．若a∥α，b∥β，α∥β，则a∥bC．若a⊥α，b⊥β，α⊥β，则a⊥bD．若a?α，b?β，a∥b，则α∥β参考答案：C【考点】命题的真假判断与应用；空间中直线与平面之间的位置关系．【专题】综合题；空间位置关系与距离．【分析】对四个选项中的命题依据相关的立体几何知识逐一判断即可【解答】解：对于选项A，将一个圆锥放到平面上，则它的每条母线与平面所成的角都是相等的，故“若a，b与α所成的角相等，则a∥b“错；对于选项B，若a∥α，b∥β，α∥β，则a与b位置关系可能是平行，相交或异面，故B错；对于选项C，若a⊥α，b⊥β，α⊥β，则a⊥b是正确的，两个平面垂直时，与它们垂直的两个方向一定是垂直的；对于选项D，由面面平行的定理知，一个面中两条相交线分别平行于另一个平面中的两条线才能得出面面平行，故D错．故选C．【点评】本题以立体几何中线面位置关系为题面考查了命题真假的判断，熟练掌握空间中点线面的位置关系是解答的关键3. 点为不等式组所表示的平面区域上的动点，则最小值为（）A． B． C． D．参考答案：D如图所示，不等式组所表示的平面区域为图中阴影部分．由可得，故．的几何意义为直线的斜率，故当点与点重合时直线的斜率的最小，此时．4. 等差数列的前n项和为，且，则（）(A)8 (B)9 (C)1 0 (D) 11参考答案：B略5. 已知正六棱柱的底面边长和侧棱长均为，其三视图中的俯视图如图所示，则其左视图的面积是（）（A）（B）（C）（D）参考答案：A正六棱柱的左视图是一个以AB长为宽，高为2的矩形，所以左视图的面积为，选A.6. 已知、均为锐角，若的（）A．充分而不必要条件 B．必要而不充分条件C．充要条件 D．既不充分也不必要条件参考答案：答案：C7. 已知一个几何体是由上下两部分构成的组合体，其三视图如下，若图中圆的半径为，等腰三角形的腰长为，则该几何体的表面积是（）A. B. C. D.参考答案：A略8. 设α、β、γ为平面，m、n、l为直线，则m⊥β的一个充分条件是（）A．α⊥β，α∩β=l，m⊥l B．α∩γ=m，α⊥γ，β⊥γC．α⊥γ，β⊥γ，m⊥αD．n⊥α，n⊥β，m⊥α参考答案：D【考点】LW：直线与平面垂直的判定．【分析】根据面面垂直的判定定理可知选项A是否正确，根据平面α与平面β的位置关系进行判定可知选项B和C是否正确，根据垂直于同一直线的两平面平行，以及与两平行平面中一个垂直则垂直于另一个平面，可知选项D正确．【解答】解：α⊥β，α∩β=l，m⊥l，根据面面垂直的判定定理可知，缺少条件m?α，故不正确；α∩γ=m，α⊥γ，β⊥γ，而α与β可能平行，也可能相交，则m与β不一定垂直，故不正确；α⊥γ，β⊥γ，m⊥α，而α与β可能平行，也可能相交，则m与β不一定垂直，故不正确；n⊥α，n⊥β，?α∥β，而m⊥α，则m⊥β，故正确故选D9. 已知抛物线和所围成的封闭曲线如图所示，给定点，若在此封闭曲线上恰有三对不同的点，满足每一对点关于点对称，则实数的取值范围是（）（A）（B）（C）（D）参考答案：D考点：函数与方程10. 若复数z满足z（1﹣i）=|1﹣i|+i，则z的实部为（）A．B．﹣1 C．1 D．参考答案：A【考点】复数代数形式的混合运算．【分析】z（1﹣i）=|1﹣i|+i，化为z=，再利用复数的运算法则、实部的定义即可得出．【解答】解：∵z（1﹣i）=|1﹣i|+i，∴z===+i，∴z的实部为．故选：A．二、填空题:本大题共7小题,每小题4分,共28分11. 函数的定义域是，单调递减区间是________________________．参考答案：（-∞，0）∪（2，+∞）， (2，＋∞)12. 如图，椭圆C：，与两条平行直线：，：分别交于四点A，B，C，D，且四边形ABCD的面积为，则直线AD的斜率为________．参考答案：【分析】设D的坐标，四边形的面积等于2个三角形的面积之和可得D的横坐标，代入椭圆方程求出D的纵坐标，进而求出直线AD的斜率．【详解】解：设，由椭圆的对称性，可得，由题意，所以，代入椭圆中可得，即，所以，所以直线AD的方程为，故答案为：【点睛】本题考查了直线与椭圆的知识，待定系数法是解决本题很好的途径，准确运算是解题的关键.13. 过点且与相切的直线方程为．参考答案：14. 在中，,则的面积等于_________.参考答案：15. 若的展开式中各项系数之和为64，则展开式的常数项为．参考答案：﹣540【考点】DB：二项式系数的性质．【分析】依据二项式系数和为2n，列出方程求出n，利用二项展开式的通项公式求出常数项．【解答】解：若的展开式中各项系数之和为2n=64，解得n=6，则展开式的常数项为=﹣540，故答案为：﹣540．16. 文：已知等差数列的首项为3，公差为4，则该数列的前项和________．参考答案：17. 已知中AC=4，AB=2，若G为的重心，则。

数学（理科）一、选择题：本大题共12 小题，每题 5 分，在每题给出的四个选项中，只有一项为哪一项符合题目要求的。

1. 已知复数z 知足，则复数z 在复平面内对应的点所在象限为A. 第一象限B. 第二象限C. 第三象限D. 第四象限【答案】【分析】D复数知足，∴，则复数在复平面内对应的点在第四象限，应选 D.2. 已知全集，会合为A. B. C. D.【答案】 B【分析】【剖析】化简会合A、 B，利用补集与交集运算即可获得结果【详解】因为.，所以或.所以.应选 B.【点睛】此题考察会合的交并补运算，考察不等式的解法，属于基础题3. 若命题p为：为.A.B.C.D.【答案】 C【分析】【剖析】依据全称命题的否认为特称命题即可获得结果.【详解】依据的构成方法得，为. 应选C.【点睛】全称命题的一般形式是：，，其否认为. 存在性命题的一般形式是，，其否认为.4. 朱世杰是历史上最伟大的数学家之一，他所著的《四元玉鉴》卷中“如像招数”五问中有以下问题：“今有官司差夫一千九百八十四人筑堤，只云初日差六十四人，次日转多八人，每人日支米三升”．其粗心为“官府陆续差遣1984 人前去修建堤坝，第一天派出64 人，从次日开始每日派出的人数比前一天多8 人，修建堤坝的每人每日赋发大米 3 升”，在该问题中的 1984 人所有差遣到位需要的天数为A. 14B. 16C. 18D. 20【答案】 B【分析】【剖析】利用等差数列的通项公式及前n 项和公式即可获得结果.【详解】依据题意设每日派出的人数构成数列，剖析可得数列是首项. 公差为8 的等差数列，设1984 人所有差遣到位需要n 天，则. 解得 n=16. 应选 B.【点睛】此题考察等差数列的通项公式、前n 项和公式的应用，考察推理能力与计算能力，属于基础题 .5.以下图，分别以正方形 ABCD两邻边 AB、AD为直径向正方形内做两个半圆，交于点 O．若向正方形内扔掷一颗质地平均的小球 ( 小球落到每点的可能性均同样 ) ，则该球落在暗影部分的概率为A. B.C. D.【答案】 C【分析】【剖析】计算正方形与暗影的面积，依据面积概型公式获得答案.【详解】法一：设正方形的边长为 2. 则这两个半圆的并集所在地区的面积为，所以该质点落入这两个半圆的并集所在区城内的概率为. 故选C.法二：设正方形的边长为域的面积为2. 过O作 OF垂直于 AB，OE垂直于 AD.则这两个半圆的并集所在区，所以该质点落入这两个半圆的并集所在地区的概率为，应选 C.【点睛】解决几何概型问题常有种类有：长度型、角度型、面积型、体积型，求与面积有关的几何概型问题关鍵是计算问题的总面积以及事件的面积；几何概型问题还有以下几点简单造成失分，在备考时要高度关注：（ 1）不可以正确判断事件是古典概型仍是几何概型致使错误；（2）基本领件对应的地区测度掌握禁止致使错误；（ 3）利用几何概型的概率公式时 , 忽略考证事件能否等可能性致使错误 .6. 已知定义在R 上的函数知足：(1) ；(2)为奇函数；(3) 当时，图象连续且恒成立，则的大小关系正确的为A. B.C. D.【答案】 C【分析】【剖析】先明确函数的周期性、奇偶性与单一性，把问题转变为在上利用单一性比较大小的问题 .【详解】因为，所以函数是周期为 2 的周期函数 . 又由为奇函数，所以有，所以函数为奇函数，又由当时，图象连续，且恒成立，得函数在区间（-1，1）内单一递加，而.所以.应选 C.【点睛】此题综合考察了函数的图象与性质，波及到周期性、单一性、对称性，利用单一性比较大小，解题重点怎样把自变量转变到同一个单一区间上，属于中档题.7.一正方体被两平面截去部分后剩下几何体的三视图以下图，则该几何体的表面积为A. B.C. D.【答案】 B【分析】【剖析】作出几何体的直观图，察看截去几何体的结构特色，代入数据计算．【详解】由题中条件及三视图可知该几何体是由棱长为 2 的正方体被平面截去了两个三棱锥后剩下的几何体，以下图，该几何体的表面三角形有，，，，，，由对称性只要计算，的大小，因为，. 所以该几何体的表面积为.应选 B.【点睛】由三视图画出直观图的步骤和思虑方法：1、第一看俯视图，依据俯视图画出几何体的直观图； 2、察看正视图和侧视图找到几何体前、后、左、右的高度；3、画出整体，然后再依据三视图进行调整.8.以下图，边长为 2 的正方形 ABCD中， E 为 BC边中点，点 P 在对角线 BD上运动，过点 P 作 AE的垂线，垂足为F，当最小时，A. B. C. D.【答案】 D【分析】【剖析】由图易知向量所成角为钝角 , 联合题意可知当最小时，即为向量在向量方向上的投影最小，确立点P 的地点，从而获得结果.【详解】依题，由图易知向量所成角为钝角，所以，所以当最小时，即为向量在向量方向上的投影最小，数形联合易知点 P 在点 D时,最小（以下图），在三角形 ADE中，由等面积可知，所以，从而. 所以.应选 D.【点睛】此题考察了平面向量数目积的定义及运算，向量的线性运算，考察了数形联合的思想，考察了计算能力，属于中档题.9. 已知双曲线的左、右焦点分别为，左、右极点分别为A、B，过点的直线与双曲线 C的右支交于P 点，且的外接圆面积为A. B. C. D.【答案】 C【分析】【剖析】由可知：，从而易得，利用正弦定理可得外接圆的半径，获得的外接圆面积 .【详解】因为，所以，由已知得 A（-1.0 ），B（1，0），（2，0），且，所以，在三角形 ABP中，由正弦定理得 . ，所以三角形APB的外接圆的面积为. 应选 C.【点睛】此题考察了双曲线的简单几何性质，平面向量数目积的几何意义，正弦定理，考察了推理论证能力，计算能力，属于中档题.10.利用一半径为 4cm的圆形纸片 ( 圆心为 O)制作一个正四棱锥．方法以下：(1)以 O为圆心制作一个小的圆；(2)在小的圆内制作一内接正方形ABCD；(3) 以正方形ABCD的各边向外作等腰三角形，使等腰三角形的极点落在大圆上( 如图 ) ；(4)将正方形 ABCD作为正四棱锥的底，四个等腰三角形作为正四棱锥的侧面折起，使四个等腰三角形的极点重合，问：要使所制作的正四棱锥体积最大，则小圆的半径为A. B. C. D.【答案】 C【分析】【剖析】设小圆的半径为，连 OD. OH.OH与 AD交于点 M，表示正四棱锥的体积，利用导数研究函数的最值，即可获得结果.【详解】设小圆的半径为，连 OD.OH. OH与 AD交于点 M，则. 因为大圆半径R=4，所以，在正四棱锥中，以下图，.所以记，所以令，易知，时，取最大值，所以小圆半径为时，V最大。

2020届河北省衡水中学高三下学期全国第三次联考数学（理）试卷★祝考试顺利★ (解析版)一、选择题：在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知集合{}20M x x x =+>,(){}ln 10N x x =->,则（ ）A. M N ⊇B. M N ⊆C. ()1,M N ⋂=+∞D. ()2,M N ⋃=+∞【答案】A 【解析】解出集合M 、N ,利用集合的包含关系和交集、并集的定义可判断各选项的正误.【详解】{}()()20,10,M x x x =+>=-∞-⋃+∞,(){}{}()ln 10112,N x x x x =->=->=+∞,所以,M N ⊇,()2,M N =+∞,()(),10,M N =-∞-+∞.故选：A.2. 已知复数2(2)z i =+,则z 的虚部为（ ） A. 3 B. 3iC. 4D. 4i【答案】C 【解析】根据复数的代数形式的乘法法则计算即可得解； 【详解】解：2(2)34z i i =+=+,所以z 的虚部为4. 故选：C .3. 以下统计表和分布图取自《清华大学2019年毕业生就业质量报告》.国内1583 55.8％94 3.8％290 19.9％1967 29.0％出国（境）699 24.6％137 5.5％199 13.7％1035 15.3％就业490 17.3％2224 89.2％943 64.8％3657 53.9％签三方就154 5.4％1656 66.4％864 59.4％2674 39.4％业灵活就业336 11.8％568 22.8％79 5.4％983 14.5％未就业64 2.3％39 1.6％23 1.6％126 1.9％合计2836 100.0％2494 100.0％1455 100.0％6785 100.0％清华大学2019年毕业生去向分布情况统计表清华大学2019年毕业生签三方就业单位所在省（区、市）分布图则下列选项错误．．的是（）.A. 清华大学2019年毕业生中,大多数本科生选择继续深造,大多数硕士生选择就业B. 清华大学2019年毕业生中,硕士生的就业率比本科生高C. 清华大学2019年签三方就业的毕业生中,本科生的就业城市比硕士生的就业城市分散D. 清华大学2019年签三方就业毕业生中,留北京人数超过一半【答案】D【解析】选项A在表中找出本科生选择继续深造达80.4％,硕士生选择就业达89.2％,则判断选项A正确；选项B在表中找出硕士生的就业率达89.2％,本科生的就业率达17.3％,则判断选项B正确；。

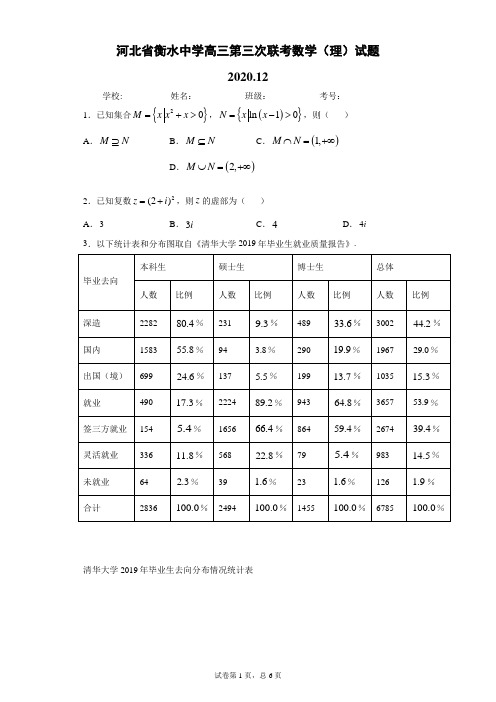
河北省衡水中学高三第三次联考数学（理）试题2020.12学校:___________姓名：___________班级：___________考号：___________ 1．已知集合{}20M x x x =+>，(){}ln 10N x x =->，则（ ）A ．M N ⊇B ．M N ⊆C ．()1,M N ⋂=+∞D ．()2,M N ⋃=+∞2．已知复数2(2)z i =+，则z 的虚部为（ ） A ．3B ．3iC ．4D ．4i3．以下统计表和分布图取自《清华大学2019年毕业生就业质量报告》.清华大学2019年毕业生去向分布情况统计表清华大学2019年毕业生签三方就业单位所在省（区、市）分布图则下列选项错误．．的是（ ）.A ．清华大学2019年毕业生中，大多数本科生选择继续深造，大多数硕士生选择就业B ．清华大学2019年毕业生中，硕士生的就业率比本科生高C ．清华大学2019年签三方就业的毕业生中，本科生的就业城市比硕士生的就业城市分散D ．清华大学2019年签三方就业的毕业生中，留北京人数超过一半 4．若圆22(2)(1)5x y -+-=关于直线10(0,0)ax by a b +-=>>对称，则21a b+的最小值为( ) A ．4B．C ．9D．5．要使得满足约束条件42y x y x x y ⎧⎪-⎨⎪+⎩，的变量,x y 表示的平面区域为正方形，则可增加的一个约束条件为（ ） A ．4x y +≤B ．4x y +C ．6x y +D ．6x y +6．若{}n a 是公比为(0)q q ≠的等比数列，记n S 为{}n a 的前n 项和，则下列说法正确的是（ ）A ．若{}n a 是递增数列，则10,0a q <<B ．若{}n a 是递减数列，则10,01a q ><<C ．若0q >，则4652S S S +>D ．若1n nb a =，则{}n b 是等比数列7．为了得到函数()sin g x x =的图象，需将函数()sin 6f x x π⎛⎫=- ⎪⎝⎭的图象（ ） A ．向左平移6π个单位长度 B ．向右平移6π个单位长度 C ．向左平移56π个单位长度 D ．向右平移56π个单位长度 8．设()f x 是定义在R 上的奇函数，且当0x 时，1()sin 23f x x x =-.若2tan 5a f π⎛⎫= ⎪⎝⎭，32log cos 5b f π⎛⎫= ⎪⎝⎭，2cos 5c f π⎛⎫= ⎪⎝⎭大小关系为（ ）A ．a b c <<B ．b c a <<C ．b a c <<D ．c b a <<9．如图是由等边△AIE 和等边△KGC 构成的六角星，图中的B ，D ，F ，H ，J ，L 均为三等分点，两个等边三角形的中心均为O .若OA mOC nOJ =+，则mn=（ ）A ．12B ．23C ．34D ．110．区块链是数据存储､传输､加密算法等计算机技术的新型应用模式，图论是区块链技术的一个主要的数学模型,在一张图中有若干点，有的点与点之间有边相连，有的没有边相连，边可以是直线段，也可以是曲线段，我们规定图中无重边(即两个点之间最多只有一条边)且无孤立点(即对于每个点，都至少存在另外一个点与之相连)，现有A ，B ，C ，D 四个点，若图中恰有3条边，则满足上述条件的图的个数为（ ）A ．4B ．8C ．12D ．1611．地球的公转轨道可以看作是以太阳为一个焦点的椭圆，根据开普勒行星运动第二定律，可知太阳和地球的连线在相等的时间内扫过相等的面积，某同学结合物理和地理知识得到以下结论：①地球到太阳的距离取得最小值和最大值时，地球分别位于图中A 点和B 点；②已知地球公转轨道的长半轴长约为149600000千米，短半轴长约为149580000千米，则该椭圆的离心率约为1.因此该椭圆近似于圆形：③已知我国每逢春分（3月21日前后）和秋分（9月23日前后），地球会分别运行至图中C 点和D 点，则由此可知我国每年的夏半年（春分至秋分）比冬半年（当年秋分至次年春分）要少几天.以上结论正确的是（ ）A ．①B ．①②C ．②③D ．①③12．正方体1111ABCD A B C D -的棱长为2，在A ，B ，C ，D ，1C ，1D 这六个顶点中.选择两个点与1A ，1B 构成正三棱锥P ，在剩下的四个顶点中选择两个点与1A ，1B 构成正三棱锥Q ，M 表示P 与Q 的公共部分，则M 的体积为（ ）A ．13B ．4C ．23D ．113．62x x ⎛⎫- ⎪⎝⎭的展开式中2x 的系数为_________.(用数字作答) 14．记n S 为正项等差数列{}n a 的前n 项和，若13471,a a a S =⋅=，则n S =_________. 15．若抛物线()220y px p =>的焦点到双曲线22222y x p -=的一个焦点的距离为p 的值为_________.16．已知函数()()21xf x kx k e x =+--，若()0f x <的解集中恰有三个整数，则实数k 的取值范围为______.17．在锐角△ABC 中，内角A ，B ，C 所对的边分别为a ，b ，c ，若cos cos c B b C =，BC 边上的高12AD =，4sin 5BAC ∠=.（1）求BC 的长：（2）过点A 作AE AB ⊥，垂足为A ，且CAE ∠为锐角，AE =sin ACE ∠. 18．如图，在三棱锥A BCD -中，AB ⊥平面BCD ，E 为棱AC 上的一点，且BE ⊥平面ACD .（1）证明：BC CD ⊥；（2）设1BC CD ==.BC 与平面ACD 所成的角为45︒.求二面角B AD C --的大小. 19．2020年1月10日，中国工程院院士黄旭华和中国科学院院士曾庆存荣获2019年度国家最高科学技术奖.曾庆存院士是国际数值天气预报奠基人之一，他的算法是世界数值天气预报核心技术的基础，在气象预报中，过往的统计数据至关重要，如图是根据甲地过去50年的气象记录所绘制的每年高温天数(若某天气温达到35 ℃及以上，则称之为高温天)的频率分布直方图.若某年的高温天达到15天及以上，则称该年为高温年，假设每年是否为高温年相互独立，以这50年中每年高温天数的频率作为今后每年是否为高温年的概率.（1）求今后4年中，甲地至少有3年为高温年的概率.（2）某同学在位于甲地的大学里勤工俭学，成为了校内奶茶店(消费区在户外)的店长，为了减少高温年带来的损失，该同学现在有两种方案选择：方案一：不购买遮阳伞，一旦某年为高温年，则预计当年的收入会减少6000元；方案二：购买一些遮阳伞，费用为5000元，可使用4年，一旦某年为高温年，则预计当年的收入会增加1000元.以4年为期，试分析该同学是否应该购买遮阳伞？20．已知椭圆22221(0)x y a b a b+=>>的左､右焦点分别为12,F F ，且12F F =过椭圆的右焦点2F 作长轴的垂线与椭圆，在第一象限交于点P ，且满足127PF PF =.（1）求椭圆的标准方程；（2）若矩形ABCD 的四条边均与椭圆相切，求该矩形面积的取值范围.21．已知函数()2,()ln x f x e x g x x x =+-=+，若1x 是函数()f x 的零点，2x 是函数()g x 的零点.（1）比较1x 与2x 的大小； （2）证明：()()210f x g x +<.22．在直角坐标系xOy 中，曲线C 的参数方程为222x t y t t =-⎧⎨=-⎩(t 为参数)，曲线C 上异于原点的两点M ，N 所对应的参数分别为12,t t .以坐标原点O 为极点，x 轴的正半轴为极轴建立极坐标系，曲线D 的极坐标方程为2sin a ρθ=. （1）当121,3t t ==时，直线MN 平分曲线D ，求a 的值；（2）当1a =时，若122t t +=直线MN 被曲线D 求直线MN 的方程.23．已知函数()|1|2|3|,()|1|f x x x g x a x =++-=-. （1）求()8f x 的解集；（2）当[1,3]x ∈-时，()()f x g x 恒成立，求实数a 的取值范围.参考答案1．A 【解析】 【分析】解出集合M 、N ，利用集合的包含关系和交集、并集的定义可判断各选项的正误. 【详解】{}()()20,10,M x x x =+>=-∞-⋃+∞，(){}{}()ln 10112,N x x x x =->=->=+∞,所以，M N ⊇，()2,M N =+∞，()(),10,M N =-∞-+∞.故选：A. 【点睛】本题考查集合包含关系的判断，同时也考查了集合的交集和并集运算、二次不等式与对数不等式的求解，考查计算能力，属于基础题. 2．C 【解析】 【分析】根据复数的代数形式的乘法法则计算即可得解； 【详解】解：2(2)34z i i =+=+，所以z 的虚部为4. 故选：C . 【点睛】本题考查复数代数形式的乘法，复数的相关概念，属于基础题. 3．D 【解析】 【分析】选项A 在表中找出本科生选择继续深造达80.4％，硕士生选择就业达89.2％，则判断选项A 正确；选项B 在表中找出硕士生的就业率达89.2％，本科生的就业率达17.3％，则判断选项B 正确；选项C 在表中分析出本科生的就业城市主要分散在北京、广东、上海，硕士生的就业城市主要集中在北京，则判断选项C 正确；选项D 在表中分析出留北京人数仅博士生达到了51.2%，本科生与硕士生都没有达到一半，判断选项D 错误即可. 【详解】选项A ：清华大学2019年毕业生中，本科生选择继续深造达80.4％，硕士生选择就业达89.2％，故选项A 正确；选项B ：清华大学2019年毕业生中，硕士生的就业率达89.2％，本科生的就业率达17.3％，故选项B 正确；选项C ：清华大学2019年签三方就业的毕业生中，本科生的就业城市主要分散在北京、广东、上海，硕士生的就业城市主要集中在北京，故选项C 正确；选项D ：清华大学2019年签三方就业的毕业生中，留北京人数仅博士生达到了51.2%，本科生与硕士生都没有达到一半，故选项D 错误. 故选：D. 【点睛】本题考查统计表与分布图，是基础题. 4．C 【解析】 【分析】利用“乘1法”与基本不等式的性质即可得出． 【详解】解：由题意可知，圆心(2,1)在直线10ax by ， 则21a b +=， 又因为0a >，0b >， 所以212122()(2)5549b aa b a b a b a b+=++=+++=， 当且仅当22b a a b =且21a b +=即13a =，13b =时取等号，此时取得最小值9． 故选：C ． 【点睛】本题考查了“乘1法”与基本不等式的性质，属于基础题． 5．C 【解析】 【分析】设新增加的约束条件为x y c +，根据正方形两组对边的距离相等，得到方程解得即可； 【详解】解：根据正方形的性质可设新增加的约束条件为x y c +，两组对边的距离相等，故d ===，所以6c =或2c =-(舍去). 如图所示故选:C . 【点睛】本题考查二元不等式组表示的平面区域，两平行线间的距离公式的应用，属于基础题. 6．D 【解析】 【分析】选项A ，B ，C 中，分别取特殊数列满足条件，但得不出相应的结论，说明选项A ，B ，C 都是错误的，选项D 中，利用等比数列的定义可以证明结论正确. 【详解】A 选项中，12,3a q ==，满足{}n a 单调递增，故A 错误；B 选项中，11,2a q =-=，满足{}n a 单调递减，故B 错误；C 选项中，若111,2a q ==，则656554,a a S S S S <-<-，故C 错误； D 选项中，111(0)n n n n b a q b a q++==≠，所以{}n b 是等比数列.故D 正确. 故选：D. 【点睛】本题考查了等比数列的定义，考查了数列的单调性，考查了特值排除法，属于基础题. 7．D 【解析】 【分析】先将函数()sin 6f x x π⎛⎫=-⎪⎝⎭用诱导公式变形为5()sin 6f x x π⎛⎫=+⎪⎝⎭，结合三角函数图象的平移变换规律，得到答案. 【详解】5()sin sin sin sin 6666f x x x x x πππππ⎛⎫⎛⎫⎛⎫⎛⎫=-=--=-+=+⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭, 由5()sin 6f x x π⎛⎫=+ ⎪⎝⎭的图象得到函数()sin g x x =的图象， 向右56π个单位长度即可. 故选：D. 【点睛】本题主要考查三角函数图象的平移变换，要注意三角函数图象的平移变换是在“x ”的基础上进行的，解决此类题还需熟记口诀“左加右减”. 8．B 【解析】 【分析】根据题意当0x 时2()1cos 203f x x '=->，()f x 是定义在R 上的奇函数,则()f x 在定义域上单调递增，2tan tan 154ππ>=，20cos 15π<<，32log cos 05π<，由函数的单调性可得出答案. 【详解】由题意知由当0x 时,2()1cos 203f x x '=->，所以()f x 在[)0+，∞上单调递增，且()00f =又()f x 是定义在R 上的奇函数，所以()f x 在(]0-∞，上单调递增. 所以()f x 在定义域上单调递增. 又因为28tantan tan 15204πππ=>=，20cos 15π<<，所以32log cos 05π<， 由()f x 在定义域上单调递增，则3222tan cos log cos 555f f f πππ⎛⎫⎛⎫⎛⎫>> ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭所以b c a <<. 故选：B . 【点睛】本题考查函数的奇偶性和单调性的综合应用，利用单调性比较大小，考查三角函数值大小的的比较，对数值大小的比较，属于中档题 9．B 【解析】 【分析】以点O 为坐标原点，OD 为x 轴，OA 为y 轴建立平面直角坐标系，设等边三角形的边长为,,A C J 的坐标，由向量的运算可求得,m n 的值，可得答案.【详解】由平行四边形法则，22()23OA OB OJ OC OJ OJ OC OJ =+=++=+，所以2m =，3n =，所以23m n = 以点O 为坐标原点，OD 为x 轴，OA 为y 轴建立如图所示的平面直角坐标系，设等边三角形的边长为3=，由B ，D ，F ，H ，J ，L 均为三等分点， 则2323OA =⨯=,23OJ =所以())0,2,03，，A J C⎛⎫- ⎪ ⎪⎝⎭()0,2OA =,()3,1OC =,3OJ ⎛⎫=- ⎪ ⎪⎝⎭)OA mOC nOJ mn m ⎛⎫⎫=+=+=- ⎪⎪⎪⎪⎝⎭⎭所以032m -=⎪=⎩，解得32n m =⎧⎨=⎩ 所以23m n = 故选：B . 【点睛】本题考查向量的线性运算，建立直角坐标系是解决本题的关键，也是解决的向量问题的常用方法，属于中档题.【解析】 【分析】先求出A ，B ，C ，D 四点最可确定6条边，再由题得到满足条件的图的个数. 【详解】 如图，A ，B ，C ，D 四点最可确定AB ，AC ，AD ，BC ，BD ，CD 共6条边. 由题意知恰有3条边且无孤立点，所以满足条件的图有36416C -=(个).故选：D. 【点睛】本题主要考查组合的应用，意在考查学生对这些知识的理解掌握水平. 11．A 【解析】 【分析】根据椭圆的几何性质可判断命题①的正误；利用椭圆的离心率公式可判断命题②的正误；根据开普勒行星运动第二定律可判断命题③的正误.综合可得出结论. 【详解】由椭圆的几何性质可知，当地球到太阳的距离取得最小值和最大值时，地球分别位于图中A 点和B 点，命题①正确；1495800001149600000b a =≈，则该椭圆的离心率0c e a ===≈，命题②错误；根据开普勒行星运动第二定律，地球从D 点到C 点运行的速度较快，因此经历的时间较短，因此夏半年比冬半年多几天，命题③错误. 故选：A.本题考查与椭圆性质相关的命题真假的判断，涉及椭圆焦半径、离心率的应用，考查推理能力，属于中等题. 12．A 【解析】 【分析】根据题意，设平面11A BC 与平面11AB D 的交线为EF ，则M 为四面体11A B EF ， 取11A B 的中点O ，连EO 接，可得EO ⊥平面11A B F ，然后，分别求出EO 与11A B F S △ 即可求出M 的体积1113A B F V EO S =⋅⋅△ 【详解】如图，由题意知，P 和Q 分别为三棱锥111B A BC -和三棱锥111A AB D -，设平面11A BC 与平面11AB D 的交线为EF ，则M 为四面体11A B EF ，取11A B 的中点O ，连接EO ，可得1EO =， 1112112A B F S =⨯⨯=△， 可得EO ⊥平面11A B F ，则M 的体积为1111111333A B F V EO S =⋅⋅=⨯⨯=△故选：A 【点睛】本题考查空间几何体的体积问题，属于简单题. 13．60 【解析】 【分析】先求出二项式展开式的通项6216(2)r r rr T C x -+=-，再令622r -=即得解.【详解】由题得()6162166(2)(2)rr r r r r rr T C x x C x ---+=⋅-⋅=-.令622r -=，解得2r ，所以2x 的系数为226(2)60C ⋅-=.故答案为：60 【点睛】本题主要考查利用二项式定理求指定项的系数，意在考查学生对该知识的理解掌握水平. 14．23122n n - 【解析】 【分析】设等差数列的公差为d ，根据已知求出3d =，再利用等差数列求和公式求解. 【详解】设等差数列的公差为d ， 由题得173474772a a a a S a +⋅==⨯=， 所以37,a =所以1+27,3d d =∴=.所以2(1)313222n n n S n n n -=+⨯=-. 故答案为：23122n n -.【点睛】本题主要考查等差数列的基本量计算，考查等差中项的应用和求和，意在考查学生对这些知识的理解掌握水平. 15．2 【解析】 【分析】求出双曲线的焦点坐标以及抛物线的焦点坐标，利用两点间的距离公式可得出关于p 的等式，由此可解得p 的值.【详解】抛物线的焦点为,02p F ⎛⎫⎪⎝⎭，双曲线的方程可化为222212y x p p -=，所以223c p =，所以其一个焦点化为()1F ，所以1FF p ===2p =. 故答案为：2. 【点睛】本题考查利用双曲线和抛物线的焦点坐标求参数，考查计算能力，属于基础题. 16．3243,54e e ⎡⎫⎪⎢⎣⎭ 【解析】 【分析】把()0f x <转化为()12xx k x e ++<，设1()x x g x e +=，()()2h x k x =+，则若()0f x <的解集中恰有三个整数解等价于()g x 的图像在()h x 的图像上方所对应的x 的取值范围中恰好有三个整数解，利用数形结合找到满足题意的不等式，解不等式即可求得实数k 的取值范围. 【详解】解：()0f x <等价于()210xkx k e x +--<，即()12xx k x e ++<， 设1()x x g x e+=，()()2h x k x =+，则上面不等式转化为()()h x g x <， 直线()()2h x k x =+横过定点()2,0-，要使()0f x <的解集中恰有三个整数，只需()g x 的图像在()h x 的图像上方所对应的x 的取值范围中恰好有三个整数解. 因为()()2(1)1x xx x e x e g x e e -+⋅-'==,所以(),0x ∈-∞时，0g x ，()g x 单调递增；()0,x ∈+∞时，0g x ，()g x 单调递减；所以1x =时，()()max 01g x g ==，且()10g -=，x →-∞时，()g x →-∞；x →+∞时，()0g x →， 根据根据上述画出()g x 的图像图下图所示：当0k ≤时，画出()(),g x h x 的图像如图所示：从图中可以看出，[)1,x ∈-+∞时，()g x 的图像横在()h x 的图像上方，所以()()h x g x <所以的x 的取值范围中，整数解有无穷多个，不符合题意； 当0k >时，画出()(),g x h x 的图像如图所示：从图像可得：要使()g x 的图像在()h x 的图像上方所对应的x 的取值范围中恰好有三个整数解，只需满足：()()()()22{33g h g h >≤，所以233445k e ke ⎧>⎪⎪⎨⎪≤⎪⎩，解得：324354k e e ≤<. 综上，324354k e e≤<. 故答案为：3243,54e e ⎡⎫⎪⎢⎣⎭ 【点睛】本题主要考查不等式的解的问题，考查数形结合，利用导数求函数单调性和最值，属于难题. 17．（1）12BC =（2）sin 5ACE ∠= 【解析】 【分析】(1)根据正弦定理、两角和的正弦公式化简已知的式子，得到B C =，根据等腰三角形的性质，得2BAC BAD ∠=∠，利用二倍角公式求出BAD ∠的正弦、余弦，进而求出BAD ∠的正切值，即可出BC 的长 (2)利用43cos cos sin ,sin 255EAC BAC BAC EAC π⎛⎫∠=-∠=∠=∠= ⎪⎝⎭，求出AC AB ==，然后，分别利用余弦和正弦定理即可求解解：（1）由cos cos c B b C =及正弦定理得sinCcos sin cos B B C = 即sin()0B C -=. 因为,22B C ππ⎛⎫-∈-⎪⎝⎭，所以.B C = 因为ABC 为锐角三角形，且4sin 5BAC ∠=， 所以3cos 5BAC ∠=. 又因为根据等腰三角形的性质， 可得，2BAC BAD ∠=∠， 所以232cos 15BAD ∠-=则cos BAD ∠=所以1sin tan 2BAD BAD ∠=∠= 所以6BD =，所以12BC = （2）由题意得43cos cos sin ,sin 255EAC BAC BAC EAC π⎛⎫∠=-∠=∠=∠=⎪⎝⎭AC AB ===在ACE △，因为222cos 2AE AC CE CAE AE AC+-∠=⋅所以9CE =. 由sin sin CE AECAE ACE=∠∠得sin 5ACE ∠= 【点睛】本题考查正弦定理、余弦定理、两角和的正弦公式以及二倍角公式，属于中档题. 18．（1）见解析（2）60︒. 【解析】（1）根据线面垂直性质，以及线面垂直的判定定理，先得到CD ⊥平面.ABE ，进而可得BC CD ⊥；（2）先由题意，得到45BCE BCA ︒∠=∠=，求得1BC AB ==，以C 为坐标原点，CD 方向为x 轴正方向，CB 方向为y 轴正方向，建立空间直角坐标系C xyz -，求出两平面ACD 和ABD 的法向量，根据向量夹角公式，即可求出结果.【详解】（1）证明：因为BE ⊥平面ACD ，CD ⊂平面ACD ， 所以BE CD ⊥.因为AB ⊥平面BCD ，CD ⊂平面BCD ， 所以AB CD ⊥. 因为ABBE B =，所以CD ⊥平面.ABE因为BC ⊂平面ABE ，所以BC CD ⊥.（2）解：因为BE ⊥平面ACD ，BCE ∠即为BC 与平面ACD 所成的角， 所以45BCE BCA ︒∠=∠=，所以1BC AB ==，以C 为坐标原点，CD 方向为x 轴正方向，CB 方向为y 轴正方向，建立空间直角坐标系C xyz -则(0,0,0),(1,0,0),(0,1,0),(0,1,1)C D B A(1,0,0),(0,1,1),(1,1,0),(0,0,1)CD CA BD BA ===-=设平面ACD 的一个法向量为()111,,n x y z =， 平面ABD 的一个法向量为()222,,m x y z =则00CD n CA n ⎧⋅=⎨⋅=⎩，00BD m BA m ⎧⋅=⎨⋅=⎩即11100x y z =⎧⎨+=⎩，2220x y z -=⎧⎨=⎩，令121,1y x ==可得(0,1,1),(1,1,0)n m =-= 所以1cos ,2n m n m n m⋅<>==由图知，二面角B AD C --的平面角为锐角，所以二面角B AD C --的大小为60︒. 【点睛】本题主要考查证明线线垂直，以及求二面角的大小，熟记线面垂直的判定定理及性质，灵活运用空间向量的方法求二面角即可，属于常考题型. 19．（1）0.0272（2）应该购买遮阳伞 【解析】 【分析】（1）先求出某年为高温年的概率为0.2，再根据~(4,0.2)X B ，求出今后4年中，甲地至少有3年为高温年的概率；（2）求出两种方案损失的收入的期望，再决定是否应该购买遮阳伞. 【详解】解：（1）由题意知，某年为高温年的概率为(0.030.01)50.2+⨯=， 设今后4年中高温年出现X 年，则~(4,0.2)X B 故44()0.20.8,0,1,2,3,4kkkP X k C k -===3314(3)0.20.80.0256P X C ===， 4404(4)0.20.80.0016P X C ==⋅=，(3)(3)(4)0.02560.00160.0272P X P X P X ==+==+=.（2）若选择方案一，不购买遮阳伞，设今后4年共损失1Y 元， 则()1460000.24800E Y =⨯⨯=若选择方案二，购买遮阳伞，设今后4年共损失2Y 元， 则()25000410000.24200E Y =-⨯⨯=(元) 则()()12E Y E Y >，故该同学应该购买遮阳伞. 【点睛】本题主要考查互斥事件的概率和独立重复试验的概率的求法，考查二项分布的期望的计算，意在考查学生对这些知识的理解掌握水平.20．（1）2214x y +=（2）[]8,10【解析】 【分析】（1）易知c =2PF x =，17PF x =，根据勾股定理计算得到2a =，得到椭圆方程.（2）考虑矩形边与坐标轴平行和不平行两种情况，联立方程组根据0∆=得到,m n 和k 的关系，计算边长得到面积表达式，根据均值不等式计算得到答案. 【详解】（1）由12F F =c =设2PF x =，因为127PF PF =，所以17PF x =，在Rt △12PF F 中，2221212PF PF F F =+，即224912x x =+，所以12x =， 所以284a x ==，解得2222,1a b a c ==-=，所以椭圆的标准方程为2214x y +=.（2）记矩形面积为S ，当矩形一边与坐标轴平行时，易知8S =.当矩形的边与坐标轴不平行时，根据对称性，设其中一边所在直线方程为y kx m =+， 则对边所在直线方程为y kx m =-， 另一边所在的直线方程为1y x n k =-+，则对边所在直线方程为1y x n k=--， 联立2244x y y kx m⎧+=⎨=+⎩，得()()222148410k x kmx m +++-=，由题意知()()222264161140k m m k∆=--+=，整理得2241km +=，矩形的一边长为1d =，同理2241n k +=，矩形的另一边长为2d =，122|4|1mnk S d d k =⋅==+44==44== 因为0k ≠，所以20k >，所以2212k k+≥(当且仅当21k =时等号成立)， 所以22990,142k k ⎛⎤∈ ⎥⎝⎦++52,2⎛⎤⎥⎝⎦，所以(8,10]S ∈. 综上所述，该矩形面积的取值范围为[]8,10. 【点睛】本题考查了求椭圆方程，椭圆外接矩形的面积范围，意在考查学生的计算能力和综合应用能力.21．（1）12x x <，见解析（2）见解析 【解析】 【分析】方法一：利用()20=+-=xf x e x ，利用2=-x e x 对不等式进行放缩，可得()111111ln 2ln 12ln 10x x e x x x x -+-++=-+≤，进而利用()g x 单调递增，且()10g x <和()20g x =，即可比较1x 与2x 的大小方法二：设()11111ln ln 2xH x x x x e =+=-+，令函数()ln 2,0tH t t e t =-+>，从而判断出函数()g x 的单调性，即可利用函数的单调性即可比较1x 与2x 的大小 (2) 令函数()()()h x f x g x =-，则()()()()1122,h x g x h x f x =-=，要证()()210f x g x +<，即证()()21f x g x <-，只要证：()()21h x h x <，最后通过证明函数()h x 在区间[]12,x x 上的单调性进行证明即可.【详解】（1）解:()11120xf x e x =+-=()11111ln ln 2x g x x x x e =+=-+方法一：()111111ln 2ln 12ln 10xx e x x x x -+-++=-+≤因为11x ≠，所以11ln 10x x -+<，所以()10g x <. 因为()20g x =，且()g x 单调递增，所以12x x < 方法二：设()11111ln ln 2xH x x x x e =+=-+，令函数()ln 2,0tH t t e t =-+>则1()t H t e t'=-，则()00010t H t e t '=-= 则函数()H t 在区间()00,t 上单调递增，()H t 在区间()0,t +∞上单调递减，所以()0max 00001()ln 220t H t H t t e t t ==-+=--+< 所以()10g x '<因为()20g x =，且()g x 单调递增，所以12x x < （2）证明：令函数()()()h x f x g x =-， 则()()()()1122,h x g x h x f x =-=.要证()()210f x g x +<，即证()()21f x g x <- 只要证：()()21h x h x <，只要证：函数()h x 在区间[]12,x x 上单调递减. 由题意得()()()ln 2xh x f x g x e x =-=--()22211(),x x h x e h x e x x ''=-=-因为()222ln 0g x x x =+= 所以2221ln lnx x x =-= 所以()2222211,0x x e h x e x x '==-= 因为()h x '单调递增，所以在区间[]12,x x 上，()0h x ' 所以()h x 在区间[]12,x x 上单调递减. 所以原命题得证. 【点睛】本题考查利用构造函数比较大小，主要通过求导判断函数的单调性进行判断大小，属于难题. 22．（1）1a =（2）y =或2y =+【解析】 【分析】（1）求出直线MN 的方程和曲线D 的直角坐标方程，然后利用直线MN 过点()0,a 求出答案；（2）由122t t +=MN k 然后可设直线MN的方程为y m =+，然后根据直线MN 被曲线D建立方程求解即可. 【详解】（1）因为121,3t t ==，所以(1,1),(1,3)M N --. 所以直线MN 的方程为21y x =+. 曲线D 的方程可化为222()x y a a +-=因为直线MN 平分曲线D ，所以直线MN 过点()0,a ， 所以1a =.（2）由题意可知()()()()()()22112212121212121222222MNt t t t t t t t y y k x x t t t t ----+--====-----曲线D 的方程为22(1)1y x +-= 设直线MN的方程为y m =+，圆心D 到直线MN 的距离为.d因为22212d ⎛+= ⎝⎭，所以221122m ⎛⎫-⎛⎫+= ⎪ ⎪ ⎪⎝⎭⎝⎭所以0m =或2m =，所以直线MN的方程为y =或2y =+【点睛】设圆的半径为r ，圆心到直线的距离为d ，弦长为AB ，则有2222AB r d ⎛⎫=+ ⎪⎝⎭.23．（1）1313xx ⎧⎫-⎨⎬⎩⎭∣（2）(,2]-∞ 【解析】 【分析】（1）利用分类讨论法解绝对值不等式得解； （2）对x 分三种情况1x =、[1,1)x 、(1,3]x ∈讨论，分别求出每一种情况下的实数a 的取值范围，最后综合即得解. 【详解】解：（1）由题意得35,1()|1|2|3|7,1335,3x x f x x x x x x x -+<-⎧⎪=++-=-+-≤≤⎨⎪->⎩当1x <-时，()8f x 得1x ≥-，所以此时无解；当13x -时，由()8f x ，即78x -+≤，解得13x -； 当3x >时，由()8f x ，即358x -≤，解得1333x< 综上，解集为1313x x ⎧⎫-⎨⎬⎩⎭∣.（2）①当1x =时，()()f x g x 显然恒成立. ②当[1,1)x时，()7,()(1)f x x g x a x =-=-因为()()f x g x 恒成立， 所以7(1)x a x --，即76111x ax x-=+--恒成立. 令6()1,[1,1)1F x x x=+∈--则min ()a F x 显然()F x 在区间[1,1)-上为增函数， 所以min ()(1)4F x F =-=，所以4a .③当(1,3]x ∈时，()7,()(1)f x x g x a x =-=-. 因为()()f x g x 恒成立， 所以7(1)x a x --，即76111x a x x -=-+--恒成立. 令6()1,(1,3]1G x x x =-+∈-，则min ()a G x 显然()G x 在区间(1,3]上为减函数， 所以min ()(3)2G x G ==， 所以2a .综上所述，实数a 的取值范围为(,2]-∞. 【点睛】本题主要考查绝对值不等式的解法，考查绝对值不等式的恒成立问题，考查函数的单调性求最值，意在考查学生对这些知识的理解掌握水平和分析推理能力.。

2020届河北省衡水中学高三下学期三模数学（理）试卷注意事项：1．答题前填写好自己的姓名、班级、考号等信息 2．请将答案正确填写在答题卡上第I 卷（选择题）一、选择题1.设集合3A x x =<，{}2,B x x k k ==∈Z ，则A B =（ ）A.{}0,2B.{}2,2-C.2,0,2D.{}2,1,0,1,2--2.若复数z 满足1z i i ⋅=-+，则z 的共轭复数z -在复平面内对应的点位于（ ） A.第一象限B.第二象限C.第三象限D.第四象限3.设实数x ，y 满足条件202300x y x y x y +-≤⎧⎪-+>⎨⎪-≤⎩则1x y ++的最大值为（ ）A.1B.2C.3D.44.平面向量a 与b 的夹角为60︒， ()2,0,1a b ==，则2a b +等于( ) A. 125.如图，是函数()f x 的部分图象，则()f x 的解析式可能是（ ）A.()|sin cos |f x x x =+B.22()sin cos f x x x =+C.()|sin ||cos |f x x x =+D.()sin ||cos ||f x x x =+6.已知二项式121(2)n x x+的展开式中，二项式系数之和等于64，则展开式中常数项等于（ ） A.240B.120C.48D.367.祖冲之是中国南北朝时期的数学家和天文学家，他在数学方面的突出贡献是将圆周率的精确度计算到小数点后第7位，也就是3.1415926和3.1415927之间，这一成就比欧洲早了1000多年，我校“爱数学”社团的同学，在祖冲之研究圆周率的方法启发下，自制了一套计算圆周率的数学实验模型.该模型三视图如图所示，模型内置一个与其各个面都相切的球，该模型及其内球在同一方向有开口装置.实验的时候，同学们随机往模型中投掷大小相等，形状相同的玻璃球，通过计算落在球内的玻璃球数量，来估算圆周率的近似值.已知某次实验中，某同学一次投掷了1000个玻璃球，请你根据祖冲之的圆周率精确度（取小数点后三位）估算落在球内的玻璃球数量（ ）A.297B.302C.307D.3128.设函数()()2sin f x x ωϕ=+， x R ∈，其中0ω>，ϕπ<.若528f π⎛⎫= ⎪⎝⎭，1108f π⎛⎫= ⎪⎝⎭，且()f x 的最小正周期大于2π，则 A. 23ω=， 12πϕ= B. 23ω=， 1112πϕ=- C. 13ω=， 1124πϕ=- D. 13ω=，724πϕ= 9.甲、乙、丙、丁四人参加冬季滑雪比赛，有两人获奖．在比赛结果揭晓之前，四人的猜测如下表，其中“√”表示猜测某人获奖，“×”表示猜测某人未获奖，而“〇”则表示对某人是否获奖未发表意见．已知四个人中有且只有两个人的猜测是正确的，那么两名获奖者是（ ）A.乙丁B.乙丙C.丙丁D.甲丁10.已知椭圆()2222:10x y C a b a b+=>>的左、右焦点分别为1F ，2F ．2F 也是抛物线()2:20E y px p =>的焦点，点A 为C 与E 的一个交点，且直线1AF 的倾斜角为45︒，则C 的离心率为（ ）A.121 C.3111.已知0a <，不等式1ln 0a x x e a x +⋅+≥对任意的实数1x >都成立，则实数a 的最小值为（ ） A.2e -B.e -C.e 2-D.1e-12.已知正方体1111ABCD A B C D -的外接球的表面积为27π，1A DB △与11A DC △的重心分别为E ，F ，球O 与该正方体的各条棱都相切，则球O 被EF 所在直线截的弦长为（ ）B. C.第II 卷（非选择题）二、填空题（题型注释）13.已知双曲线的一个焦点与抛物线28y x =的焦点F 重合，抛物线的准线与双曲线交于A ，B 两点，且OAB 的面积为6（O 为原点），则双曲线的标准方程为______．14.2020年初，我国突发新冠肺炎疫情.面对“突发灾难”，举国上下心，继解放军医疗队于除夕夜飞抵武汉，各省医疗队也陆续增援，纷纷投身疫情防控与病人救治之中.为分担“逆行者”的后顾之忧，某大学学生志愿者团队开展“爱心辅学”活动，为抗疫前线工作者子女在线辅导功课.现随机安排甲、乙、丙3名志愿者为某学生辅导数学、物理、化学、生物4门学科，每名志愿者至少辅导1门学科，每门学科由1名志愿者辅导，则数学学科恰好由甲辅导的概率为______.15.海洋蓝洞是地球罕见的自然地理现象，被誉为“地球给人类保留宇宙秘密的最后遗产”，我国拥有世界上已知最深的海洋蓝洞．若要测量如图所示的海洋蓝洞的口径(即A ，B 两点间的距离)，现取两点C ，D ，测得CD ＝80，∠ADB ＝135°，∠BDC ＝∠DCA ＝15°，∠ACB ＝120°，则图中海洋蓝洞的口径为________．16.已知圆22:4O x y +=点()2,2A ，直线l 与圆O 交于P Q ，两点，点E 在直线l 上且满足2PQ QE →→=.若22248AE AP +=，则弦PQ 中点M 的横坐标的取值范围为_____________.三、解答题（题型注释）17.已知等差数列n a 的公差为d ，n S 是数列{}n a 的前n 项和，等比数列{}n b 的公比为()1q q ≠，n T 是数列{}n b 的前n 项和，330a b +=，11b =，33T =，d q =-．（1）求数列{}n b 的通项公式；（2）是否存在正整数λ，使得关于k 的不等式()3010k S λ+≤有解？若λ存在，求出λ的值；若λ不存在，说明理由．18.如图，在多面体ABCDP 中，ABC 是边长为4的等边三角形，PA AC =，BD CD ==PC PB ==，点E 为BC 的中点，平面BDC ⊥平面ABC ．（1）求证：//DE 平面PAC（2）线段BC 上是否存在一点T ，使得二面角T DA B --为直二面角？若存在，试指出点T 的位置；若不存在，请说明理由．19.如图在平面直角坐标系xOy 中，已知椭圆()2222:10x y C a b a b+=>>，短轴长为4．（I ）求椭圆C 的方程；（2）若与原点距离为1的直线1:l y kx m =+与椭圆C 相交于A ，B 两点，直线2l 与1l 平行，且与椭圆C 相切于点M （O ，M 位于直线1l 的两侧）．记MAB △，OAB 的面积分别为1S ，2S 若12S S λ=，求实数λ的取值范围．20.2019年由“杂交水稻之父”袁隆平团队研发的第三代杂交水稻10月21日至22日首次公开测产，经测产专家组评定，最终亩产为1046.3千克．第三代杂交水稻的综合优势，可以推动我国的水稻生产向更加优质、高产、绿色和可持续方向发展．某企业引进一条先进的年产量为100万件的食品生产线，计划以第三代杂交水稻为原料进行深加工．已知该生产线生产的产品的质量以某项指标值[]()70,100k k ∈为衡量标准，其产品等级划分如下表．为了解该产品的生产效益，该企业先进行试生产，并从中随机抽取了1000件产品，测量了每件产品的质量指标值，得到如下的产品质量指标值的频率分布直方图．（1）若从质量指标值不小于85的产品中，采用分层抽样的方法抽取7件产品，然后从这7件产品中任取3件，求产品的质量指标值[)90,95k ∈的件数X 的分布列及数学期望； （2）将频率视为概率，从该产品中有放回地随机抽取3件，记“抽出的产品中至少有1件是合格及以上等级”为事件A ．求事件A 发生的概率；（3）若每件产品的质量指标值k 与利润y （单位：元）的关系如下表所示；（14t <<）试确定t 的值，使得该生产线的年盈利取得最大值，并求出最大值（参考数值：ln 20.7≈，ln3 1.1≈，ln5 1.6≈）21.已知函数()l e n xm f x x xx =+-()m ∈R ．（1）当1em =时，求函数()f x 的最小值； （2）若2e 2m ≥，()22e x m x g x x-=，求证：()()f x g x <．22.在直角坐标系xOy 中．直线l 的参数方程为00cos sin x x t y y t ϕϕ=+⎧⎨=+⎩（t 为参数，[)0,ϕπ∈）．以坐标原点为极点，x 轴的正半轴为极轴，建立极坐标系，圆C 的极坐标方程为8cos 3πρθ⎛⎫=-⎪⎝⎭． （1）化圆C 的极坐标方程为直角坐标标准方程；（2）设点()00,P x y ，圆心()002,2C x y ，若直线l 与圆C 交于M 、N 两点，求PM PNPN PM+的最大值． 23.已知函数()3f x ax =-，不等式()2f x ≤的解集为{}15x x ≤≤． （1）解不等式()()211f x f x <+-；（2）若3m ≥，3n ≥，()()3f m f n +=，求证：141m n+≥．参考答案1.C【解析】1.求出集合A ，利用交集的定义可得出集合AB .{}{}333A x x x x =<=-<<，{}2,B x x k k ==∈Z ，因此，{}2,0,2A B =-.故选：C. 2.D【解析】2.先根据1z i i ⋅=-+求出z ，再求出z -，即得z -在复平面内对应的点所在的象限.由1z i i ⋅=-+得21(1)1,1i i iz i z i i i--+-+===+∴=-. 所以z -对应的点为(1,1)-，在第四象限. 故选：D. 3.C【解析】3.由约束条件作出可行域，化目标函数为直线方程的斜截式，数形结合得到最优解，联立方程组求出最优解的坐标，代入目标函数得答案．作出不等式组对应的可行域，如图所示，由++1z x y =可得1y x z =-+-， 将直线l ：1y x z =-+-进行平移， 当l 与AB 重合时，目标函数z 达到最大值， 因为AB 过点（0，2）； ∴z max ＝0+2+1＝3． 故选：C ．4.B【解析】4.因为2,1a b ==， a 与b 的夹角为60︒，故cos601a b a b ⋅=⋅=，则244a b +=+=B 。

2020届河北省衡水中学高三下学期全国第三次联考数学（理）试题一、单选题1．已知集合{}20M x x x =+>，(){}ln 10N x x =->，则（ ）A ．M N ⊇B ．M N ⊆C ．()1,M N ⋂=+∞D ．()2,M N ⋃=+∞【答案】A【解析】解出集合M 、N ，利用集合的包含关系和交集、并集的定义可判断各选项的正误. 【详解】{}()()20,10,M x x x =+>=-∞-⋃+∞，(){}{}()ln 10112,N x x x x =->=->=+∞,所以，M N ⊇，()2,M N =+∞，()(),10,M N =-∞-+∞.故选：A. 【点睛】本题考查集合包含关系的判断，同时也考查了集合的交集和并集运算、二次不等式与对数不等式的求解，考查计算能力，属于基础题. 2．已知复数2(2)z i =+，则z 的虚部为（ ） A ．3 B ．3i C ．4D ．4i【答案】C【解析】根据复数的代数形式的乘法法则计算即可得解； 【详解】解：2(2)34z i i =+=+，所以z 的虚部为4. 故选：C . 【点睛】本题考查复数代数形式的乘法，复数的相关概念，属于基础题.3．以下统计表和分布图取自《清华大学2019年毕业生就业质量报告》.本科生硕士生博士生总体毕业去向人数比例人数比例人数比例人数比例深造228280.4％2319.3％48933.6％300244.2％国内158355.8％94 3.8％29019.9％196729.0％出国（境）69924.6％137 5.5％19913.7％103515.3％就业49017.3％222489.2％94364.8％365753.9％签三方就业154 5.4％165666.4％86459.4％267439.4％灵活就业33611.8％56822.8％79 5.4％98314.5％未就业64 2.3％39 1.6％23 1.6％126 1.9％合计2836100.0％2494100.0％1455100.0％6785100.0％清华大学2019年毕业生去向分布情况统计表清华大学2019年毕业生签三方就业单位所在省（区、市）分布图则下列选项错误．．的是（）.A．清华大学2019年毕业生中，大多数本科生选择继续深造，大多数硕士生选择就业B．清华大学2019年毕业生中，硕士生的就业率比本科生高C．清华大学2019年签三方就业的毕业生中，本科生的就业城市比硕士生的就业城市分散D．清华大学2019年签三方就业的毕业生中，留北京人数超过一半【答案】D【解析】选项A 在表中找出本科生选择继续深造达80.4％，硕士生选择就业达89.2％，则判断选项A 正确；选项B 在表中找出硕士生的就业率达89.2％，本科生的就业率达17.3％，则判断选项B 正确；选项C 在表中分析出本科生的就业城市主要分散在北京、广东、上海，硕士生的就业城市主要集中在北京，则判断选项C 正确；选项D 在表中分析出留北京人数仅博士生达到了51.2%，本科生与硕士生都没有达到一半，判断选项D 错误即可. 【详解】选项A ：清华大学2019年毕业生中，本科生选择继续深造达80.4％，硕士生选择就业达89.2％，故选项A 正确；选项B ：清华大学2019年毕业生中，硕士生的就业率达89.2％，本科生的就业率达17.3％，故选项B 正确；选项C ：清华大学2019年签三方就业的毕业生中，本科生的就业城市主要分散在北京、广东、上海，硕士生的就业城市主要集中在北京，故选项C 正确；选项D ：清华大学2019年签三方就业的毕业生中，留北京人数仅博士生达到了51.2%，本科生与硕士生都没有达到一半，故选项D 错误. 故选：D. 【点睛】本题考查统计表与分布图，是基础题.4．若圆22(2)(1)5x y -+-=关于直线10(0,0)ax by a b +-=>>对称，则21a b+的最小值为（ ）A ．4B ．C ．9D ．【答案】C【解析】由已知得，若圆关于直线对称，即直线必然经过圆心，故有圆心(2,1)在直线10ax by 上，则21a b +=，然后，利用基本不等式关于“1”的用法即可求解.【详解】由题意知圆心(2,1)在直线10ax by 上，则21a b +=.又因为0,0a b >>，所以212122(2)59b a a b a b a b a b ⎛⎫+=++=++ ⎪⎝⎭，当且仅当22b a a b =时，即13a b ==时取等号，此时，min219a b ⎛⎫+= ⎪⎝⎭故选：C 【点睛】本题考查基本不等式关于“1”的用法，属于基础题.5．要使得满足约束条件42y x y x x y ⎧⎪-⎨⎪+⎩，的变量,x y 表示的平面区域为正方形，则可增加的一个约束条件为（ ） A ．4x y +≤ B ．4x y +C ．6x y +D ．6x y +【答案】C【解析】设新增加的约束条件为x y c +，根据正方形两组对边的距离相等，得到方程解得即可； 【详解】解：根据正方形的性质可设新增加的约束条件为x y c +，两组对边的距离相等，故2222d ===，所以6c =或2c =-(舍去). 如图所示【点睛】本题考查二元不等式组表示的平面区域，两平行线间的距离公式的应用，属于基础题. 6．若{}n a 是公比为(0)q q ≠的等比数列，记n S 为{}n a 的前n 项和，则下列说法正确的是（ ）A ．若{}n a 是递增数列，则10,0a q <<B ．若{}n a 是递减数列，则10,01a q ><<C ．若0q >，则4652S S S +>D ．若1n nb a =，则{}n b 是等比数列 【答案】D【解析】选项A ，B ，C 中，分别取特殊数列满足条件，但得不出相应的结论，说明选项A ，B ，C 都是错误的，选项D 中，利用等比数列的定义可以证明结论正确. 【详解】A 选项中，12,3a q ==，满足{}n a 单调递增，故A 错误；B 选项中，11,2a q =-=，满足{}n a 单调递减，故B 错误；C 选项中，若111,2a q ==，则656554,a a S S S S <-<-，故C 错误； D 选项中，111(0)n n n n b a q b a q++==≠，所以{}n b 是等比数列.故D 正确. 故选：D. 【点睛】本题考查了等比数列的定义，考查了数列的单调性，考查了特值排除法，属于基础题. 7．为了得到函数()sin g x x =的图象，需将函数()sin 6f x x π⎛⎫=- ⎪⎝⎭的图象（ ） A ．向左平移6π个单位长度 B ．向右平移6π个单位长度 C ．向左平移56π个单位长度 D ．向右平移56π个单位长度【解析】先将函数()sin 6f x x π⎛⎫=-⎪⎝⎭用诱导公式变形为5()sin 6f x x π⎛⎫=+⎪⎝⎭，结合三角函数图象的平移变换规律，得到答案. 【详解】5()sin sin sin sin 6666f x x x x x πππππ⎛⎫⎛⎫⎛⎫⎛⎫=-=--=-+=+⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭, 由5()sin 6f x x π⎛⎫=+ ⎪⎝⎭的图象得到函数()sin g x x =的图象， 向右56π个单位长度即可. 故选：D. 【点睛】本题主要考查三角函数图象的平移变换，要注意三角函数图象的平移变换是在“x ”的基础上进行的，解决此类题还需熟记口诀“左加右减”.8．设()f x 是定义在R 上的奇函数，且当0x 时，1()sin 23f x x x =-.若2tan5a f π⎛⎫= ⎪⎝⎭，32log cos 5b f π⎛⎫= ⎪⎝⎭，2cos 5c f π⎛⎫=⎪⎝⎭大小关系为（ ） A ．a b c << B ．b c a <<C ．b a c <<D ．c b a <<【答案】B【解析】根据题意当0x 时2()1cos 203f x x '=->，()f x 是定义在R 上的奇函数,则()f x 在定义域上单调递增，2tantan 154ππ>=，20cos 15π<<，32log cos 05π<，由函数的单调性可得出答案. 【详解】由题意知由当0x 时,2()1cos 203f x x '=->，所以()f x 在[)0+，∞上单调递增，且()00f =又()f x 是定义在R 上的奇函数，所以()f x 在(]0-∞，上单调递增. 所以()f x 在定义域上单调递增. 又因为28tantan tan 15204πππ=>=，20cos 15π<<，所以32log cos 05π<，由()f x 在定义域上单调递增，则3222tan cos log cos 555f f f πππ⎛⎫⎛⎫⎛⎫>>⎪⎪ ⎪⎝⎭⎝⎭⎝⎭所以b c a <<. 故选：B . 【点睛】本题考查函数的奇偶性和单调性的综合应用，利用单调性比较大小，考查三角函数值大小的的比较，对数值大小的比较，属于中档题9．如图是由等边△AIE 和等边△KGC 构成的六角星，图中的B ，D ，F ，H ，J ，L 均为三等分点，两个等边三角形的中心均为O .若OA mOC nOJ =+，则mn=（ ）A ．12B ．23C ．34D ．1【答案】B【解析】以点O 为坐标原点，OD 为x 轴，OA 为y 轴建立平面直角坐标系，设等边三角形的边长为23得出点,,A C J 的坐标，由向量的运算可求得,m n 的值，可得答案. 【详解】由平行四边形法则，22()23OA OB OJ OC OJ OJ OC OJ =+=++=+，所以2m =，3n =，所以23m n = 以点O 为坐标原点，OD 为x 轴，OA 为y 轴建立如图所示的平面直角坐标系，设等边三角形的边长为23()()222333-=，由B ，D ，F ，H ，J ，L 均为三等分点， 则2323OA =⨯=,233OJ =所以())230,23,1，，A J C⎛⎫⎪ ⎪⎝⎭()0,2OA =,()3,1OC =,23OJ ⎛⎫= ⎪ ⎪⎝⎭)23233,13,33n OA mOC nOJ mn m m ⎛⎫⎫=+=+-=- ⎪⎪ ⎪⎪⎝⎭⎭所以23302nm m ⎧-=⎪⎨⎪=⎩，解得32n m =⎧⎨=⎩ 所以23m n = 故选：B . 【点睛】本题考查向量的线性运算，建立直角坐标系是解决本题的关键，也是解决的向量问题的常用方法，属于中档题.10．区块链是数据存储､传输､加密算法等计算机技术的新型应用模式，图论是区块链技术的一个主要的数学模型,在一张图中有若干点，有的点与点之间有边相连，有的没有边相连，边可以是直线段，也可以是曲线段，我们规定图中无重边(即两个点之间最多只有一条边)且无孤立点(即对于每个点，都至少存在另外一个点与之相连)，现有A，B，C，D四个点，若图中恰有3条边，则满足上述条件的图的个数为（）A．4B．8C．12D．16【答案】D【解析】先求出A，B，C，D四点最可确定6条边，再由题得到满足条件的图的个数. 【详解】如图，A，B，C，D四点最可确定AB，AC，AD，BC，BD，CD共6条边.由题意知恰有3条边且无孤立点，所以满足条件的图有36416C-=(个).故选：D.【点睛】本题主要考查组合的应用，意在考查学生对这些知识的理解掌握水平.11．地球的公转轨道可以看作是以太阳为一个焦点的椭圆，根据开普勒行星运动第二定律，可知太阳和地球的连线在相等的时间内扫过相等的面积，某同学结合物理和地理知识得到以下结论：①地球到太阳的距离取得最小值和最大值时，地球分别位于图中A点和B点；②已知地球公转轨道的长半轴长约为149600000千米，短半轴长约为149580000千米，则该椭圆的离心率约为1.因此该椭圆近似于圆形：③已知我国每逢春分（3月21日前后）和秋分（9月23日前后），地球会分别运行至图中C点和D点，则由此可知我国每年的夏半年（春分至秋分）比冬半年（当年秋分至次年春分）要少几天.以上结论正确的是（）A．①B．①②C．②③D．①③【答案】A【解析】根据椭圆的几何性质可判断命题①的正误；利用椭圆的离心率公式可判断命题②的正误；根据开普勒行星运动第二定律可判断命题③的正误.综合可得出结论. 【详解】由椭圆的几何性质可知，当地球到太阳的距离取得最小值和最大值时，地球分别位于图中A 点和B 点，命题①正确；1495800001149600000b a =≈，则该椭圆的离心率222210c a b b e a a a -⎛⎫===-≈ ⎪⎝⎭，命题②错误；根据开普勒行星运动第二定律，地球从D 点到C 点运行的速度较快，因此经历的时间较短，因此夏半年比冬半年多几天，命题③错误. 故选：A. 【点睛】本题考查与椭圆性质相关的命题真假的判断，涉及椭圆焦半径、离心率的应用，考查推理能力，属于中等题.12．正方体1111ABCD A B C D -的棱长为2，在A ，B ，C ，D ，1C ，1D 这六个顶点中.选择两个点与1A ，1B 构成正三棱锥P ，在剩下的四个顶点中选择两个点与1A ，1B 构成正三棱锥Q ，M 表示P 与Q 的公共部分，则M 的体积为（ ） A ．13B ．24C ．23D ．1【答案】A【解析】根据题意，设平面11A BC 与平面11AB D 的交线为EF ，则M 为四面体11A B EF ， 取11A B 的中点O ，连EO 接，可得EO ⊥平面11A B F ，然后，分别求出EO 与11A B F S △ 即可求出M 的体积1113A B F V EO S =⋅⋅△ 【详解】如图，由题意知，P 和Q 分别为三棱锥111B A BC -和三棱锥111A AB D -，设平面11A BC 与平面11AB D 的交线为EF ，则M 为四面体11A B EF ，取11A B 的中点O ，连接EO ，可得1EO =， 1112112A B F S =⨯⨯=△， 可得EO ⊥平面11A B F ，则M 的体积为1111111333A B F V EO S =⋅⋅=⨯⨯=△故选：A 【点睛】本题考查空间几何体的体积问题，属于简单题.二、填空题13．62x x ⎛⎫- ⎪⎝⎭的展开式中2x 的系数为_________.(用数字作答) 【答案】60【解析】先求出二项式展开式的通项6216(2)rr rr T C x -+=-，再令622r -=即得解.【详解】由题得()6162166(2)(2)rr rr r r rr T C x x C x ---+=⋅-⋅=-.令622r -=，解得2r ，所以2x 的系数为226(2)60C ⋅-=.故答案为：60 【点睛】本题主要考查利用二项式定理求指定项的系数，意在考查学生对该知识的理解掌握水平.14．记n S 为正项等差数列{}n a 的前n 项和，若13471,a a a S =⋅=，则n S =_________. 【答案】23122n n - 【解析】设等差数列的公差为d ，根据已知求出3d =，再利用等差数列求和公式求解. 【详解】设等差数列的公差为d ， 由题得173474772a a a a S a +⋅==⨯=，所以37,a =所以1+27,3d d =∴=.所以2(1)313222n n n S n n n -=+⨯=-. 故答案为：23122n n -.【点睛】本题主要考查等差数列的基本量计算，考查等差中项的应用和求和，意在考查学生对这些知识的理解掌握水平.15．若抛物线()220y px p =>的焦点到双曲线22222y x p -=的一个焦点的距离为p 的值为_________.【答案】2【解析】求出双曲线的焦点坐标以及抛物线的焦点坐标，利用两点间的距离公式可得出关于p 的等式，由此可解得p 的值. 【详解】抛物线的焦点为,02p F ⎛⎫⎪⎝⎭，双曲线的方程可化为222212y x p p -=，所以223c p =，所以其一个焦点化为()1F ，所以12FF p ===2p =.故答案为：2. 【点睛】本题考查利用双曲线和抛物线的焦点坐标求参数，考查计算能力，属于基础题. 16．已知函数()()21xf x kx k e x =+--，若()0f x <的解集中恰有三个整数，则实数k 的取值范围为______. 【答案】3243,54e e ⎡⎫⎪⎢⎣⎭【解析】把()0f x <转化为()12xx k x e ++<，设1()x x g x e +=，()()2h x k x =+，则若()0f x <的解集中恰有三个整数解等价于()g x 的图像在()h x 的图像上方所对应的x 的取值范围中恰好有三个整数解，利用数形结合找到满足题意的不等式，解不等式即可求得实数k 的取值范围. 【详解】解：()0f x <等价于()210xkx k e x +--<，即()12xx k x e ++<， 设1()x x g x e+=，()()2h x k x =+，则上面不等式转化为()()h x g x <， 直线()()2h x k x =+横过定点()2,0-，要使()0f x <的解集中恰有三个整数，只需()g x 的图像在()h x 的图像上方所对应的x 的取值范围中恰好有三个整数解.因为()()2(1)1x xx x e x e g x e e -+⋅-'==,所以(),0x ∈-∞时，0g x ，()g x 单调递增；()0,x ∈+∞时，0g x ，()g x 单调递减；所以1x =时，()()max 01g x g ==，且()10g -=，x →-∞时，()g x →-∞；x →+∞时，()0g x →， 根据根据上述画出()g x 的图像图下图所示：当0k ≤时，画出()(),g x h x 的图像如图所示：从图中可以看出，[)1,x ∈-+∞时，()g x 的图像横在()h x 的图像上方，所以()()h x g x <所以的x 的取值范围中，整数解有无穷多个，不符合题意；当0k >时，画出()(),gx h x 的图像如图所示：从图像可得：要使()g x 的图像在()h x 的图像上方所对应的x 的取值范围中恰好有三个整数解，只需满足：()()()()22{33g h g h >≤，所以233445k e ke ⎧>⎪⎪⎨⎪≤⎪⎩，解得：324354k e e ≤<. 综上，324354k e e ≤<. 故答案为：3243,54e e ⎡⎫⎪⎢⎣⎭【点睛】本题主要考查不等式的解的问题，考查数形结合，利用导数求函数单调性和最值，属于难题.三、解答题17．在锐角△ABC 中，内角A ，B ，C 所对的边分别为a ，b ，c ，若cos cos c B b C =，BC 边上的高12AD =，4sin 5BAC ∠=. （1）求BC 的长：（2）过点A 作AE AB ⊥，垂足为A ，且CAE ∠为锐角，AE =sin ACE ∠.【答案】（1）12BC =（2）sin ACE ∠=【解析】(1)根据正弦定理、两角和的正弦公式化简已知的式子，得到B C =，根据等腰三角形的性质，得2BAC BAD ∠=∠，利用二倍角公式求出BAD ∠的正弦、余弦，进而求出BAD ∠的正切值，即可出BC 的长 (2)利用43cos cos sin ,sin 255EAC BAC BAC EAC π⎛⎫∠=-∠=∠=∠= ⎪⎝⎭，求出AC AB ===【详解】解：（1）由cos cos c B b C =及正弦定理得sinCcos sin cos B B C = 即sin()0B C -=. 因为,22B C ππ⎛⎫-∈-⎪⎝⎭，所以.B C = 因为ABC 为锐角三角形，且4sin 5BAC ∠=， 所以3cos 5BAC ∠=. 又因为根据等腰三角形的性质， 可得，2BAC BAD ∠=∠， 所以232cos 15BAD ∠-=则cos BAD ∠=所以1sin ,tan 52BAD BAD ∠=∠= 所以6BD =，所以12BC = （2）由题意得43cos cos sin ,sin 255EAC BAC BAC EAC π⎛⎫∠=-∠=∠=∠=⎪⎝⎭2265AC AB AD BD ==+=在ACE △，因为222cos 2AE AC CE CAE AE AC+-∠=⋅所以9CE =. 由sin sin CE AECAE ACE=∠∠得5sin 5ACE ∠= 【点睛】本题考查正弦定理、余弦定理、两角和的正弦公式以及二倍角公式，属于中档题. 18．如图，在三棱锥A BCD -中，AB ⊥平面BCD ，E 为棱AC 上的一点，且BE ⊥平面ACD .（1）证明：BC CD ⊥；（2）设1BC CD ==.BC 与平面ACD 所成的角为45︒.求二面角B AD C --的大小. 【答案】（1）见解析（2）60︒.【解析】（1）根据线面垂直性质，以及线面垂直的判定定理，先得到CD ⊥平面.ABE ，进而可得BC CD ⊥；（2）先由题意，得到45BCE BCA ︒∠=∠=，求得1BC AB ==，以C 为坐标原点，CD 方向为x 轴正方向，CB 方向为y 轴正方向，建立空间直角坐标系C xyz -，求出两平面ACD 和ABD 的法向量，根据向量夹角公式，即可求出结果. 【详解】（1）证明：因为BE ⊥平面ACD ，CD ⊂平面ACD ， 所以BE CD ⊥.因为AB ⊥平面BCD ，CD ⊂平面BCD ， 所以AB CD ⊥.因为AB BE B=，所以CD⊥平面.ABE因为BC⊂平面ABE，所以BC CD⊥.（2）解：因为BE⊥平面ACD ，BCE∠即为BC与平面ACD所成的角，所以45BCE BCA︒∠=∠=，所以1BC AB==，以C为坐标原点，CD方向为x轴正方向，CB方向为y轴正方向，建立空间直角坐标系C xyz-则(0,0,0),(1,0,0),(0,1,0),(0,1,1)C D B A(1,0,0),(0,1,1),(1,1,0),(0,0,1)CD CA BD BA===-=设平面ACD的一个法向量为()111,,n x y z=，平面ABD的一个法向量为()222,,m x y z=则CD nCA n⎧⋅=⎨⋅=⎩，BD mBA m⎧⋅=⎨⋅=⎩即111xy z=⎧⎨+=⎩，222x yz-=⎧⎨=⎩，令121,1y x==可得(0,1,1),(1,1,0)n m=-=所以1cos,2n mn mn m⋅<>==由图知，二面角B AD C--的平面角为锐角，所以二面角B AD C--的大小为60︒. 【点睛】本题主要考查证明线线垂直，以及求二面角的大小，熟记线面垂直的判定定理及性质，灵活运用空间向量的方法求二面角即可，属于常考题型.19．2020年1月10日，中国工程院院士黄旭华和中国科学院院士曾庆存荣获2019年度国家最高科学技术奖.曾庆存院士是国际数值天气预报奠基人之一，他的算法是世界数值天气预报核心技术的基础，在气象预报中，过往的统计数据至关重要，如图是根据甲地过去50年的气象记录所绘制的每年高温天数(若某天气温达到35 ℃及以上，则称之为高温天)的频率分布直方图.若某年的高温天达到15天及以上，则称该年为高温年，假设每年是否为高温年相互独立，以这50年中每年高温天数的频率作为今后每年是否为高温年的概率.（1）求今后4年中，甲地至少有3年为高温年的概率.（2）某同学在位于甲地的大学里勤工俭学，成为了校内奶茶店(消费区在户外)的店长，为了减少高温年带来的损失，该同学现在有两种方案选择：方案一：不购买遮阳伞，一旦某年为高温年，则预计当年的收入会减少6000元；方案二：购买一些遮阳伞，费用为5000元，可使用4年，一旦某年为高温年，则预计当年的收入会增加1000元.以4年为期，试分析该同学是否应该购买遮阳伞？ 【答案】（1）0.0272（2）应该购买遮阳伞【解析】（1）先求出某年为高温年的概率为0.2，再根据~(4,0.2)X B ，求出今后4年中，甲地至少有3年为高温年的概率；（2）求出两种方案损失的收入的期望，再决定是否应该购买遮阳伞. 【详解】解：（1）由题意知，某年为高温年的概率为(0.030.01)50.2+⨯=， 设今后4年中高温年出现X 年，则~(4,0.2)X B 故44()0.20.8,0,1,2,3,4kkkP X k C k -===3314(3)0.20.80.0256P X C ===， 4404(4)0.20.80.0016P X C ==⋅=，(3)(3)(4)0.02560.00160.0272P X P X P X ==+==+=.（2）若选择方案一，不购买遮阳伞，设今后4年共损失1Y 元， 则()1460000.24800E Y =⨯⨯=若选择方案二，购买遮阳伞，设今后4年共损失2Y 元， 则()25000410000.24200E Y =-⨯⨯=(元) 则()()12E Y E Y >，故该同学应该购买遮阳伞. 【点睛】本题主要考查互斥事件的概率和独立重复试验的概率的求法，考查二项分布的期望的计算，意在考查学生对这些知识的理解掌握水平.20．已知椭圆22221(0)x y a b a b+=>>的左､右焦点分别为12,F F ，且12F F =过椭圆的右焦点2F 作长轴的垂线与椭圆，在第一象限交于点P ，且满足127PF PF =.（1）求椭圆的标准方程；（2）若矩形ABCD 的四条边均与椭圆相切，求该矩形面积的取值范围.【答案】（1）2214x y +=（2）[]8,10【解析】（1）易知c =，设2PF x =，17PF x =，根据勾股定理计算得到2a =，得到椭圆方程.（2）考虑矩形边与坐标轴平行和不平行两种情况，联立方程组根据0∆=得到,m n 和k 的关系，计算边长得到面积表达式，根据均值不等式计算得到答案. 【详解】（1）由12F F =c =，设2PF x =，因为127PF PF =，所以17PF x =，在Rt △12PF F 中，2221212PF PF F F =+，即224912x x =+，所以12x =， 所以284a x ==，解得2222,1a b a c ==-=，所以椭圆的标准方程为2214x y +=.（2）记矩形面积为S ，当矩形一边与坐标轴平行时，易知8S =.当矩形的边与坐标轴不平行时，根据对称性，设其中一边所在直线方程为y kx m =+， 则对边所在直线方程为y kx m =-， 另一边所在的直线方程为1y x n k =-+，则对边所在直线方程为1y x n k=--，联立2244x y y kx m⎧+=⎨=+⎩，得()()222148410k x kmx m +++-=，由题意知()()222264161140k m m k∆=--+=，整理得2241km +=，矩形的一边长为1d =，同理2241n k+=，矩形的另一边长为2d =，122|4|1mnk S d d k =⋅==+44==44== 因为0k ≠，所以20k >，所以2212k k+≥(当且仅当21k =时等号成立)， 所以22990,142k k ⎛⎤∈ ⎥⎝⎦++52,2⎛⎤⎥⎝⎦，所以(8,10]S ∈. 综上所述，该矩形面积的取值范围为[]8,10. 【点睛】本题考查了求椭圆方程，椭圆外接矩形的面积范围，意在考查学生的计算能力和综合应用能力.21．已知函数()2,()ln x f x e x g x x x =+-=+，若1x 是函数()f x 的零点，2x 是函数()g x 的零点.（1）比较1x 与2x 的大小； （2）证明：()()210f x g x +<.【答案】（1）12x x <，见解析（2）见解析【解析】方法一：利用()20=+-=xf x e x ，利用2=-x e x 对不等式进行放缩，可得()111111ln 2ln 12ln 10x x e x x x x -+-++=-+≤，进而利用()g x 单调递增，且()10g x <和()20g x =，即可比较1x 与2x 的大小方法二：设()11111ln ln 2xH x x x x e =+=-+，令函数()ln 2,0tH t t e t =-+>，从而判断出函数()g x 的单调性，即可利用函数的单调性即可比较1x 与2x 的大小 (2) 令函数()()()h x f x g x =-，则()()()()1122,h x g x h x f x =-=，要证()()210f x g x +<，即证()()21f x g x <-，只要证：()()21h x h x <，最后通过证明函数()h x 在区间[]12,x x 上的单调性进行证明即可. 【详解】（1）解:()11120xf x e x =+-=()11111ln ln 2x g x x x x e =+=-+方法一：()111111ln 2ln 12ln 10xx e x x x x -+-++=-+≤因为11x ≠，所以11ln 10x x -+<，所以()10g x <. 因为()20g x =，且()g x 单调递增，所以12x x < 方法二：设()11111ln ln 2xH x x x x e =+=-+，令函数()ln 2,0tH t t e t =-+>则1()tH t e t'=-，则()00010t H t e t '=-= 则函数()H t 在区间()00,t 上单调递增，()H t 在区间()0,t +∞上单调递减，所以()0max 00001()ln 220tH t H t t e t t ==-+=--+< 所以()10g x '<因为()20g x =，且()g x 单调递增，所以12x x < （2）证明：令函数()()()h x f x g x =-， 则()()()()1122,h x g x h x f x =-=.要证()()210f x g x +<，即证()()21f x g x <-只要证：()()21h x h x <，只要证：函数()h x 在区间[]12,x x 上单调递减. 由题意得()()()ln 2xh x f x g x e x =-=--()22211(),x x h x e h x e x x ''=-=-因为()222ln 0g x x x =+= 所以2221ln lnx x x =-= 所以()2222211,0x x e h x e x x '==-= 因为()h x '单调递增，所以在区间[]12,x x 上，()0h x '所以()h x 在区间[]12,x x 上单调递减. 所以原命题得证. 【点睛】本题考查利用构造函数比较大小，主要通过求导判断函数的单调性进行判断大小，属于难题.22．在直角坐标系xOy 中，曲线C 的参数方程为222x t y t t=-⎧⎨=-⎩(t 为参数)，曲线C 上异于原点的两点M ，N 所对应的参数分别为12,t t .以坐标原点O 为极点，x 轴的正半轴为极轴建立极坐标系，曲线D 的极坐标方程为2sin a ρθ=. （1）当121,3t t ==时，直线MN 平分曲线D ，求a 的值；（2）当1a =时，若122t t +=直线MN 被曲线D求直线MN 的方程.【答案】（1）1a =（2）y =或2y =+【解析】（1）求出直线MN 的方程和曲线D 的直角坐标方程，然后利用直线MN 过点()0,a 求出答案；（2）由122t t +=MN k =MN的方程为y m =+，然后根据直线MN 被曲线D. 【详解】（1）因为121,3t t ==，所以(1,1),(1,3)M N --. 所以直线MN 的方程为21y x =+. 曲线D 的方程可化为222()x y a a +-=因为直线MN 平分曲线D ，所以直线MN 过点()0,a ， 所以1a =.（2）由题意可知()()()()()()22112212121212121222222MNt t t t t t t t y y k x x t t t t ----+--====-----曲线D 的方程为22(1)1y x +-= 设直线MN的方程为y m =+，圆心D 到直线MN 的距离为.d因为2221d +=⎝⎭，所以22112m -⎛⎫+= ⎪⎝⎭⎝⎭所以0m =或2m =，所以直线MN的方程为y =或2y =+【点睛】设圆的半径为r ，圆心到直线的距离为d ，弦长为AB ，则有2222AB r d ⎛⎫=+ ⎪⎝⎭.23．已知函数()|1|2|3|,()|1|f x x x g x a x =++-=-. （1）求()8f x 的解集；（2）当[1,3]x ∈-时，()()f x g x 恒成立，求实数a 的取值范围.【答案】（1）1313xx ⎧⎫-⎨⎬⎩⎭∣（2）(,2]-∞ 【解析】（1）利用分类讨论法解绝对值不等式得解； （2）对x 分三种情况1x =、[1,1)x、(1,3]x ∈讨论，分别求出每一种情况下的实数a 的取值范围，最后综合即得解. 【详解】解：（1）由题意得35,1()|1|2|3|7,1335,3x x f x x x x x x x -+<-⎧⎪=++-=-+-≤≤⎨⎪->⎩当1x <-时，()8f x 得1x ≥-，所以此时无解；当13x -时，由()8f x ，即78x -+≤，解得13x -； 当3x >时，由()8f x ，即358x -≤，解得1333x< 综上，解集为1313xx ⎧⎫-⎨⎬⎩⎭∣. （2）①当1x =时，()()f x g x 显然恒成立. ②当[1,1)x时，()7,()(1)f x x g x a x =-=-因为()()f x g x 恒成立， 所以7(1)x a x --，即76111x ax x-=+--恒成立. 令6()1,[1,1)1F x x x=+∈--则min ()a F x 显然()F x 在区间[1,1)-上为增函数， 所以min ()(1)4F x F =-=，所以4a .③当(1,3]x ∈时，()7,()(1)f x x g x a x =-=-. 因为()()f x g x 恒成立， 所以7(1)x a x --，即76111x a x x -=-+--恒成立. 令6()1,(1,3]1G x x x =-+∈-，则min ()a G x 显然()G x 在区间(1,3]上为减函数， 所以min ()(3)2G x G ==， 所以2a .综上所述，实数a 的取值范围为(,2]-∞. 【点睛】本题主要考查绝对值不等式的解法，考查绝对值不等式的恒成立问题，考查函数的单调性求最值，意在考查学生对这些知识的理解掌握水平和分析推理能力.。

河北衡水中学2020届全国高三第三次联合考试理科数学注意事项：1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上相应的位置。

2．全部答案在答题卡上完成，答在本试卷上无效。

3．回答选择题时，选出每小题答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

回答非选择题时，将答案用0.5 mm 黑色笔迹签字笔写在答题卡上。

4．考试结束后，将本试卷和答题卡一并交回。

一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目的要求的。

1．设集合{}22A x x =-<<，{}20B x x x m =-+<，若{}23A B x x =-<<，则实数m =A ．6-B ．6C ．5D ．22．已知()()2i i 55i a ++=+，则实数a =A ．0B ．1C ．2D ．33．已知双曲线2212x y a a -=-与椭圆2215x y +=的焦点相同，则该双曲线的离心率为A B ．43C.D ．34．设()f x 是定义在R 上的奇函数，且在区间(],0-∞上单调递增，则 A ．2321(log 3)(log 2)(log )3f f f <<B ．2231(log )(log 3)(log 2)3f f f <<C ．2321(log )(log 2)(log 3)3f f f <<D ．3221(log 2)(log )(log 3)3f f f <<5．为庆祝中华人民共和国成立70周年，2019年10月1日晚，金水桥南，百里长街成为舞台，3290名联欢群众演员跟着音乐的旋律，用手中不时变幻色彩的光影屏，流动着拼组出五星红旗、祖国万岁、长城等各式图案和文字.光影激滟间，以《红旗项》《我们走在大路上》《在希望的田野上》《领航新时代》四个章节，展现出中华民族从站起来、富起来到强起来的伟大飞跃，在每名演员的手中都有一块光影屏，每块屏有1024颗灯珠，若每个灯珠的开、关各表示一个信息，则每块屏可以表示出不同图案的个数为A ．2048B ．10242C ．21024D ．102410246．已知等差数列{}n a 中，前5项的和n S 满足51525S <<，则公差d 的取值范围为A ．13,22⎛⎫ ⎪⎝⎭B ．(1,4)C ．(1,3)D ．1,12⎛⎫ ⎪⎝⎭7．“勾3股4弦5”是勾股定理的一个特例，据记载，西周时期的数学家商高曾经和周公讨论过“勾3股4弦5”的问题，比毕达哥拉斯发现勾股定理早了500多年.如图，在矩形ABCD 中，ABC △满足“勾3股4弦5”，且AB= 3，E 为AD 上的一点，BE AC ⊥，若BA BE AC λμ=+，则λμ+的值为 A ．925- B ．725C ．1625D ．18．执行如图所示的程序框图，则输出S 的值为 A ．0 BC．1D．19．在长方体1111ABCD A B C D -中，E F G 、、分别为棱111AA C D DD 、、的中点，1=2AB AA AD =，则异面直线EF 与BG 所成角的大小为A ．30B ．60C ．90D ．12010．将函数cos 23y x π⎛⎫=+ ⎪⎝⎭的图象向左平移8π个单位长度，然后再将所得图像上所有点的横坐标扩大为原来的2倍（纵坐标不变），所得图象对应的函数解析式为A ．cos 12y x π⎛⎫=+ ⎪⎝⎭B ．7cos 412y x π⎛⎫=+ ⎪⎝⎭C ．sin 412y x π⎛⎫=+ ⎪⎝⎭D ．sin 12y x π⎛⎫=-+ ⎪⎝⎭11．已知5123456012345671(2)(1)x x a x a a x a x a x a x a x a x x-+--=+++++++，则4a =A ．21B ．42C ．35-D ．210-12．已知函数22,0()=ln(1),0x x x f x x x ⎧--≤⎨+>⎩，若方程1()2f x mx m =+-恰有四个不相等的实数根，则实数的取值范围是A ．121,e 2-⎡⎫⎢⎪⎢⎭⎣B ．121,e 2-⎛⎫⎪⎝⎭C ．121,e 2⎛⎫⎪⎝⎭D ．121e ,2⎛⎫- ⎪⎝⎭二、填空题：本题共4小题，每小题5分，共20分。

河北省衡水市高考数学三模试卷（理科）姓名:________ 班级:________ 成绩:________一、选择题 (共12题；共24分)1. （2分）已知集合则等于（）A . {0,1}B . {1}C . {-1,1}D . {-1,0,1}2. （2分）(2017·鄂尔多斯模拟) 设i为虚数单位，（﹣3+4i）2=a+bi（a，b∈R），则下列判断正确的是（）A . |a+bi|=5B . a+b=1C . a﹣b=﹣17D . ab=1683. （2分）已知是数列{}的前n项和，，那么数列{}是（）A . 等比数列B . 当p≠0时为等比数列C . 当p≠0，p≠1时为等比数列D . 不可能为等比数列4. （2分）若实数，则函数的图象的一条对称轴方程为（）A .B .C .D .5. （2分） (2017高二上·潮阳期末) 执行如图的程序框图，则输出S的值为（）A . 2B . ﹣3C . ﹣D .6. （2分）(2017·沈阳模拟) 某几何体的三视图如图所示，则其体积为（）A . 4B . 8C .D .7. （2分） (2016高一上·宁波期中) 已知偶函数f（x）在区间[0，+∞）单调递减，则满足的实数x的取值范围是（）A . （，）B . [ ，）C . （，）D . [ ，）8. （2分） (2017高二下·莆田期末) 某班周四上午有4节课，下午有2节课，安排语文、数学、英语、物理、体育、音乐6门课，若要求体育不排在上午第一、二节，并且体育课与音乐课不相邻，（上午第四节与下午第一节理解为相邻），则不同的排法总数为（）A . 312B . 288C . 480D . 4569. （2分） (2015高三下·湖北期中) 已知A，B为双曲线E的左，右顶点，点M在E上，△ABM为等腰三角形，顶角为120°，则E的离心率为（）A .B . 2C .D .10. （2分） (2016高二下·市北期中) 函数f（x）=Asin（ωx+φ）（A＞0，|φ|＜）的图象如图所示，为了得到g（x）=sin（2x+ ）的图象，则只需将f（x）的图象（）A . 向右平移个单位长度B . 向右平移个单位长度C . 向左平移个单位长度D . 向左平移个单位长度11. （2分）已知正三棱锥P-ABC的主视图和俯视图如图所示,则此三棱锥的外接球的表面积为（）A . 4πB . 12πC .D .12. （2分） (2017高二下·红桥期末) 已知函数f（x）= sin2x﹣cos2x+1，下列结论中错误的是（）A . f（x）的图象关于（，1）中心对称B . f（x）在（，）上单调递减C . f（x）的图象关于x= 对称D . f（x）的最大值为3二、填空题 (共4题；共5分)13. （2分） (2018高三上·嘉兴期末) 直角中，，为边上的点，且，则 ________；若，则 ________．14. （1分）(2017·福建模拟) 设不等式，表示的平面区域为M，若直线y=k（x+2）上存在M内的点，则实数k的最大值是________．15. （1分）在研究吸烟与患肺癌的关系中，通过收集数据、整理分析数据得“有99%以上的把握认为吸烟与患肺癌有关”．对以下说法：（1）在100个吸烟者中至少有99人患有肺癌；（2）某个人吸烟，那么这个人有99%的概率患有肺癌；（3）在100个吸烟者中一定有患肺癌的人；（4）在100个吸烟者中可能一个患肺癌的人也没有．其中正确的是________ ．（填上所有正确的序号）16. （1分） (2016高二上·浦东期中) 在数列{an}中，Sn是其前n项和，若Sn=n2+1，n∈N* ，则an=________．三、解答题 (共5题；共50分)17. （10分） (2017高一下·宿州期中) 在△ABC中，a，b，c分别为内角A，B，C所对的边且asinB= bcosA（1）求A.（2）若a=3，b=2c，求△ABC的面积．18. （5分）(2017·芜湖模拟) 如图1，在直角梯形ABCD中，AD∥BC，AD⊥DC，BC=2AD=2DC，四边形ABEF 是正方形．将正方形ABEF沿AB折起到四边形ABE1F1的位置，使平面ABE1F1⊥平面ABCD，M为AF1的中点，如图2．（I）求证：AC⊥BM；（Ⅱ）求平面CE1M与平面ABE1F1所成锐二面角的余弦值．19. （10分） (2017高二下·启东期末) 在校运动会上，甲、乙、丙三位同学每人均从跳远，跳高，铅球，标枪四个项目中随机选一项参加比赛，假设三人选项目时互不影响，且每人选每一个项目时都是等可能的（1）求仅有两人所选项目相同的概率；（2）设X为甲、乙、丙三位同学中选跳远项目的人数，求X的分布列和数学期望E（X）20. （10分）已知过点A(1，0)且斜率为k的直线l与圆C：(x-2)2+(y-3)2=1交于M ， N两点.（1）求k的取值范围；（2）=12，其中O为坐标原点，求|MN|.21. （15分） (2019高三上·城关期中) 设函数 .（1）求过点的切线方程；（2）若方程有3个不同的实根，求的取值范围。