5算法设计技术1-蛮力法和分治法_823204234

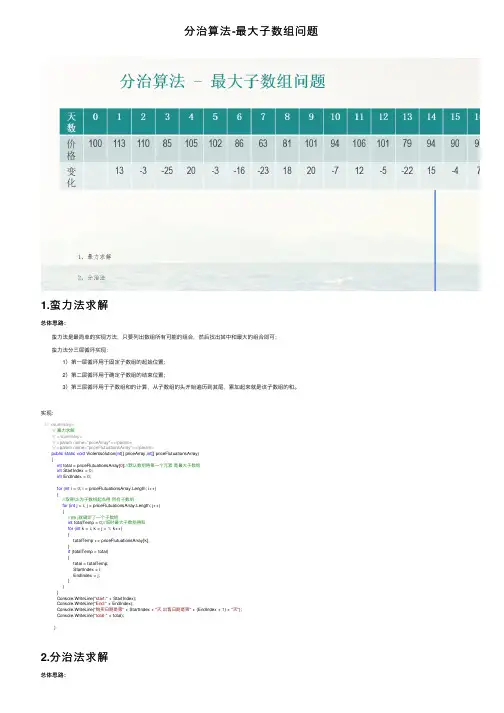
分治算法-最⼤⼦数组问题1.蛮⼒法求解总体思路： 蛮⼒法是最简单的实现⽅法，只要列出数组所有可能的组合，然后找出其中和最⼤的组合即可； 蛮⼒法分三层循环实现： 1）第⼀层循环⽤于固定⼦数组的起始位置； 2）第⼆层循环⽤于确定⼦数组的结束位置； 3）第三层循环⽤于⼦数组和的计算，从⼦数组的头开始遍历到其尾，累加起来就是该⼦数组的和。

实现：///<summary>///暴⼒求解///</summary>///<param name="priceArray"></param>///<param name="priceFlutuationsArray"></param>public static void Violentsolution(int[] priceArray,int[] priceFlutuationsArray){int total = priceFlutuationsArray[0];//默认数组得第⼀个元素是最⼤⼦数组int StartIndex = 0;int EndIndex = 0;for (int i = 0; i < priceFlutuationsArray.Length; i++){//取得以i为⼦数组起点得所有⼦数组for (int j = i; j < priceFlutuationsArray.Length; j++){//由i j就确定了⼀个⼦数组int totalTemp = 0;//临时最⼤⼦数组得和for (int k = i; k < j + 1; k++){totalTemp += priceFlutuationsArray[k];}if (totalTemp > total){total = totalTemp;StartIndex = i;EndIndex = j;}}}Console.WriteLine("start:" + StartIndex);Console.WriteLine("End:" + EndIndex);Console.WriteLine("购买⽇期是第" + StartIndex + "天出售⽇期是第" + (EndIndex + 1) + "天");Console.WriteLine("total:" + total);}2.分治法求解总体思路： 分治法的精髓： 1）分--将问题分解为规模更⼩的⼦问题； 2）治--将这些规模更⼩的⼦问题逐个击破； 3）合--将已解决的⼦问题合并，最终得出“母”问题的解； 所以原数组的最⼤⼦数组求法： 1）分--将原数组拆分成两部分，每个部分再拆分成新的两部分......直到数组被分得只剩下⼀个元素； 2）治--每个⼩型的数组找最⼤⼦数组，只有⼀个元素的数组，解就是该元素； 3）合--将两个⼩型数组合并为⼀个数组，其中解有三种可能：左边的返回值⼤，右边的返回值⼤，中间存在⼀个更⼤的⼦数组和； 返回值应选最⼤的；实现：using System;using System.Collections.Generic;using System.Linq;using System.Text;using System.Threading.Tasks;namespace最⼤⼦数组问题{class Program{//最⼤⼦数组的结构体struct SubArray{public int startIndex;public int endIndex;public int total;}static void Main(string[] args){int[] priceArray = { 100, 113, 110, 85, 105, 102, 86, 63, 81, 101, 94, 106, 101, 79, 94, 90, 97 };int[] pf = new int[priceArray.Length - 1];//价格波动的数组for (int i = 1; i < priceArray.Length; i++){pf[i - 1] = priceArray[i] - priceArray[i - 1];}SubArray subArray = GetMaxSubArray(0, pf.Length - 1, pf);Console.WriteLine(subArray.startIndex);Console.WriteLine(subArray.endIndex);Console.WriteLine("我们在第" + subArray.startIndex + "天买⼊，在第" + (subArray.endIndex + 1) + "天卖出");Console.ReadKey();}///<summary>///这个⽅法⽤来取得array这个数组从low到high得最⼤⼦数组///</summary>///<param name="low"></param>///<param name="high"></param>///<param name="array"></param>static SubArray GetMaxSubArray(int low,int high,int[] array){if (low == high){SubArray subarray;subarray.startIndex = low;subarray.endIndex = high;subarray.total = array[low];return subarray;}int mid = (low + high)/2; //低区间[low,mid] ⾼区间[mid+1,high]SubArray subArray1= GetMaxSubArray(low, mid, array);SubArray subArray2=GetMaxSubArray(mid+1, high, array);SubArray subArray3 = GetMaxSub(low, mid, high, array);if (subArray1.total >= subArray2.total && subArray1.total >= subArray3.total){return subArray1;}else if (subArray2.total >= subArray1.total && subArray2.total >= subArray3.total){return subArray2;}else{return subArray3;}}static SubArray GetMaxSub(int low,int mid,int high,int[] array){//从【low,mid】找到最⼤⼦数组[i,mid]int total1 = array[mid];int startIndex = mid;int totalTemp = 0;for (int i = mid; i >= low; i--){totalTemp += array[i];if (totalTemp > total1){total1 = totalTemp;startIndex = i;}}//从【mid+1,high】找到最⼤⼦数组[mid+1,j]int total2 = array[mid + 1];int endIndex = mid + 1;totalTemp = 0;for (int j = mid + 1; j <= high; j++) {totalTemp += array[j];if (totalTemp > total2){total2 = totalTemp;endIndex = j;}}SubArray subArray3;subArray3.startIndex = startIndex; subArray3.endIndex = endIndex; subArray3.total = total1 + total2;return subArray3;}}}。

五⼤算法设计思想（转载）⼀分治法1.1 概念： 将⼀个难以直接解决的⼤问题，分割成⼀些规模较⼩的相同问题，以便各个击破，分⽽治之。

1.2 思想策略： 对于⼀个规模为n的问题，若该问题可以容易地解决（⽐如说规模n较⼩）则直接解决，否则将其分解为k个规模较⼩的⼦问题，这些⼦问题互相独⽴且与原问题形式相同，递归地解这些⼦问题，然后将各⼦问题的解合并得到原问题的解。

1.3 特征：1) 该问题的规模缩⼩到⼀定的程度就可以容易地解决2) 该问题可以分解为若⼲个规模较⼩的相同问题，即该问题具有最优⼦结构性质。

3) 利⽤该问题分解出的⼦问题的解可以合并为该问题的解；4) 该问题所分解出的各个⼦问题是相互独⽴的，即⼦问题之间不包含公共的⼦⼦问题。

1.4 对特征的解析：第⼀条特征是绝⼤多数问题都可以满⾜的，因为问题的计算复杂性⼀般是随着问题规模的增加⽽增加；第⼆条特征是应⽤分治法的前提它也是⼤多数问题可以满⾜的，此特征反映了递归思想的应⽤；第三条特征是关键，能否利⽤分治法完全取决于问题是否具有第三条特征，如果具备了第⼀条和第⼆条特征，⽽不具备第三条特征，则可以考虑⽤贪⼼法或动态规划法。

第四条特征涉及到分治法的效率，如果各⼦问题是不独⽴的则分治法要做许多不必要的⼯作，重复地解公共的⼦问题，此时虽然可⽤分治法，但⼀般⽤动态规划法较好。

1.5 基本步骤：1 分解：将原问题分解为若⼲个规模较⼩，相互独⽴，与原问题形式相同的⼦问题；2 解决：若⼦问题规模较⼩⽽容易被解决则直接解，否则递归地解各个⼦问题3 合并：将各个⼦问题的解合并为原问题的解。

1.6 适⽤分治法求解的经典问题：1）⼆分搜索2）⼤整数乘法3）Strassen矩阵乘法4）棋盘覆盖5）合并排序6）快速排序7）线性时间选择8）最接近点对问题9）循环赛⽇程表10）汉诺塔⼆动态规划2.1 概念 每次决策依赖于当前状态，⼜随即引起状态的转移。

⼀个决策序列就是在变化的状态中产⽣出来的，所以，这种多阶段最优化决策解决问题的过程就称为动态规划。

1分治法1.1基本概念在计算机科学中，分治法是一种很重要的算法。

字面上的解释是“分而治之”，就是把一个复杂的问题分成两个或更多的相同或相似的子问题，再把子问题分成更小的子问题……直到最后子问题可以简单的直接求解，原问题的解即子问题的解的合并。

这个技巧是很多高效算法的基础，如排序算法(快速排序，归并排序)，傅立叶变换(快速傅立叶变换)……任何一个可以用计算机求解的问题所需的计算时间都与其规模有关。

问题的规模越小，越容易直接求解，解题所需的计算时间也越少。

例如，对于n个元素的排序问题，当n=1时，不需任何计算。

n=2时，只要作一次比较即可排好序。

n=3时只要作3次比较即可，…。

而当n较大时，问题就不那么容易处理了。

要想直接解决一个规模较大的问题，有时是相当困难的。

1.2基本思想及策略分治法的设计思想是：将一个难以直接解决的大问题，分割成一些规模较小的相同问题，以便各个击破，分而治之。

分治策略是：对于一个规模为n的问题，若该问题可以容易地解决（比如说规模n较小）则直接解决，否则将其分解为k个规模较小的子问题，这些子问题互相独立且与原问题形式相同，递归地解这些子问题，然后将各子问题的解合并得到原问题的解。

这种算法设计策略叫做分治法。

如果原问题可分割成k个子问题，1<k≤n，且这些子问题都可解并可利用这些子问题的解求出原问题的解，那么这种分治法就是可行的。

由分治法产生的子问题往往是原问题的较小模式，这就为使用递归技术提供了方便。

在这种情况下，反复应用分治手段，可以使子问题与原问题类型一致而其规模却不断缩小，最终使子问题缩小到很容易直接求出其解。

这自然导致递归过程的产生。

分治与递归像一对孪生兄弟，经常同时应用在算法设计之中，并由此产生许多高效算法。

1.3分治法适用的情况分治法所能解决的问题一般具有以下几个特征：1) 该问题的规模缩小到一定的程度就可以容易地解决2) 该问题可以分解为若干个规模较小的相同问题，即该问题具有最优子结构性质。

实验项目1：蛮力法与分治法应用1、目的与要求：实验目的：了解蛮力法和分治法的基本思想，学会运用蛮力法和分治法解决实际系统设计应用中碰到的问题。

实验要求：用蛮力法实现选择、冒泡排序，或旅行商问题、背包问题等问题（任选其中之一）。

用分治法实现合并排序或快速排序。

要求写出算法的伪代码描述，并编写程序实现之，相关算法放在函数内实现，主程序给出测试用例，要设计足够多的相关测试用例，验证程序的正确性。

注意观察程序执行结果和运行的时间。

实验报告要求给出问题定义及算法的伪代码描述，程序设计的代码，算法的测试用例及结果，并分析算法的时间效率，回答指导书中的思考题。

2、实验内容：（2）用分治法实现快速排序、合并排序算法。

本实验主要是用分治法实现合并排序，快速排序程序等。

合并排序算法描述：MergeSort ( A[0...p-1] )// input 待排序数组A[0..n-1]// output 非降序排列的数组A[0..n-1]if ( n>1 ) {//至少有2个元素Copy A[0.. n/2-1 ] to B[0.. n/2-1 ];Copy A[n/2..n-1 ] to C[0.. n/2-1 ];MergeSort ( B[0.. n/2-1 ] );MergeSort (C[0.. n/2-1 ]t);Merge (B, C, A); //复制回数组a快速排序算法描述：QuickSort ( A[1.. r ] ){if (l<r) s=Partition( A[l,r] ); // s 是分裂位置QuickSort ( A[l..s-1] ); //对左半段排序QuickSort ( A[s+1,r); //对右半段排序}Partition ( A[l..r] ){p=A[[l] ;i = l; j = r + 1;repeatedrepeated i=i+1; until A[i]> p // 将>= x的元素交换到左边区域repeated i=i+1; until A[i]> p // <= x的元素交换到右边区域Swap( A[i], A[j] )Until i>jSwap( A[i] = a[j] );Swap( A[l], A[j] )return j;要求先给出算法的伪代码，然后用C++或其他程序设计语言编写程序实现之，并设计相关的测试用例，验证程序的正确性。

实验四求最近点对算法1.算法设计思路：设共有n个点，找其中距离最近的两点及其距离。

（1）蛮力法：蛮力法的思路是把所有点之间距离比较找出中间最小的。

先假设最短距离是第一个元素和第二个元素的距离，然后求第一个元素与其后的（n-1）个元素各自的距离，若比之前记录的最短距离小则记录当前值···求第i个元素与其后的（n-i）个元素各自的距离，记录之前所得到的所有距离中的最小值，直到计算到第（n-1）个元素与第n个元素的距离，此时记录的距离即为这n个元素中的最短距离。

（2）分治法：分治法是把一个大的问题划分成相似的小问题，采用递归的思想。

找中线把n个元素分成左右两部分元素分别求得两边的最短距离，然后取两者中的最小者记为l，在中线两边分别取l的距离，记录该距离范围内点的个数，中线左边有L个元素，右边有R个元素，求左边元素到右边元素的距离看其是否小于之前记录的最短距离，小则记录下来，此时的右边元素只取y值和左边元素y值距离小于l的（减少循环次数）。

循环结束即可找到最小的距离。

2.程序代码：#include<iostream>#include<cstdlib>#include<ctime>#include<cmath>using std::cout;using std::endl;#define N 5int x[N],y[N],record[N]; //产生原始点数据，x坐标放在x[]中，y坐标放在y[]中。

double Min;//////////////////////////产生随机数组/////////////////////////////void randnum(){int i;srand(time(0));for (i=0;i<N;i++){x[i]=rand()%N;cout<<x[i]<<' ';}cout<<endl;for (i=0;i<N;i++){y[i]=rand()%N;cout<<y[i]<<' ';}cout<<endl;}//////////////////////////////交换数组元素/////////////////////////// void swap(int & a, int & b){int temp=a;a=b;b=temp;}///////////////////////////////求平方///////////////////////////////////int square(int x){return x*x;}/////////////////////////////////////求两点之间距离////////////////////double lengthf(int x1,int y1,int x2,int y2){return sqrt(square(x1-x2)+square(y1-y2));}//////////////////////////////////求两者中最小者////////////////////// double min(double a,double b){if (a>=b)return b;elsereturn a;}////////////////////////////对平面数组排序//////////////////////////// void sort(int A[]){int i,j;for (i=0;i<N;i++)record[i]=i;for (j=1;j<N;j++){i=j;while (i>=0&&A[i]<A[i-1]){swap(A[i],A[i-1]);swap(record[i-1],record[i]); //得到x排序后对应的原y的坐标i--;}}cout<<"排序后的元素数组："<<endl;for (i=0;i<N;i++)cout<<A[i]<<' ';cout<<endl;for (i=0;i<N;i++)cout<<record[i]<<' ';cout<<endl;}///////////////////////////穷举法找最小点对///////////////////////////////double exhaustion(){int i,j,k1,k2;double num;double length;num=10000;k1=k2=-1;for (j=0;j<N-1;j++){for (i=j+1;i<N;i++){length=lengthf(x[i],y[i],x[j],y[j]);if (length<num){num=length;k1=i;k2=j;}}}cout<<"平面数组最短距离是："<<endl;cout<<"min="<<num<<endl;cout<<"对应数组下标及点坐标为："<<endl;cout<<"i="<<k1<<','<<k2<<endl;cout<<"(x1,y1)="<<'('<<x[k1]<<','<<y[k1]<<')'<<endl<<"(x2,y2)="<<'('<<x[k2]<<','<<y[k2]<<')' <<endl;return num;}////////////////////////////////////分治法////////////////////////////////*************************************************************************/double merge(int left,int right){double mlength;if (right==left)mlength=10e-6;if (right==left+1)mlength=lengthf(x[right],y[record[right]],x[left],y[record[left]]); //两个点时求最小值if (right-left==2)mlength=min(min(lengthf(x[right-1],y[record[right-1]],x[left],y[record[left]]),lengthf(x[right],y[re cord[right]],x[left+1],y[record[left+1]])),lengthf(x[right],y[record[right]],x[left],y[record[left]]));//三个点时求最大值return mlength;}double divide(int left,int right){if (right-left<=2){Min=merge(left,right);}else{double l1,l2,mi; //l1记录划分区域后左半面最小距离，l2记录右半面最小距离，min为两者中较小者，m为全部中的最小者int rem1,rem2,l; //记录获得最短距离对应的两个点//int il,jl,ir,jr;int i,j;int R,L;R=L=0; //记录划分小区域后的左半块和右半块个有多少元素l1=l2=Min=100;l=(right-left+1)/2-1; //中线位置///////////////////////////////////////////////////l1=divide(left,l);l2=divide(l+1,right);if (l1<l2){Min=l1;//cout<<"两半面最短距离是："<<min;else{Min=l2;//cout<<"两半面最短距离是："<<min;}///////////////////得到右半块元素数R//cout<<"min="<<min<<endl;for (i=l+1;i<N;i++){if (x[i]-x[l]<=Min)R++;else break;}//cout<<"R="<<R<<endl;/////////////////////得到左半块元素数Lfor (i=l;i>=0;i--){if (x[l]-x[i]<=Min)L++;else break;}//cout<<"L="<<L<<endl;if (L!=0&&R!=0){for (i=l-L+1;i<=l;i++)for (j=l+1;j<=l+R;j++){if (y[record[j]]-y[record[i]]<Min||-Min<y[record[j]]-y[record[i]]){mi=lengthf(x[i],y[record[i]],x[j],y[record[j]]);if (mi<Min){Min=mi;rem1=i;rem2=j;}}}// cout<<"min="<<min<<endl;//cout<<"rem1="<<rem1<<endl<<"rem2="<<rem2<<endl;}return Min;}/***********************************************************************///////////////////////////////////主函数///////////////////////////////////int main(){//double a;randnum();cout<<"***************************遍历法*************************"<<endl;exhaustion();cout<<"***************************分治法*************************"<<endl;sort(x);divide(0,N-1);cout<<"元素组中最短距离为："<<endl;cout<<"min="<<Min<<endl;return 0;}3.实验数据及实验结果：实验数据：随机产生的五个点坐标分别为：（1，3），（4，2），（3，0），（2，0），（0，3）实验结果：用蛮力法得到平面数组最短距离为：min=1用分治法得到平面数组最短距离为：min=14.实验总结：从本次试验中得到的领悟是：分治法事把问题分解成两个相似小问题，子问题和原来的大问题解决方法一样所以可以用递归，分治法重要是找到递归出口，什么时候递归结束，一般都有元素个数的限制。

蛮力法与分治法求解最近对问题1、蛮力法蛮力法是一种简单直接地解决问题的方法，常常直接基于问题的描述和所涉及的概念定义，来求解问题。

虽然巧妙和高效的算法很少来自于蛮力法，但它仍是一种重要的算法设计策略：（1）适用泛围广，是能解决几乎所有问题的一般性方法；（2）常用于一些非常基本、但又十分重要的算法（排序、查找、矩阵乘法和字符串匹配等）；（3）解决一些规模小或价值低的问题；（4）可以做为同样问题的更高效算法的一个标准；（5）可以通过对蛮力法的改进来得到更好的算法。

2、分治法分治法，就是分而治之即把一个复杂的问题分成两个或更多的相同或相似的子问题，再把子问题分成更小的子问题直到问题解决。

分治法在求解问题时，效率比较高，也是一种重要的算法策略：（1）该问题的规模缩小到一定的程度就可以容易地解决；（2）该问题可以分解为若干个规模较小的相同问题，即该问题具有最优子结构性质；（3）利用该问题分解出的子问题的解可以合并为该问题的解；（4）该问题所分解出的各个子问题是相互独立的，即子问题之间不包含公共的子子问题。

算法的基本思想及复杂度分析1．蛮力法（1）基本思想蛮力法求解最近对问题的过程是：分别计算每一对点之间的距离，然后通过排序找出距离最小的一对，为了避免对同一对点计算两次距离，只考虑i<j的那些点对（P i，P j）。

（2）复杂度分析算法的基本操作是计算两个点的欧几里得距离。

在求欧几里得距离时，我们要避免求平方根操作，因为求平方根时要浪费时间，而在求解此问题时，求解平方根并没什么更大的意义。

如果被开方的数越小，则它的平方根也越小。

因此，算法的基本操作就是求平方即可，其执行次数为：T(n)=∑-=11n i ∑+=n i j 12 =2∑-=-11)(n i i n =n （n-1）=O （n2） 2.分治法（1）基本思想用分治法解决最近对问题，就是将集合S 分成两个子集S1和S2，每个子集中有n/2个点。

《算法设计与分析》实验报告一学号： 1004091130 姓名：金玉琦日期：2011-11-03得分：一、实验内容：分别用蛮力法，分治法和动态规划法射击最大字段和问题的算法，比较不同算法的时间性能。

二、所用算法的基本思想及复杂度分析：1.蛮力法1）基本思想蛮力法求解最大子段和问题的设计思想很简单, 依次从第1 个数开始计算长度为1 ,2 , ⋯, n 的子段和, 将这一阶段的最大子段和保存起来, 再从第2 个数开始计算长度为1 ,2 , ⋯, n - 1 的子段和, 将这一阶段的最大子段和与前一阶段求得的最大子段和比较, 取较大者保存起来, 以此类推, 最后保存的即是整个序列的最大子段和。

2）复杂度分析时间复杂度是O(n2);2.分治法1）基本思想划分: 按照平衡子问题的原则, 将序列( a1 , a2 , ⋯, a n ) 划分成长度相同的两个子序列( a1 , ⋯, a n/ 2 ) 和( a n/ 2 + 1 , ⋯, a n ) , 则会出现以下3 种情况:① a1 , ⋯, a n 的最大子段和= a1 , ⋯, a n/ 2 的最大子段和;②a1 , ⋯, a n 的最大子段和= a n/ 2 + 1 , ⋯, a n 的最大子段和;③a1 , ⋯, a n 的最大子段和= Σjk = i a k , 且1 ≤i ≤n/ 2 , n/ 2 + 1 ≤j ≤n。

比较在划分阶段的3 种情况下的最大子段和, 取三者之中的较大者为原问题的解。

2）复杂度分析算法的时间复杂性为O( n log2 n)。

3.动态规划法1）基本思想动态规划法求解最大子段和问题的关键就在于确定动态规划函数。

求解的主要思想如下：将序列(a1,a2,……,a n)中的从第1个数字到第i个数字之间的最大子段和存入数组b[i]中，则b数组中的最大元素就是所求。

b数组求法如下：b[i-1]+a i ,b[i-1]>0b[i]=a i,b[i-1]<=02）复杂度分析动态规划的时间复杂度是O(n)三、源程序及注释：#define MAX 10000#include <IOSTREAM>#include <TIME.H>#include <WINDOWS.H>using namespace std;//蛮力法int BF_Sum(int n[],int l,int &index1,int &index2){int max=0;int sum=0;int i,j;for (i=0;i<l-1;i++){sum=n[i];for(j=i+1;j<l;j++){if(sum>=max){index1=i;index2=j;max=sum;}sum+=n[j];}}return max;}//分治法int DC_Sum(int n[],int l,int r){int sum=0,s1=0,s2=0;int lefts=0,rights=0;int leftsum=0,rightsum=0;int center;int i;if(l==r){if(n[l]>0)sum=n[l];elsesum=0;}else{center=(l+r)/2;leftsum=DC_Sum(n,l,center);rightsum=DC_Sum(n,center+1,r);for(i=center;i>=l;i--){lefts+=n[i];if(lefts>=s1) s1=lefts;}for(i=center+1;i<=r;i++){rights+=n[i];if(rights>=s2) s2=rights;}sum=s1+s2;if(sum<leftsum) sum=leftsum;if(sum<rightsum) sum=rightsum; }return sum;}//动态规划法int DY_Sum(int a[],int l){int sum=0;int *b=(int *)malloc(l*sizeof(int)); b[0]=a[0];for(int i=1;i<l;i++){if(b[i-1]>0)b[i]=b[i-1]+a[i];elseb[i]=a[i];}for(int j=0;j<l;j++)if(b[j]>sum)sum=b[j];delete []b;return sum;}void main(){int num[MAX];int i;int n;int index1,index2;LARGE_INTEGER begin,end,frequency; QueryPerformanceFrequency(&frequency);//生成随机序列//////////cout<<"输入序列大小：";cin>>n;srand(time(0));for (i=0;i<n;i++){if(rand()%2==0)num[i]=rand()/30;elsenum[i]=(-1)*rand()/30;if(n<=100)cout<<num[i]<<" ";}cout<<endl;//蛮力法//cout<<"\n蛮力法:"<<endl;cout<<"最大子段和:";QueryPerformanceCounter(&begin);cout<<BF_Sum(num,n,index1,index2)<<endl; QueryPerformanceCounter(&end);if(n<=100){cout<<"最大子段:";cout<<"从"<<num[index1]<<"到"<<num[index2]<<endl;}cout<<"时间:"<<(double)(end.QuadPart-begin.QuadPart)/frequency.QuadPart <<"s"<<endl;//分治法/////////////////////////////////////////cout<<"\n分治法:"<<endl;cout<<"最大子段和:";QueryPerformanceCounter(&begin);cout<<DC_Sum(num,0,n)<<endl;QueryPerformanceCounter(&end);cout<<"时间:"<<(double)(end.QuadPart-begin.QuadPart)/frequency.QuadPart<<"s"<<endl;//动态规划法/////////////////////////////////////cout<<"\n动态规划法:"<<endl;cout<<"最大子段和:";QueryPerformanceCounter(&begin);cout<<DY_Sum(num,n)<<endl;QueryPerformanceCounter(&end);cout<<"时间:"<<(double)(end.QuadPart-begin.QuadPart)/frequency.QuadPart<<"s"<<endl;}四、运行输出结果：五、调试和运行程序过程中产生的问题、采取的措施及获得的相关经验教训：调试过程中，蛮力法会出现计算错误。