计组-加法器实验报告

加法器电路设计实验报告【加法器电路设计实验报告】一、实验目的本实验的主要目标是通过实际操作，设计并实现一个基础的加法器电路，以深入理解数字逻辑电路的设计原理和工作方式。

通过对半加器、全加器以及多位加法器的设计与搭建，进一步熟悉集成门电路的应用，掌握组合逻辑电路的设计方法，并能对电路的逻辑功能进行有效的验证与分析。

二、实验原理加法器是数字系统中的基本运算单元，其核心工作原理基于二进制数的加法规则。

在最基础的层面上，一个半加器（Half Adder）用于计算两个一位二进制数的和，同时产生一个进位输出；而全加器（Full Adder）在此基础上增加了处理来自低位的进位输入，可以完成三位二进制数的相加。

对于多位二进制数的加法，可以通过级联多个全加器来实现。

1. 半加器：由两个异或门（XOR）实现“和”输出，一个与门（AND）实现“进位”输出，即S=A XOR B，Cout=A AND B。

2. 全加器：除了接收两个数据输入A和B外，还接收一个进位输入Cin，同样由异或门计算“和”，但“进位”输出需要考虑三个输入的与或逻辑关系，即S=A XOR B XOR Cin，Cout=(A AND B) OR (B AND Cin) OR (A AND Cin)。

三、实验步骤1. 半加器设计：首先，利用集成电路库中的逻辑门元件构建半加器，将A 和B作为异或门的输入得到和信号S，将A和B分别连接到与门的两个输入端得到进位信号Cout。

2. 全加器设计：在半加器的基础上，增加一个输入端Cin代表低位的进位，同样运用异或门和与门组合形成全加器的逻辑结构，根据全加器的逻辑表达式连接各门电路。

3. 多位加法器设计：为了实现多位二进制数的加法，将若干个全加器按照从低位到高位的顺序级联起来，每级全加器的进位输出连接到下一级的进位输入。

四、实验结果及分析经过电路设计与仿真测试，成功实现了从半加器到多位加法器的功能转化。

当给定两组多位二进制数后，所设计的加法器电路能够准确无误地计算出它们的和，并正确显示进位信息。

姓名班级 1 学号
实验日期节次教师签字成绩
加法计算器
1.实验目的
熟悉掌握有关时序逻辑电路的组成原理；
通过设计一个简单的计算器，掌握组合逻辑电路、时序逻辑电路的分析和设计方法；
了解及掌握中规模集成电路，了解各个芯片的管脚图及结构图。

能够掌握全加器、计数器等的功能及实现方法；
锻炼自己的动手实践能力，并自己设计电路，培养自己的兴趣。

2.总体设计方案或技术路线
设计一个多功能计算器，它能实现简单的加法运算，只能显示结果为0—16的和数，并能够在数码管上显示，加法运算的实现要求：用四个开关代表四位二进制数，操纵开关，输入二进制数码，则在对应的数码管1上会显示出相应的十进制数，即代表被加数；用同样的方法在另外的四个开关上输入二进制数，则在对应的数码管2上还会出现相应的十进制数，即代表加数；当加数与被加数都输入后，在数码管3和数码管4上出现两数的和，两个数码管可以显示到和的十位。

3.实验电路图
4.仪器设备名称、型号和技术指标
直流稳压电源、试验箱、万用表；
2个74LS00D、1个74LS283D、1个74LS04D、2个74LS08D、1个74LS20D；
单刀双掷开关9个、导线若干。

一、实验目的1. 理解加法器的基本原理和结构。

2. 掌握加法器的使用方法和调试技巧。

3. 通过实际操作，加深对数字电路基础知识的理解。

二、实验器材1. 实验箱2. 加法器芯片（如741）3. 逻辑分析仪4. 万用表5. 连接线6. 电源三、实验原理加法器是一种基本的数字电路，用于实现两个或多个数字的加法运算。

本实验以半加器和全加器为基础，通过级联实现多位数的加法运算。

1. 半加器：完成两个一位二进制数相加，并产生和与进位。

2. 全加器：在半加器的基础上增加一个进位输入端，实现多位数的加法运算。

四、实验步骤1. 搭建电路：- 将加法器芯片插入实验箱的相应位置。

- 根据实验要求，连接输入端、输出端和电源。

- 使用逻辑分析仪观察输入信号和输出信号。

2. 半加器测试：- 将两个一位二进制数输入到半加器的两个输入端。

- 观察逻辑分析仪的输出，验证半加器的功能。

3. 全加器测试：- 将两个一位二进制数和一个进位信号输入到全加器的三个输入端。

- 观察逻辑分析仪的输出，验证全加器的功能。

4. 多位数加法测试：- 将多位二进制数输入到全加器的相应输入端。

- 观察逻辑分析仪的输出，验证多位数的加法运算。

5. 实验结果分析：- 对比理论计算结果和实验结果，分析实验误差原因。

五、实验结果与分析1. 半加器测试：- 输入：A=0, B=0- 输出：和=0，进位=0- 输入：A=1, B=0- 输出：和=1，进位=0- 输入：A=0, B=1- 输出：和=1，进位=0- 输入：A=1, B=1- 输出：和=0，进位=12. 全加器测试：- 输入：A=0, B=0, 进位=0- 输出：和=0，进位=0- 输入：A=1, B=0, 进位=0- 输出：和=1，进位=0- 输入：A=0, B=1, 进位=0- 输出：和=1，进位=0- 输入：A=1, B=1, 进位=0- 输出：和=0，进位=13. 多位数加法测试：- 输入：A=1010，B=1101，进位=0- 输出：和=10111，进位=1实验结果表明，加法器能够实现预期的功能，实验结果与理论计算基本一致。

杭州电子科技大学计算机学院
实验报告
实验项目：实验2-超前进位加法器设计实验
课程名称：计算机组成原理与系统结构课程设计
姓名：学号：同组姓名：学号：
实验位置（机号）：
实验日期：指导教师：
二、结果
思考题：
（1）综合得到的电路图，它和想要设计的电路在引脚的输入输出方面是完全相同的，但是相比较内部的RTL图，实验实现的结果是相同的，但是我编写的实验代码并没有调用实验一的全加器设计。

（2）尝试编写8位超前进位加法器设计实验
module add_8 ( input [7:0]a, input [7:0]b, input cin, output [7:0] s, output co );
wire [7:0]c_tmp;
wire [7:0]g;
wire [7:0]p;。

计组实验报告(共10篇)计组实验报告计算机组成原理实验报告一一、算术逻辑运算器1. 实验目的与要求：目的：①掌握算术逻辑运算器单元ALU（74LS181）的工作原理。

②掌握简单运算器的数据传输通道。

③验算由74LS181等组合逻辑电路组成的运输功能发生器运输功能。

④能够按给定数据，完成实验指定的算术/逻辑运算。

要求：完成实验接线和所有练习题操作。

实验前，要求做好实验预习，掌握运算器的数据传送通道和ALU 的特性，并熟悉本实验中所用的模拟开关的作用和使用方法。

实验过程中，要认真进行实验操作，仔细思考实验有关的内容，把自己想得不太明白的问题通过实验去理解清楚，争取得到最好的实验结果，达到预期的实验教学目的。

实验完成后，要求每个学生写出实验报告。

2. 实验方案：1．两片74LS181（每片4位）以并/串联形式构成字长为8为的运算器。

2．8为运算器的输出经过一个输入双向三态门（74LS245）与数据总线相连，运算器的两个数据输入端分别与两个8位寄存器（74LS273）DR1和DR2的输出端相连，DR1和DR2寄存器是用于保存参加运算的数据和运算的结果。

寄存器的输入端于数据总线相连。

3．8位数据D7~D0（在“INPUT DEVICE”中）用来产生参与运算的数据，并经过一个输出三态门（74LS245）与数据总线相连。

数据显示灯（BUS UNIT）已与数据总线相连，用来显示数据总线上所内容。

4．S3、S2、S1、S0是运算选择控制端，由它们决定运算器执行哪一种运算（16种算术运算或16种逻辑运算）。

5．M是算术/逻辑运算选择，M＝0时，执行算术运算，M＝1时，执行逻辑运算。

6．Cn是算术运算的进位控制端，Cn=0(低电平)，表示有进位，运算时相当于在最低位上加进位1，Cn=1(高电平)，表示无进位。

逻辑运算与进位无关。

7．ALU-B是输出三态门的控制端，控制运算器的运算结果是否送到数据总线BUS上。

低电平有效。

计算机组成原理加法器实验实训报告一、实验目的本次实验旨在通过实际操作加法器电路，加深对计算机组成原理中加法器的理解，掌握加法器的工作原理和实验操作技能。

二、实验内容1. 搭建基本加法器电路2. 进行加法器实验3. 分析实验结果并撰写实验报告三、实验器材和工具1. 电路实验箱2. 电源3. 电路连接线4. 示波器5. 多用途数字实验仪6. 逻辑门集成电路四、实验步骤1. 搭建基本加法器电路1) 将逻辑门集成电路插入电路实验箱中2) 连接逻辑门的输入端和输出端3) 接入电源并进行必要的调试2. 进行加法器实验1) 输入两个二进制数，并将其连接到逻辑门输入端2) 观察输出端的变化3) 调节输入信号，验证加法器的正确性和稳定性3. 分析实验结果1) 记录实验数据2) 分析实验结果，对比理论值和实际值的差异3) 总结实验中的经验和问题，并提出改进建议五、实验数据1. 输入数据：A = 1010B = 11012. 输出数据：Sum = xxxCarryout = 1六、实验结果分析通过实验，我们成功搭建了基本加法器电路，并进行了加法器实验。

实验结果表明，加法器能够正确地对两个二进制数进行加法运算，并输出正确的结果。

通过比对理论值和实际值，我们发现存在一定的偏差，可能是由于电路连接不良或逻辑门延迟等因素导致。

在今后的实验中，我们需要注意电路连接质量和信号延迟，以提高实验结果的准确性和稳定性。

七、实验总结通过本次加法器实验，我们加深了对计算机组成原理中加法器的理解，掌握了基本的加法器实验操作技能。

我们也发现了一些问题并提出了改进建议。

在今后的学习和实验中，我们将继续加强对计算机组成原理的学习，不断提升实验操作能力，为今后的科研工作和实际应用打下坚实的基础。

八、参考资料1. 《计算机组成原理》（第五版），唐朔飞，张善民，电子工业出版社2. 《数字逻辑与计算机设计》（第三版），David M. Harris，Sarah L. Harris，清华大学出版社以上是本次计算机组成原理加法器实验实训报告的全部内容，谢谢阅读。

《计算机组成原理》课程设计实验报告1 任务描述掌握运算器的原理及其设计方法的基础上，利用TD-CMA 计算机组成原理教学实验系统的CPLD单元或FPGA单元，使用Quartus II 软件,使用Verilog或VHDL语言设计方式实现一8位并行进位并行加法器,并进行验证。

2 实验设备该实验所使用的是TD-CMA实验箱及PC机一台。

3 设计原理和方法3.1 工作原理加法器是执行二进制加法运算的逻辑部件，也是CPU 运算器的基本逻辑部件（减法可以通过补码相加来实现）。

加法器又分为半加器和全加器（FA），不考虑低位的进位，只考虑两个二进制数相加，得到和以及向高位进位的加法器为半加器，而全加器是在半加器的基础上又考虑了低位过来的进位信号。

3.2 设计方法对加法器进位的逻辑表达式做推导：C0 = 0Ci+1 = AiBi + AiCi + BiCi设gi = AiBi；pi = Ai + Bi，则有Ci+1 = gi + piCi由于gi、pi 只和Ai、Bi 有关，这样Ci+1 就只和Ai、Ai-1、…、A0，Bi、Bi-1、…B0 及C0有关。

所以各位的进位Ci、Ci-1、…、C1 就可以并行地产生。

转化为VHDL语言即为：sum(n)<=ain(n) xor bin(n) xor h(n);h(n+1):=(ain(n) and bin(n)) or (h(n) and ain(n)) or (h(n) and bin(n));3.3设计思想本算法的核心思想是把8 位加法器分成两个4 位加法器，先求出低4 位加法器的各个进位，特别是向高4 位加法器的进位C4。

然后，高4 位加法器把C4 作为初始进位，使用低4 位加法器相同的方法来完成计算。

每一个4 位加法器在计算时，又分成了两个2 位的加法器。

4 设计过程（1）根据上述加法器的逻辑原理使用 Quartus II 软件编辑相应的电路原理图并进行编译，其在EPM1270 芯片中对应的引脚如图，框外文字表示I/O 号，框内文字表示该引脚的含义。

加法器实验报告加法器实验报告概述：本次实验旨在设计和实现一个加法器电路，通过对电路的搭建和测试，验证加法器的正确性和可行性。

加法器是计算机中最基本的算术运算器之一，其在数字逻辑电路中扮演着重要的角色。

1. 实验背景加法器是一种基本的数字逻辑电路，用于实现数字的加法运算。

在计算机中，加法器被广泛应用于算术逻辑单元(ALU)和中央处理器(CPU)等部件中，用于进行各种数值计算和逻辑运算。

因此，了解和掌握加法器的工作原理和设计方法对于理解计算机原理和数字电路设计具有重要意义。

2. 实验目的本次实验的主要目的是通过设计和实现一个4位二进制加法器电路，验证加法器的正确性和可行性。

具体要求如下：- 设计并搭建一个4位二进制加法器电路；- 对电路进行测试，验证其加法运算的正确性；- 分析电路的性能和优化空间。

3. 实验原理加法器是通过逻辑门电路实现的。

在本次实验中，我们将使用全加器电路来实现4位二进制加法器。

全加器是一种能够实现两个二进制位相加并考虑进位的电路。

通过将多个全加器连接起来，可以实现更高位数的二进制加法器。

4. 实验步骤4.1 设计加法器电路的逻辑功能首先，我们需要确定加法器电路的逻辑功能。

在这个实验中，我们需要实现两个4位二进制数的相加运算，并输出结果。

具体的逻辑功能可以通过真值表或逻辑表达式来描述。

4.2 搭建电路根据逻辑功能的要求，我们可以使用逻辑门电路来搭建加法器。

在本次实验中，我们将使用多个全加器电路来实现4位二进制加法器。

通过将多个全加器连接起来，可以实现更高位数的二进制加法器。

4.3 进行电路测试在搭建完电路后，我们需要对电路进行测试，以验证其加法运算的正确性。

可以通过输入一些测试用例，并比较输出结果与预期结果是否一致来进行测试。

5. 实验结果与分析通过对加法器电路的测试，我们可以得到加法器的输出结果。

通过比较输出结果与预期结果，可以验证加法器的正确性。

同时，我们还可以分析电路的性能和优化空间，例如进一步提高加法器的速度和减少功耗等。

计算机组成原理实验课程实验报告实验名称运算器实验
实验二运算器
一．实验目的
了解简单运算器的数据传输通路。

验证运算功能发生器的组合功能。

掌握算术逻辑运算加、减、与的工作原理。

二．实验环境
Quartus 2 9.1
三．实验基本原理及步骤
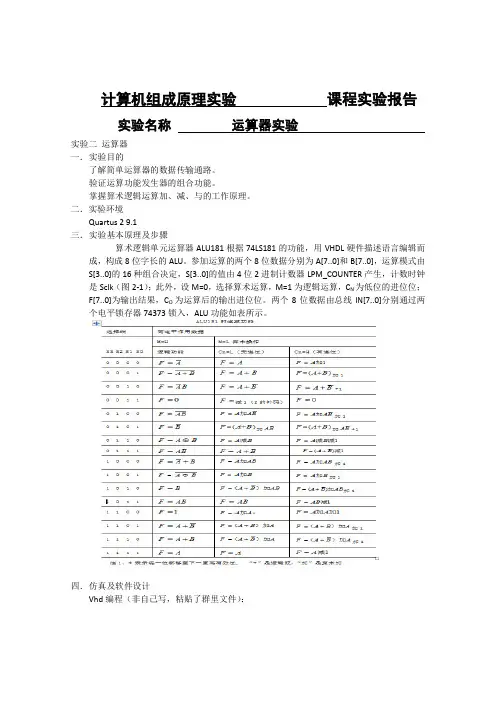
算术逻辑单元运算器ALU181根据74LS181的功能，用VHDL硬件描述语言编辑而成，构成8位字长的ALU。

参加运算的两个8位数据分别为A[7..0]和B[7..0]，运算模式由S[3..0]的16种组合决定，S[3..0]的值由4位2进制计数器LPM_COUNTER产生，计数时钟是Sclk（图2-1）；此外，设M=0，选择算术运算，M=1为逻辑运算，C N为低位的进位位；
F[7..0]为输出结果，C O为运算后的输出进位位。

两个8位数据由总线IN[7..0]分别通过两个电平锁存器74373锁入，ALU功能如表所示。

四．仿真及软件设计
Vhd编程（非自己写，粘贴了群里文件）：
将编程存为器件以及定制74373b，如图
bdf电路图:
五．实验结果分析及回答问题（或测试环境及测试结果）实验问题：
发现是
后来将IN[7…0]改为IN[7..0]
运行成功
仿真结果：
经检验结果正确：。